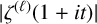 $|\zeta ^{(\ell )}(1+{i}t)|$
$|\zeta ^{(\ell )}(1+{i}t)|$
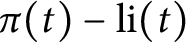 $\pi (t)-\operatorname {\textrm {li}}(t)$
$\pi (t)-\operatorname {\textrm {li}}(t)$
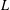 $L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$-FUNCTIONS IN THE EXTENDED SELBERG CLASS