Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T15:43:24.941Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ABSENCE OF ZEROS IN INFINITE ARITHMETIC PROGRESSION FOR CERTAIN ZETA FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  15 August 2018

TEERAPAT SRICHAN
TEERAPAT SRICHAN*
Affiliation:
Department of Mathematics, Faculty of Science, Kasetsart University, Bangkok 10900, Thailand email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Putnam [‘On the non-periodicity of the zeros of the Riemann zeta-function’, Amer. J. Math.76 (1954), 97–99] proved that the sequence of consecutive positive zeros of 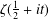$\unicode[STIX]{x1D701}(\frac{1}{2}+it)$ does not contain any infinite arithmetic progression. We extend this result to a certain class of zeta functions.

Keywords

arithmetic progressionRiemann zeta functionzeros of zeta functions

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 3 , December 2018 , pp. 376 - 382
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the Thailand Research Fund (MRG6080210).

References

Lapidus, M. L. and van Frankenhuijsen, M., Fractal Geometry, Complex Dimensions and Zeta Functions (Springer, New York, 2006).Google Scholar
Li, X. and Radziwiłł, M., ‘The Riemann zeta function on vertical arithmetic progressions’, Int. Math. Res. Not. 2015(2) (2015), 325–354.Google Scholar
Putnam, C. R., ‘On the non-periodicity of the zeros of the Riemann zeta-function’, Amer. J. Math. 76 (1954), 97–99.Google Scholar
Titchmarch, E. C., The Riemann Zeta-Function, 2nd edn (Oxford University Press, Oxford, 1986).Google Scholar