We show that for all 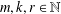 $m,k,r\in \mathbb{N}$, there is an
$m,k,r\in \mathbb{N}$, there is an 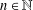 $n\in \mathbb{N}$ such that whenever
$n\in \mathbb{N}$ such that whenever 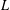 $L$ is a Latin square of order
$L$ is a Latin square of order  $m$ and the Cartesian product
$m$ and the Cartesian product 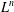 $L^{n}$ of
$L^{n}$ of  $n$ copies of
$n$ copies of 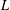 $L$ is
$L$ is  $r$-coloured, there is a monochrome Latin subsquare of
$r$-coloured, there is a monochrome Latin subsquare of 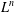 $L^{n}$, isotopic to
$L^{n}$, isotopic to 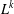 $L^{k}$. In particular, for every prime
$L^{k}$. In particular, for every prime 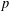 $p$ and for all
$p$ and for all 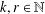 $k,r\in \mathbb{N}$, there is an
$k,r\in \mathbb{N}$, there is an 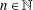 $n\in \mathbb{N}$ such that whenever the multiplication table
$n\in \mathbb{N}$ such that whenever the multiplication table 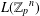 $L({\mathbb{Z}_{p}}^{n})$ of the group
$L({\mathbb{Z}_{p}}^{n})$ of the group 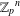 ${\mathbb{Z}_{p}}^{n}$ is
${\mathbb{Z}_{p}}^{n}$ is  $r$-coloured, there is a monochrome Latin subsquare of order
$r$-coloured, there is a monochrome Latin subsquare of order 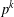 $p^{k}$. On the other hand, we show that for every group
$p^{k}$. On the other hand, we show that for every group 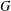 $G$ of order
$G$ of order 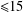 $\leq 15$, there is a 2-colouring of
$\leq 15$, there is a 2-colouring of 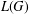 $L(G)$ without a nontrivial monochrome Latin subsquare.
$L(G)$ without a nontrivial monochrome Latin subsquare.
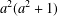 $a^{2}(a^{2}+1)$
$a^{2}(a^{2}+1)$
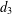 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
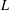 $L$-EMBEDDED BANACH BIMODULES
$L$-EMBEDDED BANACH BIMODULES
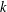 $k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES
$k$-HESSIAN IN FRACTIONAL SOBOLEV SPACES