Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T15:37:34.526Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Size of an Expression in the Nyman–Beurling-Báez–Duarte Criterion for the Riemann Hypothesis

Published online by Cambridge University Press:  20 November 2018

Helmut Maier  and
Michael Th. Rassias
Helmut Maier
Affiliation:
Department of Mathematics, University of Ulm, Helmholtzstrasse 18, 89081 Ulm, Germany, e-mail: [email protected]
Michael Th. Rassias
Affiliation:
Institute of Mathematics, University of Zurich, CH-8057, Zurich, Switzerland, e-mail : [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A crucial role in the Nyman-Beurling-Báez-Duarte approach to the Riemann Hypothesis is played by the distance

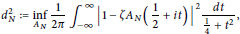$$d_{N}^{2}:=\underset{{{A}_{N}}}{\mathop{\inf }}\,\frac{1}{2\pi }\int _{-\infty }^{\infty }{{\left| 1-\zeta {{A}_{N}}\left( \frac{1}{2}+it \right) \right|}^{2}}\frac{dt}{\frac{1}{4}+{{t}^{2}}},$$

where the infimum is over all Dirichlet polynomials

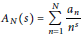$${{A}_{N}}\left( s \right)\,=\,\sum\limits_{n=1}^{N}{\frac{{{a}_{n}}}{{{n}^{s}}}}$$

of length 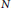$N$. In this paper we investigate 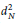$d_{N}^{2}$ under the assumption that the Riemann zeta function has four nontrivial zeros off the critical line.

Keywords

30C1511M26Riemann hypothesisRiemann zeta functionNyman–Beurling–Bá-Duarte criterion
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 622 - 627
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Bäez-Duarte, L., Balazard, M., Landreau, B., and Saias, E., Notes sur lafonction f de Riemann. III. Adv. Math. 149(2000), no. 1, 130–144. http://dx.doi.Org/10.1006/aima.1999.1861Google Scholar
[2] Bäez-Duarte, L., Balazard, M., Landreau, B., and Saias, E., Etüde de Vautocorrelation multiplicative de lafonction ‘partiefractionnaire'. Ramanujan J. 9(2005), no. 1-2, 215–240. http://dx.doi.Org/10.1007/s11139-005-0834-4Google Scholar
[3] Bettin, S., Conrey, J. B., and Farmer, D. W., An optimal choice of Dirichlet polynomiah for the Nyman-Beurling criterion. Proc. Steklov Inst. Math. 280(2013), suppl. 2, S30-S36. http://dx.doi.Org/10.1134/S0081543813030036Google Scholar
[4] Burnol, J. F., A lower bound in an approximation problem involving the zeros of the Riemann zeta function. Adv. Math. 170(2002), 56-70. http://dx.doi.Org/10.1006/aima.2001.2066Google Scholar
[5] Titchmarsh, E. C., The theory of the Riemann Zeta-function. Second ed., The Clarendon Press, Oxford University Press, New York, 1986.Google Scholar