This article concerns the existence and multiplicity of solutions for the following class of non-linear elliptic equations with variable exponents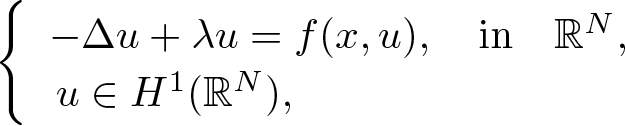 \begin{equation*}\left\{\begin{array}{l}-\Delta u+\lambda u=f(x,u), \quad \text{in} \quad \mathbb{R}^N, \\\,u\in H^{1}(\mathbb{R}^N),\\\end{array}\right.\end{equation*}
\begin{equation*}\left\{\begin{array}{l}-\Delta u+\lambda u=f(x,u), \quad \text{in} \quad \mathbb{R}^N, \\\,u\in H^{1}(\mathbb{R}^N),\\\end{array}\right.\end{equation*}
where λ > 0, 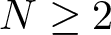 $N\geq 2$ and
$N\geq 2$ and  $f:\mathbb{R}^N \times \mathbb{R} \to \mathbb{R}$ is a function of the following types:
$f:\mathbb{R}^N \times \mathbb{R} \to \mathbb{R}$ is a function of the following types:
Type 1: The subcritical case: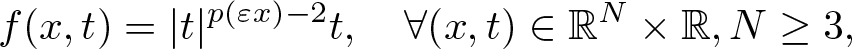 \begin{equation*}f(x,t)=|t|^{p(\varepsilon x)-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
\begin{equation*}f(x,t)=|t|^{p(\varepsilon x)-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
Type 2: The critical case: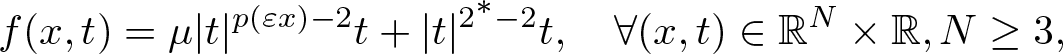 \begin{equation*}f(x,t)=\mu|t|^{p(\varepsilon x)-2}t+|t|^{2^*-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
\begin{equation*}f(x,t)=\mu|t|^{p(\varepsilon x)-2}t+|t|^{2^*-2}t, \quad \forall (x,t) \in \mathbb{R}^N\times \mathbb{R}, N\geq3, \end{equation*}
Type 3: The exponential subcritical growth case: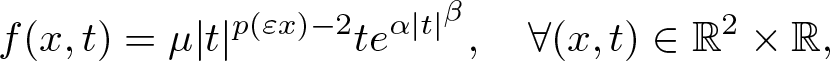 \begin{equation*} f(x,t)=\mu|t|^{p(\varepsilon x)-2}te^{\alpha|t|^\beta}, \quad \forall (x,t) \in \mathbb{R}^2\times \mathbb{R}, \end{equation*}
\begin{equation*} f(x,t)=\mu|t|^{p(\varepsilon x)-2}te^{\alpha|t|^\beta}, \quad \forall (x,t) \in \mathbb{R}^2\times \mathbb{R}, \end{equation*}
where parameterɛ > 0, α > 0, 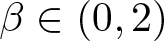 $\beta \in (0,2)$,
$\beta \in (0,2)$,  $2^*=\frac{2N}{N-2}$ if
$2^*=\frac{2N}{N-2}$ if 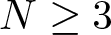 $N \geq 3$ and
$N \geq 3$ and 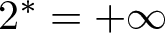 $2^*=+\infty$ if N = 2. Related to the function
$2^*=+\infty$ if N = 2. Related to the function  $p:\mathbb{R}^{N}\rightarrow \mathbb{R}$, we assume that it is a continuous function with
$p:\mathbb{R}^{N}\rightarrow \mathbb{R}$, we assume that it is a continuous function with 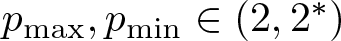 $p_{\max}, p_{\min} \in (2,2^*)$, where
$p_{\max}, p_{\min} \in (2,2^*)$, where 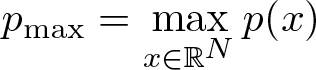 $p_{\max}=\displaystyle \max_{x \in \mathbb{R}^N}p(x)$ and
$p_{\max}=\displaystyle \max_{x \in \mathbb{R}^N}p(x)$ and 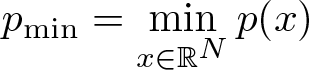 $p_{\min}=\displaystyle \min_{x \in \mathbb{R}^N}p(x)$.
$p_{\min}=\displaystyle \min_{x \in \mathbb{R}^N}p(x)$.
We show that for each λ > 0 the number of solutions is associated with the number of global maximum or global minimum points of p when ɛ is small enough. The proof of is based on the variational methods, Ekeland’s variational principle, Trundiger–Moser inequality, and the monotonicity of the ground state energy with respect to p. Our results extend those of Cao and Noussair (Multiplicity of positive and nodal solutions for nonlinear elliptic problem in 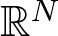 $\mathbb{R}^{N}$. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 13 (1996), 567–588) and Ji, Wang and Wu (A monotone property of the ground state energy to the scalar field equation and applications. J. Lond. Math. Soc., II. Ser. 100 (2019), 804–824).
$\mathbb{R}^{N}$. Ann. Inst. Henri Poincaré, Anal. Non Linéaire. 13 (1996), 567–588) and Ji, Wang and Wu (A monotone property of the ground state energy to the scalar field equation and applications. J. Lond. Math. Soc., II. Ser. 100 (2019), 804–824).