Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T09:06:48.253Z Has data issue: false hasContentIssue false
  • English
  • Français

Zeta Functions and the Log Behaviour of Combinatorial Sequences

Published online by Cambridge University Press:  21 July 2015

William Y. C. Chen ,
Jeremy J. F. Guo  and
Larry X. W. Wang
William Y. C. Chen
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, People’s Republic of China ([email protected]; [email protected])
Jeremy J. F. Guo
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, People’s Republic of China ([email protected]; [email protected])
Larry X. W. Wang
Affiliation:
Center for Combinatorics, Nankai University, Tianjin 300071, People’s Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we use the Riemann zeta function ζ(x) and the Bessel zeta function ζμ(x) to study the log behaviour of combinatorial sequences. We prove that ζ(x) is log-convex for x > 1. As a consequence, we deduce that the sequence {|B2n|/(2n)!}n ≥ 1 is log-convex, where Bn is the nth Bernoulli number. We introduce the function θ(x) = (2ζ(x)Γ(x + 1)) 1/x, where Γ(x) is the gamma function, and we show that logθ(x) is strictly increasing for x ≥ 6. This confirms a conjecture of Sun stating that the sequence 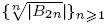is strictly increasing. Amdeberhan et al. defined the numbers an(μ) = 2 2n+1 (n + 1)!(μ+ 1)nζμ(2n) and conjectured that the sequence {an(μ)}n≥1 is log-convex for μ = 0 and μ = 1. By proving that ζμ(x) is log-convex for x > 1 and μ > -1, we show that the sequence {an(≥)}n>1 is log-convex for any μ > - 1. We introduce another function θμ,(x) involving ζμ(x) and the gamma function Γ(x) and we show that logθμ(x) is strictly increasing for x > 8e(μ + 2)2. This implies that

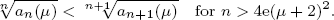
Based on Dobinski’s formula, we prove that

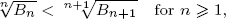
where Bn is the nth Bell number. This confirms another conjecture of Sun. We also establish a connection between the increasing property of 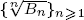and Holder’s inequality in probability theory.

Keywords

log-convexityRiemann zeta functionBernoulli numberBell numberBessel zeta functionNarayana numberPrimary 05A2011B68
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 3 , October 2015 , pp. 637 - 651
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alzer, H., Sharp upper and lower bounds for the gamma function, Proc. R. Soc. Edinb. A 139 (2009), 709–718.Google Scholar
2.Amdeberhan, T., Moll, V. H. and Vignat, C., A probabilistic interpretation of a sequence related to Narayana polynomials, Online J. Analytic Combinat. 8 (2013), Paper 1.Google Scholar
3.Andrews, G. E., Askey, R. and Roy, R., Special functions (Cambridge University Press, 1999).CrossRefGoogle Scholar
4.Artin, E., The gamma function (Holt, Rinehart and Winston, New York, 1964).Google Scholar
5.Bell, E. T., Exponential numbers, Am. Math. Mon. 41 (1934), 411–419.Google Scholar
6.Carlitz, L., A sequence of integers related to the Bessel function, Proc. Am. Math. Soc. 14 (1963), 1–9.CrossRefGoogle Scholar
7.Chamber, L. G., An upper bound for the first zero of Bessel functions, Math. Comp. 38 (1982), 589–591.Google Scholar
8.Lasalle, M., Two integer sequences related to Catalan numbers, J. Combin. Theory A 119 (2012), 923–935.Google Scholar
9.Luca, F. and Stănică, P., On some conjectures on the monotonicity of some combinatorial sequences, J. Combin. Number Theory 4 (2012), 1–10.Google Scholar
10.OEIS Foundation Inc., The online encyclopedia of integer sequences, available at http://oeis.org.Google Scholar
11.Roman, S. M. and Rota, Gian-Carlo, The umbral calculus, Adv. Math. 27 (1978), 95–188.Google Scholar
12.Rota, G.-C., The number of partitions of a set, Am. Math. Mon. 71 (1964), 498–504.CrossRefGoogle Scholar
13.Sachkov, V. N., Probabilistic methods in combinatorial analysis (Cambridge University Press, 1997).Google Scholar
14.Smith, D. E., Source Book in Mathematics, Volumes 1 and 2 (Dover, New York, 1959).Google Scholar
15.Sun, Z., Conjectures involving arithmetical sequences, in Numbers theory: arithmetic, Shangri-La, Proc. 6th China–Japan Seminar, Shang-hai, August 15–17, 2011 (ed. Kanemitsu, S., Li, H. and Liu, J.), pp. 244–258 (World Scientific, 2013).Google Scholar
16.Wang, Y. and Zhu, B., Proofs of some conjectures on monotonicity of number-theoretic and combinatorial sequences, Sci. China A 57(11 (2014), 2429–2435.Google Scholar