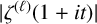Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-10T23:10:38.509Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE LARGE VALUES OF $|\zeta ^{(\ell )}(1+{i}t)|$

Part of: Multiplicative number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  05 January 2023

ZIKANG DONG Open the ORCID record for ZIKANG DONG [Opens in a new window]  and
BIN WEI Open the ORCID record for BIN WEI [Opens in a new window]
ZIKANG DONG
Affiliation:
CNRS LAMA 8050, Laboratoire d’analyse et de mathématiques appliquées, Université Paris-Est Créteil, 61 avenue du Général de Gaulle, 94010 Créteil Cedex, France e-mail: [email protected]
BIN WEI*
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the large values of the derivatives of the Riemann zeta function 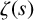$\zeta (s)$ on the 1-line. We give a larger lower bound for 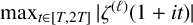$\max _{t\in [T,2T]}|\zeta ^{(\ell )}(1+{i} t)|$, which improves the previous result established by Yang [‘Extreme values of derivatives of the Riemann zeta function’, Mathematika 68 (2022), 486–510].

Keywords

extreme valuesRiemann zeta function

MSC classification

Primary: 11M06: $zeta (s)$ and $L(s, chi)$
Secondary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 217 - 223
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the China Scholarship Council (CSC) for his study in France. The second author is supported by Natural Science Foundation of Tianjin City (Grant No. 19JCQNJC14200).

References

Bondarenko, A. and Seip, K., ‘ Note on the resonance method for the Riemann zeta function ’, in: 50 Years with Hardy Spaces, Operator Theory: Advances and Applications, 261 (eds. Baranov, A., Kisliakov, S. and Nikolski, N.) (Birkhäuser/Springer, Cham, 2018), 121–139.10.1007/978-3-319-59078-3_6CrossRefGoogle Scholar
Dong, Z. and Wei, B., ‘On large values of $\mid \zeta \left(\sigma +\mathrm{it}\right)\mid$ ’, Preprint, 2022, arXiv:2110.04278.Google Scholar
Granville, A. and Soundararajan, K., ‘Extreme values of $\mid \zeta \left(1+\mathrm{it}\right)\mid$ ’, in: The Riemann Zeta Function and Related Themes: Papers in Honour of Professor K. Ramachandra, Ramanujan Mathematical Society Lecture Notes Series, 2 (eds. Balsubramanian, R. and Srinivas, K.) (International Press, Mysore, 2006), 65–80.Google Scholar
Littlewood, J. E., ‘On the Riemann zeta-function’, Proc. Lond. Math. Soc. (2) 24 (1925), 175–201.Google Scholar
Soundararajan, K., ‘Extreme values of zeta and $L$ -functions’, Math. Ann. 342 (2008), 467–486.CrossRefGoogle Scholar
Titchmarsh, E. C., ‘On an inequality satisfied by the zeta-function of Riemann’, Proc. Lond. Math. Soc. 28 (1928), 70–80.10.1112/plms/s2-28.1.70CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (Oxford University Press, New York, 1986).Google Scholar
Yang, D., ‘Extreme values of derivatives of the Riemann zeta function’, Mathematika 68 (2022), 486–510.10.1112/mtk.12130CrossRefGoogle ScholarPubMed