Research Article
Near-rings of polynomials over groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-7
-
- Article
-
- You have access
- Export citation
Localizations of injective modules
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 289-299
-
- Article
-
- You have access
- Export citation
Small isomorphisms between operator algebras
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 121-131
-
- Article
-
- You have access
- Export citation
Subsimple, injective, retract
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 301-302
-
- Article
-
- You have access
- Export citation
On pseudo-distributive near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 133-141
-
- Article
-
- You have access
- Export citation
On ideally finite Lie algebras which are lower semi-modular
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 9-11
-
- Article
-
- You have access
- Export citation
Length functions on hypercentral groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 303-304
-
- Article
-
- You have access
- Export citation
Semigroups of high rank
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 13-34
-
- Article
-
- You have access
- Export citation
Almost diagonal systems in asymptotic integration
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 143-158
-
- Article
-
- You have access
- Export citation
A generalization of centralizer near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 159-165
-
- Article
-
- You have access
- Export citation
Analogues of the braid group whose graphs are stars
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 35-39
-
- Article
-
- You have access
- Export citation
On a relation between the topology and the intrinsic and extrinsic geometries of a compact submanifold
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 305-311
-
- Article
-
- You have access
- Export citation
Extensions of characters from Hall π-subgroups of π-separable groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 313-317
-
- Article
-
- You have access
- Export citation
C*-Algebras of inverse semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 41-58
-
- Article
-
- You have access
- Export citation
An extended Hamburger moment problem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 167-183
-
- Article
-
- You have access
- Export citation
On the (J, pn, qn) method of summation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 59-66
-
- Article
-
- You have access
- Export citation
Automorphisms of normal transformation semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-205
-
- Article
-
- You have access
- Export citation
The ideal structure of idempotent-generated transformation semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 319-331
-
- Article
-
- You have access
- Export citation
On certain semigroups arising from radicals of matrix rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 67-72
-
- Article
-
- You have access
- Export citation
The countable neighbourhood property and tensor products
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 207-215
-
- Article
-
- You have access
- Export citation

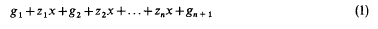
 . On the other hand one can get from Theorems 1 and 3 of [3] that the Nagasawa theorem can be extended to some operator algebras as follows:
. On the other hand one can get from Theorems 1 and 3 of [3] that the Nagasawa theorem can be extended to some operator algebras as follows: , then there is no room for injectives in
, then there is no room for injectives in  or as functions Φ:
or as functions Φ: provided
provided 
 the class of Lie algebras all of whose maximal subalgebras have codimension 1 in
the class of Lie algebras all of whose maximal subalgebras have codimension 1 in 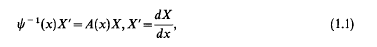
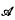 be a group of automorphisms of
be a group of automorphisms of 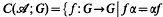 for all α∈
for all α∈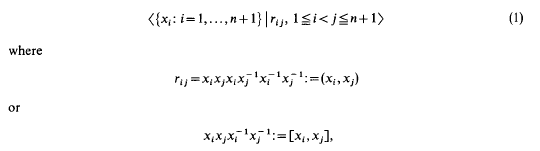

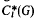 determined by the completion of
determined by the completion of 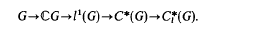
 ,
, 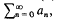 with the partial sum
with the partial sum 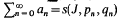 if the series
if the series
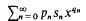 converge to the sum functions
converge to the sum functions 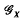 be the group of all bijections of
be the group of all bijections of 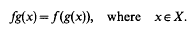
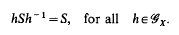
 the semigroup (under composition) of all total transformations from
the semigroup (under composition) of all total transformations from  of all partial transformations of
of all partial transformations of