Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:37:39.143Z Has data issue: false hasContentIssue false
  • English
  • Français

The ideal structure of idempotent-generated transformation semigroups

Published online by Cambridge University Press:  20 January 2009

M. A. Reynolds  and
R. P. Sullivan
M. A. Reynolds
Affiliation:
Mathematics Department, University of Western Australia, Nedlands, 6009, Western Australia
R. P. Sullivan
Affiliation:
Mathematics Department, University of Western Australia, Nedlands, 6009, Western Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a set and 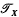the semigroup (under composition) of all total transformations from X into itself. In ([6], Theorem 3) Howie characterised those elements of 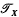that can be written as a product of idempotents in 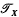different from the identity. We gather from review articles that his work was later extended by Evseev and Podran [3, 4] (and independently for finite X by Sullivan [15]) to the semigroup 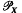of all partial transformations of X into itself. Howie's result was generalized in a different direction by Kim [8], and it has also been considered in both a topological and a totally ordered setting (see [11] and [14] for brief summaries of this latter work). In addition, Magill [10] investigated the corresponding idea for endomorphisms of a Boolean ring, while J. A. Erdos [2] resolved the analogous problem for linear transformations of a finite–dimensional vector space.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 3 , October 1985 , pp. 319 - 331
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups (Math. Surveys, no. 7, Amer. Math. Soc, Providence, RI, Vol. 1, 1961; Vol. 2, 1967).Google Scholar
2.Erdos, J. A., On products of idempotent matrices, Glasgow Math. J. 8 (1967), 118–122.CrossRefGoogle Scholar
3.Evseev, A. E. and Podran, N. E., Semigroups of transformations generated by idempotents with given projection characteristics, Isv. Vyss. Ucebn. Zaved. Mat. 12 (103), 1970, 30–36.Google Scholar
4.Evseev, A. E. and Podran, N. E., Semigroups of transformations generated by idempotents with given defect, Izv. Vyss. Ucebn. Zaved. Mat. 2 (117) 1972, 44–50.Google Scholar
5.Fitzgerald, D. G. and Preston, G. B., Divisibility of binary relations, Bull. Austral. Math. Soc. 5 (1971), 75–86.CrossRefGoogle Scholar
6.Howie, J. M., The subsemigroup generated by the idempotents of a full transformation semigroup, J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
7.Howie, J. M., Some subsemigroups of infinite full transformation semigroups, Proc. Royal Soc. Edin. 88A (1981), 159–167.CrossRefGoogle Scholar
8.Bai Kim, Jin, Idempotents in symmetric semigroups, J. Combin. Theory 13 (1972), 155–161.CrossRefGoogle Scholar
9.Ljapin, E. S., Semigroups, 3 ed. (Vol. 3, Translations Math. Monographs, Amer. Math. Soc, Providence, RI, 1974).Google Scholar
10.Magill, K. D. Jr., The semigroup of endomorphisms of a Boolean ring, J. Austral. Math. Soc. (Series A) 11 (1970), 411–416.CrossRefGoogle Scholar
11.Magill, K. D. Jr., X-structure spaces of semigroups generated by idempotents, J. London Math. Soc. 3 (1971), 321–325.CrossRefGoogle Scholar
12.Monk, J. D., Introduction to Set Theory (McGraw-Hill, NY, 1969).Google Scholar
13.Rosser, J. B., Simplified Independence Proofs (Academic, NY, 1969).Google Scholar
14.Schein, B. M., Products of idempotent order-preserving transformations of arbitrary chains, Semigroup Forum 11 (1975/1976), 297–309.CrossRefGoogle Scholar
15.Sullivan, R. P., A study in the theory of transformation semigroups (Ph.D. thesis, Monash University, 1969).Google Scholar
16.Symons, J. S. V., Normal transformation semigroups, J. Austral. Math. Soc. (Series A) 22 (1976), 385–390.CrossRefGoogle Scholar
17.Vorobev, N. N., Defect ideals of associative systems, Leningrad Gos. Univ. Ucen. Zap., Ser. Mat. Nauk 16 (1949), 47–53.Google Scholar
18.Vorobev, N. N., On symmetric associative systems, Leningrad Gos. Ped. Inst. Ucen. Zap. 89 (1953), 161–166.Google Scholar