Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:54:50.678Z Has data issue: false hasContentIssue false
  • English
  • Français

An extended Hamburger moment problem

Published online by Cambridge University Press:  20 January 2009

Olav Njåstad
Olav Njåstad
Affiliation:
University of Trondheim—NthN-7034 TrondheimNorway
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

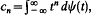The classical Hamburger moment problem can be formulated as follows: Given a sequence {cn:n=0,1,2,…} of real numbers, find necessary and sufficient conditions for the existence of a distribution function ψ (i.e. a bounded, real-valued, non-decreasing function) on (– ∞,∞) with infinitely many points of increase, such that , n = 0,1,2, … This problem was posed and solved by Hamburger [5] in 1921. The corresponding problem for functions ψ on the interval [0,∞) had already been treated by Stieltjes [15] in 1894. The characterizations were in terms of positivity of Hankel determinants associated with the sequence {cn}, and the original proofs rested on the theory of continued fractions. Much work has since been done on questions connected with these problems, using orthogonal functions and extension of positive definite functionals associated with the sequence. Accounts of the classical moment problems with later developments can be found in [1,4,14]. Good modern accounts of the theory of orthogonal polynomials can be found in [2,3].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 2 , June 1985 , pp. 167 - 183
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Akiezer, N. I., The Classical Moment Problem and some Related Questions in Analysis (Hafner Publishing Company, New York, 1965).Google Scholar
2.Brezinski, C., Padé-type Approximation and General Orthogonal Polynomials (Birkhäuser Verlag, Basel-Boston Stuttgart, 1980).CrossRefGoogle Scholar
3.Chihara, T. S., Introduction to Orthogonal Polynomials (Mathematics and its applications series, Gordon, 1978).Google Scholar
4.Freud, G., Orthogonal Polynomials (Pergamon Press, New York, 1971).Google Scholar
5.Hamburger, H., Über eine Erweiterung des Stieltjesschen Momentproblems, Parts I, II, III, Math. Ann. 81 (1920), 235–319, 82 (1921), 120-164, 168-187.CrossRefGoogle Scholar
6.Jones, William B. and Thron, W. J., Orthogonal Laurent polynomials and Gaussian quadrature', Quantum Mechanics in Mathematics, Chemistry and Physics (Eds., Gustafson, K. and Reinhardt, W. P., Plenum Publishing Corp., New York, 1981), 449–455.CrossRefGoogle Scholar
7.Jones, William B. and Thron, W. J., Survey of continued fractions methods of solving moment problems and related topics, Analytic Theory of Continued Fractions,Proceedings, Loen, Norway, 1981 (Lecture notes in mathematics, No. 932, Springer Verlag, Berlin, 1982), 4–37.CrossRefGoogle Scholar
8.Jones, William B., Njåstad, Olav and Thron, W. J., Two-point Padé expansions for a family of analytic functions, J. Comp. Appl. Math. 9 (1983), 105–123.CrossRefGoogle Scholar
9.Jones, William B., Njåstad, Olav and Thron, W. J., Continued fractions and strong Hamburger moment problems, Proc. London Math. Soc. (3) 47 (1983), 363–384.CrossRefGoogle Scholar
10.Jones, William B., Njåstad, Olav and Thron, W. J., Orthogonal Laurent polynomials and the strong Hamburger moment problem, J. Math. Anal. App., to appear.Google Scholar
11.Jones, William B., Thron, W. J. and Waadeland, H., A strong Stieltjes moment problem, Trans. Amer. Math. Soc. (1980), 503–528.CrossRefGoogle Scholar
12.Njåstad, Olav and Thron, W. J., The theory of sequences of orthogonal L-polynomials, Padé Approximants and Continued Fractions, (Eds., Waadeland, Haakon and Wallin, Hans), Det Kongelige Norske Videnskabers Selskab, Skrifter (1983) No. 1, 54–91.Google Scholar
13.Njåstad, Olav and Thron, W. J., Unique solvability of the strong Hamburger moment problem, J. Austral. Math. Soc. (Series A) 39 (1985), 15 pages.Google Scholar
14.Shohat, J. A. and Tamarkin, J. D., The Problem of Moments (Mathematical Surveys No. 1, Amer. Math. Soc., Providence, R.I., 1943).CrossRefGoogle Scholar
15.Stieltjes, T. J., ReschÉrches sur les fractions continues, Ann. Fac. Sci, Toulouse 8 (1984), J, 1–122; 9 (1898), A, 1-47; Oeuvres 2 402-566.CrossRefGoogle Scholar