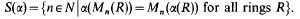Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:09:46.286Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain semigroups arising from radicals of matrix rings

Published online by Cambridge University Press:  20 January 2009

A. D. Sands
A. D. Sands
Affiliation:
Department of Mathematical SciencesThe University DundeeDD1 4HN, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a ring we shall mean an associative ring not necessarily containing an identity element. The fundamental definitions and properties of radicals may be found in Divinsky [2]. Similarly we refer to Howie [3] for the semigroup concepts.

If R is a ring Mn(R) will denote the ring of n × n matrices with entries from R. For many important radicals α it has been shown that α(Mn(R)) = Mn(α(R)) for all rings R and all positive integers n. However this is not the case for all radicals α. Associated with each radical α we define a set of positive integers S(α) by

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 1 , February 1985 , pp. 67 - 72
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, vol 1 (Mathematical Surveys, 7, American Mathematical Society, 1961).Google Scholar
2.Divinsky, N. J., Rings and Radicals (Allen and Unwin, 1965).Google Scholar
3.Howie, J. M., An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
4.Sands, A. D., Prime Ideals in Matrix Rings, Proc. Glasgow Math. Assoc. 2 (1956), 193–195.CrossRefGoogle Scholar
5.Snider, R. L., Lattices of Radicals, Pacific J. Math. 40 (1972), 207–220.CrossRefGoogle Scholar