Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:58:34.422Z Has data issue: false hasContentIssue false
  • English
  • Français

Subsimple, injective, retract

Published online by Cambridge University Press:  20 January 2009

Shalom Feigelstock  and
Aaron Klein
Shalom Feigelstock
Affiliation:
Bar-Ilan University
Aaron Klein
Affiliation:
Ramat-Gan Israel 52100
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Simple and subsimple objects were introduced in [6]. It was shown that if there are enough simple objects in a category 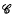, then there is no room for injectives in 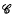. This idea was exploited in [6] and [2] to show that several classes of groups, rings and classes belonging to other categories do not possess non-trivial injectives or retracts. In this note, the above results will be strengthened by introducing a weaker condition than subsimple of [6]. As a consequence, and by employing some embedding theorems, we show that some important classes do not possess non-trivial retracts.

All the categories are assumed to have a zero object.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 3 , October 1985 , pp. 301 - 302
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Boone, W. W. and Higman, G., An algebraic characterization of groups with soluble word problem, J. Austr. Math. Soc. 18 (1974), 41–53.CrossRefGoogle Scholar
2.Feigelstock, S. and Klein, A., Retracts and injectives, Canad. Math. Bull. 25 (4) (1982), 462–467.CrossRefGoogle Scholar
3.Hall, P., Some constructions for locally finite groups, J. London Math. Soc. 34 (1959), 305–319.CrossRefGoogle Scholar
4.Herrlich, P. and Strecker, G. E., Category Theory (Allyn and Bacon, Boston, 1973).Google Scholar
5.Higman, G., Neumann, B. H. and Neumann, H., Embedding theorems for groups, J. London Math. Soc. 24 (1949), 247–254.CrossRefGoogle Scholar
6.Klein, A., Injectives and simple objects, J. Pure and Appl. Alg. 15 (1979), 243–245.CrossRefGoogle Scholar
7.Thompson, R. J., Embeddings into finitely generated simple groups which preserve the word problem, Word Problem II (Studies in Logic and the Foundations of Math., North-Holland, Amsterdam-New York, 1980), 401–441.Google Scholar