During the last fifteen years there has been a paradigm shift in the continuum modelling of granular materials; most notably with the development of rheological models, such as the 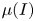 $\mu (I)$-rheology (where
$\mu (I)$-rheology (where 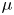 $\mu$ is the friction and I is the inertial number), but also with significant advances in theories for particle segregation. This paper details theoretical and numerical frameworks (based on OpenFOAM
$\mu$ is the friction and I is the inertial number), but also with significant advances in theories for particle segregation. This paper details theoretical and numerical frameworks (based on OpenFOAM ) which unify these currently disconnected endeavours. Coupling the segregation with the flow, and vice versa, is not only vital for a complete theory of granular materials, but is also beneficial for developing numerical methods to handle evolving free surfaces. This general approach is based on the partially regularized incompressible
) which unify these currently disconnected endeavours. Coupling the segregation with the flow, and vice versa, is not only vital for a complete theory of granular materials, but is also beneficial for developing numerical methods to handle evolving free surfaces. This general approach is based on the partially regularized incompressible 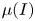 $\mu (I)$-rheology, which is coupled to the gravity-driven segregation theory of Gray & Ancey (J. Fluid Mech., vol. 678, 2011, pp. 353–588). These advection–diffusion–segregation equations describe the evolving concentrations of the constituents, which then couple back to the variable viscosity in the incompressible Navier–Stokes equations. A novel feature of this approach is that any number of differently sized phases may be included, which may have disparate frictional properties. Further inclusion of an excess air phase, which segregates away from the granular material, then allows the complex evolution of the free surface to be captured simultaneously. Three primary coupling mechanisms are identified: (i) advection of the particle concentrations by the bulk velocity, (ii) feedback of the particle-size and/or frictional properties on the bulk flow field and (iii) influence of the shear rate, pressure, gravity, particle size and particle-size ratio on the locally evolving segregation and diffusion rates. The numerical method is extensively tested in one-way coupled computations, before the fully coupled model is compared with the discrete element method simulations of Tripathi & Khakhar (Phys. Fluids, vol. 23, 2011, 113302) and used to compute the petal-like segregation pattern that spontaneously develops in a square rotating drum.
$\mu (I)$-rheology, which is coupled to the gravity-driven segregation theory of Gray & Ancey (J. Fluid Mech., vol. 678, 2011, pp. 353–588). These advection–diffusion–segregation equations describe the evolving concentrations of the constituents, which then couple back to the variable viscosity in the incompressible Navier–Stokes equations. A novel feature of this approach is that any number of differently sized phases may be included, which may have disparate frictional properties. Further inclusion of an excess air phase, which segregates away from the granular material, then allows the complex evolution of the free surface to be captured simultaneously. Three primary coupling mechanisms are identified: (i) advection of the particle concentrations by the bulk velocity, (ii) feedback of the particle-size and/or frictional properties on the bulk flow field and (iii) influence of the shear rate, pressure, gravity, particle size and particle-size ratio on the locally evolving segregation and diffusion rates. The numerical method is extensively tested in one-way coupled computations, before the fully coupled model is compared with the discrete element method simulations of Tripathi & Khakhar (Phys. Fluids, vol. 23, 2011, 113302) and used to compute the petal-like segregation pattern that spontaneously develops in a square rotating drum.