3.1. Effect of liquid cross-flow velocity, orientation and wall superheat

Four different values of $Re_l$, viz., 10, 50, 100 and 170 are considered to study the effect of free stream velocity in both upward and horizontal cross-flow of saturated liquid. The major axis of the elliptical heater is aligned to the flow direction ($\theta =0^{\circ }$) in these simulations while the aspect ratio is fixed as $\varGamma =0.6$. Correspondingly, the square root of the Froude number is calculated as 0.12, 0.6, 1.2 and 2.04, respectively, for different $Re_l$ that signifies a successively growing influence of flow inertia. The non-dimensional wall superheat, $Ja_v/Pr_v$ , is varied from 0.3 to 1.2 at each $Re_l$, and is an important parameter affecting the interfacial dynamics by controlling the rate of vapour generation that is subsequently infused into the vapour wake.

The effect of different upward cross-flow velocities on the interface evolution at $Ja_v/Pr_v=0.6$ is presented in figure 5. A periodic ebullition is observed at $Re_l=10$ as shown in figure 5($a$), involving various stages such as bubble growth at the top of the heater, necking and pinch-off, recoil of the remaining vapour mass, and subsequent undulations leading to the next bubble formation and release cycle. Such a quasi-steady nature is characteristic of natural convection film boiling where bubble removal is governed by Rayleigh–Taylor instability. This is expected to be the case with a dominant effect of buoyancy at a low value of Fr. A similar interface evolution is also seen at $Re_l=50$ from figure 5($b$). However, an increase in the bubble release frequency is observed that indicates an additional effect of flow inertia on vapour removal, although being quite subtle with respect to the interface morphology. At $Re_l=100$, the influence of inertia becomes more prominent with the vapour wake dynamics visibly affected by the liquid flow, as shown in figure 5($c$). A combined effect of inertia and buoyancy results in a larger pinch-off distance ($t=0.74\ \textrm {s}$) along with a thinner film at the bottom of the cylinder. Further, a loss of the periodic nature of film boiling can be seen accompanied by a random detachment of bubbles from the vapour wake. Upon further increase in flow velocity at $Re_l=170$, a thin film is wrapped around the bottom half of the cylinder, and a steady and thick vapour wake along with a trailing column is formed behind the elliptical cylinder. Further, small bubbles are observed to release from the top of the vapour mass. While such a steady interface morphology indicates a suppression of vortex shedding at the $Re_l$ value under consideration, it is also inherently different from that observed for a circular cylinder ($\varGamma =1$) under similar conditions (Singh & Premachandran Reference Singh and Premachandran2018b). This shows the effect of elliptical geometry in the present configuration on vapour removal in terms of accentuating the rate at which kinetic energy of the vapour is carried into the wake.

Figure 5. Interface evolution with different upward liquid cross-flow velocities over an elliptical cylinder $(b / \lambda _o = 0.5,\varGamma =0.6)$ for water $(p / p_c = 0.99)$ at $Ja_v / Pr_v = 0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l = 10$ ($\sqrt {Fr} = 0.12$), ($b$) $Re_l = 50$ ($\sqrt {Fr}= 0.6$), ($c$) $Re_l = 100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l = 170$ ($\sqrt {Fr} = 2.04$).

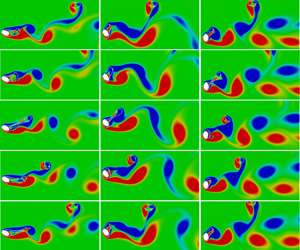
Figure 6 shows the effect of free stream velocity on interface evolution in horizontal cross-flow at $Ja_v/Pr_v =0.6$. From figure 6($a$) at $Re_l=10$, similar phases of interface evolution are observed as for upward cross-flow with buoyancy predominantly determining the vapour morphology. However, a much thicker film can be seen in the bottom portion of the cylinder, which can be attributed to a constriction in the vapour removal due to buoyancy, and is discussed in § 3.2. This also leads to a much lower bubble release frequency compared with upward flow orientation. Nonetheless, the voluminous vapour mass at the top of the elliptical heater is observed to be slightly deflected sideways even with a minimal effect of liquid flow. At $Re_l=50$, the effect of flow inertia can be clearly visualized from figure 6($b$) with the bubbles releasing from the top right-hand portion of the heater at a higher frequency, while the role of buoyancy is verified from the periodic nature of ebullition. Such a competing effect of inertia and buoyancy causes a recirculation in the vapour film leading to a vapour bulge at the bottom of the heater, as analysed in an earlier study for $\varGamma =1$ (Singh & Premachandran Reference Singh and Premachandran2019). However, with the present aspect ratio of 0.6, the bulge is more prominent as compared with a circular cylinder due to the ellipse orientation blocking vapour passage against a significant influence of buoyancy at $\sqrt {Fr}=0.6$. At $Re_l=100$, the vapour wake shifts entirely to the rear of the elliptical cylinder as shown in figure 6($c$). While the vapour wake shows a slight tendency to rise even with a weak effect of gravity, the overall vapour morphology along with a random detachment of bubbles from the tail end of the wake indicates that the aperiodic interface evolution is primarily governed by flow inertia in contrast to Rayleigh–Taylor instability at lower velocities. Upon further increase in cross-flow velocity, it is seen from figure 6($d$) at $Re_l=170$ that the vapour wake is again formed at the cylinder rear with the front stagnation region covered with a thin and steady film. However, an interesting build-up of the instability is observed in distinct phases, as also marked in Figure 6($d$). Initially, the instability evolves from the top rear portion of the cylinder (phase I) with small bubbles detached from the end, which characterizes a smaller effect of gravity being overcome by the dominant liquid flow. Further, the ellipse orientation along the flow causes a rapid infusion of vapour into the wake leading to a thick vapour mass in the entire rear portion of the heater (phase II). Subsequently the effect of Kelvin–Helmholtz instability on the interface becomes pronouncedly visible (phase III), which eventually leads to tearing of the vapour sheet behind the ellipse (phase IV). Such interesting interfacial features indicate a significant effect of the bluff-body geometry on film boiling behaviour along with relative strengths of buoyancy and flow inertia in the mixed regime.

Figure 6. Interface evolution with different horizontal liquid cross-flow velocities over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ for water $(p/p_c =0.99)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l = 10$ ($\sqrt {Fr} = 0.12$), ($b$) $Re_l = 50$ ($\sqrt {Fr}= 0.6$), ($c$) $Re_l = 100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l = 170$ ($\sqrt {Fr} = 2.04$).

The non-dimensional parameter $Ja_v/Pr_v$ is varied from 0.3 to 1.2 in the present simulations to assess the effect of wall superheat on the interfacial dynamics. With upward cross-flow of liquid, a periodic ebullition cycle is observed at $Re_l=10$ for all the wall superheats, as discussed previously for $Ja_v/Pr_v =0.6$. At subsequently larger values of $Re_l$, stable vapour columns are formed due to enhanced vapour generation at elevated wall superheats, with small bubbles releasing from their tail end. However, with the aiding influence of cross-flow velocity on carrying the vapour into the wake, such vapour jets are observed at successively lower degrees of superheat as $Re_l$ increases. This is clearly depicted in figure 7 for $Re_l=50$ and 100, and also seen from figure 5($d$) for $Re_l=170$. Additionally, a lesser portion of the heater wall is wrapped with a thin film as the liquid cross-flow velocity increases leading to a thicker wake behind the heater, as seen prominently for $Re_l=170$ in figure 5($d$). Such an observation is analogous to the case of a circular cylinder with regard to vapour flow separation (Singh & Premachandran Reference Singh and Premachandran2018b). With horizontal cross-flow orientation, periodic bubble release is observed for $Re_l=10$ and 50 at different values of $Ja_v/Pr_v$. However, the orthogonal gravity and flow fields do not support formation of stable columns at any of the wall superheats investigated in this study. Further, the interfacial dynamics at a lower non-dimensional superheat of 0.3 corresponding to $Re_l=170$ is shown in figure 8 for both the cross-flow orientations. For upward liquid flow, a transient vapour wake with random detachment of bubbles is observed from figure 8($a$), in contrast to a steady wake with a trailing column formed at $Ja_v/Pr_v =0.6$ and beyond. Similarly from figure 8($b$) for horizontal cross-flow, the interface is seen to evolve in a considerably different manner when compared with $Ja_v/Pr_v =0.6$, with the instability evolution essentially restricted to phase I described with respect to figure 6($d$). The subsequent phases are eliminated on account of reduced vapour generation at a lower superheat. The above discussion highlights the role of wall superheat as a major factor affecting the film boiling dynamics in the mixed regime that affects the evolution rate leading to a change in the interface morphology altogether under certain conditions.

Figure 7. Interface morphology showing formation of vapour columns in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $\theta =0^{\circ }$ and elevated wall superheats: ($a$) $Re_l=50, Ja_v/Pr_v =1.2$ and ($b$) $Re_l=100, Ja_v/Pr_v =0.9$.

Figure 8. Interface evolution over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ for water $(p/p_c =0.99)$ at $Re_l=170, Ja_v/Pr_v =0.3$ and $\theta =0^{\circ }$: ($a$) upward cross-flow and ($b$) horizontal cross-flow. (For interface evolution at $Ja_v/Pr_v =0.6$, one may refer to figures 5 and 6.)

The heat transfer is quantified by means of the Nusselt number and the corresponding values for the present set of simulations are shown in figure 9. The space-averaged Nusselt number variation with upward cross-flow at $Ja_v/Pr_v =0.6$ and 1.2 is plotted in figures 9($a$) and 9($b$), respectively. At $Ja_v/Pr_v =0.6$, a quasi-steady variation is obtained concomitant to periodic ebullition under Rayleigh–Taylor instability for $Re_l=10$ and 50. An increase in the ebullition frequency is seen at $Re_l=50$, depicting considerable effect of flow inertia at a low magnitude of Froude number. The transient Nusselt number variation at $Re_l=100$ corresponds to the aperiodic interface evolution presented previously. At the same time, a steady vapour structure near the elliptical heater comprising of a thin film and thick vapour wake leads to a constant Nusselt number for $Re_l=170$. Further, a decrease in bubble release period with superheat is evident from the Nusselt number distribution shown in figure 9($b$) at $Ja_v/Pr_v =1.2$ and $Re_l=10$. At all subsequent $Re_l$ values, stable vapour columns are formed with the particular conditions aided by the elliptical heater orientation as discussed earlier, resulting in the Nusselt number remaining constant with time. Corresponding to horizontal liquid flow and similar levels of wall superheat, the space-averaged Nusselt number distribution is shown in figures 9($c$) and 9($d$). A quite low bubble release frequency is observed at $Re_l=10$ compared with upflow due to the major axis of the elliptical heater oriented normal to the direction of buoyancy, which is the dominant factor controlling vapour removal at such low value of $Re_l$. Nonetheless, an increase in the frequency is observed with cross-flow velocity as well as wall superheat. For $Re_l=100$, the Nusselt number variation is in accordance with the random interface evolution. A steady vapour region near the wall along with the wake fluctuations primarily confined away from the wall, as presented in figure 6($d$) at $Ja_v/Pr_v =0.6$, results in a constant Nusselt number for $Re_l=170$.

Figure 9. Nusselt number with different liquid flow velocities and wall superheats for water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $\theta =0^{\circ }$. Corresponding to ($a{,}b$) upward and ($c{,}d$) horizontal cross-flow; the temporal variation of space-averaged Nusselt number at various $Re_l$ is shown for ($a{,}c$) $Ja_v/Pr_v =0.6$ and ($b{,}d$) $Ja_v/Pr_v =1.2$. Time-averaged values of the Nusselt number for all the parameters considered are shown in panel ($e$).

Figure 9($e$) shows the time-averaged Nusselt number values obtained with various parameters in the present set of simulations. For both the liquid flow orientations, an increase in Nusselt number with $Re_l$ is observed that depicts an appreciable influence of flow inertia on heat transfer even at low cross-flow velocities, thereby marking the onset of the mixed regime. On the other hand, the wall superheat is observed to weakly affect the heat transfer especially at low cross-flow velocities, where an augmentation of the bubble release frequency is largely offset by a thicker film near the heater wall at elevated superheats. Even at higher $Re_l$ values, the Nusselt number is almost invariant once a steady vapour region is formed near the wall at a particular degree of superheat. Furthermore, the heat transfer with upward liquid flow directly aiding buoyancy in the mixed regime is higher as compared with horizontal cross-flow configuration, except at $Re_l=170$. A high magnitude of Froude number $(\sqrt {Fr}=2.04)$ corresponding to $Re_l=170$ implies film boiling occurring in the purely inertial regime, where the liquid flow inertia drives the interfacial dynamics. As such, the flow direction becomes trivial leading to same magnitude of the Nusselt number for both cross-flow directions. A similar coincidence of heat transfer magnitude would have been expected for $Re_l=10$, with conditions approaching natural convection film boiling due to minimal effect of liquid flow. However, the relative orientation of the elliptical heater and gravity differs in both cases as the angle of incidence $(\theta =0^{\circ })$ is defined with respect to the flow direction, which leads to significantly lower Nusselt number values with horizontal cross-flow at $Re_l=10$. Incidentally, the Nusselt number values at $Re_l=10$ with upward cross-flow are slightly higher than those obtained at even $Re_l=50$ with horizontal cross-flow for all superheats, thereby highlighting the effect of elliptical geometry in aiding vapour removal and improving the heat transfer. Consequently, the effect of important geometrical parameters on film boiling characteristics in the mixed regime is investigated in the next sections.

3.2. Effect of aspect ratio $(\varGamma )$

The aspect ratio is an important parameter that affects the front stagnation region of the elliptical heater for a fixed orientation, which is a critical zone for film boiling heat transfer and vapour generation. As such, the vapour removal passage is altered with a change in the aspect ratio thereby affecting the rate of vapour infusion into the wake, interface morphology and associated heat transfer rates. While important results for $\varGamma =0.6$ have been presented in § 3.1, two other aspect ratios, viz., $\varGamma =0.4$ and 0.8 are considered here to investigate the film boiling behaviour at a fixed value of $\theta =0^{\circ }$. The analysis also includes a comparison with circular heater geometry ($\varGamma =1$) (Singh & Premachandran Reference Singh and Premachandran2018b, Reference Singh and Premachandran2019) under similar conditions. The non-dimensional wall superheat is fixed at 0.6 in the simulations. Similar to the previous section, four different magnitudes of $Re_l$ in the range 10–170 are considered with both upward and horizontal liquid cross-flow configurations. Since the characteristic dimension normal to the flow remains the same for different aspect ratios with $\theta =0^{\circ }$, the Froude number magnitude at each $Re_l$ also remains unchanged ($\sqrt {Fr}=0.12\text {--}2.04$). This assumes importance from the view of determining the sole effect of $\varGamma$ on interface evolution and heat transfer under similar hydrodynamic and thermal conditions.

Figure 10 shows the interface evolution for $\varGamma =0.4$ and 0.8 at several $Re_l$ values in upward cross-flow corresponding to $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, quasi-steady film boiling is observed at $Re_l=10$ similar to $\varGamma =0.6$, and is not presented here. At $Re_l=50$, the bubble pinch-off after vapour growth occurs at a relatively larger distance from the heater wall, as shown in figure 10($a$) ($t=0.97\ \textrm {s}$). This is accompanied by a limited recoil of the remaining vapour mass on account of surface tension, resulting in the vapour undulations confined to only a small top portion of the heater. A major portion of the heater wall thus remains blanketed by a thin vapour film. Such a behaviour is ascribed to the combined action of buoyancy and inertia along the elongated elliptical profile, and also leads to a certain loss of the periodic nature of ebullition. Further, the effect of lower aspect ratio is also seen with the formation of a stable vapour column at $Re_l=100$ itself for the present wall superheat in contrast to $\varGamma =0.6$. At $Re_l=170$, figure 10($c$) shows a thin vapour column to be preceded by a thicker wake that reinforces the argument regarding vapour flow separation occurring earlier at increased cross-flow velocities, irrespective of the aspect ratio. At the same time, the thickness of the wake is lower as compared with $\varGamma =0.6$ due to the heater profile, which indicates a delayed vapour wake separation at lower aspect ratios. For $\varGamma =0.8$, the interface evolution is essentially similar to $\varGamma =0.6$ up to $Re_l=100$, with the bubble release becoming transient at $Re_l=100$ due to flow inertia as shown in figure 10($d$). With further increase in cross-flow velocity at $Re_l=170$, a long vapour sheet is seen to form behind the heater from figure 10($e$). While bubbles are detached randomly from the top of the sheet, the sheet itself is torn at some instants ($t=0.535\ \textrm {s}$) due to an interaction with the liquid flow. The behaviour, though quite different from a steady vapour region formed at lower aspect ratios, is characteristically similar to that observed for a circular cylinder (Singh & Premachandran Reference Singh and Premachandran2018b).

Figure 10. Interface evolution with different heater aspect ratios and $Re_l$ (mentioned alongside each case) in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a\text {--}c$) $\varGamma =0.4$ and ($d{,}e$) $\varGamma =0.8$. (For interface evolution at $\varGamma =0.6$ with the same non-dimensional wall superheat, one may refer to figure 5.)

With horizontal cross-flow, the bubble release is periodic at $Re_l=10$ and 50 for $\varGamma =0.4$ as well as 0.8 accompanied by the formation of a thick film below the heater, as seen from figures 11($a$) and 11($b$) at $Re_l=10$. A similar observation was earlier made for $\varGamma =0.6$ from figure 6($a$). Further, the interface morphology at $Re_l=170$ is presented in figures 11($c$) and 11($d$) corresponding to $\varGamma =0.4$ and 0.8, respectively. For $\varGamma =0.4$, the instability evolves in a similar manner as described in figure 6($d$) for $\varGamma =0.6$. However, in comparison, the growth of the vapour wake is much more rapid while no tearing of the vapour sheet due to Kelvin–Helmholtz instability is observed behind the ellipse. This can directly be attributed to the enhanced rate at which the vapour kinetic energy is carried into the wake due to the lower heater aspect ratio coupled with its orientation along the strong flow inertia. On the other hand, for a higher aspect ratio of 0.8, the interface evolution is limited to the phase prior to vapour wake growth. Overall, it is observed that varied wake profiles can result for an elliptical heater in the mixed regime solely based on geometric considerations. This renders the mathematical prediction of wake profiles to be quite difficult, with several other factors including an interplay of buoyancy and inertia and the cross-flow orientation significantly affecting the vapour wake dynamics.

Figure 11. Interface evolution with different heater aspect ratios for ($a{,}b$) $Re_l=10$ and ($c{,}d$) $Re_l=170$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$. (For interface evolution at $\varGamma =0.6$ with the same non-dimensional wall superheat, one may refer to figure 6.)

Furthermore, the thick vapour film formed beneath the heater with horizontal cross-flow at a low $Re_l$ value of 10 is shown in figure 12 for different aspect ratios, along with the vapour temperature distribution. While the vapour removal occurs mainly due to buoyancy under these conditions, the orientation of the major axis normal to gravity offers a constriction to the vapour passage towards the top region of the cylinder. The blockage is more severe at a lower aspect ratio of 0.4 where the situation resembles a downward facing surface with the stagnation points forming the edges of such a surface. The situation subsequently eases out as $\varGamma$ increases allowing a smaller escape route for the vapour. A higher temperature is observed adjacent to the heater wall with a thicker vapour film that is detrimental to the heat transfer rates obtained, as already seen for $\varGamma =0.6$ earlier, and further discussed for other aspect ratios.

Figure 12. Instantaneous temperature distribution and interface morphology in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=10, Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$, showing the effect of heater aspect ratio on vapour removal, thereby affecting film thickness around the cylinder and heat transfer: ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$.

The temporal variation of space-averaged Nusselt number in upward cross-flow at $\varGamma =0.4$ and 0.8 is plotted in figures 13($a$) and 13($b$), respectively, for different $Re_l$. The Nusselt number distribution follows from the nature of ebullition and wake dynamics for each case. For $\varGamma =0.4$, a loss of periodic ebullition can be observed at $Re_l=50$ with vapour recoil affecting only a small upper portion of the heater. A constant Nusselt number is obtained at $Re_l=100$ and 170 due to formation of stable vapour jets even at a low wall superheat, which is an artefact of the heater geometry. On the other hand, no such stable vapour structures are formed for $\varGamma =0.8$ as confirmed from figure 13($b$). Even at $Re_l=170$, the vapour sheet formed behind the elliptical heater is unstable due to rigorous interaction with the liquid flow, as seen previously, resulting in a transient Nusselt number variation. Further, the frequency of periodic bubble release at $Re_l=10$ is much lower as compared with $\varGamma =0.4$. Additionally, it is also observed that the variation of space-averaged Nusselt number from minimum to maximum value is lower for $\varGamma =0.4$ with enhanced vapour infusion into the wake, which limits the vapour undulations post recoil to a small region near the heater wall. With horizontal cross-flow, the space-averaged Nusselt number variation is presented in figures 13($c$) and 13($d$). Here an opposite trend compared with upward flow is notable regarding the bubble release frequency at lower $Re_l$ values, which is shown to increase with the aspect ratio. This is due to the heater profile blocking upward vapour passage with buoyancy more severely at a lower aspect ratio, as discussed in figure 12. An increase in flow inertia, though, alleviates such an effect to an extent, affecting the interface morphology for all the aspect ratios. However, at $Re_l=170$, the Nusselt number is constant for $\varGamma =0.4$ due to a thick and stable vapour wake behind the heater, while very rapid fluctuations are seen corresponding to $\varGamma =0.8$ which are characteristic of vortex shedding behind the heater affecting the vapour morphology. While such fluctuations are also observed for a circular heater (Singh & Premachandran Reference Singh and Premachandran2019) at the present wall superheat, the absence of these at lower values of $\varGamma$ indicates a mutual interaction of vapour and liquid wakes, with the vapour dynamics also affecting the liquid flow characteristics.

Figure 13. Nusselt number with different heater aspect ratios for water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$. The temporal variation of space-averaged Nusselt number at various $Re_l$ is shown for ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$, corresponding to both ($a{,}b$) upward and ($c{,}d$) horizontal cross-flow. Time-averaged values of the Nusselt number for all the parameters considered are shown in panel ($e$). (For space-averaged Nusselt number at $\varGamma =0.6$, one may refer to figure 9.)

The time-averaged Nusselt number values obtained with the present set of parameters are shown in figure 13($e$). From the observations up until this stage in the present work, it can be deduced that the film boiling behaviour in the mixed regime for a given thermal condition of the heater wall is determined primarily by the geometric configuration of the bluff body and a combined influence of buoyancy and flow inertia as per the cross-flow direction. With upward cross-flow, both these factors aid in efficient vapour removal from the heater without any hindrance caused to the vapour flow by the geometric orientation. As such, a minimal variation is seen in the Nusselt number at $Re_l=10$ with bubble release occurring primarily due to buoyancy in a periodic manner. As the effect of flow inertia increases with $Re_l$, a rise in the Nusselt number is seen corresponding to all aspect ratios. However, for $\varGamma =0.4$, the geometric profile of the heater is the dominant factor governing vapour removal even at low $Re_l$ values, which has been discussed previously with regard to figures 10($a$) and 13($a$). As a result, the increase in Nusselt number with flow inertia is not as steep as observed for increasingly higher aspect ratios. As $\varGamma$ increases, the influence of geometry gradually diminishes, while an increase in cross-flow velocity substantially increases the Nusselt number with the formation of a thin stable film over a larger area of the heater wall. This explains the increase in heat transfer with aspect ratio observed at higher $Re_l$ values in figure 13($e$). With horizontal cross-flow, the heater orientation causes a constriction to vapour flow under buoyancy that is accentuated at lower values of $\varGamma$, as described earlier. Thus at a low $Re_l$ value of 10, the heat transfer rate is observed to be considerably smaller than in upward cross-flow for $\varGamma =0.4$. As $\varGamma$ increases, the blockage to vapour passage eases out leading to a linear increase in the Nusselt number. Eventually, the Nusselt number magnitude at $\varGamma =1$ is almost the same as obtained with upward cross-flow, which indeed should be the case with conditions close to pool boiling. Similarly at $Re_l=170$, the Nusselt number is almost independent of the cross-flow orientation due to a predominant effect of inertia ($\sqrt {Fr}=2.04$) driving film boiling dynamics. At the same time, the Nusselt number at intermediate values of $Re_l$ is higher for upward cross-flow, with a comparable influence of buoyancy and inertia aiding each other in the mixed regime.

3.3. Effect of angle of incidence $(\theta )$

From the previous results, it has been established that the geometrical configuration of the elliptical heater coupled with other film boiling parameters in the mixed regime determines the overall interface dynamics and heat transfer. However, the simulations up until this stage have been performed considering the major axis of the ellipse to be aligned along the free stream flow ($\theta =0^{\circ }$). As such, an investigation with different angles of incidence becomes imperative to comprehensively assess the effect of heater geometry on the film boiling behaviour. To this effect, three different values of $\theta$, viz., $30^{\circ }, 60^{\circ }$ and $90^{\circ }$ are considered here corresponding to different heater aspect ratios. The investigation has also been extended to different wall superheats and $Re_l$ values (10–170) as presented subsequently for both liquid cross-flow orientations. However, for each geometric configuration, the magnitude of $Re_l$ is carefully selected to conform to the critical limits reported for flow transition to a three-dimensional nature in single phase flow (Thompson et al. Reference Thompson, Radi, Rao, Sheridan and Hourigan2014; Paul et al. Reference Paul, Prakash, Vengadesan and Pulletikurthi2016). Corresponding to the various conditions, the magnitude of the Froude number varies as $\sqrt {Fr}=0.086\text {--}1.86$, which again ascertains a significant influence of buoyancy in addition to flow inertia.

The interface evolution in upward liquid cross-flow with different angles of incidence is presented in figure 14 for two different aspect ratios at $Re_l=100$ and $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, a thin vapour column was observed at $\theta =0^{\circ }$ previously under similar conditions. However, a discrete bubble release in a periodic manner at subsequently higher angles of incidence is shown in figure 14($a$–$c$). The periodic ebullition indicates that even at a high $Re_l$ value of 100 the effect of flow inertia is overshadowed by buoyancy for these heater orientations. This is, however, conceivable due to a reduction in the magnitude of the Froude number as $\theta$ increases for a given aspect ratio. Nonetheless, the bubble pinch-off occurs at a larger distance from the wall for $\theta =30^{\circ }$. It is also observed that the vapour film is relatively thin over the portion of the heater directly facing the liquid flow. This leads to a much thinner vapour region below the heater at $\theta =90^{\circ }$ when compared with a similar configuration with regard to vapour removal for horizontal cross-flow (figure 12). The constriction to vapour flow is, though, still evident from a visibly thick film due to which buoyancy cannot easily overcome surface tension, leading to severe undulations at the top of the heater during the bubble growth phase ($t=0.63\ \textrm {s}$ and 0.65 s). For $\varGamma =0.6$, the Froude number again reduces with $\theta$, but the magnitude is higher than $\varGamma =0.4$ for each case. As such the random bubble release at $\theta =0^{\circ }$ (figure 5$c$) gradually attains a quasi-steady nature with the effect of flow inertia perceivable up to $\theta =60^{\circ }$ (for instance, $t=0.66\ \textrm {s}$ and 0.7 s in figure 14$e$). The ebullition becomes essentially periodic at $\theta =90^{\circ }$, where no undulations are observed during bubble growth unlike $\varGamma =0.4$ along with a thin film in the bottom region of the heater since the vapour passage becomes easier for a higher aspect ratio.

Figure 14. Interface evolution with different angles of incidence for ($a\text {--}c$) $\varGamma =0.4$ and ($d\text {--}f$) $\varGamma =0.6$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a{,}d$) $\theta =30^{\circ }$, ($b{,}e$) $\theta =60^{\circ }$ and ($c,\kern0.05em f$) $\theta =90^{\circ }$. (For interface evolution at $\theta =0^{\circ }$ with the same non-dimensional wall superheat, one may refer to figures 5 and 10.)

For $\varGamma =0.8$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$, the interface evolution occurs under a slightly enhanced influence of flow inertia for various angles of incidence, and is not presented in figure 14. Instead, the interface morphology obtained with different values of $Re_l$ at $\theta =60^{\circ }$ is shown in figure 15 with upward cross-flow. A periodic film boiling cycle at $Re_l=50$ is replaced by an increasingly transient interfacial dynamics as $Re_l$ increases. Such a characteristic behaviour with variation in cross-flow velocity is observed at all angles of incidence with $\varGamma =0.8$. While the periodic ebullition occurs in a similar manner at different values of $\theta$, a certain difference in the vapour profiles at higher $Re_l$ values is observed compared with $\theta =0^{\circ }$ (figure 10), especially with regard to the vapour sheet formed behind the heater at $Re_l=170$. Nonetheless, the heater orientation has a smaller influence on vapour morphology, in contrast to a substantial change in the ebullition process observed at lower aspect ratios under a given set of conditions. Further, simulations have also been performed considering a higher non-dimensional superheat of 1.2 at $Re_l=100$ for various values of $\varGamma$ and $\theta$. Stable vapour columns are formed in almost all these cases, which have been depicted for $\theta =60^{\circ }$ in figure 16. It is seen that as $\varGamma$ increases, a larger proportion of the heater area is covered by the vapour wake behind the heater.

Figure 15. Interface evolution for ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $\theta =60^{\circ }$ and $Ja_v/Pr_v =0.6$. (For interface evolution at $\theta =0^{\circ }$ and $\varGamma =0.8$, one may refer to figure 10.)

Figure 16. Vapour column formation for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100, \theta =60^{\circ }$ and $Ja_v/Pr_v =1.2$.

The space-averaged Nusselt number distribution at $Re_l=100$ and $Ja_v/Pr_v =0.6$ with upward cross-flow is plotted in figure 17($a$–$c$) for different values of $\varGamma$ and $\theta$. For $\varGamma =0.4$, a completely periodic Nusselt number variation concomitant with the interface evolution is obtained at all angles other than $\theta =0^{\circ }$ for which the Nusselt number is constant due to the formation of a stable vapour column. The frequency of periodic ebullition is observed to decrease with an increase in $\theta$ as the heater orientation offers an increasing resistance to the vapour flow. Further, the undulations observed during the vapour growth phase at $\theta =90^{\circ }$ are also evident from the oscillating Nusselt number variation during each cycle. The effect of flow inertia indicated by a loss in periodicity can be seen at larger heater inclinations with an increase in the aspect ratio. Additionally, as a larger portion of the heater wall is affected by the vapour dynamics during an ebullition cycle for higher values of $\theta$, the corresponding variation in the Nusselt number from minimum to maximum value is observed to increase for all the aspect ratios. The time-averaged Nusselt number values for the various cases investigated with $\varGamma =0.8$ are shown in figure 17($d$). While there is a significant rise in heat transfer as $Re_l$ increases, the comparative influence of heater orientation on the Nusselt number is quite low, with any appreciable increase observed only at higher $Re_l$ values. However, this is not the case at lower aspect ratios for which the time-averaged Nusselt number values corresponding to different $\theta$ and $Re_l$ at $Ja_v/Pr_v =0.6$ are presented in figure 17($e$). In general, the Nusselt number is shown to increase with $\theta$ for all the aspect ratios except $\varGamma =1$, where the definition of $\theta$ is trivial. The increase is significant at $\varGamma =0.4$, while the effect diminishes gradually at subsequently higher values of $\varGamma$ corresponding to both $Re_l$ magnitudes. This in turn leads to a trend (barring a few anomalies that are discussed next) where the Nusselt number decreases with aspect ratio for $\theta =30^{\circ }$ and beyond, and is in contrast to the observation at $\theta =0^{\circ }$. However, a closer investigation of the data reveals that an increase in Nusselt number with $\theta$ for a given aspect ratio is not commensurate to a corresponding increase in the characteristic dimension normal to the flow ($D$), thereby leading to a reduction in heat transfer as $\theta$ increases. This essentially translates into an increase in heat transfer coefficient with $\varGamma$ at all angles of incidence, which is directly reflected in the plot for $\theta =0^{\circ }$ with $D$ being constant for all the aspect ratios. The aforementioned discussion is also directly in line with the results for a circular cylinder (Singh & Premachandran Reference Singh and Premachandran2018b), where an increase in the characteristic dimension relative to the capillary length scale ($\lambda _o$) has a detrimental effect on heat transfer.

Figure 17. Nusselt number showing the effect of angle of incidence on heat transfer in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$. Space-averaged Nusselt number variation at $Ja_v/Pr_v =0.6$, $Re_l=100$ and different values of $\theta$ is shown for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$. Time-averaged values of the Nusselt number for various parameters considered are shown in panels ($d\text {--}f$).

Further, some differences are observed with regard to the Nusselt number trend outlined in the preceding text, which can be traced to the specific interface morphologies. One such observation relates to especially low values of Nusselt number obtained at $Re_l=50$ with $\theta =90^{\circ }$ for all values of $\varGamma$. This is due to a much thicker vapour film formed beneath the heater at $Re_l=50$ compared with $Re_l=100$, as shown in figure 18. While such a thick film is an artefact of a constriction to vapour flow due to the heater orientation, the action of liquid flow at a higher $Re_l$ value of 100 is able to effectively squeeze out the vapour from the underside of the heater directly facing the flow. However, this is not the case at $Re_l=50$ leading to a severe impairment in heat transfer. Additionally, a slightly thicker film even for $Re_l=100$ at a lower aspect ratio of 0.4 leads to a quite low value of Nusselt number at the said conditions in figure 17(e). Furthermore, the variation of time-averaged Nusselt number with heater geometry as described above is also verified from similar trends observed at an enhanced non-dimensional wall superheat of 1.2 and $Re_l=100$, as shown in figure 17($\,f$).

Figure 18. Interface morphology en route bubble pinch-off in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =90^{\circ }$, showing the effect of angle of incidence in conjunction with $Re_l$ on film thickness around the cylinder: ($a$) $\varGamma =0.4$ and ($b$) $\varGamma =0.6$.

The effect of heater orientation relative to free stream flow on the film boiling dynamics is further discussed considering horizontal cross-flow configuration. Figure 19 shows the interface evolution with different angles of incidence for two different aspect ratios at $Re_l=100$ and $Ja_v/Pr_v =0.6$. For $\varGamma =0.4$, the interface dynamics obtained from an earlier investigation at $\theta =0^{\circ }$ is transient in nature with the vapour wake lying entirely behind the heater under the influence of cross-flow. The ebullition becomes increasingly periodic at subsequently higher values of $\theta$ as seen from figure 19($a$–$c$), with a reduction in the magnitude of the Froude number similar to upward cross-flow. While a decrease in Froude number implies a more pronounced effect of buoyancy, the vapour flow due to buoyancy is restricted to varying degrees with different heater orientations leading to an accumulation of vapour on the underside of the heater directly facing the flow. Under such conditions in the mixed regime, a competing effect of buoyancy and inertia forces causes a recirculation in the vapour film leading to a vapour bulge or thick film region. The extent and location of such a recirculation near the heater wall is observed to vary with heater orientation, and is further presented by plotting streamlines in figure 20. For $\theta =0^{\circ }$, the recirculation is confined to the thick vapour wake formed behind the heater under a dominant effect of flow inertia at a higher Froude number, and is indicative of a direct effect of the bluff body rather than arising from an interplay of buoyancy and inertia. However, there is an increased effect of buoyancy at $\theta =30^{\circ }$, while the vapour removal under buoyancy is severely restricted due to the heater orientation. This leads to a vapour bulge in the lower region of the cylinder side facing the flow as shown in figure 20($b$). At $\theta =60^{\circ }$, the vapour can escape more easily from the underside of the heater with buoyancy leading to a thinner and more uniform recirculation region as highlighted in figure 20($c$). Further, the constriction to buoyancy-driven vapour removal is completely absent at $\theta =90^{\circ }$, while the horizontal liquid flow has a further squeezing effect on the vapour side directly facing the flow as also described previously for upward cross-flow. Such a concerted action of buoyancy and inertia leads to a much thinner vapour film near the heater wall. Additionally, the effect of instantaneous vapour wake profiles on the liquid flow is also visualized from figure 20 that indicates a coupling of the vapour and liquid wake behaviour under the present conditions.

Figure 19. Interface evolution with different angles of incidence for ($a\text {--}c$) $\varGamma =0.4$ and ($d\text {--}f$) $\varGamma =0.6$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a{,}d$) $\theta =30^{\circ }$, ($b{,}e$) $\theta =60^{\circ }$ and ($c,\kern0.05em f$) $\theta =90^{\circ }$. (For interface evolution at $\theta =0^{\circ }$ with $\varGamma =0.6$ and same non-dimensional wall superheat, one may refer to figure 6.)

Figure 20. Instantaneous view of streamlines near an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.4)$ with different angles of incidence in horizontal cross-flow of water $(p/p_c =0.99)$ at $Re_l=100$ and $Ja_v/Pr_v =0.6$: ($a$) $\theta =0^{\circ }$, ($b$) $\theta =30^{\circ }$, ($c$) $\theta =60^{\circ }$ and ($d$) $\theta =90^{\circ }$. All of the above views correspond to the time instant, $t = 0.7\ \textrm {s}$.

The interface evolution at the aforementioned conditions with a lower heater aspect ratio of 0.6 is presented in figure 19($d$–$\,f$). As with $\varGamma =0.4$, film boiling becomes increasingly periodic at higher values of $\theta$. However, an enhanced effect of flow inertia persists up until higher heater inclinations, with relatively higher Froude number magnitudes at a higher aspect ratio. As such, an elongated vapour wake can be seen at $\theta =30^{\circ }$ along with a quite small vapour bulge beneath the heater. Although the recirculation region becomes more prominent for $\theta =60^{\circ }$ with increased buoyancy effect, it is still confined to the lower portion of the heater with the oncoming liquid flow in contrast to $\varGamma =0.4$. Such a thick vapour region near the wall was previously observed for $\theta =0^{\circ }$ only at a lower $Re_l$ value of 50 (figure 6$b$). At $\theta =90^{\circ }$, the recirculation again disappears on account of heater orientation being favourable to buoyancy, and a much thinner vapour film is observed as compared with $\varGamma =0.4$. The overall results put forth the significance of the Froude number as the major parameter governing film boiling behaviour in the mixed regime. Additionally, under such an interplay of buoyancy and inertia forces for both the cross-flow directions, their relative effects are determined by the orientation of the elliptical heater showing a coupled effect of geometry and hydrodynamics on the interface evolution. This adds a further degree of complexity compared with a circular heater, where the heater orientation is inconsequential.

In figure 21, the interface evolution at a higher aspect ratio of 0.8 is presented for two different cross-flow velocities and wall superheats at $\theta =60^{\circ }$. At $Re_l=100$ and $Ja_v/Pr_v =0.6$, the bubble release is periodic as compared with a random vapour release obtained at $\theta =0^{\circ }$ previously. The vapour bulge beneath the heater is, however, much smaller than observed at lower aspect ratios showing a lesser constriction to buoyancy governed vapour passage. With increase in $Re_l$ to 170, a random bubble release is again observed with the vapour wake concentrated in an upward region behind the heater as shown in figure 21($b$). At the same time, an increase in wall superheat at $Re_l=100$ also leads to a significant change in the vapour morphology due to enhanced vapour generation. As such, an elongated wake covering the entire rear portion of the heater is observed. The characteristic nature of these changes with $Re_l$ and $Ja_v/Pr_v$, though, is along expected lines, and in consonance with the discussion in previous sections at $\theta =0^{\circ }$.

Figure 21. Interface evolution in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $\theta =60^{\circ }$: ($a$) $Re_l=100, Ja_v/Pr_v =0.6$, ($b$) $Re_l=170, Ja_v/Pr_v =0.6$ and ($c$) $Re_l=100, Ja_v/Pr_v =1.2$.

The temporal variation of space-averaged Nusselt number with horizontal cross-flow at $Re_l=100$ and $Ja_v/Pr_v =0.6$ is plotted in figure 22($a$–$c$) for different values of $\varGamma$ and $\theta$. The Nusselt number distribution is concomitant with the interface evolution described in previous paragraphs for the various cases. However, amongst the cases with periodic ebullition, no noticeable change in bubble release frequency is observed for $\varGamma =0.4$ and also for $\varGamma =0.8$ at a later time. In fact, the frequency is seen to increase with angle at $\varGamma =0.6$ which is in stark contrast to the observation with upward cross-flow. This can, however, be attributed to the opposing effects of heater orientation in aiding or opposing buoyancy-driven vapour removal with regard to the two cross-flow orientations, which have already been discussed in detail. The time-averaged Nusselt number values for the various cases investigated with $\varGamma =0.8$ are shown in figure 22($d$), while the values obtained at other aspect ratios for different conditions are presented in figures 22($e$) and 22($\,f$). The trends, with slight differences, can be broadly related to the discussion for upward cross-flow. However, two major instances of peculiar behaviour can be observed from these results. The first relates to a higher heat transfer compared with upward liquid flow (figure 17) for a few cases at higher angles of incidence. While such an observation is completely counter-intuitive with buoyancy aiding flow inertia in liquid upflow, it stems from the prominent role of heater orientation on the interfacial dynamics. For upward cross-flow, an increase in the angle of incidence has a detrimental effect on vapour removal due to buoyancy, as well as liquid flow. However, with horizontal cross-flow, while higher values of $\theta$ entail a lower influence of flow inertia with a reduction in Froude number, the buoyancy-driven vapour removal is simultaneously enhanced leading to higher heat transfer rates compared with upflow under certain conditions. Thus an additional degree to the interplay between buoyancy and inertia is imposed by the heater orientation that already depends substantially on the Froude number as well as the cross-flow orientation, thereby establishing a strong coupling between the angle of incidence and Froude number.

Figure 22. Nusselt number showing the effect of angle of incidence on heat transfer in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$. Space-averaged Nusselt number variation at $Ja_v/Pr_v =0.6, Re_l=100$ and different values of $\theta$ is shown for ($a$) $\varGamma =0.4$, ($b$) $\varGamma =0.6$ and ($c$) $\varGamma =0.8$. Time-averaged values of the Nusselt number for various parameters considered are shown in panels ($d\text {--}f$).

Another major anomaly that can be observed from the results concerns a reduction in heat transfer with increase in $Re_l$ under a given set of conditions, as seen at $\theta =60^{\circ }$ and $90^{\circ }$ with $Re_l=10$ and 50 for $\varGamma =0.8$, and a few other cases in figure 22($e$). This is directly a consequence of the cross-flow orientation since such an observation does not relate to any of the results for upward cross-flow, and is explained further in figure 23. The interface morphology prior to bubble pinch-off at $\varGamma =0.8$ and $Ja_v/Pr_v =0.6$ is shown for $Re_l=10$ and 50 in figure 23($a$), with a fixed heater orientation of $60^{\circ }$. At $Re_l=50$, a recirculation zone near the heater wall is clearly evident from figure 23($c$) that forms with an interplay of buoyancy and inertia, as has been described previously for various conditions. On the other hand, at $Re_l=10$ the effect of buoyancy is much stronger along with the heater geometry not offering any major resistance to the vapour flow. As such, the vapour smoothly flows over the ellipse driven strongly by the buoyancy force, as seen from the streamlines in figure 23($b$). For $Re_l=50$, the recirculation leads to a thick film with a higher temperature in the affected zone near the wall, which causes the impairment in heat transfer observed in figure 22($d$). Further, such an effect is dependent on several parameters including heater geometry as shown previously, thereby affecting the heat transfer to different extents under various conditions.

Figure 23. ($a$) Interface morphology prior to bubble pinch-off for $Re_l=10$ and 50 in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.8)$ at $Ja_v/Pr_v =0.6$ and $\theta =60^{\circ }$. Comparison of instantaneous temperature distribution in the vapour film and streamlines near the cylinder is shown for ($b$) $Re_l=10$ and ($c$) $Re_l=50$.

At this stage, it is prudent to briefly discuss the two-dimensional nature of the present film boiling simulations. With no prior study performed for film boiling over an ellipse with liquid cross-flow, the qualitative as well as quantitative insights obtained from the present two-dimensional simulations form an important first step towards plugging a discernible gap existing in the literature. While the operating conditions correspond to the mixed regime with low magnitudes of the Froude number, these have also been selected while considering the limitation of the current study being two-dimensional. At system pressures near-critical conditions, the interfacial dynamics in film boiling is closer to a two-dimensional situation (Son & Dhir Reference Son and Dhir1998). Additionally, low values of $Re_l$ are employed as discussed in the beginning of this section. Furthermore, several studies (Panzarella, Davis & Bankoff Reference Panzarella, Davis and Bankoff2000; Aursand, Davis & Ytrehus Reference Aursand, Davis and Ytrehus2018) have relied on two-dimensional models to obtain significant insights pertaining to nonlinear dynamics and thermocapillary effects in horizontal pool film boiling, where the physics is inherently three-dimensional. Based on the aforementioned considerations, it is expected that the observations from the present study are not just limited to two-dimensional scenarios, and the physical insights would very well apply to real problems. For instance, the recirculation mechanism identified as impairing the heat transfer, results from the competing influence of buoyancy and inertia along the circumferential direction of the elliptical heater, which would exist in the mixed regime even when velocity along the longitudinal axis is present for three-dimensional cases. At the same time, the location and extent of the recirculation may vary depending on the film boiling conditions including any three-dimensional effects. Such an observation from the present study assumes a greater significance considering that the effect in the thin vapour film would be quite difficult to ascertain from experiments. Similar arguments can be applied to other aspects of interface evolution and vapour wake dynamics presented in this work, even if exact quantitative predictions can be better obtained from three-dimensional simulations or experiments that are missing from the literature as yet.

Another major feature of the present work is the quantification of heat transfer under different conditions in the mixed regime. In this regard, the results with upward cross-flow for $\varGamma =1$ have been shown to be in close agreement with available experimental data, thereby ensuring the validity of the present simulations. Additionally, the two-dimensional simulations offer much more flexibility to account for the influence of various parameters on the film boiling behaviour at a reasonable computational cost. This has been a major consideration in some previous film boiling studies (Esmaeeli & Tryggvason Reference Esmaeeli and Tryggvason2004) relying on two-dimensional simulations to obtain parametric heat transfer data that is in reasonable agreement with empirical results.

3.4. Liquid and vapour wake dynamics in the mixed regime

Based on the results obtained in the previous sections, it is overall observed that the interfacial dynamics and associated heat transfer in the mixed regime of film boiling over an ellipse are determined by a coupled effect and complex interplay of several parameters, including a prominent effect of the geometrical configuration of the heater as well as the cross-flow orientation. This results in substantially varying film boiling characteristics including wake profiles as shown for various conditions investigated in the present study. A closer examination of the interplay of buoyancy and inertia at different conditions in the mixed regime, that forms the central theme of the present work, is presented in this section. Further, the mutual interaction of liquid and vapour wakes for different cases is also discussed.

To assess the comparative influence of buoyancy and inertia for a fixed heater geometry, fast Fourier transform (FFT) analysis of the space-averaged Nusselt number in upward liquid cross-flow with different Reynolds number is presented in figure 24, corresponding to $Ja_v/Pr_v =0.3, \varGamma =0.6$ and $\theta =0^{\circ }$. Here, the amplitude is normalized with respect to the dominant frequency observed in each case, and the typical interface morphology is also shown alongside. A dominant frequency is observed at $f_1=3.91\ \textrm {Hz}$ from figure 24($a$) for $Re_l=10$, and is followed by several superharmonics that are exact multiples of $f_1$. Further, $f_1$ corresponds to the frequency of the periodic ebullition driven primarily by buoyancy at such a low value of $Re_l$ (and $Fr$). This indicates that the bubble release occurring under Rayleigh–Taylor instability governs the heat transfer over the elliptical heater. At $Re_l=50$, an almost similar nature of the FFT plot is observed. However, a higher magnitude of the dominant frequency (5.48 Hz) points to an additional effect of flow inertia in aiding bubble release that eventually determines the heat transfer. The effect of inertia is not directly discernible from the interface morphology, which evolves almost identically to $Re_l=10$. At $Re_l=100$, while a dominant peak can be identified from figure 24($c$), it is saddled between several subharmonics and superharmonics. This characterizes a loss of the quasi-steady nature of ebullition under an enhanced influence of flow inertia. Upon further increase in $Re_l$ to 170, multiple frequencies with comparable magnitude are observed on account of random bubble release, with $\sqrt {Fr}=2.04$ implying film boiling occurring in the purely inertial regime. The deductions from the present analysis are in line with those for a circular cylinder (Singh & Premachandran Reference Singh and Premachandran2018b) under similar conditions, which can be expected for the same characteristic dimension resulting from the present configuration of the elliptical heater.

Figure 24. Normalized FFT analysis of the space-averaged Nusselt number with different Reynolds numbers in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.3$ and $\theta =0^{\circ }$: ($a$) $Re_l=10$ ($\sqrt {Fr}=0.12$), ($b$) $Re_l=50$ ($\sqrt {Fr}=0.6$), ($c$) $Re_l=100$ ($\sqrt {Fr}=1.2$) and ($d$) $Re_l=170$ ($\sqrt {Fr}=2.04$).

Further, FFT analysis of the space-averaged Nusselt number in horizontal cross-flow with different angles of incidence and $\varGamma =0.6$ is presented in figure 25, corresponding to $Ja_v/Pr_v =0.6$ and $Re_l=100$. While multiple frequencies at $\theta =0^{\circ }$ and $30^{\circ }$ indicate a random and transient nature of interfacial dynamics, a periodic ebullition governs the heat transfer at higher angles of incidence as evidenced from clearly demarcated peak frequencies in the FFT plots. Such a behaviour can be ascribed to a more prominent effect of buoyancy due to a reduction in the magnitude of Froude number with an increase in $\theta$, as has been described earlier in § 3.3. It can, however, be noted from the interface morphologies presented alongside that the liquid flow does affect the interface evolution at $\theta =60^{\circ }$ and $90^{\circ }$ for a higher $Re_l$ value of 100, as seen from the vapour bulge near the wall and diagonal nature of bubble release. However, there is a pronounced effect of buoyancy along with the heater orientation aiding buoyancy-driven at these angles of incidence, which curtails the randomness arising out of the effect of flow inertia and leads to a periodic ebullition that eventually governs the heat transfer. As such, the magnitude of the dominant frequency is also observed to become higher as $\theta$ increases from $60^{\circ }$ to $90^{\circ }$. Furthermore, the analysis from figures 24 and 25 establishes the Froude number as a key parameter dictating heat transfer in the mixed regime, irrespective of the cross-flow orientation or geometric configuration of the elliptical heater.

Figure 25. Normalized FFT analysis of the space-averaged Nusselt number with different angles of incidence in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $Re_l=100$: ($a$) $\theta =0^{\circ }$, ($b$) $\theta =30^{\circ }$, ($c$) $\theta =60^{\circ }$ and ($d$) $\theta =90^{\circ }$.

To take a closer look at the mutual interaction of liquid and vapour wakes in the mixed regime of film boiling over an elliptical heater, instantaneous contours of the non-dimensional vorticity are plotted for different conditions along with the vapour morphology. The vorticity $\varOmega$ is non-dimensionalized as $\omega =\varOmega D/U$. Figure 26 shows the contours of $\omega$ obtained in upward liquid cross-flow for different Reynolds number values with $Ja_v/Pr_v =0.6, \varGamma =0.6$ and $\theta =0^{\circ }$. From figure 26($a$) at $Re_l=50$, a strong pair of counter-rotating vortices can be seen in the saturated liquid behind the growing vapour mass ($t=0.625\ \textrm {s}$). With further growth of the vapour at the top of the heater, these extend as asymmetric vorticity patches in the liquid wake. However, as the bubble pinch-off stage is reached ($t=0.705\ \textrm {s}$), the vorticity around the liquid–vapour interface becomes substantially higher in comparison. This indicates a significant effect of buoyancy in addition to a relatively smaller effect of flow inertia, with bubble release primarily occurring under Rayleigh–Taylor instability. In a previous study for single phase flow over an ellipse (Paul, Prakash & Vengadesan Reference Paul, Prakash and Vengadesan2014), it has been established that the critical Reynolds number beyond which the steady flow bifurcates into unsteady vortex shedding is approximately 87.5, for $\varGamma =0.6$ and $\theta =0^{\circ }$ as per the current configuration. From figure 26($b$) for $Re_l=100$, it is observed that asymmetric vorticity patches extend from near the wall along the length of the vapour wake, while vortex shedding starts only beyond the bubble mass. Eventually the bubble detaches and rises ($t=0.76\ \textrm {s}$) preventing vortex shedding to fully establish in the liquid flow region. Thus, while the interface evolves under a prominent influence of liquid flow inertia, the above observation reveals an inherent effect of the vapour wake dynamics itself on the liquid wake characteristics. This is further seen in a more pronounced manner at $Re_l=170$, where bifurcation of the liquid flow into characteristic vortex shedding is altogether prevented with the formation of a steady vapour wake behind the heater. Subsequently, the contours of $\omega$ for the same set of parameters in horizontal cross-flow are plotted in figure 27. Since the detached bubbles do not move directly in line with the free stream flow due to orthogonal gravity and flow fields, a more continuous vortex street is established beyond the vapour wake at $Re_l=100$ compared with upward cross-flow. At $Re_l=170$, a voluminous vapour wake is formed behind the heater, with the different stages of interface evolution and effect of Kelvin–Helmholtz instability described earlier in figure 6($d$). The thick vapour wake again affects the liquid wake nature, even though vortex shedding can be observed beyond the vapour region at several instants. Interestingly the value of $Re_l=50$ is much below the critical Reynolds number with the present heater geometry as mentioned earlier. Still vortices can be seen emanating from the tip of the vapour wake as well as adjacent to the film beneath the heater wall, thereby showing the effect of vapour wake profile on the liquid flow in addition to the bluff-body geometry. Additionally, a long vorticity patch along with a smaller vortex is observed in the trail of the rising bubble, which is eventually shed as a vortex along the liquid flow ($t=0.8\ \textrm {s}$).

Figure 26. Instantaneous non-dimensional vorticity contours with different $Re_l$ in upward cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$.

Figure 27. Instantaneous non-dimensional vorticity contours with different $Re_l$ in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5,\varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a$) $Re_l=50$, ($b$) $Re_l=100$ and ($c$) $Re_l=170$.

Further, the non-dimensional vorticity contours are plotted for similar conditions but different aspect ratios of the elliptical heater in figure 28. For $\varGamma =0.4$ and $\theta =0^{\circ }$, the $Re_l$ values considered in the present study are much lower than the corresponding magnitude of the critical Reynolds number (Paul et al. Reference Paul, Prakash and Vengadesan2014). Thus the steady vapour region formed behind the heater for both the cross-flow orientations and particular $Re_l$, although resulting from an accentuated rate of vapour infusion due to a lower aspect ratio, also broadly conforms to the liquid flow behaviour expected under the present conditions as shown in figures 28($a$) and 28($c$). For $\varGamma =0.8$, a more rigorous effect of the liquid flow on the vapour wake is observed, especially with horizontal cross-flow at $Re_l=170$. As shown in figure 28($d$), the vapour wake fluctuations and bubble detachment are primarily governed by the alternate vortex shedding process, while the small bubbles are carried along the typical alleyway in unsteady flow behind the cylinder. The current analysis is also extended to different orientations of the elliptical heater in figure 29, where the contours of $\omega$ are plotted in horizontal liquid cross-flow for different values of $\theta$ with $Re_l=100, Ja_v/Pr_v =0.6$ and $\varGamma =0.6$. The intensity of vortex shedding is observed to increase with an increase in $\theta$, with the vortex street behind the heater becoming quite dense for $\theta =90^{\circ }$. While this follows directly as an influence of the bluff-body configuration, the vapour wake during bubble growth phase has a wider span along the vertical direction due to buoyancy-driven vapour removal becoming more prominent at higher angles of incidence. Since the vortices originate from the tips of the vapour region as also discussed earlier, the span of the vorticity field in the saturated liquid becomes wider at $\theta =60^{\circ }$ and $90^{\circ }$ compared with $\theta =30^{\circ }$.

Figure 28. Instantaneous non-dimensional vorticity contours for ($a{,}b$) upward ($Re_l=100$) and ($c{,}d$) horizontal ($Re_l=170$) cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5)$ at $Ja_v/Pr_v =0.6$ and $\theta =0^{\circ }$: ($a{,}c$) $\varGamma =0.4$ and ($b{,}d$) $\varGamma =0.8$. (For contours at $\varGamma =0.6$ with similar conditions, one may refer to figures 26 and 27.)

Figure 29. Instantaneous non-dimensional vorticity contours in horizontal cross-flow of water $(p/p_c =0.99)$ over an elliptical cylinder $(b/\lambda _o=0.5, \varGamma =0.6)$ at $Ja_v/Pr_v =0.6$ and $Re_l=100$: ($a$) $\theta =30^{\circ }$, ($b$) $\theta =60^{\circ }$ and ($c$) $\theta =90^{\circ }$. (For contours at $\theta =0^{\circ }$ with similar conditions, one may refer to figure 27.)

The aforementioned discussion characterizes a mutual interaction of the liquid and vapour wakes under different conditions in the investigated mixed regime of film boiling over an ellipse, which is quite significant considering that a discernible gap regarding the same exists even in classical film boiling studies for a circular cylinder. Here, it can be mentioned that the qualitative nature of these results established for the first time is not expected to change for three-dimensional cases. Simultaneously, two-dimensional simulations allow characterization of the mutual wake interaction under the influence of various parameters at a much lower computational cost. While the veracity of the above analysis based on vorticity contours can be exactly established only through future three-dimensional simulations or experiments, the present observations can also serve as an important reference for such studies. As such, the present analysis assumes a greater significance in the absence of any prior empirical or three-dimensional data, as also discussed towards the end of § 3.3.

3.5. Shape factor ($\psi$): correlation for heat transfer

With the extensive set of simulations performed in the present study, a correlation for the time-averaged Nusselt number (subsequently referred to as $Nu$) is arrived at in this section to comprehensively predict the heat transfer in the mixed regime of film boiling over an elliptical heater. It can be noted that a heat transfer correlation for saturated film boiling over a circular heater geometry has been proposed in an earlier study by the present authors (Singh & Premachandran Reference Singh and Premachandran2018b) under similar conditions in the mixed regime with upward liquid cross-flow. Subsequently in another study (Singh & Premachandran Reference Singh and Premachandran2019), a reduction factor as a function of the Froude number was proposed to quantify the heat transfer with horizontal cross-flow of liquid over a circular cylinder. These correlations comprehensively account for the various hydrodynamic, thermal and geometric parameters that are observed to affect the film boiling heat transfer. An attempt is made to quantify the heat transfer in the present case while avoiding an altogether new formulation, considering that the interfacial dynamics results from an interplay of similar parameters in addition to the elliptical geometry. To this effect, a shape factor ($\psi$) is conceived as a function of the geometrical parameters of the ellipse such that

(3.1)\begin{equation} Nu_e=\psi Nu_c, \end{equation}

where the subscripts $e$ and $c$ denote elliptical ($\varGamma <1$) and circular ($\varGamma =1$) heater geometries, respectively. Further, it has been shown previously that the Nusselt number increases with the aspect ratio of the heater for $\theta =0^{\circ }$, while broadly showing a decreasing trend with $\varGamma$ for other values of $\theta$. Thus the Nusselt number can be directly related to the elliptical geometry based on a parameter $\varGamma ^{'}$ which is defined as

(3.2)\begin{equation} \varGamma^{'}=\varGamma + \frac{\theta}{\varGamma}. \end{equation}

It should be mentioned that the unit of $\theta$ is radians in (3.2). For upward cross-flow, the heater orientation has a consistent effect on vapour removal due to buoyancy as well as flow inertia. As such, the shape factor is suitably determined by fitting a polynomial to the simulation data. However, a coupled effect of heater orientation and the Froude number is observed with horizontal cross-flow, as has been discussed previously in § 3.3. Under these conditions, a close fit based on the simulation results is obtained with the inclusion of an additional logarithmic function in the functional form of the shape factor. Eventually, the expression for the shape factor is obtained as

(3.3)\begin{equation} \psi (\varGamma,\theta,Fr)=\left(1+\delta_h\gamma\left(\varGamma^{'},Fr\right)\right)\left(-0.045\varGamma^{'2}+0.2\varGamma^{'}+0.825\right), \end{equation}

where

(3.4)\begin{equation} \gamma\left(\varGamma^{'},Fr\right)=-0.08x_1+0.065x_2+0.1x_1 x_2+0.2x_1^{3}+0.08x_1 x_2^{2}, \end{equation}

with $x_1=ln(\varGamma ^{'})$, $x_2=ln(\sqrt {Fr})$, and $\delta _h$ being unity for horizontal cross-flow and zero for upward cross-flow. It must be carefully noted that the Nusselt number calculated using the above expression relates only to the convective heat transfer, since the radiation contribution in the present study is negligible as already mentioned in § 2.2.2. Further, the shape factor is strictly derived for the mixed regime only, while a detailed analysis would be required to characterize the same in the purely inertial regime of forced convection film boiling. The parity plot for the time-averaged Nusselt number obtained from the present simulations and predicted using (3.1)–(3.4) is shown in figure 30. The maximum deviation from the plot is observed to be within $\pm 12\,\%$ for all data points, which is quite a reasonable fit for boiling data.

Figure 30. Parity plot for the time-averaged Nusselt number obtained from the present simulations and the proposed correlation in terms of the shape factor ($\psi$).