We numerically investigate both single and multiple droplet dissolution with droplets consisting of less dense liquid dissolving in a denser host liquid. In this situation, buoyancy can lead to convection and thus plays an important role in the dissolution process. The significance of buoyancy is quantified by the Rayleigh number 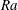 $Ra$, which is the buoyancy force over the viscous damping force. In this study,
$Ra$, which is the buoyancy force over the viscous damping force. In this study, 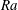 $Ra$ spans almost four decades from 0.1 to 400. We focus on how the mass flux, characterized by the Sherwood number
$Ra$ spans almost four decades from 0.1 to 400. We focus on how the mass flux, characterized by the Sherwood number 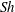 $Sh$, and the flow morphologies depend on
$Sh$, and the flow morphologies depend on 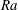 $Ra$. For single droplet dissolution, we first show the transition of the
$Ra$. For single droplet dissolution, we first show the transition of the 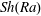 $Sh(Ra)$ scaling from a constant value to
$Sh(Ra)$ scaling from a constant value to 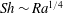 $Sh\sim Ra^{1/4}$, which confirms the experimental results by Dietrich et al. (J. Fluid Mech., vol. 794, 2016, pp. 45–67). The two distinct regimes, namely the diffusively and the convectively dominated regimes, exhibit different flow morphologies: when
$Sh\sim Ra^{1/4}$, which confirms the experimental results by Dietrich et al. (J. Fluid Mech., vol. 794, 2016, pp. 45–67). The two distinct regimes, namely the diffusively and the convectively dominated regimes, exhibit different flow morphologies: when 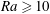 $Ra\geqslant 10$, a buoyant plume is clearly visible, which contrasts sharply with the pure diffusion case at low
$Ra\geqslant 10$, a buoyant plume is clearly visible, which contrasts sharply with the pure diffusion case at low 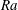 $Ra$. For multiple droplet dissolution, the well-known shielding effect comes into play at low
$Ra$. For multiple droplet dissolution, the well-known shielding effect comes into play at low 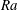 $Ra$, so that the dissolution rate is slower as compared to the single droplet case. However, at high
$Ra$, so that the dissolution rate is slower as compared to the single droplet case. However, at high 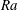 $Ra$, convection becomes more and more dominant so that a collective plume enhances the mass flux, and remarkably the multiple droplets dissolve faster than a single droplet. This has also been found in the experiments by Laghezza et al. (Soft Matt., vol. 12 (26), 2016, pp. 5787–5796). We explain this enhancement by the formation of a single, larger plume rather than several individual plumes. Moreover, there is an optimal
$Ra$, convection becomes more and more dominant so that a collective plume enhances the mass flux, and remarkably the multiple droplets dissolve faster than a single droplet. This has also been found in the experiments by Laghezza et al. (Soft Matt., vol. 12 (26), 2016, pp. 5787–5796). We explain this enhancement by the formation of a single, larger plume rather than several individual plumes. Moreover, there is an optimal 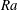 $Ra$ at which the enhancement is maximized, because the single plume is narrower at larger
$Ra$ at which the enhancement is maximized, because the single plume is narrower at larger 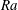 $Ra$, which thus hinders the enhancement. Our findings demonstrate a new mechanism in collective droplet dissolution, which is the merging of the plumes, which leads to non-trivial phenomena, contrasting the shielding effect.
$Ra$, which thus hinders the enhancement. Our findings demonstrate a new mechanism in collective droplet dissolution, which is the merging of the plumes, which leads to non-trivial phenomena, contrasting the shielding effect.