We investigate experimentally the planar paths displayed by cylinders falling freely in a thin-gap cell containing liquid at rest, by varying the elongation ratio and the Archimedes number of the cylinders, and the solid-to-fluid density ratio. In the investigated conditions, the oscillatory falling motion features two main characteristics: the mean fall velocity $\overline {u_v}$ does not scale with the gravitational velocity, which overestimates $\overline {u_v}$ and is unable to capture the influence of the density ratio on it; and high-amplitude oscillations of the order of $\overline {u_v}$ are observed for both translational and rotational velocities. To model the body behaviour, we propose a force balance, including proper and added inertia terms, the buoyancy force and vortical contributions accounting for the production of vorticity at the body surface and its interaction with the cell walls. Averaging the equations over a temporal period provides a mean force balance that governs the mean fall velocity of the cylinder, revealing that the coupling between the translational and rotational velocity components induces a mean upward inertial force responsible for the decrease of $\overline {u_v}$. This mean force balance also provides a normalization for the frequency of oscillation of the cylinder in agreement with experimental measurements. We then consider the instantaneous force balance experienced by the body, and propose three contributions for the modelling of the vortical force. These can be interpreted as drag, lift and history forces, and their dependence on the control parameters is adjusted on the basis of the experimental measurements.

The added mass force resulting from the acceleration of a body in a fluid is of fundamental and practical interest in dispersed multiphase flows. Euler–Lagrange (EL) and Euler–Euler (EE) simulations require closure terms for the added mass force in order to accurately couple the conserved variables between phases. Presently, a more thorough understanding of the added mass force in a multi-particle system is developed based on potential flow resulting in a resistance matrix formulation analogous to Stokesian dynamics. This formulation is then used to generate a dataset of added mass resistance matrices for large systems of randomly generated particles. This methodology is used to create a volume fraction corrected binary model for predicting the added mass force in large systems as well as generate statistics of the added mass force in such systems. This work provides clarification to the theory of the added mass force for particle clouds, and modelling options that may be implemented in existing EL and EE codes.

Fluid dynamics systems driven by dominant, near-periodic dynamics are common across wakes, jets, rotating machinery and high-speed flows. Traditional modal decomposition techniques have been used to gain insight into these flows, but can require many modes to represent key physical processes. With the aim of generating modes that intuitively convey the underlying physical mechanisms, we propose an intrinsic phase-based proper orthogonal decomposition (IPhaB POD) method, which creates energetically ranked modes that evolve along a characteristic cycle of the dominant near-periodic dynamics. Our proposed formulation is set in the time domain, which is particularly useful in cases where the cyclical content is imperfectly periodic. We formally derive IPhaB POD within a POD framework that therefore inherits the energetically ranked decomposition and optimal low-rank representation inherent to POD. As part of this derivation, a dynamical systems representation is utilized, facilitating a definition of phase within the system's near-periodic cycle in the time domain. An expectation operator and inner product are also constructed relative to this definition of phase in a manner that allows for the various cycles within the data to demonstrate imperfect periodicity. The formulation is tested on two sample problems: a simple, low Reynolds number aerofoil wake, and a complex, high-speed pulsating shock wave problem. The method is compared to space-only POD, spectral POD (SPOD) and cyclostationary SPOD. The method is shown to better isolate the dominant, near-periodic global dynamics in a time-varying IPhaB mean, and isolate the tethered, local-in-phase dynamics in a series of time-varying modes.

In freely decaying stably stratified turbulent flows, numerical evidence shows that the horizontal displacement of Lagrangian tracers is diffusive while the vertical displacement converges towards a stationary distribution, as shown numerically by Kimura & Herring (J. Fluid Mech., vol. 328, 1996, pp. 253–269). Here, we develop a stochastic model for the vertical dispersion of Lagrangian tracers in stably stratified turbulent flows that aims to replicate and explain the emergence of a stationary probability distribution for the vertical displacement of such tracers. More precisely, our model is based on the assumption that the dynamical evolution of the tracers results from the competing effects of buoyancy forces that tend to bring a vertically perturbed fluid parcel (carrying tracers) to its equilibrium position and turbulent fluctuations that tend to disperse tracers. When the density of a fluid parcel is allowed to change due to molecular diffusion, a third effect needs to be taken into account: irreversible mixing. Indeed, ‘mixing’ dynamically and irreversibly changes the equilibrium position of the parcel and affects the buoyancy force that ‘stirs’ it on larger scales. These intricate couplings are modelled using a stochastic resetting process (Evans & Majumdar, Phys. Rev. Lett., vol. 106, issue 16, 2011, 160601) with memory. More precisely, Lagrangian tracers in stratified turbulent flows are assumed to follow random trajectories that obey a Brownian process. In addition, their stochastic paths can be reset to a given position (corresponding to the dynamically changing equilibrium position of a density structure containing the tracers) at a given rate. Scalings for the model parameters as functions of the molecular properties of the fluid and the turbulent characteristics of the flow are obtained by analysing the dynamics of an idealised density structure. Even though highly idealised, the model has the advantage of being analytically solvable. In particular, we show the emergence of a stationary distribution for the vertical displacement of Lagrangian tracers. We compare the predictions of this model with direct numerical simulation data at various Prandtl numbers 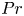$Pr$, the ratio of kinematic viscosity to molecular diffusion.

The transformation of internal waves on a stepwise underwater obstacle is studied in the linear approximation. The transmission and reflection coefficients are derived for a two-layer fluid. The results are obtained and presented as functions of incident wave wavenumber, density ratio of layers, pycnocline position, and height of the bottom step. Excitation coefficients of evanescent modes are also calculated, and their importance is demonstrated. This allows one to estimate the number of evanescent modes necessary to take into account to attain the required accuracy for the transformation coefficients.

This work presents an experimental investigation of the effects of vortex shedding suppression on the properties and recovery of turbulent wakes. Four plates, properly modified so that they produce different vortex shedding strengths, are tested using high speed particle image velocimetry and hot-wire anemometry, and analysed using spectral proper orthogonal decomposition, mean-flow linear stability analysis and various turbulence statistics. When present, vortex shedding is found to exhibit a characteristic frequency that scales with the mean shear, providing a link between the mean flow and the main turbulent motion. To achieve full suppression of shedding, we combine the effects of porosity and fractal perimeter. The mean shear is then decreased to the point where the flow becomes convectively unstable and shedding vanishes. In that case, the onset of self-similarity is delayed, compared with the case with vortex shedding, and appears after another large-scale structure, the secondary vortex street, emerges. It is also found that both large- and small-scale intermittency are starkly reduced when shedding is absent. A simple theoretical representation of the wake dynamics explains the evolution of the wake properties and its connection to the coherent structures in the flow.

When one fluid is injected into a confined geometry such as a porous medium filled with another immiscible fluid, even at an extremely low injection speed, rapid filling of several pore spaces accompanied by retraction of multiple fluid–fluid interfaces can be observed. Such processes with fast liquid redistribution within the solid structure, called Haines jumps, are ubiquitous in many multiphase flow systems, which can impact fluid trapping, energy dissipation and hysteretic saturation in various engineering applications. Inspired by this mechanism, here, we propose a dual-channel structure to realise controlled Haines jumps during fluid displacement processes. Via theoretical analysis and numerical simulations, we show that the dynamics of fluid interfaces during Haines jumps can be quantitatively correlated with the driving capillary pressure and dissipating viscous stress, which enables simultaneous determination of the fluid viscosity and interfacial tension in the dual-channel multiphase system.

We investigate nonlinear energy transfer for channel flows at friction Reynolds numbers $Re_{\tau }=180$ and $590$. The key feature of the analysis is that we quantify the energy transferred from a source mode to a recipient mode, with each mode characterised by a streamwise wavenumber and a spanwise wavenumber. This is achieved through an explicit examination of the triadic interactions of the nonlinear energy transfer term in the spectral turbulent kinetic energy equation. First, we quantify the nonlinear energy transfer gain and loss for individual Fourier modes. The gain and loss cannot be obtained without expanding the nonlinear triadic interactions. Second, we quantify the nonlinear energy transfer budgets for three types of modes. Each type of mode is characterised by a specific region in streamwise–spanwise wavenumber space. We find that a transverse cascade from streamwise-elongated modes to spanwise-elongated modes exists for all three types of modes. Third, we quantify the forward and inverse cascades between resolved scales and subgrid scales in the spirit of large-eddy simulations. For the cutoff wavelength range that we consider, the forward and inverse cascades between the resolved scales and subgrid scales result in a net forward cascade from the resolved scales to the subgrid scales. The shape of the net forward cascade curve with respect to the cutoff wavelength resembles the net forward cascade predicted by the Smagorinsky eddy viscosity.

The small-scale velocity gradient is connected to fundamental properties of turbulence at the large scales. By neglecting the viscous and non-local pressure Hessian terms, we derive a restricted Euler model for the turbulent flow along an undeformed free surface and discuss the associated stable/unstable manifolds. The model is compared with the data collected by high-resolution imaging on the free surface of a turbulent water tank with negligible surface waves. The joint probability density function (p.d.f.) of the velocity gradient invariants exhibits a distinct pattern from the one in the bulk. The restricted Euler model captures the enhanced probability along the unstable branch of the manifold and the asymmetry of the joint p.d.f. Significant deviations between the experiments and the prediction are evident, however, in particular concerning the compressibility of the surface flow. These results highlight the enhanced intermittency of the velocity gradient and the influence of the free surface on the energy cascade.

The concept of vortex lock-in for a single circular cylinder in an oscillating flow, induced through acoustic forcing, is revisited. Multiple cylinder diameters are investigated over a Reynolds number range between 500 and 7200. The lock-in behaviour is investigated quantitatively through hot-wire anemometry and planar particle image velocimetry measurements. The results corroborate previous findings describing the frequency range over which vortex lock-in occurs. It is found that the cylinder location in a standing wave (pressure node or velocity node) had a significant influence on the lock-in behaviour. A novel scaling which captures the onset of vortex lock-in is proposed which demonstrates that the Strouhal number is important in predicting the amplitude of the velocity fluctuations required to induce lock-in. Velocity fields also reveal the existence of bimodal vortex shedding during lock-in. This is confirmed using snapshot proper orthogonal decomposition which demonstrates that symmetric and alternate shedding modes are simultaneously present during lock-in and that symmetric shedding is inherent to the near wake region only. Reduced-order reconstruction of the instantaneous velocity fields confirmed that features associated with the forcing frequency control the shear layer roll-up up to $x/d=2.1$ while the influence of the asymmetric mode is simply to skew the trajectory of the vortex pair. Since vortex roll-up and the cylinder wake ends at $x/d=2.1$, the emergence of spectral content at $0.5f_e$ is attributed to a wavelength doubling measured between the vortical structures in the flow field.

Nonlinear hydroelastic waves along a compressed ice sheet lying on top of a two-dimensional fluid of infinite depth are investigated. Based on a Hamiltonian formulation of this problem and by applying techniques from Hamiltonian perturbation theory, a Hamiltonian Dysthe equation is derived for the slowly varying envelope of modulated wavetrains. This derivation is further complicated here by the presence of cubic resonances for which a detailed analysis is given. A Birkhoff normal form transformation is introduced to eliminate non-resonant triads while accommodating resonant ones. It also provides a non-perturbative scheme to reconstruct the ice-sheet deformation from the wave envelope. Linear predictions on the modulational instability of Stokes waves in sea ice are established, and implications for the existence of solitary wave packets are discussed for a range of values of ice compression relative to ice bending. This Dysthe equation is solved numerically to test these predictions. Its numerical solutions are compared with direct simulations of the full Euler system, and very good agreement is observed.

An efficient compression scheme for modal flow analysis is proposed and validated on data sequences of compressible flow through a linear turbomachinery blade row. The key feature of the compression scheme is a minimal, user-defined distortion of the mutual distance of any snapshot pair in phase space. Through this imposed feature, the model reduction process preserves the temporal dynamics contained in the data sequence, while still decreasing the spatial complexity. The mathematical foundation of the scheme is the fast Johnson–Lindenstrauss transformation (FJLT) which uses randomized projections and a tree-based spectral transform to accomplish the embedding of a high-dimensional data sequence into a lower-dimensional latent space. The compression scheme is coupled to a proper orthogonal decomposition and dynamic mode decomposition analysis of flow through a linear blade row. The application to a complex flow-field sequence demonstrates the efficacy of the scheme, where compression rates of two orders of magnitude are achieved, while incurring very small relative errors in the dominant temporal dynamics. This FJLT technique should be attractive to a wide range of modal analyses of large-scale and multi-physics fluid motion.

We study the formation of dust-free regions above hot horizontal surfaces of uniform temperature and propose relations for its height in the limit of small particle inertia and gravitational effects. By including particle inertia, thermophoretic, gravitational and viscous effects, we conduct Lagrangian simulations of particle dynamics in a natural convection boundary layer over a horizontal surface. Trajectory analysis of the particles inside the boundary layer on the surface reveals the existence of two separatrices originating from a saddle point, which form the boundary of the dust-free region. These separatrices for low gravitational effects follow the boundary layer thickness, but are of much lower height and also depend on the dimensionless thermophoretic number ($Th$) and Prandtl number ($Pr$). We obtain a relation for the dimensionless height of the dust-free region ($\eta _{df}$) as a function of $Pr$ and $Th$, for low dimensionless gravitational number ($Gn$); the numerical solution of this equation gives us the dust-free region height for any $Th$ and $Pr$. We then obtain scaling laws for $\eta _{df}$ using the boundary layer equations corresponding to the $Pr \gg 1$ and $Pr \ll 1$ cases; these scaling laws are shown to be valid respectively for $Pr>1$ and $Pr<1$, except in the large $\eta$ limit for $Pr>1$, where $\eta$ is the boundary layer similarity variable. We then obtain an empirical relation in this large $\eta$ limit using the numerical solutions of the boundary layer equations for the intermediate $Pr$ case to obtain scaling laws for dust-free region height for the whole range of $Pr \ll 1$ to $Pr \gg 1$.

In recent years, the generalised quasilinear (GQL) approximation has been developed and its efficacy tested against purely quasilinear (QL) approximations. GQL systematically interpolates between QL and fully nonlinear dynamics by employing a generalised Reynolds decomposition. Here, we examine an exact statistical closure for the GQL equations on the doubly periodic $\beta$-plane. Closure is achieved at second order using a generalised cumulant approach which we term GCE2. GCE2 is shown to yield improved performance over statistical representations of purely QL dynamics (CE2) and thus enables direct statistical simulation of complex mean flows that do not entirely fall within the remit of pure QL theory. Despite the existence of an exact closure, GCE2 like CE2 admits the possibility of a rank instability that leads to differences with statistics obtained from GQL. Recognition of this instability is a necessary step before further progress can be made with the GCE2 statistical closure.

The nonlinear stability of two-dimensional (2-D) plane Couette flow subject to a constant throughflow is analysed at finite and asymptotically large Reynolds numbers $\textit {Re}$. The speed of this throughflow is quantified by the non-dimensional throughflow number $\eta$. The base flow exhibits a linear instability provided $\eta \gtrsim 3.35$, with multi-deck upper and lower branch structures developing in the limit $1\ll \eta \ll \mathit {O}(\textit {Re})$. This instability provides a springboard for the computation of nonlinear travelling waves which bifurcate subcritically from the linear neutral curve, allowing us to map out a neutral surface at different values of $\eta$. Using strongly nonlinear critical layer theory, we investigate the waves that bifurcate from the upper branch at asymptotically large $\textit {Re}$. This asymptotic structure exists provided the throughflow number is larger than the critical value of $\eta _c\approx 1.20$ and is shown to give quantitatively similar results to the numerical solutions at Reynolds numbers of $\mathit {O}(10^5)$.

We study linear convective instability in a mushy layer formed by solidification of a binary alloy, cooled by either an isothermal perfectly conducting boundary or an imperfectly conducting boundary where the surface temperature depends linearly on the surface heat flux. A companion paper (Hitchen & Wells, J. Fluid Mech., 2025, in press) showed how thermal and salinity conditions impact mush structure. We here quantify the impact on convective instability, described by a Rayleigh number characterising the ratio of buoyancy to dissipative mechanisms. Two limits emerge for a perfectly conducting boundary. When the salinity-dependent freezing-point depression is large versus the temperature difference across the mush, convection penetrates throughout the depth of a high-porosity mush. The other limit, which we will call the Stefan limit, has small freezing-point depression and inhibits convection, which localises at onset to a high-porosity boundary layer near the mush–liquid interface. Scaling arguments characterise variation of the critical Rayleigh number and wavenumber based on the potential energy contained in order-one aspect ratio convective cells over the high-porosity regions. The Stefan number characterises the ratio of latent and sensible heats, and has moderate impact on stability via modification of the background temperature and porosity. For imperfectly conducting boundaries, the changing surface temperature causes stability to decrease over time in the limit of large freezing-point depression, but in the Stefan limit combines with the decreasing porosity to yield non-monotonic variation of the critical Rayleigh number. We discuss the implications for convection in growing sea ice.

Turbulent boundary layers on immersed objects can be significantly altered by the pressure gradients imposed by the flow outside the boundary layer. The interaction of turbulence and pressure gradients can lead to complex phenomena such as relaminarization, history effects and flow separation. The angular momentum integral (AMI) equation (Elnahhas & Johnson, J. Fluid Mech., vol. 940, 2022, A36) is extended and applied to high-fidelity simulation datasets of non-zero pressure gradient turbulent boundary layers. The AMI equation provides an exact mathematical equation for quantifying how turbulence, free-stream pressure gradients and other effects alter the skin friction coefficient relative to a baseline laminar boundary layer solution. The datasets explored include flat-plate boundary layers with nearly constant adverse pressure gradients, a boundary layer over the suction surface of a two-dimensional NACA 4412 airfoil and flow over a two-dimensional Gaussian bump. Application of the AMI equation to these datasets maps out the similarities and differences in how boundary layers interact with favourable and adverse pressure gradients in various scenarios. Further, the fractional contribution of the pressure gradient to skin friction attenuation in adverse-pressure-gradient boundary layers appears in the AMI equation as a new Clauser-like parameter with some advantages for understanding similarities and differences related to upstream history effects. The results highlight the applicability of the integral-based analysis to provide quantitative, interpretable assessments of complex boundary layer physics.

A super-stable granular heap is a pile of grains whose free surface is inclined above the angle of repose, and which forms when particles are poured onto a plane that is confined laterally by frictional sidewalls that are separated by a narrow gap. During continued mass supply, the heap free surface gradually steepens until all the inflowing grains can flow out of the domain. As soon as the supply of grains is stopped, the heap is progressively eroded, and if the base of the domain is inclined above the angle of repose, then all the grains eventually flow out. This phenomenology is modelled using a system of two-dimensional width-averaged mass and momentum balances that incorporate the sidewall friction. The granular material is assumed to be incompressible and satisfy the partially regularized $\mu (I)$-rheology. This is implemented in OpenFOAM$^{\circledR}$ and compared against small-scale experiments that study the formation, steady-state behaviour and drainage of a super-stable heap. The simulations accurately capture the dense liquid-like flows as well as the evolving heap shape. The steady uniform flow that develops along the heap surface has non-trivial inertial number dependence through its depth. Super-stable heaps are therefore a sensitive rheometer that can be used to determine the dependence of the friction $\mu$ on the inertial number $I$. However, these flows are challenging to simulate because the free-surface inertial number is high, and can exceed the threshold for ill-posedness even for the partially regularized theory.

Aqueous suspensions of cornstarch abruptly increase their viscosity on raising either shear rate or stress, and display the formation of large-amplitude waves when flowing down inclined channels. The two features have been recently connected using constitutive models designed to describe discontinuous shear thickening. By including time-dependent relaxation and spatial diffusion of the frictional contact density responsible for shear thickening, an analysis of steady sheet flow and its linear stability is presented. The inclusion of such effects is motivated by the need to avoid an ill-posed mathematical problem in thin-film theory and the resulting failure to select any preferred wavelength for unstable linear waves. Relaxation, in particular, eliminates an ultraviolet catastrophe in the spectrum of unstable waves and furnishes a preferred wavelength at which growth is maximized. The nonlinear dynamics of the unstable waves is briefly explored. It is found that the linear instability saturates once disturbances reach finite amplitude, creating steadily propagating nonlinear waves. These waves take the form of a series of steep, shear-thickened steps that translate relatively slowly in comparison with the mean flow.