Coupled free-flow and porous-medium systems appear in a variety of industrial and environmental applications. Fluid flow in the free-flow domain is typically described by the (Navier–)Stokes equations while Darcy’s law is applied in the porous medium. The correct choice of coupling conditions on the fluid–porous interface is crucial for accurate numerical simulations of coupled problems. We found out that the Beavers–Joseph interface condition, which is widely used not only for fluid flow parallel to the porous layer but also for filtration problems, is unsuitable for arbitrary flow directions. To validate our statement, we provide several examples and compare numerical simulation results for the coupled Stokes–Darcy problems to the pore-scale resolved models. We show also that the Beavers–Joseph parameter cannot be fitted for arbitrary flow directions.

When a drop impacts a dry surface at high velocity, it atomises into secondary droplets. These small droplets are generated by one of two types of splashes: either by a prompt splash from the spreading rim at the surface or by a thin corona splash, which levitates from the surface. This study investigates the splashing mechanisms experimentally using multiple high-resolution cameras and characterises the outcome of both splashing types at high Weber and Reynolds numbers. We demonstrate that the prompt splash is well described by the Rayleigh–Taylor instability of the rapidly advancing liquid lamella and determine the boundaries defining this splashing regime, which allows us to distinguish the prompt from the corona splash. Furthermore, we provide an expression to estimate the elapsed time during which the secondary droplets are generated, which is then implemented in the theory of Riboux & Gordillo (Phys. Rev. Lett., vol. 113 (2), 2014, 024507). This theoretical approach together with detailed quantification of the splashing outcome allows us to completely predict the outcome of both splashing types, which includes the mean size, velocity and total ejected volume of the secondary droplets. The detailed model proposed here can be indeed used to understand, characterise and predict more accurately the underlying physics in several applications.

Natural convection in porous media is a fundamental process for the long-term storage of CO2 in deep saline aquifers. Typically, details of mass transfer in porous media are inferred from the numerical solution of the volume-averaged Darcy–Oberbeck–Boussinesq (DOB) equations, even though these equations do not account for the microscopic properties of a porous medium. According to the DOB equations, natural convection in a porous medium is uniquely determined by the Rayleigh number. However, in contrast with experiments, DOB simulations yield a linear scaling of the Sherwood number with the Rayleigh number ($Ra$) for high values of $Ra$ ($Ra\gg 1300$). Here, we perform direct numerical simulations (DNS), fully resolving the flow field within the pores. We show that the boundary layer thickness is determined by the pore size instead of the Rayleigh number, as previously assumed. The mega- and proto-plume sizes increase with the pore size. Our DNS results exhibit a nonlinear scaling of the Sherwood number at high porosity, and for the same Rayleigh number, higher Sherwood numbers are predicted by DNS at lower porosities. It can be concluded that the scaling of the Sherwood number depends on the porosity and the pore-scale parameters, which is consistent with experimental studies.

Vortex interactions behind step cylinders with diameter ratio $D/d=2$ and 2.4 at Reynolds number ($Re_{D}$) 150 were investigated by directly solving the three-dimensional Navier–Stokes equations. In accordance with previous studies, three spanwise vortex cells were captured: S-, N- and L-cell vortices. In this paper, we focused on vortex interactions between the N- and L-cell vortices, especially the vortex dislocations and subsequent formations of vortex loop structures. The phase difference accumulation process of every pair of corresponding N- and L-cell vortices and its effects on the vortex dislocations were investigated. We revealed that the total phase difference between N- and L-cell vortices was accumulated by two physically independent mechanisms, namely different shedding frequencies and different convective velocities of these two cells. The second mechanism has never been reported before. The relative importance of these two mechanisms varied periodically in the phase difference accumulation process of every pair of corresponding N- and L-cell vortices. This variation caused the vortex dislocation process and the subsequent formation of the loop structures to change from one N-cell cycle to another. Our long-time observations also revealed an interruption of the conventional antisymmetric vortex interactions between two subsequent N-cell cycles in this wake. Moreover, the trigger value and the threshold value in the phase difference accumulation processes were identified and discussed. Both values contribute to better understanding of the vortex dislocations in this kind of wake flow. Finally, the universality of our discussions and conclusions was investigated.

We present a new theoretical model describing gravity–capillary waves in orbitally shaken cylindrical containers. Our model can account for both one-layer free-surface and two-layer interfacial wave systems. A set of modal equations for irrotational waves is formulated that we complement with viscous damping rates to incorporate energy dissipation. This approach allows us to calculate explicit formulas for the phase shifts between wave and shaker which are practically important for the mixing efficiency in orbitally shaken bioreactors. Resonance dynamics is described using eight dimensionless numbers, revealing a variety of different effects influencing the forced wave amplitudes. As an unexpected result, the model predicts the formation of novel spiral wave patterns resulting from a damping-induced symmetry breaking mechanism. For validation, we compare theoretical amplitudes, fluid velocities and phase shifts with three different and independent experiments and, when using the slightly deviating experimental values of the resonance frequencies, find a good agreement within the theoretical limits.

We present results from direct numerical simulations of flows in spherical and oblate spheroidal shells, driven both by precession and thermal convection, with Ekman number $Ek=10^{-4}$, non-diffusive Rayleigh numbers from $Ra=0.1$ to $Ra=10$ and unity Prandtl number. The applied precessional forcing spans seven orders of magnitude. Our experiments show a clear transition between a convective state and a precessing flow that can be approximated by a reduced dynamical model. The change in the flow is apparent in visualizations and a decomposition of the velocity into symmetric and antisymmetric components. For the flow dominated by precession, some parameter combinations show two stable solutions that can be realized by a hysteresis or a strong thermal forcing. An increase of the Rayleigh number at a constant precession rate exhibits established scaling properties for the heat transfer, with exponents $2/7$ and $6/5$.

‘Ground effect’ refers to the enhanced performance enjoyed by fliers or swimmers operating close to the ground. We derive a number of exact solutions for this phenomenon, thereby elucidating the underlying physical mechanisms involved in ground effect. Unlike previous analytic studies, our solutions are not restricted to particular parameter regimes, such as ‘weak’ or ‘extreme’ ground effect, and do not even require thin aerofoil theory. Moreover, the solutions are valid for a hitherto intractable range of flow phenomena, including point vortices, uniform and straining flows, unsteady motions of the wing, and the Kutta condition. We model the ground effect as the potential flow past a wing inclined above a flat wall. The solution of the model requires two steps: firstly, a coordinate transformation between the physical domain and a concentric annulus; and secondly, the solution of the potential flow problem inside the annulus. We show that both steps can be solved by introducing a new special function which is straightforward to compute. Moreover, the ensuing solutions are simple to express and offer new insight into the mathematical structure of ground effect. In order to identify the missing physics in our potential flow model, we compare our solutions against new experimental data. The experiments show that boundary layer separation on the wing and wall occurs at small angles of attack, and we suggest ways in which our model could be extended to account for these effects.

Pressure and shear-driven flows of a confined film of fluid overlying a periodic one-dimensional topography of arbitrary shape are considered for prediction of the effective hydraulic permeability in the Stokes flow regime. The other surface confining the fluid may be a planar no-slip wall, an identically patterned wall, a free surface or a surface with prescribed shear. Analytical predictions are obtained using spectral analysis and the domain perturbation method under the assumption of small pattern size to pitch ratio. Using a novel decomposition of the channel height effects into exponentially and algebraically decaying components, a simple surface-metrology-dependent relationship which connects the eigenvalues of the effective permeability tensor is obtained. Two representative topographies are assessed numerically: the infinitely differentiable topography of a phase-modulated sinusoid which has multiple local extrema and zero crossings and the non-differentiable triangular-wave topography. Non-differentiability in the form of corners of triangular patterns and the cusps of scalloped patterns are not found to be an impediment to meaningful and numerically accurate asymptotic predictions of effective permeability and effective slip, contradicting an earlier suggestion from the literature. Several distinct applications of the theory to the friction-reduction and shear-stability performance of the recently developed lubricant impregnated patterned surfaces as well as to scalloped and trapezoidal drag-reduction riblets are discussed, with comparison to experimental data from the literature for the last application. Analytical approximations which have an extended domain of numerical accuracy are also proposed.

Wave forecasting in ocean and coastal waters commonly relies on spectral models based on the spectral action balance equation. These models assume that different wave components are statistically independent and as a consequence cannot resolve wave interference due to statistical correlation between crossing waves, as may be found in, for instance, a focal zone. This study proposes a statistical model for the evolution of wave fields over non-uniform currents and bathymetry that retains the information on the correlation between different wave components. To this end, the quasi-coherent model (Smit & Janssen, J. Phys. Oceanogr., vol. 43, 2013, pp. 1741–1758) is extended to allow for wave–current interactions. The outcome is a generalized action balance model that predicts the evolution of the wave statistics over variable media, while preserving the effect of wave interferences. Two classical examples of wave–current interaction are considered to demonstrate the statistical contribution of wave interferences: (1) swell field propagation over a jet-like current and (2) the interaction of swell waves with a vortex ring. In both examples cross-correlation terms lead to development of prominent interference structures, which significantly change the wave statistics. Comparison with results of the SWAN model demonstrates that retention of cross-correlation terms is essential for accurate prediction of wave statistics in shear-current-induced focal zones.

In this article, we consider the modelling of stationary incompressible and isothermal one-dimensional fluid flow through a long pipeline. The approximation of the average pressure in the developed model by the arithmetic mean of inlet and outlet pressures leads to the known empirical Darcy–Weisbach equation. Most importantly, we also present another improved approach that is more accurate because the average pressure is estimated by integrating the pressure along the pipeline. Through appropriate transformation, we show the difference between the Darcy–Weisbach equation and the improved model that should be treated as a Darcy–Weisbach model error, in multiplicative and additive form. This error increases when the overall pressure drop increases. This symptomatic phenomenon is discussed in detail. In addition, we also consider four methods of estimating the coefficient of friction, assess the impact of pressure difference on the estimated average flow velocity and, based on experimental data, we show the usefulness of new proposals in various applications.

Direct numerical simulation of the Navier–Stokes equations has been used to investigate the Taylor–Couette flow with an imposed pulsatile axial pressure gradient resulting in a spiral Poiseuille flow modulated by an oscillating forcing. Keeping the Reynolds and Taylor numbers constant, both the amplitude and frequency of the oscillating component are varied to span a small region of the phase space. In the narrow-gap geometry considered in this study, the base flow (spiral Poiseuille flow) is in the turbulent regime whereas the oscillating component is laminar. It has been found that the effect of the oscillation is to induce a global flow laminarization provided the frequency is sufficiently small (at constant amplitude) or the amplitude is sufficiently large (at constant frequency). The coupling between steady and oscillating components has been analysed with the help of long-time and phase-averaged statistics. The reverse transition mechanism has been associated to an anisotropic modification of the Reynolds stress tensor components, which has been shown to be caused by an alteration of the pressure–strain interaction.

We use a multiple-scale expansion to average the wave action balance equation over an ensemble of sea-surface velocity fields characteristic of the ocean mesoscale and submesoscale. Assuming that the statistical properties of the flow are stationary and homogeneous, we derive an expression for a diffusivity tensor of surface-wave action density. The small parameter in this expansion is the ratio of surface current speed to gravity wave group speed. For isotropic currents, the action diffusivity is expressed in terms of the kinetic energy spectrum of the flow. A Helmholtz decomposition of the sea-surface currents into solenoidal (vortical) and potential (divergent) components shows that, to leading order, the potential component of the surface velocity field has no effect on the diffusivity of wave action: only the vortical component of the sea-surface velocity results in diffusion of surface-wave action. We validate our analytic results for the action diffusivity by Monte Carlo ray-tracing simulations through an ensemble of stochastic velocity fields.

We study the equilibrium of two phases following gravity segregation under the influence of capillary heterogeneity. Such processes are important in a number of porous media applications, e.g. determining reservoir composition, secondary migration, gravity drainage enhanced oil recovery and CO$_{2}$ storage in aquifers. Solutions are derived for three-dimensional saturation distribution $S_{w}(x,y,z)$ and given as an analytical formula apart from a constant $P_{c}^{0}$ which is determined by numerical integration. The first solution assumes hydrostatic pressure and applies to cases without capillary entry pressure ($P_{c}(S_{w}=1)=0$). The solution can be used for validation of numerical simulations and we show a close match for a number of cases. A second analytical solution is derived, extending the first, to cases of random log-normally distributed permeability fields. A formula for ensemble average saturation solution is presented and a comparison to solutions of various realizations is discussed. When capillary entry pressure is present, the solution based on hydrostatic pressure may be inaccurate due to entry pressure trapping which occurs when regions of $S_{w}=1$ are present. Using numerical simulation, we extend the solution to include estimations of entry pressure trapping for a range of parameters and show its applicability. The comparison of analytical and numerical results helps illustrate and draw insight on the trapping mechanism.

The permanent precession of a baroclinic geophysical vortex is reproduced, under the quasi-geostrophic approximation, using three potential vorticity anomaly modes in spherical geometry. 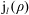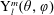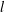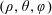The potential vorticity modes involve the spherical Bessel functions of the first kind $\text{j}_{l}(\unicode[STIX]{x1D70C})$ and the spherical harmonics $\text{Y}_{l}^{m}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$, where $l$ is the degree, $m$ is the order, and $(\unicode[STIX]{x1D70C},\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$ are the spherical coordinates. The vortex precession is interpreted as the horizontal and circular advection by a large-amplitude background flow associated with the spherical mode 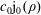$c_{0}\text{j}_{0}(\unicode[STIX]{x1D70C})$ of the small-amplitude zonal mode 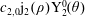$c_{2,0}\text{j}_{2}(\unicode[STIX]{x1D70C})\text{Y}_{2}^{0}(\unicode[STIX]{x1D703})$ tilted by a small-amplitude mode 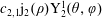$c_{2,1}\text{j}_{2}(\unicode[STIX]{x1D70C})\text{Y}_{2}^{1}(\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$, where 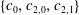$\{c_{0},c_{2,0},c_{2,1}\}$ are constant potential vorticity modal amplitudes. An approximate time-dependent, closed-form solution for the potential vorticity anomaly is given. In this solution the motion of the potential vorticity field is periodic but not rigid. The vortex precession frequency 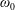$\unicode[STIX]{x1D714}_{0}$ depends linearly on the amplitudes 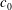$c_{0}$ and 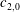$c_{2,0}$ of the modal components of order 0, while the slope of the precessing axis depends on the ratio between the modal amplitude 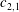$c_{2,1}$ and 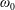$\unicode[STIX]{x1D714}_{0}$.

We revisit the optimal heat transport problem for Rayleigh–Bénard convection in which a rigorous upper bound on the Nusselt number, $Nu$, is sought as a function of the Rayleigh number, $Ra$. Concentrating on the two-dimensional problem with stress-free boundary conditions, we impose the time-averaged heat equation as a constraint for the bound using a novel two-dimensional background approach thereby complementing the ‘wall-to-wall’ approach of Hassanzadeh et al. (J. Fluid Mech., vol. 751, 2014, pp. 627–662). Imposing the same symmetry on the problem, we find correspondence with their maximal result for $Ra\leqslant Ra_{c}:=4468.8$ but, beyond that, the results from the two approaches diverge. The bound produced by the two-dimensional background field approaches that produced by the one-dimensional background field from below as the length of computational domain $L\rightarrow \infty$. On lifting the imposed symmetry, the optimal two-dimensional temperature background field reverts to being one-dimensional, giving the best bound $Nu\leqslant 0.055Ra^{1/2}$ compared to $Nu\leqslant 0.026Ra^{1/2}$ in the non-slip case. We then show via an inductive bifurcation analysis that introducing two-dimensional temperature and velocity background fields (in an attempt to impose the time-averaged Boussinesq equations) is also unable to lower the bound. This then exhausts the background approach for the two-dimensional (and by extension three-dimensional) Rayleigh–Bénard problem with the bound remaining stubbornly $Ra^{1/2}$ while data seem more to scale like $Ra^{1/3}$ for large $Ra$. Finally, we show that adding a velocity background field to the formulation of Wen et al. (Phys. Rev. E., vol. 92, 2015, 043012), which is able to use an extra vorticity constraint due to the stress-free condition to lower the bound to $Nu\leqslant O(Ra^{5/12})$, also fails to further improve the bound.

We tackle the question of how anisotropy in flows subject to background rotation favours structures elongated along the rotation axis, especially in turbulent flows. A new, wave-free mechanism is identified that challenges the current understanding of the process. Inertial waves propagating near the rotation axis (Staplehurst et al. J. Fluid Mech., vol. 598, 2008, pp. 81–105; Yarom & Sharon, Nat. Phys., vol. 10(7), 2014, pp. 510–514) are generally accepted as the most efficient mechanism to transport energy anisotropically. They have been shown to transfer energy to large anisotropic, columnar structures. Nevertheless, they cannot account for the formation of simpler steady anisotropic phenomena such as Taylor columns. Here, we experimentally show that more than one mechanism involving the Coriolis force may promote anisotropy. In particular, in the limit of fast rotation, that is at low Rossby number, anisotropy favouring the direction of rotation of the average of a turbulent flow arises neither because of inertial waves nor following the same mechanism as in steady Taylor columns, but from an interplay between the Coriolis force and average advection.

We derive the upper limit for power extraction from an open-channel flow with lateral bypass representing tidal power or run-of-river plants for the complete range of blockage $\unicode[STIX]{x1D70E}$, Froude number $Fr_{2}$ and turbine head $H_{T}$. For this, a generic turbine model is used: a momentum and energy sink distributed over the geometric blocking $\unicode[STIX]{x1D70E}$ of the channel allowing lateral bypass. It is indicated that existing models neglect important aspects of the free-surface deformation due to the energy extraction, yielding unphysical behaviour at high blockage, high Froude number or high turbine head. The asymptotic validity of existing theories for $\unicode[STIX]{x1D70E}\rightarrow 0$, $Fr_{2}\rightarrow 0$, $H_{T}\rightarrow 0$ becomes evident: firstly, by comparing existing theories with the presented general theory; and secondly, by the experimental validation of the existing and presented theories. The accompanying systematic experimental study comprises a wide range of blockage ratios, $0.25\leqslant \unicode[STIX]{x1D70E}\leqslant 1.0$, of downstream Froude numbers, $0.2\leqslant Fr_{2}\leqslant 0.5$, and of different turbine heads, $H_{T}$, measured in multiples of the specific energy $E_{0}$ of the undisturbed flow. The subsequent model-based optimisation allows an indication of the optimal turbine head $H_{T,opt}/E_{0}$ as well as the maximal obtainable coefficient of performance $C_{P,opt}$ as a function of $\unicode[STIX]{x1D70E}$ and $Fr_{2}$ or downstream water depth $h_{2}/E_{0}$, respectively. The theory reveals points of operation in which there is a surge wave in the tailwater. The new physical insight and optimisation results may serve for plant design and operation, as well as for investment decisions.

We consider the two-dimensional steady channel flow of a rarefied gas over a backward facing step in the limit of large Knudsen numbers. The free-molecular problem is solved analytically for both diffuse and specular-reflecting channel boundaries, and the solutions are validated through comparison with direct simulation Monte Carlo calculations. Prescribing the density and temperature differences between the inlet and outlet external equilibrium conditions, the results for the density- and temperature-drop-driven flows are analysed and contrasted, revealing higher flow velocities and mass flow rates in the former. While the flow rate is unaffected by the step geometry in the specular case, it increases with the step size in the diffuse-reflecting set-up. At conditions where small flow velocities occur, flow detachment is observed in the form of streamlines connecting the step edge stagnation points. Considering the problem at finite Knudsen numbers, the collisionless-flow regime breaks down at higher Knudsen numbers for lower gas speed flows, followed by the occurrence of step flow separation and recirculation.

We present an experimental investigation of steady particle-driven gravity currents with Reynolds numbers in the range 500–1600, and with the ratio of the initial current speed to the fall speed of the particles, $S=u_{0}/u_{fall}$, in the range $5<S<160$. We identify three regimes: (i) For $S<10$, the particles settle close to the source at a velocity corresponding to their fall speed, consistent with the observation of sedimenting fronts in classical settling column experiments. (ii) In the range $10<S<40$, a steady gravity current develops within the tank. The experiments show that the depth of the gravity current gradually decreases away from the source and dye added to the source liquid appears above the gravity current along its entire length, suggesting that there is a sedimentation front, so that the volume and momentum fluxes of the current gradually decrease with distance from the source. We find that as $S$ increases, the descent speed of the sedimentation front decreases relative to the fall speed of the particles, and the run-out length of the gravity current increases. We note that the density of the interstitial fluid corresponds to the density of the ambient fluid, so that any reduction in buoyancy of the gravity current is attributed to the sedimentation of particles on the floor of the tank and we do not observe lofting of the interstitial fluid. (iii) For $40<S<160$, the gravity currents reach the end of our experimental tank and we no longer observe a sedimentation front. For these experiments, it appears that the entrainment at the top of the current begins to match the sedimentation and so the current depth does not change significantly over the scale of the tank, but a larger scale experimental system would be needed to explore the full run-out behaviour for these larger values of $S$. For the intermediate case, $10<S<40$, we develop a model for the conservation of volume, momentum and buoyancy fluxes in the current, accounting for the sedimentation front and the release of fluid at the top surface of the gravity current, and we compare this with our new experimental data.