A component U of the complement of the Julia set of an entire function ƒ is a wandering domain if the sets ƒn(U) are mutually disjoint, where n ∈ℕ and ƒn is the n-th iterate of ƒ. Examples are given of entire ƒ of order , which have multiply-connected wandering domains. An example is given where the connectivity is infinite.

A continuous ℤ⊗TG action on a subshift of finite type consists of a subshift of finite type with its shift transformation, together with a group, G, of homeomorphisms of the subshift and a group automorphism T, so that the commutation relation σ ° g = Tg ° ∑A is any positive entropy subshift of finite type, G is any finite group and T is any automorphism of G then there is a non-trivial ℤ⊗TG action on ∑A. We then classify all such actions up to ‘almost topological‘ conjugacy.

Charles Conley has shown that for a flow on a compact metric space, a point x is chain recurrent if and only if any attractor which contains the & ω-limit set of x also contains x. In this paper we show that the same statement holds for a continuous map of a compact metric space to itself, and additional equivalent conditions can be given. A stronger result is obtained if the space is locally connected.It follows, as a special case, that if a map of the circle to itself has no periodic points then every point is chain recurrent. Also, for any homeomorphism of the circle to itself, the chain recurrent set is either the set of periodic points or the entire circle. Finally, we use the equivalent conditions mentioned above to show that for any continuous map f of a compact space to itself, if the non-wandering set equals the chain recurrent set then f does not permit Ω-explosions. The converse holds on manifolds.

We classify finite-to-one factor maps between shifts of finite type up to almost topological conjugacy.

Let f be a continuous map from the circle into itself of degree one, having a periodic orbit of rotation number p/q ≠ 0. If (p, q) = 1 then we prove that f has a twist periodic orbit of period q and rotation number p/q (i.e. a periodic orbit which behaves as a rotation of the circle with angle 2πp/q). Also, for this map we give the best lower bound of the topological entropy as a function of the rotation interval if one of the endpoints of the interval is an integer.

Let δ be a closed *-derivation on a commutative C*-algebra , suppose that is dense in for some n = 1, 2, …, ∞, and let be a linear operator satisfying the locality condition

It is shown that , for some finite integer p≤n and functions lm on X. Estimates on the coefficients lm are obtained and applied to flows and local flows.

We study the measure theoretic properties of the complex exponential map E(z) = ez.An particular, we show that the equivalence relation generated by E is recurrent and that E has no quasi-conformal deformations. This enables us to give some information concerning Devaney's semi-conjugacy between E and the shift map on sequences of integers.

A class of vector fields on the 2-torus, which includes Cherry fields, is studied. Natural paths through this class are defined and it is shown that the parameters for which the vector field is unstable is the closure of has irrational rotation number}, where ƒ is a certain map of the circle and Rt is rotation through t. This is shown to be a Cantor set of zero Hausdorff dimension. The Cherry fields are shown to form a family of codimension one submanifolds of the set of vector fields. The natural paths are shown to be stable paths.

Let λ > 1 be a real eigenvalue of an automorphism of the two dimensional torus. We prove that for a dense, open subset of intervals the sequence where {x} denotes the fractional part of x and χ[a, b] the characteristic function of [a, b], satisfies the local limit theorem with respect to Lebesgue measure on [0, 1].

This paper concerns Smale diffeomorphisms of compact oriented surfaces. Relationships are found between the isotopy class of the map and the dynamics of its basic sets. The form of the dynamical properties involves restrictions on periods and reduced zeta functions.

An example is given of an area-preserving monotone twist map such that a uniformly hyperbolic structure exists on the closure of its Birkhoff maximizing orbits.

The paper contains the proof of the fact that every solvable locally compact separable group is the range of a cocycle of an ergodic automorphism. The proof is based on the theory of representations of canonical anticommutation relations and the orbit theory of dynamical systems. The slight generalization of reasoning shows further that this result holds for amenable Lie groups as well and can be also extended to almost connected amenable locally compact separable groups.

In this paper we show that Birkhoff periodic orbits actually exist for arbitrary monotone twist maps satisfying the graph intersection property.

We define a new property of a Borel group action on a Lebesgue measure space, which we call approximate transitivity. Our main results are (i) a type III0 hyperfinite factor is ITPFI if and only if its flow of weights is approximately transitive, and (ii) for ergodic transformations preserving a finite measure, approximate transitivity implies zero entropy.

We give an example of a compact metric space X and a strictly ergodic homeomorphism T of X with invariant probability μ such that for every x ∈ X the set is not generic for μ × μ} is countable.

The unstable-unstable pair bifurcation is a bifurcation in which two unstable fixed points or periodic orbits of the same period coalesce and disappear as a system paremeter is raised. For parameter values just above that at which unstable orbits are destroyed there can be chaotic transients. Then, as the bifurcation is approached from above, the average length of a chaotic transient diverges, and, below the bifurcation point, the chaotic transient may be regarded as having been converted into a chaotic attractor. It is argued that unstable-unstable pair bifurcations should be expected to occur commonly in dynamical systems. This bifurcation is an example of the crisis route to chaos. The most striking fact about unstable-unstable pair bifurcation crises is that long chaotic transients persist even for parameter values relatively far from the bifurcation point. These long-lived chaotic transients may prevent the time asymptotic state from being reached during experiments. An expression giving a lower bound for the average lifetime of a chaotic transient is derived and shown to agree well with numerical experiments. In particular, this bound on the average lifetime, (τ), satisfies

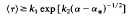
for α near α*, where k1 and k2 are constants and α* is the value of the parameter a at which the crisis occurs. Thus, as a approaches α* from above, (τ) increases more rapidly than any power of (α − α*)−1. Finally, we discuss the effect of adding bounded noise (small random perturbations) on these phenomena and argue that the chaotic transients should be lengthened by noise.

We study which algebraic integers λ ≥ l arise as the growth rate of a mapping class of a surface and give conditions that are necessary and perhaps sufficient. Flow equivalence and twisted Lefschetz zeta functions are used to generate families of λ's. Examples and open problems are included

Periodic points of piecewise monotonic transformations are investigated using an oriented graph, whose closed paths represent the periodic orbits of the transformation. In the first part it is shown that the inverse of the ζ-function is a kind of characteristic polynomial of this graph, which is a power series if the graph is infinite. In the second part, the sets are determined, which can occur as{ with and where T is a monotonic mod one transformation.

We prove that if f: M2→ M2 is pseudo-Anosov and if g ⋍ f then there is a closed subset X ⊂ M2 and a continuous surjection π: X→ M that is homotopic to inclusion such that f ° π = π ° g|X.

Every rational function ƒ with degree has a unique invariant probability ƒƒ that maximizes entropy. It has been conjectured that the system (ƒ, μƒ) is equivalent to the one sided Bernoulli shift . In this paper we prove that there exists m >0 such that (ƒm, ƒƒ) is equivalent to .