Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Robinson, Derek W.
1987.
Smooth derivations on abelian C*-dynamical systems.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 42,
Issue. 2,
p.
247.


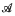 , suppose that
, suppose that 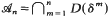 is dense in
is dense in 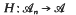 be a linear operator satisfying the locality condition
be a linear operator satisfying the locality condition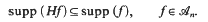
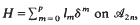 , for some finite integer
, for some finite integer 