Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:37:42.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of the family of Cherry fields on the torus

Published online by Cambridge University Press:  19 September 2008

Colin Boyd
Colin Boyd
Affiliation:
SES 5.2.2, MLB 5/56, B.T.R.L., Martlesham Heath, Ipswich 1P5 7RE, England
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

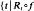A class of vector fields on the 2-torus, which includes Cherry fields, is studied. Natural paths through this class are defined and it is shown that the parameters for which the vector field is unstable is the closure of has irrational rotation number}, where ƒ is a certain map of the circle and Rt is rotation through t. This is shown to be a Cantor set of zero Hausdorff dimension. The Cherry fields are shown to form a family of codimension one submanifolds of the set of vector fields. The natural paths are shown to be stable paths.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 5 , Issue 1 , March 1985 , pp. 27 - 46
Copyright
Copyright © Cambridge University Press 1985

References

REFERENCES

[1]Arnold, V. I.. Small denominators, I. Mappings of the circumference onto itself. AMS Translations, Series 2, 46, 213–284.CrossRefGoogle Scholar
[2]Besicovitch, A. S. & Taylor, S. J.. On the complementary intervals of a linear closed set of zero Lebesgue measure. J. London Math. Soc. 29 (1954), 449–459.CrossRefGoogle Scholar
[3]Cherry, T. M.. Analytic quasi-periodic curves of discontinuous type on a torus. Proc. London Math. Soc. 44 (1938), 175–215.CrossRefGoogle Scholar
[4]Dieudonné, J.. Foundations of Modern Analysis. Academic Press, 1969.Google Scholar
[5]Herman, M.. Mesure de Lebesgue et nombre de rotation. In: Geometry and Topology Rio de Janeiro 1976. Lecture Notes in Mathematics vol. 597, Springer-Verlag, 1977.Google Scholar
[6]Hirsch, M. W., Pugh, C. C. & Shub, M.. Invariant Manifolds. Lecture Notes in Mathematics vol. 583. Springer-Verlag, 1977.CrossRefGoogle Scholar
[7]Hurewicz, W. & Wallman, H.. Dimension Theory. Princeton, 1941.Google Scholar
[8]Palis, J. Jr. & de Melo, W.. Geometric Theory of Dynamical Systems. Springer-Verlag, 1982.CrossRefGoogle Scholar
[9]Sell, G. R.. Smooth linearization near a fixed point. Preprint, Minnesota, 1983.Google Scholar
[10]Sotomayor, J.. Generic one parameter families of vector fields on two-dimensional manifolds. Pub. Math. Inst. Hautes Études Scientifiques, 43 (1973), 6–46.Google Scholar
[11]van Strien, S. J.. One parameter families of vector fields. Thesis, Utrecht, 1982.Google Scholar
[12]Taylor, S. J.. Introduction to Measure and Integration. Cambridge University Press, 1966.Google Scholar