Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hofbauer, Franz
1986.
Piecewise invertible dynamical systems.
Probability Theory and Related Fields,
Vol. 72,
Issue. 3,
p.
359.
Misiurewicz, Michał
1986.
Rotation intervals for a class of maps of the real line into itself.
Ergodic Theory and Dynamical Systems,
Vol. 6,
Issue. 1,
p.
117.
Dufour, Jean-Paul
1989.
Existence de cycles pour des multi-applications du cercle.
Ergodic Theory and Dynamical Systems,
Vol. 9,
Issue. 1,
p.
47.
Baladi, V.
and
Keller, G.
1990.
Zeta functions and transfer operators for piecewise monotone transformations.
Communications in Mathematical Physics,
Vol. 127,
Issue. 3,
p.
459.
Keller, Gerhard
and
Nowicki, Tomasz
1992.
Spectral theory, zeta functions and the distribution of periodic points for Collet-Eckmann maps.
Communications in Mathematical Physics,
Vol. 149,
Issue. 1,
p.
31.
Esquembre, Francisco
1993.
Twist orbits for non continuous maps of degree one.
Bulletin of the Australian Mathematical Society,
Vol. 47,
Issue. 3,
p.
415.
Buzzi, Jérôme
2009.
Encyclopedia of Complexity and Systems Science.
p.
953.
Buzzi, Jérôme
2009.
Ergodic Theory.
p.
633.
BUZZI, JÉRÔME
2009.
Maximal entropy measures for piecewise affine surface homeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 6,
p.
1723.
Buzzi, Jérôme
2009.
New Trends in Mathematical Physics.
p.
95.
Buzzi, Jérôme
2012.
Mathematics of Complexity and Dynamical Systems.
p.
63.
E. Rubin, Jonathan
Signerska-Rynkowska, Justyna
D. Touboul, Jonathan
and
Vidal, Alexandre
2017.
Wild oscillations in a nonlinear neuron model with resets: (Ⅱ) Mixed-mode oscillations.
Discrete & Continuous Dynamical Systems - B,
Vol. 22,
Issue. 10,
p.
4003.
BANDTLOW, OSCAR F.
and
RUGH, HANS HENRIK
2018.
Entropy continuity for interval maps with holes.
Ergodic Theory and Dynamical Systems,
Vol. 38,
Issue. 6,
p.
2036.
Anušić, Ana
Bruin, Henk
and
Činč, Jernej
2020.
Topological properties of Lorenz maps derived from unimodal maps.
Journal of Difference Equations and Applications,
Vol. 26,
Issue. 8,
p.
1174.
Efremova, L. S.
and
Makhrova, E. N.
2021.
One-dimensional dynamical systems.
Russian Mathematical Surveys,
Vol. 76,
Issue. 5,
p.
821.
Efremova, Lyudmila Sergeevna
and
Makhrova, Elena Nikolaevna
2021.
Одномерные динамические системы.
Успехи математических наук,
Vol. 76,
Issue. 5(461),
p.
81.
Efremova, L. S.
2021.
Geometrically Integrable Maps in the Plane and Their Periodic Orbits.
Lobachevskii Journal of Mathematics,
Vol. 42,
Issue. 10,
p.
2315.
Tesarčík, Jan
and
Pravec, Vojtěch
2023.
On distributional spectrum of piecewise monotonic maps.
Aequationes mathematicae,
Vol. 97,
Issue. 1,
p.
133.
Cholewa, Łukasz
and
Oprocha, Piotr
2024.
Renormalization in Lorenz maps - completely invariant sets and periodic orbits.
Advances in Mathematics,
Vol. 456,
Issue. ,
p.
109890.
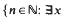 with
with 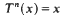 and
and 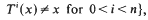 where T is a monotonic mod one transformation.
where T is a monotonic mod one transformation.