Several papers have, as their raison d’être, the exploration of the generalised Lau product associated to a homomorphism 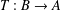 $T:B\rightarrow A$ of Banach algebras. In this short note, we demonstrate that the generalised Lau product is isomorphic as a Banach algebra to the usual direct product
$T:B\rightarrow A$ of Banach algebras. In this short note, we demonstrate that the generalised Lau product is isomorphic as a Banach algebra to the usual direct product 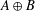 $A\oplus B$. We also correct some misleading claims made about the relationship between this generalised Lau product and an older construction of Monfared [‘On certain products of Banach algebras with applications to harmonic analysis’, Studia Math. 178(3) (2007), 277–294].
$A\oplus B$. We also correct some misleading claims made about the relationship between this generalised Lau product and an older construction of Monfared [‘On certain products of Banach algebras with applications to harmonic analysis’, Studia Math. 178(3) (2007), 277–294].
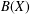 $B(X)$
$B(X)$