Article contents
COMPACTNESS OF SPACES OF CONVEX AND SIMPLE QUADRILATERALS
Published online by Cambridge University Press: 09 September 2016
Abstract
The space of shapes of quadrilaterals can be identified with 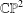 $\mathbb{CP}^{2}$. We deal with the subset of
$\mathbb{CP}^{2}$. We deal with the subset of 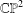 $\mathbb{CP}^{2}$ corresponding to convex quadrilaterals and the subset which corresponds to simple (that is, without self-intersections) quadrilaterals. We provide a complete description of the topological closures in
$\mathbb{CP}^{2}$ corresponding to convex quadrilaterals and the subset which corresponds to simple (that is, without self-intersections) quadrilaterals. We provide a complete description of the topological closures in 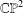 $\mathbb{CP}^{2}$ of both spaces. Although the interior of each space is homeomorphic to a disjoint union
$\mathbb{CP}^{2}$ of both spaces. Although the interior of each space is homeomorphic to a disjoint union 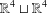 $\mathbb{R}^{4}\sqcup \mathbb{R}^{4}$, their closures are topologically different. In particular, the boundary of the space corresponding to convex quadrilaterals is homeomorphic to a pair of three-dimensional spheres glued along a Möbius strip while the boundary of the space corresponding to simple quadrilaterals is more complicated.
$\mathbb{R}^{4}\sqcup \mathbb{R}^{4}$, their closures are topologically different. In particular, the boundary of the space corresponding to convex quadrilaterals is homeomorphic to a pair of three-dimensional spheres glued along a Möbius strip while the boundary of the space corresponding to simple quadrilaterals is more complicated.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 507 - 521
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by


