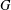Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maslei, Aleksandr Viktorovich
2017.
О числах Геринга-Мартина-Тана и числах Тана элементарных подгрупп $\operatorname{PSL}(2,\mathbb{C})$.
Математические заметки,
Vol. 102,
Issue. 2,
p.
255.
Maslei, A. V.
2017.
Gehring–Martin–Tan numbers and Tan numbers of elementary subgroups of PSL(2,ℂ).
Mathematical Notes,
Vol. 102,
Issue. 1-2,
p.
219.