Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T12:05:53.606Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST NONNEGATIVE CURVATURE ON SOME FAKE 6- AND 14-DIMENSIONAL PROJECTIVE SPACES

Part of: Global differential geometry

Published online by Cambridge University Press:  27 July 2016

PRIYANKA RAJAN  and
FREDERICK WILHELM
PRIYANKA RAJAN
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA email [email protected]
FREDERICK WILHELM*
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We apply the lifting theorem of Searle and the second author to put metrics of almost nonnegative curvature on the fake 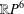$\mathbb{R}P^{6}$s of Hirsch and Milnor and on the analogous fake 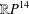$\mathbb{R}P^{14}$s.

Keywords

liftingalmost nonnegative curvaturefake ℝPn

MSC classification

Primary: 53C20: Global Riemannian geometry, including pinching
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 304 - 315
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Abresch, U., Durán, C., Püttmann, T. and Rigas, A., ‘Wiedersehen metrics and exotic involutions of Euclidean spheres’, J. reine angew. Math. 605 (2007), 1–21.Google Scholar
Baez, J., ‘The octonions’, Bull. Amer. Math. Soc. 39 (2002), 145–205.CrossRefGoogle Scholar
Brumfiel, G., ‘On the homotopy groups of BPL and PL/O’, Ann. of Math. (2) 88 (1968), 291–311.Google Scholar
Burago, Y., Gromov, M. and Perelman, G., ‘A. D. Alexandrov spaces with curvatures bounded from below’, I, Uspekhi Mat. Nauk 47 (1992), 3–51.Google Scholar
Davis, M., ‘Some group actions on homotopy spheres of dimensions seven and fifteen’, Amer. J. Math. 104 (1982), 59–90.Google Scholar
Eells, J. and Kuiper, N. H., ‘An invariant for certain smooth manifolds’, Ann. Mat. Pura Appl. 60 (1962), 93–110.Google Scholar
Gromoll, D. and Meyer, W., ‘An exotic sphere with nonnegative sectional curvature’, Ann. of Math. (2) 100 (1974), 401–406.Google Scholar
Grove, K., Verdiani, L., Wilking, B. and Ziller, W., ‘Non-negative curvature obstructions in cohomogeneity one and the Kervaire spheres’, Ann. Sc. Norm. Super. Pisa Cl. Sci. 5(2) (2006), 159–170.Google Scholar
Grove, K. and Ziller, W., ‘Curvature and symmetry of milnor spheres’, Ann. of Math. (2) 152 (2000), 331–367.Google Scholar
He, C., ‘New examples of obstructions to non-negative sectional curvatures in cohomogeneity one manifolds’, Trans. Amer. Math. Soc. 366 (2014), 6093–6118.CrossRefGoogle Scholar
Hirsch, M. and Milnor, J., ‘Some curious involutions of spheres’, Bull. Amer. Math. Soc. 70(3) (1964), 372–377.Google Scholar
Kervaire, M. and Milnor, J., ‘Groups of homotopy spheres I’, Ann. of Math. (2) 77 (1963), 504–537.Google Scholar
Milnor, J., ‘On manifolds homeomorphic to the 7-sphere’, Ann. of Math. (2) 64 (1956), 399–405.Google Scholar
Schwachhöfer, L. and Tuschmann, W., ‘Metrics of positive Ricci curvature on quotient spaces’, Math. Ann. 330(1) (2004), 59–91.Google Scholar
Schwachhöfer, L. and Tuschmann, W., Almost nonnegative curvature and cohomogeneity one’, Preprint no. 62, Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig, http://www.mis.mpg.de/cgi-bin/preprints.pl.Google Scholar
Searle, C. and Wilhelm, F., ‘How to lift positive Ricci curvature’, Geom. Topol. 19 (2015), 1409–1475.Google Scholar
Shimada, N., ‘Differentiable structures on the 15-sphere and Pontriagin classes of certain manifolds’, Nagoya Math. J. 12 (1957), 37–69.Google Scholar
Wall, C., ‘Classification of (n - 1)-connected 2n-manifolds’, Ann. of Math. (2) 75 (1962), 163–189.Google Scholar
Wilhelm, F., ‘Exotic spheres with lots of positive curvatures’, J. Geom. Anal. 11(1) (2001), 161–186.Google Scholar