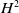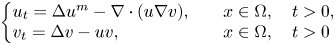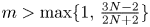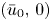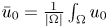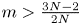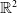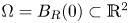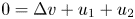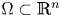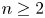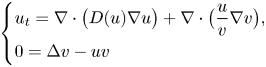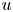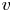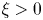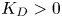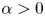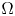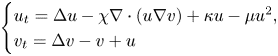47 results
18 - Chemotaxis and Detection
- from Part II - Single Bacteria
-
- Book:
- The Physics of Bacteria
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 190-202
-
- Chapter
- Export citation
3 - Molecular Communication in Biological Systems
-
- Book:
- Molecular Communication
- Published online:
- 12 December 2024
- Print publication:
- 19 December 2024, pp 37-51
-
- Chapter
- Export citation
Dynamical behaviour of a logarithmically sensitive chemotaxis model under time-dependent boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stabilization in a chemotaxis system modelling T-cell dynamics with simultaneous production and consumption of signals
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 April 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
The fully parabolic multi-species chemotaxis system in
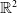 $\mathbb{R}^{2}$
$\mathbb{R}^{2}$
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 January 2024, pp. 675-706
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the global existence of solutions to chemotaxis system for two populations in dimension two
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 2106-2128
- Print publication:
- December 2023
-
- Article
- Export citation
Finite-time blow-up in a repulsive chemotaxis-consumption system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1150-1166
- Print publication:
- August 2023
-
- Article
- Export citation
Stationary solutions to the Keller–Segel equation on curved planes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 327-343
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chemotactic and temperature-dependent responses of the Strongyloidoidea superfamily of nematodes
-
- Journal:
- Parasitology / Volume 149 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 05 October 2021, pp. 116-123
-
- Article
- Export citation
Natural variation in host-finding behaviour of gastropod parasitic nematodes (Phasmarhabditis spp.) exposed to host-associated cues
-
- Journal:
- Journal of Helminthology / Volume 95 / 2021
- Published online by Cambridge University Press:
- 24 February 2021, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a repulsion Keller–Segel system with a logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 153-181
-
- Article
- Export citation
Immediate smoothing and global solutions for initial data in L1 × W1,2 in a Keller–Segel system with logistic terms in 2D
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 1204-1224
- Print publication:
- August 2021
-
- Article
- Export citation
Does indirectness of signal production reduce the explosion-supporting potential in chemotaxis–haptotaxis systems? Global classical solvability in a class of models for cancer invasion (and more)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 618-651
-
- Article
- Export citation
7 - SSAs for Reaction–Diffusion–Advection Processes
-
- Book:
- Stochastic Modelling of Reaction–Diffusion Processes
- Published online:
- 04 November 2019
- Print publication:
- 30 January 2020, pp 192-225
-
- Chapter
- Export citation
The role of carbon dioxide in nematode behaviour and physiology
-
- Journal:
- Parasitology / Volume 147 / Issue 8 / July 2020
- Published online by Cambridge University Press:
- 11 October 2019, pp. 841-854
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gastropod parasitic nematodes (Phasmarhabditis sp.) are attracted to hyaluronic acid in snail mucus by cGMP signalling
-
- Journal:
- Journal of Helminthology / Volume 94 / 2020
- Published online by Cambridge University Press:
- 15 November 2018, e9
-
- Article
- Export citation
Sharp decay estimates in a bioconvection model with quadratic degradation in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 939-955
- Print publication:
- October 2018
-
- Article
- Export citation
Thermodynamically consistent Navier–Stokes–Cahn–Hilliard models with mass transfer and chemotaxis
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 595-644
-
- Article
- Export citation