Let $\sigma \in (0,\,2)$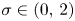 , $\chi ^{(\sigma )}(y):={\mathbf 1}_{\sigma \in (1,2)}+{\mathbf 1}_{\sigma =1} {\mathbf 1}_{y\in B(\mathbf {0},\,1)}$
, $\chi ^{(\sigma )}(y):={\mathbf 1}_{\sigma \in (1,2)}+{\mathbf 1}_{\sigma =1} {\mathbf 1}_{y\in B(\mathbf {0},\,1)}$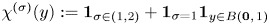 , where $\mathbf {0}$
, where $\mathbf {0}$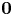 denotes the origin of $\mathbb {R}^n$
denotes the origin of $\mathbb {R}^n$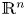 , and $a$
, and $a$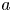 be a non-negative and bounded measurable function on $\mathbb {R}^n$
be a non-negative and bounded measurable function on $\mathbb {R}^n$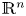 . In this paper, we obtain the boundedness of the non-local elliptic operator
. In this paper, we obtain the boundedness of the non-local elliptic operator\[ Lu(x):=\int_{\mathbb{R}^n}\left[u(x+y)-u(x)-\chi^{(\sigma)}(y)y\cdot\nabla u(x)\right]a(y)\,\frac{{\rm d}y}{|y|^{n+\sigma}} \]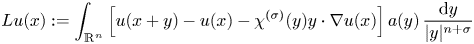
from the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$ to the space $\mathrm {BMO}(\mathbb {R}^n)$
to the space $\mathrm {BMO}(\mathbb {R}^n)$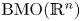 , and from the Sobolev space based on the Hardy space $H^1(\mathbb {R}^n)$
, and from the Sobolev space based on the Hardy space $H^1(\mathbb {R}^n)$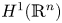 to $H^1(\mathbb {R}^n)$
to $H^1(\mathbb {R}^n)$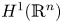 . Moreover, for any $\lambda \in (0,\,\infty )$
. Moreover, for any $\lambda \in (0,\,\infty )$ , we also obtain the unique solvability of the non-local elliptic equation $Lu-\lambda u=f$
, we also obtain the unique solvability of the non-local elliptic equation $Lu-\lambda u=f$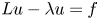 in $\mathbb {R}^n$
in $\mathbb {R}^n$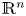 , with $f\in \mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$
, with $f\in \mathrm {BMO}(\mathbb {R}^n)\cap (\bigcup _{p\in (1,\infty )}L^p(\mathbb {R}^n))$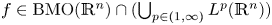 or $H^1(\mathbb {R}^n)$
or $H^1(\mathbb {R}^n)$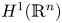 , in the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)$
, in the Sobolev space based on $\mathrm {BMO}(\mathbb {R}^n)$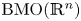 or $H^1(\mathbb {R}^n)$
or $H^1(\mathbb {R}^n)$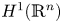 . The boundedness and unique solvability results given in this paper are further devolvement for the corresponding results in the scale of the Lebesgue space $L^p(\mathbb {R}^n)$
. The boundedness and unique solvability results given in this paper are further devolvement for the corresponding results in the scale of the Lebesgue space $L^p(\mathbb {R}^n)$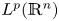 with $p\in (1,\,\infty )$
with $p\in (1,\,\infty )$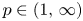 , established by H. Dong and D. Kim [J. Funct. Anal. 262 (2012), 1166–1199], in the endpoint cases of $p=1$
, established by H. Dong and D. Kim [J. Funct. Anal. 262 (2012), 1166–1199], in the endpoint cases of $p=1$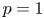 and $p=\infty$
and $p=\infty$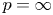 .
.
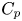 estimates via $M^{\sharp }$
estimates via $M^{\sharp }$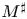 function
function