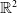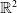1. Introduction
The well-known classical parabolic–parabolic Keller–Segel model reads as [Reference Keller and Segel24]
 \begin{equation} \begin{cases} \partial _t u=\Delta u-\alpha \nabla \cdot (u\nabla v), &\quad x\in \mathbb{R}^2,\quad t\gt 0,\\[5pt] \tau \partial _t v=\Delta v-\beta v+\gamma u, &\quad x\in \mathbb{R}^2,\quad t\gt 0,\\[5pt] \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial _t u=\Delta u-\alpha \nabla \cdot (u\nabla v), &\quad x\in \mathbb{R}^2,\quad t\gt 0,\\[5pt] \tau \partial _t v=\Delta v-\beta v+\gamma u, &\quad x\in \mathbb{R}^2,\quad t\gt 0,\\[5pt] \end{cases} \end{equation}
where
![]() $u=u(x,t)$
and
$u=u(x,t)$
and
![]() $v=v(x,t)$
denote the cell density and the concentration of the chemical substance, respectively.
$v=v(x,t)$
denote the cell density and the concentration of the chemical substance, respectively.
![]() $\alpha$
and
$\alpha$
and
![]() $\gamma$
are positive constants. The constants
$\gamma$
are positive constants. The constants
![]() $\tau$
and
$\tau$
and
![]() $\beta$
are non-negative. The system (1.1) can be regarded as one of the simplest models to describe the overall behaviour of cells under the influence of chemotaxis, that is the motion of cells partially orient their movement towards higher concentration of a certain chemical substance produced by cells themselves. A striking feature of the Keller–Segel system is that the behaviour of solutions is determined by the total mass of cells which remains constant over time, see [Reference Calvez and Corrias5, Reference Herrero and Velázquez16, Reference Mizoguchi31, Reference Nagai and Ogawa34] for instance. Namely, given a non-negative and suitable smooth initial data
$\beta$
are non-negative. The system (1.1) can be regarded as one of the simplest models to describe the overall behaviour of cells under the influence of chemotaxis, that is the motion of cells partially orient their movement towards higher concentration of a certain chemical substance produced by cells themselves. A striking feature of the Keller–Segel system is that the behaviour of solutions is determined by the total mass of cells which remains constant over time, see [Reference Calvez and Corrias5, Reference Herrero and Velázquez16, Reference Mizoguchi31, Reference Nagai and Ogawa34] for instance. Namely, given a non-negative and suitable smooth initial data
![]() $u_0$
, any solution with
$u_0$
, any solution with
![]() $m=\|u_0\|_{L^1(\mathbb{R}^2)}\lt 8\pi/(\alpha \gamma )$
exists globally, while blow-up solution appears if
$m=\|u_0\|_{L^1(\mathbb{R}^2)}\lt 8\pi/(\alpha \gamma )$
exists globally, while blow-up solution appears if
![]() $m\gt 8\pi/(\alpha \gamma )$
. Note that the main idea to prove the global existence is based on the following free energy functional,
$m\gt 8\pi/(\alpha \gamma )$
. Note that the main idea to prove the global existence is based on the following free energy functional,
which is a monotonic non-increasing function with respect to time variable. In view of this fact, Calvez and Corrias use a minimisation principle for entropy functionals and Onofri’s inequality to derive a priori estimates under the sub-critical mass
![]() $m\lt 8\pi/(\alpha \gamma )$
, where the assumptions
$m\lt 8\pi/(\alpha \gamma )$
, where the assumptions
![]() $u_0\log\! \big(1+|x|^2\big)\in L^1(\mathbb{R}^2)$
and
$u_0\log\! \big(1+|x|^2\big)\in L^1(\mathbb{R}^2)$
and
![]() $u_0\log u_0\in L^1(\mathbb{R}^2)$
are necessary [Reference Calvez and Corrias5], while these extra assumptions have been removed by applying a modified free energy functional with the Moser–Trudinger inequality in unbounded domain [Reference Mizoguchi31].
$u_0\log u_0\in L^1(\mathbb{R}^2)$
are necessary [Reference Calvez and Corrias5], while these extra assumptions have been removed by applying a modified free energy functional with the Moser–Trudinger inequality in unbounded domain [Reference Mizoguchi31].
For the parabolic–elliptic Keller–Segel system (i.e. taking
![]() $\tau =0$
in (1.1)2)
$\tau =0$
in (1.1)2)
the above two-dimensional mass threshold phenomenon also exists. See [Reference Blanchet, Dolbeault and Perthame4, Reference Diaz, Nagai and Rakotoson8, Reference Nagai33] for the global well-posedness results and [Reference Biler and Nadzieja3, Reference Blanchet, Dolbeault and Perthame4] for the blow-up arguments. The main feature to prove the global existence of solutions in this simplified chemotaxis system over (1.1) is that
![]() $v$
could be expressed by the fundamental solution of the elliptic equation, then it leads to a single parabolic problem for
$v$
could be expressed by the fundamental solution of the elliptic equation, then it leads to a single parabolic problem for
![]() $u$
. For example, if
$u$
. For example, if
![]() $\beta =0$
, an explicit expression for
$\beta =0$
, an explicit expression for
![]() $v$
takes form like
$v$
takes form like
![]() $v=\gamma K\ast u$
, so (1.1)
$v=\gamma K\ast u$
, so (1.1)
![]() $_1$
becomes
$_1$
becomes
where
![]() $K=-(1/2\pi )\log |\cdot |$
. A direct application of the logarithmic Hardy–Littlewood–Sobolev inequality (see [Reference Beckner2]) on the corresponding free energy yields the global existence of solutions if
$K=-(1/2\pi )\log |\cdot |$
. A direct application of the logarithmic Hardy–Littlewood–Sobolev inequality (see [Reference Beckner2]) on the corresponding free energy yields the global existence of solutions if
![]() $m\lt 8\pi/(\alpha \gamma )$
[Reference Blanchet, Dolbeault and Perthame4].
$m\lt 8\pi/(\alpha \gamma )$
[Reference Blanchet, Dolbeault and Perthame4].
Compared with the one-population chemotaxis system (1.1), an interesting and complex question is to derive sharp conditions to recognise global existence and blow-up of solutions for the following multi-species chemotaxis model in
![]() $\mathbb{R}^2$
,
$\mathbb{R}^2$
,
 \begin{equation} \begin{cases} \begin{split} \partial _t u_i=&\Delta u_i-\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), &i\in \mathcal{I}=\{1,\cdots,n\}, \\ \tau _j\partial _t v_j=&\Delta v_j-\beta _jv_j+\sum \limits ^n_{i=1}\gamma _{i,j}u_i, &j\in \mathcal{J}=\{1,\cdots,m\}, \end{split} \end{cases} \end{equation}
\begin{equation} \begin{cases} \begin{split} \partial _t u_i=&\Delta u_i-\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), &i\in \mathcal{I}=\{1,\cdots,n\}, \\ \tau _j\partial _t v_j=&\Delta v_j-\beta _jv_j+\sum \limits ^n_{i=1}\gamma _{i,j}u_i, &j\in \mathcal{J}=\{1,\cdots,m\}, \end{split} \end{cases} \end{equation}
where
![]() $\tau _j\geq 0$
,
$\tau _j\geq 0$
,
![]() $j\in \mathcal{J}$
. This model was first proposed by Wolansky in [Reference Wolansky42] to describe the chemotactic movement of
$j\in \mathcal{J}$
. This model was first proposed by Wolansky in [Reference Wolansky42] to describe the chemotactic movement of
![]() $n$
populations with respect to
$n$
populations with respect to
![]() $m$
chemical substances. Here,
$m$
chemical substances. Here,
![]() $u_i=u_i(x,t)$
denotes the density of
$u_i=u_i(x,t)$
denotes the density of
![]() $i$
-th population, and
$i$
-th population, and
![]() $v_j=v_j(x,t)$
represents the concentration of
$v_j=v_j(x,t)$
represents the concentration of
![]() $j$
-th chemical signal. The total number of species
$j$
-th chemical signal. The total number of species
![]() $|\mathcal I|=n\geq 1$
is assumed to be finite.
$|\mathcal I|=n\geq 1$
is assumed to be finite.
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
and
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
and
![]() $\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
define a pair of
$\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
define a pair of
![]() $n\times m$
matrices for the sensitivity parameter and the production/consumption rate, respectively.
$n\times m$
matrices for the sensitivity parameter and the production/consumption rate, respectively.
![]() $\beta _j\in \mathbb{R}$
,
$\beta _j\in \mathbb{R}$
,
![]() $j\in \mathcal{J}$
, presents the growth/degradation rate for chemical substance. We introduce
$j\in \mathcal{J}$
, presents the growth/degradation rate for chemical substance. We introduce
![]() $\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
$\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
![]() $\beta _{j,l}=\beta _j\delta _{j,l}$
as a
$\beta _{j,l}=\beta _j\delta _{j,l}$
as a
![]() $m\times m$
diagonal matrix for convenience, where
$m\times m$
diagonal matrix for convenience, where
![]() $\delta _{j,l}$
satisfies
$\delta _{j,l}$
satisfies
 \begin{align*} \delta _{j,l}=\begin{cases} 1,&\text{if}\quad j=l,\\[5pt] 0,&\text{if}\quad j\neq l. \end{cases} \end{align*}
\begin{align*} \delta _{j,l}=\begin{cases} 1,&\text{if}\quad j=l,\\[5pt] 0,&\text{if}\quad j\neq l. \end{cases} \end{align*}
It is very important to understand the multi-species chemotaxis in biology, and this phenomenon has been observed in numerous experiments. We take the following two examples. First one is that a system with two different species, reacting on one common chemical, appears in the cell sorting process during the early aggregation state of mound formation [Reference Weijer40]. And a two-species chemotaxis system with two chemicals has been proposed in [Reference Knútsdóttir, Pálsson and Edelstein-Keshet25] to imitate the breast cancer metastatic process. The readers could see [Reference Horstmann20, Reference Horstmann and Lucia21] for other biological motivations.
Just recently, some authors have started to look more closely at the parabolic–elliptic case of (1.2) (i.e.
![]() $\tau _j=0$
) for
$\tau _j=0$
) for
![]() $n$
-populations interacting via a self-produced chemical agent. Consider (1.2) with
$n$
-populations interacting via a self-produced chemical agent. Consider (1.2) with
![]() $|\mathcal{I}|=|\mathcal{J}|=n$
is subject to symmetric sensitivity coefficients matrix
$|\mathcal{I}|=|\mathcal{J}|=n$
is subject to symmetric sensitivity coefficients matrix
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times n}$
with non-negative entries, zero matrix
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times n}$
with non-negative entries, zero matrix
![]() $\boldsymbol{\beta }$
and unit matrix
$\boldsymbol{\beta }$
and unit matrix
![]() $\boldsymbol{\gamma }$
, that is,
$\boldsymbol{\gamma }$
, that is,
 \begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^n_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), \\[9pt] -\Delta v_j=u_j, \quad i,j \in \mathcal{I}=\{1,\cdots,n\}. \\[5pt] \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^n_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), \\[9pt] -\Delta v_j=u_j, \quad i,j \in \mathcal{I}=\{1,\cdots,n\}. \\[5pt] \end{cases} \end{equation}
Karmakar and Wolansky [Reference Karmakar and Wolansky22] had derived the global well-posedness of weak solutions with respect to time in the sub-critical regime
where
![]() $m_i=\|u_0\|_{L^1(\mathbb{R}^2)}$
. Furthermore, the borderline case of critical mass
$m_i=\|u_0\|_{L^1(\mathbb{R}^2)}$
. Furthermore, the borderline case of critical mass
![]() $\Lambda _{\mathcal{I}}(\boldsymbol{{m}})=0$
, and
$\Lambda _{\mathcal{I}}(\boldsymbol{{m}})=0$
, and
![]() $\Lambda _{\mathcal{K}}(\boldsymbol{{m}})\gt 0$
,
$\Lambda _{\mathcal{K}}(\boldsymbol{{m}})\gt 0$
,
![]() $\forall \,\emptyset \neq \mathcal{K} \subsetneq \mathcal{I}$
, has been considered in [Reference Karmakar and Wolansky23]. It shows that a free energy solution exists globally in time. According to analogous results about (1.1) mentioned above, it is expected that if the condition
$\forall \,\emptyset \neq \mathcal{K} \subsetneq \mathcal{I}$
, has been considered in [Reference Karmakar and Wolansky23]. It shows that a free energy solution exists globally in time. According to analogous results about (1.1) mentioned above, it is expected that if the condition
![]() $\Lambda _{\mathcal{K}}(\boldsymbol{{m}})\geq 0$
for some
$\Lambda _{\mathcal{K}}(\boldsymbol{{m}})\geq 0$
for some
![]() $\emptyset \neq \mathcal{K} \subset \mathcal{I}$
is violated, a finite-time blow-up solution appears. Using the second-moment techniques in [Reference He and Tadmor15], some solutions of (1.3) blow-up in finite time provided
$\emptyset \neq \mathcal{K} \subset \mathcal{I}$
is violated, a finite-time blow-up solution appears. Using the second-moment techniques in [Reference He and Tadmor15], some solutions of (1.3) blow-up in finite time provided
![]() $\Lambda _{\mathcal{I}}(\boldsymbol{{m}})\lt 0$
. While the basic strategy to prove global existence is the logarithmic Hardy–Littlewood–Sobolev inequality for system, see [Reference Shafrir and Wolansky38] for details. In particular, in the case of parabolic–elliptic system (1.2) with
$\Lambda _{\mathcal{I}}(\boldsymbol{{m}})\lt 0$
. While the basic strategy to prove global existence is the logarithmic Hardy–Littlewood–Sobolev inequality for system, see [Reference Shafrir and Wolansky38] for details. In particular, in the case of parabolic–elliptic system (1.2) with
![]() $|\mathcal{I}|=2$
,
$|\mathcal{I}|=2$
,
![]() $|\mathcal{J}|=1$
, Espejo et al. [Reference Conca, Espejo and Vilches7, Reference Espejo, Vilches and Conca12] discovered a threshold curve to help us to determine whether the solutions of system are blow-up or global in time. See related works for parabolic–elliptic system (1.2) with
$|\mathcal{J}|=1$
, Espejo et al. [Reference Conca, Espejo and Vilches7, Reference Espejo, Vilches and Conca12] discovered a threshold curve to help us to determine whether the solutions of system are blow-up or global in time. See related works for parabolic–elliptic system (1.2) with
![]() $|\mathcal{I}|=|\mathcal{J}|=2$
in [Reference Hong, Wang and Wang18, Reference Hong, Wang, Yu and Zhang19]. Moreover, [Reference Espejo, Stevens and Suzuki9–
Reference Espejo, Stevens and Velázquez11, Reference Espejo, Vilches and Conca13] could be refereed to characterise the simultaneous or non-simultaneous blow-up results in two-species model.
$|\mathcal{I}|=|\mathcal{J}|=2$
in [Reference Hong, Wang and Wang18, Reference Hong, Wang, Yu and Zhang19]. Moreover, [Reference Espejo, Stevens and Suzuki9–
Reference Espejo, Stevens and Velázquez11, Reference Espejo, Vilches and Conca13] could be refereed to characterise the simultaneous or non-simultaneous blow-up results in two-species model.
However, it should be noted that fewer papers have been considered on Cauchy problem of the fully parabolic multi-species (i.e.
![]() $\tau _j\gt 0$
in (1.2)) than the parabolic–elliptic case. For a two-dimensional bounded domain, the author and coauthors have researched the initial boundary problems of (1.2), and we have tried to find optimal conditions on the global existence or blow-up in [Reference Lin27–Reference Lin and Zhong30]. In this article, under a conflict-free situation given by Definition 1
$\tau _j\gt 0$
in (1.2)) than the parabolic–elliptic case. For a two-dimensional bounded domain, the author and coauthors have researched the initial boundary problems of (1.2), and we have tried to find optimal conditions on the global existence or blow-up in [Reference Lin27–Reference Lin and Zhong30]. In this article, under a conflict-free situation given by Definition 1
![]() $(ii)$
, a sufficient (or possibly optimal) condition on the global solvability of the Cauchy problem for parabolic–parabolic system (1.2) with arbitrary
$(ii)$
, a sufficient (or possibly optimal) condition on the global solvability of the Cauchy problem for parabolic–parabolic system (1.2) with arbitrary
![]() $|\mathcal{I}|=n\geq 1$
and
$|\mathcal{I}|=n\geq 1$
and
![]() $|\mathcal{J}|=m\geq 1$
has been obtained. For simplicity, we assume
$|\mathcal{J}|=m\geq 1$
has been obtained. For simplicity, we assume
![]() $\tau _j=1$
for all
$\tau _j=1$
for all
![]() $j\in \mathcal{J}$
in (1.2) and consider
$j\in \mathcal{J}$
in (1.2) and consider
 \begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), &i\in \mathcal{I}, \\[5pt] \partial _t v_j=\Delta v_j-\beta _jv_j+\sum \limits ^n_{i=1}\gamma _{i,j}u_i, &j\in \mathcal{J}, \\[5pt] u_{i0}(x)=u_i(x,0), v_{j0}(x)=v_j(x,0),&i\in \mathcal{I},\quad j\in \mathcal{J}, \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), &i\in \mathcal{I}, \\[5pt] \partial _t v_j=\Delta v_j-\beta _jv_j+\sum \limits ^n_{i=1}\gamma _{i,j}u_i, &j\in \mathcal{J}, \\[5pt] u_{i0}(x)=u_i(x,0), v_{j0}(x)=v_j(x,0),&i\in \mathcal{I},\quad j\in \mathcal{J}, \end{cases} \end{equation}
with initial data
![]() $\boldsymbol{{u}}_0=(u_{10},\cdots,u_{n0})$
and
$\boldsymbol{{u}}_0=(u_{10},\cdots,u_{n0})$
and
![]() $ \boldsymbol{{v}}_0=(v_{10},\cdots,v_{m0})$
satisfying
$ \boldsymbol{{v}}_0=(v_{10},\cdots,v_{m0})$
satisfying
 \begin{equation} \begin{cases} &u_{i0}(x)\in C^0(\mathbb{R}^2)\cap L^1(\mathbb{R}^2)\cap L^1\!\left(\mathbb{R}^2,\log \!\left(1+|x|^2\right)dx\right)\cap L^{\infty }(\mathbb{R}^2),\\[5pt] &u_{i0}\geq 0\quad \text{and}\quad u_{i0}\not \equiv 0,\quad i\in \mathcal{I},\\[5pt] &v_{j0}(x)\in W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2)\quad \text{with some}\,\,p\gt 2,\quad j\in \mathcal{J}. \end{cases} \end{equation}
\begin{equation} \begin{cases} &u_{i0}(x)\in C^0(\mathbb{R}^2)\cap L^1(\mathbb{R}^2)\cap L^1\!\left(\mathbb{R}^2,\log \!\left(1+|x|^2\right)dx\right)\cap L^{\infty }(\mathbb{R}^2),\\[5pt] &u_{i0}\geq 0\quad \text{and}\quad u_{i0}\not \equiv 0,\quad i\in \mathcal{I},\\[5pt] &v_{j0}(x)\in W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2)\quad \text{with some}\,\,p\gt 2,\quad j\in \mathcal{J}. \end{cases} \end{equation}
Before stating our main results, let us go over some notations and definitions in [Reference Wolansky42].
is the number to quantify the tendency of a population
![]() $i$
towards a population
$i$
towards a population
![]() $k$
by taking an accounting of the action of all the agents, where
$k$
by taking an accounting of the action of all the agents, where
![]() $\boldsymbol{\alpha }_i=(\alpha _{i,1},\cdots,\alpha _{i,m})^T$
and
$\boldsymbol{\alpha }_i=(\alpha _{i,1},\cdots,\alpha _{i,m})^T$
and
![]() $\boldsymbol{\gamma }_i=(\gamma _{i,1},\cdots,\gamma _{i,m})^T$
. The condition
$\boldsymbol{\gamma }_i=(\gamma _{i,1},\cdots,\gamma _{i,m})^T$
. The condition
![]() $\lambda _{i,k}\gt 0$
means that a population
$\lambda _{i,k}\gt 0$
means that a population
![]() $i$
is attracted by a population
$i$
is attracted by a population
![]() $k$
; otherwise, the population
$k$
; otherwise, the population
![]() $i$
is repelled from the population
$i$
is repelled from the population
![]() $k$
if
$k$
if
![]() $\lambda _{i,k}\lt 0$
. Especially, a population is self-attracting (resp. self-repelling) if
$\lambda _{i,k}\lt 0$
. Especially, a population is self-attracting (resp. self-repelling) if
![]() $\lambda _{i,i}\gt 0$
(resp.
$\lambda _{i,i}\gt 0$
(resp.
![]() $\lambda _{i,i}\lt 0$
). A pair
$\lambda _{i,i}\lt 0$
). A pair
![]() $(i,k)$
of populations
$(i,k)$
of populations
![]() $i,k\in I$
is said to be in a conflict if
$i,k\in I$
is said to be in a conflict if
![]() $\lambda _{i,k}\times \lambda _{k,i}\lt 0$
. In general,
$\lambda _{i,k}\times \lambda _{k,i}\lt 0$
. In general,
![]() $\boldsymbol{\lambda }=(\lambda _{i,k})_{i,k\in \mathcal{I}}$
is not symmetric. We assume that there exist nonzero constants
$\boldsymbol{\lambda }=(\lambda _{i,k})_{i,k\in \mathcal{I}}$
is not symmetric. We assume that there exist nonzero constants
![]() $a_1,\cdots,a_n$
satisfying
$a_1,\cdots,a_n$
satisfying
then
![]() $D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is symmetric, where
$D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is symmetric, where
![]() $D_{\boldsymbol{{a}}}=\text{Diag}\{a_1,\cdots,a_n\}$
. If
$D_{\boldsymbol{{a}}}=\text{Diag}\{a_1,\cdots,a_n\}$
. If
![]() $\boldsymbol{\lambda }$
is non-singular, there exists a
$\boldsymbol{\lambda }$
is non-singular, there exists a
![]() $m\times m$
symmetric matrix
$m\times m$
symmetric matrix
![]() $\boldsymbol{{B}}$
which transforms
$\boldsymbol{{B}}$
which transforms
![]() $\boldsymbol{\gamma }_i$
into
$\boldsymbol{\gamma }_i$
into
![]() $a_i\boldsymbol{\alpha }_i$
for all
$a_i\boldsymbol{\alpha }_i$
for all
![]() $i\in \mathcal{I}$
, i.e.
$i\in \mathcal{I}$
, i.e.
In fact, denote
 \begin{align*} \boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}=\left [ \begin{array}{c} \boldsymbol{\alpha }^T_1\\[5pt] \vdots \\[5pt] \boldsymbol{\alpha }^T_n \end{array} \right ],\,\, \boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}=\left [ \begin{array}{c} \boldsymbol{\gamma }^T_1\\[5pt] \vdots \\[5pt] \boldsymbol{\gamma }^T_n \end{array} \right ]. \end{align*}
\begin{align*} \boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}=\left [ \begin{array}{c} \boldsymbol{\alpha }^T_1\\[5pt] \vdots \\[5pt] \boldsymbol{\alpha }^T_n \end{array} \right ],\,\, \boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}=\left [ \begin{array}{c} \boldsymbol{\gamma }^T_1\\[5pt] \vdots \\[5pt] \boldsymbol{\gamma }^T_n \end{array} \right ]. \end{align*}
First, we observe that the ranks
![]() $R(\boldsymbol{\alpha })=R(\boldsymbol{\gamma })=n$
due to
$R(\boldsymbol{\alpha })=R(\boldsymbol{\gamma })=n$
due to
![]() $\boldsymbol{\lambda }=\boldsymbol{\alpha }\boldsymbol{\gamma }^T$
is non-singular. Then, there exists a solution
$\boldsymbol{\lambda }=\boldsymbol{\alpha }\boldsymbol{\gamma }^T$
is non-singular. Then, there exists a solution
![]() $X=(x_{i,j})_{m\times m}$
to a linear system of equations
$X=(x_{i,j})_{m\times m}$
to a linear system of equations
![]() $ \boldsymbol{\gamma }X=D_{\boldsymbol{{a}}}\boldsymbol{\alpha }$
since both the ranks of its coefficient matrix and augmented matrix equal to
$ \boldsymbol{\gamma }X=D_{\boldsymbol{{a}}}\boldsymbol{\alpha }$
since both the ranks of its coefficient matrix and augmented matrix equal to
![]() $n$
. Finally, the choice
$n$
. Finally, the choice
![]() $\boldsymbol{{B}}=X^T$
fulfils (1.8). Moreover, using the symmetry of
$\boldsymbol{{B}}=X^T$
fulfils (1.8). Moreover, using the symmetry of
![]() $D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
, one is able to show that
$D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
, one is able to show that
![]() $ \boldsymbol{\gamma }\boldsymbol{{B}}^T\boldsymbol{\gamma }^T=\boldsymbol{\gamma }\boldsymbol{{B}}\boldsymbol{\gamma }^T$
. This implies that
$ \boldsymbol{\gamma }\boldsymbol{{B}}^T\boldsymbol{\gamma }^T=\boldsymbol{\gamma }\boldsymbol{{B}}\boldsymbol{\gamma }^T$
. This implies that
![]() $\boldsymbol{{B}}$
can be symmetric.
$\boldsymbol{{B}}$
can be symmetric.
Now we give the following definitions throughout this paper.
Definition 1.
![]() $(i)$
A pair
$(i)$
A pair
![]() $(i,k)$
of populations
$(i,k)$
of populations
![]() $i,k\in \mathcal{I}$
is said to be in a conflict if
$i,k\in \mathcal{I}$
is said to be in a conflict if
![]() $\lambda _{i,k}\times \lambda _{k,i}\lt 0$
. All populations are mutually attractive if
$\lambda _{i,k}\times \lambda _{k,i}\lt 0$
. All populations are mutually attractive if
![]() $\lambda _{i,k}\gt 0$
,
$\lambda _{i,k}\gt 0$
,
![]() $\forall \,i,k\in \mathcal{I}$
.
$\forall \,i,k\in \mathcal{I}$
.
![]() $(ii)$
System (1.5) is called a conflict-free system if
$(ii)$
System (1.5) is called a conflict-free system if
![]() $\lambda _{i,k}\times \lambda _{k,i}\gt 0$
,
$\lambda _{i,k}\times \lambda _{k,i}\gt 0$
,
![]() $\forall \,i,k\in \mathcal{I}$
, and if there exist positive constants
$\forall \,i,k\in \mathcal{I}$
, and if there exist positive constants
![]() $a_1,\cdots,a_n$
such that (1.7) is valid.
$a_1,\cdots,a_n$
such that (1.7) is valid.
The main result of this article is stated as follows.
Theorem 1.1.
Let
![]() $\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
,
$\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
,
![]() $\boldsymbol{\lambda }=(\lambda _{i,k})_{n\times n}$
,
$\boldsymbol{\lambda }=(\lambda _{i,k})_{n\times n}$
,
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
with full column rank
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
with full column rank
![]() $R(\boldsymbol{\alpha })=m$
, and
$R(\boldsymbol{\alpha })=m$
, and
![]() $\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
$\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
![]() $\beta _{j,l}=\beta _j\delta _{j,l}$
,
$\beta _{j,l}=\beta _j\delta _{j,l}$
,
![]() $\beta _{j}\in \mathbb{R}$
,
$\beta _{j}\in \mathbb{R}$
,
![]() $j,l\in \mathcal{J}$
. Assume that (1.5) is a conflict-free system with initial data
$j,l\in \mathcal{J}$
. Assume that (1.5) is a conflict-free system with initial data
![]() $(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
satisfying (1.6). Suppose that there exist positive constants
$(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
satisfying (1.6). Suppose that there exist positive constants
![]() $a_1,\cdots,a_n$
and a positive definite matrix
$a_1,\cdots,a_n$
and a positive definite matrix
![]() $\boldsymbol{{R}}=(r_{i,k})_{n\times n}$
with
$\boldsymbol{{R}}=(r_{i,k})_{n\times n}$
with
![]() $r_{i,k}\geq 0$
,
$r_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
, such that
$i,k\in \mathcal{I}$
, such that
Then for any initial data satisfying
the corresponding initial boundary value problem (1.5) possesses a unique smooth global solution.
We would like to give an explanation for assumptions in Theorem 1.1. First, since
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
is required to be full column rank, it ensures that
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
is required to be full column rank, it ensures that
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}=\boldsymbol{\alpha }^T\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
is a positive definite matrix if
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}=\boldsymbol{\alpha }^T\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
is a positive definite matrix if
![]() $\boldsymbol{{R}}$
is chosen to be positive definition. Condition (1.9) can probably be viewed as one of necessary condition for the existence of energy functional for the conflict-free system (1.5) (see [Reference Horstmann20, Reference Lin and Zhong30, Reference Wolansky42]). In order to handle the whole domain case better in this paper, we use a modified free energy functional
$\boldsymbol{{R}}$
is chosen to be positive definition. Condition (1.9) can probably be viewed as one of necessary condition for the existence of energy functional for the conflict-free system (1.5) (see [Reference Horstmann20, Reference Lin and Zhong30, Reference Wolansky42]). In order to handle the whole domain case better in this paper, we use a modified free energy functional
![]() $\mathcal{F}$
as
$\mathcal{F}$
as
 \begin{align*} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\\[5pt] &-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx. \end{split} \end{align*}
\begin{align*} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\\[5pt] &-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx. \end{split} \end{align*}
Second, condition (1.10) can be regarded as an optimality condition to guarantee the global existence of solution to (1.5). This is because if
![]() $D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is a positive definite matrix with
$D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is a positive definite matrix with
![]() $\lambda _{i,k}\geq 0$
,
$\lambda _{i,k}\geq 0$
,
![]() $\forall \,i,k\in \mathcal{I}$
, then (1.10) is actually equivalent to the following sub-critical mass condition obtained in [Reference Lin and Zhong30, Reference Wolansky42]
$\forall \,i,k\in \mathcal{I}$
, then (1.10) is actually equivalent to the following sub-critical mass condition obtained in [Reference Lin and Zhong30, Reference Wolansky42]
Indeed, let
![]() $\boldsymbol{{R}}=(r_{i,k})_{n\times n}=D^{-1}_{\boldsymbol{{a}}}\boldsymbol{\lambda }^T$
. Then in terms of
$\boldsymbol{{R}}=(r_{i,k})_{n\times n}=D^{-1}_{\boldsymbol{{a}}}\boldsymbol{\lambda }^T$
. Then in terms of
![]() $\lambda _{i,k}=\boldsymbol{\alpha }^T_i\cdot \boldsymbol{\gamma }_k$
and
$\lambda _{i,k}=\boldsymbol{\alpha }^T_i\cdot \boldsymbol{\gamma }_k$
and
![]() $R(\boldsymbol{\alpha })=m$
,
$R(\boldsymbol{\alpha })=m$
,
![]() $\boldsymbol{{B}}=\boldsymbol{\alpha }^{T}{\boldsymbol{{R}}}^{-1}\boldsymbol{\alpha }$
is a positive definite matrix which satisfies
$\boldsymbol{{B}}=\boldsymbol{\alpha }^{T}{\boldsymbol{{R}}}^{-1}\boldsymbol{\alpha }$
is a positive definite matrix which satisfies
![]() $\boldsymbol{{B}}\boldsymbol{\gamma }_i=a_i\boldsymbol{\alpha }_i$
,
$\boldsymbol{{B}}\boldsymbol{\gamma }_i=a_i\boldsymbol{\alpha }_i$
,
![]() $\forall \,\,i\in \mathcal{I}$
. Moreover, we obtain
$\forall \,\,i\in \mathcal{I}$
. Moreover, we obtain
from
![]() $r_{i,k}={\lambda _{k,i}}/a_i\geq 0$
,
$r_{i,k}={\lambda _{k,i}}/a_i\geq 0$
,
![]() $i,k\in \mathcal{I}$
.
$i,k\in \mathcal{I}$
.
Theorem 1.1 gives a sharp criterion on the global existence of the general chemotaxis system (1.5). Hence, a large amount of known global existence results are particular cases in our paper. We give several typical examples here. It is obvious that the sub-critical mass condition (1.10) recovers the threshold condition, i.e.
![]() $m\lt 8\pi/(\alpha \gamma )$
, for global regularity of the Keller–Segel model (1.1). When
$m\lt 8\pi/(\alpha \gamma )$
, for global regularity of the Keller–Segel model (1.1). When
![]() $|\mathcal{I}|=2$
,
$|\mathcal{I}|=2$
,
![]() $|\mathcal{J}|=1$
, consider a chemotaxis system involving two species that interact via one-single chemical signal [Reference Weijer40]
$|\mathcal{J}|=1$
, consider a chemotaxis system involving two species that interact via one-single chemical signal [Reference Weijer40]
 \begin{equation} \left\{\begin{array}{l} \partial _t u_i=\Delta u_i-\alpha _{i,1}\nabla \cdot (u_i\nabla v_1),\quad i\in \mathcal{I}=\{1,2\}, \\[5pt] \partial _tv_{1}=\Delta v_1-v_1+\gamma _{1,1}u_1+\gamma _{2,1}u_2, \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l} \partial _t u_i=\Delta u_i-\alpha _{i,1}\nabla \cdot (u_i\nabla v_1),\quad i\in \mathcal{I}=\{1,2\}, \\[5pt] \partial _tv_{1}=\Delta v_1-v_1+\gamma _{1,1}u_1+\gamma _{2,1}u_2, \end{array}\right. \end{equation}
with
![]() $\alpha _{i,1}\gt 0$
,
$\alpha _{i,1}\gt 0$
,
![]() $\gamma _{i,1}=1$
,
$\gamma _{i,1}=1$
,
![]() $i=1,2$
. Note that
$i=1,2$
. Note that
![]() $\lambda _{i,k}=\alpha _{i,1}\gt 0$
,
$\lambda _{i,k}=\alpha _{i,1}\gt 0$
,
![]() $i,k=1,2$
. Then, (1.9) can be satisfied if one takes
$i,k=1,2$
. Then, (1.9) can be satisfied if one takes
![]() $a_i=1/\alpha _{i,1}$
and chooses a positive definite matrix
$a_i=1/\alpha _{i,1}$
and chooses a positive definite matrix
 \begin{align*} \boldsymbol{{R}}=\left [ \begin{array}{c@{\quad}c} \alpha ^2_{1,1}(1+\epsilon )&\alpha _{1,1}\alpha _{2,1}(1-\epsilon )\\[5pt] \alpha _{1,1}\alpha _{2,1}(1-\epsilon )&\alpha ^2_{2,1}(1+\epsilon ) \end{array} \right ] \end{align*}
\begin{align*} \boldsymbol{{R}}=\left [ \begin{array}{c@{\quad}c} \alpha ^2_{1,1}(1+\epsilon )&\alpha _{1,1}\alpha _{2,1}(1-\epsilon )\\[5pt] \alpha _{1,1}\alpha _{2,1}(1-\epsilon )&\alpha ^2_{2,1}(1+\epsilon ) \end{array} \right ] \end{align*}
for some small
![]() $\epsilon \in (0,1)$
. Then, (1.10) reads as
$\epsilon \in (0,1)$
. Then, (1.10) reads as
 \begin{equation} \begin{cases} 8\pi \gt \alpha _{1,1}(1+\epsilon )m_1,\\[5pt] 8\pi \gt \alpha _{2,1}(1+\epsilon )m_2,\\[5pt] 8\pi \!\left (\dfrac{m_1}{\alpha _{1,1}}+\dfrac{m_2}{\alpha _{2,1}}\right )\gt (m_1+m_2)^2+\epsilon (m_1-m_2)^2. \end{cases} \end{equation}
\begin{equation} \begin{cases} 8\pi \gt \alpha _{1,1}(1+\epsilon )m_1,\\[5pt] 8\pi \gt \alpha _{2,1}(1+\epsilon )m_2,\\[5pt] 8\pi \!\left (\dfrac{m_1}{\alpha _{1,1}}+\dfrac{m_2}{\alpha _{2,1}}\right )\gt (m_1+m_2)^2+\epsilon (m_1-m_2)^2. \end{cases} \end{equation}
However, (1.12) can be simplified as
![]() $m_1\lt 8\pi/\alpha _{1,1}$
,
$m_1\lt 8\pi/\alpha _{1,1}$
,
![]() $m_2\lt 8\pi/\alpha _{2,1}$
and
$m_2\lt 8\pi/\alpha _{2,1}$
and
![]() $(m_1+m_2)^2\lt 8\pi \!\left (m_1/\alpha _{1,1}+m_2/\alpha _{2,1}\right )$
by letting
$(m_1+m_2)^2\lt 8\pi \!\left (m_1/\alpha _{1,1}+m_2/\alpha _{2,1}\right )$
by letting
![]() $\epsilon \rightarrow 0$
, which coincides with global existence condition for (1.11) in a bounded domain ([Reference Lin27, Theorem 1.1]).
$\epsilon \rightarrow 0$
, which coincides with global existence condition for (1.11) in a bounded domain ([Reference Lin27, Theorem 1.1]).
Now suppose that
![]() $|\mathcal{I}|=|\mathcal{J}|=n$
,
$|\mathcal{I}|=|\mathcal{J}|=n$
,
![]() $\boldsymbol{\beta }=\boldsymbol{0}$
,
$\boldsymbol{\beta }=\boldsymbol{0}$
,
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times n}$
with
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times n}$
with
![]() $\alpha _{i,j}\geq 0$
is positive definite, and
$\alpha _{i,j}\geq 0$
is positive definite, and
![]() $\boldsymbol{\gamma }$
is an unit matrix. Then, (1.5) becomes
$\boldsymbol{\gamma }$
is an unit matrix. Then, (1.5) becomes
 \begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^n_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), \\[8pt] \partial _tv_{j}=\Delta v_j+u_j, \quad i,j \in \mathcal{I}=\{1,\cdots,n\}. \\[5pt] \end{cases} \end{equation}
\begin{equation} \begin{cases} \partial _t u_i=\Delta u_i-\sum \limits ^n_{j=1}\alpha _{i,j}\nabla \cdot (u_i\nabla v_j), \\[8pt] \partial _tv_{j}=\Delta v_j+u_j, \quad i,j \in \mathcal{I}=\{1,\cdots,n\}. \\[5pt] \end{cases} \end{equation}
Taking
![]() $a_i=1$
and
$a_i=1$
and
![]() $\lambda _{i,k}=\alpha _{i,k}$
,
$\lambda _{i,k}=\alpha _{i,k}$
,
![]() $i,k\in \mathcal{I}$
, one can find that Cauchy problem (1.13) has a global solution if (1.4) is valid. This global result is similar to that of the parabolic–elliptic system (1.3) [Reference He and Tadmor15, Reference Karmakar and Wolansky22].
$i,k\in \mathcal{I}$
, one can find that Cauchy problem (1.13) has a global solution if (1.4) is valid. This global result is similar to that of the parabolic–elliptic system (1.3) [Reference He and Tadmor15, Reference Karmakar and Wolansky22].
The idea to show the global existence is to derive an a prior estimate for modified total entropy
For this purpose, we need to give a lower bound for
![]() $\mathcal{F}$
. In this situation, the last term consisting of
$\mathcal{F}$
. In this situation, the last term consisting of
![]() $u_i$
and
$u_i$
and
![]() $v_j$
in
$v_j$
in
![]() $\mathcal{F}$
could be controlled by
$\mathcal{F}$
could be controlled by
![]() $\mathcal{S}$
and the last second term under (1.10). For the case of single variable, a common approach to achieve this goal is to use the well-known Moser–Trudinger inequality [Reference Moser32, Reference Trudinger39]
$\mathcal{S}$
and the last second term under (1.10). For the case of single variable, a common approach to achieve this goal is to use the well-known Moser–Trudinger inequality [Reference Moser32, Reference Trudinger39]
where
![]() $\Omega \subset \mathbb{R}^2$
is a bounded domain. For initial Neumann boundary value problem (1.1), Nagai et al. [Reference Nagai, Senba and Yoshida36] had used a version of (1.14) in the Sobolev space
$\Omega \subset \mathbb{R}^2$
is a bounded domain. For initial Neumann boundary value problem (1.1), Nagai et al. [Reference Nagai, Senba and Yoshida36] had used a version of (1.14) in the Sobolev space
![]() $W^{1,2}$
(see also [Reference Chang and Yang6]) to obtain the global existence of solution if
$W^{1,2}$
(see also [Reference Chang and Yang6]) to obtain the global existence of solution if
![]() $m\lt 8\pi/(\alpha \gamma )$
. Later, Mizoguchi [Reference Mizoguchi31] applies (1.14) to get a similar global result for Cauchy problem (1.1) in
$m\lt 8\pi/(\alpha \gamma )$
. Later, Mizoguchi [Reference Mizoguchi31] applies (1.14) to get a similar global result for Cauchy problem (1.1) in
![]() $\mathbb{R}^2$
. Hence, we expect the Moser–Trudinger inequality for vector is valid for our problem. Shafrir and Wolansky [Reference Shafrir and Wolansky38] had proved the following Moser–Trudinger inequality for system. For
$\mathbb{R}^2$
. Hence, we expect the Moser–Trudinger inequality for vector is valid for our problem. Shafrir and Wolansky [Reference Shafrir and Wolansky38] had proved the following Moser–Trudinger inequality for system. For
![]() $\forall \,\,\rho _i\in H^1(\mathbb{S}^2)$
satisfying
$\forall \,\,\rho _i\in H^1(\mathbb{S}^2)$
satisfying
![]() $\int _{\mathbb{S}^2}\rho _i=0,\,\,i\in \mathcal{I}$
, there exists a constant
$\int _{\mathbb{S}^2}\rho _i=0,\,\,i\in \mathcal{I}$
, there exists a constant
![]() $C\gt 0$
such that
$C\gt 0$
such that
 \begin{align*} \Phi _{\mathbb{S}^2}(\boldsymbol{\rho })= \frac{1}{2}\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k -\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\geq -C\end{align*}
\begin{align*} \Phi _{\mathbb{S}^2}(\boldsymbol{\rho })= \frac{1}{2}\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k -\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\geq -C\end{align*}
if and only if
 \begin{align*} \left \{ \begin{array}{l} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})\geq 0,\quad \forall \,\emptyset \neq \mathcal{K}\subset \mathcal{I},\\[9pt] \text{if}\,\,\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})=0\,\,\text{for some}\,\,\mathcal{K},\,\,\text{then}\,\,s_{i,i}+\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}\setminus \{i\}}(\boldsymbol{{M}})\gt 0,\,\,\forall \,{i\in \mathcal{K}}, \end{array} \right . \end{align*}
\begin{align*} \left \{ \begin{array}{l} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})\geq 0,\quad \forall \,\emptyset \neq \mathcal{K}\subset \mathcal{I},\\[9pt] \text{if}\,\,\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})=0\,\,\text{for some}\,\,\mathcal{K},\,\,\text{then}\,\,s_{i,i}+\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}\setminus \{i\}}(\boldsymbol{{M}})\gt 0,\,\,\forall \,{i\in \mathcal{K}}, \end{array} \right . \end{align*}
where
![]() $\mathbb{S}^2\subset \mathbb{R}^3$
is the unit sphere,
$\mathbb{S}^2\subset \mathbb{R}^3$
is the unit sphere,
![]() $\mathcal{I}=\{1,2,\cdots,n\}$
,
$\mathcal{I}=\{1,2,\cdots,n\}$
,
![]() $\boldsymbol{{M}}\,:\!=\,\{M_1,\cdots,M_n\}\in (\mathbb{R}_{+})^n$
,
$\boldsymbol{{M}}\,:\!=\,\{M_1,\cdots,M_n\}\in (\mathbb{R}_{+})^n$
,
![]() $\boldsymbol{{S}}\,:\!=\,(s_{i,k})_{n\times n}$
is a positive definite matrix with
$\boldsymbol{{S}}\,:\!=\,(s_{i,k})_{n\times n}$
is a positive definite matrix with
![]() $s_{i,k}\geq 0$
,
$s_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
, and
$i,k\in \mathcal{I}$
, and
![]() $\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}$
is given by
$\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}$
is given by
We will firstly transform the above Moser–Trudinger inequality for system to
![]() $\mathbb{R}^2$
via the stereographic projection and next use it to show that
$\mathbb{R}^2$
via the stereographic projection and next use it to show that
![]() $\mathcal{S}$
is bounded under the assumption (1.10). Then, one invokes the Moser iterative to obtain the global existence of solutions to (1.5). Finally, we should point out that such idea has been used to establish the global well-posedness of solutions to initial Neumann boundary value problem for multi-species and chemicals in a two-dimensional bounded domain [Reference Lin and Zhong30].
$\mathcal{S}$
is bounded under the assumption (1.10). Then, one invokes the Moser iterative to obtain the global existence of solutions to (1.5). Finally, we should point out that such idea has been used to establish the global well-posedness of solutions to initial Neumann boundary value problem for multi-species and chemicals in a two-dimensional bounded domain [Reference Lin and Zhong30].
Our second object is to show certain conflict-free parabolic system admits a global solution for any initial data. More precisely,
Theorem 1.2.
Let
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
,
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
,
![]() $\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
,
$\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
,
![]() $\boldsymbol{\lambda }=(\lambda _{i,k})_{n\times n}$
and
$\boldsymbol{\lambda }=(\lambda _{i,k})_{n\times n}$
and
![]() $\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
$\boldsymbol{\beta }=(\beta _{j,l})_{m\times m}$
with
![]() $\beta _{j,l}=\beta _j\delta _{j,l}$
,
$\beta _{j,l}=\beta _j\delta _{j,l}$
,
![]() $\beta _{j}\in \mathbb{R}$
,
$\beta _{j}\in \mathbb{R}$
,
![]() $j,l\in \mathcal{J}$
. Assume that (1.5) is a conflict-free system with initial data
$j,l\in \mathcal{J}$
. Assume that (1.5) is a conflict-free system with initial data
![]() $(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
satisfying (1.6). Suppose that there exist positive constants
$(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
satisfying (1.6). Suppose that there exist positive constants
![]() $a_1,\cdots,a_n$
and a positive definite matrix
$a_1,\cdots,a_n$
and a positive definite matrix
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
then Cauchy problem (1.5) possesses a unique smooth global solution.
Remark 1.
In addition, if
![]() $\beta _j\gt 0$
for all
$\beta _j\gt 0$
for all
![]() $j\in \mathcal{J}$
in Theorem 1.2, then the solution to (1.5) is uniformly bounded with respect to time.
$j\in \mathcal{J}$
in Theorem 1.2, then the solution to (1.5) is uniformly bounded with respect to time.
Remark 2.
As mentioned above, the existence of
![]() $\boldsymbol{{B}}$
in Theorem 1.2 can be ensured if
$\boldsymbol{{B}}$
in Theorem 1.2 can be ensured if
![]() $D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is negative definite and
$D_{\boldsymbol{{a}}}\boldsymbol{\lambda }$
is negative definite and
![]() $R(\boldsymbol{\alpha })=m$
. Hence, one may assert that there exists a unique global smooth solution, provided that the self-repelling effects are strong enough in the sense that
$R(\boldsymbol{\alpha })=m$
. Hence, one may assert that there exists a unique global smooth solution, provided that the self-repelling effects are strong enough in the sense that
![]() $\lambda _{ii}\lt 0$
,
$\lambda _{ii}\lt 0$
,
![]() $i\in \mathcal{I}$
, is negative sufficiently large. Following are two prototypical examples. Consider (1.1) with
$i\in \mathcal{I}$
, is negative sufficiently large. Following are two prototypical examples. Consider (1.1) with
![]() $\alpha \lt 0,\gamma \gt 0$
, the local solution can in fact be extended for all times. As an application of Theorem 1.2 on two-species system (1.11) with
$\alpha \lt 0,\gamma \gt 0$
, the local solution can in fact be extended for all times. As an application of Theorem 1.2 on two-species system (1.11) with
![]() $\alpha _{i,1}\lt 0$
,
$\alpha _{i,1}\lt 0$
,
![]() $\gamma _{i,1}\gt 0$
,
$\gamma _{i,1}\gt 0$
,
![]() $i=1,2$
, one would derive the global stability by choosing
$i=1,2$
, one would derive the global stability by choosing
![]() $a_1=-1/(\alpha _{1,1}\gamma _{2,1})$
,
$a_1=-1/(\alpha _{1,1}\gamma _{2,1})$
,
![]() $a_2=-1/(\alpha _{2,1}\gamma _{1,1})$
and
$a_2=-1/(\alpha _{2,1}\gamma _{1,1})$
and
![]() $\boldsymbol{{B}}=(1/(\gamma _{1,1}\gamma _{2,1}))_{1\times 1}$
.
$\boldsymbol{{B}}=(1/(\gamma _{1,1}\gamma _{2,1}))_{1\times 1}$
.
Compared with the proof of Theorem 1.1, the main difference to prove Theorem 1.2 is to derive a prior estimates for the modified total entropy
![]() $\mathcal{S}$
through the following modified free energy functional
$\mathcal{S}$
through the following modified free energy functional
This paper is organised as follows. In Section 2, we would like to establish the local existence of smooth solutions and present some basic inequalities. Theorem 1.1 will be proved in Section 3. The existence of modified free energy functional
![]() $\mathcal{F}$
will be shown firstly, then the stepwise bounds on the total entropy,
$\mathcal{F}$
will be shown firstly, then the stepwise bounds on the total entropy,
![]() $L^2$
and
$L^2$
and
![]() $L^{\infty }$
norms under the condition (1.10) will end the proof of this theorem. In Section 4, we will prove Theorem 1.2 by making use of
$L^{\infty }$
norms under the condition (1.10) will end the proof of this theorem. In Section 4, we will prove Theorem 1.2 by making use of
![]() $\mathcal{G}$
. In appendix, the proof of Lemma 2.1 will be contained.
$\mathcal{G}$
. In appendix, the proof of Lemma 2.1 will be contained.
We introduce some notations which will be used later. Let
![]() $|\mathcal I|=n\geq 1$
denote the total number of species, and
$|\mathcal I|=n\geq 1$
denote the total number of species, and
![]() $|\mathcal{J}|=m\geq 1$
represent the total number of chemical substances.
$|\mathcal{J}|=m\geq 1$
represent the total number of chemical substances.
![]() $|\Omega |$
is the Lebesgue measure of
$|\Omega |$
is the Lebesgue measure of
![]() $\Omega \subset \mathbb{R}^2$
. For
$\Omega \subset \mathbb{R}^2$
. For
![]() $\alpha _{i,j}$
,
$\alpha _{i,j}$
,
![]() $\gamma _{i,j}$
,
$\gamma _{i,j}$
,
![]() $b_{i,j}$
,
$b_{i,j}$
,
![]() $r_{i,k}$
,
$r_{i,k}$
,
![]() $t_{i,j}$
,
$t_{i,j}$
,
![]() $a_i$
,
$a_i$
,
![]() $\beta _{j}\in \mathbb{R}$
,
$\beta _{j}\in \mathbb{R}$
,
![]() $i,k\in \mathcal{I}$
,
$i,k\in \mathcal{I}$
,
![]() $j\in \mathcal{J}$
, we define
$j\in \mathcal{J}$
, we define
 \begin{align*} \alpha ^* & =\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|\alpha _{i,j}|\}, \,\,\gamma ^*=\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|\gamma _{i,j}|\},\,\,b^*=\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|b_{i,j}|\},\,\,r^*=\max \limits _{i,k\in \mathcal{I}}\{|r_{i,k}|\},\\ t^* & =\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|t_{i,j}|\},\,\,a^*=\max \limits _{i\in \mathcal{I}}\{|a_i|\}, \,\,\beta ^*=\max \limits _{j\in \mathcal{J}}\{|\beta _j|\},\,\,\beta _*=\min \limits _{j\in \mathcal{J}}\{\beta _j\}\,\,\text{if}\,\,\beta _j\gt 0. \end{align*}
\begin{align*} \alpha ^* & =\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|\alpha _{i,j}|\}, \,\,\gamma ^*=\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|\gamma _{i,j}|\},\,\,b^*=\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|b_{i,j}|\},\,\,r^*=\max \limits _{i,k\in \mathcal{I}}\{|r_{i,k}|\},\\ t^* & =\max \limits _{i\in \mathcal{I},j\in \mathcal{J}}\{|t_{i,j}|\},\,\,a^*=\max \limits _{i\in \mathcal{I}}\{|a_i|\}, \,\,\beta ^*=\max \limits _{j\in \mathcal{J}}\{|\beta _j|\},\,\,\beta _*=\min \limits _{j\in \mathcal{J}}\{\beta _j\}\,\,\text{if}\,\,\beta _j\gt 0. \end{align*}
2. Preliminaries
In this section, we list some lemmas which will be frequently used throughout this paper. Under some certain assumption on the initial data, we assert that Cauchy problem (1.5) admits a local classical solution. A number of fundamental properties, such as uniqueness, positivity, and regularity, have also been obtained in the following lemma.
Lemma 2.1.
Suppose that
![]() $\boldsymbol{{u}}_0\in [C^0(\mathbb{R}^2)\cap L^1(\mathbb{R}^2)\cap L^{\infty }(\mathbb{R}^2)]^n$
and
$\boldsymbol{{u}}_0\in [C^0(\mathbb{R}^2)\cap L^1(\mathbb{R}^2)\cap L^{\infty }(\mathbb{R}^2)]^n$
and
![]() $ \boldsymbol{{v}}_0\in [W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2)]^m$
for some
$ \boldsymbol{{v}}_0\in [W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2)]^m$
for some
![]() $p\gt 2$
. Then, there exists a positive constant
$p\gt 2$
. Then, there exists a positive constant
![]() $T_{\max }\in (0,\infty ]$
such that the Cauchy problem (1.5) has a unique solution
$T_{\max }\in (0,\infty ]$
such that the Cauchy problem (1.5) has a unique solution
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})$
satisfying
$(\boldsymbol{{u}},\boldsymbol{{v}})$
satisfying
 \begin{equation} \begin{cases} \boldsymbol{{u}}\in \left [C^0([0,T_{\max }];\ L^1(\mathbb{R}^2))\cap C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^n,\\[5pt]\boldsymbol{{v}}\in \left [C^0([0,T_{\max }];\ W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2))\cap C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^m. \end{cases} \end{equation}
\begin{equation} \begin{cases} \boldsymbol{{u}}\in \left [C^0([0,T_{\max }];\ L^1(\mathbb{R}^2))\cap C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^n,\\[5pt]\boldsymbol{{v}}\in \left [C^0([0,T_{\max }];\ W^{1,p}(\mathbb{R}^2)\cap W^{1,1}(\mathbb{R}^2))\cap C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^m. \end{cases} \end{equation}
Moreover, it holds that
-
(i)
 $(\boldsymbol{{u}},\boldsymbol{{v}})$
solves (1.5) classically in
$(\boldsymbol{{u}},\boldsymbol{{v}})$
solves (1.5) classically in
 $\mathbb{R}^2\times (0,T_{\max })$
;
$\mathbb{R}^2\times (0,T_{\max })$
; -
(ii) If
 $T_{\max }\lt \infty$
, then
$T_{\max }\lt \infty$
, then
 \begin{align*} \limsup _{t\rightarrow T_{\max }}\left (\sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}\right )=\infty ; \end{align*}
\begin{align*} \limsup _{t\rightarrow T_{\max }}\left (\sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}\right )=\infty ; \end{align*}
-
(iii)
 $u_i\gt 0$
in
$u_i\gt 0$
in
 $\mathbb{R}^2\times (0,T_{\max })$
,
$\mathbb{R}^2\times (0,T_{\max })$
,
 $i\in \mathcal{I}$
;
$i\in \mathcal{I}$
; -
(iv) For
 $t\in (0,T_{\max })$
,
$t\in (0,T_{\max })$
,
 $\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}=\|u_{i0}\|_{L^1(\mathbb{R}^2)}=m_i$
,
$\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}=\|u_{i0}\|_{L^1(\mathbb{R}^2)}=m_i$
,
 $i\in \mathcal{I}$
;
$i\in \mathcal{I}$
; -
(v) For
 $q\geq 1$
,
$q\geq 1$
,
 $T\in (0,T_{\max })$
, then there exists a constant
$T\in (0,T_{\max })$
, then there exists a constant
 $A_q=A_q(q,\beta ^*,\gamma ^*,\|\boldsymbol{{u}}_0\|_{L^1(\mathbb{R}^2)},\|\boldsymbol{{v}}_0\|_{L^q(\mathbb{R}^2)},T)\gt 0$
such that
Moreover,
$A_q=A_q(q,\beta ^*,\gamma ^*,\|\boldsymbol{{u}}_0\|_{L^1(\mathbb{R}^2)},\|\boldsymbol{{v}}_0\|_{L^q(\mathbb{R}^2)},T)\gt 0$
such that
Moreover, \begin{align*} \sum \limits ^m_{j=1}\|v_j(\cdot,t)\|_{L^q(\mathbb{R}^2)}\leq A_q,\quad t\in (0,T). \end{align*}
\begin{align*} \sum \limits ^m_{j=1}\|v_j(\cdot,t)\|_{L^q(\mathbb{R}^2)}\leq A_q,\quad t\in (0,T). \end{align*}
 $A_q$
is independent of
$A_q$
is independent of
 $T$
if
$T$
if
 $\beta _j\gt 0$
for all
$\beta _j\gt 0$
for all
 $j\in \mathcal{J}$
.
$j\in \mathcal{J}$
.
Proof. For the case
![]() $|\mathcal{I}|=|\mathcal{J}|=1$
to system (1.5) in
$|\mathcal{I}|=|\mathcal{J}|=1$
to system (1.5) in
![]() $\mathbb{R}^n$
(
$\mathbb{R}^n$
(
![]() $n\geq 3$
), Winkler has proved these properties in [Reference Winkler41, Proposition 1.1]. One can apply similar arguments to obtain the desired results. Please see the proof in appendix.
$n\geq 3$
), Winkler has proved these properties in [Reference Winkler41, Proposition 1.1]. One can apply similar arguments to obtain the desired results. Please see the proof in appendix.
The following inequalities are very important to derive a prior estimates for solutions.
Lemma 2.2.
Let
![]() $\eta \in (0,1)$
. Then for any non-negative function
$\eta \in (0,1)$
. Then for any non-negative function
![]() $f\in L^1(\mathbb{R}^2)\cap H^1(\mathbb{R}^2)$
, one has
$f\in L^1(\mathbb{R}^2)\cap H^1(\mathbb{R}^2)$
, one has
where
![]() $c=c(\eta )\rightarrow \infty$
as
$c=c(\eta )\rightarrow \infty$
as
![]() $\eta \rightarrow 0$
.
$\eta \rightarrow 0$
.
Proof. Inequality (2.2) has been shown in [Reference Yamada43, Lemma 2.3], and (2.3)–(2.4) have been proved in [Reference Nagai and Yamada37, Lemmas 2.3–2.4].
Now, the Gagliardo–Nirenberg inequality will be given as follows.
Lemma 2.3.
Let
![]() $1\leq p\lt \infty$
,
$1\leq p\lt \infty$
,
![]() $1\leq q,r\leq \infty$
and
$1\leq q,r\leq \infty$
and
![]() $\theta \in [0,1]$
such that
$\theta \in [0,1]$
such that
Then for any
![]() $u(x)\in W^{1,r}(\mathbb{R}^2)\cap L^{q}(\mathbb{R}^2)$
, there exists a constant
$u(x)\in W^{1,r}(\mathbb{R}^2)\cap L^{q}(\mathbb{R}^2)$
, there exists a constant
![]() $c=c(p,q,r)\gt 0$
such that
$c=c(p,q,r)\gt 0$
such that
Proof. The proof of this lemma has been given in [Reference Giga, Giga and Saal14, Theorem 6.1.1].
3. Proof of Theorem 1.1
In this section, the proof of Theorem 1.1 will be divided into several steps.
Now we would like to give an equality for the modified free energy functional
![]() $ \mathcal{F}$
. Notice that the equality for one-single variable can be found in [Reference Nagai and Ogawa34, Proposition 4.1].
$ \mathcal{F}$
. Notice that the equality for one-single variable can be found in [Reference Nagai and Ogawa34, Proposition 4.1].
Lemma 3.1.
Let
![]() $\alpha _{i,j},\beta _{j},\gamma _{i,j}\in \mathbb{R}$
,
$\alpha _{i,j},\beta _{j},\gamma _{i,j}\in \mathbb{R}$
,
![]() $i\in \mathcal{I}$
,
$i\in \mathcal{I}$
,
![]() $j\in \mathcal{J}$
and
$j\in \mathcal{J}$
and
![]() $T\gt 0$
. Let
$T\gt 0$
. Let
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})$
be a local solution of (1.5) with initial data
$(\boldsymbol{{u}},\boldsymbol{{v}})$
be a local solution of (1.5) with initial data
![]() $(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
. Assume that there exist positive constants
$(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
. Assume that there exist positive constants
![]() $a_1,\cdots,a_n$
and a positive definite matrix
$a_1,\cdots,a_n$
and a positive definite matrix
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
Then,
 \begin{align} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\left (\partial _t\boldsymbol{{v}}\right )dx +\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\Bigg \{u_i\!\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[5pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\Bigg \}dx\\[5pt] =&\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j \right )dx+\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx \nonumber \end{align}
\begin{align} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\left (\partial _t\boldsymbol{{v}}\right )dx +\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\Bigg \{u_i\!\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[5pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\Bigg \}dx\\[5pt] =&\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j \right )dx+\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx \nonumber \end{align}
for
![]() $ t\in (0,T)$
, where
$ t\in (0,T)$
, where
![]() $\mathcal{F}$
is given by
$\mathcal{F}$
is given by
 \begin{align*} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx. \end{align*}
\begin{align*} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx. \end{align*}
Moreover, there exists a constant
![]() $c\gt 0$
such that
$c\gt 0$
such that
 \begin{align} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx\nonumber\\[9pt] &+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\Bigg \{u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[9pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\Bigg \}dx\\[9pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+c,\quad t\in (0,T).\nonumber \end{align}
\begin{align} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx\nonumber\\[9pt] &+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\Bigg \{u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[9pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\Bigg \}dx\\[9pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+c,\quad t\in (0,T).\nonumber \end{align}
Proof. Multiplying both sides of
![]() $i$
-th equation in (1.5) by
$i$
-th equation in (1.5) by
![]() $a_i\log\! (u_i+1)$
, integrating by parts and summing them with respect to
$a_i\log\! (u_i+1)$
, integrating by parts and summing them with respect to
![]() $i$
, we have
$i$
, we have
 \begin{align} \frac{d}{dt}&\left [\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right ]\nonumber\\[9pt] =&-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx +\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\frac{u_i}{u_i+1}\nabla u_i\cdot \nabla v_jdx. \end{align}
\begin{align} \frac{d}{dt}&\left [\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right ]\nonumber\\[9pt] =&-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx +\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\frac{u_i}{u_i+1}\nabla u_i\cdot \nabla v_jdx. \end{align}
By the symmetry of
![]() $\boldsymbol{{B}}$
, it is clear that
$\boldsymbol{{B}}$
, it is clear that
 \begin{align*} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\right ]\\[8pt] =&\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left [\nabla \!\left (\partial _tv_j\right )\cdot \nabla v_l+\nabla v_j\cdot \nabla \!\left (\partial _tv_l\right ) \right ]dx\\[8pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_l\partial _tv_j+v_j\partial _tv_l\right )dx\\[8pt] =&\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla \!\left (\partial _tv_j\right )\cdot \nabla v_ldx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}\left (v_l\partial _tv_j+v_j\partial _tv_l\right )dx\\[8pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\partial _tv_j\right )\left (\Delta v_l-\beta _{l}v_l\right )dx\\[8pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx, \end{align*}
\begin{align*} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\right ]\\[8pt] =&\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left [\nabla \!\left (\partial _tv_j\right )\cdot \nabla v_l+\nabla v_j\cdot \nabla \!\left (\partial _tv_l\right ) \right ]dx\\[8pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_l\partial _tv_j+v_j\partial _tv_l\right )dx\\[8pt] =&\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla \!\left (\partial _tv_j\right )\cdot \nabla v_ldx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}\left (v_l\partial _tv_j+v_j\partial _tv_l\right )dx\\[8pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\partial _tv_j\right )\left (\Delta v_l-\beta _{l}v_l\right )dx\\[8pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx, \end{align*}
and then using (3.1) and the
![]() $j$
-th equation in (1.5), it implies that
$j$
-th equation in (1.5), it implies that
 \begin{align*} \begin{split} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\right ]\\[5pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\partial _tv_j\partial _tv_ldx+\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,l}\int _{\mathbb{R}^2}u_i\partial _tv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j \right )dx\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_i\partial _tv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx\right ]\\[5pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\partial _tv_j\partial _tv_ldx+\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,l}\int _{\mathbb{R}^2}u_i\partial _tv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j \right )dx\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_i\partial _tv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx. \end{split} \end{align*}
Since
 \begin{align*} \begin{split} \frac{d}{dt}\left ({-}\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\right )=&-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}v_j\partial _tu_idx\\[5pt] &-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_i\partial _tv_jdx \end{split} \end{align*}
\begin{align*} \begin{split} \frac{d}{dt}\left ({-}\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\right )=&-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}v_j\partial _tu_idx\\[5pt] &-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_i\partial _tv_jdx \end{split} \end{align*}
and
 \begin{align*} \begin{split} -\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}v_j\partial _tu_idx=&-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\left (\Delta u_i-\sum \limits ^m_{l=1}\alpha _{i,l}\nabla \cdot (u_i\nabla v_l)\right )v_jdx\\[5pt] =&\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx, \end{split} \end{align*}
\begin{align*} \begin{split} -\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}v_j\partial _tu_idx=&-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\left (\Delta u_i-\sum \limits ^m_{l=1}\alpha _{i,l}\nabla \cdot (u_i\nabla v_l)\right )v_jdx\\[5pt] =&\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx, \end{split} \end{align*}
one can obtain
 \begin{align*} \begin{split} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\right ]\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx, \end{split} \end{align*}
\begin{align*} \begin{split} \frac{d}{dt}&\left [\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\right ]\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx, \end{split} \end{align*}
which together with (3.4) yields that
 \begin{align*} \begin{split} \frac{d}{dt}\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx\\[5pt] &+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{2u_i+1}{u_i+1}\nabla u_i\cdot \nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &+\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{d}{dt}\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx\\[5pt] &+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{2u_i+1}{u_i+1}\nabla u_i\cdot \nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j} v_j\right )\right |^2dx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx\\[5pt] =&-\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &-\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &+\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx. \end{split} \end{align*}
Hence, we have proved (3.2).
By means of the positivity of
![]() $\boldsymbol{{B}}$
, there exists a constant
$\boldsymbol{{B}}$
, there exists a constant
![]() $c_1\gt 0$
such that
$c_1\gt 0$
such that
then we have
 \begin{align*} &\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx\\[5pt]& \leq \beta ^*\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}\left |\partial _tv_j\right | |v_l|dx\\[5pt]& \leq \frac{1}{2c_1}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\partial _tv_j\right |^2dx+\frac{c_1(b^*\beta ^*|\mathcal{J}|)^2}{2}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}v^2_jdx\\[5pt]& \leq \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\partial _tv_j\partial _tv_ldx+\frac{c_1(b^*\beta ^*|\mathcal{J}|)^2}{2}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}v^2_jdx \end{align*}
\begin{align*} &\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}\left (v_j\partial _tv_l-v_l\partial _tv_j\right )dx\\[5pt]& \leq \beta ^*\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}\left |\partial _tv_j\right | |v_l|dx\\[5pt]& \leq \frac{1}{2c_1}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\partial _tv_j\right |^2dx+\frac{c_1(b^*\beta ^*|\mathcal{J}|)^2}{2}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}v^2_jdx\\[5pt]& \leq \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\partial _tv_j\partial _tv_ldx+\frac{c_1(b^*\beta ^*|\mathcal{J}|)^2}{2}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}v^2_jdx \end{align*}
due to Young’s inequality. Employing (3.2) and the boundedness of
![]() $v_j$
in
$v_j$
in
![]() $L^2$
space, we can obtain a constant
$L^2$
space, we can obtain a constant
![]() $c\gt 0$
such that (3.3) holds for all
$c\gt 0$
such that (3.3) holds for all
![]() $t\in (0,T)$
.
$t\in (0,T)$
.
Remark 3. Let us define
 \begin{align*} \begin{split} \mathcal{E}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\log u_idx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx. \end{split} \end{align*}
\begin{align*} \begin{split} \mathcal{E}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\log u_idx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx. \end{split} \end{align*}
Then,
![]() $d\mathcal{E}[\boldsymbol{{u}},\boldsymbol{{v}}]/dt\leq 0$
for
$d\mathcal{E}[\boldsymbol{{u}},\boldsymbol{{v}}]/dt\leq 0$
for
![]() $t\in (0,T)$
if one has (3.1) and
$t\in (0,T)$
if one has (3.1) and
![]() $\boldsymbol{{B}}D_{\boldsymbol{\beta }}$
is symmetric.
$\boldsymbol{{B}}D_{\boldsymbol{\beta }}$
is symmetric.
We list the Moser–Trudinger inequality for system on the two-dimensional unit sphere [Reference Shafrir and Wolansky38, Theorem 2 (ii)].
Lemma 3.2.
Let
![]() $\mathbb{S}^2\subset \mathbb{R}^3$
be the unit sphere. Assume
$\mathbb{S}^2\subset \mathbb{R}^3$
be the unit sphere. Assume
![]() $\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
is a positive definite matrix with
$\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
is a positive definite matrix with
![]() $s_{i,k}\geq 0$
,
$s_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
, and
$i,k\in \mathcal{I}$
, and
![]() $\boldsymbol{{M}}\in (\mathbb{R}_{+})^n$
. Then for
$\boldsymbol{{M}}\in (\mathbb{R}_{+})^n$
. Then for
![]() $\rho _i\in H^1(\mathbb{S}^2)$
satisfying
$\rho _i\in H^1(\mathbb{S}^2)$
satisfying
![]() $\int _{\mathbb{S}^2}\rho _i=0,\,\,i\in \mathcal{I}$
,
$\int _{\mathbb{S}^2}\rho _i=0,\,\,i\in \mathcal{I}$
,
 \begin{equation} \left \{ \begin{array}{l@{\quad}l@{\quad}l@{\quad}l} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})\geq 0,\quad \forall \,\emptyset \neq \mathcal{K}\subset \mathcal{I},\\[5pt]\text{if}\,\,\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})=0\,\,\textit{for some}\,\,\mathcal{K},\,\,\textit{then}\,\,s_{i,i}+\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}\setminus \{i\}}(\boldsymbol{{M}})\gt 0,\,\,\forall \,{i\in \mathcal{K}}, \end{array} \right . \end{equation}
\begin{equation} \left \{ \begin{array}{l@{\quad}l@{\quad}l@{\quad}l} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})\geq 0,\quad \forall \,\emptyset \neq \mathcal{K}\subset \mathcal{I},\\[5pt]\text{if}\,\,\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}})=0\,\,\textit{for some}\,\,\mathcal{K},\,\,\textit{then}\,\,s_{i,i}+\Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}\setminus \{i\}}(\boldsymbol{{M}})\gt 0,\,\,\forall \,{i\in \mathcal{K}}, \end{array} \right . \end{equation}
is the necessary and sufficient condition for the existence of a constant
![]() $B\gt 0$
such that
$B\gt 0$
such that
 \begin{equation} \begin{split} \Phi _{\mathbb{S}^2}(\boldsymbol{\rho })= \frac{1}{2}\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\geq -B. \end{split} \end{equation}
\begin{equation} \begin{split} \Phi _{\mathbb{S}^2}(\boldsymbol{\rho })= \frac{1}{2}\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\geq -B. \end{split} \end{equation}
Now we use the stereographic projection
![]() $\mathcal{S}$
to transform the inequality for system in Lemma 3.2 to
$\mathcal{S}$
to transform the inequality for system in Lemma 3.2 to
![]() $\mathbb{R}^2$
. In fact, we associate with each
$\mathbb{R}^2$
. In fact, we associate with each
![]() $\rho _i\,:\,\mathbb{S}^2\rightarrow \mathbb{R}^2$
a function
$\rho _i\,:\,\mathbb{S}^2\rightarrow \mathbb{R}^2$
a function
![]() $\widetilde{\rho }_i\,:\,\mathbb{R}^2\rightarrow \mathbb{S}^2$
via the transformation
$\widetilde{\rho }_i\,:\,\mathbb{R}^2\rightarrow \mathbb{S}^2$
via the transformation
 \begin{equation} \begin{split} \begin{cases} \widetilde{\rho }_i\leftrightarrow &\rho _i=\widetilde{\rho }_i\circ \mathcal{S},\\[5pt] \rho _i\leftrightarrow &\widetilde{\rho }_i= \rho _i\circ \mathcal{S}^{-1},\quad i\in \mathcal{I}. \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} \begin{cases} \widetilde{\rho }_i\leftrightarrow &\rho _i=\widetilde{\rho }_i\circ \mathcal{S},\\[5pt] \rho _i\leftrightarrow &\widetilde{\rho }_i= \rho _i\circ \mathcal{S}^{-1},\quad i\in \mathcal{I}. \end{cases} \end{split} \end{equation}
By a simple calculation, we have
Lemma 3.3.
Let
![]() $\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
be a positive definite matrix with
$\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
be a positive definite matrix with
![]() $s_{i,k}\geq 0$
,
$s_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
. Then for
$i,k\in \mathcal{I}$
. Then for
![]() $\widetilde{\rho }_i\in H^1(\mathbb{R}^2)$
,
$\widetilde{\rho }_i\in H^1(\mathbb{R}^2)$
,
![]() $i\in \mathcal{I}$
, condition (3.5) is the necessary and sufficient condition for the existence of a constant
$i\in \mathcal{I}$
, condition (3.5) is the necessary and sufficient condition for the existence of a constant
![]() $B\gt 0$
such that
$B\gt 0$
such that
 \begin{equation} \begin{split} \frac{1}{2}&\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{R}^2}\nabla \widetilde{\rho }_i\cdot \nabla \widetilde{\rho }_kdx-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k} \widetilde{\rho }_k\right)H(x)dx\right )\\[5pt] &+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx\geq -B, \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1}{2}&\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{R}^2}\nabla \widetilde{\rho }_i\cdot \nabla \widetilde{\rho }_kdx-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k} \widetilde{\rho }_k\right)H(x)dx\right )\\[5pt] &+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx\geq -B, \end{split} \end{equation}
where
![]() $H(x)=4/\big(1+|x|^2\big)^2$
.
$H(x)=4/\big(1+|x|^2\big)^2$
.
Proof. Let
![]() $\rho _i\in H^1(\mathbb{S}^2)$
,
$\rho _i\in H^1(\mathbb{S}^2)$
,
![]() $i\in \mathcal{I}$
. Then, we take
$i\in \mathcal{I}$
. Then, we take
for
![]() $\rho _i$
in (3.6), and obtain that
$\rho _i$
in (3.6), and obtain that
 \begin{equation} \begin{split} \frac{1}{2}&\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\\[5pt] &+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{S}^2}\rho _k\geq -B \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1}{2}&\sum _{i,k\in \mathcal{I}}s_{i,k}\int _{\mathbb{S}^2}\nabla \rho _i\cdot \nabla \rho _k-\sum _{i\in \mathcal{I}}M_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)\right )\\[5pt] &+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{S}^2}\rho _k\geq -B \end{split} \end{equation}
with some constant
![]() $B\gt 0$
if and only if (3.5) is valid. Using the transformation (3.7), one derives that
$B\gt 0$
if and only if (3.5) is valid. Using the transformation (3.7), one derives that
![]() $\int _{\mathbb{S}^2}\rho _k=\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx$
, and
$\int _{\mathbb{S}^2}\rho _k=\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx$
, and
as well as
 \begin{align*} \int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)=\int _{\mathbb{R}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\widetilde{\rho }_k\right)H(x)dx. \end{align*}
\begin{align*} \int _{\mathbb{S}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\rho _k\right)=\int _{\mathbb{R}^2}\exp \!\left(\sum \limits _{k\in \mathcal{I}}s_{i,k}\widetilde{\rho }_k\right)H(x)dx. \end{align*}
Under the condition (1.10), utilising the above Moser–Trudinger inequality for system in the whole space, we can give an estimate on the interaction term consisting of
![]() $u_i$
and
$u_i$
and
![]() $v_j$
in
$v_j$
in
![]() $ \mathcal{F}$
at the first step. The idea is mainly combined with some of the work in [Reference Calvez and Corrias5] and [Reference Mizoguchi31] and has been applied to one-species or two-species chemotaxis system with two chemicals [Reference Hong, Wang, Yu and Zhang19, Reference Nagai, Seki and Yamada35].
$ \mathcal{F}$
at the first step. The idea is mainly combined with some of the work in [Reference Calvez and Corrias5] and [Reference Mizoguchi31] and has been applied to one-species or two-species chemotaxis system with two chemicals [Reference Hong, Wang, Yu and Zhang19, Reference Nagai, Seki and Yamada35].
Lemma 3.4.
Suppose
![]() $\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
with
$\boldsymbol{\alpha }=(\alpha _{i,j})_{n\times m}$
with
![]() $R(\boldsymbol{\alpha })=m$
,
$R(\boldsymbol{\alpha })=m$
,
![]() $\beta _{j}\in \mathbb{R}$
,
$\beta _{j}\in \mathbb{R}$
,
![]() $j\in \mathcal{J}$
,
$j\in \mathcal{J}$
,
![]() $\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
and
$\boldsymbol{\gamma }=(\gamma _{i,j})_{n\times m}$
and
![]() $T\gt 0$
. Assume that
$T\gt 0$
. Assume that
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})$
is a local solution of Cauchy problem (1.5) with initial data
$(\boldsymbol{{u}},\boldsymbol{{v}})$
is a local solution of Cauchy problem (1.5) with initial data
![]() $(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
. Suppose that there exist positive constants
$(\boldsymbol{{u}}_0,\boldsymbol{{v}}_0)$
. Suppose that there exist positive constants
![]() $a_1,\cdots,a_n$
and a positive definite matrix
$a_1,\cdots,a_n$
and a positive definite matrix
![]() $\boldsymbol{{R}}=(r_{i,k})_{n\times n}$
with
$\boldsymbol{{R}}=(r_{i,k})_{n\times n}$
with
![]() $r_{i,k}\geq 0$
,
$r_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
, such that
$i,k\in \mathcal{I}$
, such that
Then for any
there exist a small
![]() $\epsilon \gt 0$
and a constant
$\epsilon \gt 0$
and a constant
![]() $c\gt 0$
such that
$c\gt 0$
such that
 \begin{align*} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx &\leq \frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] & \quad +\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &\quad -\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c, \end{align*}
\begin{align*} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx &\leq \frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] & \quad +\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &\quad -\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c, \end{align*}
where
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}=\boldsymbol{\alpha }^T\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
and
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}=\boldsymbol{\alpha }^T\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
and
![]() $H(x)=4/\big(1+|x|^2\big)^2$
.
$H(x)=4/\big(1+|x|^2\big)^2$
.
Proof. From our assumption,
![]() $\boldsymbol{{B}}$
is a positive definite matrix satisfying
$\boldsymbol{{B}}$
is a positive definite matrix satisfying
![]() $\boldsymbol{{B}}\boldsymbol{\gamma }_i=a_i\boldsymbol{\alpha }_i$
,
$\boldsymbol{{B}}\boldsymbol{\gamma }_i=a_i\boldsymbol{\alpha }_i$
,
![]() $\forall \,i\in \mathcal{I}$
. Define
$\forall \,i\in \mathcal{I}$
. Define
![]() $\boldsymbol{{T}}\,:\!=\,(t_{i,j})_{n\times m}=\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
. Then it is easy to find that
$\boldsymbol{{T}}\,:\!=\,(t_{i,j})_{n\times m}=\boldsymbol{{R}}^{-1}\boldsymbol{\alpha }$
. Then it is easy to find that
and
Moreover, one can pick a positive definite matrix
![]() $\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
with
$\boldsymbol{{S}}=(s_{i,k})_{n\times n}$
with
![]() $s_{i,k}=(1+\epsilon )r_{i,k}\geq 0$
,
$s_{i,k}=(1+\epsilon )r_{i,k}\geq 0$
,
![]() $i,k\in \mathcal{I}$
, such that
$i,k\in \mathcal{I}$
, such that
and
Note that Lemma 2.1
![]() $(v)$
will help us to find a constant
$(v)$
will help us to find a constant
![]() $A_1\gt 0$
such that
$A_1\gt 0$
such that
Chosen
![]() $\epsilon \gt 0$
small enough, (3.10) implies
$\epsilon \gt 0$
small enough, (3.10) implies
 \begin{equation}{} \begin{split} \sum \limits _{i\in \mathcal{K}}a_im_i\left [8\pi -(1+\epsilon )^2\sum \limits _{k\in \mathcal{K}}a_kr_{i,k}m_k\right ]\gt 0,\quad \forall \,\,\emptyset \neq \mathcal{K} \subset \mathcal{I}. \end{split} \end{equation}
\begin{equation}{} \begin{split} \sum \limits _{i\in \mathcal{K}}a_im_i\left [8\pi -(1+\epsilon )^2\sum \limits _{k\in \mathcal{K}}a_kr_{i,k}m_k\right ]\gt 0,\quad \forall \,\,\emptyset \neq \mathcal{K} \subset \mathcal{I}. \end{split} \end{equation}
Let
 \begin{align*} \overline{\rho }_i(t)& \,:\!=\,\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)-s\sum \limits ^n_{k=1}r_{i,k}\right )_{+},\quad \widetilde{\rho }_i(t)\,:\!=\,\left (\sum \limits ^m_{j=1}t_{i,j}v_j(t)-s\right )_{+},\quad i\in \mathcal{I},\\[5pt] \overline{\Omega }_i(t) & \,:\!=\,\left \{x\in \mathbb{R}^2\,:\,\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)\gt s\sum \limits ^n_{k=1}r_{i,k}\right \},\quad \widetilde{\Omega }_i(t)\,:\!=\,\left \{x\in \mathbb{R}^2:\sum \limits ^m_{j=1}t_{i,j}v_j(t)\gt s\right \},\quad i\in \mathcal{I}, \end{align*}
\begin{align*} \overline{\rho }_i(t)& \,:\!=\,\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)-s\sum \limits ^n_{k=1}r_{i,k}\right )_{+},\quad \widetilde{\rho }_i(t)\,:\!=\,\left (\sum \limits ^m_{j=1}t_{i,j}v_j(t)-s\right )_{+},\quad i\in \mathcal{I},\\[5pt] \overline{\Omega }_i(t) & \,:\!=\,\left \{x\in \mathbb{R}^2\,:\,\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)\gt s\sum \limits ^n_{k=1}r_{i,k}\right \},\quad \widetilde{\Omega }_i(t)\,:\!=\,\left \{x\in \mathbb{R}^2:\sum \limits ^m_{j=1}t_{i,j}v_j(t)\gt s\right \},\quad i\in \mathcal{I}, \end{align*}
and
We claim some facts in the following. First, since
![]() $\widetilde{\rho }_i(t)\in H^1_0(\widetilde{\Omega }_i(t))$
and
$\widetilde{\rho }_i(t)\in H^1_0(\widetilde{\Omega }_i(t))$
and
![]() $\nabla \widetilde{\rho }_i(t)=\sum \limits ^m_{j=1}t_{i,j}\nabla v_j(t)$
in
$\nabla \widetilde{\rho }_i(t)=\sum \limits ^m_{j=1}t_{i,j}\nabla v_j(t)$
in
![]() ${\Omega }(t)$
, then
${\Omega }(t)$
, then
![]() $\widetilde{\rho }_i(t)\in H^1_0({\Omega }(t))$
for all
$\widetilde{\rho }_i(t)\in H^1_0({\Omega }(t))$
for all
![]() $i\in \mathcal{I}$
. Second, the Lebesgue measure of
$i\in \mathcal{I}$
. Second, the Lebesgue measure of
![]() $\Omega (t)$
, denoted by
$\Omega (t)$
, denoted by
![]() $|\Omega (t)|$
, is finite. This is because
$|\Omega (t)|$
, is finite. This is because
 \begin{align*} s\cdot |\Omega (t)|\leq s\sum \limits ^n_{i=1}|\widetilde{\Omega }_i(t)| \leq \sum \limits ^n_{i=1}\left \|\sum \limits ^m_{j=1}t_{i,j}v_j(\cdot,t)\right \|_{L^1(\mathbb{R}^2)}\leq c_1 \end{align*}
\begin{align*} s\cdot |\Omega (t)|\leq s\sum \limits ^n_{i=1}|\widetilde{\Omega }_i(t)| \leq \sum \limits ^n_{i=1}\left \|\sum \limits ^m_{j=1}t_{i,j}v_j(\cdot,t)\right \|_{L^1(\mathbb{R}^2)}\leq c_1 \end{align*}
implies that
![]() $|\Omega (t)|\leq c_{1}/s$
. Third,
$|\Omega (t)|\leq c_{1}/s$
. Third,
![]() $|\overline{\Omega }_i(t)|\leq c_{1}/s$
holds out due to
$|\overline{\Omega }_i(t)|\leq c_{1}/s$
holds out due to
Finally, without loss of generality, we assume
![]() $|\Omega (t)|\geq 1$
and
$|\Omega (t)|\geq 1$
and
![]() $|\overline{\Omega }_i(t)|\gt 0$
for all
$|\overline{\Omega }_i(t)|\gt 0$
for all
![]() $i\in \mathcal{I}$
. If
$i\in \mathcal{I}$
. If
![]() $|\overline{\Omega }_i(t)|=0$
for some
$|\overline{\Omega }_i(t)|=0$
for some
![]() $i\in \mathcal{I}$
, classical techniques are sufficient to analyse this case.
$i\in \mathcal{I}$
, classical techniques are sufficient to analyse this case.
Fixing
![]() $i\in \mathcal{I}$
, it is obvious that
$i\in \mathcal{I}$
, it is obvious that
 \begin{align*} a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx & = a_i\int _{\overline{\Omega }_i(t)}u_i\!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j}v_j\right )dx+a_i\int _{\mathbb{R}^2\setminus \overline{\Omega }_i(t)}u_i\!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j}v_j\right )dx\\[5pt]& \leq a_i\int _{\overline{\Omega }_i(t)}u_i \overline{\rho }_idx+sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )\\[5pt]& \leq a_i\int _{\mathbb{R}^2}u_i \overline{\rho }_idx+sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right ). \end{align*}
\begin{align*} a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx & = a_i\int _{\overline{\Omega }_i(t)}u_i\!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j}v_j\right )dx+a_i\int _{\mathbb{R}^2\setminus \overline{\Omega }_i(t)}u_i\!\left (\sum \limits ^{m}_{j=1}\alpha _{i,j}v_j\right )dx\\[5pt]& \leq a_i\int _{\overline{\Omega }_i(t)}u_i \overline{\rho }_idx+sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )\\[5pt]& \leq a_i\int _{\mathbb{R}^2}u_i \overline{\rho }_idx+sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right ). \end{align*}
Denote
![]() $u^*_i=m_i\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)\left (\int _{\mathbb{R}^2}\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)dx\right )^{-1}$
. Then,
$u^*_i=m_i\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)\left (\int _{\mathbb{R}^2}\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)dx\right )^{-1}$
. Then,
![]() $\|u^*_i\|_1=m_i$
and a classical entropy minimisation in [Reference Calvez and Corrias5, Lemma 2.1] implies that the function
$\|u^*_i\|_1=m_i$
and a classical entropy minimisation in [Reference Calvez and Corrias5, Lemma 2.1] implies that the function
satisfies
 \begin{align*} \mathcal{E}\!\left (u_i;\,(1+\epsilon )\overline{\rho }_i+\log H\right ) & \geq \mathcal{E}\!\left (u^*_i;\,(1+\epsilon )\overline{\rho }_i+\log H\right )\\[5pt] & =m_i\log m_i-m_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)dx\right )-m_i\log\! (4\pi ). \end{align*}
\begin{align*} \mathcal{E}\!\left (u_i;\,(1+\epsilon )\overline{\rho }_i+\log H\right ) & \geq \mathcal{E}\!\left (u^*_i;\,(1+\epsilon )\overline{\rho }_i+\log H\right )\\[5pt] & =m_i\log m_i-m_i\log \!\left (\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp ({(1+\epsilon )\overline{\rho }_i(x,t)})H(x)dx\right )-m_i\log\! (4\pi ). \end{align*}
Combining the aforementioned findings, we arrive at the following
 \begin{align*} &(1+\epsilon )a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx- a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt]& \leq (1+\epsilon )a_i\int _{\mathbb{R}^2}u_i\overline{\rho }_idx- a_i\int _{\mathbb{R}^2}u_i\log u_i dx+(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )\\[5pt]& \leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [{(1+\epsilon )\overline{\rho }_i(x,t)}\right ]H(x)dx\right \}-a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx\\[5pt] & \quad +(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log \frac{4\pi }{m_i}\\[5pt]& \leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [(1+\epsilon )\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)-s\sum \limits ^n_{k=1}r_{i,k}\right )_+\right ]H(x) dx\right \}\\[5pt] &\quad -a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log \frac{4\pi }{m_i}, \end{align*}
\begin{align*} &(1+\epsilon )a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx- a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt]& \leq (1+\epsilon )a_i\int _{\mathbb{R}^2}u_i\overline{\rho }_idx- a_i\int _{\mathbb{R}^2}u_i\log u_i dx+(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )\\[5pt]& \leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [{(1+\epsilon )\overline{\rho }_i(x,t)}\right ]H(x)dx\right \}-a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx\\[5pt] & \quad +(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log \frac{4\pi }{m_i}\\[5pt]& \leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [(1+\epsilon )\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j(t)-s\sum \limits ^n_{k=1}r_{i,k}\right )_+\right ]H(x) dx\right \}\\[5pt] &\quad -a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log \frac{4\pi }{m_i}, \end{align*}
where the choice of matrix
![]() $\boldsymbol{{S}}$
allows one to conclude that
$\boldsymbol{{S}}$
allows one to conclude that
 \begin{align*} & (1+\epsilon )a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx- a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &\leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [\sum \limits ^n_{k=1}s_{i,k}\left (\sum \limits ^m_{j=1}t_{k,j}v_j-s\right )_{+}\right ]H(x)dx\right \}\\[5pt] & \quad -a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_{2i}\\[5pt] &= a_im_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]-a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_{2i}, \end{align*}
\begin{align*} & (1+\epsilon )a_i\sum \limits ^{m}_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx- a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &\leq a_im_i\log \!\left \{\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left [\sum \limits ^n_{k=1}s_{i,k}\left (\sum \limits ^m_{j=1}t_{k,j}v_j-s\right )_{+}\right ]H(x)dx\right \}\\[5pt] & \quad -a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_{2i}\\[5pt] &= a_im_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]-a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_{2i}, \end{align*}
where
![]() $c_{2i}=(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log\! (4\pi/m_i)$
,
$c_{2i}=(1+\epsilon )sa_im_i\left (\sum \limits ^n_{k=1}r_{i,k}\right )+a_im_i\log\! (4\pi/m_i)$
,
![]() $i\in \mathcal{I}$
. Then, summing it with respect to
$i\in \mathcal{I}$
. Then, summing it with respect to
![]() $i$
from
$i$
from
![]() $i=1$
to
$i=1$
to
![]() $i=n$
, we get
$i=n$
, we get
 \begin{align} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\leq &\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_im_i\log \left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\nonumber\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}c_{2i}.\nonumber \end{align}
\begin{align} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\leq &\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_im_i\log \left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\nonumber\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}c_{2i}.\nonumber \end{align}
Choose
Since (3.11) implies that
 \begin{align*} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}}) & = 8\pi \sum \limits _{i\in \mathcal{K}}M_i-\sum \limits _{i,k\in \mathcal{K}}s_{i,k}M_iM_k\\[5pt] &=(1+\epsilon )\left [8\pi \sum \limits _{i\in \mathcal{K}}a_im_i-(1+\epsilon )^2\sum \limits _{i,k\in \mathcal{K}}a_ia_kr_{i,k}m_im_k\right ]\\[5pt]& \gt 0,\quad \forall \,\,\emptyset \neq \mathcal{K}\subset \mathcal{I}, \end{align*}
\begin{align*} \Lambda ^{\boldsymbol{{S}}}_{\mathcal{K}}(\boldsymbol{{M}}) & = 8\pi \sum \limits _{i\in \mathcal{K}}M_i-\sum \limits _{i,k\in \mathcal{K}}s_{i,k}M_iM_k\\[5pt] &=(1+\epsilon )\left [8\pi \sum \limits _{i\in \mathcal{K}}a_im_i-(1+\epsilon )^2\sum \limits _{i,k\in \mathcal{K}}a_ia_kr_{i,k}m_im_k\right ]\\[5pt]& \gt 0,\quad \forall \,\,\emptyset \neq \mathcal{K}\subset \mathcal{I}, \end{align*}
then the Moser–Trudinger inequality for system in Lemma 3.3 helps us to get that
 \begin{align*} &\sum \limits ^n_{i=1} M_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\\[5pt] &=(1+\epsilon )\sum \limits ^n_{i=1}a_im_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\\[5pt]& \leq \frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}s_{i,k}\int _{\mathbb{R}^2}\nabla \widetilde{\rho }_i\cdot \nabla \widetilde{\rho }_k dx+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx+B\\[5pt]& \leq \frac{1}{2}(1+\epsilon )\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx+c_3, \end{align*}
\begin{align*} &\sum \limits ^n_{i=1} M_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\\[5pt] &=(1+\epsilon )\sum \limits ^n_{i=1}a_im_i\log \!\left [\frac{1}{4\pi }\int _{\mathbb{R}^2}\exp \!\left (\sum \limits ^n_{k=1}s_{i,k}\widetilde{\rho }_k\right )H(x)dx\right ]\\[5pt]& \leq \frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}s_{i,k}\int _{\mathbb{R}^2}\nabla \widetilde{\rho }_i\cdot \nabla \widetilde{\rho }_k dx+\frac{1}{4\pi }\sum \limits _{i,k\in \mathcal{I}}M_is_{i,k}\int _{\mathbb{R}^2}\widetilde{\rho }_kH(x)dx+B\\[5pt]& \leq \frac{1}{2}(1+\epsilon )\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx+c_3, \end{align*}
where we have used the bound of
![]() $\|v_j\|_{L^1(\mathbb{R}^2)}$
,
$\|v_j\|_{L^1(\mathbb{R}^2)}$
,
![]() $j\in \mathcal{J}$
, and
$j\in \mathcal{J}$
, and
![]() $\int _{\mathbb{R}^2}H(x)dx=4\pi$
. This together with (3.12) and the positivity of
$\int _{\mathbb{R}^2}H(x)dx=4\pi$
. This together with (3.12) and the positivity of
![]() $\boldsymbol{{B}}$
implies that
$\boldsymbol{{B}}$
implies that
 \begin{align*} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx & \leq \frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}c_{2i}+\frac{c_3}{(1+\epsilon )^2}. \end{align*}
\begin{align*} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx & \leq \frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}c_{2i}+\frac{c_3}{(1+\epsilon )^2}. \end{align*}
Therefore, we have finished the proof of this lemma.
As a consequence of Lemma 3.4, the bound on modified total entropy
![]() $\mathcal{S}$
could be obtained.
$\mathcal{S}$
could be obtained.
Lemma 3.5.
Let
![]() $T\gt 0$
. Under the same assumptions in Lemma 3.4, there exists a constant
$T\gt 0$
. Under the same assumptions in Lemma 3.4, there exists a constant
![]() $c=c(T)\gt 0$
such that
$c=c(T)\gt 0$
such that
and
hold out for
![]() $t\in (0,T)$
.
$t\in (0,T)$
.
Proof. Notice that positive definite matrix
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}= \boldsymbol{\alpha }^{T}{\boldsymbol{{R}}}^{-1}\boldsymbol{\alpha }$
satisfies
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}= \boldsymbol{\alpha }^{T}{\boldsymbol{{R}}}^{-1}\boldsymbol{\alpha }$
satisfies
Then thanks to Lemma 3.1, there exists a modified free energy functional
![]() $\mathcal{F}$
given by
$\mathcal{F}$
given by
 \begin{equation} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx \end{split} \end{equation}
\begin{equation} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]=&\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _{l}v_jv_l\right )dx \end{split} \end{equation}
satisfying
 \begin{align} \frac{d}{dt}\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]&+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\bigg \{u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[5pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\bigg \}dx\nonumber\\[5pt]& \leq \frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+c_1\\[5pt]& \leq \frac{a^*\alpha ^*|\mathcal{I}||\mathcal{J}|}{4}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\left |\nabla v_j\right |^2dx+c_1\nonumber \end{align}
\begin{align} \frac{d}{dt}\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]&+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\bigg \{u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\nonumber\\[5pt] &+\left |\nabla \!\left (\log\! (u_i+1)-\frac{1}{2}\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2\bigg \}dx\nonumber\\[5pt]& \leq \frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\left |\nabla \!\left (\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+c_1\\[5pt]& \leq \frac{a^*\alpha ^*|\mathcal{I}||\mathcal{J}|}{4}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\left |\nabla v_j\right |^2dx+c_1\nonumber \end{align}
with some constant
![]() $c_1\gt 0$
. Moreover, Lemma 3.4 implies the existence of small
$c_1\gt 0$
. Moreover, Lemma 3.4 implies the existence of small
![]() $\epsilon \gt 0$
such that
$\epsilon \gt 0$
such that
 \begin{align} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx \leq &\frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\nonumber\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_2\nonumber \end{align}
\begin{align} \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx \leq &\frac{1}{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\nonumber\\[5pt] &+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1) dx\\[5pt] &-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+c_2\nonumber \end{align}
is true with some
![]() $c_2\gt 0$
. On the one hand, one has
$c_2\gt 0$
. On the one hand, one has
 \begin{equation} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]\geq &\frac{\epsilon }{1+\epsilon }\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx+\frac{\epsilon }{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx-c_2 \end{split} \end{equation}
\begin{equation} \begin{split} \mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]\geq &\frac{\epsilon }{1+\epsilon }\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx+\frac{\epsilon }{2(1+\epsilon )}\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx+\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx-c_2 \end{split} \end{equation}
from (3.15) and (3.17). On the other hand, we have
 \begin{align*} \begin{split} \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx&=\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] &- \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx, \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx&=\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] &- \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}u_iv_jdx, \end{split} \end{align*}
which together with (3.17) ensures that
 \begin{align*} \begin{split} \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\leq &\frac{1+\epsilon }{\epsilon }\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] &- \frac{1+\epsilon }{2\epsilon }\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx\\[5pt] &-\frac{1}{\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{(1+\epsilon )c_2}{\epsilon }. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\nabla v_j\cdot \nabla v_ldx\leq &\frac{1+\epsilon }{\epsilon }\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\sum \limits ^{n}_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] &- \frac{1+\epsilon }{2\epsilon }\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _{l}\int _{\mathbb{R}^2}v_jv_ldx\\[5pt] &-\frac{1}{\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+\frac{(1+\epsilon )c_2}{\epsilon }. \end{split} \end{align*}
Further, using the positivity of
![]() $\boldsymbol{{B}}$
and the bound on the
$\boldsymbol{{B}}$
and the bound on the
![]() $\|v_j\|_{L^2(\mathbb{R}^2)}$
by Lemma 2.1
$\|v_j\|_{L^2(\mathbb{R}^2)}$
by Lemma 2.1
![]() $(v)$
, there exists a constant
$(v)$
, there exists a constant
![]() $c_3\gt 0$
such that
$c_3\gt 0$
such that
 \begin{align*} \sum \limits ^m_{j=1}\int _{\mathbb{R}^2}|\nabla v_j|^2dx\leq &\frac{(1+\epsilon )c_3}{\epsilon }\left (\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+1\right ). \end{align*}
\begin{align*} \sum \limits ^m_{j=1}\int _{\mathbb{R}^2}|\nabla v_j|^2dx\leq &\frac{(1+\epsilon )c_3}{\epsilon }\left (\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+1\right ). \end{align*}
Applying above inequalities and from (3.16), it follows that
 \begin{equation} \begin{split} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] \leq & \frac{(1+\epsilon )c_3a^*\alpha ^*|\mathcal{I}||\mathcal{J}|}{4\epsilon }\left (\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+1\right )+c_1 \end{split} \end{equation}
\begin{equation} \begin{split} \frac{d}{dt}&\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]+\frac{1}{2}\int _{\mathbb{R}^2}\left (\partial _t\boldsymbol{{v}}\right )^T\boldsymbol{{B}}\!\left (\partial _t\boldsymbol{{v}}\right )dx+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] \leq & \frac{(1+\epsilon )c_3a^*\alpha ^*|\mathcal{I}||\mathcal{J}|}{4\epsilon }\left (\mathcal{F}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx+1\right )+c_1 \end{split} \end{equation}
for
![]() $t\in (0,T)$
. To estimate the second term on the right side of (3.19), we first observe that
$t\in (0,T)$
. To estimate the second term on the right side of (3.19), we first observe that
 \begin{align*} \begin{split} -\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx=&\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx\\[5pt] &-\frac{2\log 2}{1+\epsilon }\sum \limits ^n_{i=1}a_im_i\\[5pt] \leq &\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx, \end{split} \end{align*}
\begin{align*} \begin{split} -\frac{1}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log H(x)dx=&\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx\\[5pt] &-\frac{2\log 2}{1+\epsilon }\sum \limits ^n_{i=1}a_im_i\\[5pt] \leq &\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx, \end{split} \end{align*}
where we take the derivative of the right term to see that
 \begin{align*} \begin{split} \frac{d}{dt}&\left (\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx\right )\\[5pt] =&-\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\nabla \!\left [\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right ]\cdot \nabla \log\! \big(1+|x|^2\big)dx\\[5pt] &-\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{\nabla u_i}{u_i+1}\cdot \nabla \log\! \big(1+|x|^2\big)dx \\ \leq &\frac{1}{2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &+\frac{2}{(1+\epsilon )^2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\big|\nabla \log\! \big(1+|x|^2\big)\big|^2dx\\[5pt] &+\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\log\! (u_i+1)\Delta \log\! \big(1+|x|^2\big)dx\\[5pt] \leq &\frac{1}{2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+10\sum \limits ^n_{i=1}a_im_i \quad \text{for}\,\,t\in (0,T), \end{split} \end{align*}
\begin{align*} \begin{split} \frac{d}{dt}&\left (\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i(x)\log\! \big(1+|x|^2\big)dx\right )\\[5pt] =&-\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\nabla \!\left [\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right ]\cdot \nabla \log\! \big(1+|x|^2\big)dx\\[5pt] &-\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{\nabla u_i}{u_i+1}\cdot \nabla \log\! \big(1+|x|^2\big)dx \\ \leq &\frac{1}{2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx\\[5pt] &+\frac{2}{(1+\epsilon )^2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\big|\nabla \log\! \big(1+|x|^2\big)\big|^2dx\\[5pt] &+\frac{2}{1+\epsilon }\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\log\! (u_i+1)\Delta \log\! \big(1+|x|^2\big)dx\\[5pt] \leq &\frac{1}{2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}u_i\left |\nabla \!\left (\log\! (u_i+1)-\sum \limits ^m_{j=1}\alpha _{i,j}v_j\right )\right |^2dx+10\sum \limits ^n_{i=1}a_im_i \quad \text{for}\,\,t\in (0,T), \end{split} \end{align*}
by Young’s inequality, since
 \begin{align*} \big|\nabla \log\! \big(1+|x|^2\big)\big|= \left |\frac{2x}{1+|x|^2}\right |\leq 1,\quad \big|\Delta \log\! \big(1+|x|^2\big)\big|= \left |\frac{4}{\big(1+|x|^2\big)^2}\right |\leq 4, \end{align*}
\begin{align*} \big|\nabla \log\! \big(1+|x|^2\big)\big|= \left |\frac{2x}{1+|x|^2}\right |\leq 1,\quad \big|\Delta \log\! \big(1+|x|^2\big)\big|= \left |\frac{4}{\big(1+|x|^2\big)^2}\right |\leq 4, \end{align*}
and
![]() $\log\! (s+1)\leq s$
for all
$\log\! (s+1)\leq s$
for all
![]() $s\gt 0$
. Thereby, denoting
$s\gt 0$
. Thereby, denoting
one derives that
with
![]() $c_4=10\sum \limits ^n_{i=1}a_im_i+c_1$
, where the Gronwall argument means that
$c_4=10\sum \limits ^n_{i=1}a_im_i+c_1$
, where the Gronwall argument means that
Hence, we have proved (3.13)–(3.14) due to (3.18), the choices of positive
![]() $a_i$
,
$a_i$
,
![]() $i\in \mathcal{I}$
, the positivity of
$i\in \mathcal{I}$
, the positivity of
![]() $\boldsymbol{{B}}$
and the bound on the
$\boldsymbol{{B}}$
and the bound on the
![]() $\|v_j\|_{L^2(\mathbb{R}^2)}$
,
$\|v_j\|_{L^2(\mathbb{R}^2)}$
,
![]() $j\in \mathcal{J}$
.
$j\in \mathcal{J}$
.
A straightforward argument [Reference Nagai, Senba and Yoshida36, Lemma 3.6] could be indeed used to obtain
![]() $L^2$
estimates for the solutions by the bound on
$L^2$
estimates for the solutions by the bound on
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
Lemma 3.6.
For
![]() $T\gt 0$
, there exists a constant
$T\gt 0$
, there exists a constant
![]() $c=c(T)\gt 0$
such that
$c=c(T)\gt 0$
such that
Proof. From Lemma 3.5, there exists a constant
![]() $c_1=c_1(T)\gt 0$
such that
$c_1=c_1(T)\gt 0$
such that
and
We multiply the
![]() $i$
-the equation in (1.5) by
$i$
-the equation in (1.5) by
![]() $u_i$
and integrate them over
$u_i$
and integrate them over
![]() $\mathbb{R}^2$
to have
$\mathbb{R}^2$
to have
 \begin{equation} \begin{split} \frac{1}{2}\frac{d}{dt}\left (\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx\right )=&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\Delta v_jdx\\[5pt] =&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\left (\partial _t v_j+\beta _jv_j-\sum \limits ^n_{k=1}\gamma _{k,j}u_k\right )dx\\[5pt] =&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx+\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}\alpha _{i,j}\gamma _{k,j}\int _{\mathbb{R}^2}u^2_iu_kdx\\[5pt] &-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u^2_iv_jdx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\partial _tv_jdx \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1}{2}\frac{d}{dt}\left (\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx\right )=&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\Delta v_jdx\\[5pt] =&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\left (\partial _t v_j+\beta _jv_j-\sum \limits ^n_{k=1}\gamma _{k,j}u_k\right )dx\\[5pt] =&-\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}|\nabla u_i|^2dx+\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}\alpha _{i,j}\gamma _{k,j}\int _{\mathbb{R}^2}u^2_iu_kdx\\[5pt] &-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u^2_iv_jdx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\partial _tv_jdx \end{split} \end{equation}
for
![]() $t\in (0,T)$
. It is clear that
$t\in (0,T)$
. It is clear that
 \begin{align*} \begin{split} &\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}\alpha _{i,j}\gamma _{k,j}\int _{\mathbb{R}^2}u^2_iu_kdx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u^2_iv_jdx\\[5pt] &\leq \frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}|\alpha _{i,j}||\gamma _{k,j}|\int _{\mathbb{R}^2}\left(u^3_i+u^3_k\right)dx+\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}||\beta _j|\int _{\mathbb{R}^2}\left(u^3_i+v^3_j\right)dx\\[5pt] &\leq \frac{\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^3_idx+\frac{\alpha ^*\beta ^*|\mathcal{I}|A^3_3}{2}\\[5pt] &\leq \frac{c_1\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\eta _i\int _{\mathbb{R}^2}|\nabla u_i|^2dx\\[5pt] &\qquad +\frac{\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}c_{2i}m_i+\frac{\alpha ^*\beta ^*|\mathcal{I}|A^3_3}{2}, \end{split} \end{align*}
\begin{align*} \begin{split} &\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}\alpha _{i,j}\gamma _{k,j}\int _{\mathbb{R}^2}u^2_iu_kdx-\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u^2_iv_jdx\\[5pt] &\leq \frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^n_{k=1}\sum \limits ^m_{j=1}|\alpha _{i,j}||\gamma _{k,j}|\int _{\mathbb{R}^2}\left(u^3_i+u^3_k\right)dx+\frac{1}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}||\beta _j|\int _{\mathbb{R}^2}\left(u^3_i+v^3_j\right)dx\\[5pt] &\leq \frac{\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^3_idx+\frac{\alpha ^*\beta ^*|\mathcal{I}|A^3_3}{2}\\[5pt] &\leq \frac{c_1\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\eta _i\int _{\mathbb{R}^2}|\nabla u_i|^2dx\\[5pt] &\qquad +\frac{\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|}{2}\sum \limits ^n_{i=1}c_{2i}m_i+\frac{\alpha ^*\beta ^*|\mathcal{I}|A^3_3}{2}, \end{split} \end{align*}
where we have used Young’s inequality and the following facts
![]() $\sum \limits ^m_{j=1}\|v_j\|_{L^3(\mathbb{R}^2)}\leq A_3$
hold due to Lemma 2.1
$\sum \limits ^m_{j=1}\|v_j\|_{L^3(\mathbb{R}^2)}\leq A_3$
hold due to Lemma 2.1
![]() $(v)$
, and for any
$(v)$
, and for any
![]() $\eta _i\in (0,1)$
,
$\eta _i\in (0,1)$
,
![]() $i\in \mathcal{I}$
,
$i\in \mathcal{I}$
,
 \begin{align*} \begin{split} \int _{\mathbb{R}^2}u^3_idx&\leq \eta _i\left (\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right )\left (\int _{\mathbb{R}^2}|\nabla u_i|^2dx\right )+c_{2i}\int _{\mathbb{R}^2}u_idx\\[5pt] &\leq c_1\eta _i \int _{\mathbb{R}^2}|\nabla u_i|^2dx+c_{2i}m_i,\quad i\in \mathcal{I}, \end{split} \end{align*}
\begin{align*} \begin{split} \int _{\mathbb{R}^2}u^3_idx&\leq \eta _i\left (\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right )\left (\int _{\mathbb{R}^2}|\nabla u_i|^2dx\right )+c_{2i}\int _{\mathbb{R}^2}u_idx\\[5pt] &\leq c_1\eta _i \int _{\mathbb{R}^2}|\nabla u_i|^2dx+c_{2i}m_i,\quad i\in \mathcal{I}, \end{split} \end{align*}
exists with
![]() $c_{2i}=c_{2i}(\eta _i)\gt 0$
from (2.4). As for the rightmost integral of (3.21), we first use Hölder’s inequality to find that
$c_{2i}=c_{2i}(\eta _i)\gt 0$
from (2.4). As for the rightmost integral of (3.21), we first use Hölder’s inequality to find that
Applying the Gagliardo–Nirenberg inequality with
![]() $c_3\gt 0$
to have
$c_3\gt 0$
to have
and it infers that
 \begin{align*} \begin{split} -\frac{1}{2}&\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\partial _tv_jdx\\[5pt] \leq &\frac{c_3}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}|\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\| u_i\|_{L^2(\mathbb{R}^2)}\|\partial _tv_j\|_{L^2(\mathbb{R}^2)}\\[5pt] \leq &\frac{c_3\alpha ^*|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\eta _i\|\nabla u_i\|^2_{L^2(\mathbb{R}^2)}+\frac{c_3\alpha ^*}{8}\left (\sum \limits ^n_{i=1}\frac{1}{\eta _i}\|u_i\|^2_{L^2(\mathbb{R}^2)}\right ) \cdot \left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right ) \end{split} \end{align*}
\begin{align*} \begin{split} -\frac{1}{2}&\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}u^2_i\partial _tv_jdx\\[5pt] \leq &\frac{c_3}{2}\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}|\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\| u_i\|_{L^2(\mathbb{R}^2)}\|\partial _tv_j\|_{L^2(\mathbb{R}^2)}\\[5pt] \leq &\frac{c_3\alpha ^*|\mathcal{J}|}{2}\sum \limits ^n_{i=1}\eta _i\|\nabla u_i\|^2_{L^2(\mathbb{R}^2)}+\frac{c_3\alpha ^*}{8}\left (\sum \limits ^n_{i=1}\frac{1}{\eta _i}\|u_i\|^2_{L^2(\mathbb{R}^2)}\right ) \cdot \left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right ) \end{split} \end{align*}
by Young’s inequality. Hence, (3.21) gives us that
 \begin{equation} \begin{split} &\frac{d}{dt}\left (\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx\right )+\sum \limits ^n_{i=1}\left \{2-\alpha ^*\left [c_1\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|\eta _i\right \}\int _{\mathbb{R}^2}|\nabla u_i|^2dx\\[5pt] &\leq \frac{c_3\alpha ^*}{4}\left (\sum \limits ^n_{i=1}\frac{1}{\eta _i} \|u_i\|^2_{L^2(\mathbb{R}^2)}\right )\left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right )\\[5pt] &\quad +\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|\sum \limits ^n_{i=1}c_{2i}m_i+\alpha ^*\beta ^*|\mathcal{I}|A^3_3\quad \text{for}\,\,t\in (0,T). \end{split} \end{equation}
\begin{equation} \begin{split} &\frac{d}{dt}\left (\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx\right )+\sum \limits ^n_{i=1}\left \{2-\alpha ^*\left [c_1\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|\eta _i\right \}\int _{\mathbb{R}^2}|\nabla u_i|^2dx\\[5pt] &\leq \frac{c_3\alpha ^*}{4}\left (\sum \limits ^n_{i=1}\frac{1}{\eta _i} \|u_i\|^2_{L^2(\mathbb{R}^2)}\right )\left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right )\\[5pt] &\quad +\alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|\sum \limits ^n_{i=1}c_{2i}m_i+\alpha ^*\beta ^*|\mathcal{I}|A^3_3\quad \text{for}\,\,t\in (0,T). \end{split} \end{equation}
Because
 \begin{align*} \|u_i\|^2_{L^2(\mathbb{R}^2)}&\leq c_4\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\| u_i\|_{L^1(\mathbb{R}^2)}=c_4m_i\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\\[5pt]& \leq \|\nabla u_i\|^2_{L^2(\mathbb{R}^2)}+\frac{c^2_4m^2_i}{4} \end{align*}
\begin{align*} \|u_i\|^2_{L^2(\mathbb{R}^2)}&\leq c_4\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\| u_i\|_{L^1(\mathbb{R}^2)}=c_4m_i\|\nabla u_i\|_{L^2(\mathbb{R}^2)}\\[5pt]& \leq \|\nabla u_i\|^2_{L^2(\mathbb{R}^2)}+\frac{c^2_4m^2_i}{4} \end{align*}
is right for some
![]() $c_4\gt 0$
, we take
$c_4\gt 0$
, we take
![]() $\eta _i=1/\{\alpha ^*\left [c_1\!\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|\}\gt 0$
,
$\eta _i=1/\{\alpha ^*\left [c_1\!\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|\}\gt 0$
,
![]() $i\in \mathcal{I}$
, small enough in (3.22) to arrive at
$i\in \mathcal{I}$
, small enough in (3.22) to arrive at
 \begin{align*} \begin{split} y^{\prime}(t)&+\left [1-\frac{c_3(\alpha ^*)^2\left [c_1\!\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|}{4}\left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right )\right ]y(t)\\[5pt] \leq\ & \alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|\sum \limits ^n_{i=1}c_{2i}m_i+\frac{c^2_4}{4}\sum \limits ^n_{i=1}m^2_i+\alpha ^*\beta ^*|\mathcal{I}|A^3_3 \end{split} \end{align*}
\begin{align*} \begin{split} y^{\prime}(t)&+\left [1-\frac{c_3(\alpha ^*)^2\left [c_1\!\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )+c_3\right ]|\mathcal{J}|}{4}\left (\sum \limits ^m_{j=1}\|\partial _tv_j\|^2_{L^2(\mathbb{R}^2)}\right )\right ]y(t)\\[5pt] \leq\ & \alpha ^*\left (\beta ^*+2\gamma ^*|\mathcal{I}|\right )|\mathcal{J}|\sum \limits ^n_{i=1}c_{2i}m_i+\frac{c^2_4}{4}\sum \limits ^n_{i=1}m^2_i+\alpha ^*\beta ^*|\mathcal{I}|A^3_3 \end{split} \end{align*}
for
![]() $t\in (0,T)$
, where
$t\in (0,T)$
, where
![]() $y(t)\,:\!=\,\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx$
. Together with (3.20), the
$y(t)\,:\!=\,\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}u^2_idx$
. Together with (3.20), the
![]() $L^2$
estimates for the solutions can be obtained by solving this ODE.
$L^2$
estimates for the solutions can be obtained by solving this ODE.
Proof of Theorem
1.1. Let
![]() $0\lt T\leq \infty$
. Once one has
$0\lt T\leq \infty$
. Once one has
![]() $L^2$
estimates on
$L^2$
estimates on
![]() $u_i$
,
$u_i$
,
![]() $i\in \mathcal{I}$
, then
$i\in \mathcal{I}$
, then
![]() $L^p$
-
$L^p$
-
![]() $L^q$
estimates for the heat semigroup in Lemma 5.1 ensure that for
$L^q$
estimates for the heat semigroup in Lemma 5.1 ensure that for
![]() $r\in (1,\infty )$
, we have
$r\in (1,\infty )$
, we have
with some
![]() $c\gt 0$
. Consequently, applying the Moser iteration technique [Reference Alikakos1] with (3.23), it means that
$c\gt 0$
. Consequently, applying the Moser iteration technique [Reference Alikakos1] with (3.23), it means that
Therefore, the global result in Theorem 1.1 is an immediate consequence of the extensibility criterion in Lemma 2.1.
4. Proof of Theorem 1.2
Under strong self-repelling effect, the global existence of the Cauchy problem (1.5) with arbitrary initial data will be established in this section. As with the above treatment of the proof of Theorem 1.1, the main approach is to give a bound on the modified total entropy
![]() $\mathcal{S}$
. For this purpose, we would like to create a differential inequality for
$\mathcal{S}$
. For this purpose, we would like to create a differential inequality for
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
Lemma 4.1.
Assume that there exist positive constants
![]() $a_1,\cdots,a_n$
and a positive definite matrix
$a_1,\cdots,a_n$
and a positive definite matrix
![]() $\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
$\boldsymbol{{B}}=(b_{j,l})_{m\times m}$
such that
Let
with some
![]() $D_1,D_2\gt 0$
. Then, there exist a constant
$D_1,D_2\gt 0$
. Then, there exist a constant
![]() $c_1=c_1(a^*,b^*,\alpha ^*,\beta ^*,A_2,D_1,D_2,\|\boldsymbol{{u}}_0\|_{L^1(\mathbb{R}^2)},|\mathcal{I}|$
,
$c_1=c_1(a^*,b^*,\alpha ^*,\beta ^*,A_2,D_1,D_2,\|\boldsymbol{{u}}_0\|_{L^1(\mathbb{R}^2)},|\mathcal{I}|$
,
![]() $|\mathcal{J}|)\gt 0$
such that
$|\mathcal{J}|)\gt 0$
such that
where
![]() $\mathcal{G}$
is given by
$\mathcal{G}$
is given by
Moreover, if
![]() $\beta _j\gt 0$
for all
$\beta _j\gt 0$
for all
![]() $j\in \mathcal{J}$
, then there exist a constant
$j\in \mathcal{J}$
, then there exist a constant
![]() $c_2\gt 0$
independent of
$c_2\gt 0$
independent of
![]() $T$
such that
$T$
such that
Proof. Given
![]() $a_i\gt 0$
, testing the
$a_i\gt 0$
, testing the
![]() $i$
-th equation in (1.5) by
$i$
-th equation in (1.5) by
![]() $a_i\log\! (u_i+1)$
and summing the results with respect to
$a_i\log\! (u_i+1)$
and summing the results with respect to
![]() $i$
, we get
$i$
, we get
 \begin{equation} \begin{split} &\frac{d}{dt}\left [\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right ] +\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\frac{u_i}{u_i+1}\nabla u_i\cdot \nabla v_jdx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx\quad \text{for}\quad t\in (0,T). \end{split} \end{equation}
\begin{equation} \begin{split} &\frac{d}{dt}\left [\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\right ] +\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\frac{u_i}{u_i+1}\nabla u_i\cdot \nabla v_jdx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_jdx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx\quad \text{for}\quad t\in (0,T). \end{split} \end{equation}
Moreover, we observe that
 \begin{equation*} \begin{split} \frac{1}{2}&\frac{d}{dt}\left [\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _lv_jv_l\right )\right ]dx\\[5pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}(\Delta v_l-\beta _lv_l)\partial _tv_jdx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx \\ =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\Delta v_j-\beta _jv_j\right )\left (\Delta v_l-\beta _lv_l\right )dx\\[5pt] &+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_ldx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,j}\beta _l\int _{\mathbb{R}^2}u_iv_ldx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\quad \text{for}\quad t\in (0,T) \end{split} \end{equation*}
\begin{equation*} \begin{split} \frac{1}{2}&\frac{d}{dt}\left [\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _lv_jv_l\right )\right ]dx\\[5pt] =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}(\Delta v_l-\beta _lv_l)\partial _tv_jdx+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx \\ =&-\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\Delta v_j-\beta _jv_j\right )\left (\Delta v_l-\beta _lv_l\right )dx\\[5pt] &+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,j}\int _{\mathbb{R}^2}\nabla u_i\cdot \nabla v_ldx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\gamma _{i,j}\beta _l\int _{\mathbb{R}^2}u_iv_ldx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\quad \text{for}\quad t\in (0,T) \end{split} \end{equation*}
and that
 \begin{equation} \begin{split} D_1\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\leq & \sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\Delta v_j-\beta _jv_j\right )\left (\Delta v_l-\beta _lv_l\right )dx\\[5pt] \leq &D_2\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx. \end{split} \end{equation}
\begin{equation} \begin{split} D_1\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\leq & \sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\Delta v_j-\beta _jv_j\right )\left (\Delta v_l-\beta _lv_l\right )dx\\[5pt] \leq &D_2\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx. \end{split} \end{equation}
Then employing
![]() $\sum \limits ^m_{j=1}b_{j,l}\gamma _{i,j}=-a_i\alpha _{i,l}$
by (4.1), it is obvious that
$\sum \limits ^m_{j=1}b_{j,l}\gamma _{i,j}=-a_i\alpha _{i,l}$
by (4.1), it is obvious that
 \begin{equation} \begin{split} \frac{d}{dt}&\mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+D_1\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\\[5pt] \leq &\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\quad \text{for}\quad t\in (0,T) \end{split} \end{equation}
\begin{equation} \begin{split} \frac{d}{dt}&\mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]+\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+D_1\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\\[5pt] \leq &\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx-\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u_iv_jdx\\[5pt] &+\frac{1}{2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\quad \text{for}\quad t\in (0,T) \end{split} \end{equation}
due to (4.2) and (4.3). Since
![]() $\log\! (u_i+1)\leq \sqrt{u}_i$
,
$\log\! (u_i+1)\leq \sqrt{u}_i$
,
![]() $\|u_i\|_{L^1(\mathbb{R}^2)}=m_i$
,
$\|u_i\|_{L^1(\mathbb{R}^2)}=m_i$
,
![]() $i\in \mathcal{I}$
, and
$i\in \mathcal{I}$
, and
hold out, an application of Young’s inequality gives that
 \begin{equation} \begin{split} &\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}(\Delta v_j-\beta _jv_j)\log\! (u_i+1)dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}v_j\log\! (u_i+1)dx\\[5pt] &\leq \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i|\alpha _{i,j}|\int _{\mathbb{R}^2}|\Delta v_j-\beta _jv_j|\sqrt{u_i}dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i|\alpha _{i,j}||\beta _j|\int _{\mathbb{R}^2}|v_j|\sqrt{u_i}dx\\[5pt] &\leq \frac{D_1}{4}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx+\frac{(a^*\alpha ^*)^2|\mathcal{I}||\mathcal{J}|}{D_1}\sum \limits ^n_{i=1}m_i+a^*\alpha ^*\beta ^*A_2\sum \limits ^n_{i=1}m^{1/2}_i. \end{split} \end{equation}
\begin{equation} \begin{split} &\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}\Delta v_j\log\! (u_i+1)dx\\[5pt] &=\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\int _{\mathbb{R}^2}(\Delta v_j-\beta _jv_j)\log\! (u_i+1)dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}v_j\log\! (u_i+1)dx\\[5pt] &\leq \sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i|\alpha _{i,j}|\int _{\mathbb{R}^2}|\Delta v_j-\beta _jv_j|\sqrt{u_i}dx+\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i|\alpha _{i,j}||\beta _j|\int _{\mathbb{R}^2}|v_j|\sqrt{u_i}dx\\[5pt] &\leq \frac{D_1}{4}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx+\frac{(a^*\alpha ^*)^2|\mathcal{I}||\mathcal{J}|}{D_1}\sum \limits ^n_{i=1}m_i+a^*\alpha ^*\beta ^*A_2\sum \limits ^n_{i=1}m^{1/2}_i. \end{split} \end{equation}
Note that
![]() $A_2$
is uniformly bounded with respect to time variable if
$A_2$
is uniformly bounded with respect to time variable if
![]() $\beta _j\gt 0$
for all
$\beta _j\gt 0$
for all
![]() $j\in \mathcal{J}$
. However, Lemma 2.2 tells us
$j\in \mathcal{J}$
. However, Lemma 2.2 tells us
Then, one has
 \begin{equation} \begin{split} -\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u_iv_jdx\leq & \sum \limits ^n_{i=1}\frac{\pi a_i}{2m_i}\int _{\mathbb{R}^2}u^2_idx+\frac{(\alpha ^*\beta ^*)^2|\mathcal{J}|}{2\pi }\left (\sum \limits ^n_{i=1}a_im_i\right )\left (\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}v^2_jdx\right )\\[5pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+\pi \sum \limits ^n_{i=1}a_i+\frac{(\alpha ^*\beta ^*A_2|\mathcal{J}|)^2}{2\pi }\left (\sum \limits ^n_{i=1}a_im_i\right ) \end{split} \end{equation}
\begin{equation} \begin{split} -\sum \limits ^n_{i=1}\sum \limits ^{m}_{j=1}a_i\alpha _{i,j}\beta _j\int _{\mathbb{R}^2}u_iv_jdx\leq & \sum \limits ^n_{i=1}\frac{\pi a_i}{2m_i}\int _{\mathbb{R}^2}u^2_idx+\frac{(\alpha ^*\beta ^*)^2|\mathcal{J}|}{2\pi }\left (\sum \limits ^n_{i=1}a_im_i\right )\left (\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}v^2_jdx\right )\\[5pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+\pi \sum \limits ^n_{i=1}a_i+\frac{(\alpha ^*\beta ^*A_2|\mathcal{J}|)^2}{2\pi }\left (\sum \limits ^n_{i=1}a_im_i\right ) \end{split} \end{equation}
and
 \begin{align} \frac{1}{2}&\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\nonumber\\[5pt] \leq &\beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j||\partial _tv_l|dx\nonumber\\[5pt] \leq & \beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j||\Delta v_l-\beta _lv_l|dx+\beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j|\left |\sum \limits ^n_{i=1}\alpha _{i,l}u_i\right |dx\\[5pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+\frac{D_1}{4}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\nonumber\\[5pt] &+\frac{\left(\alpha ^*b^*\beta ^*A_2|\mathcal{J}|^2\right)^2}{2\pi }\sum \limits ^n_{i=1}\frac{m_i}{a_i}+\pi \sum \limits ^n_{i=1}a_i+\frac{(b^*\beta ^*A_2|\mathcal{J}|)^2}{D_1}\quad \text{for}\quad t\in (0,T).\nonumber \end{align}
\begin{align} \frac{1}{2}&\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\beta _l\int _{\mathbb{R}^2}(v_j\partial _tv_l-v_l\partial _tv_j)dx\nonumber\\[5pt] \leq &\beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j||\partial _tv_l|dx\nonumber\\[5pt] \leq & \beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j||\Delta v_l-\beta _lv_l|dx+\beta ^*\sum \limits ^m_{j=1}\sum \limits ^m_{l=1}|b_{j,l}|\int _{\mathbb{R}^2}|v_j|\left |\sum \limits ^n_{i=1}\alpha _{i,l}u_i\right |dx\\[5pt] \leq &\frac{1}{4}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx+\frac{D_1}{4}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\nonumber\\[5pt] &+\frac{\left(\alpha ^*b^*\beta ^*A_2|\mathcal{J}|^2\right)^2}{2\pi }\sum \limits ^n_{i=1}\frac{m_i}{a_i}+\pi \sum \limits ^n_{i=1}a_i+\frac{(b^*\beta ^*A_2|\mathcal{J}|)^2}{D_1}\quad \text{for}\quad t\in (0,T).\nonumber \end{align}
Putting (4.5)–(4.8) together, then there exists a constant
![]() $c_1\gt 0$
such that
$c_1\gt 0$
such that
![]() $\mathcal{G}$
satisfies
$\mathcal{G}$
satisfies
Now if
![]() $\beta _j\gt 0$
for all
$\beta _j\gt 0$
for all
![]() $j\in \mathcal{J}$
, combining (2.2) with (4.4) yields that
$j\in \mathcal{J}$
, combining (2.2) with (4.4) yields that
 \begin{align*} \begin{split} \frac{D_1}{2}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\,\geq\, &\frac{D_1}{2D_2}\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}b_{j,l}\int _{\mathbb{R}^2}(\Delta v_j-\beta _jv_j)(\Delta v_l-\beta _lv_l)dx\\[5pt] \geq\, &\frac{D_1\beta _*}{2D_2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _lv_jv_l\right )dx\\[5pt] =\, &\frac{D_1\beta _*}{D_2} \mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]- \frac{D_1\beta _*}{D_2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] \geq\, &\frac{D_1\beta _*}{D_2} \mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{D_1\beta _*}{D_2}\sum \limits ^n_{i=1}a_im_i\eta _i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx-c_2\beta _*\sum \limits ^n_{i=1}a_im_i, \end{split} \end{align*}
\begin{align*} \begin{split} \frac{D_1}{2}\sum \limits ^{m}_{j=1}\int _{\mathbb{R}^2}\left |\Delta v_j-\beta _jv_j\right |^2dx\,\geq\, &\frac{D_1}{2D_2}\sum \limits ^{m}_{j=1}\sum \limits ^{m}_{l=1}b_{j,l}\int _{\mathbb{R}^2}(\Delta v_j-\beta _jv_j)(\Delta v_l-\beta _lv_l)dx\\[5pt] \geq\, &\frac{D_1\beta _*}{2D_2}\sum \limits ^{m}_{j=1}\sum \limits ^m_{l=1}b_{j,l}\int _{\mathbb{R}^2}\left (\nabla v_j\cdot \nabla v_l+\beta _lv_jv_l\right )dx\\[5pt] =\, &\frac{D_1\beta _*}{D_2} \mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]- \frac{D_1\beta _*}{D_2}\sum \limits ^n_{i=1}a_i\int _{\mathbb{R}^2}(u_i+1)\log\! (u_i+1)dx\\[5pt] \geq\, &\frac{D_1\beta _*}{D_2} \mathcal{G}[\boldsymbol{{u}},\boldsymbol{{v}}]-\frac{D_1\beta _*}{D_2}\sum \limits ^n_{i=1}a_im_i\eta _i\int _{\mathbb{R}^2}\frac{|\nabla u_i|^2}{u_i+1}dx-c_2\beta _*\sum \limits ^n_{i=1}a_im_i, \end{split} \end{align*}
where
![]() $\eta _i\in (0,1)$
,
$\eta _i\in (0,1)$
,
![]() $i\in \mathcal{I}$
and
$i\in \mathcal{I}$
and
![]() $c_2\gt 0$
are constants. Taking
$c_2\gt 0$
are constants. Taking
![]() $\eta _i=\frac{D_2}{2D_1m_i\beta _*}$
,
$\eta _i=\frac{D_2}{2D_1m_i\beta _*}$
,
![]() $i\in \mathcal{I}$
, we collect the above two inequalities to obtain
$i\in \mathcal{I}$
, we collect the above two inequalities to obtain
Proof of Theorem 1.2. Thanks to Lemma 4.1, we conclude that
![]() $ \mathcal{G}$
is bounded. Therefore, there exists a constant
$ \mathcal{G}$
is bounded. Therefore, there exists a constant
![]() $c\gt 0$
such that
$c\gt 0$
such that
 \begin{align*} & \sum \limits ^n_{i=1}\|(u(\cdot,t)+1)\log\! (u(\cdot,t)+1)\|_{L^1(\mathbb{R}^2)}\leq c\quad \text{for}\quad t\in (0,T),\\& \sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|_{L^2(\mathbb{R}^2)}\leq c\quad \text{for}\quad t\in (0,T). \end{align*}
\begin{align*} & \sum \limits ^n_{i=1}\|(u(\cdot,t)+1)\log\! (u(\cdot,t)+1)\|_{L^1(\mathbb{R}^2)}\leq c\quad \text{for}\quad t\in (0,T),\\& \sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|_{L^2(\mathbb{R}^2)}\leq c\quad \text{for}\quad t\in (0,T). \end{align*}
Similar to the proof of Theorem 1.1, the global result can be obtained through a classic and standard method.
Acknowledgements
The author thanks the anonymous referee very much for carefully reading our manuscript and giving positive and valuable comments.
Funding
K. Lin is supported by Natural Science Foundation of Sichuan Province (No. 2022NSFSC1837) and Guanghua Talent Project of Southwestern University of Finance and Economics.
Competing interest
None
Appendix
In this section, we will prove Lemma 2.1. The following lemma collects some basic facts on the asymptotics of the heat semigroup
![]() $(e^{t\Delta })_{t\geq 0}$
, given by
$(e^{t\Delta })_{t\geq 0}$
, given by
where
![]() $\phi \in C^0(\mathbb{R}^2)\cap L^{\infty }(\mathbb{R}^2)$
and the Gaussian heat kernel is denoted by
$\phi \in C^0(\mathbb{R}^2)\cap L^{\infty }(\mathbb{R}^2)$
and the Gaussian heat kernel is denoted by
![]() $G(z,t)\,:\!=\,(4\pi t)^{-1}e^{-\frac{|z|^2}{4t}}$
,
$G(z,t)\,:\!=\,(4\pi t)^{-1}e^{-\frac{|z|^2}{4t}}$
,
![]() $z\in \mathbb{R}^2$
,
$z\in \mathbb{R}^2$
,
![]() $t\gt 0$
.
$t\gt 0$
.
Lemma 5.1.
Let
![]() $(e^{t\Delta })_{t\geq 0}$
be the heat semigroup in
$(e^{t\Delta })_{t\geq 0}$
be the heat semigroup in
![]() $\mathbb{R}^2$
. Then, the following properties are true.
$\mathbb{R}^2$
. Then, the following properties are true.
![]() $(i)$
Let
$(i)$
Let
![]() $\omega \in \mathbb{N}^n_0$
. Then
$\omega \in \mathbb{N}^n_0$
. Then
is valid for all
![]() $\phi \in C^{|\omega |}(\mathbb{R}^2)\cap W^{|\omega |,\infty }(\mathbb{R}^2)$
.
$\phi \in C^{|\omega |}(\mathbb{R}^2)\cap W^{|\omega |,\infty }(\mathbb{R}^2)$
.
![]() $(ii)$
If
$(ii)$
If
![]() $1\leq r_1\leq r_2\leq \infty$
and
$1\leq r_1\leq r_2\leq \infty$
and
![]() $\omega \in \mathbb{N}^n_0$
, then there exist a constant
$\omega \in \mathbb{N}^n_0$
, then there exist a constant
![]() $c(r_1,r_2,|\omega |)\gt 0$
such that
$c(r_1,r_2,|\omega |)\gt 0$
such that
holds for all
![]() $\phi \in L^{r_1}(\mathbb{R}^2)$
. In particular,
$\phi \in L^{r_1}(\mathbb{R}^2)$
. In particular,
![]() $c(r_1,r_2,|\omega |)=1$
if
$c(r_1,r_2,|\omega |)=1$
if
![]() $|\omega |=0$
and
$|\omega |=0$
and
![]() $r_1=r_2$
.
$r_1=r_2$
.
Proof. Please see [Reference Winkler41, Lemma 2.1] and [Reference Giga, Giga and Saal14] for details.
Proof of Lemma 2.1 . The proof of Lemma 2.1 will be divided into several steps.
First Step: local existence. The contraction mapping theorem will be used to prove the local existence of mild solutions. Let
and let
![]() $T$
be a fixed positive number below. Set
$T$
be a fixed positive number below. Set
equipped with the norm
 \begin{align*} \begin{split} \|(\boldsymbol{{u}},\boldsymbol{{v}})\|_{X}=\max \limits _{0\leq t\leq T}\Big \{&\sum \limits ^n_{i=1}\left [\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}+\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}\right ]\\[5pt] &+\sum \limits ^m_{j=1}\left [\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}\right ]\Big \} \end{split} \end{align*}
\begin{align*} \begin{split} \|(\boldsymbol{{u}},\boldsymbol{{v}})\|_{X}=\max \limits _{0\leq t\leq T}\Big \{&\sum \limits ^n_{i=1}\left [\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}+\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}\right ]\\[5pt] &+\sum \limits ^m_{j=1}\left [\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}\right ]\Big \} \end{split} \end{align*}
for
![]() $t\in [0,T]$
. Moreover, define
$t\in [0,T]$
. Moreover, define
Then, it is easy to see that
![]() $E$
is a closed convex subset of
$E$
is a closed convex subset of
![]() $X$
. Consider a nonlinear mapping
$X$
. Consider a nonlinear mapping
![]() $\Pi \,:\,E\mapsto X$
such that for any
$\Pi \,:\,E\mapsto X$
such that for any
![]() $(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\in E$
,
$(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\in E$
,
where
![]() $\boldsymbol{{u}}=(u_1,\cdots,u_n)$
and
$\boldsymbol{{u}}=(u_1,\cdots,u_n)$
and
![]() $\boldsymbol{{v}}=(v_1,\cdots,v_m)$
satisfy
$\boldsymbol{{v}}=(v_1,\cdots,v_m)$
satisfy
and
respectively. By the estimates for the heat semigroup in Lemma 5.1
![]() $(ii)$
to (A1), there exists a constant
$(ii)$
to (A1), there exists a constant
![]() $c_1=c_1(p)\gt 0$
such that
$c_1=c_1(p)\gt 0$
such that
 \begin{align*} \begin{split} \sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}\leq &\sum \limits ^n_{i=1}\|e^{t\Delta }u_{i0}\|_{L^{\infty }(\mathbb{R}^2)}+c_1\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}|\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}} \|\widetilde{u}_i(\cdot,s)\nabla \widetilde{v}_j(\cdot,s)\|_{L^p({\mathbb{R}^2})}ds,\\[5pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{\infty }(\mathbb{R}^2)} +c_1\alpha ^*\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}} \left (\sum \limits ^n_{i=1}\|\widetilde{u}_i(\cdot,s)\|_{L^\infty ({\mathbb{R}^2})}\right )\\[5pt] &\cdot \left (\sum \limits ^m_{j=1}\|\nabla \widetilde{v}_j(\cdot,s)\|_{L^p({\mathbb{R}^2})}\right )ds\\[5pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{\infty }(\mathbb{R}^2)}+\frac{2c_1p\alpha ^*R^2}{p-2}T^{\frac{1}{2}-\frac{1}{p}},\quad t\in [0,T]. \end{split} \end{align*}
\begin{align*} \begin{split} \sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}\leq &\sum \limits ^n_{i=1}\|e^{t\Delta }u_{i0}\|_{L^{\infty }(\mathbb{R}^2)}+c_1\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\alpha _{i,j}|\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}} \|\widetilde{u}_i(\cdot,s)\nabla \widetilde{v}_j(\cdot,s)\|_{L^p({\mathbb{R}^2})}ds,\\[5pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{\infty }(\mathbb{R}^2)} +c_1\alpha ^*\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}} \left (\sum \limits ^n_{i=1}\|\widetilde{u}_i(\cdot,s)\|_{L^\infty ({\mathbb{R}^2})}\right )\\[5pt] &\cdot \left (\sum \limits ^m_{j=1}\|\nabla \widetilde{v}_j(\cdot,s)\|_{L^p({\mathbb{R}^2})}\right )ds\\[5pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{\infty }(\mathbb{R}^2)}+\frac{2c_1p\alpha ^*R^2}{p-2}T^{\frac{1}{2}-\frac{1}{p}},\quad t\in [0,T]. \end{split} \end{align*}
Similarly, one also has
 \begin{align*} \begin{split} \sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{1}(\mathbb{R}^2)} \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{1}(\mathbb{R}^2)} +c_2\alpha ^*\int ^t_0(t-s)^{-\frac{1}{2}} \left (\sum \limits ^n_{i=1}\|\widetilde{u}_i(\cdot,s)\|_{L^\infty ({\mathbb{R}^2})}\right )\\[1pt] &\cdot \left (\sum \limits ^m_{j=1}\|\nabla \widetilde{v}_j(\cdot,s)\|_{L^1({\mathbb{R}^2})}\right )ds\\[1pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{1}(\mathbb{R}^2)}+2c_2\alpha ^*R^2T^{\frac{1}{2}},\quad t\in [0,T], \end{split} \end{align*}
\begin{align*} \begin{split} \sum \limits ^n_{i=1}\|u_i(\cdot,t)\|_{L^{1}(\mathbb{R}^2)} \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{1}(\mathbb{R}^2)} +c_2\alpha ^*\int ^t_0(t-s)^{-\frac{1}{2}} \left (\sum \limits ^n_{i=1}\|\widetilde{u}_i(\cdot,s)\|_{L^\infty ({\mathbb{R}^2})}\right )\\[1pt] &\cdot \left (\sum \limits ^m_{j=1}\|\nabla \widetilde{v}_j(\cdot,s)\|_{L^1({\mathbb{R}^2})}\right )ds\\[1pt] \leq &\sum \limits ^n_{i=1}\|u_{i0}\|_{L^{1}(\mathbb{R}^2)}+2c_2\alpha ^*R^2T^{\frac{1}{2}},\quad t\in [0,T], \end{split} \end{align*}
with some
![]() $c_2\gt 0$
. Moreover, one can apply Lemma 5.1
$c_2\gt 0$
. Moreover, one can apply Lemma 5.1
![]() $(ii)$
to find constants
$(ii)$
to find constants
![]() $c_3$
,
$c_3$
,
![]() $c_4\gt 0$
such that
$c_4\gt 0$
such that
 \begin{align*} \begin{split} \sum \limits ^m_{j=1}\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)} \leq &\sum \limits ^m_{j=1}e^{|\beta _j|t}\|v_{j0}\|_{L^{1}(\mathbb{R}^2)} +\gamma ^*\sum \limits ^m_{j=1}e^{|\beta _j|t}\int ^t_0 \left \|\sum \limits ^n_{i=1}\widetilde{u}_i(\cdot,s)\right \|_{L^1({\mathbb{R}^2})}ds\\[1pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|v_{j0}\|_{L^{1}(\mathbb{R}^2)}+\gamma ^*e^{\beta ^*T}R|\mathcal{J}|T,\quad t\in [0,T], \end{split} \end{align*}
\begin{align*} \begin{split} \sum \limits ^m_{j=1}\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)} \leq &\sum \limits ^m_{j=1}e^{|\beta _j|t}\|v_{j0}\|_{L^{1}(\mathbb{R}^2)} +\gamma ^*\sum \limits ^m_{j=1}e^{|\beta _j|t}\int ^t_0 \left \|\sum \limits ^n_{i=1}\widetilde{u}_i(\cdot,s)\right \|_{L^1({\mathbb{R}^2})}ds\\[1pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|v_{j0}\|_{L^{1}(\mathbb{R}^2)}+\gamma ^*e^{\beta ^*T}R|\mathcal{J}|T,\quad t\in [0,T], \end{split} \end{align*}
 \begin{equation}{} \begin{split} \sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}\leq & \sum \limits ^m_{j=1} e^{|\beta _j|t}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+c_3\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\gamma _{i,j}|e^{|\beta _j|t}\int ^t_0(t-s)^{-\frac{1}{2}}\|\widetilde{u}_i(\cdot,s)\|_{L^p(\mathbb{R}^2)}ds\\[5pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+c_3\gamma ^*e^{\beta ^*t}|\mathcal{J}|\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\\[5pt] &\cdot \|\widetilde{u}_i(\cdot,s)\|^{\frac{p-1}{p}}_{L^{\infty }(\mathbb{R}^2)}\|\widetilde{u}_i(\cdot,s)\|^{\frac{1}{p}}_{L^{1}(\mathbb{R}^2)}ds\\[5pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+2c_3\gamma ^*e^{\beta ^*T}R|\mathcal{J}|T^{\frac{1}{2}},\quad t\in [0,T], \end{split} \end{equation}
\begin{equation}{} \begin{split} \sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}\leq & \sum \limits ^m_{j=1} e^{|\beta _j|t}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+c_3\sum \limits ^n_{i=1}\sum \limits ^m_{j=1}|\gamma _{i,j}|e^{|\beta _j|t}\int ^t_0(t-s)^{-\frac{1}{2}}\|\widetilde{u}_i(\cdot,s)\|_{L^p(\mathbb{R}^2)}ds\\[5pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+c_3\gamma ^*e^{\beta ^*t}|\mathcal{J}|\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\\[5pt] &\cdot \|\widetilde{u}_i(\cdot,s)\|^{\frac{p-1}{p}}_{L^{\infty }(\mathbb{R}^2)}\|\widetilde{u}_i(\cdot,s)\|^{\frac{1}{p}}_{L^{1}(\mathbb{R}^2)}ds\\[5pt] \leq\, &e^{\beta ^*T}\sum \limits ^m_{j=1}\|\nabla v_{j0}\|_{L^{p}(\mathbb{R}^2)}+2c_3\gamma ^*e^{\beta ^*T}R|\mathcal{J}|T^{\frac{1}{2}},\quad t\in [0,T], \end{split} \end{equation}
Hence,
![]() $\Pi$
maps
$\Pi$
maps
![]() $E$
into
$E$
into
![]() $E$
if we choose
$E$
if we choose
![]() $T$
small enough.
$T$
small enough.
We now show that the mapping is a contraction. Indeed, for
![]() $(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})\in E$
,
$(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})\in E$
,
![]() $(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\in E$
, we have
$(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\in E$
, we have
where
![]() $I_i$
,
$I_i$
,
![]() $i=1,2,\cdots,5$
is introduced as follows,
$i=1,2,\cdots,5$
is introduced as follows,
 \begin{align*} I_1(t)=&\sum \limits ^n_{i=1}\Bigg \|\int ^t_0\nabla \cdot e^{(t-s)\Delta }\Big [(\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s))\Big (\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \overline{v}_j(\cdot,s)\Big )\\[5pt] &+\widetilde{u}_i(\cdot,s)\sum \limits ^m_{j=1}\alpha _{i,j}\Big ( \nabla \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\Big ]ds\Bigg \|_{L^{\infty }(\mathbb{R}^2)}\\[5pt] \leq\, &c_1\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}}\left \|\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j} \nabla \overline{v}_j(\cdot,s)\right \|_{L^p(\mathbb{R}^2)}ds\\[5pt] &+c_1\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}}\left \|\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \Big ( \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\right \|_{L^p(\mathbb{R}^2)}ds\\[5pt] \leq\, &\frac{4c_1p\alpha ^*R}{p-2}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{align*}
\begin{align*} I_1(t)=&\sum \limits ^n_{i=1}\Bigg \|\int ^t_0\nabla \cdot e^{(t-s)\Delta }\Big [(\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s))\Big (\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \overline{v}_j(\cdot,s)\Big )\\[5pt] &+\widetilde{u}_i(\cdot,s)\sum \limits ^m_{j=1}\alpha _{i,j}\Big ( \nabla \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\Big ]ds\Bigg \|_{L^{\infty }(\mathbb{R}^2)}\\[5pt] \leq\, &c_1\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}}\left \|\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j} \nabla \overline{v}_j(\cdot,s)\right \|_{L^p(\mathbb{R}^2)}ds\\[5pt] &+c_1\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}-\frac{1}{p}}\left \|\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \Big ( \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\right \|_{L^p(\mathbb{R}^2)}ds\\[5pt] \leq\, &\frac{4c_1p\alpha ^*R}{p-2}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{align*}
 \begin{align*} \begin{split} I_2(t)=&\sum \limits ^n_{i=1}\Bigg \|\int ^t_0\nabla \cdot e^{(t-s)\Delta }\Big [(\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s))\Big (\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \overline{v}_j(\cdot,s)\Big )\\[5pt] &+\widetilde{u}_i(\cdot,s)\sum \limits ^m_{j=1}\alpha _{i,j}\Big ( \nabla \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\Big ]ds\Bigg \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &c_2\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\left \|\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j} \nabla \overline{v}_j(\cdot,s)\right \|_{L^1(\mathbb{R}^2)}ds\\[5pt] &+c_2\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\left \|\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \Big ( \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\right \|_{L^1(\mathbb{R}^2)}ds\\[5pt] \leq\, &4c_2\alpha ^*RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
\begin{align*} \begin{split} I_2(t)=&\sum \limits ^n_{i=1}\Bigg \|\int ^t_0\nabla \cdot e^{(t-s)\Delta }\Big [(\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s))\Big (\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \overline{v}_j(\cdot,s)\Big )\\[5pt] &+\widetilde{u}_i(\cdot,s)\sum \limits ^m_{j=1}\alpha _{i,j}\Big ( \nabla \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\Big ]ds\Bigg \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &c_2\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\left \|\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j} \nabla \overline{v}_j(\cdot,s)\right \|_{L^1(\mathbb{R}^2)}ds\\[5pt] &+c_2\sum \limits ^n_{i=1}\int ^t_0(t-s)^{-\frac{1}{2}}\left \|\widetilde{u}_i(\cdot,s)\right \|_{L^{\infty }(\mathbb{R}^2)}\left \|\sum \limits ^m_{j=1}\alpha _{i,j}\nabla \Big ( \overline{v}_j(\cdot,s)-\widetilde{v}_j(\cdot,s)\Big )\right \|_{L^1(\mathbb{R}^2)}ds\\[5pt] \leq\, &4c_2\alpha ^*RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
 \begin{align*} \begin{split} I_3(t)=&\sum \limits ^m_{j=1}\left \|\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )ds\right \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &\gamma ^*e^{|\beta ^*|T}|\mathcal{J}|\sum \limits ^n_{i=1}\int ^t_0\left \| \overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{1}(\mathbb{R}^2)}ds\\[5pt] \leq\, &\gamma ^*e^{|\beta ^*|T}|\mathcal{J}|T\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
\begin{align*} \begin{split} I_3(t)=&\sum \limits ^m_{j=1}\left \|\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )ds\right \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &\gamma ^*e^{|\beta ^*|T}|\mathcal{J}|\sum \limits ^n_{i=1}\int ^t_0\left \| \overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right \|_{L^{1}(\mathbb{R}^2)}ds\\[5pt] \leq\, &\gamma ^*e^{|\beta ^*|T}|\mathcal{J}|T\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
 \begin{align*} \begin{split} I_4(t)=&\sum \limits ^m_{j=1}\left \|\nabla \left [\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )\right ]\right \|_{L^{p}(\mathbb{R}^2)}\\[5pt] \leq\, &2c_3\gamma ^*e^{\beta ^*T}|\mathcal{J}|RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
\begin{align*} \begin{split} I_4(t)=&\sum \limits ^m_{j=1}\left \|\nabla \left [\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )\right ]\right \|_{L^{p}(\mathbb{R}^2)}\\[5pt] \leq\, &2c_3\gamma ^*e^{\beta ^*T}|\mathcal{J}|RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T], \end{split} \end{align*}
 \begin{align*} \begin{split} I_5(t)=&\sum \limits ^m_{j=1}\left \|\nabla \left [\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )\right ]\right \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &2c_4\gamma ^*e^{\beta ^*T}|\mathcal{J}|RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T]. \end{split} \end{align*}
\begin{align*} \begin{split} I_5(t)=&\sum \limits ^m_{j=1}\left \|\nabla \left [\int ^t_0 e^{(t-s)(\Delta -\beta _j)}\left (\sum \limits ^n_{i=1}\gamma _{i,j}\left (\overline{u}_i(\cdot,s)-\widetilde{u}_i(\cdot,s)\right )\right )\right ]\right \|_{L^{1}(\mathbb{R}^2)}\\[5pt] \leq\, &2c_4\gamma ^*e^{\beta ^*T}|\mathcal{J}|RT^{\frac{1}{2}}\|(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})-(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})\|_{X},\quad t\in [0,T]. \end{split} \end{align*}
So
![]() $\Pi$
is a contraction if
$\Pi$
is a contraction if
![]() $T$
is sufficiently small. Thus from Banach’s fixed point theorem,
$T$
is sufficiently small. Thus from Banach’s fixed point theorem,
![]() $\Pi$
has a fixed point in the sense that
$\Pi$
has a fixed point in the sense that
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})=\Pi (\boldsymbol{{u}},\boldsymbol{{v}})$
. Since the choice of above
$(\boldsymbol{{u}},\boldsymbol{{v}})=\Pi (\boldsymbol{{u}},\boldsymbol{{v}})$
. Since the choice of above
![]() $T$
depends only on
$T$
depends only on
![]() $R$
,
$R$
,
![]() $\alpha ^*$
,
$\alpha ^*$
,
![]() $\beta ^*$
,
$\beta ^*$
,
![]() $\gamma ^*$
,
$\gamma ^*$
,
![]() $p$
and
$p$
and
![]() $|\mathcal{I}|$
,
$|\mathcal{I}|$
,
![]() $|\mathcal{J}|$
, a standard argument implies that
$|\mathcal{J}|$
, a standard argument implies that
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})$
can be extended up to some
$(\boldsymbol{{u}},\boldsymbol{{v}})$
can be extended up to some
![]() $T_{\max }$
, and
$T_{\max }$
, and
 \begin{equation}{} \begin{split} \limsup _{t\rightarrow T_{\max }}&\left\{\sum \limits ^n_{i=1}\left [\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}+\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}\right ]\right.\\[5pt] &\left. +\sum \limits ^m_{j=1}\left [\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}\right ]\right\}=\infty \end{split} \end{equation}
\begin{equation}{} \begin{split} \limsup _{t\rightarrow T_{\max }}&\left\{\sum \limits ^n_{i=1}\left [\|u_i(\cdot,t)\|_{L^{\infty }(\mathbb{R}^2)}+\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}\right ]\right.\\[5pt] &\left. +\sum \limits ^m_{j=1}\left [\|v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{p}(\mathbb{R}^2)}+\|\nabla v_j(\cdot,t)\|_{L^{1}(\mathbb{R}^2)}\right ]\right\}=\infty \end{split} \end{equation}
holds if
![]() $T_{\max }\lt \infty$
.
$T_{\max }\lt \infty$
.
Second Step: Regularity. Since
![]() $e^{t\Delta }$
and
$e^{t\Delta }$
and
![]() $\nabla \cdot$
commute on
$\nabla \cdot$
commute on
![]() $C^1(\mathbb{R}^2;\,\mathbb{R}^2)\cap L^1(\mathbb{R}^2;\,\mathbb{R}^2)$
, a straightforward regularity argument in [Reference Hillen, Painter and Winkler17, Lemma 3.3] which includes standard semigroup techniques and bootstrap procedure, and the parabolic Schauder estimates [Reference Ladyzenskaja, Solonnikov and Ural’ceva26] imply that
$C^1(\mathbb{R}^2;\,\mathbb{R}^2)\cap L^1(\mathbb{R}^2;\,\mathbb{R}^2)$
, a straightforward regularity argument in [Reference Hillen, Painter and Winkler17, Lemma 3.3] which includes standard semigroup techniques and bootstrap procedure, and the parabolic Schauder estimates [Reference Ladyzenskaja, Solonnikov and Ural’ceva26] imply that
![]() $(\boldsymbol{{u}},\boldsymbol{{v}})\in \left [C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^{m+n}$
. In fact, abbreviating
$(\boldsymbol{{u}},\boldsymbol{{v}})\in \left [C^{2,1}(\mathbb{R}^2\times (0,T_{\max }))\right ]^{m+n}$
. In fact, abbreviating
![]() $F_i(x,t)=\sum \limits ^m_{j=1}\alpha _{i,j}u_i(x,t)\nabla v_j(x,t)$
for some
$F_i(x,t)=\sum \limits ^m_{j=1}\alpha _{i,j}u_i(x,t)\nabla v_j(x,t)$
for some
![]() $i\in \mathcal{I}$
and from the regularity for the mild solution, we rewritten (1.5)
$i\in \mathcal{I}$
and from the regularity for the mild solution, we rewritten (1.5)
![]() $_i$
as
$_i$
as
with continuous and bounded
![]() $\mathcal{F}_i$
in
$\mathcal{F}_i$
in
![]() $\mathbb{R}^2\times [0,T]$
. Then the Step 2 in [Reference Hillen, Painter and Winkler17, Lemma 3.3] tells that
$\mathbb{R}^2\times [0,T]$
. Then the Step 2 in [Reference Hillen, Painter and Winkler17, Lemma 3.3] tells that
![]() $u_i$
is a very weak solution to (A6), i.e.
$u_i$
is a very weak solution to (A6), i.e.
 \begin{align*} \begin{split} &-\int ^T_0\int _{\mathbb{R}^2}u_i\phi _t-\int _{\mathbb{R}^2}u_{i0}\phi (\cdot,0)=\int ^T_0\int _{\mathbb{R}^2}u_i\Delta \phi \\[5pt] &+\int ^T_0\int _{\mathbb{R}^2}F_i\cdot \nabla \phi \quad \text{for all}\,\,\phi \in C^{\infty }_0(\mathbb{R}^2\times [0,T)). \end{split} \end{align*}
\begin{align*} \begin{split} &-\int ^T_0\int _{\mathbb{R}^2}u_i\phi _t-\int _{\mathbb{R}^2}u_{i0}\phi (\cdot,0)=\int ^T_0\int _{\mathbb{R}^2}u_i\Delta \phi \\[5pt] &+\int ^T_0\int _{\mathbb{R}^2}F_i\cdot \nabla \phi \quad \text{for all}\,\,\phi \in C^{\infty }_0(\mathbb{R}^2\times [0,T)). \end{split} \end{align*}
Moreover, one can improve the regularity of very weak solution by introducing another solution
![]() $\overline{u}_i$
to the following initial boundary problem
$\overline{u}_i$
to the following initial boundary problem
 \begin{align*} \begin{cases} \partial _t \overline{u}_i=\Delta \overline{u}_i-\nabla \cdot F_i,\quad x\in B_R,\,\,t\in (\tau,T), \\[5pt] \overline{u}_i|_{\partial B_R}=u_i, \quad t\in (\tau,T),\\[5pt] \overline{u}(x,\tau )=u(x,\tau ),\quad x\in B_R, \\[5pt] \end{cases} \end{align*}
\begin{align*} \begin{cases} \partial _t \overline{u}_i=\Delta \overline{u}_i-\nabla \cdot F_i,\quad x\in B_R,\,\,t\in (\tau,T), \\[5pt] \overline{u}_i|_{\partial B_R}=u_i, \quad t\in (\tau,T),\\[5pt] \overline{u}(x,\tau )=u(x,\tau ),\quad x\in B_R, \\[5pt] \end{cases} \end{align*}
where
![]() $0\lt \tau \lt T$
,
$0\lt \tau \lt T$
,
![]() $R\gt 0$
. Then a similar way in the Step 3 in [Reference Hillen, Painter and Winkler17, Lemma 3.3] makes sure that
$R\gt 0$
. Then a similar way in the Step 3 in [Reference Hillen, Painter and Winkler17, Lemma 3.3] makes sure that
![]() $\nabla u_i\in L^2_{loc}(\mathbb{R}^2\times (\tau,T))$
and
$\nabla u_i\in L^2_{loc}(\mathbb{R}^2\times (\tau,T))$
and
 \begin{align*} \begin{split} &-\int ^{T}_\tau \int _{\mathbb{R}^2}u_i\phi _t-\int _{\mathbb{R}^2}u_{i}(\cdot,\tau )\phi (\cdot,\tau )=-\int ^T_\tau \int _{\mathbb{R}^2}\nabla u_i\cdot \nabla \phi \\[5pt] &+\int ^T_\tau \int _{\mathbb{R}^2}F_i\cdot \nabla \phi \quad \text{for all}\,\,\phi \in C^{\infty }_0(\mathbb{R}^2\times [\tau,T)). \end{split} \end{align*}
\begin{align*} \begin{split} &-\int ^{T}_\tau \int _{\mathbb{R}^2}u_i\phi _t-\int _{\mathbb{R}^2}u_{i}(\cdot,\tau )\phi (\cdot,\tau )=-\int ^T_\tau \int _{\mathbb{R}^2}\nabla u_i\cdot \nabla \phi \\[5pt] &+\int ^T_\tau \int _{\mathbb{R}^2}F_i\cdot \nabla \phi \quad \text{for all}\,\,\phi \in C^{\infty }_0(\mathbb{R}^2\times [\tau,T)). \end{split} \end{align*}
Hence,
![]() $\nabla \cdot F_i\in L^2_{loc}(\mathbb{R}^2\times [\tau,T])$
, which together with parabolic regularity theory [Reference Knútsdóttir, Pálsson and Edelstein-Keshet25] asserts that
$\nabla \cdot F_i\in L^2_{loc}(\mathbb{R}^2\times [\tau,T])$
, which together with parabolic regularity theory [Reference Knútsdóttir, Pálsson and Edelstein-Keshet25] asserts that
![]() $u_i\in L^2((\tau,T);W^{2,2}_{loc}(\mathbb{R}^2))$
and
$u_i\in L^2((\tau,T);W^{2,2}_{loc}(\mathbb{R}^2))$
and
![]() $u_i\in L^p((\tau,T);W^{2,p}_{loc}(\mathbb{R}^2))$
for all
$u_i\in L^p((\tau,T);W^{2,p}_{loc}(\mathbb{R}^2))$
for all
![]() $p\in (1,\infty )$
by the embedding theorem. Then invoking parabolic Schauder theory, we have
$p\in (1,\infty )$
by the embedding theorem. Then invoking parabolic Schauder theory, we have
![]() $u_i\in C^{2+\gamma,1+\frac{\gamma }{2}}_{loc}(\mathbb{R}^2\times (\tau,T))$
with some
$u_i\in C^{2+\gamma,1+\frac{\gamma }{2}}_{loc}(\mathbb{R}^2\times (\tau,T))$
with some
![]() $\gamma \in (0, 1)$
, and
$\gamma \in (0, 1)$
, and
![]() $u_i$
solves the
$u_i$
solves the
![]() $i$
-th equation in (1.5) classically in
$i$
-th equation in (1.5) classically in
![]() $\mathbb{R}^2\times (\tau,T)$
. The proof is complete due to the arbitrary choice of
$\mathbb{R}^2\times (\tau,T)$
. The proof is complete due to the arbitrary choice of
![]() $\tau$
.
$\tau$
.
Third Step: Uniqueness, positivity and mass conservation. Construct a non-increasing cut-off function
![]() $h(x)\in C^{\infty }(\mathbb{R})$
to fulfil
$h(x)\in C^{\infty }(\mathbb{R})$
to fulfil
![]() $h(x)\equiv 1$
in
$h(x)\equiv 1$
in
![]() $({-}\infty, 0]$
and
$({-}\infty, 0]$
and
![]() $h(x)\equiv 0$
in
$h(x)\equiv 0$
in
![]() $[1,\infty )$
. And for
$[1,\infty )$
. And for
![]() $K\gt 0$
, set
$K\gt 0$
, set
![]() $\xi _K(x)\,:\!=\,h(|x|-K)$
,
$\xi _K(x)\,:\!=\,h(|x|-K)$
,
![]() $x\in \mathbb{R}^2$
. Under the help of cut-off function
$x\in \mathbb{R}^2$
. Under the help of cut-off function
![]() $\xi _K$
, one can utilise localisation arguments to prove uniqueness, positivity and mass conservation of solutions to (1.5). Let us point out that such results were already obtained by Winkler in single-species case. We just describe the following main steps of the proof and refer to [Reference Winkler41, Lemmas 2.4–2.7] for more details.
$\xi _K$
, one can utilise localisation arguments to prove uniqueness, positivity and mass conservation of solutions to (1.5). Let us point out that such results were already obtained by Winkler in single-species case. We just describe the following main steps of the proof and refer to [Reference Winkler41, Lemmas 2.4–2.7] for more details.
Now we prove the uniqueness. Proceeding as in [Reference Winkler41, Lemma 2.4], given
![]() $T\gt 0$
and two solutions
$T\gt 0$
and two solutions
![]() $(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})$
and
$(\overline{\boldsymbol{{u}}},\overline{\boldsymbol{{v}}})$
and
![]() $(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})$
in
$(\widetilde{\boldsymbol{{u}}},\widetilde{\boldsymbol{{v}}})$
in
![]() $\mathbb{R}^2\times (0,T)$
, we let
$\mathbb{R}^2\times (0,T)$
, we let
![]() $\boldsymbol{{w}}=\overline{\boldsymbol{{u}}}-\widetilde{\boldsymbol{{u}}}$
and
$\boldsymbol{{w}}=\overline{\boldsymbol{{u}}}-\widetilde{\boldsymbol{{u}}}$
and
![]() $\boldsymbol{{z}}=\overline{\boldsymbol{{v}}}-\widetilde{\boldsymbol{{v}}}$
and obtain by applying straightforward procedure to (1.5) that
$\boldsymbol{{z}}=\overline{\boldsymbol{{v}}}-\widetilde{\boldsymbol{{v}}}$
and obtain by applying straightforward procedure to (1.5) that
With the help of cut-off function
![]() $\xi _K$
and Young’s inequality, we have
$\xi _K$
and Young’s inequality, we have
 \begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_Kw^2_{i}dx\leq &-\frac{1}{4}\int _{\mathbb{R}^2}\xi ^2_K|\nabla w_i|^2dx+4\int _{\mathbb{R}^2}|\nabla \xi _K|^2w^2_idx\\[5pt] &+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_Kw^2_i\left (\sum \limits ^m_{j=1}|\nabla \overline{v}_j|^2\right )dx\\[5pt] &+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K(\widetilde{u}_i)^2\left (\sum \limits ^m_{j=1}|\nabla z_j|^2\right )dx\\[5pt] &+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _kw^2_i\nabla \xi _K\cdot \nabla \overline{v}_jdx\\[5pt] &+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _K\widetilde{u}_iw_i\nabla \xi _K\cdot \nabla z_jdx \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_Kw^2_{i}dx\leq &-\frac{1}{4}\int _{\mathbb{R}^2}\xi ^2_K|\nabla w_i|^2dx+4\int _{\mathbb{R}^2}|\nabla \xi _K|^2w^2_idx\\[5pt] &+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_Kw^2_i\left (\sum \limits ^m_{j=1}|\nabla \overline{v}_j|^2\right )dx\\[5pt] &+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K(\widetilde{u}_i)^2\left (\sum \limits ^m_{j=1}|\nabla z_j|^2\right )dx\\[5pt] &+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _kw^2_i\nabla \xi _K\cdot \nabla \overline{v}_jdx\\[5pt] &+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _K\widetilde{u}_iw_i\nabla \xi _K\cdot \nabla z_jdx \end{split} \end{align*}
 \begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx\leq &\int _{\mathbb{R}^2}|\nabla \xi _K|^2\|\nabla z_j|^2dx+(\beta ^*+(\gamma ^*)^2)\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx\\[5pt] &+\frac{|\mathcal{I}|}{4}\int _{\mathbb{R}^2}\xi ^2_K\left (\sum \limits ^n_{i=1}|\nabla w_i|^2\right )dx. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx\leq &\int _{\mathbb{R}^2}|\nabla \xi _K|^2\|\nabla z_j|^2dx+(\beta ^*+(\gamma ^*)^2)\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx\\[5pt] &+\frac{|\mathcal{I}|}{4}\int _{\mathbb{R}^2}\xi ^2_K\left (\sum \limits ^n_{i=1}|\nabla w_i|^2\right )dx. \end{split} \end{align*}
By Hölder’s, Young’s and the Gagliardo–Nirenberg inequalities,
 \begin{equation}{} \begin{split} (\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_Kw^2_i\left (\sum \limits ^m_{j=1}|\nabla \overline{v}_j|^2\right )dx\leq & c_5(\alpha ^*)^2|\mathcal{J}|\|\xi _Kw_i\|^2_{L^{\frac{2q}{q-2}}(\mathbb{R}^2)}\\[5pt] \leq &c_5c_6(\alpha ^*)^2|\mathcal{J}|\|\nabla (\xi _Kw_i)\|^{\frac{4}{q}}_{L^2(\mathbb{R}^2)}\|\xi _Kw_i\|^{\frac{2(q-2)}{q}}_{L^2(\mathbb{R}^2)}\\[5pt] \leq &\frac{1}{8}\int _{\mathbb{R}^2}\xi ^2_K|\nabla w_i|^2dx+\frac{1}{8}\int _{\mathbb{R}^2}|\nabla \xi _K|^2w^2_idx\\[5pt] &+c_7\int _{\mathbb{R}^2}\xi ^2_Kw^2_idx, \end{split} \end{equation}
\begin{equation}{} \begin{split} (\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_Kw^2_i\left (\sum \limits ^m_{j=1}|\nabla \overline{v}_j|^2\right )dx\leq & c_5(\alpha ^*)^2|\mathcal{J}|\|\xi _Kw_i\|^2_{L^{\frac{2q}{q-2}}(\mathbb{R}^2)}\\[5pt] \leq &c_5c_6(\alpha ^*)^2|\mathcal{J}|\|\nabla (\xi _Kw_i)\|^{\frac{4}{q}}_{L^2(\mathbb{R}^2)}\|\xi _Kw_i\|^{\frac{2(q-2)}{q}}_{L^2(\mathbb{R}^2)}\\[5pt] \leq &\frac{1}{8}\int _{\mathbb{R}^2}\xi ^2_K|\nabla w_i|^2dx+\frac{1}{8}\int _{\mathbb{R}^2}|\nabla \xi _K|^2w^2_idx\\[5pt] &+c_7\int _{\mathbb{R}^2}\xi ^2_Kw^2_idx, \end{split} \end{equation}
 \begin{align*} (\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K(\widetilde{u}_i)^2\left (\sum \limits ^m_{j=1}|\nabla z_j|^2\right )dx \leq & c^2_8(\alpha ^*)^2|\mathcal{J}|\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_j|^2dx, \end{align*}
\begin{align*} (\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K(\widetilde{u}_i)^2\left (\sum \limits ^m_{j=1}|\nabla z_j|^2\right )dx \leq & c^2_8(\alpha ^*)^2|\mathcal{J}|\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_j|^2dx, \end{align*}
where we set
![]() $c_5=\sup _{t\in (0,T)}\sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|^2_{L^q(\mathbb{R}^2)}$
and
$c_5=\sup _{t\in (0,T)}\sum \limits ^m_{j=1}\|\nabla v_j(\cdot,t)\|^2_{L^q(\mathbb{R}^2)}$
and
![]() $c_8=\sup _{t\in (0,T)}\sum \limits ^n_{i=1}\|\widetilde{u}_i\|_{L^{\infty }(\mathbb{R}^2)}$
. By the finiteness
$c_8=\sup _{t\in (0,T)}\sum \limits ^n_{i=1}\|\widetilde{u}_i\|_{L^{\infty }(\mathbb{R}^2)}$
. By the finiteness
![]() $\|(\nabla \overline{v}_j,\nabla z_j)\|_{L^q(\mathbb{R}^2)}$
for
$\|(\nabla \overline{v}_j,\nabla z_j)\|_{L^q(\mathbb{R}^2)}$
for
![]() $j\in \mathcal{J}$
,
$j\in \mathcal{J}$
,
![]() $\|(\widetilde{u}_i, w_i)\|_{L^{\infty }(\mathbb{R}^2)}$
for
$\|(\widetilde{u}_i, w_i)\|_{L^{\infty }(\mathbb{R}^2)}$
for
![]() $i\in \mathcal{I}$
and
$i\in \mathcal{I}$
and
![]() $supp\,\,\xi _K\subset ({-}K,K)$
, we find that
$supp\,\,\xi _K\subset ({-}K,K)$
, we find that
![]() $y_K(t)\,:\!=\,\frac{1}{2}\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}\xi ^2_Kw^2_{i}dx+\frac{1}{4|\mathcal{I}|}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx$
satisfies
$y_K(t)\,:\!=\,\frac{1}{2}\sum \limits ^n_{i=1}\int _{\mathbb{R}^2}\xi ^2_Kw^2_{i}dx+\frac{1}{4|\mathcal{I}|}\sum \limits ^m_{j=1}\int _{\mathbb{R}^2}\xi ^2_K|\nabla z_{j}|^2dx$
satisfies
 \begin{align*} \begin{split} y^{\prime}_K(t)\leq & c_9y_K(t)+c_9\sum \limits ^n_{i=1}\|w_i\|^{\frac{q-1}{q}}_{L^1(B_{R+1}\backslash B_R)}+c_9\sum \limits ^n_{i=1}\|w_i\|_{L^1(B_{R+1}\backslash B_R)}\\[5pt] &+c_9\sum \limits ^m_{j=1}\|\nabla z_j\|^{\frac{q-2}{q-1}}_{L^1(B_{R+1}\backslash B_R)}\quad \text{for}\,\,t\in (0,T), \end{split} \end{align*}
\begin{align*} \begin{split} y^{\prime}_K(t)\leq & c_9y_K(t)+c_9\sum \limits ^n_{i=1}\|w_i\|^{\frac{q-1}{q}}_{L^1(B_{R+1}\backslash B_R)}+c_9\sum \limits ^n_{i=1}\|w_i\|_{L^1(B_{R+1}\backslash B_R)}\\[5pt] &+c_9\sum \limits ^m_{j=1}\|\nabla z_j\|^{\frac{q-2}{q-1}}_{L^1(B_{R+1}\backslash B_R)}\quad \text{for}\,\,t\in (0,T), \end{split} \end{align*}
where due to
![]() $y_K(0)=0$
and (2.1), an integration over
$y_K(0)=0$
and (2.1), an integration over
![]() $(0,T)$
shows that
$(0,T)$
shows that
![]() $y_K(t)\rightarrow 0$
as
$y_K(t)\rightarrow 0$
as
![]() $K\rightarrow \infty$
. Hence
$K\rightarrow \infty$
. Hence
![]() $\overline{\boldsymbol{{u}}}=\widetilde{\boldsymbol{{u}}}$
and
$\overline{\boldsymbol{{u}}}=\widetilde{\boldsymbol{{u}}}$
and
![]() $\overline{\boldsymbol{{v}}}=\widetilde{\boldsymbol{{v}}}$
in
$\overline{\boldsymbol{{v}}}=\widetilde{\boldsymbol{{v}}}$
in
![]() $\mathbb{R}^2\times (0,T)$
.
$\mathbb{R}^2\times (0,T)$
.
To prove the positivity of
![]() $u_i$
,
$u_i$
,
![]() $i\in \mathcal{I}$
, it is sufficient to make sure that
$i\in \mathcal{I}$
, it is sufficient to make sure that
![]() $u_i$
is non-negative in
$u_i$
is non-negative in
![]() $\mathbb{R}^2\times (0,T)$
for each
$\mathbb{R}^2\times (0,T)$
for each
![]() $T\in (0,T_{\max })$
by the strong maximum principle and (1.6). Denote
$T\in (0,T_{\max })$
by the strong maximum principle and (1.6). Denote
![]() $u^{-}_{i}=\max \{-u_i,0\}$
. A direct computation shows that
$u^{-}_{i}=\max \{-u_i,0\}$
. A direct computation shows that
 \begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_{i})^2dx\leq &-\frac{1}{2}\int _{\mathbb{R}^2}\xi ^2_K|\nabla u^{-}_i|^2dx+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K|u^{-}_i|^2\left (\sum \limits ^m_{j=1}|\nabla v_j|^2\right )dx\\[5pt] &+4\int _{\mathbb{R}^2}|u^{-}_i|^2|\nabla \xi _K|^2dx+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _K(u^{-}_i)^2\nabla \xi _K\cdot \nabla v_jdx. \end{split} \end{align*}
\begin{align*} \begin{split} \frac{1}{2}\frac{d}{dt}\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_{i})^2dx\leq &-\frac{1}{2}\int _{\mathbb{R}^2}\xi ^2_K|\nabla u^{-}_i|^2dx+(\alpha ^*)^2|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K|u^{-}_i|^2\left (\sum \limits ^m_{j=1}|\nabla v_j|^2\right )dx\\[5pt] &+4\int _{\mathbb{R}^2}|u^{-}_i|^2|\nabla \xi _K|^2dx+2\sum \limits ^m_{j=1}\alpha _{i,j}\int _{\mathbb{R}^2}\xi _K(u^{-}_i)^2\nabla \xi _K\cdot \nabla v_jdx. \end{split} \end{align*}
Since
![]() $\nabla v_j\in L^{\infty }((0,T);\,L^{p}(\mathbb{R}^2))$
with
$\nabla v_j\in L^{\infty }((0,T);\,L^{p}(\mathbb{R}^2))$
with
![]() $p\gt 2$
, using a similar approach in (A7) shows the existence of
$p\gt 2$
, using a similar approach in (A7) shows the existence of
![]() $c_{10}\gt 0$
such that
$c_{10}\gt 0$
such that
 \begin{align*} \begin{split} (\alpha ^*)^2&|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K|u^{-}_i|^2\left (\sum \limits ^m_{j=1}|\nabla v_j|^2\right )dx\\[5pt] \leq & c_5(\alpha ^*)^2|\mathcal{J}|\|\xi _Ku^{-}_i\|^2_{L^{\frac{2q}{q-2}}(\mathbb{R}^2)}\\[5pt] \leq & \frac{1}{2}\int _{\mathbb{R}^2}\xi ^2_K|\nabla u^{-}_i|^2dx+\frac{1}{2}\int _{\mathbb{R}^2}|\nabla \xi _K|^2(u^{-}_i)^2dx+c_{10}\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_i)^2dx. \end{split} \end{align*}
\begin{align*} \begin{split} (\alpha ^*)^2&|\mathcal{J}|\int _{\mathbb{R}^2}\xi ^2_K|u^{-}_i|^2\left (\sum \limits ^m_{j=1}|\nabla v_j|^2\right )dx\\[5pt] \leq & c_5(\alpha ^*)^2|\mathcal{J}|\|\xi _Ku^{-}_i\|^2_{L^{\frac{2q}{q-2}}(\mathbb{R}^2)}\\[5pt] \leq & \frac{1}{2}\int _{\mathbb{R}^2}\xi ^2_K|\nabla u^{-}_i|^2dx+\frac{1}{2}\int _{\mathbb{R}^2}|\nabla \xi _K|^2(u^{-}_i)^2dx+c_{10}\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_i)^2dx. \end{split} \end{align*}
On the other hand, we follow a procedure in proving uniqueness and conclude that
![]() $g_K(t)\,:\!=\,\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_{i})^2dx$
fulfils
$g_K(t)\,:\!=\,\int _{\mathbb{R}^2}\xi ^2_K(u^{-}_{i})^2dx$
fulfils
![]() $g_K(t)\rightarrow 0$
as
$g_K(t)\rightarrow 0$
as
![]() $K\rightarrow \infty$
. Hence non-negativity of
$K\rightarrow \infty$
. Hence non-negativity of
![]() $u_i$
,
$u_i$
,
![]() $i\in \mathcal{I}$
, has been proved.
$i\in \mathcal{I}$
, has been proved.
Fourth Step:
![]() $L^q$
estimates for
$L^q$
estimates for
![]() $v_j$
,
$v_j$
,
![]() $j\in \mathcal{J}$
. Integrating
$j\in \mathcal{J}$
. Integrating
![]() $j$
-th equation in (1.5) over
$j$
-th equation in (1.5) over
![]() $\mathbb{R}^2\times (0,T)$
directly, it results in
$\mathbb{R}^2\times (0,T)$
directly, it results in
 \begin{align*} \|v_j(\cdot,t)\|_{L^1(\mathbb{R}^2)}\leq \begin{cases} &\|v_{j0}\|_{L^1(\mathbb{R}^2)}+t\sum \limits ^n_{i=1}|\gamma _{i,j}|\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad \text{if}\quad \beta _j=0,\\[5pt] &e^{-\beta _jt}\|v_{j0}\|_{L^1(\mathbb{R}^2)}+\frac{1}{|\beta _j|}\left |1-e^{-\beta _jt}\right |\sum \limits ^n_{i=1}|\gamma _{i,j}|\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad \text{if}\quad \beta _j\neq 0. \end{cases} \end{align*}
\begin{align*} \|v_j(\cdot,t)\|_{L^1(\mathbb{R}^2)}\leq \begin{cases} &\|v_{j0}\|_{L^1(\mathbb{R}^2)}+t\sum \limits ^n_{i=1}|\gamma _{i,j}|\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad \text{if}\quad \beta _j=0,\\[5pt] &e^{-\beta _jt}\|v_{j0}\|_{L^1(\mathbb{R}^2)}+\frac{1}{|\beta _j|}\left |1-e^{-\beta _jt}\right |\sum \limits ^n_{i=1}|\gamma _{i,j}|\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad \text{if}\quad \beta _j\neq 0. \end{cases} \end{align*}
For
![]() $q\gt 1$
, applying Lemma 5.1 to (A2) we infer that
$q\gt 1$
, applying Lemma 5.1 to (A2) we infer that
 \begin{align*} \begin{split} \|v_j(\cdot,t)\|_{L^{q}(\mathbb{R}^2)} \leq &e^{|\beta _j|t}\|v_{j0}\|_{L^{q}(\mathbb{R}^2)} +e^{|\beta _j|t}\sum \limits ^n_{i=1}|\gamma _{i,j}|\int ^t_0(t-s)^{-1+\frac{1}{q}} \left \|\widetilde{u}_i(\cdot,s)\right \|_{L^1({\mathbb{R}^2})}ds\\[5pt] \leq &e^{\beta ^*T}\|v_{j0}\|_{L^{q}(\mathbb{R}^2)}+q\gamma ^*e^{\beta ^*T}T^{\frac{1}{q}}\sum \limits ^n_{i=1}\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad j\in \mathcal{J},\quad t\in [0,T]. \end{split} \end{align*}
\begin{align*} \begin{split} \|v_j(\cdot,t)\|_{L^{q}(\mathbb{R}^2)} \leq &e^{|\beta _j|t}\|v_{j0}\|_{L^{q}(\mathbb{R}^2)} +e^{|\beta _j|t}\sum \limits ^n_{i=1}|\gamma _{i,j}|\int ^t_0(t-s)^{-1+\frac{1}{q}} \left \|\widetilde{u}_i(\cdot,s)\right \|_{L^1({\mathbb{R}^2})}ds\\[5pt] \leq &e^{\beta ^*T}\|v_{j0}\|_{L^{q}(\mathbb{R}^2)}+q\gamma ^*e^{\beta ^*T}T^{\frac{1}{q}}\sum \limits ^n_{i=1}\|u_{i0}\|_{L^1(\mathbb{R}^2)},\quad j\in \mathcal{J},\quad t\in [0,T]. \end{split} \end{align*}
Hence, we have obtained
![]() $L^q$
estimates for
$L^q$
estimates for
![]() $v_j$
,
$v_j$
,
![]() $j\in \mathcal{J}$
, and found that the upper bound is independent of time variable if
$j\in \mathcal{J}$
, and found that the upper bound is independent of time variable if
![]() $\beta _j\gt 0$
,
$\beta _j\gt 0$
,
![]() $\forall \,\,j\in \mathcal{J}$
.
$\forall \,\,j\in \mathcal{J}$
.
Fifth Step: Criterion. If
![]() $T_{\max }\lt \infty$
and there exists a constant
$T_{\max }\lt \infty$
and there exists a constant
![]() $c_{11}\gt 0$
such that
$c_{11}\gt 0$
such that
Then from the mass conservation
![]() $\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}=\|u_{i0}\|_{L^1(\mathbb{R}^2)}$
,
$\|u_i(\cdot,t)\|_{L^1(\mathbb{R}^2)}=\|u_{i0}\|_{L^1(\mathbb{R}^2)}$
,
![]() $i\in \mathcal{I}$
, and the boundedness of
$i\in \mathcal{I}$
, and the boundedness of
![]() $L^1$
estimate for
$L^1$
estimate for
![]() $v_j(\cdot,t)$
,
$v_j(\cdot,t)$
,
![]() $j\in \mathcal{J}$
, for all
$j\in \mathcal{J}$
, for all
![]() $t\in (0,T_{\max })$
and the following fact
$t\in (0,T_{\max })$
and the following fact
is right with some
![]() $c_{12}\gt 0$
because of (A3)–(A4), we claim that (A5) implies
$c_{12}\gt 0$
because of (A3)–(A4), we claim that (A5) implies
![]() $T_{\max }$
cannot be finite.
$T_{\max }$
cannot be finite.