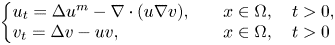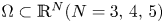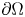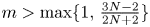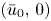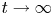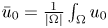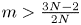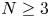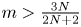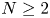Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T05:17:37.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Global boundedness and large time behaviour in a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant

Part of: Physiological, cellular and medical topics Representations of solutions Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  30 April 2024

Minghua Zhang ,
Chunlai Mu  and
Hongying Yang
Minghua Zhang
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P.R. China ([email protected]; [email protected])
Chunlai Mu
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P.R. China ([email protected]; [email protected])
Hongying Yang
Affiliation:
School of Sciences, Shihezi University, Shihezi 832000, P.R. China ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the following quasilinear chemotaxis system with consumption of chemoattractant

\[ \left\{\begin{array}{@{}ll} u_t=\Delta u^{m}-\nabla\cdot(u\nabla v),\quad & x\in \Omega,\quad t>0,\\ v_t=\Delta v-uv,\quad & x\in \Omega,\quad t>0\\ \end{array}\right. \]
in a bounded domain $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ with smooth boundary $\partial \Omega$. It is shown that if $m>\max \{1,\,\frac {3N-2}{2N+2}\}$, for any reasonably smooth nonnegative initial data, the corresponding no-flux type initial-boundary value problem possesses a globally bounded weak solution. Furthermore, we prove that the solution converges to the spatially homogeneous equilibrium $(\bar {u}_0,\,0)$ in an appropriate sense as $t\rightarrow \infty$, where $\bar {u}_0=\frac {1}{|\Omega |}\int _\Omega u_0$. This result not only partly extends the previous global boundedness result in Fan and Jin (J. Math. Phys. 58 (2017), 011503) and Wang and Xiang (Z. Angew. Math. Phys. 66 (2015), 3159–3179) to $m>\frac {3N-2}{2N}$ in the case $N\geq 3$, but also partly improves the global existence result in Zheng and Wang (Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 669–686) to $m>\frac {3N}{2N+2}$ when $N\geq 2$.

Keywords

boundednesschemotaxisweak solutionlarge time behaviourquasilinear

MSC classification

Primary: 35B40: Asymptotic behavior of solutions
Secondary: 35D30: Weak solutions 35K51: Initial-boundary value problems for second-order parabolic systems 92C17: Cell movement (chemotaxis, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 26
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

Chemotaxis is one of the most important components in the process of reproduction and migration, it describes the biased movement of biological species or cells towards chemotaxis substances. In this paper, we study the following quasilinear chemotaxis system with consumption of chemoattractant

(1.1)\begin{equation} \left\{\begin{array}{@{}ll} u_t=\Delta u^m-\nabla\cdot (u\nabla v),\quad & x\in \Omega, t>0,\\ v_t=\Delta v - uv,\quad & x\in \Omega, t>0,\\ (\nabla u^m- u\nabla v)\cdot \nu=\nabla v\cdot \nu=0,\quad & x\in \partial\Omega, t>0,\\ {u(x,0)=u_0(x)},\quad v(x,0)=v_0(x),\quad & x\in \Omega\\ \end{array}\right.\end{equation}

in a bounded domain $\Omega \subset \mathbb {R}^N$ with smooth boundary $\partial \Omega,$ where $m>1$ is a constant, $\nu$ denotes the outer normal derivative on $\partial \Omega$, $u(x,\,t)$ and $v(x,\,t)$ denote the density of cells population and the concentration of oxygen, respectively. And the initial data $(u_0,\,v_0)$ satisfies

(1.2)\begin{equation} \left\{ \begin{array}{@{}ll} u_0\in W^{1,\infty}(\Omega)~~\text{ with }~u_0\geq 0 \text{ and } u_0\not\equiv 0,\\ v_0\in W^{1,\infty}(\Omega)~~\text{ with } v_0\geq0~\text{ in }~\bar{\Omega}.\\ \end{array} \right. \end{equation}

To better understand the chemotaxis model (1.1), we recall several previous works. Firstly, we recall the following system that has been studied for more than ten years,

(1.3)\begin{equation} \left\{\begin{array}{@{}ll} u_t=\nabla\cdot( D(u)\nabla u)-\nabla\cdot (u\nabla v),\quad & x\in \Omega, t>0,\\ \displaystyle{ v_t=\Delta v - uv},\quad & x\in \Omega, t>0,\\ \end{array}\right.\end{equation}

where the function $D(u)$ denotes the diffusive function of cells, and the effect of $D(u)$ on the global solvability of solutions has attracted widespread attention. Note that for the corresponding no-flux type initial-boundary value problem (1.3), for the case of $D(u)=1$ and $N\geq 2$, Tao [Reference Tao12] proved that system (1.3) possesses a unique global bounded classical solution under the assumption that $\|v_0\|_{L^\infty (\Omega )}$ is small. Especially, the domain is convex when $N=3$, Tao and Winkler [Reference Tao and Winkler14] removed the smallness condition of initial data and proved that the system admits at least one global weak solution for arbitrarily large initial data; moreover, they showed that this solution is eventually smooth and converges to the constant equilibria in the large time limit.

Considering the quasilinear diffusion function $D(u)\geq D_0(u+1)^{m-1}$ with some constant $D_0>0$, if $N\geq 2$ and the domain is convex, Wang et al. [Reference Wang, Mu and Zhou20] established the globally bounded classical solution when $m>2-\frac 2N$. Subsequently, Wang et al. [Reference Wang, Mu, Lin and Zhao19] removed the convexity assumption and showed that the global solution is locally bounded if $m>2-\frac {6}{N+4}$ with $N\geq 3$. In addition, Zheng and Wang [Reference Zheng and Wang41] improved the global existence result for the case $m>\frac {3N}{2N+2}$.

Furthermore, taking account of the degenerate diffusion function $D(u)\geq D_0u^{m-1}$ with some constant $D_0>0$, under the assumption $m>\frac {3N-2}{2N}$, $N\geq 3$, the globally bounded weak solution was obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], and the asymptotic behaviour of solution was obtained in [Reference Fan and Jin5]. And for the convex domain case, the global existence result of the weak solution was further raised to the case $m>\frac {3N}{2N+2}(N\geq 2)$ in [Reference Zheng and Wang41]. Since then, no further research was conducted.

Besides, chemotaxis processes with signal absorption coupling to the fluid motion are often considered, such as the following chemotaxis system which describes the movement of bacterial cells to oxygen in incompressible fluids [Reference Tuval, Cisneros, Dombrowski, Wolgemuth, Kessler and Goldstein18]

(1.4)\begin{equation} \left\{\begin{array}{@{}ll} u_t+\mathcal {V}\cdot\nabla u=\nabla\cdot( D(u)\nabla u)-\nabla\cdot (uS\nabla v), & \quad x\in \Omega, t>0,\\ \displaystyle{ v_t+\mathcal {V}\cdot\nabla v=\Delta v - uv}, & \quad x\in \Omega, t>0,\\ \displaystyle{\mathcal {V}_t+\kappa(\mathcal {V}\cdot\nabla)\mathcal {V}=\Delta\mathcal {V}-\nabla P+u\nabla\phi,\quad \nabla\cdot\mathcal {V}=0}, & \quad x\in \Omega, t>0,\\ \end{array}\right.\end{equation}

where $S$ is a given chemotactic sensitivity function, $\kappa \in \mathbb {R}$ is a constant, $P$ is the pressure, $\phi$ is the gravitational force, and $\mathcal {V}$ is the velocity of the fluid. Note that if the effect of fluids is absent (i.e. $\mathcal {V}=0$), system (1.4) is reduced to system (1.3). Readers who are interested in the study of (1.4) could refer to [Reference Cao1–Reference Di Francesco, Lorz and Markowich3, Reference Jin6, Reference Lorz10, Reference Tao and Winkler15, Reference Tao and Winkler16, Reference Wang21–Reference Wang and Xie23, Reference Winkler26–Reference Winkler33, Reference Zhang and Li36–Reference Zheng and Qi40]. Particularly, we point out that when $D(u)=mu^{m-1}$, there is a long process of how far $m$ can ensure the solvability of system (1.4) with $\kappa =0$ in $\Omega \subset \mathbb {R}^3$. When $S$ is a scalar function, Francesco et al. [Reference Di Francesco, Lorz and Markowich3] proved global bounded weak solutions for $m\in (\tfrac {7+\sqrt {217}}{12},\,2]$, Tao and Winkler [Reference Tao and Winkler16] established the existence of global weak solutions for $m>\frac {8}{7}$, Winkler [Reference Winkler31] and Jin [Reference Jin6] enhanced the boundedness result to $m>\frac {9}{8}$ and $m>1$, respectively. When $S$ is a given parameter matrix, Winkler [Reference Winkler28] presented the boundedness of solutions in convex domains for $m>\frac {7}{6}$. Additionally, this result was extended to the case $m>\frac {10}{9}$ [Reference Zheng37], $m>\frac {65}{63}$ [Reference Tian and Xiang17], and $m>\frac {11}{4}-\sqrt {3}$ [Reference Zheng and Ke39]. Recently, Winkler [Reference Winkler34, corollary 1.4] has shown that the system admits a globally bounded weak solution for $m>1$ in the convex domain.

Comparing the results of systems (1.3) and (1.4) in three dimensions, we see that the conditions of parameter $m>\frac {7}{6}$ [Reference Fan and Jin5, Reference Wang and Xiang24] and $m>\frac {9}{8}$ [Reference Zheng and Wang41] are worse than $m>1$ [Reference Jin6, Reference Winkler34] from the point of ensuring the solvability of the solution. Therefore, it is a natural question whether the range of $m$ of system (1.1) in higher dimensions is wider than that in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. If the range of $m$ can be extended, what is the large time behaviour of the corresponding solution? Indeed, those questions are partially answered by the main results of this paper.

Main idea: As aforementioned, under the assumption $m>\frac {3N-2}{2N}$, the global boundedness weak solution of system (1.1) has been obtained in [Reference Fan and Jin5, Reference Wang and Xiang24], thus we focus on the case $m\leq \frac {3N-2}{2N}$. Without loss of generality, we shall assume that $2>m>1$ in the sequel. Note that the term $\int _\Omega (u_\varepsilon +\varepsilon )^{p-m+1}|\nabla v_\varepsilon |^2$ was decoupled into two parts in [Reference Fan and Jin5, Reference Wang and Xiang24], namely the integrals containing only $u_\varepsilon$ and $\nabla v_\varepsilon$ separately. In this paper, inspired by [Reference Winkler34], we choose $p=m+1$ to be the dissipative part of the inequality describing the evolution of $\int _\Omega (u_\varepsilon +\varepsilon )|\nabla v_\varepsilon |^2$. Unfortunately, there are additional bad terms that must be addressed. Therefore, we construct a new functional

\[ y(t)=\tilde{C_1}\int_\Omega (u_\varepsilon+\varepsilon)^{m+1}+\tilde{C_2}\int_\Omega (u_\varepsilon+\varepsilon)^{3-m}+\int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2+\tilde{C_3}\int_\Omega |\nabla v_\varepsilon|^4 \]

to obtain the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$ for $2>m>1$, which is the most critical step. Next, under the assumption of $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$ (where $N=3,\,4,\,5$), the boundedness of functional $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$ for large $p$ and large $q$ can be obtained. And then by the iteration procedure in [Reference Tao and Winkler13, theorem A.1], we get the uniform bounds for $\|u_\varepsilon \|_{L^\infty (\Omega )}$ and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$.

At first, we introduce the following definition of weak solutions.

Definition 1.1 For a global weak solution of (1.1), we mean a pair of nonnegative functions $(u,\,v)$ satisfying

\[ u\in L^\infty((0,\infty);L^\infty(\Omega)),\quad \nabla u^m \in L^2_{loc}([0, \infty);L^2(\Omega)),\quad v\in L^\infty((0,\infty);L^\infty(\Omega)), \]

and for any $\varphi \in C_0^{\infty } (\bar {\Omega }\times [0,\, \infty ))$,

\begin{align*} & -\int_0^{\infty}\int_{\Omega}u\varphi_t-\int_{\Omega}u_0\varphi({\cdot},0)={-}\int_0^\infty\int_\Omega \nabla u^m\cdot \nabla\varphi+\int_0^\infty\int_\Omega u\nabla v\cdot\nabla\varphi,\\ & {-\int_0^{\infty}\int_{\Omega}v\varphi_t-\int_{\Omega}v_0\varphi({\cdot},0)}={-\int_0^\infty\int_{\Omega}\nabla v\cdot\nabla\varphi-\int_0^\infty\int_{\Omega}vu\cdot\varphi}. \end{align*}

The main results are stated as follows.

Theorem 1.2 Let $\Omega \subset \mathbb {R}^N~(N=3,\,4,\,5)$ be a bounded domain with smooth boundary, assume that

\[ m>\max\Bigg\{1,\frac{3N-2}{2N+2}\Bigg\}, \]

then system (1.1) with (1.2) at least has one globally bounded weak solution.

Remark 1.3 For the case $3\leq N\leq 5$, our theorem 1.2 extends the previous results in [Reference Fan and Jin5, Reference Wang and Xiang24, Reference Zheng and Wang41]. In addition, our result is consistent with the associated fluid-free system [Reference Jin6, Reference Winkler34] for $N=3$.

Remark 1.4 In this paper, our method is motivated by Winkler [Reference Winkler34], but we can only solve the case for $N=3,\,4,\,5$, whether it can be further solved for the case $N>5$ is uncertain. Fortunately, we have removed the convexity assumption on the domain in [Reference Winkler34].

Remark 1.5 In the case $N=3,\,4$, we can find that if $m=1$ the system must be imposed on the smallness condition of the initial data [Reference Tao12]. As we all know, the condition $m>1$ means that the diffusion is stronger than $m=1$. From these points of view, our result is optimal. But in the case $N=5$, it is not clear whether the assumptions of $m>\frac {13}{12}$ is optimal to ensure global boundedness of the solution.

As a byproduct of theorem 1.2, large time behaviour of the solution to system (1.1) can be achieved.

Theorem 1.6 Under the assumptions of theorem 1.2, the global weak solution constructed in theorem 1.2 satisfies

(1.5)\begin{equation} u({\cdot},t)\stackrel{\ast}\rightharpoonup \bar{u}_0~in~ L^\infty(\Omega),\quad v({\cdot},t)\rightarrow 0 ~in~ L^\infty(\Omega)\end{equation}

as $t\rightarrow \infty$, where $\bar {u}_0:=\frac {1}{|\Omega |}\int _\Omega u_0$.

The rest of this paper is organized as follows. In § 2, we introduce the approximated system (2.1) and provide the local existence of the approximated solution and some crucial properties. In § 3, we present some important estimates, and obtain the global bounded classical solution to the approximate system (2.1). In § 4, we deduce some convergence properties and complete the proof of theorem 1.2 by an approximation procedure. Finally, in § 5, we establish the convergence of the solution.

2. Approximate problems and crucial properties

In this section, in order to construct a weak solution of (1.1), we consider the following approximate problems

(2.1)\begin{equation} \left\{\begin{array}{@{}ll} (u_\varepsilon)_t=\Delta(u_\varepsilon+\varepsilon)^{m}-\nabla\cdot(u_\varepsilon\nabla v_\varepsilon),\quad & x\in \Omega, t>0,\\ \displaystyle{ (v_\varepsilon)_t=\Delta v_\varepsilon - u_\varepsilon v_\varepsilon},\quad & x\in \Omega, t>0,\\ \displaystyle{\dfrac{\partial u_\varepsilon}{\partial\nu}=\dfrac{\partial v_\varepsilon}{\partial\nu}=0},\quad & x\in \partial\Omega, t>0,\\ \displaystyle{u_\varepsilon(x,0)=u_{0}(x),\quad v_\varepsilon(x,0)=v_{0}(x)},~~ & x\in \Omega\\ \end{array}\right.\end{equation}

for $\varepsilon \in (0,\,1)$.

For each $\varepsilon \in (0,\,1)$, the regularized problem (2.1) is locally solvable in the classical sense.

Lemma 2.1 Suppose that $\Omega \subset \mathbb {R}^N (N\geq 3)$ is a bounded domain with smooth boundary. Assume that the initial data $(u_0,\,v_0)$ fulfils (1.2). Then problem (2.1) has a unique classical solution

(2.2)\begin{align} \left\{\begin{array}{@{}ll} u_\varepsilon\in C^0(\bar{\Omega}\times[0,T_{\max,\varepsilon}))\cap C^{2,1}(\bar{\Omega}\times(0,T_{\max,\varepsilon}))\cap L^\infty_{loc}([0,T_{\max,\varepsilon});W^{1,\infty}(\Omega)),\\ v_\varepsilon \in C^0(\bar{\Omega}\times[0,T_{\max,\varepsilon}))\cap C^{2,1}(\bar{\Omega}\times(0,T_{\max,\varepsilon}))\cap L^\infty_{loc}([0,T_{\max,\varepsilon});W^{1,\infty}(\Omega)),\\ \end{array}\right.\end{align}

where $T_{\max,\varepsilon }$ denotes the maximal existence time. Moreover, if $T_{\max,\varepsilon }<\infty$, then

(2.3)\begin{equation} \|u_\varepsilon({\cdot}, t)\|_{L^\infty(\Omega)}+\|v_\varepsilon({\cdot}, t)\|_{W^{1,\infty}(\Omega)}\rightarrow\infty~~ \mbox{as}~~ t \rightarrow T_{\max,\varepsilon}.\end{equation}

Proof. The local existence, extensibility criterion, and regularity of (2.1) are well-established (see [Reference Wang, Mu and Zhou20]), the uniqueness can be achieved by the same procedure as in [Reference Horstmann and Winkler7, Reference Winkler25], so we omit the details of the proof for the sake of brevity.

Lemma 2.2 The solution $(u_\varepsilon,\, v_\varepsilon )$ of (2.1) satisfies

(2.4)\begin{align} \|u_\varepsilon({\cdot},t)\|_{L^1(\Omega)}& =\|u_{0}\|_{L^1(\Omega)}\text{ for all }t\in (0, T_{\max,\varepsilon}), \end{align}
(2.5)\begin{align} \|v_\varepsilon({\cdot},t)\|_{L^\infty(\Omega)}& \leq\|v_{0}\|_{L^\infty(\Omega)}\text{ for all } t\in (0, T_{\max,\varepsilon}). \end{align}

Proof. A direct integration in the first equation in (2.1) yields (2.4). Equation (2.5) follows from an application of the maximum principle to the second equation in (2.1).

In order to prove the main result, we state two basic lemmas which will be used later. The first is Gagliardo–Nirenberg inequality.

Lemma 2.3 Let $\Omega \subset \mathbb {R}^N(N\geq 3)$ be a bounded smooth domain

(2.6)\begin{equation} 1\leq r< q<\frac{N(p+m-1)}{N-2}, \end{equation}

then there exists $C>0$ such that

(2.7)\begin{equation} \int_\Omega \varphi^q\leq C\left\{\left(\int_\Omega \varphi^{p+m-3}|\nabla \varphi|^2\right)^{\frac{\frac{q}{2r}-\frac{1}{2}}{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}}\|\varphi\|_{L^r(\Omega)}^{\frac{{\frac{p+m-1}{2}+\frac{q}{N}-\frac{q}{2}}}{{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}}}+\|\varphi\|_{L^r(\Omega)}^{q}\right\} \end{equation}

for all $\varphi \in C^1(\Omega )\cap L^r(\Omega )$.

Particularly, if $q=p+m-1+\frac {2r}{N}$, then there exists $C>0$ such that

(2.8)\begin{equation} \int_\Omega \varphi^q\leq C\left\{\left(\int_\Omega \varphi^{p+m-3}|\nabla \varphi|^2\right)\|\varphi\|_{L^r(\Omega)}^{\frac{{\frac{p+m-1}{2}+\frac{q}{N}-\frac{q}{2}}}{{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}}}+\|\varphi\|_{L^r(\Omega)}^{q}\right\} \end{equation}

for all $\varphi \in C^1(\Omega )\cap L^r(\Omega )$.

Proof. Condition (2.6) entails that

\[ a=\frac{\frac{p+m-1}{2r}-\frac{p+m-1}{2q}}{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}\in(0,1), \]

and hence the Gagliardo–Nirenberg inequality provides $C_1>0$ satisfying

\begin{align*} \int_\Omega \varphi ^q & = \|\varphi^\frac{p+m-1}{2}\|_{L^{\frac{2q}{p+m-1}}(\Omega)}^{\frac{2q}{p+m-1}}\\ & \leq C_1\|\nabla \varphi^{\frac{p+m-1}{2}}\|_{L^2(\Omega)}^{\frac{2qa}{p+m-1}}\cdot\|\varphi^{\frac{p+m-1}{2}}\|_{L^{\frac{2r}{p+m-1}}(\Omega)}^{\frac{2q(1-a)}{p+m-1}} +C_1 \|\varphi^{\frac{p+m-1}{2}}\|_{L^{\frac{2r}{p+m-1}}(\Omega)}^{\frac{2q}{p+m-1}}\\ & = C_2 \Bigg\{\left(\int_\Omega \varphi^{p+m-3}|\nabla \varphi|^2\right)^{\frac{qa}{p+m-1}}\cdot \|\varphi\|_{L^r(\Omega)}^{q(1-a)}+\|\varphi\|_{L^r(\Omega)}^q\Bigg\} \end{align*}

for all $\varphi \in C^1({\Omega })\cap L^r (\Omega )$ with $C_2=C_1\max \{1,\,\frac {(p+m-1)^2}{4}\}$. Note that

\[ \frac{qa}{p+m-1}=\frac{\frac{q}{2r}-\frac{1}{2}}{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}\text{ and }q(1-a)=\frac{{\frac{p+m-1}{2}+\frac{q}{N}-\frac{q}{2}}}{{\frac{p+m-1}{2r}+\frac{1}{N}-\frac{1}{2}}}. \]

Thus, (2.7) is proved. Moreover, since $\frac {qa}{p+m-1}=\frac {\frac {q}{2r}-\frac {1}{2}}{\frac {p+m-1}{2r}+\frac {1}{N}-\frac {1}{2}}=1$ with the additional assumption $q=p+m-1+\frac {2r}{N}$, (2.8) results from (2.7).

The next is interpolation inequality.

Lemma 2.4 (Lemma 3.3 of [Reference Wang and Xiang24])

Suppose that $q>\max \{1,\,\frac {N-2}{2}\}$ and ${\Omega \subset \mathbb {R}^N(N\geq 3)}$ is a bounded domain with smooth boundary. Moreover, assume that

(2.9)\begin{equation} \lambda\in\Bigg[2q+2, \frac{N(2q+1)-2(q+1)}{N-2} \Bigg],\end{equation}

then there exists $C > 0$ such that for all $\varphi \in C^2(\bar {\Omega })$ fulfilling $\varphi \cdot \frac {\partial \varphi }{\partial \nu }= 0$ on $\partial \Omega$, we have

(2.10)\begin{equation} \|\nabla\varphi\|_{L^\lambda(\Omega)}\leq C\||\nabla\varphi|^{q-1}D^2\varphi\|_{L^2(\Omega)}^{\frac{2(\lambda-N)}{(2q-N+2)\lambda}} \|\varphi\|_{L^\infty(\Omega)}^{\frac{2qN-(N-2)\lambda}{(2q-N+2)\lambda}}+C\|\varphi\|_{L^\infty(\Omega)}.\\ \end{equation}

3. Uniform estimates for ($u_\varepsilon,\,v_\varepsilon$) and global boundedness of approximate solutions

In this section, we establish some priori estimates for solutions and get the global boundedness of approximate solutions (2.1). Firstly, we apply standard testing procedures to establish a differential inequality for the first equation in (2.1).

Lemma 3.1 Let $p>1$ and $\Omega \subset \mathbb {R}^N$ be a bounded domain with smooth boundary. Assume $(u_\varepsilon,\,v_\varepsilon )$ is a classical solution to system (2.1) on $[0,\,T_{\max,\varepsilon })$. Then for all $t\in (0,\,T_{\max,\varepsilon })$ and $\varepsilon \in (0,\,1)$, we can see that

(3.1)\begin{align} & \frac{1}{p}\frac{{\rm d}}{{\rm d}t}\int_{\Omega}(u_\varepsilon+\varepsilon)^p +\frac{m(p-1)}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{p+m-3}|\nabla u_\varepsilon|^2\notag\\ &\quad \leq \frac{p-1}{2m}\int_\Omega(u_\varepsilon+\varepsilon)^{p-m+1}|\nabla v_\varepsilon|^2.\end{align}

Proof. We multiply the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{p-1}$ integrating by parts and together with Young's inequality to obtain

(3.2)\begin{equation} \begin{aligned} & {\frac{1}{p}\frac{{\rm d}}{{\rm d}t}\|u_\varepsilon+\varepsilon\|^{p}_{L^{p}(\Omega)}+m({{p}-1})\int_{\Omega}(u_\varepsilon+\varepsilon)^{m+{p}-3}|\nabla u_\varepsilon|^2}\\ & \qquad{\leq(p-1)\int_\Omega (u_\varepsilon+\varepsilon)^{p-2}u_\varepsilon\nabla v_\varepsilon\cdot\nabla u_\varepsilon} \\ & \qquad{\leq \frac{m(p-1)}{2} \int_{\Omega}(u_\varepsilon+\varepsilon)^{m+{p}-3}|\nabla u_\varepsilon|^2+\frac{p-1}{2m}\int_\Omega(u_\varepsilon+\varepsilon)^{p-m+1}|\nabla v_\varepsilon|^2} \end{aligned} \end{equation}

for all $t\in (0,\, T_{\max,\varepsilon })$, which results in (3.1).

Lemma 3.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume $2>m>1$, then for all $\varepsilon \in (0,\,1)$, there exists $C>0$ independent of $\varepsilon$ such that the solution of (2.1) satisfies

(3.3)\begin{align} \int_\Omega (u_\varepsilon+\varepsilon)^{m+1}& \leq C \quad\mbox{for~all}~t\in(0,T_{\max,\varepsilon}), \end{align}
(3.4)\begin{align} \int_t^{t+\tau}\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2 & \leq C \text{ for all }t\in(0,T_{\max,\varepsilon}-\tau), \end{align}
(3.5)\begin{align} \int_t^{t+\tau}\int_\Omega|\nabla u_\varepsilon|^2 & \leq C \text{ for all }t\in(0,T_{\max,\varepsilon}-\tau) \end{align}

with $\tau :=\min \{1,\,\frac {T_{\max,\varepsilon }}{2}\}$.

Proof. The proof is divided into five steps.

Step 1. Using (3.1) to $u_\varepsilon$ with $p:=m+1$, for all $t\in (0,\,T_{\max,\varepsilon })$ we get

(3.6)\begin{align} \frac{1}{m+1}\frac{{\rm d}}{{\rm d}t}\int_{\Omega}(u_\varepsilon+\varepsilon)^{m+1} +\frac{m^2}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2 \leq \frac{1}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{2}|\nabla v_\varepsilon|^2.\end{align}

Step 2. For any $\eta _1>0$, one can find four positive constants $C_1,\,C_2(\eta _1),\,C_3$, and $\widetilde {C}$ such that

(3.7)\begin{align} & \frac{{\rm d}}{{\rm d}t}\int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2+\int_\Omega(u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+2\int_\Omega (u _\varepsilon+\varepsilon)|D^2 v_\varepsilon|^2\notag\\ & \quad\leq \eta_1\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2+C_1\int_\Omega |\nabla u_\varepsilon|^2\notag\\ & \qquad+C_2(\eta_1)\int_\Omega |\nabla v_\varepsilon|^2|D^2 v_\varepsilon|^2+C_3\int_\Omega |\nabla v_\varepsilon|^2+\widetilde{C}\quad\mbox{for~all~}t\in(0,T_{\max,\varepsilon}). \end{align}

Indeed, on the basis of (2.5) and the identities $\nabla v_\varepsilon \cdot \nabla \Delta v_\varepsilon =\frac {1}{2}\Delta |\nabla v_\varepsilon |^2-|D^2 v_\varepsilon |^2$ and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$, upon integrating by parts, for all $t\in (0,\,T_{\max,\varepsilon })$, we compute

(3.8)\begin{align} & \frac{{\rm d}}{{\rm d}t} \int_\Omega(u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2\notag\\ & \quad = \int_\Omega (u_\varepsilon)_t\cdot|\nabla v_\varepsilon|^2+2\int_\Omega (u_\varepsilon+\varepsilon)\nabla v_\varepsilon\cdot \nabla (v_\varepsilon)_t\notag\\ & \quad =\int_{\Omega} |\nabla {v}|^2\{\Delta(u_\varepsilon+\varepsilon)^{m}-\nabla\cdot(u_\varepsilon\nabla v_\varepsilon)\}\notag\\ & \qquad+2\int_\Omega (u_\varepsilon+\varepsilon)\nabla v_\varepsilon\cdot\{\nabla\Delta v_\varepsilon-\nabla(u_\varepsilon v_\varepsilon)\}\notag\\ & \quad ={-}2m\int_\Omega (u_\varepsilon+\varepsilon)^{m-1}\nabla u_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon+2\int_\Omega u_\varepsilon\nabla v_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon\notag\\ & \qquad+\int_\Omega (u_\varepsilon+\varepsilon)\Delta|\nabla v_\varepsilon|^2-2\int_\Omega (u_\varepsilon+\varepsilon)|D^2 v_\varepsilon|^2\notag\\ & \qquad-2\int_\Omega (u_\varepsilon+\varepsilon)v_\varepsilon\nabla u_\varepsilon\cdot\nabla v_\varepsilon-2\int_\Omega (u_\varepsilon+\varepsilon)u_\varepsilon|\nabla v_\varepsilon|^2\notag\\ & \quad ={-}2m\int_\Omega (u_\varepsilon+\varepsilon)^{m-1}\nabla u_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon+2\int_\Omega u_\varepsilon\nabla v_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon\notag\\ & \qquad-2\int_\Omega \nabla u_\varepsilon(D^2v_\varepsilon\cdot\nabla v_\varepsilon)+\int_{\partial\Omega} u_\varepsilon \cdot \frac{\partial|\nabla v_\varepsilon|^2}{\partial\nu}-2\int_\Omega (u_\varepsilon+\varepsilon)|D^2 v_\varepsilon|^2\notag\\ & \qquad-2\int_\Omega (u_\varepsilon+\varepsilon)v_\varepsilon\nabla u_\varepsilon\cdot\nabla v_\varepsilon-2\int_\Omega (u_\varepsilon+\varepsilon)u_\varepsilon|\nabla v_\varepsilon|^2. \end{align}

Now, we will estimate the right-hand side of (3.8). To this end, given any $\eta _1>0$, utilize Young's inequality to see that for all $t\in (0,\,T_{\max,\varepsilon })$ satisfies

(3.9)\begin{align} & -2m\int_\Omega (u_\varepsilon+\varepsilon)^{m-1}\nabla u_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon\notag\\ & \quad \leq \eta_1 \int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2+\frac{m^2}{\eta_1}\int_\Omega|\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2, \end{align}
(3.10)\begin{align} & 2\int_\Omega u_\varepsilon\nabla v_\varepsilon\cdot D^2v_\varepsilon\cdot\nabla v_\varepsilon\notag\\ & \leq\frac{1}{2} \int_\Omega u_\varepsilon^2|\nabla v_\varepsilon|^2+2\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2\nonumber\\ & \leq\frac{1}{2} \int_\Omega (u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2 +2 \int_\Omega\ {|\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2}, \end{align}

and

(3.11)\begin{equation} -2\int_\Omega \nabla u_\varepsilon(D^2v_\varepsilon\cdot\nabla v_\varepsilon)\leq \int_\Omega |\nabla u_\varepsilon|^2+\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2.\end{equation}

Next, we will estimate the boundary integral in (3.8). According to [Reference Nagai, Senba and Yoshida11], there exists $c_2>0$ such that $\partial _\nu |\nabla \varphi |^2 \leq c_2|\nabla \varphi |^2$ on $\partial \Omega$ for all $\varphi \in C^2(\bar {\Omega })$ with $\partial _\nu \varphi |_{\partial \Omega }=0$. And notice the equivalent trace inequality [Reference Xiang35, P.1186]: for all $\epsilon >0$, one has

\[ \|w\|_{L^2(\partial\Omega)}\leq\epsilon\|\nabla w\|_{L^2(\Omega)}+C(\epsilon)\|w\|_{L^1(\Omega)},\quad\forall~w\in H^1(\Omega). \]

Now, for any $\epsilon >0$, it follows that for all $t\in(0,T_{\max,\varepsilon})$,

(3.12)\begin{align} \int_{\partial\Omega} u_\varepsilon \cdot \frac{\partial|\nabla v_\varepsilon|^2}{\partial\nu} & \leq c_2\int_{\partial\Omega} u_\varepsilon |\nabla v_\varepsilon|^2\leq c_2 \int_{\partial\Omega}|\nabla v_\varepsilon|^4+ \frac{c_2}{4}\int_{\partial\Omega}u_\varepsilon^2\notag\\ & \leq c_2 \int_{\partial\Omega}|\nabla v_\varepsilon|^4+\epsilon\int_\Omega |\nabla u_\varepsilon|^2+ C(\epsilon)\Bigg(\int_\Omega u_\varepsilon\Bigg)^2. \end{align}

Moreover, let $c_3$ denote the embedding constant for trace embedding $W^{1,1}(\Omega )\hookrightarrow L^1(\partial \Omega )$ [Reference Evans4]. Using lemma 2.4 for $v_\varepsilon$ with $q:=2$, $\lambda :=6$, $3\leq N\leq 5$, and (2.5), one has

(3.13)\begin{equation} \int_\Omega |\nabla v_\varepsilon|^6\leq C \int_\Omega |\nabla v_\varepsilon|^2|D^2 v_\varepsilon|^2 +C \quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{equation}

This combined with Young's inequality yields

(3.14)\begin{align} c_2\int_{\partial\Omega} |\nabla {v_\varepsilon}|^{4} & \leq 2c_2c_3\int_\Omega |\nabla v_\varepsilon|^2 \nabla |\nabla {v_\varepsilon}|^{2}+c_2c_3\int_\Omega |\nabla {v_\varepsilon}|^{4}\notag\\ & \leq \frac{1}{32}\int_\Omega |\nabla |{\nabla v_\varepsilon}|^{2}|^2+(c_2c_3+32{c_2^2c_3^2})\int_\Omega |\nabla {v_\varepsilon}|^{4}\notag\\ & = {\frac{1}{8}\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2+(c_2c_3+32{c_2^2c_3^2})\int_\Omega |\nabla {v_\varepsilon}|^{4}}\notag\\ & \leq{\frac{1}{4}\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2+c_4}\quad~\mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{align}

Therefore, combining (3.12), (3.14) and (2.4) by letting $\epsilon =1$, the boundary integral in (3.8) can be simplified to

\[ \int_{\partial\Omega} u_\varepsilon\frac{\partial|\nabla v_\varepsilon|^2}{\partial\nu}\leq \frac{1}{4}\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2+ \int_\Omega |\nabla u_\varepsilon|^2 +C \quad~\mbox{for all}~t\in(0,T_{\max,\varepsilon}). \]

Next, using (2.5) and Young's inequality, it is obvious that for all $t\in (0,\,T_{\max,\varepsilon })$,

(3.15)\begin{equation} \begin{aligned} -2\int_\Omega (u_\varepsilon+\varepsilon)v_\varepsilon\nabla u_\varepsilon\cdot\nabla v_\varepsilon & \leq \frac{1}{4}\int_\Omega(u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+4\int_\Omega v_\varepsilon^2 |\nabla u_\varepsilon|^2\\ & \leq \frac{1}{4}\int_\Omega(u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+4\|v_{0}\|_{L^\infty(\Omega)}^2\int_\Omega |\nabla u_\varepsilon|^2. \end{aligned} \end{equation}

Since $\varepsilon \in (0,\,1)$, and using Young's inequality, it follows that for all $t\in (0,\,T_{\max,\varepsilon })$,

(3.16)\begin{equation} \begin{aligned} -2\int_\Omega (u_\varepsilon+\varepsilon)u_\varepsilon|\nabla v_\varepsilon|^2 & \leq{-}2\int_\Omega (u_\varepsilon+\varepsilon)(u_\varepsilon+\varepsilon-1)|\nabla v_\varepsilon|^2\\ & ={-}2\int_\Omega (u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+2\int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2\\ & \leq{-}\frac{7}{4}\int_\Omega (u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+4\int_\Omega |\nabla v_\varepsilon|^2. \end{aligned} \end{equation}

From (3.9)–(3.16), we obtain (3.7) upon letting $C_1:=2+4\|v_0\|_{L^\infty (\Omega )}$, $C_2 (\eta _1):=\frac {m^2}{\eta _1}+\frac {13}{4}$ and $C_3=4$.

Step 3. In order to absorb the third term on the right-hand side of (3.7), our goal is to show that the integral $\int _\Omega |\nabla v_\varepsilon |^4$ satisfies

(3.17)\begin{align} \displaystyle{\frac{{\rm d}}{{\rm d}t}\int_\Omega |\nabla v_\varepsilon|^4+\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2 \leq C_4\int_\Omega|\nabla u_\varepsilon|^2 +C_5}\quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{align}

In fact, using the second equation in (2.1) along with the pointwise identities $\nabla v_\varepsilon \cdot \nabla \Delta v_\varepsilon =\frac {1}{2}\Delta |\nabla v_\varepsilon |^2-|D^2 v_\varepsilon |^2$ and $\nabla |\nabla v_\varepsilon |^2=2D^2v_\varepsilon \cdot \nabla v_\varepsilon$, we differentiate $\int _\Omega |\nabla {v_\varepsilon }|^4$ directly and integrate by parts to yield

(3.18)\begin{equation} \begin{aligned} {\frac{1}{4}\frac{{\rm d}}{{\rm d}t}\int_\Omega|\nabla{v_\varepsilon}|^4} & = {\int_{\Omega} |\nabla {v_\varepsilon }|^{2}\nabla {v_\varepsilon }\cdot\nabla(\Delta {v_\varepsilon }-u_\varepsilon v_\varepsilon )}\\ & ={\frac{1}{{2}}\int_{\Omega} |\nabla {v_\varepsilon }|^{2}\Delta |\nabla {v_\varepsilon }|^2-\int_{\Omega} |\nabla {v_\varepsilon }|^{2}|D^2 {v_\varepsilon }|^2}\\ & \quad -{\int_\Omega v_\varepsilon{|\nabla v_\varepsilon }|^{2}\nabla {v_\varepsilon } \nabla u_\varepsilon -\int_\Omega u_\varepsilon |\nabla {v_\varepsilon }|^4 }\\ & ={-\frac{1}{{2}}\int_{\Omega} \left|\nabla |\nabla {v_\varepsilon }|^{2}\right|^2+\frac{1}{{2}}\int_{\partial\Omega} |\nabla {v_\varepsilon }|^{2}\frac{\partial |\nabla {v_\varepsilon }|^{2}}{\partial\nu_\varepsilon}}-\int_\Omega |\nabla v_\varepsilon|^2|D^2 v_\varepsilon|^2\\ & \quad-{\int_\Omega v_\varepsilon{|\nabla v_\varepsilon }|^{2}\nabla {v_\varepsilon } \nabla u_\varepsilon-\int_\Omega u_\varepsilon |\nabla {v_\varepsilon }|^4 }\\ & \leq{-\int_\Omega |\nabla v_\varepsilon|^2|D^2 v_\varepsilon|^2+\frac{1}{{2}}\int_{\partial\Omega} |\nabla {v_\varepsilon }|^{2}\frac{\partial |\nabla {v_\varepsilon }|^{2}}{\partial\nu_\varepsilon }}\\ & \quad-{\int_\Omega v_\varepsilon{|\nabla v_\varepsilon }|^{2}\nabla {v_\varepsilon } \nabla u_\varepsilon -\int_\Omega u_\varepsilon |\nabla {v_\varepsilon }|^4}\quad \text{ for all }t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

Applying Young's inequality, for all $\delta >0$, we obtain

(3.19)\begin{align} -\int_\Omega v_\varepsilon{|\nabla v_\varepsilon }|^{2}\nabla {v_\varepsilon } \nabla u_\varepsilon\leq \frac{\|v_\varepsilon\|_{L^\infty(\Omega)}^2}{4\delta}\int_\Omega |\nabla u_\varepsilon|^2+\delta\int_\Omega {|\nabla v_\varepsilon }|^6\quad~\mbox{for all}~t\in(0,T_{\max,\varepsilon}).\end{align}

In light of (3.13), we can choose a suitable $\delta$ such that exists a constant $c_1>0$ satisfying

(3.20)\begin{equation} \delta\int_\Omega {|\nabla v_\varepsilon }|^6\leq \frac{1}{2}\int_\Omega {|\nabla v_\varepsilon }|^2|D^2 v_\varepsilon|^2+c_1 \quad~\mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{equation}

Similar to (3.14), the boundary integral in (3.18) fulfils

(3.21)\begin{equation} \begin{aligned} \int_{\partial\Omega}\frac{\partial |\nabla {v_\varepsilon}|^2}{\partial\nu} |\nabla {v_\varepsilon}|^{2} & \leq c_2\int_{\partial\Omega} |\nabla {v_\varepsilon}|^{4}\\ & \leq{\frac{1}{4}\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2+c_4}\quad\text{ for all }t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

From (3.18)–(3.21), we obtain (3.17) upon an obvious choice of $C_4:=\frac {\|v_0\|_{L^\infty (\Omega )}^2}{\delta }$ and $C_5:=4c_1+4c_4$.

Step 4. Let the term $\int _\Omega |\nabla u_\varepsilon |^2$ of both (3.7) and (3.17) appears on the left-hand side of an inequality. Namely, for all $t\in (0,\,T_{\max,\varepsilon })$ and for any $\eta _2>0$, there exists $C_6(\eta _2):=\eta _2^{\frac {m-1}{m-2}}\cdot (\frac {2-m}{2m})^{\frac {1}{2-m}}$ such that

(3.22)\begin{equation} \begin{aligned} & \frac{1}{3-m}\frac{{\rm d}}{{\rm d}t}\int_{\Omega}(u_\varepsilon+\varepsilon)^{3-m}+\frac{(2-m)m}{2}\int_\Omega|\nabla u_\varepsilon|^2\\ & \quad\leq \frac{2-m}{2m}\int_\Omega(u_\varepsilon+\varepsilon)^{4-2m}|\nabla v_\varepsilon|^2\\ & \quad\leq \eta_2 \int_\Omega (u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+C_6(\eta_2)\int_\Omega|\nabla v_\varepsilon|^2. \end{aligned} \end{equation}

Actually, due to $2>m>1$, using (3.1) to $u_\varepsilon$ with $p:=3-m$, and upon Young's inequality the result is obtained.

Step 5. Subtly combining (3.6), (3.7), (3.17) and (3.22), let

(3.23)\begin{equation} \begin{aligned} y(t) & :=\frac{1}{2m^2(m+1)}\int_\Omega (u_\varepsilon+\varepsilon)^{m+1}+\frac{4C_1+8{C_2(\eta_1)}C_4}{m(2-m)(3-m)}\int_\Omega (u_\varepsilon+\varepsilon)^{3-m}\\ & \quad+\int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2+2{C_2(\eta_1)}\int_\Omega |\nabla v_\varepsilon|^4 \quad~ \mbox{for all}~ t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

Due to $2>m>1$, we can see that

(3.24)\begin{equation} \begin{aligned} & y'(t)+y(t)+\frac{1}{4}\int_\Omega(u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2 +\Big(C_1+2{C_2(\eta_1)}C_4\Big)\int_\Omega|\nabla u_\varepsilon|^2\\ & \qquad+\frac{3}{4}\int_\Omega(u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+{C_2(\eta_1)}\int_\Omega |\nabla v_\varepsilon|^2|D^2v_\varepsilon|^2 \\ & \quad\leq \eta_2\frac{4C_1+8{C_2(\eta_1)}C_4}{2-m}\int_\Omega(u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2\\ & \qquad +\Bigg(\frac{\big(4C_1+8{C_2(\eta_1)}C_4\big){C_6(\eta_2)}}{m(2-m)}+C_3\Bigg)\int_\Omega|\nabla v_\varepsilon|^2\\ & \qquad+\eta_1\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2+2{C_2(\eta_1)}C_5\\ & \qquad+\frac{1}{2m^2(m+1)}\int_\Omega (u_\varepsilon+\varepsilon)^{m+1}+\frac{4C_1+8{C_2(\eta_1)}C_4}{m(2-m)(3-m)}\int_\Omega (u_\varepsilon+\varepsilon)^{3-m}\\ & \qquad+\int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2+2{C_2(\eta_1)}\int_\Omega |\nabla v_\varepsilon|^4 +\widetilde{C}\quad~ \mbox{for all}~ t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

Choose suitable $\eta _1$ and $\eta _2$ such that $\eta _1=\frac {1}{16}$ and $\eta _2\frac {4C_1+8{C_2(\eta _1)}C_4}{2-m}=\frac {1}{2}$. In view of lemma 2.3, Young's inequality, and (2.4), there exists $c_1>0$ such that

(3.25)\begin{equation} \begin{aligned} & \frac{1}{2m^2(m+1)}\int_\Omega (u_\varepsilon+\varepsilon)^{m+1}+\frac{4C_1+8{C_2(\eta_1)}C_4}{m(2-m)(3-m)}\int_\Omega (u_\varepsilon+\varepsilon)^{3-m}\\ & \quad\leq \frac{1}{8}\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2+c_1 \quad\mbox{for all } t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

Using Young's inequality, we have

(3.26)\begin{align} \int_\Omega (u_\varepsilon+\varepsilon)|\nabla v_\varepsilon|^2\leq \frac{1}{4}\int_\Omega (u_\varepsilon+\varepsilon)^2|\nabla v_\varepsilon|^2+\int_\Omega |\nabla v_\varepsilon|^2\quad \mbox{for all}~ t\in(0,T_{\max,\varepsilon}). \end{align}

Upon Young's inequality and (3.20), there exist $c_2 ~\mbox {and} ~c_3>0$ such that

(3.27)\begin{equation} \begin{aligned} & \int_\Omega|\nabla v_\varepsilon|^2+\Bigg(\frac{\big(4C_1+8{C_2(\eta_1)}C_4\big){C_6(\eta_2)}}{m(2-m)}+C_3\Bigg)\int_\Omega|\nabla v_\varepsilon|^2+2C_4\int_\Omega |\nabla v_\varepsilon|^4\\ & \quad\leq 2\delta {C_2(\eta_1)} \int_\Omega|\nabla v_\varepsilon|^6+c_2\\ & \quad\leq {C_2(\eta_1)} \int_\Omega {|\nabla v_\varepsilon }|^2|D^2 v_\varepsilon|^2+c_3\quad\mbox{for all}~ t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

It follows from (3.24)–(3.27) that

(3.28)\begin{equation} y'(t)+y(t)+h(t)\leq \widehat{C} \quad \mbox{for all}~ t\in(0,T_{\max,\varepsilon}), \end{equation}

where $h(t):=\frac {1}{16}\int _\Omega (u_\varepsilon +\varepsilon )^{2m-2}|\nabla u_\varepsilon |^2 +(C_1+2{C_2(\eta _1)}C_4)\int _\Omega |\nabla u_\varepsilon |^2$ and $\widehat {C}:=2{C_2(\eta _1)}C_5+c_1+c_3+\widetilde {C}$. By an ordinary differential equations (ODE) comparison argument, it yields

\[ y(t)\leq \max\{\widehat{C}, y(0)\}\quad \mbox{for all}~ t\in(0,T_{\max,\varepsilon}), \]

which implies (3.3). Finally, integration of (3.28) shows that (3.4)–(3.5) hold.

According to lemma 3.2, the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$ can be obtained without any restriction on $m$ except for the condition $2>m>1$. Next, we use the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$ to establish a further estimate for solutions to the approximated system (2.1). As in [Reference Tao and Winkler13], we provide an estimate on $\nabla v_\varepsilon$. The proof of the following lemma is the same as that in lemma 3.2 of [Reference Wang and Xiang24], so we omit it.

Lemma 3.3 Let $q>1$, then for all $\varepsilon \in (0,\,1),$ we have

(3.29)\begin{equation} \begin{aligned} & \displaystyle{\frac{{\rm d}}{{\rm d}t}\int_\Omega |\nabla v_\varepsilon|^{2q}+\frac{2(q-1)}{q}\int_\Omega |\nabla |\nabla v_\varepsilon|^q|^2+q\int_\Omega|\nabla v_\varepsilon|^{2(q-1)}|D^2v_\varepsilon|^2}\\ & \quad{\quad\leq q(2q-2+\sqrt{N})^2\|v_0\|_{L^\infty(\Omega)}^2\int_\Omega u_\varepsilon^2|\nabla v_\varepsilon|^{2q-2}+C_7} \end{aligned} \end{equation}

for all $t\in (0,\,T_{\max,\varepsilon })$ with a positive constant $C_7.$

Next, we will estimate the combination of $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$.

Lemma 3.4 Assume that $2>m>1$, then for all $p>2$ and any $q>1$, one can find three constants $C_8,\,C_9,\,C_{10}>0$ such that

(3.30)\begin{equation} \begin{aligned} & F'_\varepsilon(t)+F_\varepsilon(t)+\frac{p(p-1)}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{p+m-3}|\nabla u_\varepsilon|^2\\ & \quad \leq C_8 \int_\Omega (u_\varepsilon+\varepsilon)^{\frac{(p-m+1)(2q+2)}{2q}}+C_9\int_\Omega (u_\varepsilon+\varepsilon)^{q+1}\\ & \qquad+\int_\Omega (u_\varepsilon+\varepsilon)^{p}+C_{10} \quad\mbox{for all }t\in(0,T_{\max,\varepsilon}), \end{aligned} \end{equation}

where the function $F_\varepsilon (t)$ is defined as

(3.31)\begin{equation} F_\varepsilon(t):=\int_\Omega(u_\varepsilon+\varepsilon)^p+\int_\Omega |\nabla v_\varepsilon|^{2q} \quad \mbox{for all}~t\in(0,T_{\max,\varepsilon})~\mbox{and}~\varepsilon\in(0,1).\end{equation}

Proof. Combining lemma 3.1 with lemma 3.3 and using $m>1$, we obtain

(3.32)\begin{equation} \begin{aligned} & F'_\varepsilon(t)+F_\varepsilon(t)+\frac{p(p-1)}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{p+m-3}|\nabla u_\varepsilon|^2\\ & \qquad +\frac{2(q-1)}{q}\int_\Omega |\nabla |\nabla v_\varepsilon|^q|^2+q\int_\Omega|\nabla v_\varepsilon|^{2(q-1)}|D^2v_\varepsilon|^2\\ & \quad\leq \frac{p(p-1)}{2m}\int_\Omega(u_\varepsilon+\varepsilon)^{p-m+1}|\nabla v_\varepsilon|^2 +q(2q-2+\sqrt{N})^2\|v_0\|_{L^\infty(\Omega)}^2\int_\Omega u_\varepsilon^2|\nabla v_\varepsilon|^{2q-2}\\ & \qquad+C_7+\int_\Omega(u_\varepsilon+\varepsilon)^p+\int_\Omega |\nabla v_\varepsilon|^{2q}\quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{aligned} \end{equation}

Next, by Young's inequality for any $\eta _3>0$, we have

\[ \frac{p(p-1)}{2m}\int_\Omega(u_\varepsilon+\varepsilon)^{p-m+1}|\nabla v_\varepsilon|^2\leq \eta_3\int_\Omega|\nabla v_\varepsilon|^{2q+2}+C(\eta_3)\int_\Omega(u_\varepsilon+\varepsilon)^{\frac{(p-m+1)(2q+2)}{2q}}, \]

and

\[ q(2q-2+\sqrt{N})^2\|v_0\|_{L^\infty(\Omega)}^2\int_\Omega u_\varepsilon^2|\nabla v_\varepsilon|^{2q-2}\leq \eta_3 \int_\Omega|\nabla v_\varepsilon|^{2q+2}+C(\eta_3)\int_\Omega(u_\varepsilon+\varepsilon)^{q+1}. \]

Using interpolation inequality (2.10) and Young's inequality, we can choose a suitably $\eta _3$ such that

\[ 2\eta_3 \int_\Omega|\nabla c_\varepsilon|^{2q+2}+\int_\Omega |\nabla v_\varepsilon|^{2q}\leq q\int_\Omega|\nabla v_\varepsilon|^{2(q-1)}|D^2v_\varepsilon|^2+c_1\quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \]

It follows from (3.32) that (3.30) holds.

Therefore, we obtain the boundedness of $\int _\Omega (u_\varepsilon +\varepsilon )^p+\int _\Omega |\nabla v_\varepsilon |^{2q}$ with $p>2$ and $q>1$.

Lemma 3.5 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$, whenever $p>2$ and $q>1$ are such that

(3.33)\begin{equation} \frac{p-m+1}{m-1+\frac{m+1}{N}}<2q<2p+2m-4+\frac{4(m+1)}{N}, \end{equation}

then for all $\varepsilon \in (0,\,1)$, we can find a constant $C=C(p,\,q)>0$ satisfying

(3.34)\begin{equation} \int_\Omega (u_\varepsilon+\varepsilon)^p+\int_\Omega |\nabla v_\varepsilon|^{2q}\leq C \quad~\mbox{for all}~t\in(0,T_{\max,\varepsilon}).~ \end{equation}

Proof. Using the boundedness of $\|u_\varepsilon +\varepsilon \|_{L^{m+1}(\Omega )}$ to (2.8) with $r:=m+1$, there exists $C_{11}>0$ such that for all $\varepsilon \in (0,\,1)$ satisfies

(3.35)\begin{align} \int_\Omega(u_\varepsilon+\varepsilon)^{p+m-1+\frac{2(m+1)}{N}}\leq C_{11} \int_\Omega (u_\varepsilon+\varepsilon)^{p+m-3}|\nabla u_\varepsilon|^2+C_{11}\quad\mbox{for all}~ t\in(0,T_{\max,\varepsilon}). \end{align}

Moreover, $m>\max \{1,\,\frac {3N-2}{2N+2}\}$ ensures that hypothesis (3.33) holds. (3.33) asserts that $q+1< p+m-1+\frac {2(m+1)}{N}$ and

\begin{align*} 0& <\frac{(p-m+1)(2q+2)}{2q}=p-m+1+\frac{2(p-m+1)}{2q}\\ & < p-m+1+2\Bigg(m-1+\frac{m+1}{N}\Bigg) = p+m-1+\frac{2(m+1)}{N}. \end{align*}

Consequently, utilizing Young's inequality, we obtain

(3.36)\begin{equation} \int_\Omega (u_\varepsilon+\varepsilon)^{\frac{(p-m+1)(2q+2)}{2q}}<\frac{p(p-1)}{6 C_8 C_{11}} \int_\Omega (u_\varepsilon+\varepsilon)^{p+m-1+\frac{2(m+1)}{N}}+c_1 \quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}), \end{equation}

and

(3.37)\begin{align} \int_\Omega (u_\varepsilon+\varepsilon)^{q+1}< \frac{p(p-1)}{6C_9C_{11}} \int_\Omega (u_\varepsilon+\varepsilon)^{p+m-1+\frac{2(m+1)}{N}}+c_2 \quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{align}

Since $p< p+m-1+\frac {2(m+1)}{N}$, it is similar to deduce

(3.38)\begin{align} \int_\Omega (u_\varepsilon+\varepsilon)^{p}<\frac{p(p-1)}{6C_{11}} \int_\Omega (u_\varepsilon+\varepsilon)^{p+m-1+\frac{2(m+1)}{N}}+c_3\quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}). \end{align}

Collecting (3.35)–(3.38) and (3.30), it follows that

\[ F'_\varepsilon(t)+F_\varepsilon(t)\leq c_4 \quad \mbox{for all}~t\in(0,T_{\max,\varepsilon}) \]

with $c_4>0$. It is obvious to obtain (3.34) by a comparison argument.

By means of Moser–Alikakos iteration procedure, an application of the above to suitably large but fixed $p$ and $q$ yields bounds in $L^\infty (\Omega )\times W^{1,\infty }(\Omega )$.

Lemma 3.6 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$. Then there exists $C>0$ such that for all $\varepsilon \in (0,\,1)$ the solution of (2.1) satisfies

(3.39)\begin{equation} \|u_\varepsilon\|_{L^\infty(\Omega)}\leq C \quad \mbox{for all}~t>0, \end{equation}

and

(3.40)\begin{equation} \|v_\varepsilon\|_{W^{1,\infty}(\Omega)}\leq C \quad \mbox{for all}~t>0. \end{equation}

Proof. In light of using the result of lemma 3.5, lemma A.1 in [Reference Tao and Winkler13], and (2.5), we derive

\[ \|u_\varepsilon\|_{L^\infty(\Omega)}+\|v_\varepsilon\|_{W^{1,\infty}(\Omega)}\leq C \quad\mbox{for all } t\in(0, T_{\max,\varepsilon}) \]

where $C > 0$ is independent of $\varepsilon \in (0,\, 1)$. From this and the extensibility criterion (2.3), it is evident that $T_{\max,\varepsilon }=\infty$, which finishes the proof.

4. Global bounded weak solutions to system (1.1)

In order to finish the proof of theorem 1.2, we will give some regularity properties with $(u_\varepsilon,\,v_\varepsilon )$ in this section.

Lemma 4.1 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$, then we get

(4.1)\begin{equation} \int_0^\infty\int_\Omega u_\varepsilon v_\varepsilon\leq \int_\Omega v_0 \quad\mbox{for all } \varepsilon \in(0,1), \end{equation}

and

(4.2)\begin{equation} \int_0^\infty\int_\Omega |\nabla v_\varepsilon|^2\leq \frac{1}{2}\int_\Omega v^2_0 \quad\mbox{for all } \varepsilon \in(0,1). \end{equation}

Proof. Multiplying the second equation of (2.1) by 1 and $v_\varepsilon$ separately, upon integrating by parts, and integrating with respect to $t$, we obtain

\[ \int_\Omega v_\varepsilon({\cdot},t)+\int_0^t\int_\Omega u_\varepsilon v_\varepsilon=\int_\Omega v_0 \]

and

\[ \frac{1}{2}\int_\Omega v_\varepsilon^2+\int_0^t\int_\Omega |\nabla v_\varepsilon|^2+\int_0^t\int_\Omega u_\varepsilon v_\varepsilon^2=\frac{1}{2}\int_\Omega v^2_0 \]

for all $\varepsilon \in (0,\,1)$. As a result, we immediately obtain (4.1) and (4.2).

Lemma 4.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume that $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$, then for any $T>0$ there exists $C(T)>0$ such that

(4.3)\begin{equation} \int_0^T\|\partial_t (u_\varepsilon+\varepsilon)^{m}({\cdot},t)\|_{({W_0^{N,2}(\Omega)})^\ast}{\rm d}t\leq C(T)\quad \mbox{for all}~ \varepsilon \in(0,1), \end{equation}

and

(4.4)\begin{equation} \int_0^T\int_\Omega |\nabla (u_\varepsilon+\varepsilon)^{m}|^2\leq C(T) \quad \mbox{for all}~ \varepsilon \in(0,1). \end{equation}

Proof. Due to lemma 3.2, for any $T>0$, we have

(4.5)\begin{equation} \int_0^T \int_\Omega|\nabla u_\varepsilon|^2\leq C(T), \end{equation}

and

(4.6)\begin{equation} \int_0^T \int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}|\nabla u_\varepsilon|^2\leq C(T), \end{equation}

which indicates (4.4) is valid. Due to lemma 3.6, there exists a positive constant $c_1>0$ such that $0< u_\varepsilon < c_1$ in $\Omega \times (0,\,\infty )$ for all $\varepsilon \in (0,\,1)$. Multiplying the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{m-1}$, one has

\[ \frac{1}{m}\frac{{\rm d}}{{\rm d}t}\int_{\Omega}(u_\varepsilon+\varepsilon)^m+\frac{m(m-1)}{2}\int_\Omega(u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2 \leq \frac{m-1}{2m} (c_1+1)\int_\Omega|\nabla v_\varepsilon|^2, \]

integrating with respect to $t$ and using (4.2), which indicates

(4.7)\begin{equation} \int_0^t \int_\Omega(u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2\leq C. \end{equation}

Next, multiplying the first equation of (2.1) by $(u_\varepsilon +\varepsilon )^{m}\psi$ with $\psi \in C^\infty _0(\Omega )$, and integrating over $\Omega$, for all $\varepsilon \in (0,\,1)$, we obtain

(4.8)\begin{equation} \begin{aligned} \frac{1}{m}\int_\Omega\partial_t(u_\varepsilon+\varepsilon)^{m}\cdot\psi & ={-}m\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}\nabla u_\varepsilon\cdot\nabla \psi\\ & \quad -m(m-1)\int_\Omega (u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2\psi\\ & \quad+\int_\Omega u_\varepsilon (u_\varepsilon+\varepsilon)^{m-1} \nabla v_\varepsilon\cdot \nabla \psi\\ & \quad +(m-1)\int_\Omega u_\varepsilon(u_\varepsilon+\varepsilon)^{m-2}\nabla u_\varepsilon\cdot \nabla v_\varepsilon\psi. \end{aligned} \end{equation}

Using the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$ and Young's inequality, it yields

(4.9)\begin{equation} \begin{aligned} -m\int_\Omega (u_\varepsilon+\varepsilon)^{2m-2}\nabla u_\varepsilon\cdot\nabla \psi & \leq m(c_1+1)^{2m-2} \|\nabla\psi\|_{L^\infty(\Omega)}\cdot\int_\Omega |\nabla u_\varepsilon|\\ & \leq C\Bigg(\int_\Omega |\nabla u_\varepsilon|^2+4|\Omega|\Bigg)\cdot \|\nabla\psi\|_{L^\infty(\Omega)}, \end{aligned} \end{equation}

and

(4.10)\begin{equation} -m\int_\Omega (u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2\psi\leq m \|\psi\|_{L^\infty(\Omega)}\cdot\Bigg(\int_\Omega (u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2\Bigg). \end{equation}

Moreover, by the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$ and $\|\nabla v_\varepsilon \|_{L^\infty (\Omega )}$, we get

(4.11)\begin{equation} \int_\Omega u_\varepsilon (u_\varepsilon+\varepsilon)^{m-1} \nabla v_\varepsilon\cdot \nabla \psi\leq C \|\nabla\psi\|_{L^\infty(\Omega)}, \end{equation}

and

(4.12)\begin{equation} m\int_\Omega u_\varepsilon(u_\varepsilon+\varepsilon)^{m-2}\nabla u_\varepsilon\cdot \nabla v_\varepsilon\psi\leq C \|\psi\|_{L^\infty(\Omega)}\Bigg(\int_\Omega (u_\varepsilon+\varepsilon)^{2m-3}|\nabla u_\varepsilon|^2\Bigg). \end{equation}

According to (4.6)–(4.12) and the continuity of the embedding $W_0^{N,2}(\Omega )\hookrightarrow W^{1,\infty }(\Omega )$, there exists $C(T)>0$ such that

\[ \int_0^T\|\partial_tu_\varepsilon({\cdot},t)^{m}\|_{(W_0^{N,2}(\Omega))^\ast}\leq C(T)\quad \mbox{for all}~ \varepsilon \in(0,1). \]

The proof of this lemma is completed.

Lemma 4.3 Let $2>m>\max \{1,\,\frac {3N-2}{2N+2}\}$, then for any $T>0$ there exists $C(T)>0$ such that

(4.13)\begin{equation} \|\frac{\partial v_\varepsilon}{\partial t}\|_{L^2(0,T;(W^{1,2}(\Omega))^*)}\leq C(T) \quad \mbox{for all}~ \varepsilon \in(0,1). \end{equation}

Proof. Multiplying $\psi (x)$ on both sides of the second equation with $\psi (x)\in W^{1,2}(\Omega )$, and integrating over $\Omega$ and using the Hölder inequality, we have

\[ \int_\Omega \frac{\partial v_\varepsilon}{\partial t} \psi ={-}\int_\Omega\nabla v_\varepsilon\cdot\nabla \psi-\int_\Omega u_\varepsilon v_\varepsilon\psi \leq \|\nabla v_\varepsilon\|_{L^2(\Omega)}\|\nabla \psi\|_{L^2(\Omega)}+\|u_\varepsilon v_\varepsilon\|_{L^2(\Omega)}\|\psi\|_{L^2(\Omega)}. \]

By the boundedness of $\|u_\varepsilon \|_{L^\infty (\Omega )}$ and $\|v_\varepsilon \|_{L^\infty (\Omega )}$, it shows that

(4.14)\begin{equation} \| \frac{\partial v_\varepsilon}{\partial t}\|_{(W^{1,2}(\Omega))^*}\leq \|\nabla v_\varepsilon\|_{L^2(\Omega)}+\|u_\varepsilon v_\varepsilon\|_{L^2(\Omega)}\leq C+\|\nabla v_\varepsilon\|_{L^2(\Omega)}. \end{equation}

Combining (4.2) and (4.14), it follows that

\[ \| \frac{\partial v_\varepsilon}{\partial t}\|^2_{L^2(0,T;(W^{1,2}(\Omega))^*)}\leq\int_0^T\int_\Omega|\nabla v_\varepsilon|^2+\int_0^T \int_\Omega |u_\varepsilon v_\varepsilon|^2\leq C(T). \]

The proof of throrem 1.2. Lemma 3.6 shows that there exists $(\varepsilon _j)_{j\in \mathbb {N}}\subset (0,\,1)$ such that $\varepsilon _j\rightarrow 0$ as $j\rightarrow \infty$ and that $u_{\varepsilon _j}\stackrel {\ast }\rightharpoonup u$ in $L^\infty (\Omega \times (0,\,\infty ))$ and $\nabla v_{\varepsilon _j}\stackrel {\ast }\rightharpoonup \nabla v$ in $L^\infty (\Omega \times (0,\,\infty ))$ hold. Lemma 4.2 implies that $(u_\varepsilon ^{m})_{\varepsilon \in (0,1)}$ is bounded in $L^2([0,T];W^{1,2}(\Omega ))$. Hence, $\nabla u_{\varepsilon _j}^{m} \rightharpoonup \nabla u^{m}$ in $L^2_{loc}([0,\,\infty );L^2(\Omega ))$. Furthermore, using the Aubin–Lions lemma and $(\partial _tu_\varepsilon ^{m})_{\varepsilon \in (0,1)}$ is bounded in $L^1([0,T];(W_0^{N,2}(\Omega ))^\ast )$, it yields $u^{m}_{\varepsilon _j}\rightarrow u^{m}$ in $L^2([0,T];L^2(\Omega ))$. By the Riesz lemma and $m>1$, we have $u_{\varepsilon _j}\rightarrow u$ a.e. in $\Omega \times (0,\,\infty )$. Likewise, by lemmas 3.6 and 4.3, it follows that $v_{\varepsilon _j}\rightarrow v$ in $L^2([0,T];L^2(\Omega ))$ and a.e. in $\Omega \times (0,\,\infty )$. Because of these convergence properties, one may readily prove that $(u,\,v)$ is a global weak solution of (1.1) in the sense of definition 1.1. Consequently, $(u,\,v)$ is a global bounded weak solution of (1.1) by lemma 3.6. The proof is completed. $\square$

5. Large time behaviour

This section discusses the asymptotic behaviour of the system for large time. Motivated by [Reference Fan and Jin5, Reference Winkler28], the required properties of the solutions are first presented.

Lemma 5.1 Let $m>\max \{1,\,\frac {3N-2}{2N+2}\}$, then there exists $\theta \in (0,\,1)$ such that for some $C>0$, we obtain

(5.1)\begin{equation} \|v_\varepsilon({\cdot},t)\|_{C^{\theta,\frac{\theta}{2}}(\bar{\Omega}\times[t,t+1])}\leq C \quad \mbox{for all } t\geq0, \end{equation}

and for all $\tau >0$, we can find $C(\tau )>0$ such that

(5.2)\begin{equation} \|\nabla v_\varepsilon({\cdot},t)\|_{C^{\theta,\frac{\theta}{2}}(\bar{\Omega}\times[t,t+1])}\leq C \quad \mbox{for all } t\geq\tau. \end{equation}

Proof. In view of lemma 3.6, $-u_\varepsilon v_\varepsilon$ is bounded in $L^\infty (\Omega \times (0,\,\infty ))$ for all $\varepsilon \in (0,\,1)$. Therefore, applying the standard parabolic regularity theory [Reference Ladyzhenskaia, Solonnikov and Ural'tseva8, Chapter III], both estimates (5.1) and (5.2) are obtained.

Lemma 5.2 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$ and $p>\max \{1,\,m-1\}$, then there exists $C>0$ such that

(5.3)\begin{equation} \int_0^\infty\int_\Omega |\nabla (u_\varepsilon+\varepsilon)^{\frac{p+m-1}{2}}|\leq C \quad \mbox{for all}~ \varepsilon \in(0,1). \end{equation}

Proof. By virtue of lemma 3.6, there exists a positive constant $c_1>0$ such that $0< u_\varepsilon < c_1$ in $\Omega \times (0,\,\infty )$ for all $\varepsilon \in (0,\,1)$. From lemma 3.1 and $p>\max \{1,\,m-1\}$, it follows that

\[ \int_\Omega (u_\varepsilon+\varepsilon)^{p-m+1}|\nabla v_\varepsilon|^2 \leq (c_1+1)^{p-m+1} \int_\Omega |\nabla v_\varepsilon|^2 \text{ for all } t>0 \mbox{ and } \varepsilon \in(0,1). \]

Therefore, an integration of (3.1) shows that

\begin{align*} & \frac{2m(p-1)}{(p+m-1)^2}\int_0^t\int_\Omega |\nabla (u_\varepsilon+\varepsilon)^{\frac{p+m-1}{2}}|\notag\\ & \quad \leq \frac{1}{p}\int_\Omega (u_0+\varepsilon)^p+\frac{p-1}{2m}(c_1+1)^{p-m+1} \int_0^t\int_\Omega |\nabla v_\varepsilon|^2 \end{align*}

for all $\varepsilon \in (0,\,1)$, which together with (4.2) indicate that (5.3) is valid.

Lemma 5.3 Let $\Omega \subset \mathbb {R}^N(N=3,\,4,\,5)$ be a bounded domain with smooth boundary. Assume that $m>\max \{1,\,\frac {3N-2}{2N+2}\}$, then there exist $C>0$ such that

(5.4)\begin{equation} \|\partial_t u_\varepsilon({\cdot},t)\|_{({W_0^{2,2}(\Omega)})^\ast}\leq C,\quad \mbox{for all}~t>0~\mbox{and}~\varepsilon \in(0,1). \end{equation}

Particularly,

(5.5)\begin{equation} \|u_\varepsilon({\cdot},t)-u_\varepsilon({\cdot},s)\|_{({W_0^{2,2}(\Omega)})^\ast}\leq C|t-s|,\quad \mbox{for all}~t\geq0, s\geq0~\mbox{and}~\varepsilon \in(0,1). \end{equation}

Proof. Multiplying the first equation of (2.1) by $\psi$ with $\psi \in C^\infty _0(\Omega )$, and integrating over $\Omega$, one has

(5.6)\begin{equation} \begin{aligned} \int_\Omega\partial_t u_\varepsilon\cdot\psi & ={-}\int_\Omega \nabla(u_\varepsilon+\varepsilon)^{m}\cdot\nabla \psi+\int_\Omega u_\varepsilon\nabla v_\varepsilon\cdot\nabla\psi\\ & =\int_\Omega (u_\varepsilon+\varepsilon)^m\Delta\psi+\int_\Omega u_\varepsilon\nabla v_\varepsilon\cdot\nabla\psi \quad\mbox{for all }t>0. \end{aligned} \end{equation}

According to lemma 3.6, there exist two positive constants $c_1,\,c_2>0$ such that $0< u_\varepsilon < c_1$ and $|\nabla v_\varepsilon |\leq c_2$ in $\Omega \times (0,\,\infty )$ for all $\varepsilon \in (0,\,1)$. Then (5.6) implies

\[ \Bigg|\int_\Omega \partial_tu_\varepsilon({\cdot},t)\cdot\psi\Bigg|\leq (c_1+1)^m\int_\Omega|\Delta\psi|+c_1c_2\int_\Omega|\nabla\psi|\quad\mbox{for all }t>0\mbox{ and }\varepsilon \in(0,1), \]

and

\[ \|\partial_tu_\varepsilon({\cdot},t)\|^2_{({W_0^{2,2}(\Omega)})^\ast}=\mathop{\sup}\limits_{{\psi\in W_0^{2,2}(\Omega),\|\psi\|_{{W_0^{2,2}(\Omega)}}=1}}\Bigg|\int_\Omega \partial_tu_\varepsilon({\cdot},t)\cdot\psi\Bigg|^2\leq C. \]

This indicates that (5.4) and (5.5) are valid.

With the above information on solutions, the convergence of $u$ is shown as follows.

Lemma 5.4 Let $m>\max \{1,\,\frac {3N-2}{2N+2}\}~(\mbox {where}~ N=3,\,4,\,5)$ and $(u,\,v)$ as given by theorem 1.2, we can see that

(5.7)\begin{equation} u({\cdot},t)\stackrel{\ast}\rightharpoonup \bar{u}_0 \text{ in } L^\infty(\Omega)~\mbox{as } t\rightarrow\infty.\end{equation}

Proof. Similar to lemma 5.1 of [Reference Winkler28] and lemma 3.16 of [Reference Fan and Jin5], the proof of this lemma can be completed. In fact, assuming the lemma is false, then there exists a sequence $(t_j)_{j\subset \mathbb {N}}\subset (0,\,\infty )$ such that $t_j\rightarrow \infty$ as $j\rightarrow \infty$, and such that for some $\tilde {\psi }\in L^1(\Omega )$ one has

(5.8)\begin{equation} \int_\Omega u(x,t_j)\tilde{\psi}(x){\rm d}x-\int_\Omega \bar{u}_0\tilde{\psi}(x){\rm d}x\geq c_1\quad\mbox{for all}~j\subset\mathbb{N} \end{equation}

with $c_1>0$. Note that theorem 1.2 implies that there exists a positive constant $c_2>0$ such that $0< u< c_2$ for a.e. $(x,\,t)\in \Omega \times (0,\,\infty )$. And then using the density of $C_0^\infty (\Omega )$ in $L^1(\Omega )$ in choosing $\psi \in C_0^\infty (\Omega )$ such that $\|\psi -\tilde {\psi }\|_{L^1(\Omega )}\leq \frac {c_1}{4c_2}$, (5.8) yields

(5.9)\begin{equation} \begin{aligned} \int_\Omega u(x,t_j){\psi}(x){\rm d}x-\int_\Omega \bar{u}_0{\psi}(x){\rm d}x & \geq\int_\Omega u(x,t_j)\tilde{\psi}(x){\rm d}x-\int_\Omega \bar{u}_0\tilde{\psi}(x){\rm d}x\\ & \quad-\{\|u(x,t_j)\|_{L^\infty(\Omega)}+\bar{u}_0\}\|\psi-\tilde{\psi}\|_{L^1(\Omega)}\\ & \geq \frac{c_1}{2}\quad\mbox{for all } j\subset\mathbb{N}. \end{aligned} \end{equation}

Due to $L^\infty (\Omega )\hookrightarrow (W_0^{2,2}(\Omega ))^\ast$ is compact, using Arzelà–Ascoli theorem, the equicontinuity properties (5.5) and the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$ in $C^0([0,\infty );L^\infty (\Omega ))$ ensure that $u_\varepsilon \rightarrow u$ in $C_{loc}^0([0,\,\infty );(W_0^{2,2}(\Omega ))^\ast )$ holds. According to (5.5), there exists a positive constant $c_3>0$ such that

\[ \|u_\varepsilon({\cdot},t)-u_\varepsilon({\cdot},s)\|_{({W_0^{2,2}(\Omega)})^\ast}\leq c_3|t-s|,\quad \mbox{for all}~t\geq0, s\geq0~\mbox{and}~\varepsilon \in(0,1). \]

Then, taking limits to get

\[ \|u({\cdot},t)-u({\cdot},s)\|_{({W_0^{2,2}(\Omega)})^\ast}\leq c_3|t-s|,\quad \mbox{for all}~t\geq0, s\geq0. \]

If let $\tau \in (0,\,1)$ such that $\tau \leq \frac {c_1}{4c_3\|\psi \|_{W_0^{2,2}(\Omega )}}$, then for all $j\subset \mathbb {N}$ and each $t\in (t_j,\,t_j+\tau )$ one has

\begin{align*} \Bigg|\int_\Omega u(x,t_j){\psi}(x){\rm d}x-\int_\Omega u(x,t){\psi}(x){\rm d}x\Bigg|& \leq \|u(x,t_j)-u(x,t)\|_{({W_0^{2,2}(\Omega)})^\ast}\|\psi\|_{W_0^{2,2}(\Omega)}\\ & \leq c_3|t_j-t|\cdot\|\psi\|_{W_0^{2,2}(\Omega)}\\ & \leq \frac{c_1}{4}, \end{align*}

which together with (5.9) implies that

(5.10)\begin{align} \int_\Omega u(x,t){\psi}(x){\rm d}x-\int_\Omega \bar{u}_0{\psi}(x){\rm d}x\geq \frac{c_1}{4} \quad\mbox{for all } t\in(t_j,t_j+\tau)\mbox{ and each } j\subset\mathbb{N}. \end{align}

Next, we will prove (5.10) contradicts lemma 5.2. Taking the Poincaré constant $c_4>0$ such that

\[ \int_\Omega \bigg|\varphi(x)-\frac{1}{|\Omega|}\int_\Omega \varphi(x)\bigg|^2{\rm d}x\leq c_4\int_\Omega|\nabla\varphi|^2\quad\mbox{for all }\varphi\in W^{1,2}(\Omega). \]

Fix any $p>1$ such that $p\geq \max \{1,\,m-1,\,3-m\}$, and using lemma 5.2, it is obvious that

(5.11)\begin{equation} \begin{aligned} \int_0^\infty\int_\Omega\bigg|u_\varepsilon^{\frac{p+m-1}{2}}(x,t)-a_\varepsilon^{\frac{p+m-1}{2}}(t)\bigg|^2{\rm d}x{\rm d}t & \leq c_4\int_\Omega\bigg|\nabla u_\varepsilon^{\frac{p+m-1}{2}}\bigg|^2 \\ & \leq c_4\int_\Omega\bigg|\nabla (u_\varepsilon+\varepsilon)^{\frac{p+m-1}{2}}\bigg|^2\\ & \leq c_5 \end{aligned} \end{equation}

for all $\varepsilon \in (0,\,1)$, where $a_\varepsilon (t):=(\frac {1}{|\Omega |}\int _\Omega u_\varepsilon ^{\frac {p+m-1}{2}})^{\frac {2}{p+m-1}}$ and $c_5>0$. Using the convergence property $u_\varepsilon \rightarrow u$ a.e. in $\Omega \times (0,\,\infty )$ as $\varepsilon \rightarrow 0$, the boundedness of $(u_\varepsilon )_{\varepsilon \in (0,1)}$ in $L^\infty (\Omega \times (0,\,\infty ))$ and the dominated convergence theorem, one obtains

(5.12)\begin{equation} a_\varepsilon(t)\rightarrow a(t)\quad\mbox{for a.e.} ~t>0, \mbox{ as } \varepsilon\rightarrow0, \end{equation}

where $a(t):=(\frac {1}{|\Omega |}\int _\Omega u^{\frac {p+m-1}{2}})^{\frac {2}{p+m-1}}$. Again using $u_\varepsilon \rightarrow u$ a.e. in $\Omega \times (0,\,\infty )$ as $\varepsilon \rightarrow 0$ and Fatou's lemma, (5.11) and (5.12) imply that

(5.13)\begin{equation} \int_0^\infty\int_\Omega|u_\varepsilon^{\frac{p+m-1}{2}}(x,t)-a^{\frac{p+m-1}{2}}(t)|^2{\rm d}x{\rm d}t\leq c_5. \end{equation}

Review the following inequality: If $\mu >1$, then $\frac {\xi ^\mu -\eta ^\mu }{\xi -\eta }\geq \eta ^{\mu -1}$ for all $\xi,\,\eta \leq 0$ with $\xi \neq \eta$. And since by the Hölder inequality, and the $L^1(\Omega )$ conservation of $u$ means that

\[ \bar{u}_0=\frac{1}{|\Omega|}\int_\Omega u\leq \frac{1}{|\Omega|}\left(\int_\Omega u^{\frac{p+m-1}{2}}\right)^{\frac{2}{p+m-1}}\cdot|\Omega|^{\frac{p+m-3}{p+m-1}}=a(t). \]

Thus, on the left-hand side of (5.13) indicates

\begin{align*} \int_\Omega|u^{\frac{p+m-1}{2}}(x,t)-a^{\frac{p+m-1}{2}}(t)|^2{\rm d}x& \geq a^{p+m-3}(t)\int_\Omega|u(x,t)-a(t)|^2{\rm d}x\\ & \geq \bar{u}_0^{p+m-3}\cdot\int_\Omega|u(x,t)-a(t)|^2{\rm d}x, \end{align*}

and

(5.14)\begin{equation} \int_0^\infty\int_\Omega|u(x,t)-a(t)|^2{\rm d}x{\rm d}t\leq c_6:=\frac{c_5}{\bar{u}_0^{p+m-3}}. \end{equation}

Now, we introduce

\[ u_j(x,s):=u(x,t_j+s), \quad (x,s)\in\Omega \times (0,\tau)\text{ for all }j\subset\mathbb{N}, \]

and

\[ a_j(s):=a(t_j+s),\quad s\in(0,\tau),\text{ for all }j\subset\mathbb{N}. \]

Therefore, (5.14) implies that

\[ \int_0^\tau\int_\Omega |u_j(x,s)-a_j(s)|^2{\rm d}x{\rm d}t=\int_{t_j}^{t_j+\tau}\int_\Omega|u(x,t)-a(t)|^2{\rm d}x{\rm d}t\rightarrow 0 \text{ as }j\rightarrow\infty, \]

which means

(5.15)\begin{equation} u_j(x,s)-a_j(s)\rightarrow 0 \text{ in } L^2(\Omega\times(0,\tau)) \text{ as } j\rightarrow\infty. \end{equation}

By the definition of $a(t)$ and the boundedness of $u(x,\,t)$, $(a_j)_{j\subset \mathbb {N}}$ is bounded in $L^2((0,\,\tau ))$. Then, for some nonnegative $a_\infty \in L^2((0,\,\tau ))$ satisfying

(5.16)\begin{equation} a_j\rightharpoonup a_\infty \text{ in } L^2((0,\tau))\text{ as }j\rightarrow\infty. \end{equation}

By utilizing the $L^1(\Omega )$ conservation of $u$, we have

\begin{align*} \int_0^\tau \int_\Omega (u_j(x,s)-a_j(s)){\rm d}x{\rm d}s& =\tau \bar{u}_0|\Omega|-|\Omega|\int_0^\tau a_j(s){\rm d}s\\ & \rightarrow \tau \bar{u}_0|\Omega|-|\Omega|\int_0^\tau a_\infty(s){\rm d}s\text{ as } j\rightarrow\infty, \end{align*}

which combined with (5.15), one has

(5.17)\begin{equation} \int_0^\tau a_\infty(s){\rm d}s=\tau \bar{u}_0. \end{equation}

On the other hand, (5.10) and (5.17) show that

\begin{align*} \frac{c_1}{4}& \leq\int_0^\tau\int_\Omega u_j(x,s)\psi(x){\rm d}x{\rm d}s-\int_0^\tau\int_\Omega \bar{u}_0\psi(x){\rm d}x{\rm d}s\\ & =\int_0^\tau \int_\Omega (u_j(x,s)-a_j(s)){\rm d}x{\rm d}s+\int_0^\tau \int_\Omega a_j(s)\psi(x){\rm d}x{\rm d}s-\tau\bar{u}_0\int_\Omega \psi(x){\rm d}x\\ & =\int_0^\tau \int_\Omega (u_j(x,s)-a_j(s)){\rm d}x{\rm d}s+\int_0^\tau a_j(s){\rm d}s\cdot\int_\Omega \psi(x){\rm d}x\\ & \rightarrow \int_0^\tau a_\infty(s){\rm d}s\cdot\int_\Omega \psi(x){\rm d}x-\tau\bar{u}_0\int_\Omega \psi(x){\rm d}x=0\text{ as }j\rightarrow\infty. \end{align*}

This is a contradiction and then the proof of this lemma is completed.

Finally, the convergence of $v$ can be obtained.

Lemma 5.5 Let $m>\max \{1,\frac {3N-2}{2N+2}\}~(\mbox {where}~ N=3,\,4,\,5)$ and $(u,\,v)$ as given by theorem 1.2, we obtain

(5.18)\begin{equation} v({\cdot},t)\rightarrow 0 \text{ in } L^\infty(\Omega)~\mbox{as } t\rightarrow\infty. \end{equation}

Proof. Similar to lemma 5.2 of [Reference Winkler28] and lemma 3.17 of [Reference Fan and Jin5], the proof of this lemma can be completed. Similarly, assume the lemma is false, then there exist two sequences $(x_j)_{j\subset \mathbb {N}}\subset \Omega$ and $(t_j)_{j\subset \mathbb {N}}\subset (0,\,\infty )$ such that $t_j\rightarrow \infty$ as $j\rightarrow \infty$ satisfies

(5.19)\begin{equation} v(x_j,t_j)\geq c_1~\quad\mbox{for all}~j\subset\mathbb{N} \end{equation}

with $c_1>0$, where passing to subsequences we may assume that there exists $x_0\in \bar {\Omega }$ such that $x_j\rightarrow x_0$ as $j\rightarrow \infty$. Due to lemma 5.1, $v$ is uniformly continuous in $\cup _{j\in \mathbb {N}}(\bar {\Omega }\times [t_j,\,t_j+1])$, which entails that there exist $\delta >0$, $\tau \in (0,\,1)$ and $B:=B_\delta (x_0)\cap \Omega$ such that

(5.20)\begin{equation} v(x,t)\geq \frac{c_1}{2} ~\quad\mbox{for~all~} x\in B, t\in (t_j,t_j+\tau)~\text{ and }j\in\mathbb{N}. \end{equation}

Now, let $u_j(x,\,s):=u(x,\,t_j+s)\mbox { and } v_j(x,\,s):=v(x,\,t_j+s)~\mbox {for } x\in \Omega,\, s\in (0,\,\tau ) \mbox{ and }j\in \mathbb {N}$, then from (4.1), we noticed that

(5.21)\begin{equation} \begin{aligned} \int_0^\tau \int_B u_j(x,s)v_j(x,s){\rm d}x{\rm d}s & =\int_{t_j}^{t_j+\tau} \int_B u(x,t)v(x,t){\rm d}x{\rm d}t\\ & \leq \int_{t_j}^{\infty} \int_B u(x,t)v(x,t){\rm d}x{\rm d}t\\ & \rightarrow 0\text{ as }j\rightarrow\infty. \end{aligned} \end{equation}

On the other hand, let $\psi (x):=\chi _B(x)$ for $x\in \Omega$, then in light of lemma 5.4, it follows that

\begin{align*} & \Bigg|{\int_{t_j}^{t_j+\tau}\int_\Omega u(x,t)\chi_B(x){\rm d}x{\rm d}t-\bar{u}_0\tau|B|}\Bigg|\\ & \quad=\Bigg|\int_{t_j}^{t_j+\tau}\Bigg\{\int_\Omega u(x,t)\chi_B(x){\rm d}x-\int_\Omega\bar{u}_0\chi_B(x){\rm d}x\Bigg\}{\rm d}t\Bigg|\\ & \quad\leq \tau \sup_{t\in(t_j,t_j+\tau)}\Bigg|\Bigg\{\int_\Omega u(x,t)\chi_B(x){\rm d}x{\rm d}t-\int_\Omega\bar{u}_0\chi_B(x){\rm d}x\Bigg\}\Bigg|\\ & \quad\rightarrow 0\text{ as }j\rightarrow\infty, \end{align*}

and that hence

(5.22)\begin{equation} {\int_{0}^{\tau}\int_\Omega u_j(x,s){\rm d}x{\rm d}s\rightarrow\bar{u}_0\tau|B|} \text{ as }j\rightarrow\infty.\end{equation}

In summary, the combination of (5.20) and (5.21) indicates that

\begin{align*} \frac{c_1}{2}\bar{u}_0\tau|B|& =\liminf_{j\rightarrow\infty}\bigg\{\frac{c_1}{2}\int_{0}^{\tau}\int_\Omega u(x,s){\rm d}x{\rm d}s\bigg\}\\ & \leq \int_0^\tau \int_B u_j(x,s)v_j(x,s){\rm d}x{\rm d}s, \end{align*}

which contradicts (5.21), then the proof of this lemma is completed.

The proof of theorem 1.6. The claimed convergence properties are precisely asserted by lemmas 5.4 and 5.5. $\square$

Acknowledgements

The second author is partially supported by the NSFC (Grant No. 12271064), the Chongqing Talent Support program (Grant No. cstc2022ycjh-bgzxm0169), Natural Science Foundation of Chongqing (Grant No. CSTB2023NSCQ-LZX0089), the Fundamental Research Funds for the Central Universities (Grant Nos. 2022CDJJCLK002, 2020CDJQY-Z001, 2019CDJCYJ001), Chongqing Key Laboratory of Analytic Mathematics and Applications, and Key Laboratory of Nonlinear Analysis and its Applications (Chongqing University), Ministry of Education.  The third author is partially supported by the Interdisciplinary Research Program of Shihezi University (Grant No. JCYJ202316), Corps Science and Technology Plan Project (Grant No. 2023CB008-13), and Launch Project of High-Level Talent Scientific Research of Shihezi University (Grant No. 2022ZK008).

References

Cao, X.. Global classical solutions in chemotaxis(–Navier)–Stokes system with rotational flux term. J. Differ. Equ. 261 (2016), 6883–6914.CrossRefGoogle Scholar
Cao, X. and Lankeit, J.. Global classical small-data solutions for a three-dimensional chemotaxis Navier–Stokes system involving matrix-valued sensitivities. Calc. Var. Part. Differ. Equ. 55 (2016), 107.CrossRefGoogle Scholar
Di Francesco, M., Lorz, A. and Markowich, P.. Chemotaxis–fluid coupled model for swimming bacteria with nonlinear diffusion: global existence and asymptotic behavior. Discrete Contin. Dyn. Syst. 28 (2010), 1437–1453.CrossRefGoogle Scholar
Evans, L. C., Partial Differential Equations (Providence, RI: American Mathematical Society, 2010).Google Scholar
Fan, L. and Jin, H.. Global existence and asymptotic behavior to a chemotaxis system with consumption of chemoattractant in higher dimensions. J. Math. Phys. 58 (2017), 011503.CrossRefGoogle Scholar
Jin, C., Global bounded solution in three-dimensional chemotaxis–Stokes model with arbitrary porous medium slow diffusion. eprint arXiv:2101.11235.Google Scholar
Horstmann, D. and Winkler, M.. Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215 (2005), 52–107.CrossRefGoogle Scholar
Ladyzhenskaia, O. A., Solonnikov, V. A. and Ural'tseva, N. N.. Linear and quasi-linear equations of parabolic type (Providence: American Mathematical Society, 1968).CrossRefGoogle Scholar
Lions, P.. Résolution de problèmes elliptiques quasilinéaires. Arch. Rational Mech. Anal. 74 (1980), 335–353.CrossRefGoogle Scholar
Lorz, A.. Coupled chemotaxis fluid model. Math. Models Methods Appl. Sci. 20 (2010), 987–1004.CrossRefGoogle Scholar
Nagai, T., Senba, T. and Yoshida, K.. Application of the Trudinger–Moser inequality to a parabolic system of chemotaxis. Funkcial. Ekvac. 40 (1997), 411–433.Google Scholar
Tao, Y.. Boundedness in a chemotaxis model with oxygen consumption by bacteria. J. Math. Anal. Appl. 381 (2011), 521–529.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Boundedness in a quasilinear parabolic–parabolic Keller–Segel system with subcritical sensitivity. J. Differ. Equ. 252 (2012), 692–715.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equ. 252 (2012), 2520–2543.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Global existence and boundedness in a Keller–Segel–Stokes model with arbitrary porous medium diffusion. Discrete Contin. Dyn. Syst. 32 (2012), 1901–1914.CrossRefGoogle Scholar
Tao, Y. and Winkler, M.. Locally bounded global solutions in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion. Ann. Inst. H. Poincaré C Anal. Non Linéaire 30 (2013), 157–178.CrossRefGoogle Scholar
Tian, Y. and Xiang, Z.. Global boundedness to a 3D chemotaxis–Stokes system with porous medium cell diffusion and general sensitivity. Adv. Nonlinear Anal. 12 (2022), 23–53.CrossRefGoogle Scholar
Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C., Kessler, J. and Goldstein, R.. Bacterial swimming and oxygen transport near contact lines. Proc. Natl. Acad. Sci. USA 102 (2005), 2277–2282.CrossRefGoogle ScholarPubMed
Wang, L., Mu, C., Lin, K. and Zhao, J.. Global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Z. Angew. Math. Phys. 66 (2015), 1633–1648.CrossRefGoogle Scholar
Wang, L., Mu, C. and Zhou, S.. Boundedness in a parabolic–parabolic chemotaxis system with nonlinear diffusion. Z. Angew. Math. Phys. 65 (2014), 1137–1152.CrossRefGoogle Scholar
Wang, W.. Global boundedness of weak solutions for a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 268 (2020), 7047–7091.CrossRefGoogle Scholar
Wang, Y.. Boundedness in a 2D chemotaxis–Stokes system with general sensitivity and nonlinear diffusion. Comput. Math. Appl. 76 (2018), 818–830.CrossRefGoogle Scholar
Wang, Y. and Xie, L.. Boundedness for a 3D chemotaxis–Stokes system with porous medium diffusion and tensor-valued chemotactic sensitivity. Z. Angew. Math. Phys. 68 (2017), 29.CrossRefGoogle Scholar
Wang, Y. and Xiang, Z.. Global existence and boundedness in a higher-dimensional quasilinear chemotaxis system. Z. Angew. Math. Phys. 66 (2015), 3159–3179.CrossRefGoogle Scholar
Winkler, M.. Boundedness in the higher-dimensional parabolic–parabolic chemotaxis system with logistic source. Commun. Partial Differ. Equ. 35 (2010), 1516–1537.CrossRefGoogle Scholar
Winkler, M.. Global large-data solutions in a chemotaxis–(Navier–)Stokes system modeling cellular swimming in fluid drops. Commun. Partial Differ. Equ. 37 (2012), 319–351.CrossRefGoogle Scholar
Winkler, M.. Stabilization in a two-dimensional chemotaxis–Navier–Stokes system. Arch. Ration. Mech. Anal. 211 (2014), 455–487.CrossRefGoogle Scholar
Winkler, M.. Boundedness and large time behavior in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Calc. Var. Part. Differ. Equ. 54 (2015), 3789–3828.CrossRefGoogle Scholar
Winkler, M.. Global weak solutions in a three-dimensional chemotaxis–Navier–Stokes system. Ann. Inst. H. Poincaré C Anal. Non Linéaire 33 (2016), 1329–1352.CrossRefGoogle Scholar
Winkler, M.. How far do chemotaxis-driven forces influence regularity in the Navier–Stokes system?. Trans. Am. Math. Soc. 369 (2017), 3067–3125.CrossRefGoogle Scholar
Winkler, M.. Global existence and stabilization in a degenerate chemotaxis–Stokes system with mildly strong diffusion enhancement. J. Differ. Equ. 264 (2018), 6109–6151.CrossRefGoogle Scholar
Winkler, M.. Global mass-preserving solutions in a two-dimensional chemotaxis–Stokes system with rotational flux components. J. Evol. Equ. 18 (2018), 1267–1289.CrossRefGoogle Scholar
Winkler, M.. Can rotational fluxes impede the tendency toward spatial homogeneity in nutrient Taxis(–Stokes) systems?. Int. Math. Res. Not. IMRN 11 (2021), 8106–8152.CrossRefGoogle Scholar
Winkler, M.. Chemotaxis–Stokes interaction with very weak diffusion enhancement: blow-up exclusion via detection of absorption-induced entropy structures involving multiplicative couplings. Adv. Nonlinear Stud. 22 (2022), 88–117.CrossRefGoogle Scholar
Xiang, T.. How strong a logistic damping can prevent blow-up for the minimal Keller–Segel chemotaxis system?. J. Math. Anal. Appl. 459 (2018), 1172–1200.CrossRefGoogle Scholar
Zhang, Q. and Li, Y.. Global weak solutions for the three-dimensional chemotaxis–Navier–Stokes system with nonlinear diffusion. J. Differ. Equ. 259 (2015), 3730–3754.CrossRefGoogle Scholar
Zheng, J.. Global existence and boundedness in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Ann. Mat. Pura Appl. 201 (2022), 243–288.CrossRefGoogle Scholar
Zheng, J. and Ke, Y.. Global bounded weak solutions for a chemotaxis–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 289 (2021), 182–235.CrossRefGoogle Scholar
Zheng, J. and Ke, Y.. Further study on the global existence and boundedness of the weak solution in a three-dimensional chemotaxis–Stokes system with nonlinear diffusion and general sensitivity. Commun. Nonlinear Sci. Numer. Simul. 115 (2022), 106732.CrossRefGoogle Scholar
Zheng, J. and Qi, D.. Global existence and boundedness in an $N$-dimensional chemotaxis–Navier–Stokes system with nonlinear diffusion and rotation. J. Differ. Equ. 335 (2022), 347–397.CrossRefGoogle Scholar
Zheng, J. and Wang, Y.. A note on global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Discrete Contin. Dyn. Syst. Ser. B 22 (2017), 669–686.Google Scholar