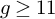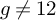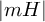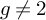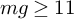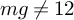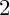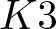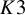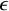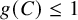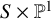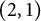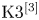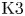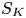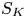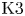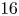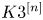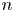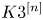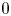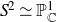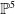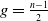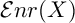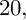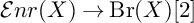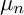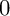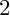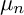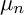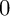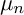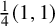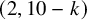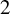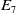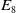76 results
ON THE DEGREE OF IRRATIONALITY OF LOW GENUS
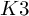 $K3$ SURFACES
$K3$ SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 19 March 2025, pp. 627-662
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MUKAI’S PROGRAM FOR NONPRIMITIVE CURVES ON K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1053-1091
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPACT MODULI OF ENRIQUES SURFACES OF DEGREE 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 February 2025, pp. 1-44
-
- Article
- Export citation
On families of K3 surfaces with real multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double EPW sextics associated with Gushel–Mukai surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
Differential forms on universal K3 surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 12 July 2024, pp. 1-9
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasimaps to moduli spaces of sheaves on a
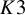 $K3$ surface
$K3$ surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 May 2024, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher Chow cycles on a family of Kummer surfaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 288-316
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Complex multiplication and Noether–Lefschetz loci of the twistor space of a K3 surface
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 17-38
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Geometric aspects on Humbert-Edge curves of type 5, Kummer surfaces and hyperelliptic curves of genus 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 612-624
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonemptiness of severi varieties on enriques surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 June 2023, e52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENRIQUES INVOLUTIONS AND BRAUER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 606-621
- Print publication:
- September 2023
-
- Article
- Export citation
Exceptional jumps of Picard ranks of reductions of K3 surfaces over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 September 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
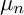 $\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
$\mu _{n}$
-ACTIONS ON K3 SURFACES IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 11-49
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deligne-Beilinson cohomology of the universal K3 surface
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 August 2022, e64
-
- Article
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation

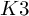



 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 

 of degree
of degree