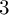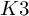1 Introduction
Given an irreducible, projective variety X of dimension n, its degree of irrationality
![]() $\operatorname {\mathrm {irr}}(X)$
is the minimal degree of a rational dominant map
$\operatorname {\mathrm {irr}}(X)$
is the minimal degree of a rational dominant map ![]() . This is a birational invariant measuring how far X is from being rational, which in recent times has been the object of a considerable amount of work; remarkable progress has been made for hypersurfaces in projective space ([Reference Bastianelli, De Poi, Ein, Lazarsfeld and UlleryBDPE+17, Reference Chen and StapletonCS20]), abelian varieties ([Reference ChenChe19, Reference MartinMar22, Reference Colombo, Martin, Naranjo and PirolaCMNP22]), hyperkähler varieties and their moduli spaces ([Reference VoisinVoi22, Reference Agostini, Barros and LaiABL23a, Reference Agostini, Barros and LaiABL23b]) and some concrete examples ([Reference Gounelas and KouvidakisGK19]). Nevertheless, the computation of
. This is a birational invariant measuring how far X is from being rational, which in recent times has been the object of a considerable amount of work; remarkable progress has been made for hypersurfaces in projective space ([Reference Bastianelli, De Poi, Ein, Lazarsfeld and UlleryBDPE+17, Reference Chen and StapletonCS20]), abelian varieties ([Reference ChenChe19, Reference MartinMar22, Reference Colombo, Martin, Naranjo and PirolaCMNP22]), hyperkähler varieties and their moduli spaces ([Reference VoisinVoi22, Reference Agostini, Barros and LaiABL23a, Reference Agostini, Barros and LaiABL23b]) and some concrete examples ([Reference Gounelas and KouvidakisGK19]). Nevertheless, the computation of
![]() $\operatorname {\mathrm {irr}}(X)$
is still a difficult problem for which very little is known in general if
$\operatorname {\mathrm {irr}}(X)$
is still a difficult problem for which very little is known in general if
![]() $n\geq 2$
.
$n\geq 2$
.
A preliminary version of this problem consists of fixing a line bundle
![]() $L\in \operatorname {\mathrm {Pic}}(X)$
and considering the following invariant of the pair
$L\in \operatorname {\mathrm {Pic}}(X)$
and considering the following invariant of the pair
![]() $(X,L)$
, closely related to the degree of irrationality of X:
$(X,L)$
, closely related to the degree of irrationality of X:
The degree of a dominant map ![]() has a natural interpretation in terms of the kernel
has a natural interpretation in terms of the kernel
![]() $E^\vee $
of the evaluation map
$E^\vee $
of the evaluation map
![]() $V \otimes \mathcal {O}_X\to L$
. Indeed, the inclusion
$V \otimes \mathcal {O}_X\to L$
. Indeed, the inclusion
![]() $V^\vee \subset H^0(E)$
describes the fibers of
$V^\vee \subset H^0(E)$
describes the fibers of
![]() $\varphi _V$
in a precise way (see Proposition 2.1 for the surface case). The degree of
$\varphi _V$
in a precise way (see Proposition 2.1 for the surface case). The degree of
![]() $\varphi _V$
turns out to be the difference between
$\varphi _V$
turns out to be the difference between
![]() $c_n(E)$
and the degree of the ‘cycle-theoretic base locus’ of sections of
$c_n(E)$
and the degree of the ‘cycle-theoretic base locus’ of sections of
![]() $V^\vee \subset H^0(E)$
. Note that the rational map induced by
$V^\vee \subset H^0(E)$
. Note that the rational map induced by
![]() $V\in \operatorname {\mathrm {Gr}}(n+1, H^0(L))$
is nothing but the composition
$V\in \operatorname {\mathrm {Gr}}(n+1, H^0(L))$
is nothing but the composition
where the second map is the projection from the linear space
![]() $\mathbb {P}\left (\ker (H^0(L)^\vee \to V^\vee )\right )$
. In the case of surfaces, the top Chern class
$\mathbb {P}\left (\ker (H^0(L)^\vee \to V^\vee )\right )$
. In the case of surfaces, the top Chern class
![]() $c_2(E)$
gives information on how secant is this linear space with respect to X, whereas the ‘cycle-theoretic base locus’ says how tangent is this linear space. If one is able to control these two invariants efficiently, then one can infer on the projections of a given degree.
$c_2(E)$
gives information on how secant is this linear space with respect to X, whereas the ‘cycle-theoretic base locus’ says how tangent is this linear space. If one is able to control these two invariants efficiently, then one can infer on the projections of a given degree.
This approach has been exploited by the first author in [Reference MorettiMor23] in order to obtain new upper bounds for the quantities
![]() $\operatorname {\mathrm {irr}}_L(X)$
and
$\operatorname {\mathrm {irr}}_L(X)$
and
![]() $\operatorname {\mathrm {irr}}(X)$
for several examples of polarized varieties
$\operatorname {\mathrm {irr}}(X)$
for several examples of polarized varieties
![]() $(X,L)$
. Among those examples, one finds polarized
$(X,L)$
. Among those examples, one finds polarized
![]() $K3$
surfaces
$K3$
surfaces
![]() $(S,L)$
with
$(S,L)$
with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
(see [Reference MorettiMor23, Theorem 1.1]). In that case the kernel bundle is moreover stable, which allowed the first author to endow the following set of special maps with a natural scheme structure:
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
(see [Reference MorettiMor23, Theorem 1.1]). In that case the kernel bundle is moreover stable, which allowed the first author to endow the following set of special maps with a natural scheme structure:
The goal of this paper is to show how, in the case of
![]() $K3$
surfaces, a combination of vector bundle techniques with tools coming from the derived category (mainly Bridgeland stability and Fourier–Mukai theory) provides new insight into these problems.
$K3$
surfaces, a combination of vector bundle techniques with tools coming from the derived category (mainly Bridgeland stability and Fourier–Mukai theory) provides new insight into these problems.
More precisely, we examine in detail the invariants
![]() $\operatorname {\mathrm {irr}}_L(S)$
and
$\operatorname {\mathrm {irr}}_L(S)$
and
![]() $W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
for polarized
$W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
for polarized
![]() $K3$
surfaces
$K3$
surfaces
![]() $(S,L)$
of low genus g, under the assumption
$(S,L)$
of low genus g, under the assumption
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. This question is already known for
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. This question is already known for
![]() $g\leq 6$
(see [Reference MorettiMor23, Theorem 1.2]); as it will become apparent in our arguments, the problem is substantially harder as long as g increases due to the complexity of the potential cycle-theoretic base loci.
$g\leq 6$
(see [Reference MorettiMor23, Theorem 1.2]); as it will become apparent in our arguments, the problem is substantially harder as long as g increases due to the complexity of the potential cycle-theoretic base loci.
Since the picture is different depending on the parity of g, we will state our results separately. For a polarized
![]() $K3$
surface
$K3$
surface
![]() $(S,L)$
of odd genus g, let us denote by
$(S,L)$
of odd genus g, let us denote by
![]() $\mathcal {M}$
the moduli space of rank
$\mathcal {M}$
the moduli space of rank
![]() $2$
stable vector bundles with
$2$
stable vector bundles with
![]() $c_1=L$
and minimal
$c_1=L$
and minimal
![]() $c_2=\lfloor \frac {g+3}{2}\rfloor $
.
$c_2=\lfloor \frac {g+3}{2}\rfloor $
.
Theorem A. Let
![]() $(S,L)$
be a very general polarized
$(S,L)$
be a very general polarized
![]() $K3$
surface of genus g.
$K3$
surface of genus g.
-
(1) If
 $g=7$
, then
$g=7$
, then
 $\operatorname {\mathrm {irr}}_L(S)=4$
and
$\operatorname {\mathrm {irr}}_L(S)=4$
and
 $W^2_4(S,L)$
is isomorphic to
$W^2_4(S,L)$
is isomorphic to
 $S\times \mathcal {M}$
.
$S\times \mathcal {M}$
. -
(2) If
 $g=9$
, then
$g=9$
, then
 $\operatorname {\mathrm {irr}}_L(S)=4$
and
$\operatorname {\mathrm {irr}}_L(S)=4$
and
 $W^2_4(S,L)$
has at least two irreducible components: a three-dimensional one (isomorphic to a
$W^2_4(S,L)$
has at least two irreducible components: a three-dimensional one (isomorphic to a
 $\mathbb P^1$
-bundle over
$\mathbb P^1$
-bundle over
 $\mathcal {M}$
) and a two-dimensional one (isomorphic to a nontrivial correspondence between S and
$\mathcal {M}$
) and a two-dimensional one (isomorphic to a nontrivial correspondence between S and
 $\mathcal {M}$
).
$\mathcal {M}$
). -
(3) If
 $g=11$
, then
$g=11$
, then
 $\operatorname {\mathrm {irr}}_L(S)=4$
and
$\operatorname {\mathrm {irr}}_L(S)=4$
and
 $W^2_4(S,L)$
has an irreducible component isomorphic to
$W^2_4(S,L)$
has an irreducible component isomorphic to
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(4) If
 $g=13$
, then
$g=13$
, then
 $\operatorname {\mathrm {irr}}_L(S)\leq 4$
and
$\operatorname {\mathrm {irr}}_L(S)\leq 4$
and
 $W^2_4(S,L)$
is at least one-dimensional.
$W^2_4(S,L)$
is at least one-dimensional.
For even genera, our results can be summarized as follows:
Theorem B. Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus g, with
$K3$
surface of genus g, with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
.
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
.
-
(1) If
 $g=8$
, then
$g=8$
, then
 $\operatorname {\mathrm {irr}}_L(S)=4$
and
$\operatorname {\mathrm {irr}}_L(S)=4$
and
 $W^2_4(S,L)$
has a component birational to a
$W^2_4(S,L)$
has a component birational to a
 $\mathbb P^3$
-bundle over S.
$\mathbb P^3$
-bundle over S. -
(2) If
 $g=10$
, then
$g=10$
, then
 $\operatorname {\mathrm {irr}}_L(S)\le 4$
and
$\operatorname {\mathrm {irr}}_L(S)\le 4$
and
 $W^2_4(S,L)$
has at least two irreducible components: a four-dimensional one (isomorphic to the Hilbert square
$W^2_4(S,L)$
has at least two irreducible components: a four-dimensional one (isomorphic to the Hilbert square
 $S^{[2]}$
) and a three-dimensional one (isomorphic to
$S^{[2]}$
) and a three-dimensional one (isomorphic to
 $\mathbb P(E)$
, where E is the stable spherical rank
$\mathbb P(E)$
, where E is the stable spherical rank
 $2$
vector bundle with
$2$
vector bundle with
 $c_2(E)=6$
).
$c_2(E)=6$
). -
(3) If
 $g=12$
, then
$g=12$
, then
 $\operatorname {\mathrm {irr}}_L(S)\le 4$
and
$\operatorname {\mathrm {irr}}_L(S)\le 4$
and
 $W^2_4(S,L)$
has a unirational three-dimensional component.
$W^2_4(S,L)$
has a unirational three-dimensional component. -
(4) If
 $g=14$
, then
$g=14$
, then
 $\operatorname {\mathrm {irr}}_L(S)\le 4$
and
$\operatorname {\mathrm {irr}}_L(S)\le 4$
and
 $W^2_4(S,L)$
has an irreducible component isomorphic to S.
$W^2_4(S,L)$
has an irreducible component isomorphic to S.
Since upper bounds for the degree of irrationality specialize in families of regular surfaces (see [Reference Chen and StapletonCS20, Proposition C]), an immediate consequence of Theorem A and Theorem B is:
Corollary C. Any polarized
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $\leq 14$
has degree of irrationality
$\leq 14$
has degree of irrationality
![]() $\leq 4$
.
$\leq 4$
.
Let us say a few words about the strategy of proof of Theorem A, which is the main body of work. The first step is the construction of rational maps ![]() of degree
of degree
![]() $\leq 4$
; by Proposition 2.1, this can be achieved by finding couples
$\leq 4$
; by Proposition 2.1, this can be achieved by finding couples
![]() $(E,\xi )\in \mathcal {M}\times S^{[\frac {g-5}{2}]}$
such that
$(E,\xi )\in \mathcal {M}\times S^{[\frac {g-5}{2}]}$
such that
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
. Via the derived category approach, we determine the locus of such couples, which leads to an explicit description of the corresponding irreducible component of
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
. Via the derived category approach, we determine the locus of such couples, which leads to an explicit description of the corresponding irreducible component of
![]() $W^2_4(S,L)$
.
$W^2_4(S,L)$
.
For instance, in genus 11 Bridgeland stability provides an isomorphism of Hilbert schemes
that, combined with Fourier–Mukai arguments, shows that
(here
![]() $\eta _E$
denotes the noncurvilinear element of
$\eta _E$
denotes the noncurvilinear element of
![]() $\mathcal {M}^{[3]}$
supported at E).
$\mathcal {M}^{[3]}$
supported at E).
In the second step (for
![]() $g=7,9,11$
), we prove that there are no degree 3 maps; this is divided into two substeps. One starts by discarding the existence of couples
$g=7,9,11$
), we prove that there are no degree 3 maps; this is divided into two substeps. One starts by discarding the existence of couples
![]() $(E,\xi )\in \mathcal {M}\times S^{[ \frac {g-3}{2}]}$
such that
$(E,\xi )\in \mathcal {M}\times S^{[ \frac {g-3}{2}]}$
such that
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
, again via derived methods. Geometrically, this means discarding the situation where the linear space we are projecting from is maximally secant to S (i.e., the base locus has the highest possible length) and is tangent to S at
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
, again via derived methods. Geometrically, this means discarding the situation where the linear space we are projecting from is maximally secant to S (i.e., the base locus has the highest possible length) and is tangent to S at
![]() $\frac {g-3}{2}$
points. For instance, in genus
$\frac {g-3}{2}$
points. For instance, in genus
![]() $g=9$
, by (twisted) Fourier–Mukai theory the condition
$g=9$
, by (twisted) Fourier–Mukai theory the condition
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
implies the existence of a rational curve in
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
implies the existence of a rational curve in
![]() $\mathcal {M}$
with a triple point; coupled with a result of Chen [Reference ChenChe02] on the singularities of rational curves on general
$\mathcal {M}$
with a triple point; coupled with a result of Chen [Reference ChenChe02] on the singularities of rational curves on general
![]() $K3$
surfaces, this gives a contradiction.
$K3$
surfaces, this gives a contradiction.
Then one has to rule out all the cases where the ‘cycle-theoretic base locus’ is strictly bigger than the ‘scheme-theoretic base locus’. This is a more special situation, in which the linear space we are projecting from is maximally secant and the singularities of the intersection with S are more complicated. In this case, we exploit systematically an ad hoc lemma relating the ‘cycle-theoretic base locus’ with the image of
![]() $V^\vee \otimes \mathcal {O}_S\to E$
(c.f. Lemma 2.4), which we combine with other vector bundle arguments.
$V^\vee \otimes \mathcal {O}_S\to E$
(c.f. Lemma 2.4), which we combine with other vector bundle arguments.
It is worth mentioning that our results suggest several patterns for the behaviour of
![]() $\operatorname {\mathrm {irr}}_L(S)$
, as g varies; here, the efforts to describe
$\operatorname {\mathrm {irr}}_L(S)$
, as g varies; here, the efforts to describe
![]() $W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
become crucial. We thus expect these two invariants to be a potential source of new questions. Some of them are gathered in a separate section at the end of the paper.
$W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
become crucial. We thus expect these two invariants to be a potential source of new questions. Some of them are gathered in a separate section at the end of the paper.
Nevertheless, it seems to us that a good understanding of this problem for arbitrary g is not accessible without further improvement of our techniques. As mentioned above, the reason is that the possible configurations of certain zero-dimensional subschemes become more and more intricate. The case of genus
![]() $14$
is somehow the first concrete realization of this problem: maps of degree
$14$
is somehow the first concrete realization of this problem: maps of degree
![]() $4$
necessarily have a ‘cycle-theoretic base locus’ bigger than the ‘scheme-theoretic base locus’. In more geometric words, there is no codimension
$4$
necessarily have a ‘cycle-theoretic base locus’ bigger than the ‘scheme-theoretic base locus’. In more geometric words, there is no codimension
![]() $3$
linear subspace in
$3$
linear subspace in
![]() $\mathbb P^{14}$
intersecting S along a subscheme of colength
$\mathbb P^{14}$
intersecting S along a subscheme of colength
![]() $18$
and being tangent to S at four distinct points.
$18$
and being tangent to S at four distinct points.
Structure of the paper. We start with a section of preliminaries, where we recall the kernel bundle approach to study linear systems (including Brill–Noether loci and key lemmas involving the local structure of the base ideal), as well as some basics on the derived category tools. Sections 3-6 deal with the cases of odd genus (namely with the proof of Theorem A) and constitute the core of the paper. In Section 7, we treat even genera (i.e., Theorem B). Finally, in Section 8 we raise several questions about the behaviour of
![]() $\operatorname {\mathrm {irr}}_L(S)$
and
$\operatorname {\mathrm {irr}}_L(S)$
and
![]() $W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
in arbitrary genus, based on our results for
$W^2_{\operatorname {\mathrm {irr}}_L(S)}(S,L)$
in arbitrary genus, based on our results for
![]() $g\leq 14$
.
$g\leq 14$
.
2 Preliminaries
Throughout this paper, we will work over the field of the complex numbers.
2.1 Projections of low degree
We fix a smooth polarized surface
![]() $(S,L)$
with
$(S,L)$
with
![]() $\mathrm {NS}(S)=\mathbb Z\cdot [L]$
. We will study linear systems
$\mathrm {NS}(S)=\mathbb Z\cdot [L]$
. We will study linear systems
![]() $V\in \mathrm {Gr}(3,H^0(L))$
, via the associated kernel bundle. Namely, one can consider the vector bundle
$V\in \mathrm {Gr}(3,H^0(L))$
, via the associated kernel bundle. Namely, one can consider the vector bundle
![]() $E^\vee $
sitting in an exact sequence
$E^\vee $
sitting in an exact sequence
and let
![]() $T:=\underline {\mathop {\mathrm {Spec}}}(\mathcal {O}_S/\mathcal {I})$
denote the base locus of the rational map
$T:=\underline {\mathop {\mathrm {Spec}}}(\mathcal {O}_S/\mathcal {I})$
denote the base locus of the rational map
![]() $\varphi _V:S \dashrightarrow \mathbb P(V^\vee )$
. Dualizing one gets an inclusion
$\varphi _V:S \dashrightarrow \mathbb P(V^\vee )$
. Dualizing one gets an inclusion
![]() $V^\vee \subset H^0(E)$
that allows to study the fibers of
$V^\vee \subset H^0(E)$
that allows to study the fibers of
![]() $\varphi _V$
(note that
$\varphi _V$
(note that
![]() $\varphi _V$
is dominant by the assumption
$\varphi _V$
is dominant by the assumption
![]() $\operatorname {\mathrm {NS}}(S)=\mathbb Z\cdot [L]$
). More precisely, the following holds:
$\operatorname {\mathrm {NS}}(S)=\mathbb Z\cdot [L]$
). More precisely, the following holds:
Proposition 2.1 [Reference MorettiMor23, Section 2].
The morphism
![]() $\tilde \varphi ={\varphi _V}|_{S\setminus T}:S\setminus T\to \mathbb {P}(V^\vee )$
satisfies:
$\tilde \varphi ={\varphi _V}|_{S\setminus T}:S\setminus T\to \mathbb {P}(V^\vee )$
satisfies:
-
(1) For every point
 $p=[s_p]\in \mathbb {P} (V^\vee )$
, one has
$p=[s_p]\in \mathbb {P} (V^\vee )$
, one has
 $\widetilde {\varphi }^{-1}(p)=Z(s_p)\cap (S\setminus T)$
where
$\widetilde {\varphi }^{-1}(p)=Z(s_p)\cap (S\setminus T)$
where
 $s_p\in V^\vee \subset H^0(E)$
.
$s_p\in V^\vee \subset H^0(E)$
. -
(2)
 $\deg (\varphi )=c_2(E)-\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )$
.
$\deg (\varphi )=c_2(E)-\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )$
.
The first preliminary lemma tells us that the degree of the map cannot be too big with respect to the colength of the base ideal
![]() $\mathcal {I}$
:
$\mathcal {I}$
:
Lemma 2.2. Let
![]() $(S,L)$
be a polarized surface and
$(S,L)$
be a polarized surface and
![]() $V\in \mathrm {Gr}(3,H^0(L))$
a linear system with finite base locus
$V\in \mathrm {Gr}(3,H^0(L))$
a linear system with finite base locus
![]() $\underline {\mathop {\mathrm {Spec}}}(\mathcal {O}_S/\mathcal {I})$
. Then
$\underline {\mathop {\mathrm {Spec}}}(\mathcal {O}_S/\mathcal {I})$
. Then
![]() $\mathrm {deg}(\varphi _V)\ge L^2- \frac {4}{3}\mathrm {colength}(\mathcal {I})$
.
$\mathrm {deg}(\varphi _V)\ge L^2- \frac {4}{3}\mathrm {colength}(\mathcal {I})$
.
Proof. There is another standard way to compute the degree of the rational map
![]() $\varphi _V$
, in terms of Hilbert–Samuel multiplicities of
$\varphi _V$
, in terms of Hilbert–Samuel multiplicities of
![]() $\mathcal {I}$
. The Hilbert–Samuel multiplicity of an ideal sheaf
$\mathcal {I}$
. The Hilbert–Samuel multiplicity of an ideal sheaf
![]() $\mathcal {I}$
at a point p is defined as
$\mathcal {I}$
at a point p is defined as
![]() $e_p(\mathcal {I}):=\mathrm {length}(\mathcal {O}_{S,p}/(f,g))$
, where
$e_p(\mathcal {I}):=\mathrm {length}(\mathcal {O}_{S,p}/(f,g))$
, where
![]() $f,g\in \mathcal {I}\otimes \mathcal {O}_{S,p}$
are general elements. Then
$f,g\in \mathcal {I}\otimes \mathcal {O}_{S,p}$
are general elements. Then
Now, by [Reference Huneke, Ma, Quy and SmirnovHMQS20, Proposition 5.7]
![]() $e_p(\mathcal {I})\le \frac {4}{3}\mathrm {colength}(\mathcal {I},p)$
(notice that
$e_p(\mathcal {I})\le \frac {4}{3}\mathrm {colength}(\mathcal {I},p)$
(notice that
![]() $\mathcal {I}\otimes \mathcal {O}_{S,p}$
has at most three generators). The lemma follows.
$\mathcal {I}\otimes \mathcal {O}_{S,p}$
has at most three generators). The lemma follows.
This has the following important implication, if one wants to study maps of degree
![]() $3,4$
in the primitive linear system of a
$3,4$
in the primitive linear system of a
![]() $K3$
surface via the kernel bundle.
$K3$
surface via the kernel bundle.
Corollary 2.3. If
![]() $\varphi _V:S \dashrightarrow \mathbb P ^2$
is a map of degree d with kernel bundle
$\varphi _V:S \dashrightarrow \mathbb P ^2$
is a map of degree d with kernel bundle
![]() $E^\vee $
, then
$E^\vee $
, then
In particular, for
![]() $(S,L)$
a polarized
$(S,L)$
a polarized
![]() $K3$
surface of genus g with
$K3$
surface of genus g with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
: if
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
: if
![]() $d=3$
only the minimal
$d=3$
only the minimal
![]() $c_2=\lfloor \frac {g+3}{2} \rfloor $
is possible, and if
$c_2=\lfloor \frac {g+3}{2} \rfloor $
is possible, and if
![]() $d=4$
, only the two lowest
$d=4$
, only the two lowest
![]() $c_2$
are possible.
$c_2$
are possible.
Proof. The inequality follows from the previous lemma, together with the observation that
![]() $c_2(E)=L^2-\mathrm {colength}( \mathcal I)$
. For the second part, observe that under the assumption
$c_2(E)=L^2-\mathrm {colength}( \mathcal I)$
. For the second part, observe that under the assumption
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
the kernel bundle
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
the kernel bundle
![]() $E^\vee $
is stable; otherwise, we would have
$E^\vee $
is stable; otherwise, we would have
![]() $\mathcal {O}_S\hookrightarrow E^\vee $
which contradicts the inclusion
$\mathcal {O}_S\hookrightarrow E^\vee $
which contradicts the inclusion
![]() $V\hookrightarrow H^0(L\otimes \mathcal {I})$
. Hence, by Mukai’s theory of stable vector bundles on
$V\hookrightarrow H^0(L\otimes \mathcal {I})$
. Hence, by Mukai’s theory of stable vector bundles on
![]() $K3$
surfaces ([Reference MukaiMuk87, Corollary 2.5]) we have
$K3$
surfaces ([Reference MukaiMuk87, Corollary 2.5]) we have
![]() $v(E)^2\geq -2$
(see Subsection 2.3 for the definition of
$v(E)^2\geq -2$
(see Subsection 2.3 for the definition of
![]() $v(E)$
), which in this case reads as
$v(E)$
), which in this case reads as
![]() $c_2(E)\geq \lfloor \frac {g+3}{2} \rfloor $
.
$c_2(E)\geq \lfloor \frac {g+3}{2} \rfloor $
.
In other words: If S is a
![]() $K3$
surface with
$K3$
surface with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
and
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
and
![]() $\varphi _V$
is of degree 3, then the base locus T has the highest possible length (i.e., the codimension 3 linear subspace
$\varphi _V$
is of degree 3, then the base locus T has the highest possible length (i.e., the codimension 3 linear subspace
![]() $\mathbb {P}\left (\ker (H^0(L)^\vee \to V^\vee )\right )$
is maximally secant to S).
$\mathbb {P}\left (\ker (H^0(L)^\vee \to V^\vee )\right )$
is maximally secant to S).
2.2 Brill–Noether loci
Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus g (i.e.,
$K3$
surface of genus g (i.e.,
![]() $L^2=2g-2$
), with
$L^2=2g-2$
), with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. In this subsection, we recall the construction of the Brill–Noether loci from [Reference MorettiMor23] and prove some auxiliary lemmas that will be fundamental to study them from our perspective.
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. In this subsection, we recall the construction of the Brill–Noether loci from [Reference MorettiMor23] and prove some auxiliary lemmas that will be fundamental to study them from our perspective.
The set-theoretic definition is the following:
Let us denote by
![]() $\mathcal {M}(2,L,g+1-c)$
the moduli space of stable rank 2 vector bundles with Chern classes
$\mathcal {M}(2,L,g+1-c)$
the moduli space of stable rank 2 vector bundles with Chern classes
![]() $c_1=L$
and
$c_1=L$
and
![]() $c_2=c$
(this notation is compatible with the Mukai vector introduced in the next subsection). By Proposition 2.1 (and the fact that the kernel bundle is stable, since
$c_2=c$
(this notation is compatible with the Mukai vector introduced in the next subsection). By Proposition 2.1 (and the fact that the kernel bundle is stable, since
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
) the above set-theoretic description is equivalent to
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
) the above set-theoretic description is equivalent to
where
 $$\begin{align*}W^2_d(S,L)_c & :=\Bigg\{(E,V^\vee) \;| \; E\in \mathcal{M}(2,L,g+1-c),\; \\ &\quad V^\vee\in \operatorname{\mathrm{Gr}}(3,H^0(E)),\; \mathrm{deg}\left(\bigcap_{s\in V^\vee}Z_{cycle}(s)\right)\geq c-d \Bigg\} \end{align*}$$
$$\begin{align*}W^2_d(S,L)_c & :=\Bigg\{(E,V^\vee) \;| \; E\in \mathcal{M}(2,L,g+1-c),\; \\ &\quad V^\vee\in \operatorname{\mathrm{Gr}}(3,H^0(E)),\; \mathrm{deg}\left(\bigcap_{s\in V^\vee}Z_{cycle}(s)\right)\geq c-d \Bigg\} \end{align*}$$
(note that the disjoint union is finite by Corollary 2.3).
With this second description,
![]() $W^2_d(S,L)$
carries a natural scheme structure. Indeed, for a fixed
$W^2_d(S,L)$
carries a natural scheme structure. Indeed, for a fixed
![]() $E\in \mathcal {M}(2,L,g+1-c)$
, one can show that
$E\in \mathcal {M}(2,L,g+1-c)$
, one can show that
![]() $\deg (\bigcap _{s\in V^\vee }Z_{cycle}(s))$
is an upper-semicontinuous function of
$\deg (\bigcap _{s\in V^\vee }Z_{cycle}(s))$
is an upper-semicontinuous function of
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
; a relative construction makes
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
; a relative construction makes
![]() $W^2_d(S,L)_c$
into a closed subset of the relative Grasmannian over
$W^2_d(S,L)_c$
into a closed subset of the relative Grasmannian over
![]() $\mathcal {M}(2,L,g+1-c)$
(see [Reference MorettiMor23, Section 2] for details).
$\mathcal {M}(2,L,g+1-c)$
(see [Reference MorettiMor23, Section 2] for details).
We will consider these closed subsets with the reduced scheme structure.Footnote 1
The stratification of the Brill–Noether locus
![]() $W^2_d(S,L)$
via
$W^2_d(S,L)$
via
![]() $c_2(E)$
distinguishes rational maps by the length of the base locus (i.e., distinguishes the linear spaces we are projecting from by how secant to S they are). For instance, for a
$c_2(E)$
distinguishes rational maps by the length of the base locus (i.e., distinguishes the linear spaces we are projecting from by how secant to S they are). For instance, for a
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $5$
we have
$5$
we have
where
![]() $W^2_4(S,L)_4$
is the relative Grassmannian over
$W^2_4(S,L)_4$
is the relative Grassmannian over
![]() $\mathcal {M}(2,L,2)$
(see [Reference MorettiMor23, Theorem 1.2]).
$\mathcal {M}(2,L,2)$
(see [Reference MorettiMor23, Theorem 1.2]).
More interestingly, if one fixes the second Chern class there may be different components according to the length of the base scheme of the sections of
![]() $V^\vee $
. Namely,
$V^\vee $
. Namely,
where
The length of
![]() $\bigcap _{s\in V^\vee }Z(s)$
can be seen as a measure of how tangent to S is the linear space we are projecting from, whereas the difference
$\bigcap _{s\in V^\vee }Z(s)$
can be seen as a measure of how tangent to S is the linear space we are projecting from, whereas the difference
![]() $\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )-\mathrm {length}\left (\bigcap _{s\in V^\vee }Z(s)\right )$
is a measure of how singular this tangency is.
$\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )-\mathrm {length}\left (\bigcap _{s\in V^\vee }Z(s)\right )$
is a measure of how singular this tangency is.
In the case where the finite subscheme
![]() $\bigcap _{s\in V^\vee }Z(s)$
is curvilinear (i.e., it lies on a smooth curve contained in S), we need the following lemma to study the relation between these two invariants:
$\bigcap _{s\in V^\vee }Z(s)$
is curvilinear (i.e., it lies on a smooth curve contained in S), we need the following lemma to study the relation between these two invariants:
Lemma 2.4. Let E be a rank 2 vector bundle on S, and let
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
. Assume that
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
. Assume that
![]() $\xi =\bigcap _{s\in V^\vee }Z(s)$
is curvilinear of length m at a point p, and that the cycle
$\xi =\bigcap _{s\in V^\vee }Z(s)$
is curvilinear of length m at a point p, and that the cycle
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
has degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
has degree
![]() $f\geq m$
at p. Then there exist local coordinates
$f\geq m$
at p. Then there exist local coordinates
![]() $x,y$
around p and
$x,y$
around p and
![]() $e_1,e_2$
local generators of E at p such that the image of the map
$e_1,e_2$
local generators of E at p such that the image of the map
is contained in
![]() $(x,y^m)\cdot e_1+(x^{\lceil \frac {f}{m}\rceil },x^{\lceil \frac {f-1}{m}\rceil }y,...,x^{\lceil \frac {1}{m}\rceil }y^{f-1},y^f)\cdot e_2$
.
$(x,y^m)\cdot e_1+(x^{\lceil \frac {f}{m}\rceil },x^{\lceil \frac {f-1}{m}\rceil }y,...,x^{\lceil \frac {1}{m}\rceil }y^{f-1},y^f)\cdot e_2$
.
Proof. We choose the local coordinates
![]() $x,y$
such that
$x,y$
such that
![]() $\mathcal {I}_\xi =(x,y^m)$
locally at p. Given
$\mathcal {I}_\xi =(x,y^m)$
locally at p. Given
![]() $e_1,e_2$
local generators of E at p, let
$e_1,e_2$
local generators of E at p, let
![]() $\mathcal {I}_j$
be the monomial ideal generated by monomials appearing in the j-th coordinate of sections of
$\mathcal {I}_j$
be the monomial ideal generated by monomials appearing in the j-th coordinate of sections of
![]() $V^\vee $
; we may choose
$V^\vee $
; we may choose
![]() $e_1,e_2$
so that
$e_1,e_2$
so that
![]() $x\in \mathcal {I}_1$
.
$x\in \mathcal {I}_1$
.
In this framework, three general elements
![]() $s_1,s_2,s_3$
of
$s_1,s_2,s_3$
of
![]() $V^\vee $
(giving a basis) have local expressions
$V^\vee $
(giving a basis) have local expressions
where
![]() $f_i(y)\in (y^m)$
and
$f_i(y)\in (y^m)$
and
![]() $t_i(x,y)\in \mathcal {O}_{S,p}^*$
(by the implicit function theorem).
$t_i(x,y)\in \mathcal {O}_{S,p}^*$
(by the implicit function theorem).
Of course, one has
![]() $u_i(f_i(y),y)\in (y^f)$
. Actually, since
$u_i(f_i(y),y)\in (y^f)$
. Actually, since
![]() $Z_{cycle}(s_1+\lambda s_2+\mu s_3)$
has degree
$Z_{cycle}(s_1+\lambda s_2+\mu s_3)$
has degree
![]() $\geq f$
at p, one has
$\geq f$
at p, one has
for every
![]() $\lambda ,\mu $
and every expression
$\lambda ,\mu $
and every expression
![]() $(x-f_1)t_1+\lambda (x-f_2)t_2+\mu (x-f_3)t_3=(x-f_{\lambda ,\mu }(y))\cdot t_{\lambda ,\mu }(x,y)$
with
$(x-f_1)t_1+\lambda (x-f_2)t_2+\mu (x-f_3)t_3=(x-f_{\lambda ,\mu }(y))\cdot t_{\lambda ,\mu }(x,y)$
with
![]() $f_{\lambda ,\mu }\in (y^m)$
and
$f_{\lambda ,\mu }\in (y^m)$
and
![]() $t_{\lambda ,\mu }\in \mathcal {O}_{S,p}^*$
.
$t_{\lambda ,\mu }\in \mathcal {O}_{S,p}^*$
.
This last condition implies that, after replacing
![]() $e_2$
by an appropriate combination of
$e_2$
by an appropriate combination of
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, one may assume that
$e_2$
, one may assume that
![]() $x^ky^l\notin \mathcal {I}_2$
as long as
$x^ky^l\notin \mathcal {I}_2$
as long as
![]() $f>mk+l$
. Therefore, for the new choice of local generators one has
$f>mk+l$
. Therefore, for the new choice of local generators one has
![]() $\mathcal {I}_2\subset (x^{\lceil \frac {f}{m}\rceil },x^{\lceil \frac {f-1}{m}\rceil }y,...,x^{\lceil \frac {1}{m}\rceil }y^{f-1},y^f)$
, which proves the assertion.
$\mathcal {I}_2\subset (x^{\lceil \frac {f}{m}\rceil },x^{\lceil \frac {f-1}{m}\rceil }y,...,x^{\lceil \frac {1}{m}\rceil }y^{f-1},y^f)$
, which proves the assertion.
The first natural step for constructing Brill–Noether loci is to understand whether the cycle-theoretic and the scheme-theoretic intersection coincide. The following remark will be useful:
Remark 2.5. Consider the cohomology jump loci
and the corresponding relative Grassmanian
Then the natural forgetful map
![]() $\psi _{c,m}:\mathcal G_{c,m}\longrightarrow W^2_{c-m}(S,L)_{c,m}$
is an isomorphism outside
$\psi _{c,m}:\mathcal G_{c,m}\longrightarrow W^2_{c-m}(S,L)_{c,m}$
is an isomorphism outside
![]() $\psi _{c,m}^{-1}(\mathrm {Im}(\psi _{c,m+1}))$
. Indeed, there is a well-defined inverse morphism
$\psi _{c,m}^{-1}(\mathrm {Im}(\psi _{c,m+1}))$
. Indeed, there is a well-defined inverse morphism
precisely outside the image of
![]() $\psi _{c,m+1}$
. In particular:
$\psi _{c,m+1}$
. In particular:
-
• If
 $\mathrm {dim}(\mathrm {Im}(\psi _{c,m+1}))<\mathrm {dim}(\mathrm {Im}(\psi _{c,m}))$
and
$\mathrm {dim}(\mathrm {Im}(\psi _{c,m+1}))<\mathrm {dim}(\mathrm {Im}(\psi _{c,m}))$
and
 $\mathcal {G}_{c,m}$
is smooth, then the singularities of
$\mathcal {G}_{c,m}$
is smooth, then the singularities of
 $\psi _{c,m}(\mathcal {G}_{c,m})$
are contained in
$\psi _{c,m}(\mathcal {G}_{c,m})$
are contained in
 $\psi _{c,m+1}(\mathcal G_{c,m+1})$
and
$\psi _{c,m+1}(\mathcal G_{c,m+1})$
and
 $\psi _{c,m}$
is birational.
$\psi _{c,m}$
is birational. -
• If
 $R_{c,m+1}$
is empty and
$R_{c,m+1}$
is empty and
 $R_{c,m}$
is irreducible, then
$R_{c,m}$
is irreducible, then
 $\psi _{c,m}$
is an isomorphism onto its image and
$\psi _{c,m}$
is an isomorphism onto its image and
 $\mathcal {G}_{c,m}$
is isomorphic to an irreducible component of
$\mathcal {G}_{c,m}$
is isomorphic to an irreducible component of
 $W^2_{c-m}(S,L)$
.
$W^2_{c-m}(S,L)$
.
We will mainly deal with the minimal second Chern class (i.e.,
![]() $c=\lfloor \frac {g+3}{2}\rfloor $
); in that case, we will just write
$c=\lfloor \frac {g+3}{2}\rfloor $
); in that case, we will just write
![]() $R_m,\mathcal G_m,\psi _m$
for simplicity.
$R_m,\mathcal G_m,\psi _m$
for simplicity.
To finish this subsection, let us point out an elementary lemma concerning the number of local generators of an ideal sheaf:
Lemma 2.6. Let X be a variety,
![]() $T\subset X$
a closed subscheme and
$T\subset X$
a closed subscheme and
![]() $p\in T$
a closed point. Then
$p\in T$
a closed point. Then
![]() $\dim _{\mathbb {C}}\operatorname {\mathrm {Ext}}^1_{\mathcal {O}_X}(\mathcal {O}_T,k(p))$
equals the minimal number of generators of
$\dim _{\mathbb {C}}\operatorname {\mathrm {Ext}}^1_{\mathcal {O}_X}(\mathcal {O}_T,k(p))$
equals the minimal number of generators of
![]() $\mathcal {I}_{T/X}$
at the point p.
$\mathcal {I}_{T/X}$
at the point p.
Proof. By applying the functor
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(-,k(p))$
to the short exact sequence
$\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(-,k(p))$
to the short exact sequence
we get an isomorphism
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(\mathcal {I}_{T/X},k(p))\cong \operatorname {\mathrm {Ext}}^1_{\mathcal {O}_X}(\mathcal {O}_T,k(p))$
. Now, the claim follows from the adjunction
$\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(\mathcal {I}_{T/X},k(p))\cong \operatorname {\mathrm {Ext}}^1_{\mathcal {O}_X}(\mathcal {O}_T,k(p))$
. Now, the claim follows from the adjunction
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(\mathcal {I}_{T/X},k(p))\cong \operatorname {\mathrm {Hom}}_{k}(\mathcal {I}_{T/X}\otimes k(p),k(p))$
and Nakayama’s lemma.
$\operatorname {\mathrm {Hom}}_{\mathcal {O}_X}(\mathcal {I}_{T/X},k(p))\cong \operatorname {\mathrm {Hom}}_{k}(\mathcal {I}_{T/X}\otimes k(p),k(p))$
and Nakayama’s lemma.
2.3 Bridgeland stability on
 $K3$
surfaces
$K3$
surfaces
Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface. In this subsection, we review some basic facts on the
$K3$
surface. In this subsection, we review some basic facts on the
![]() $(\alpha ,\beta )$
-plane of Bridgeland stability conditions associated to L. For a more detailed discussion, the reader may consult Bridgeland original work [Reference BridgelandBri07, Reference BridgelandBri08] or the recent survey [Reference Macrì and SchmidtMS21].
$(\alpha ,\beta )$
-plane of Bridgeland stability conditions associated to L. For a more detailed discussion, the reader may consult Bridgeland original work [Reference BridgelandBri07, Reference BridgelandBri08] or the recent survey [Reference Macrì and SchmidtMS21].
We will denote the Mukai vector of an object
![]() $E\in \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
by
$E\in \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
by
This gives an element of
![]() $\Lambda :=\mathbb {Z}\oplus \operatorname {\mathrm {Pic}}(S)\oplus \mathbb {Z}$
, which is a lattice equipped with the pairing
$\Lambda :=\mathbb {Z}\oplus \operatorname {\mathrm {Pic}}(S)\oplus \mathbb {Z}$
, which is a lattice equipped with the pairing
Let us also recall that a class
![]() $\delta \in \Lambda $
is called spherical if
$\delta \in \Lambda $
is called spherical if
![]() $\delta ^2=-2$
.
$\delta ^2=-2$
.
Given a coherent sheaf
![]() $E\in \operatorname {\mathrm {Coh}}(S)$
, we define its slope by
$E\in \operatorname {\mathrm {Coh}}(S)$
, we define its slope by
![]() $\mu _L(E)=\frac {L\cdot \operatorname {\mathrm {ch}}_1(E)}{L^2\cdot \operatorname {\mathrm {ch}}_0(E)}$
(with the convention
$\mu _L(E)=\frac {L\cdot \operatorname {\mathrm {ch}}_1(E)}{L^2\cdot \operatorname {\mathrm {ch}}_0(E)}$
(with the convention
![]() $\mu _L(E)=+\infty $
if
$\mu _L(E)=+\infty $
if
![]() $\operatorname {\mathrm {ch}}_0(E)=0$
). This leads to the usual notion of
$\operatorname {\mathrm {ch}}_0(E)=0$
). This leads to the usual notion of
![]() $\mu _L$
-stability.
$\mu _L$
-stability.
For a real number
![]() $\beta \in \mathbb {R}$
, we consider the full subcategories of
$\beta \in \mathbb {R}$
, we consider the full subcategories of
![]() $\operatorname {\mathrm {Coh}}(S)$
$\operatorname {\mathrm {Coh}}(S)$
 $$ \begin{align*} \mathcal{T}_{\beta}:=\{E\in\operatorname{\mathrm{Coh}}(S)\mid\mu_L(Q)>\beta\text{ for all quotients }E\twoheadrightarrow Q\}\\\mathcal{F}_{\beta}:=\{E\in\operatorname{\mathrm{Coh}}(S)\mid\mu_L(F)\leq\beta\text{ for all subsheaves }F\hookrightarrow E\}, \end{align*} $$
$$ \begin{align*} \mathcal{T}_{\beta}:=\{E\in\operatorname{\mathrm{Coh}}(S)\mid\mu_L(Q)>\beta\text{ for all quotients }E\twoheadrightarrow Q\}\\\mathcal{F}_{\beta}:=\{E\in\operatorname{\mathrm{Coh}}(S)\mid\mu_L(F)\leq\beta\text{ for all subsheaves }F\hookrightarrow E\}, \end{align*} $$
forming a torsion pair. The corresponding tilt gives a bounded t-structure on
![]() $\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
with heart
$\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
with heart
Finally, for
![]() $(\alpha ,\beta )\in \mathbb {R}_{>0}\times \mathbb {R}$
, let
$(\alpha ,\beta )\in \mathbb {R}_{>0}\times \mathbb {R}$
, let
![]() $Z_{\alpha ,\beta }:K_0(\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S))\to \mathbb {C}$
be the group homomorphism given by
$Z_{\alpha ,\beta }:K_0(\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S))\to \mathbb {C}$
be the group homomorphism given by
 $$\begin{align*}Z_{\alpha,\beta}(E):=-\left(v_2(E)-\beta L\cdot v_1(E)+\left(\frac{\beta^2}{2}-\frac{\alpha^2}{2}\right)L^2\cdot v_0(E)\right)+i\left(L\cdot v_1(E)-\beta L^2\cdot v_0(E)\right). \end{align*}$$
$$\begin{align*}Z_{\alpha,\beta}(E):=-\left(v_2(E)-\beta L\cdot v_1(E)+\left(\frac{\beta^2}{2}-\frac{\alpha^2}{2}\right)L^2\cdot v_0(E)\right)+i\left(L\cdot v_1(E)-\beta L^2\cdot v_0(E)\right). \end{align*}$$
Now, we have all the ingredients to state a fundamental result of Bridgeland:
Theorem 2.7 [Reference BridgelandBri08].
The pair
![]() $\sigma _{\alpha ,\beta }:=(\operatorname {\mathrm {Coh}}^\beta (S),Z_{\alpha ,\beta })$
is a Bridgeland stability condition on
$\sigma _{\alpha ,\beta }:=(\operatorname {\mathrm {Coh}}^\beta (S),Z_{\alpha ,\beta })$
is a Bridgeland stability condition on
![]() $\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
if, for every
$\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
if, for every
![]() $\delta \in \Lambda $
spherical with
$\delta \in \Lambda $
spherical with
![]() $\Im Z_{\alpha ,\beta }(\delta )=0$
and
$\Im Z_{\alpha ,\beta }(\delta )=0$
and
![]() $\delta _0>0$
, one has
$\delta _0>0$
, one has
![]() $\Re Z_{\alpha ,\beta }(\delta )>0$
.
$\Re Z_{\alpha ,\beta }(\delta )>0$
.
Remark 2.8. The associated region of stability conditions is thus an upper-half plane, from which certain holes (corresponding to points
![]() $(\alpha ,\beta )$
for which
$(\alpha ,\beta )$
for which
![]() $Z_{\alpha ,\beta }(\delta )=0$
for a spherical class
$Z_{\alpha ,\beta }(\delta )=0$
for a spherical class
![]() $\delta $
) have been removed. This can be visualized (for Picard rank 1) in [Reference Bayer and BridgelandBB17, Figure 1].
$\delta $
) have been removed. This can be visualized (for Picard rank 1) in [Reference Bayer and BridgelandBB17, Figure 1].
The fact that
![]() $\sigma _{\alpha ,\beta }$
is a Bridgeland stability condition can be essentially summarized as follows:
$\sigma _{\alpha ,\beta }$
is a Bridgeland stability condition can be essentially summarized as follows:
-
1. For every nonzero
 $E\in \operatorname {\mathrm {Coh}}^\beta (S)$
, one has the inequality
$E\in \operatorname {\mathrm {Coh}}^\beta (S)$
, one has the inequality
 $\Im Z_{\alpha ,\beta }(E)\geq 0$
, and
$\Im Z_{\alpha ,\beta }(E)\geq 0$
, and
 $\Re Z_{\alpha ,\beta }(E)<0$
whenever
$\Re Z_{\alpha ,\beta }(E)<0$
whenever
 $\Im Z_{\alpha ,\beta }(E)=0$
.
$\Im Z_{\alpha ,\beta }(E)=0$
. -
2. Every object of
 $\operatorname {\mathrm {Coh}}^\beta (S)$
admits a Harder–Narasimhan (HN for short) filtration, with respect to the notion of stability defined by the tilt slope
$\operatorname {\mathrm {Coh}}^\beta (S)$
admits a Harder–Narasimhan (HN for short) filtration, with respect to the notion of stability defined by the tilt slope  $$\begin{align*}\nu_{\alpha,\beta}(E):=\left\{ \begin{array}{@{}cl} \frac{-\Re Z_{\alpha,\beta}(E)}{\Im Z_{\alpha,\beta}(E)} & \Im Z_{\alpha,\beta}(E)>0\\ +\infty & \Im Z_{\alpha,\beta}(E)=0.\\ \end{array} \right. \end{align*}$$
$$\begin{align*}\nu_{\alpha,\beta}(E):=\left\{ \begin{array}{@{}cl} \frac{-\Re Z_{\alpha,\beta}(E)}{\Im Z_{\alpha,\beta}(E)} & \Im Z_{\alpha,\beta}(E)>0\\ +\infty & \Im Z_{\alpha,\beta}(E)=0.\\ \end{array} \right. \end{align*}$$
It is worth mentioning that Bridgeland stability conditions can be deformed continuously (more precisely, their set can be given the structure of a complex manifold), thanks to a technical condition called the support property. While we refer the reader to [Reference BayerBay19] for details, here we content ourselves with one of the main applications: There is a locally finite wall and chamber structure so that stability of objects remains unchanged along a chamber.
A numerical wall for a class
![]() $v\in \Lambda $
is the region of
$v\in \Lambda $
is the region of
![]() $\mathbb {R}_{>0}\times \mathbb {R}$
determined by an equation of the form
$\mathbb {R}_{>0}\times \mathbb {R}$
determined by an equation of the form
![]() $\nu _{\alpha ,\beta }(v)=\nu _{\alpha ,\beta }(w)$
, where
$\nu _{\alpha ,\beta }(v)=\nu _{\alpha ,\beta }(w)$
, where
![]() $w\in \Lambda $
is a class nonproportional to v. An actual wall for v is a subset of a numerical wall, at which the set of semistable objects of class v changes.
$w\in \Lambda $
is a class nonproportional to v. An actual wall for v is a subset of a numerical wall, at which the set of semistable objects of class v changes.
The structure of the walls in the
![]() $(\alpha ,\beta )$
-plane admits the following description:
$(\alpha ,\beta )$
-plane admits the following description:
Proposition 2.9. Assume that
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
, and let
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
, and let
![]() $v\in \Lambda $
be any class.
$v\in \Lambda $
be any class.
-
(1) All numerical walls for v are either semicircles centered on the
 $\beta $
-axis or lines parallel to the
$\beta $
-axis or lines parallel to the
 $\alpha $
-axis.
$\alpha $
-axis. -
(2) If
 $v_0\neq 0$
, there is a unique vertical wall with equation
$v_0\neq 0$
, there is a unique vertical wall with equation
 $\beta =\frac {L\cdot v_1}{L^2\cdot v_0}$
. If
$\beta =\frac {L\cdot v_1}{L^2\cdot v_0}$
. If
 $v_0=0$
, then there is no vertical wall.
$v_0=0$
, then there is no vertical wall. -
(3) The curve
 $H_v:\nu _{\alpha ,\beta }(v)=0$
intersects every semicircular wall at its top point. This curve is an hyperbola (if
$H_v:\nu _{\alpha ,\beta }(v)=0$
intersects every semicircular wall at its top point. This curve is an hyperbola (if
 $v_0\neq 0$
and
$v_0\neq 0$
and
 $v^2>0$
), a pair of lines (if
$v^2>0$
), a pair of lines (if
 $v_0\neq 0$
and
$v_0\neq 0$
and
 $v^2=0$
), a parabola (if
$v^2=0$
), a parabola (if
 $v^2<0$
) or a single vertical line (if
$v^2<0$
) or a single vertical line (if
 $v_0=0$
).
$v_0=0$
). -
(4) If
 $v^2\geq 0$
, then all semicircular walls are strictly nested.
$v^2\geq 0$
, then all semicircular walls are strictly nested. -
(5) If
 $v^2<0$
, then all walls intersect at the unique point
$v^2<0$
, then all walls intersect at the unique point
 $(\alpha ,\beta )$
such that
$(\alpha ,\beta )$
such that
 $Z_{\alpha ,\beta }(v)=0$
.
$Z_{\alpha ,\beta }(v)=0$
.
One should note that numerical walls may cross holes of the
![]() $(\alpha ,\beta )$
-plane; such a hole may determine the end of an actual wall. Pictures illustrating Proposition 2.9 (including this phenomenon) may be found in [Reference Macrì and SchmidtMS21, Figures 1-3].
$(\alpha ,\beta )$
-plane; such a hole may determine the end of an actual wall. Pictures illustrating Proposition 2.9 (including this phenomenon) may be found in [Reference Macrì and SchmidtMS21, Figures 1-3].
Using this structure of the walls, one can often understand how the stability of an object varies along certain regions of the
![]() $(\alpha ,\beta )$
-plane. This philosophy is specially well suited for Gieseker semistable sheaves, thanks to the following result:
$(\alpha ,\beta )$
-plane. This philosophy is specially well suited for Gieseker semistable sheaves, thanks to the following result:
Proposition 2.10 [Reference BridgelandBri08].
Let
![]() $v\in \Lambda $
be a class with
$v\in \Lambda $
be a class with
![]() $v_0>0$
, and let
$v_0>0$
, and let
![]() $\beta <\frac {L\cdot v_1}{L^2\cdot v_0}$
. Then an object
$\beta <\frac {L\cdot v_1}{L^2\cdot v_0}$
. Then an object
![]() $F\in \operatorname {\mathrm {Coh}}^\beta (S)$
of class
$F\in \operatorname {\mathrm {Coh}}^\beta (S)$
of class
![]() $v(F)=v$
is
$v(F)=v$
is
![]() $\sigma _{\alpha ,\beta }$
-semistable for every
$\sigma _{\alpha ,\beta }$
-semistable for every
![]() $\alpha \gg 0$
if, and only if, F is a Gieseker semistable sheaf (with respect to L).
$\alpha \gg 0$
if, and only if, F is a Gieseker semistable sheaf (with respect to L).
We close this subsection with an elementary trick that will be applied several times:
Lemma 2.11. Assume
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. Let
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. Let
![]() $\beta _0=\frac {a}{b}\in \mathbb {Q}$
with
$\beta _0=\frac {a}{b}\in \mathbb {Q}$
with
![]() $a,b$
coprime, and let
$a,b$
coprime, and let
![]() $E\in \operatorname {\mathrm {Coh}}^{\beta _0}(S)$
be an object with
$E\in \operatorname {\mathrm {Coh}}^{\beta _0}(S)$
be an object with
![]() $(L\cdot v_1-\beta _0 L^2\cdot v_0)(E)=\frac {1}{b}L^2$
. If E is
$(L\cdot v_1-\beta _0 L^2\cdot v_0)(E)=\frac {1}{b}L^2$
. If E is
![]() $\sigma _{\alpha _0,\beta _0}$
-semistable for some
$\sigma _{\alpha _0,\beta _0}$
-semistable for some
![]() $\alpha _0>0$
, then E is
$\alpha _0>0$
, then E is
![]() $\sigma _{\alpha ,\beta _0}$
-semistable for every
$\sigma _{\alpha ,\beta _0}$
-semistable for every
![]() $\alpha>0$
.
$\alpha>0$
.
2.4 Moduli spaces
Moduli spaces of Gieseker stable sheaves on
![]() $K3$
surfaces are well understood thanks to the work of many authors after the pioneering work of Mukai ([Reference MukaiMuk84]). In the more general context of Bridgeland stability, the following result was established by Bayer–Macrì [Reference Bayer and MacrìBM14], building on previous work of Toda [Reference TodaTod08]:
$K3$
surfaces are well understood thanks to the work of many authors after the pioneering work of Mukai ([Reference MukaiMuk84]). In the more general context of Bridgeland stability, the following result was established by Bayer–Macrì [Reference Bayer and MacrìBM14], building on previous work of Toda [Reference TodaTod08]:
Theorem 2.12. Let
![]() $v\in \Lambda $
be a primitive class, and let
$v\in \Lambda $
be a primitive class, and let
![]() $\sigma _{\alpha ,\beta }$
be a Bridgeland stability condition lying in no actual wall for v. Then there exists a moduli space
$\sigma _{\alpha ,\beta }$
be a Bridgeland stability condition lying in no actual wall for v. Then there exists a moduli space
![]() $\mathcal {M}_{\sigma _{\alpha ,\beta }}(v)$
of
$\mathcal {M}_{\sigma _{\alpha ,\beta }}(v)$
of
![]() $\sigma _{\alpha ,\beta }$
-stable objects of class v, which is a smooth projective hyperkähler variety of dimension
$\sigma _{\alpha ,\beta }$
-stable objects of class v, which is a smooth projective hyperkähler variety of dimension
![]() $v^2+2$
(in particular, it is nonempty if and only
$v^2+2$
(in particular, it is nonempty if and only
![]() $v^2\geq -2$
).
$v^2\geq -2$
).
We will be especially interested in the case of the Gieseker moduli space
![]() $\mathcal {M}:=\mathcal {M}(2,L,\frac {g-1}{2})$
, for
$\mathcal {M}:=\mathcal {M}(2,L,\frac {g-1}{2})$
, for
![]() $(S,L)$
a polarized
$(S,L)$
a polarized
![]() $K3$
surface of odd genus g with
$K3$
surface of odd genus g with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. This is a
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. This is a
![]() $K3$
surface, and results of Mukai ([Reference MukaiMuk87]) show that:
$K3$
surface, and results of Mukai ([Reference MukaiMuk87]) show that:
-
1. If
 $g\equiv 3\pmod {4}$
, then
$g\equiv 3\pmod {4}$
, then
 $\mathcal {M}$
is a fine moduli space and
$\mathcal {M}$
is a fine moduli space and
 $\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat {L}$
, where
$\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat {L}$
, where
 $\hat {L}$
is a polarization of genus g. Furthermore, the universal bundle
$\hat {L}$
is a polarization of genus g. Furthermore, the universal bundle
 $\mathcal {E}$
on
$\mathcal {E}$
on
 $S\times \mathcal {M}$
induces a Fourier–Mukai equivalence
$S\times \mathcal {M}$
induces a Fourier–Mukai equivalence
 $\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})$
.
$\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})$
. -
2. If
 $g\equiv 1\pmod {4}$
, then
$g\equiv 1\pmod {4}$
, then
 $\mathcal {M}$
is a coarse moduli space and
$\mathcal {M}$
is a coarse moduli space and
 $\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat {L}$
, where
$\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat {L}$
, where
 $\hat {L}$
is a polarization of genus
$\hat {L}$
is a polarization of genus
 $\frac {g+3}{4}$
.
$\frac {g+3}{4}$
.
In the second case, there exists an open analytic cover
![]() $\{U_i\}_{i\in I}$
of
$\{U_i\}_{i\in I}$
of
![]() $\mathcal {M}$
so that there exists a local universal sheaf
$\mathcal {M}$
so that there exists a local universal sheaf
![]() $\mathcal {E}_i$
on each
$\mathcal {E}_i$
on each
![]() $S\times U_i$
. Furthermore, there is a (nontrivial) Brauer class
$S\times U_i$
. Furthermore, there is a (nontrivial) Brauer class
![]() $\alpha \in \mathrm {Br}(\mathcal {M})$
and isomorphisms
$\alpha \in \mathrm {Br}(\mathcal {M})$
and isomorphisms
![]() $\varphi _{ij}:\mathcal {E}_j|_{U_i\cap U_j}\to \mathcal {E}_i|_{U_i\cap U_j}$
making
$\varphi _{ij}:\mathcal {E}_j|_{U_i\cap U_j}\to \mathcal {E}_i|_{U_i\cap U_j}$
making
![]() $(\{\mathcal {E}_i\},\{\varphi _{ij}\})$
into an
$(\{\mathcal {E}_i\},\{\varphi _{ij}\})$
into an
![]() $\alpha $
-twisted sheaf
$\alpha $
-twisted sheaf
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $S\times \mathcal {M}$
. This was proved by Caldararu ([Reference CaldararuCal00]). In analogy to the classical (untwisted) case of fine moduli spaces, Caldararu also showed that
$S\times \mathcal {M}$
. This was proved by Caldararu ([Reference CaldararuCal00]). In analogy to the classical (untwisted) case of fine moduli spaces, Caldararu also showed that
![]() $\mathcal {E}$
is the kernel of a Fourier–Mukai equivalence
$\mathcal {E}$
is the kernel of a Fourier–Mukai equivalence
where
![]() $\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M},\alpha )$
is the bounded derived category of
$\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M},\alpha )$
is the bounded derived category of
![]() $\alpha $
-twisted coherent sheaves on
$\alpha $
-twisted coherent sheaves on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Write
![]() $g=4n-3$
. As proved independently by Sawon ([Reference SawonSaw07]) and Markushevich ([Reference MarkushevichMar06]), one can use
$g=4n-3$
. As proved independently by Sawon ([Reference SawonSaw07]) and Markushevich ([Reference MarkushevichMar06]), one can use
![]() $\Phi _{\mathcal {E}}$
to define an isomorphism
$\Phi _{\mathcal {E}}$
to define an isomorphism
for some
![]() $k\in \mathbb {Z}$
, where
$k\in \mathbb {Z}$
, where
![]() $\mathcal {M}((0,\hat {L},k),\alpha )$
denotes the moduli space of stable
$\mathcal {M}((0,\hat {L},k),\alpha )$
denotes the moduli space of stable
![]() $\alpha $
-twisted sheaves on
$\alpha $
-twisted sheaves on
![]() $\mathcal {M}$
with twisted Mukai vector
$\mathcal {M}$
with twisted Mukai vector
![]() $(0,\hat {L},k)$
(see [Reference Huybrechts and StellariHS05] for the construction of the twisted Mukai vector depending on a B-field lift of
$(0,\hat {L},k)$
(see [Reference Huybrechts and StellariHS05] for the construction of the twisted Mukai vector depending on a B-field lift of
![]() $\alpha $
, and [Reference YoshiokaYos06] for the construction of moduli spaces of stable twisted sheaves).
$\alpha $
, and [Reference YoshiokaYos06] for the construction of moduli spaces of stable twisted sheaves).
By composing the isomorphism above with the natural map
sending (
![]() $\alpha $
-twisted) sheaves to their support, one gets a Lagrangian fibration
$\alpha $
-twisted) sheaves to their support, one gets a Lagrangian fibration
![]() $\pi $
of
$\pi $
of
![]() $S^{[n]}$
.
$S^{[n]}$
.
Since Brauer classes on curves can be trivialized, any element in
![]() $\mathcal {M}((0,\hat {L},k),\alpha )$
can be identified with an untwisted sheaf; this identification is not canonical, and hence
$\mathcal {M}((0,\hat {L},k),\alpha )$
can be identified with an untwisted sheaf; this identification is not canonical, and hence
![]() $\mathcal {M}((0,\hat {L},k),\alpha )$
is not globally isomorphic to the Gieseker moduli space
$\mathcal {M}((0,\hat {L},k),\alpha )$
is not globally isomorphic to the Gieseker moduli space
![]() $\mathcal {M}(0,\hat {L},k)$
on
$\mathcal {M}(0,\hat {L},k)$
on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Nevertheless, by fixing a trivialization on any given curve
![]() $C\in |\hat {L}|=\mathbb {P}(H^0(\mathcal {M},\hat {L}))$
, it follows that the fiber
$C\in |\hat {L}|=\mathbb {P}(H^0(\mathcal {M},\hat {L}))$
, it follows that the fiber
![]() $\pi ^{-1}(C)$
is isomorphic to the compactified Jacobian
$\pi ^{-1}(C)$
is isomorphic to the compactified Jacobian
![]() $\overline {JC}$
parametrizing rank 1, torsion-free sheaves on C of degree 0.
$\overline {JC}$
parametrizing rank 1, torsion-free sheaves on C of degree 0.
We can use these results to control the cohomology
![]() $h^1(S,E\otimes \mathcal {I}_\xi )$
for
$h^1(S,E\otimes \mathcal {I}_\xi )$
for
![]() $E\in \mathcal {M}$
and
$E\in \mathcal {M}$
and
![]() $\xi \in S^{[n]}$
:
$\xi \in S^{[n]}$
:
Lemma 2.13. For the Lagrangian fibration
![]() $\pi :S^{[n]}\overset {\cong }{\longrightarrow }\mathcal {M}((0,\hat {L},k),\alpha )\longrightarrow \mathbb {P}^n=|\hat {L}|$
, we have:
$\pi :S^{[n]}\overset {\cong }{\longrightarrow }\mathcal {M}((0,\hat {L},k),\alpha )\longrightarrow \mathbb {P}^n=|\hat {L}|$
, we have:
-
(1)
 $\pi $
sends
$\pi $
sends
 $\xi \in S^{[n]}$
to the curve
$\xi \in S^{[n]}$
to the curve
 $C_\xi :=\{E\in \mathcal {M}\, | \, h^1(E\otimes \mathcal {I}_\xi )>0\}$
in the primitive linear system of
$C_\xi :=\{E\in \mathcal {M}\, | \, h^1(E\otimes \mathcal {I}_\xi )>0\}$
in the primitive linear system of
 $\mathcal {M}$
.
$\mathcal {M}$
. -
(2) Given
 $\xi \in S^{[n]}$
, let
$\xi \in S^{[n]}$
, let
 $L_\xi \in \overline {JC_\xi }$
denote the corresponding element under any identification
$L_\xi \in \overline {JC_\xi }$
denote the corresponding element under any identification
 $\pi ^{-1}(C_\xi )\cong \overline {JC_\xi }$
. Then for any
$\pi ^{-1}(C_\xi )\cong \overline {JC_\xi }$
. Then for any
 $E\in C_\xi $
, the number
$E\in C_\xi $
, the number
 $h^1(S,E\otimes \mathcal {I}_\xi )$
equals the minimal number of local generators of
$h^1(S,E\otimes \mathcal {I}_\xi )$
equals the minimal number of local generators of
 $L_\xi $
at the point E.
$L_\xi $
at the point E.In particular, if
 $\mathrm {mult}_{E}(C_\xi )= m$
, then
$\mathrm {mult}_{E}(C_\xi )= m$
, then
 $h^1(S, E\otimes \mathcal {I}_\xi )\leq m$
.
$h^1(S, E\otimes \mathcal {I}_\xi )\leq m$
.
Proof. Since
![]() $h^2(E\otimes \mathcal {I}_\xi )=0$
for every
$h^2(E\otimes \mathcal {I}_\xi )=0$
for every
![]() $E\in \mathcal {M}$
and
$E\in \mathcal {M}$
and
![]() $\xi \in S^{[n]}$
, we have an isomorphism
$\xi \in S^{[n]}$
, we have an isomorphism
by cohomology and base change (which is still valid in the twisted setting, since it is a local property). Only the last assertion is not an immediate consequence of this isomorphism.
To complete the proof, note that all elements of
![]() $\overline {JC_\xi }$
are ideal sheaves, up to twist by a line bundle (see, e.g., [Reference D’SouzaD’S79, Proposition 3.2]). Since the curve
$\overline {JC_\xi }$
are ideal sheaves, up to twist by a line bundle (see, e.g., [Reference D’SouzaD’S79, Proposition 3.2]). Since the curve
![]() $C_\xi $
is Gorenstein (it lies on a smooth surface), the minimal number of generators of an ideal sheaf at a point is bounded by the multiplicity of the curve at that point, which finishes the proof.
$C_\xi $
is Gorenstein (it lies on a smooth surface), the minimal number of generators of an ideal sheaf at a point is bounded by the multiplicity of the curve at that point, which finishes the proof.
3 Genus 7
Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus 7 (i.e.,
$K3$
surface of genus 7 (i.e.,
![]() $L^2=12$
). The goal of this section is to prove Theorem A.(1); hence, we will assume
$L^2=12$
). The goal of this section is to prove Theorem A.(1); hence, we will assume
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
throughout the rest of this section. The upper bound
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
throughout the rest of this section. The upper bound
![]() $\operatorname {\mathrm {irr}}_L(S)\leq 4$
was already obtained in [Reference MorettiMor23]; let us recall the construction of rational dominant maps
$\operatorname {\mathrm {irr}}_L(S)\leq 4$
was already obtained in [Reference MorettiMor23]; let us recall the construction of rational dominant maps ![]() of degree 4 given there.
of degree 4 given there.
We denote by
![]() $\mathcal {M}=\mathcal {M}(2,L,3)$
the fine moduli space of stable rank 2 bundles with
$\mathcal {M}=\mathcal {M}(2,L,3)$
the fine moduli space of stable rank 2 bundles with
![]() $c_1(E)=L$
and
$c_1(E)=L$
and
![]() $c_2(E)=5$
. Any
$c_2(E)=5$
. Any
![]() $E\in \mathcal {M}$
has
$E\in \mathcal {M}$
has
![]() $h^0(E)=5$
, hence
$h^0(E)=5$
, hence
![]() $h^0(E\otimes \mathcal {I}_p)\geq 3$
for any
$h^0(E\otimes \mathcal {I}_p)\geq 3$
for any
![]() $p\in S$
(an equality holds, actually). Then the three-dimensional subspace
$p\in S$
(an equality holds, actually). Then the three-dimensional subspace
![]() $V^\vee = H^0(E\otimes \mathcal {I}_p)\subset H^0(E)$
induces by duality an element
$V^\vee = H^0(E\otimes \mathcal {I}_p)\subset H^0(E)$
induces by duality an element
![]() $V\in \operatorname {\mathrm {Gr}}(3,H^0(L))$
such that
$V\in \operatorname {\mathrm {Gr}}(3,H^0(L))$
such that
![]() $\deg (\varphi _V)\leq 4$
(by Proposition 2.1).
$\deg (\varphi _V)\leq 4$
(by Proposition 2.1).
3.1 Discarding rational maps of degree 3
A sufficient condition for having a map ![]() of degree 3 is
of degree 3 is
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 2$
for some
$h^1(E\otimes \mathcal {I}_\xi )\geq 2$
for some
![]() $\xi \in S^{[2]}$
(i.e.,
$\xi \in S^{[2]}$
(i.e.,
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
). We will prove, by means of Bridgeland stability, that such a configuration is impossible.
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
). We will prove, by means of Bridgeland stability, that such a configuration is impossible.
Observe that
![]() $h^1(E\otimes \mathcal {I}_\xi )=\hom (\mathcal {I}_\xi , E^\vee [1])$
. Furthermore,
$h^1(E\otimes \mathcal {I}_\xi )=\hom (\mathcal {I}_\xi , E^\vee [1])$
. Furthermore,
![]() $\mathcal {I}_\xi \in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
$\mathcal {I}_\xi \in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
![]() $\beta <0$
(it is
$\beta <0$
(it is
![]() $\sigma _{\alpha ,\frac {-1}{2}}$
and
$\sigma _{\alpha ,\frac {-1}{2}}$
and
![]() $\sigma _{\alpha ,\frac {-1}{3}}$
-stable for every
$\sigma _{\alpha ,\frac {-1}{3}}$
-stable for every
![]() $\alpha $
by Lemma 2.11) and
$\alpha $
by Lemma 2.11) and
![]() $E^\vee [1]\in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
$E^\vee [1]\in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
![]() $\beta \geq \frac {-1}{2}$
(it is
$\beta \geq \frac {-1}{2}$
(it is
![]() $\sigma _{\alpha ,\beta }$
-stable for all
$\sigma _{\alpha ,\beta }$
-stable for all
![]() $\alpha $
as long as
$\alpha $
as long as
![]() $\beta =\frac {-1}{3},\frac {-2}{5},\frac {-3}{7}$
by Lemma 2.11).
$\beta =\frac {-1}{3},\frac {-2}{5},\frac {-3}{7}$
by Lemma 2.11).
The numerical wall
![]() $W=W(\mathcal {I}_\xi ,E^\vee [1])$
has equation
$W=W(\mathcal {I}_\xi ,E^\vee [1])$
has equation
![]() $6(\beta ^2+\alpha ^2)+5\beta +1=0$
. Since it intersects
$6(\beta ^2+\alpha ^2)+5\beta +1=0$
. Since it intersects
![]() $\alpha =0$
at the points with
$\alpha =0$
at the points with
![]() $\beta $
-coordinates
$\beta $
-coordinates
![]() $\frac {-1}{2}$
and
$\frac {-1}{2}$
and
![]() $\frac {-1}{3}$
, it is clear that both
$\frac {-1}{3}$
, it is clear that both
![]() $\mathcal {I}_\xi $
and
$\mathcal {I}_\xi $
and
![]() $E^\vee [1]$
are semistable along W.
$E^\vee [1]$
are semistable along W.
Now, observe that any nonzero morphism
![]() $\mathcal {I}_\xi \to E^\vee [1]$
defines a short exact sequence
$\mathcal {I}_\xi \to E^\vee [1]$
defines a short exact sequence
in
![]() $\operatorname {\mathrm {Coh}}^\beta (S)$
for all
$\operatorname {\mathrm {Coh}}^\beta (S)$
for all
![]() $\frac {-1}{2}\leq \beta <\frac {-1}{3}$
(indeed, such a morphism corresponds to a stable extension of sheaves
$\frac {-1}{2}\leq \beta <\frac {-1}{3}$
(indeed, such a morphism corresponds to a stable extension of sheaves
![]() $0\to E^\vee \to F\to \mathcal {I}_\xi \to 0$
with
$0\to E^\vee \to F\to \mathcal {I}_\xi \to 0$
with
![]() $\mu _L(F)=\frac {-1}{3}$
). Moreover, F is
$\mu _L(F)=\frac {-1}{3}$
). Moreover, F is
![]() $\sigma _{\alpha ,\beta }$
-stable for all
$\sigma _{\alpha ,\beta }$
-stable for all
![]() $\alpha $
as long as
$\alpha $
as long as
![]() $\beta =\frac {-1}{2},\frac {-2}{5},\frac {-3}{8}$
(again by Lemma 2.11). Since
$\beta =\frac {-1}{2},\frac {-2}{5},\frac {-3}{8}$
(again by Lemma 2.11). Since
![]() $\nu _{\alpha ,\beta }(\mathcal {I}_\xi )>\nu _{\alpha ,\beta }(E^\vee [1])$
for
$\nu _{\alpha ,\beta }(\mathcal {I}_\xi )>\nu _{\alpha ,\beta }(E^\vee [1])$
for
![]() $(\alpha ,\beta )$
inside W, it follows that
$(\alpha ,\beta )$
inside W, it follows that
![]() $\mathcal {I}_\xi $
gets destabilized along W.
$\mathcal {I}_\xi $
gets destabilized along W.
The situation can be visualized in Figure 1. Note that W crosses the hole in the
![]() $(\alpha ,\beta )$
-plane corresponding to the spherical bundle G of Mukai vector
$(\alpha ,\beta )$
-plane corresponding to the spherical bundle G of Mukai vector
![]() $v(G)=(5,-2L,5)$
. We will denote by
$v(G)=(5,-2L,5)$
. We will denote by
![]() $\sigma _0$
the Bridgeland stability condition
$\sigma _0$
the Bridgeland stability condition
![]() $W\cap \{\beta =\frac {-3}{7}\}$
.
$W\cap \{\beta =\frac {-3}{7}\}$
.

Figure 1 Wall W and hyperbolas of related objects.
Lemma 3.1. Let
![]() $F\in \mathcal {M}(3,-L,2)$
and
$F\in \mathcal {M}(3,-L,2)$
and
![]() $E\in \mathcal {M}$
. Then:
$E\in \mathcal {M}$
. Then:
-
(1) F is destabilized along
 $W\cap \{\beta <\frac {-2}{5}\}$
, and
$W\cap \{\beta <\frac {-2}{5}\}$
, and
 $E^\vee [1]$
is destabilized along
$E^\vee [1]$
is destabilized along
 $W\cap \{\beta>\frac {-2}{5}\}$
.
$W\cap \{\beta>\frac {-2}{5}\}$
. -
(2) There is an isomorphism
 $\varphi :\mathcal {M}\overset {\cong }{\longrightarrow }\mathcal {M}(3,-L,2)$
.
$\varphi :\mathcal {M}\overset {\cong }{\longrightarrow }\mathcal {M}(3,-L,2)$
.
Proof. Let
![]() $E\in \mathcal {M}$
. Note that
$E\in \mathcal {M}$
. Note that
![]() $G\in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
$G\in \operatorname {\mathrm {Coh}}^\beta (S)$
for all
![]() $\beta <\frac {-2}{5}$
, and it is
$\beta <\frac {-2}{5}$
, and it is
![]() $\sigma _{\alpha ,\beta }$
-stable for all
$\sigma _{\alpha ,\beta }$
-stable for all
![]() $\alpha $
if
$\alpha $
if
![]() $\beta =\frac {-1}{2},\frac {-3}{7}$
; in particular, G and
$\beta =\frac {-1}{2},\frac {-3}{7}$
; in particular, G and
![]() $E^\vee [1]$
are
$E^\vee [1]$
are
![]() $\sigma _0$
-stable of the same slope. It follows that
$\sigma _0$
-stable of the same slope. It follows that
![]() $\hom (E^\vee [1],G)=0=\hom (G,E^\vee [1])$
, which gives
$\hom (E^\vee [1],G)=0=\hom (G,E^\vee [1])$
, which gives
![]() $\operatorname {\mathrm {ext}}^1(E^\vee [1],G)=\langle v(E^\vee [1],v(G)\rangle =1$
.
$\operatorname {\mathrm {ext}}^1(E^\vee [1],G)=\langle v(E^\vee [1],v(G)\rangle =1$
.
Therefore, there is a (unique) nontrivial extension
and
![]() $\varphi (E)$
must be
$\varphi (E)$
must be
![]() $\sigma $
-semistable for
$\sigma $
-semistable for
![]() $\sigma \in \{\beta =\frac {-3}{7}\}$
above
$\sigma \in \{\beta =\frac {-3}{7}\}$
above
![]() $\sigma _0$
. Otherwise, for a
$\sigma _0$
. Otherwise, for a
![]() $\sigma $
-destabilizing subobject
$\sigma $
-destabilizing subobject
![]() $R\subset \varphi (E)$
the composition
$R\subset \varphi (E)$
the composition
![]() $R\hookrightarrow \varphi (E)\twoheadrightarrow E^\vee [1]$
would be nonzero (since G is
$R\hookrightarrow \varphi (E)\twoheadrightarrow E^\vee [1]$
would be nonzero (since G is
![]() $\sigma $
-stable), and
$\sigma $
-stable), and
![]() $\sigma _0$
-stability of
$\sigma _0$
-stability of
![]() $E^\vee [1]$
would force
$E^\vee [1]$
would force
![]() $R\cong E^\vee [1]$
, which splits the extension (3.1).
$R\cong E^\vee [1]$
, which splits the extension (3.1).
By
![]() $\sigma $
-stability of
$\sigma $
-stability of
![]() $\varphi (E)$
, it follows that
$\varphi (E)$
, it follows that
![]() $\varphi (E)\in \mathcal {M}(3,-L,2)$
, and since this construction can be carried out in familiesFootnote 2, the assignment
$\varphi (E)\in \mathcal {M}(3,-L,2)$
, and since this construction can be carried out in familiesFootnote 2, the assignment
![]() $\varphi $
is a morphism of schemes. Furthermore, the sequence (3.1) destabilizes
$\varphi $
is a morphism of schemes. Furthermore, the sequence (3.1) destabilizes
![]() $\varphi (E)$
along
$\varphi (E)$
along
![]() $W\cap \{\beta <\frac {-2}{5}\}$
: G and
$W\cap \{\beta <\frac {-2}{5}\}$
: G and
![]() $E^\vee [1]$
are the factor of the HN filtration of
$E^\vee [1]$
are the factor of the HN filtration of
![]() $\varphi (E)$
for stability conditions along
$\varphi (E)$
for stability conditions along
![]() $\beta =\frac {-3}{7}$
that are below
$\beta =\frac {-3}{7}$
that are below
![]() $\sigma _0$
.
$\sigma _0$
.
By rotating the distinguished triangle, we obtain a short exact sequence
in
![]() $\operatorname {\mathrm {Coh}}^\beta (S)$
(
$\operatorname {\mathrm {Coh}}^\beta (S)$
(
![]() $\frac {-2}{5}\leq \beta <\frac {-1}{3}$
), which destabilizes
$\frac {-2}{5}\leq \beta <\frac {-1}{3}$
), which destabilizes
![]() $E^\vee [1]$
along
$E^\vee [1]$
along
![]() $W\cap \{\beta>\frac {-2}{5}\}$
. The HN factors of
$W\cap \{\beta>\frac {-2}{5}\}$
. The HN factors of
![]() $E^\vee [1]$
for stability conditions just below
$E^\vee [1]$
for stability conditions just below
![]() $W\cap \{\beta =\frac {-3}{8}\}$
will be precisely
$W\cap \{\beta =\frac {-3}{8}\}$
will be precisely
![]() $\varphi (E)$
and
$\varphi (E)$
and
![]() $G[1]$
.
$G[1]$
.
On the other hand, starting with
![]() $F\in \mathcal {M}(3,-L,2)$
, one can construct an element
$F\in \mathcal {M}(3,-L,2)$
, one can construct an element
![]() $\psi (F)\in \mathcal {M}$
arising as the (unique) nontrivial extension
$\psi (F)\in \mathcal {M}$
arising as the (unique) nontrivial extension
(for the uniqueness of such an extension, we use again the stability of F and
![]() $G[1]$
along
$G[1]$
along
![]() $\beta =\frac {-3}{8}$
). By rotating the triangle, we can destabilize F along
$\beta =\frac {-3}{8}$
). By rotating the triangle, we can destabilize F along
![]() $W\cap \{\beta <\frac {-2}{5}\}$
.
$W\cap \{\beta <\frac {-2}{5}\}$
.
The morphisms
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are inverse to each other, as easily follows from the uniqueness of the HN filtrations of
$\psi $
are inverse to each other, as easily follows from the uniqueness of the HN filtrations of
![]() $E^\vee [1]$
,
$E^\vee [1]$
,
![]() $\varphi (E)$
, F and
$\varphi (E)$
, F and
![]() $\psi (F)^\vee [1]$
just below W. This concludes the proof.
$\psi (F)^\vee [1]$
just below W. This concludes the proof.
Now, we can prove the desired cohomological bound:
Proposition 3.2. For all
![]() $E\in \mathcal {M}$
and
$E\in \mathcal {M}$
and
![]() $\xi \in S^{[2]}$
, the inequality
$\xi \in S^{[2]}$
, the inequality
![]() $h^1(E\otimes \mathcal {I}_\xi )\leq 1$
holds.
$h^1(E\otimes \mathcal {I}_\xi )\leq 1$
holds.
Proof. Assume that
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 1$
, that is, there exists a short exact sequence
$h^1(E\otimes \mathcal {I}_\xi )\geq 1$
, that is, there exists a short exact sequence
destabilizing
![]() $\mathcal {I}_\xi $
along W (with
$\mathcal {I}_\xi $
along W (with
![]() $F\in \mathcal {M}(3,-L,2)$
). Consider the short exact sequence
$F\in \mathcal {M}(3,-L,2)$
). Consider the short exact sequence
destabilizing F along
![]() $W\cap \{\beta <\frac {-2}{5}\}$
, constructed in the proof of Lemma 3.1. Then the HN factors of
$W\cap \{\beta <\frac {-2}{5}\}$
, constructed in the proof of Lemma 3.1. Then the HN factors of
![]() $\mathcal {I}_\xi $
(for stability conditions just below
$\mathcal {I}_\xi $
(for stability conditions just below
![]() $\sigma _0$
) are G and T, where T is the extension of
$\sigma _0$
) are G and T, where T is the extension of
![]() $E^\vee [1]$
by
$E^\vee [1]$
by
![]() $\psi (F)^\vee [1]$
obtained as the image of
$\psi (F)^\vee [1]$
obtained as the image of
![]() $\mathcal {I}_\xi $
under the induced map
$\mathcal {I}_\xi $
under the induced map
If
![]() $E\neq \psi (F)$
, of course we have
$E\neq \psi (F)$
, of course we have
![]() $T=E^\vee [1]\oplus \psi (F)^\vee [1]$
; otherwise, T is a nontrivial extension. Indeed, if
$T=E^\vee [1]\oplus \psi (F)^\vee [1]$
; otherwise, T is a nontrivial extension. Indeed, if
![]() $E= \psi (F)$
, then the above map of Ext-groups is an isomorphism (as follows from the long exact sequence obtained by applying the functor
$E= \psi (F)$
, then the above map of Ext-groups is an isomorphism (as follows from the long exact sequence obtained by applying the functor
![]() $\operatorname {\mathrm {Hom}}(E^\vee [1],-)$
to the sequence (3.2)).
$\operatorname {\mathrm {Hom}}(E^\vee [1],-)$
to the sequence (3.2)).
In any case, since
![]() $\operatorname {\mathrm {Hom}}(G,E^\vee [1])=0$
(recall that G are
$\operatorname {\mathrm {Hom}}(G,E^\vee [1])=0$
(recall that G are
![]() $E^\vee [1]$
are
$E^\vee [1]$
are
![]() $\sigma _0$
-stable of the same slope), we obtain that
$\sigma _0$
-stable of the same slope), we obtain that
![]() $\hom (\mathcal {I}_\xi , E^\vee [1])=\hom (T,E^\vee [1])=1$
.
$\hom (\mathcal {I}_\xi , E^\vee [1])=\hom (T,E^\vee [1])=1$
.
Recall that the kernel bundle of any degree 3 map has
![]() $c_2=5$
(Corollary 2.3). Hence, the following lemma, together with Proposition 3.2, discards the existence of degree 3 maps and concludes the proof of the equality
$c_2=5$
(Corollary 2.3). Hence, the following lemma, together with Proposition 3.2, discards the existence of degree 3 maps and concludes the proof of the equality
![]() $\mathrm {irr}_L(S)=4$
:
$\mathrm {irr}_L(S)=4$
:
Lemma 3.3. Let
![]() $E \in \mathcal M$
. Then there exists no
$E \in \mathcal M$
. Then there exists no
![]() $V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
$V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p$
and
$\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p$
and
![]() $\bigcap _{s \in V^\vee }Z(s)=\{p\}$
(i.e., the intersection as zero cycles has degree
$\bigcap _{s \in V^\vee }Z(s)=\{p\}$
(i.e., the intersection as zero cycles has degree
![]() $2$
, whereas the schematic intersection of the zero loci of the sections is a reduced point).
$2$
, whereas the schematic intersection of the zero loci of the sections is a reduced point).
Proof. We argue by contradiction. Suppose that there exists
![]() $V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
$V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p$
and
$\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p$
and
![]() $\bigcap _{s \in V^\vee }Z(s)=\{p\}$
. According to Lemma 2.4, we can choose local coordinates and local generators
$\bigcap _{s \in V^\vee }Z(s)=\{p\}$
. According to Lemma 2.4, we can choose local coordinates and local generators
![]() $e_1,e_2$
of E at p, such that the subsheaf
$e_1,e_2$
of E at p, such that the subsheaf
![]() $E_1 \subset E$
defined by
$E_1 \subset E$
defined by
![]() ${E_1}|_{S\setminus p}=E|_{S\setminus p}$
and
${E_1}|_{S\setminus p}=E|_{S\setminus p}$
and
![]() $E_1=m_p e_1+m_p^2e_2$
in a neighborhood of p has
$E_1=m_p e_1+m_p^2e_2$
in a neighborhood of p has
![]() $V^\vee \subset H^0(E_1)$
, in particular we get
$V^\vee \subset H^0(E_1)$
, in particular we get
![]() $h^0(E_1)\ge 3$
. Since the quotient
$h^0(E_1)\ge 3$
. Since the quotient
![]() $E/E_1$
is a
$E/E_1$
is a
![]() $4$
-dimensional vector space, we get
$4$
-dimensional vector space, we get
![]() $\chi (E_1)=1$
and hence
$\chi (E_1)=1$
and hence
![]() $h^1(E_1)=2$
. Let us consider the double extension
$h^1(E_1)=2$
. Let us consider the double extension
It is easy to compute that
![]() $h^0(E_1 \otimes k(p))=5$
(
$h^0(E_1 \otimes k(p))=5$
(
![]() $E_1$
has
$E_1$
has
![]() $xe_1$
,
$xe_1$
,
![]() $ye_1$
,
$ye_1$
,
![]() $x^2e_2$
,
$x^2e_2$
,
![]() $xye_2$
,
$xye_2$
,
![]() $y^2e_2$
as local generators), hence F cannot be locally free at p. We get
$y^2e_2$
as local generators), hence F cannot be locally free at p. We get
![]() $c_2(F^{**})<c_2(F)=c_2(E_1)=9$
. It suffices to prove that
$c_2(F^{**})<c_2(F)=c_2(E_1)=9$
. It suffices to prove that
![]() $F^{**}$
must be stable since there exists no stable rank
$F^{**}$
must be stable since there exists no stable rank
![]() $4$
vector bundle with these invariants. To this end, consider the commutative diagram with exact rows
$4$
vector bundle with these invariants. To this end, consider the commutative diagram with exact rows

where
![]() $V^\vee \in \mathrm {Gr}(3,H^0(E_1))$
. The map
$V^\vee \in \mathrm {Gr}(3,H^0(E_1))$
. The map
![]() $W\to H^0(L)$
is injective; indeed,
$W\to H^0(L)$
is injective; indeed,
![]() $V \to H^0(L)$
is injective (by stability of E) and the extension defining F is nonsplit (none of the maps
$V \to H^0(L)$
is injective (by stability of E) and the extension defining F is nonsplit (none of the maps
![]() $\mathcal O_S\to F$
in the definition of F split). It follows that
$\mathcal O_S\to F$
in the definition of F split). It follows that
![]() $H^0(F^*)=0$
, which is enough to conclude the stability of the kernel bundle
$H^0(F^*)=0$
, which is enough to conclude the stability of the kernel bundle
![]() $F^*$
since
$F^*$
since
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
(if T is a vector bundle destabilizing
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
(if T is a vector bundle destabilizing
![]() $F^*$
, then T must be of the form
$F^*$
, then T must be of the form
![]() $\mathcal {O}_S^{\oplus \operatorname {\mathrm {rk}} T}$
since
$\mathcal {O}_S^{\oplus \operatorname {\mathrm {rk}} T}$
since
![]() $T\hookrightarrow W\otimes \mathcal {O}_S$
, contradiction).
$T\hookrightarrow W\otimes \mathcal {O}_S$
, contradiction).
3.2 Determining
 $W^2_4(S,L)$
$W^2_4(S,L)$
In the notations of Remark 2.5,
![]() $R_2$
is empty. Hence,
$R_2$
is empty. Hence,
![]() $\psi _1:S \times \mathcal {M} \cong \mathcal {G}_1\to W^2_4(S,L)_{5,1}$
is an isomorphism. The following lemma shows that this is the unique component of the Brill–Noether locus
$\psi _1:S \times \mathcal {M} \cong \mathcal {G}_1\to W^2_4(S,L)_{5,1}$
is an isomorphism. The following lemma shows that this is the unique component of the Brill–Noether locus
![]() $W^2_4(S,L)$
:
$W^2_4(S,L)$
:
Lemma 3.4. If
![]() $S \dashrightarrow \mathbb P^2$
is a rational map of degree
$S \dashrightarrow \mathbb P^2$
is a rational map of degree
![]() $4$
, then the kernel bundle E has
$4$
, then the kernel bundle E has
![]() $c_2(E)=5$
.
$c_2(E)=5$
.
Proof. By Corollary 2.3 the only other possibility is
![]() $c_2(E)=6$
and
$c_2(E)=6$
and
![]() $V^\vee \in \mathrm {Gr}(3,H^0(E))$
with
$V^\vee \in \mathrm {Gr}(3,H^0(E))$
with
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
of degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
of degree
![]() $2$
.
$2$
.
If
![]() $\bigcap _{s\in V^\vee }Z(s)$
is a reduced point, then by Lemma 2.4 in an appropriate trivialization of E near p all sections
$\bigcap _{s\in V^\vee }Z(s)$
is a reduced point, then by Lemma 2.4 in an appropriate trivialization of E near p all sections
![]() $s\in V^\vee $
are of the form
$s\in V^\vee $
are of the form
![]() $s=ae_1+be_2$
, with
$s=ae_1+be_2$
, with
![]() $a\in m_p\setminus m_p^2$
and
$a\in m_p\setminus m_p^2$
and
![]() $b\in m_p^2$
. Since
$b\in m_p^2$
. Since
![]() $V=\bigwedge ^2 V^\vee $
, it follows that the base ideal
$V=\bigwedge ^2 V^\vee $
, it follows that the base ideal
![]() $\mathcal {I}$
satisfies
$\mathcal {I}$
satisfies
![]() $\mathcal {I}\subset \mathcal {I}_p^3$
; therefore,
$\mathcal {I}\subset \mathcal {I}_p^3$
; therefore,
![]() $\mathrm {colength}(\mathcal {I})\geq 7$
(because
$\mathrm {colength}(\mathcal {I})\geq 7$
(because
![]() $\mathcal {I}$
is generated by three elements). This implies that
$\mathcal {I}$
is generated by three elements). This implies that
![]() $c_2(E)=L^2-\mathrm {colength}(\mathcal {I})\leq 5$
.
$c_2(E)=L^2-\mathrm {colength}(\mathcal {I})\leq 5$
.
Hence, if
![]() $c_2(E)=6$
, we must have
$c_2(E)=6$
, we must have
![]() $h^0(E \otimes \mathcal I_\xi )\ge 3$
for some
$h^0(E \otimes \mathcal I_\xi )\ge 3$
for some
![]() $\xi \in S^{[2]}$
. Consider now the subsheaf
$\xi \in S^{[2]}$
. Consider now the subsheaf
![]() $E_1 \subset E$
generated by
$E_1 \subset E$
generated by
![]() $E \otimes \mathcal I_\xi $
and
$E \otimes \mathcal I_\xi $
and
![]() $\mathrm {Im}(\mathcal O_S \otimes H^0(E) \to E)$
. The quotient
$\mathrm {Im}(\mathcal O_S \otimes H^0(E) \to E)$
. The quotient
![]() $E_1/E\otimes \mathcal I_\xi $
is of length at most
$E_1/E\otimes \mathcal I_\xi $
is of length at most
![]() $2$
, since it is a principal
$2$
, since it is a principal
![]() $\mathcal {O}_\xi $
-submodule in
$\mathcal {O}_\xi $
-submodule in
![]() $E/E \otimes \mathcal I_\xi $
(it is generated by a section in
$E/E \otimes \mathcal I_\xi $
(it is generated by a section in
![]() $H^0(E)\setminus H^0(E \otimes \mathcal I_\xi )$
). This implies
$H^0(E)\setminus H^0(E \otimes \mathcal I_\xi )$
). This implies
![]() $\chi (E_1)\leq \chi (E \otimes \mathcal I_\xi )+2=2$
, and since
$\chi (E_1)\leq \chi (E \otimes \mathcal I_\xi )+2=2$
, and since
![]() $h^0(E_1)=4$
, we obtain
$h^0(E_1)=4$
, we obtain
![]() $h^1(E_1)\ge 2$
. Now, the nontrivial extension
$h^1(E_1)\ge 2$
. Now, the nontrivial extension
gives a stable torsion free sheaf F with Mukai vector
![]() $v(F)=(h^1(E_1)+2,L,2)$
, which yields a contradiction if
$v(F)=(h^1(E_1)+2,L,2)$
, which yields a contradiction if
![]() $h^1(E_1)\geq 2$
.
$h^1(E_1)\geq 2$
.
3.3 An isomorphism of Hilbert schemes
Before we move to higher genera, let us use the framework provided by Bridgeland stability to establish an isomorphism
![]() $S^{[2]}\cong \mathcal {M}^{[2]}$
(already predicted by Yoshioka [Reference YoshiokaYos01]). The arguments here will be useful in genus 11.
$S^{[2]}\cong \mathcal {M}^{[2]}$
(already predicted by Yoshioka [Reference YoshiokaYos01]). The arguments here will be useful in genus 11.
Proposition 3.5. The Hilbert schemes
![]() $S^{[2]}$
and
$S^{[2]}$
and
![]() $\mathcal {M}^{[2]}$
are isomorphic.
$\mathcal {M}^{[2]}$
are isomorphic.
Proof. Let us define a morphism
![]() $\gamma :\mathcal {M}^{[2]}\longrightarrow S^{[2]}$
as follows.
$\gamma :\mathcal {M}^{[2]}\longrightarrow S^{[2]}$
as follows.
Given a reduced element of
![]() $\mathcal {M}^{[2]}$
, supported at two distinct
$\mathcal {M}^{[2]}$
, supported at two distinct
![]() $E_1,E_2\in \mathcal {M}$
, we consider the object M fitting into an extension
$E_1,E_2\in \mathcal {M}$
, we consider the object M fitting into an extension
such that the induced elements of
![]() $\operatorname {\mathrm {Ext}}^1(E_i^\vee [1],G)$
are nonzero. Due to the action of automorphisms of
$\operatorname {\mathrm {Ext}}^1(E_i^\vee [1],G)$
are nonzero. Due to the action of automorphisms of
![]() $E_1^\vee [1]\oplus E_2^\vee [1]$
, such an object M is unique up to isomorphism.
$E_1^\vee [1]\oplus E_2^\vee [1]$
, such an object M is unique up to isomorphism.
On the other hand, given a nonreduced element of
![]() $\mathcal {M}^{[2]}$
supported at
$\mathcal {M}^{[2]}$
supported at
![]() $E\in \mathcal {M}$
with tangent direction
$E\in \mathcal {M}$
with tangent direction
![]() $T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E,E))$
, we consider the corresponding
$T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E,E))$
, we consider the corresponding
![]() $\widetilde {T}:=T^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],E^\vee [1]))$
and take the object M fitting into
$\widetilde {T}:=T^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],E^\vee [1]))$
and take the object M fitting into
such that the induced extension in
![]() $\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
is nonzero. Again, such an object M is unique up to isomorphism (due to the action of automorphisms of
$\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
is nonzero. Again, such an object M is unique up to isomorphism (due to the action of automorphisms of
![]() $\widetilde {T}$
).
$\widetilde {T}$
).
Let us assume for a moment that, in both cases, the object M is of the form
![]() $M=\mathcal {I}_\xi $
for some
$M=\mathcal {I}_\xi $
for some
![]() $\xi \in S^{[2]}$
(we will prove it below). Then this rule defines the morphism
$\xi \in S^{[2]}$
(we will prove it below). Then this rule defines the morphism
![]() $\gamma $
, which is injective on closed points (indeed, given
$\gamma $
, which is injective on closed points (indeed, given
![]() $M=\mathcal {I}_\xi $
in the image of
$M=\mathcal {I}_\xi $
in the image of
![]() $\gamma $
, the corresponding element of
$\gamma $
, the corresponding element of
![]() $\mathcal {M}^{[2]}$
can be recovered from the last HN factor of M just below
$\mathcal {M}^{[2]}$
can be recovered from the last HN factor of M just below
![]() $\sigma _0$
). Therefore,
$\sigma _0$
). Therefore,
![]() $S^{[2]}$
equals the image of
$S^{[2]}$
equals the image of
![]() $\gamma $
(both
$\gamma $
(both
![]() $\mathcal {M}^{[2]}$
and
$\mathcal {M}^{[2]}$
and
![]() $S^{[2]}$
are projective of the same dimension). Since
$S^{[2]}$
are projective of the same dimension). Since
![]() $\gamma $
is bijective on closed points and
$\gamma $
is bijective on closed points and
![]() $S^{[2]}$
is normal, it follows that
$S^{[2]}$
is normal, it follows that
![]() $\gamma $
is an isomorphism.
$\gamma $
is an isomorphism.
Hence, it only remains to prove that the objects M constructed above are of the form
![]() $M=\mathcal {I}_\xi $
,
$M=\mathcal {I}_\xi $
,
![]() $\xi \in S^{[2]}$
. Since there are no walls above W for the Mukai vector
$\xi \in S^{[2]}$
. Since there are no walls above W for the Mukai vector
![]() $(1,0,-1)$
, it suffices to check that M is
$(1,0,-1)$
, it suffices to check that M is
![]() $\sigma '$
-semistable for some stability condition
$\sigma '$
-semistable for some stability condition
![]() $\sigma '$
above W. We will assume that M comes from a nonreduced element of
$\sigma '$
above W. We will assume that M comes from a nonreduced element of
![]() $\mathcal {M}^{[2]}$
(the reduced case being similar but simpler).
$\mathcal {M}^{[2]}$
(the reduced case being similar but simpler).
Let
![]() $\sigma '$
be close enough to
$\sigma '$
be close enough to
![]() $\sigma _0$
(above W), and assume that M is not
$\sigma _0$
(above W), and assume that M is not
![]() $\sigma '$
-semistable. Since M is
$\sigma '$
-semistable. Since M is
![]() $\sigma _0$
-semistable, any destabilizing subobject
$\sigma _0$
-semistable, any destabilizing subobject
![]() $A\subset M$
is
$A\subset M$
is
![]() $\sigma _0$
-semistable of the same slope as M.
$\sigma _0$
-semistable of the same slope as M.
The composition
![]() $G\hookrightarrow M\twoheadrightarrow M/A$
is either zero or injective since G is
$G\hookrightarrow M\twoheadrightarrow M/A$
is either zero or injective since G is
![]() $\sigma _0$
-stable of the same slope as
$\sigma _0$
-stable of the same slope as
![]() $M/A$
. In the first case, we have
$M/A$
. In the first case, we have
![]() $G\hookrightarrow A$
and hence
$G\hookrightarrow A$
and hence
![]() $A/G\hookrightarrow \widetilde {T}$
. Consider the composition
$A/G\hookrightarrow \widetilde {T}$
. Consider the composition
![]() $A/G\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
. By
$A/G\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
. By
![]() $\sigma _0$
-stability of
$\sigma _0$
-stability of
![]() $E^\vee [1]$
, this morphism is either zero or surjective. If
$E^\vee [1]$
, this morphism is either zero or surjective. If
![]() $A/G\to E^\vee [1]$
is zero then either
$A/G\to E^\vee [1]$
is zero then either
![]() $A/G=0$
or
$A/G=0$
or
![]() $A/G\cong E^\vee [1]=\ker (\widetilde {T}\twoheadrightarrow E^\vee [1])$
(hence
$A/G\cong E^\vee [1]=\ker (\widetilde {T}\twoheadrightarrow E^\vee [1])$
(hence
![]() $\nu _{\sigma '}(A)<\nu _{\sigma '}(M)$
, contradiction); whereas if
$\nu _{\sigma '}(A)<\nu _{\sigma '}(M)$
, contradiction); whereas if
![]() $A/G\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
is surjective, then either
$A/G\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
is surjective, then either
![]() $A/G=\widetilde {T}$
(i.e.,
$A/G=\widetilde {T}$
(i.e.,
![]() $A=M$
, contradiction) or the extension
$A=M$
, contradiction) or the extension
![]() $0\to E^\vee [1]\to \widetilde {T}\to E^\vee [1]\to 0$
splits.
$0\to E^\vee [1]\to \widetilde {T}\to E^\vee [1]\to 0$
splits.
On the other hand, if
![]() $G\hookrightarrow M/A$
is injective, one easily checks that
$G\hookrightarrow M/A$
is injective, one easily checks that
![]() $A\hookrightarrow \widetilde {T}$
. Now, we consider the composition
$A\hookrightarrow \widetilde {T}$
. Now, we consider the composition
![]() $A\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
, which again will be either zero or surjective. If it is surjective, then either
$A\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
, which again will be either zero or surjective. If it is surjective, then either
![]() $A\cong \widetilde {T}$
(which splits
$A\cong \widetilde {T}$
(which splits
![]() $0\to G\to M\to \widetilde {T}\to 0$
) or
$0\to G\to M\to \widetilde {T}\to 0$
) or
![]() $A\cong E^\vee [1]$
(which splits
$A\cong E^\vee [1]$
(which splits
![]() $0\to E^\vee [1]\to \widetilde {T}\to E^\vee [1]\to 0$
). If
$0\to E^\vee [1]\to \widetilde {T}\to E^\vee [1]\to 0$
). If
![]() $A\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
is zero, then
$A\hookrightarrow \widetilde {T}\twoheadrightarrow E^\vee [1]$
is zero, then
![]() $A\cong E^\vee [1]=\ker (\widetilde {T}\twoheadrightarrow E^\vee [1])$
and the induced element in
$A\cong E^\vee [1]=\ker (\widetilde {T}\twoheadrightarrow E^\vee [1])$
and the induced element in
![]() $\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
is zero, which gives again a contradiction.
$\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
is zero, which gives again a contradiction.
Remark 3.6. Let
![]() $\mathcal {E}$
denote the universal vector bundle on
$\mathcal {E}$
denote the universal vector bundle on
![]() $S\times \mathcal {M}$
, and
$S\times \mathcal {M}$
, and
![]() $\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
the corresponding Fourier–Mukai equivalence. The isomorphism
$\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
the corresponding Fourier–Mukai equivalence. The isomorphism
![]() $\gamma $
in Proposition 3.5 sends
$\gamma $
in Proposition 3.5 sends
![]() $T\in \mathcal {M}^{[2]}$
to the subscheme
$T\in \mathcal {M}^{[2]}$
to the subscheme
![]() $\gamma (T)\in S^{[2]}$
whose ideal sheaf sits in a distinguished triangle
$\gamma (T)\in S^{[2]}$
whose ideal sheaf sits in a distinguished triangle
![]() $0\to G\to \mathcal {I}_{\gamma (T)}\to \Phi _{\mathcal {E}}(\mathcal {O}_T)^\vee [1]\to 0$
.
$0\to G\to \mathcal {I}_{\gamma (T)}\to \Phi _{\mathcal {E}}(\mathcal {O}_T)^\vee [1]\to 0$
.
4 Genus 9
Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus 9 (i.e.,
$K3$
surface of genus 9 (i.e.,
![]() $L^2=16$
) with
$L^2=16$
) with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. Throughout this section,
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. Throughout this section,
![]() $\mathcal {M}$
will denote the Gieseker moduli space
$\mathcal {M}$
will denote the Gieseker moduli space
![]() $\mathcal {M}(2,L,4)$
.
$\mathcal {M}(2,L,4)$
.
We have
![]() $\operatorname {\mathrm {irr}}_L(S)\leq 5$
, as proved in [Reference MorettiMor23] by considering vector bundles
$\operatorname {\mathrm {irr}}_L(S)\leq 5$
, as proved in [Reference MorettiMor23] by considering vector bundles
![]() $E\in \mathcal {M}$
. Indeed,
$E\in \mathcal {M}$
. Indeed,
![]() $h^0(E\otimes \mathcal {I}_p)=4$
for every
$h^0(E\otimes \mathcal {I}_p)=4$
for every
![]() $p\in S$
and, since
$p\in S$
and, since
![]() $c_2(E)=6$
, any three-dimensional vector space
$c_2(E)=6$
, any three-dimensional vector space
![]() $V^\vee \subset H^0(E\otimes \mathcal {I}_p)$
produces a map
$V^\vee \subset H^0(E\otimes \mathcal {I}_p)$
produces a map ![]() of degree
of degree
![]() $\leq 5$
.
$\leq 5$
.
4.1 Constructing maps of degree 4 (I)
We start by constructing maps of degree 4, by considering pairs
![]() $(E,\xi )\in \mathcal {M}\times S^{[2]}$
such that
$(E,\xi )\in \mathcal {M}\times S^{[2]}$
such that
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 1$
(i.e.,
$h^1(E\otimes \mathcal {I}_\xi )\geq 1$
(i.e.,
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
).
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
).
To this end, we consider the numerical wall W in the
![]() $(\alpha ,\beta )$
-plane defined by the Mukai vectors
$(\alpha ,\beta )$
-plane defined by the Mukai vectors
![]() $(-2,L,-4)$
and
$(-2,L,-4)$
and
![]() $(1,0,-1)$
. This wall intersects
$(1,0,-1)$
. This wall intersects
![]() $\alpha =0$
at the points with
$\alpha =0$
at the points with
![]() $\beta $
-coordinates
$\beta $
-coordinates
![]() $\frac {-1}{2}$
and
$\frac {-1}{2}$
and
![]() $\frac {-1}{4}$
; in particular, for every
$\frac {-1}{4}$
; in particular, for every
![]() $\xi \in S^{[2]}$
the ideal sheaf
$\xi \in S^{[2]}$
the ideal sheaf
![]() $\mathcal {I}_\xi $
is semistable along W, as an immediate application of Lemma 2.11. Furthermore, W crosses the hole in the
$\mathcal {I}_\xi $
is semistable along W, as an immediate application of Lemma 2.11. Furthermore, W crosses the hole in the
![]() $(\alpha ,\beta )$
-plane corresponding to the spherical bundle F with Mukai vector
$(\alpha ,\beta )$
-plane corresponding to the spherical bundle F with Mukai vector
![]() $v(F)=(3,-L,3)$
. Then:
$v(F)=(3,-L,3)$
. Then:
-
1. If
 $(E,\xi )\in \mathcal {M}\times S^{[2]}$
satisfies
$(E,\xi )\in \mathcal {M}\times S^{[2]}$
satisfies
 $\hom (\mathcal {I}_\xi , E^\vee [1])=h^1(E\otimes \mathcal {I}_\xi )\geq 1$
, then any nonzero map
$\hom (\mathcal {I}_\xi , E^\vee [1])=h^1(E\otimes \mathcal {I}_\xi )\geq 1$
, then any nonzero map
 $\mathcal {I}_\xi \to E^\vee [1]$
defines a destabilizing short exact sequence for
$\mathcal {I}_\xi \to E^\vee [1]$
defines a destabilizing short exact sequence for $$\begin{align*}0\to F\to \mathcal{I}_\xi \to E^\vee[1]\to 0 \end{align*}$$
$$\begin{align*}0\to F\to \mathcal{I}_\xi \to E^\vee[1]\to 0 \end{align*}$$
 $\mathcal {I}_\xi $
along
$\mathcal {I}_\xi $
along
 $W\cap \{\beta <\frac {-1}{3}\}$
. Moreover, since both F and
$W\cap \{\beta <\frac {-1}{3}\}$
. Moreover, since both F and
 $E^\vee [1]$
are
$E^\vee [1]$
are
 $\sigma _0$
-stable for
$\sigma _0$
-stable for
 $\sigma _0=W\cap \{\beta =\frac {-2}{5}\}$
(this follows again from Lemma 2.11), the short exact sequence above is the HN filtration of
$\sigma _0=W\cap \{\beta =\frac {-2}{5}\}$
(this follows again from Lemma 2.11), the short exact sequence above is the HN filtration of
 $\mathcal {I}_\xi $
just below
$\mathcal {I}_\xi $
just below
 $\sigma _0$
. In particular, the morphism
$\sigma _0$
. In particular, the morphism
 $\mathcal {I}_\xi \to E^\vee [1]$
is unique (up to constant).
$\mathcal {I}_\xi \to E^\vee [1]$
is unique (up to constant).
-
2. Conversely, it is easy to check that any nontrivial extension
 $0\to F\to G\to E^\vee [1]\to 0$
of
$0\to F\to G\to E^\vee [1]\to 0$
of
 $E^\vee [1]$
by F must be semistable above W. Therefore,
$E^\vee [1]$
by F must be semistable above W. Therefore,
 $G=\mathcal {I}_\xi $
for some
$G=\mathcal {I}_\xi $
for some
 $\xi \in S^{[2]}$
, since there are no actual walls for the Mukai vector
$\xi \in S^{[2]}$
, since there are no actual walls for the Mukai vector
 $(1,0,-1)$
above W.
$(1,0,-1)$
above W.According to the vanishings
 $\hom (F,E^\vee [1])=0=\hom (E^\vee [1],F)$
(recall that F and
$\hom (F,E^\vee [1])=0=\hom (E^\vee [1],F)$
(recall that F and
 $E^\vee [1]$
are
$E^\vee [1]$
are
 $\sigma _0$
-stable of the same slope), we have
$\sigma _0$
-stable of the same slope), we have  $$\begin{align*}\operatorname{\mathrm{ext}}^1(E^\vee[1],F)=\langle v(E^\vee[1]),v(F)\rangle = 2. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ext}}^1(E^\vee[1],F)=\langle v(E^\vee[1]),v(F)\rangle = 2. \end{align*}$$
In other words, for a fixed E the isomorphism classes of such nontrivial extensions are parametrized by a
 $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
We can summarize this discussion as follows:
Proposition 4.1. The locus
![]() $R_2=\{(E,\xi )\in \mathcal {M}\times S^{[2]}\;|\;h^1(E\otimes \mathcal {I}_\xi )\geq 1\}$
is a
$R_2=\{(E,\xi )\in \mathcal {M}\times S^{[2]}\;|\;h^1(E\otimes \mathcal {I}_\xi )\geq 1\}$
is a
![]() $\mathbb {P}^1$
-bundle over
$\mathbb {P}^1$
-bundle over
![]() $\mathcal {M}$
, with a closed immersion
$\mathcal {M}$
, with a closed immersion
![]() $R_2\hookrightarrow S^{[2]}$
defined by the second projection.
$R_2\hookrightarrow S^{[2]}$
defined by the second projection.
Let us also remark the following consequence of the above discussion:
Lemma 4.2. Let F be the spherical vector bundle with Mukai vector
![]() $v(F)=(3,-L,3)$
. Then for any
$v(F)=(3,-L,3)$
. Then for any
![]() $\xi \in S^{[2]}$
, we have
$\xi \in S^{[2]}$
, we have
![]() $\hom (F, \mathcal {I}_\xi )\le 1.$
$\hom (F, \mathcal {I}_\xi )\le 1.$
Proof. This follows from the uniqueness of the HN filtration of
![]() $\mathcal {I}_\xi $
just below
$\mathcal {I}_\xi $
just below
![]() $\sigma _0$
.
$\sigma _0$
.
4.2 Discarding degree
 $3$
maps
$3$
maps
According to Proposition 2.1 and Corollary 2.3, a map ![]() of degree 3 is equivalent to a pair
of degree 3 is equivalent to a pair
![]() $(E,V^\vee )$
with
$(E,V^\vee )$
with
![]() $E\in \mathcal {M}$
(i.e.,
$E\in \mathcal {M}$
(i.e.,
![]() $c_2(E)=6$
,
$c_2(E)=6$
,
![]() $h^0(E)=6$
) and
$h^0(E)=6$
) and
![]() $\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=3$
. The base ideal
$\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=3$
. The base ideal
![]() $\mathcal {I}$
of such a map has
$\mathcal {I}$
of such a map has
Recall that
![]() $\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat L$
, where
$\operatorname {\mathrm {Pic}}(\mathcal {M})=\mathbb {Z}\cdot \hat L$
, where
![]() $\hat L$
is a degree
$\hat L$
is a degree
![]() $4$
polarization.
$4$
polarization.
Lemma 4.3. There is an isomorphism
 $$ \begin{align*} R_3 & =\{ (E,\xi)\in \mathcal{M}\times S^{[3]}\;|\; h^1(E\otimes \mathcal{I}_\xi)\ge 3\} \\&\cong \{ (C,E,A) \;|\; C\in |\hat L|,E\in C, A\in \overline {JC}\text{ with }h^0(C,A\otimes k(E))\geq3\}. \end{align*} $$
$$ \begin{align*} R_3 & =\{ (E,\xi)\in \mathcal{M}\times S^{[3]}\;|\; h^1(E\otimes \mathcal{I}_\xi)\ge 3\} \\&\cong \{ (C,E,A) \;|\; C\in |\hat L|,E\in C, A\in \overline {JC}\text{ with }h^0(C,A\otimes k(E))\geq3\}. \end{align*} $$
In particular, if
![]() $(S,L)$
is very general among
$(S,L)$
is very general among
![]() $K3$
surfaces of genus
$K3$
surfaces of genus
![]() $9$
, we have
$9$
, we have
![]() $h^1(E\otimes \mathcal {I}_\xi )\le 2$
for every
$h^1(E\otimes \mathcal {I}_\xi )\le 2$
for every
![]() $(E,\xi )\in \mathcal {M}\times S^{[3]}$
.
$(E,\xi )\in \mathcal {M}\times S^{[3]}$
.
Proof. The isomorphism is just a reformulation of Lemma 2.13. For the second part, observe that the nonemptiness of
![]() $R_3$
implies that some plane quartic of the linear system
$R_3$
implies that some plane quartic of the linear system
![]() $|\hat {L}|$
has a triple point, hence it is rational. If
$|\hat {L}|$
has a triple point, hence it is rational. If
![]() $(S,L)$
is very general, then
$(S,L)$
is very general, then
![]() $(\mathcal {M},\hat L)$
must be very general among quartic surfaces; but in that case a theorem of Chen [Reference ChenChe02] ensures that all the rational curves in the linear system
$(\mathcal {M},\hat L)$
must be very general among quartic surfaces; but in that case a theorem of Chen [Reference ChenChe02] ensures that all the rational curves in the linear system
![]() $|\hat {L}|$
must be nodal, which gives a contradiction.
$|\hat {L}|$
must be nodal, which gives a contradiction.
Remark 4.4. On the other hand, if
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
and there is a curve with a triple point in
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
and there is a curve with a triple point in
![]() $|\hat L|$
, then the above discussion immediately yields
$|\hat L|$
, then the above discussion immediately yields
![]() $W^2_3(S,L)\neq \emptyset $
. It would be interesting to know whether such
$W^2_3(S,L)\neq \emptyset $
. It would be interesting to know whether such
![]() $K3$
surfaces may exist.
$K3$
surfaces may exist.
We are left to rule out the situation where the schematic intersection
![]() $\xi :=\bigcap _{s\in V^\vee }Z(s) $
is of length
$\xi :=\bigcap _{s\in V^\vee }Z(s) $
is of length
![]() $\le 2$
and
$\le 2$
and
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
![]() $3$
. First let us slightly simplify the situation:
$3$
. First let us slightly simplify the situation:
Lemma 4.5. Under these assumptions,
![]() $\xi $
is of length
$\xi $
is of length
![]() $2$
and reduced.
$2$
and reduced.
Proof. If
![]() $\xi $
is a reduced point p, then by Lemma 2.4 we have
$\xi $
is a reduced point p, then by Lemma 2.4 we have
![]() $s_p\in m_p\cdot e_1+m_p^3\cdot e_2$
for the local equations of
$s_p\in m_p\cdot e_1+m_p^3\cdot e_2$
for the local equations of
![]() $s\in V^\vee $
in an appropriate trivialization
$s\in V^\vee $
in an appropriate trivialization
![]() $E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
. In view of the isomorphism
$E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
. In view of the isomorphism
![]() $V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
$V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
![]() $\mathcal {I}$
satisfies
$\mathcal {I}$
satisfies
![]() $\mathcal {I}\otimes \mathcal {O}_{S,p}\subset m_p^4$
locally at p; this implies that the degree of the map is
$\mathcal {I}\otimes \mathcal {O}_{S,p}\subset m_p^4$
locally at p; this implies that the degree of the map is
![]() $\leq L^2-16=0$
, contradiction.
$\leq L^2-16=0$
, contradiction.
Now, assume that
![]() $\xi $
is not reduced, locally of the form
$\xi $
is not reduced, locally of the form
![]() $(x,y^2)$
at
$(x,y^2)$
at
![]() $p=\mathrm {Supp}(\xi )$
. In that case, by Lemma 2.4 we have
$p=\mathrm {Supp}(\xi )$
. In that case, by Lemma 2.4 we have
![]() $s_p\in (x,y^2)\cdot e_1+(x^2,xy,y^{3})\cdot e_2$
for all
$s_p\in (x,y^2)\cdot e_1+(x^2,xy,y^{3})\cdot e_2$
for all
![]() $s\in V^\vee $
in an appropriate trivialization
$s\in V^\vee $
in an appropriate trivialization
![]() $E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p. By the isomorphism
$E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p. By the isomorphism
![]() $V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
$V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
![]() $\mathcal {I}$
satisfies
$\mathcal {I}$
satisfies
![]() $\mathcal {I}\otimes \hat {\mathcal {O}}_{S,p}\subset (x^3,x^2y, xy^{3},y^{5})$
locally at p. Furthermore, since
$\mathcal {I}\otimes \hat {\mathcal {O}}_{S,p}\subset (x^3,x^2y, xy^{3},y^{5})$
locally at p. Furthermore, since
![]() $\mathcal {I}$
has at most three local generators at p, we obtain
$\mathcal {I}$
has at most three local generators at p, we obtain
![]() $\mathrm {colength}(\mathcal {I})\ge 11$
, contradiction.
$\mathrm {colength}(\mathcal {I})\ge 11$
, contradiction.
We are now ready to prove:
Corollary 4.6. If
![]() $(S,L)$
is a very general polarized
$(S,L)$
is a very general polarized
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $9$
, then
$9$
, then
![]() $\mathrm {irr}_L(S)= 4$
.
$\mathrm {irr}_L(S)= 4$
.
Proof. In view of Lemma 4.3 and Lemma 4.5, the only possibility for a degree 3 map is that
![]() $\bigcap _{s\in V^\vee } Z(s)$
is reduced, consisting of two distinct points
$\bigcap _{s\in V^\vee } Z(s)$
is reduced, consisting of two distinct points
![]() $p,q$
, and
$p,q$
, and
![]() $\bigcap _{s\in V^\vee } Z_{cycle}(s)=2p+q$
. A new application of Lemma 2.4 yields
$\bigcap _{s\in V^\vee } Z_{cycle}(s)=2p+q$
. A new application of Lemma 2.4 yields
![]() $V\cong \bigwedge ^2 V^\vee \subset H^0(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2)$
. We deduce
$V\cong \bigwedge ^2 V^\vee \subset H^0(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2)$
. We deduce
![]() $h^1(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2)=2$
, hence we may consider the stable extension
$h^1(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2)=2$
, hence we may consider the stable extension
It is easy to see that G is not locally free at p (G has rank 3, whereas
![]() $L \otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2$
has four local generators). Hence,
$L \otimes \mathcal {I}_p^3\otimes \mathcal {I}_q^2$
has four local generators). Hence,
![]() $G\subset G^{**}$
is a nontrivial subsheaf, in particular
$G\subset G^{**}$
is a nontrivial subsheaf, in particular
![]() $c_2(G^{**})<c_2(G)=9$
, whereas on the other hand we have
$c_2(G^{**})<c_2(G)=9$
, whereas on the other hand we have
![]() $c_2(G^{**})\ge 8$
since
$c_2(G^{**})\ge 8$
since
![]() $G^{**}$
is stable (stability follows from the fact that
$G^{**}$
is stable (stability follows from the fact that
![]() $G^*$
is a kernel bundle, with a proof similar to the stability of
$G^*$
is a kernel bundle, with a proof similar to the stability of
![]() $F^*$
in the proof of Lemma 3.3). This forces
$F^*$
in the proof of Lemma 3.3). This forces
![]() $G^{**}$
to be the spherical vector bundle with
$G^{**}$
to be the spherical vector bundle with
![]() $v(G^{**})=(3,L,3)$
.
$v(G^{**})=(3,L,3)$
.
Moreover,
![]() $G^{**}$
fits in a commutative diagram with exact rows and columns
$G^{**}$
fits in a commutative diagram with exact rows and columns

where
![]() $\mathcal J$
is an ideal of colength
$\mathcal J$
is an ideal of colength
![]() $8$
such that
$8$
such that
![]() $\mathcal J/\mathcal I_p^3\otimes \mathcal I_q^2\cong k(p)$
, hence it must have
$\mathcal J/\mathcal I_p^3\otimes \mathcal I_q^2\cong k(p)$
, hence it must have
![]() $3$
local generators at both p and q. This implies that the map
$3$
local generators at both p and q. This implies that the map
![]() $\mathcal O_S^{\oplus 2}\to G^{**}$
vanishes at p and q, hence
$\mathcal O_S^{\oplus 2}\to G^{**}$
vanishes at p and q, hence
![]() $h^0(G^{**}\otimes \mathcal I_{p,q})\ge 2$
which is a contradiction to Lemma 4.2. The proof is complete.
$h^0(G^{**}\otimes \mathcal I_{p,q})\ge 2$
which is a contradiction to Lemma 4.2. The proof is complete.
4.3 Constructing maps of degree 4 (II)
Here, we are going to present another construction of degree
![]() $4$
maps, eventually leading to an irreducible component of
$4$
maps, eventually leading to an irreducible component of
![]() $W^2_4(S,L)$
which is different from the
$W^2_4(S,L)$
which is different from the
![]() $\mathbb {P}^1$
-bundle
$\mathbb {P}^1$
-bundle
![]() $R_2$
over
$R_2$
over
![]() $\mathcal {M}$
that we described in subsection 4.1.
$\mathcal {M}$
that we described in subsection 4.1.
The idea is the following: given a nonreduced
![]() $\xi \in S^{[2]}$
(supported at
$\xi \in S^{[2]}$
(supported at
![]() $p\in S$
) and
$p\in S$
) and
![]() $E\in \mathcal {M}$
such that
$E\in \mathcal {M}$
such that
![]() $h^1(E\otimes \mathcal {I}_\xi )=1$
, we want to find suitable local generators
$h^1(E\otimes \mathcal {I}_\xi )=1$
, we want to find suitable local generators
![]() $e_1,e_2$
of E around p such that the subsheaf
$e_1,e_2$
of E around p such that the subsheaf
![]() $\tilde {E}\subset E$
locally defined as
$\tilde {E}\subset E$
locally defined as
![]() $m_pe_1+m_p^2e_2$
(and coinciding with E elsewhere) has
$m_pe_1+m_p^2e_2$
(and coinciding with E elsewhere) has
![]() $3$
global sections. One would expect the base locus of
$3$
global sections. One would expect the base locus of
![]() $\bigwedge ^2 H^0(E\otimes \mathcal {I}_\xi )$
to be
$\bigwedge ^2 H^0(E\otimes \mathcal {I}_\xi )$
to be
![]() $\mathcal {I}_\xi ^2$
at p, whereas the base locus of
$\mathcal {I}_\xi ^2$
at p, whereas the base locus of
![]() $\bigwedge ^2 H^0(\tilde {E})$
is locally contained in
$\bigwedge ^2 H^0(\tilde {E})$
is locally contained in
![]() $m_p^3$
. Hence, the two constructions should produce different rational maps, as we will indeed check.
$m_p^3$
. Hence, the two constructions should produce different rational maps, as we will indeed check.
Let us denote by
![]() $\pi _{\mathcal {M}}:\mathcal {M}\times S^{[2]}\to \mathcal {M}$
the canonical projection, by
$\pi _{\mathcal {M}}:\mathcal {M}\times S^{[2]}\to \mathcal {M}$
the canonical projection, by
![]() $S^{[2]}_{nred}\subset S^{[2]}$
the divisor of nonreduced subschemes and by
$S^{[2]}_{nred}\subset S^{[2]}$
the divisor of nonreduced subschemes and by
![]() $\pi _S:\mathcal {M}\times S^{[2]}_{nred}\to S$
the map sending a nonreduced subscheme to its support. Finally, for any
$\pi _S:\mathcal {M}\times S^{[2]}_{nred}\to S$
the map sending a nonreduced subscheme to its support. Finally, for any
![]() $E \in \mathcal {M}$
let us denote by
$E \in \mathcal {M}$
let us denote by
![]() $\mathbb P^1_E$
the immersion
$\mathbb P^1_E$
the immersion
![]() $\mathbb P^1_E=\mathbb P\left (\mathrm {Ext}^1(E^\vee [1],F)\right ) \hookrightarrow S^{[2]}$
(recall Proposition 4.1).
$\mathbb P^1_E=\mathbb P\left (\mathrm {Ext}^1(E^\vee [1],F)\right ) \hookrightarrow S^{[2]}$
(recall Proposition 4.1).
We need a preliminary lemma on the divisor
constructed in Proposition 4.1.
Lemma 4.7. The intersection
of
![]() $R_2$
with the divisor
$R_2$
with the divisor
![]() $S^{[2]}_{nred}$
of nonreduced subschemes is two-dimensional (and not empty). Furthermore, there is an irreducible component
$S^{[2]}_{nred}$
of nonreduced subschemes is two-dimensional (and not empty). Furthermore, there is an irreducible component
![]() $W_S\subset R_2\cap S^{[2]}_{nred}$
such that the two projections
$W_S\subset R_2\cap S^{[2]}_{nred}$
such that the two projections
![]() $\pi _{\mathcal {M}}:W_S\to \mathcal {M}$
and
$\pi _{\mathcal {M}}:W_S\to \mathcal {M}$
and
![]() $\pi _S:W_S\to S$
are surjective.
$\pi _S:W_S\to S$
are surjective.
Proof. First, let us show that
![]() $R_2 \not \subset S_{nred}^{[2]}$
. Assume the contrary. If
$R_2 \not \subset S_{nred}^{[2]}$
. Assume the contrary. If
![]() $\pi _S(\mathbb {P}^1_E)$
is a point for every
$\pi _S(\mathbb {P}^1_E)$
is a point for every
![]() $E\in \mathcal {M}$
, then we get an injective map
$E\in \mathcal {M}$
, then we get an injective map
![]() $\mathcal {M}\to S$
which is a contradiction. Otherwise,
$\mathcal {M}\to S$
which is a contradiction. Otherwise,
![]() $\pi _S(\mathbb {P}^1_E)$
defines a rational curve on S moving with E, contradicting the rigidity of rational curves on S.
$\pi _S(\mathbb {P}^1_E)$
defines a rational curve on S moving with E, contradicting the rigidity of rational curves on S.
Now, let us show that the intersection is nonempty (then it will be automatically two-dimensional). For the general
![]() $E\in \mathcal {M}$
, consider the degree 2 map
$E\in \mathcal {M}$
, consider the degree 2 map
![]() $D_E\to \mathbb {P}^1_E$
, where
$D_E\to \mathbb {P}^1_E$
, where
We claim that this degree 2 map must have a branch point. If
![]() $D_E$
is irreducible, this follows from Hurwitz formula. Otherwise,
$D_E$
is irreducible, this follows from Hurwitz formula. Otherwise,
![]() $D_E$
consists of two rational components; thus the image of the natural map
$D_E$
consists of two rational components; thus the image of the natural map
![]() $D_E\to S$
produces two rational curves on S. Since rational curves on S are rigid, it follows that this image (moving E) is a fixed curve C with (at most) two rational components. But the locus of length 2 subschemes supported at C is two-dimensional, hence
$D_E\to S$
produces two rational curves on S. Since rational curves on S are rigid, it follows that this image (moving E) is a fixed curve C with (at most) two rational components. But the locus of length 2 subschemes supported at C is two-dimensional, hence
![]() $R_2$
can’t be contained in this locus (recall that
$R_2$
can’t be contained in this locus (recall that
![]() $R_2$
is three-dimensional), which gives the contradiction.
$R_2$
is three-dimensional), which gives the contradiction.
Now, consider a component
![]() $W_S\subset R_2\cap S^{[2]}_{nred}$
such that the projection
$W_S\subset R_2\cap S^{[2]}_{nred}$
such that the projection
![]() $\pi _{\mathcal {M}}:W_S\to \mathcal {M}$
is surjective. This exists, since we just proved that
$\pi _{\mathcal {M}}:W_S\to \mathcal {M}$
is surjective. This exists, since we just proved that
![]() $D_E$
is irreducible for
$D_E$
is irreducible for
![]() $E\in \mathcal {M}$
general (hence
$E\in \mathcal {M}$
general (hence
![]() $\mathbb {P}^1_E$
contains a nonreduced subscheme). The general fiber of the map
$\mathbb {P}^1_E$
contains a nonreduced subscheme). The general fiber of the map
![]() $\pi _S:W_S\to S$
consists of nonreduced subschemes supported at a general point p, hence it is contained in a rational curve. We deduce that if the general fiber of
$\pi _S:W_S\to S$
consists of nonreduced subschemes supported at a general point p, hence it is contained in a rational curve. We deduce that if the general fiber of
![]() $\pi _S$
is positive-dimensional, then
$\pi _S$
is positive-dimensional, then
![]() $W_S$
is covered by rational curves (the fibers of
$W_S$
is covered by rational curves (the fibers of
![]() $\pi _S$
); hence,
$\pi _S$
); hence,
![]() $\mathcal {M}$
is covered by rational curves (recall that
$\mathcal {M}$
is covered by rational curves (recall that
![]() $W_S\to \mathcal {M}$
is dominant), contradiction. It follows that
$W_S\to \mathcal {M}$
is dominant), contradiction. It follows that
![]() $W_S\to S$
is surjective, as desired.
$W_S\to S$
is surjective, as desired.
Now, we give the new construction of rational maps of degree
![]() $4$
:
$4$
:
Lemma 4.8. There is a morphism
![]() $W_S\to W^2_4(S,L)$
generically finite onto its image.
$W_S\to W^2_4(S,L)$
generically finite onto its image.
Proof. For any (nonreduced)
![]() $\xi \in W_S$
, we have an associated E with
$\xi \in W_S$
, we have an associated E with
![]() $h^1(E\otimes \mathcal {I}_\xi )=1$
. We may consider the extension
$h^1(E\otimes \mathcal {I}_\xi )=1$
. We may consider the extension
and the subsheaf
![]() $E_1:=\mathrm {Im}(F^\vee \to E)\subset E$
. By numerical reasons, we get
$E_1:=\mathrm {Im}(F^\vee \to E)\subset E$
. By numerical reasons, we get
![]() $\mathrm {length}(E/E_1)=c_2(F^\vee )-c_2(E)=2$
, and also
$\mathrm {length}(E/E_1)=c_2(F^\vee )-c_2(E)=2$
, and also
![]() $E\otimes \mathcal {I}_\xi \subset E_1$
; indeed, by applying the functor
$E\otimes \mathcal {I}_\xi \subset E_1$
; indeed, by applying the functor
![]() ${\mathcal {H}\mathit {om}}(-,\mathcal {O}_S)$
to the sequence above we get that
${\mathcal {H}\mathit {om}}(-,\mathcal {O}_S)$
to the sequence above we get that
![]() $E_1$
is the kernel of
$E_1$
is the kernel of
![]() $E\to {\mathcal {E}\mathit {xt}}^1(\mathcal {I}_\xi ,\mathcal {O}_S)=\mathcal {O}_\xi $
. Moreover, if
$E\to {\mathcal {E}\mathit {xt}}^1(\mathcal {I}_\xi ,\mathcal {O}_S)=\mathcal {O}_\xi $
. Moreover, if
![]() $p=\operatorname {\mathrm {supp}}(\xi )$
, then
$p=\operatorname {\mathrm {supp}}(\xi )$
, then
![]() $E_1\otimes k(p)$
is three-dimensional since
$E_1\otimes k(p)$
is three-dimensional since
![]() $E_1$
is a quotient of a rank 3 locally free sheaf. It is then easy to deduce that
$E_1$
is a quotient of a rank 3 locally free sheaf. It is then easy to deduce that
![]() $(E_1)_p=e_1\cdot \mathcal {O}_{S,p}+e_2 \cdot \mathcal {I}_\xi $
for some
$(E_1)_p=e_1\cdot \mathcal {O}_{S,p}+e_2 \cdot \mathcal {I}_\xi $
for some
![]() $e_1,e_2$
local generators of
$e_1,e_2$
local generators of
![]() $E_p$
.
$E_p$
.
Note that
![]() $h^1(E_1)=1$
(since
$h^1(E_1)=1$
(since
![]() $h^1(F^\vee )=h^2(F^\vee )=0$
). It follows that the subsheaf
$h^1(F^\vee )=h^2(F^\vee )=0$
). It follows that the subsheaf
![]() $\tilde E\subset E_1$
defined as
$\tilde E\subset E_1$
defined as
![]() $\tilde E_p=e_1\cdot m_p+e_2\cdot m_p^2$
around p (and
$\tilde E_p=e_1\cdot m_p+e_2\cdot m_p^2$
around p (and
![]() $\tilde E_q=E_q$
for
$\tilde E_q=E_q$
for
![]() $q\neq p$
) satisfies
$q\neq p$
) satisfies
![]() $h^1(\tilde E)\ge 1$
(since
$h^1(\tilde E)\ge 1$
(since
![]() $\tilde E\subset E_1$
). Actually, a quick numerical check gives
$\tilde E\subset E_1$
). Actually, a quick numerical check gives
![]() $h^1(\tilde E)= 1$
and
$h^1(\tilde E)= 1$
and
![]() $\chi (\tilde E)=2$
, hence
$\chi (\tilde E)=2$
, hence
![]() $h^0(\tilde E)=3$
. The subspace
$h^0(\tilde E)=3$
. The subspace
![]() $H^0(\tilde E)\subset H^0(E)$
induces a map of degree
$H^0(\tilde E)\subset H^0(E)$
induces a map of degree
![]() $\leq 4$
by Proposition 2.1 (all sections are vanishing with order
$\leq 4$
by Proposition 2.1 (all sections are vanishing with order
![]() $2$
at p).
$2$
at p).
The corresponding morphism
![]() $W_S\to W^2_4(S,L)$
has image of dimension
$W_S\to W^2_4(S,L)$
has image of dimension
![]() $2$
, since
$2$
, since
![]() $\pi _{\mathcal {M}}:W_S \to \mathcal {M}$
is surjective and equals the composition
$\pi _{\mathcal {M}}:W_S \to \mathcal {M}$
is surjective and equals the composition
where
![]() $W^2_4(S,L)_6$
parametrizes maps of degree
$W^2_4(S,L)_6$
parametrizes maps of degree
![]() $\le 4$
having kernel bundle with
$\le 4$
having kernel bundle with
![]() $c_2=6$
(this is the notation in the preliminaries), and the right arrow is the forgetful map
$c_2=6$
(this is the notation in the preliminaries), and the right arrow is the forgetful map
![]() $(E,V^\vee )\mapsto E$
.
$(E,V^\vee )\mapsto E$
.
Now, we show that the image of
![]() $W_S\to W^2_4(S,L)$
is not contained in
$W_S\to W^2_4(S,L)$
is not contained in
![]() $R_2\subset W^2_4(S,L)$
. Namely, the above construction really yields new maps of degree
$R_2\subset W^2_4(S,L)$
. Namely, the above construction really yields new maps of degree
![]() $4$
:
$4$
:
Proposition 4.9. The locus
![]() $\mathrm {Im}(W_S)\subset W^2_4(S,L)$
is not contained in
$\mathrm {Im}(W_S)\subset W^2_4(S,L)$
is not contained in
![]() $R_2\subset W^2_4(S,L)$
.
$R_2\subset W^2_4(S,L)$
.
Proof. Recall that a rational map
![]() $S\dashrightarrow \mathbb P^2$
induced by the primitive linear system is completely determined by the couple
$S\dashrightarrow \mathbb P^2$
induced by the primitive linear system is completely determined by the couple
![]() $(E,V^\vee )$
. We have
$(E,V^\vee )$
. We have
![]() $(E,V^\vee )\in R_2$
if and only if
$(E,V^\vee )\in R_2$
if and only if
![]() $V^\vee =H^0(E\otimes \mathcal {I}_\zeta )$
for some
$V^\vee =H^0(E\otimes \mathcal {I}_\zeta )$
for some
![]() $\zeta \in S^{[2]}$
. Assume that
$\zeta \in S^{[2]}$
. Assume that
![]() $H^0(\tilde E)=H^0(E\otimes \mathcal {I}_\zeta )$
, where (following the notation of Lemma 4.8)
$H^0(\tilde E)=H^0(E\otimes \mathcal {I}_\zeta )$
, where (following the notation of Lemma 4.8)
![]() $\tilde E$
is constructed from a nonreduced
$\tilde E$
is constructed from a nonreduced
![]() $\xi \in W_S$
.
$\xi \in W_S$
.
If
![]() $\zeta $
is reduced, then all sections of
$\zeta $
is reduced, then all sections of
![]() $H^0(E\otimes \mathcal {I}_\zeta )$
vanish with order
$H^0(E\otimes \mathcal {I}_\zeta )$
vanish with order
![]() $2$
at the point where
$2$
at the point where
![]() $\xi $
is supported. Hence,
$\xi $
is supported. Hence,
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
![]() $\geq 3$
, which by Proposition 2.1 implies that
$\geq 3$
, which by Proposition 2.1 implies that
![]() $(E,V^\vee )\in W^2_3(S,L)$
, in contradiction to Corollary 4.6.
$(E,V^\vee )\in W^2_3(S,L)$
, in contradiction to Corollary 4.6.
Now, suppose that
![]() $\zeta $
is nonreduced. We get that
$\zeta $
is nonreduced. We get that
![]() $\zeta $
is supported at the point p where
$\zeta $
is supported at the point p where
![]() $\tilde E$
is not locally free. This implies that all the sections in
$\tilde E$
is not locally free. This implies that all the sections in
![]() $V^\vee $
are locally contained in the subsheaf
$V^\vee $
are locally contained in the subsheaf
![]() $e_1\cdot \mathcal {I}_\zeta +e_2\cdot m_p^2$
of E; in particular, we get
$e_1\cdot \mathcal {I}_\zeta +e_2\cdot m_p^2$
of E; in particular, we get
![]() $h^0(E\otimes \mathcal {I}_p^2)\ge 2$
. In order to finish the proof, it suffices to prove the following claim: For a general point
$h^0(E\otimes \mathcal {I}_p^2)\ge 2$
. In order to finish the proof, it suffices to prove the following claim: For a general point
![]() $p\in S$
, there is no vector bundle
$p\in S$
, there is no vector bundle
![]() $E_p\in \mathcal {M}$
such that
$E_p\in \mathcal {M}$
such that
![]() $h^0(E_p\otimes \mathcal {I}_p^2)=h^1(E_p\otimes \mathcal {I}_p^2)=2$
.
$h^0(E_p\otimes \mathcal {I}_p^2)=h^1(E_p\otimes \mathcal {I}_p^2)=2$
.
Observe that such a bundle
![]() $E_p\in \mathcal {M}$
is a singular point of the curve
$E_p\in \mathcal {M}$
is a singular point of the curve
which has arithmetic genus
![]() $3$
(recall Lemma 2.13). Therefore, if the claim is false one can consider the rational map
$3$
(recall Lemma 2.13). Therefore, if the claim is false one can consider the rational map
![]() $S\dashrightarrow \mathcal {M}$
sending a general
$S\dashrightarrow \mathcal {M}$
sending a general
![]() $p\in S$
to the unique singular point of
$p\in S$
to the unique singular point of
![]() $C_{\mathcal {I}_p^2}$
(note that if
$C_{\mathcal {I}_p^2}$
(note that if
![]() $C_{\mathcal {I}_p^2}$
has at least two singular points for every
$C_{\mathcal {I}_p^2}$
has at least two singular points for every
![]() $p\in S$
, then
$p\in S$
, then
![]() $\{C_{\mathcal {I}_p^2}\}_{p\in S}$
defines a two-dimensional family of curves on
$\{C_{\mathcal {I}_p^2}\}_{p\in S}$
defines a two-dimensional family of curves on
![]() $\mathcal {M}$
with geometric genus
$\mathcal {M}$
with geometric genus
![]() $\leq 1$
, contradiction). This rational map actually extends to a morphism
$\leq 1$
, contradiction). This rational map actually extends to a morphism
![]() $S\to \mathcal {M}$
; indeed, the finite birational morphism
$S\to \mathcal {M}$
; indeed, the finite birational morphism
must be an isomorphism, by normality of S. Now, the morphism
![]() $S\to \mathcal {M}$
is étale by Hurwitz formula, which contradicts the fact that
$S\to \mathcal {M}$
is étale by Hurwitz formula, which contradicts the fact that
![]() $\mathcal {M}$
is simply connected. This finishes the proof.
$\mathcal {M}$
is simply connected. This finishes the proof.
5 Genus 11
Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus 11 with
$K3$
surface of genus 11 with
![]() $\operatorname {\mathrm {Pic}}(S)\cong \mathbb {Z}\cdot L$
, and let
$\operatorname {\mathrm {Pic}}(S)\cong \mathbb {Z}\cdot L$
, and let
![]() $\mathcal {M}$
denote the (fine) moduli space
$\mathcal {M}$
denote the (fine) moduli space
![]() $\mathcal {M}(2,L,5)$
. Any
$\mathcal {M}(2,L,5)$
. Any
![]() $E\in \mathcal {M}$
has
$E\in \mathcal {M}$
has
![]() $h^0(E)=7$
and
$h^0(E)=7$
and
![]() $c_2(E)=7$
. For every
$c_2(E)=7$
. For every
![]() $\xi \in S^{[2]}$
, considering
$\xi \in S^{[2]}$
, considering
![]() $H^0(E\otimes \mathcal {I}_\xi )\subset H^0(E)$
one can construct maps
$H^0(E\otimes \mathcal {I}_\xi )\subset H^0(E)$
one can construct maps ![]() of degree
of degree
![]() $\leq 5$
. In particular,
$\leq 5$
. In particular,
![]() $W^2_5(S,L)$
has (a birational copy of)
$W^2_5(S,L)$
has (a birational copy of)
![]() $S^{[2]}\times \mathcal {M}$
as a component. Its singular locus determines the component of
$S^{[2]}\times \mathcal {M}$
as a component. Its singular locus determines the component of
![]() $W^2_4(S,L)$
that we will describe; see Remark 2.5.
$W^2_4(S,L)$
that we will describe; see Remark 2.5.
5.1 Constructing maps of degree 4
Our first goal is to construct rational maps of degree 4 (and to determine the component of
![]() $W^2_4(S,L)$
obtained from this construction). We can do this thanks to:
$W^2_4(S,L)$
obtained from this construction). We can do this thanks to:
Proposition 5.1. For every
![]() $E\in \mathcal {M}$
, there exists a unique
$E\in \mathcal {M}$
, there exists a unique
![]() $\xi \in S^{[3]}$
such that
$\xi \in S^{[3]}$
such that
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 2$
. In particular,
$h^1(E\otimes \mathcal {I}_\xi )\geq 2$
. In particular,
![]() $W^2_4(S,L)$
admits an irreducible component isomorphic to
$W^2_4(S,L)$
admits an irreducible component isomorphic to
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
The arguments for proving this proposition rely on Bridgeland stability. Along the proof, we will determine several explicit isomorphisms between moduli spaces of Gieseker stable sheaves on S and punctual Hilbert schemes on
![]() $\mathcal {M}$
. In particular, we will construct an isomorphism
$\mathcal {M}$
. In particular, we will construct an isomorphism
Under this isomorphism, the unique
![]() $\xi \in S^{[3]}$
such that
$\xi \in S^{[3]}$
such that
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 2$
corresponds to the unique noncurvilinear element of
$h^1(E\otimes \mathcal {I}_\xi )\geq 2$
corresponds to the unique noncurvilinear element of
![]() $\mathcal {M}^{[3]}$
which is supported on E.
$\mathcal {M}^{[3]}$
which is supported on E.
Consider
![]() $\xi \in S^{[3]}$
and
$\xi \in S^{[3]}$
and
![]() $E\in \mathcal {M}$
. The numerical wall W defined by
$E\in \mathcal {M}$
. The numerical wall W defined by
![]() $E^\vee [1]$
and
$E^\vee [1]$
and
![]() $\mathcal {I}_\xi $
has endpoints
$\mathcal {I}_\xi $
has endpoints
![]() $\beta =\frac {-1}{2}$
and
$\beta =\frac {-1}{2}$
and
![]() $\beta =\frac {-2}{5}$
. Since
$\beta =\frac {-2}{5}$
. Since
![]() $\mathcal {I}_\xi $
(resp.
$\mathcal {I}_\xi $
(resp.
![]() $E^\vee [1]$
) is
$E^\vee [1]$
) is
![]() $\sigma _{\alpha ,\frac {-1}{2}}$
-stable (resp.
$\sigma _{\alpha ,\frac {-1}{2}}$
-stable (resp.
![]() $\sigma _{\alpha ,\frac {-2}{5}}$
-stable) for every
$\sigma _{\alpha ,\frac {-2}{5}}$
-stable) for every
![]() $\alpha>0$
by Lemma 2.11, it follows that both
$\alpha>0$
by Lemma 2.11, it follows that both
![]() $\mathcal {I}_\xi $
and
$\mathcal {I}_\xi $
and
![]() $E^\vee [1]$
are semistable along W.
$E^\vee [1]$
are semistable along W.
Furthermore, there is a hole along W created by the spherical bundle G with
![]() $v(G)=(7,-3L,13)$
(so that
$v(G)=(7,-3L,13)$
(so that
![]() $W=W(\mathcal {I}_\xi , E^\vee [1])=W(G,E^\vee [1])$
). Finally, we also note that both
$W=W(\mathcal {I}_\xi , E^\vee [1])=W(G,E^\vee [1])$
). Finally, we also note that both
![]() $E^\vee [1]$
and G are
$E^\vee [1]$
and G are
![]() $\sigma _{\alpha ,\frac {-4}{9}}$
-stable for every
$\sigma _{\alpha ,\frac {-4}{9}}$
-stable for every
![]() $\alpha>0$
; we will write
$\alpha>0$
; we will write
![]() $\sigma _0:=W\cap \{\beta =\frac {-4}{9}\}$
.
$\sigma _0:=W\cap \{\beta =\frac {-4}{9}\}$
.
As usual, any nonzero morphism
![]() $\mathcal {I}_\xi \to E^\vee [1]$
is a surjection in
$\mathcal {I}_\xi \to E^\vee [1]$
is a surjection in
![]() $\operatorname {\mathrm {Coh}}^\beta (S)$
(
$\operatorname {\mathrm {Coh}}^\beta (S)$
(
![]() $\frac {-1}{2}\leq \beta <\frac {-1}{3}$
), defining a destabilization of
$\frac {-1}{2}\leq \beta <\frac {-1}{3}$
), defining a destabilization of
![]() $\mathcal {I}_\xi $
along W. In order to understand the possible number of morphisms
$\mathcal {I}_\xi $
along W. In order to understand the possible number of morphisms
![]() $\mathcal {I}_\xi \to E^\vee [1]$
, we also need to control the possible HN filtrations of
$\mathcal {I}_\xi \to E^\vee [1]$
, we also need to control the possible HN filtrations of
![]() $\mathcal {I}_\xi $
below W.
$\mathcal {I}_\xi $
below W.
As in genus 7, we achieve this by establishing several isomorphisms of (Hilbert schemes of) moduli spaces. For instance, the same arguments as in Lemma 3.1 prove:
Lemma 5.2. There is an isomorphism
![]() $\mathcal {M}\overset {\cong }{\longrightarrow }\mathcal {M}(5,-2L,8)$
sending a bundle
$\mathcal {M}\overset {\cong }{\longrightarrow }\mathcal {M}(5,-2L,8)$
sending a bundle
![]() $E\in \mathcal {M}$
to the (unique up to isomorphism) sheaf P fitting in a nontrivial extension
$E\in \mathcal {M}$
to the (unique up to isomorphism) sheaf P fitting in a nontrivial extension
The inverse is obtained by sending
![]() $P\in \mathcal {M}(5,-2L,8)$
to (the shift of the derived dual of) its last HN factor for stability conditions just below
$P\in \mathcal {M}(5,-2L,8)$
to (the shift of the derived dual of) its last HN factor for stability conditions just below
![]() $\sigma _0$
.
$\sigma _0$
.
Remark 5.3. By rotating the distinguished triangle,
![]() $0\to P\to E^\vee [1]\to G[1]\to 0$
defines a destabilization of
$0\to P\to E^\vee [1]\to G[1]\to 0$
defines a destabilization of
![]() $E^\vee [1]$
along
$E^\vee [1]$
along
![]() $W\cap \{\beta>\frac {-3}{7}\}$
.
$W\cap \{\beta>\frac {-3}{7}\}$
.
With similar arguments to those of Proposition 3.5, one obtains:
Lemma 5.4. There is an isomorphism
![]() $\mathcal {M}^{[2]}\overset {\cong }{\longrightarrow }\mathcal {M}(3,-L,3)$
.
$\mathcal {M}^{[2]}\overset {\cong }{\longrightarrow }\mathcal {M}(3,-L,3)$
.
Finally, one more step in this construction yields our desired isomorphism of Hilbert schemes:
Lemma 5.5. There is an isomorphism
![]() $\gamma :\mathcal {M}^{[3]}\overset {\cong }{\longrightarrow }\mathcal {M}(1,0,-2)=S^{[3]}$
.
$\gamma :\mathcal {M}^{[3]}\overset {\cong }{\longrightarrow }\mathcal {M}(1,0,-2)=S^{[3]}$
.
Proof. The proof is similar to that of Proposition 3.5. We define the morphism
![]() $\gamma $
as follows.
$\gamma $
as follows.
Given a reduced element of
![]() $\mathcal {M}^{[3]}$
, supported at
$\mathcal {M}^{[3]}$
, supported at
![]() $E_1,E_2,E_3\in \mathcal {M}$
, we consider the object M fitting into an extension
$E_1,E_2,E_3\in \mathcal {M}$
, we consider the object M fitting into an extension
such that the induced elements in
![]() $\operatorname {\mathrm {Ext}}^1(E_i^\vee [1],G)$
are nonzero. Such an M is unique up to isomorphism (due to the action of automorphisms of
$\operatorname {\mathrm {Ext}}^1(E_i^\vee [1],G)$
are nonzero. Such an M is unique up to isomorphism (due to the action of automorphisms of
![]() $E_1^\vee [1]\oplus E_2^\vee [1]\oplus E_3^\vee [1]$
), and of the form
$E_1^\vee [1]\oplus E_2^\vee [1]\oplus E_3^\vee [1]$
), and of the form
![]() $M=\mathcal {I}_\xi $
for some
$M=\mathcal {I}_\xi $
for some
![]() $\xi \in S^{[3]}$
(indeed M is semistable above
$\xi \in S^{[3]}$
(indeed M is semistable above
![]() $\sigma _0$
, by arguing as in Proposition 3.5).
$\sigma _0$
, by arguing as in Proposition 3.5).
If our element of
![]() $\mathcal {M}^{[3]}$
consists of a tangent direction
$\mathcal {M}^{[3]}$
consists of a tangent direction
![]() $T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E_1,E_1))$
at
$T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E_1,E_1))$
at
![]() $E_1$
and a reduced point
$E_1$
and a reduced point
![]() $E_2$
, we consider
$E_2$
, we consider
![]() $\widetilde {T}:=T^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E_1^\vee [1],E_1^\vee [1]))$
and take the object M fitting into
$\widetilde {T}:=T^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E_1^\vee [1],E_1^\vee [1]))$
and take the object M fitting into
such that the induced elements in
![]() $\operatorname {\mathrm {Ext}}^1(E_1^\vee [1],G)$
and
$\operatorname {\mathrm {Ext}}^1(E_1^\vee [1],G)$
and
![]() $\operatorname {\mathrm {Ext}}^1(E_2^\vee [1],G)$
(the former via the map
$\operatorname {\mathrm {Ext}}^1(E_2^\vee [1],G)$
(the former via the map
![]() $\operatorname {\mathrm {Ext}}^1(\widetilde {T}\oplus E_2^\vee [1],G)\to \operatorname {\mathrm {Ext}}^1(\widetilde {T},G)\to \operatorname {\mathrm {Ext}}^1(E_1^\vee [1],G)$
) are nonzero. Again, M is unique up to isomorphism and of the form
$\operatorname {\mathrm {Ext}}^1(\widetilde {T}\oplus E_2^\vee [1],G)\to \operatorname {\mathrm {Ext}}^1(\widetilde {T},G)\to \operatorname {\mathrm {Ext}}^1(E_1^\vee [1],G)$
) are nonzero. Again, M is unique up to isomorphism and of the form
![]() $M=\mathcal {I}_\xi $
for some
$M=\mathcal {I}_\xi $
for some
![]() $\xi \in S^{[3]}$
.
$\xi \in S^{[3]}$
.
Finally, given a tangent direction
![]() $T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],E^\vee [1]))$
at
$T\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],E^\vee [1]))$
at
![]() $E\in \mathcal {M}$
, it is well known that all elements of
$E\in \mathcal {M}$
, it is well known that all elements of
![]() $\mathcal {M}^{[3]}$
supported at E and containing T are parametrized by
$\mathcal {M}^{[3]}$
supported at E and containing T are parametrized by
![]() $\mathbb {P}(\operatorname {\mathrm {Ext}}^1(T,E))$
. Given such a
$\mathbb {P}(\operatorname {\mathrm {Ext}}^1(T,E))$
. Given such a
![]() $Q\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(T,E))$
, consider the corresponding
$Q\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(T,E))$
, consider the corresponding
![]() $\widetilde {Q}:=Q^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],T^\vee [1]))$
and take the object M sitting in an extension
$\widetilde {Q}:=Q^\vee [1]\in \mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],T^\vee [1]))$
and take the object M sitting in an extension
such that the induced element in
![]() $\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
(via the map
$\operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
(via the map
![]() $\operatorname {\mathrm {Ext}}^1(\widetilde {Q},G)\to \operatorname {\mathrm {Ext}}^1(T^\vee [1],G)\to \operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
) is nonzero. Again, M is unique and of the form
$\operatorname {\mathrm {Ext}}^1(\widetilde {Q},G)\to \operatorname {\mathrm {Ext}}^1(T^\vee [1],G)\to \operatorname {\mathrm {Ext}}^1(E^\vee [1],G)$
) is nonzero. Again, M is unique and of the form
![]() $M=\mathcal {I}_\xi $
, for some
$M=\mathcal {I}_\xi $
, for some
![]() $\xi \in S^{[3]}$
.
$\xi \in S^{[3]}$
.
The morphism
![]() $\gamma $
is injective on closed points, and hence, arguing as in the proof of Proposition 3.5, we obtain that
$\gamma $
is injective on closed points, and hence, arguing as in the proof of Proposition 3.5, we obtain that
![]() $\gamma $
is an isomorphism.
$\gamma $
is an isomorphism.
Now, we have all the ingredients to prove Proposition 5.1:
Proof of Proposition 5.1.
Given
![]() $\xi \in S^{[3]}$
and
$\xi \in S^{[3]}$
and
![]() $E'\in \mathcal {M}$
, we want to determine the number
$E'\in \mathcal {M}$
, we want to determine the number
![]() $\hom (\mathcal {I}_\xi , E^{\prime \vee }[1])=h^1(E'\otimes \mathcal {I}_\xi )$
. To this end, we consider the HN filtration
$\hom (\mathcal {I}_\xi , E^{\prime \vee }[1])=h^1(E'\otimes \mathcal {I}_\xi )$
. To this end, we consider the HN filtration
of
![]() $\mathcal {I}_\xi $
for stability conditions just below
$\mathcal {I}_\xi $
for stability conditions just below
![]() $\sigma _0$
, established in Lemma 5.5. The object F is nothing but
$\sigma _0$
, established in Lemma 5.5. The object F is nothing but
![]() $F=\Phi _{\mathcal {E}}(\mathcal {O}_{\gamma ^{-1}(\xi )})^\vee [1]$
, where
$F=\Phi _{\mathcal {E}}(\mathcal {O}_{\gamma ^{-1}(\xi )})^\vee [1]$
, where
![]() $\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
is the Fourier–Mukai equivalence with kernel the universal bundle
$\Phi _{\mathcal {E}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
is the Fourier–Mukai equivalence with kernel the universal bundle
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $S\times \mathcal {M}$
.
$S\times \mathcal {M}$
.
Due to the vanishing
![]() $\operatorname {\mathrm {Hom}}(G,E^{\prime \vee }[1])=0$
, we have equalities
$\operatorname {\mathrm {Hom}}(G,E^{\prime \vee }[1])=0$
, we have equalities
 $$\begin{align*}\begin{aligned} &\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\mathcal{I}_\xi, E^{\prime\vee}[1])=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(F, E^{\prime\vee}[1])=\\ &=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\Phi_{\mathcal{E}}(\mathcal{O}_{\gamma^{-1}(\xi)})^\vee[1], \Phi_{\mathcal{E}}(k(E'))^\vee[1])=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(\mathcal{M})}(k(E'),\mathcal{O}_{\gamma^{-1}(\xi)}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\mathcal{I}_\xi, E^{\prime\vee}[1])=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(F, E^{\prime\vee}[1])=\\ &=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\Phi_{\mathcal{E}}(\mathcal{O}_{\gamma^{-1}(\xi)})^\vee[1], \Phi_{\mathcal{E}}(k(E'))^\vee[1])=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(\mathcal{M})}(k(E'),\mathcal{O}_{\gamma^{-1}(\xi)}). \end{aligned} \end{align*}$$
If
![]() $E'\notin \operatorname {\mathrm {supp}} \gamma ^{-1}(\xi )$
, it immediately follows that
$E'\notin \operatorname {\mathrm {supp}} \gamma ^{-1}(\xi )$
, it immediately follows that
![]() $\hom (\mathcal {I}_\xi , E^{\prime \vee }[1])=0$
.
$\hom (\mathcal {I}_\xi , E^{\prime \vee }[1])=0$
.
On the other hand, if
![]() $E'\in \operatorname {\mathrm {supp}} \gamma ^{-1}(\xi )$
, then the equality
$E'\in \operatorname {\mathrm {supp}} \gamma ^{-1}(\xi )$
, then the equality
holds; indeed, it is a consequence of the equalities
![]() $\operatorname {\mathrm {ext}}^2(k(E'),\mathcal {O}_{\gamma ^{-1}(\xi )})= \hom (\mathcal {O}_{\gamma ^{-1}(\xi )},k(E'))=1$
and
$\operatorname {\mathrm {ext}}^2(k(E'),\mathcal {O}_{\gamma ^{-1}(\xi )})= \hom (\mathcal {O}_{\gamma ^{-1}(\xi )},k(E'))=1$
and
![]() $\chi (k(E'),\mathcal {O}_{\gamma ^{-1}(\xi )})=0$
.
$\chi (k(E'),\mathcal {O}_{\gamma ^{-1}(\xi )})=0$
.
Therefore, by applying Lemma 2.6 we obtain
 $$\begin{align*}\hom(\mathcal{I}_\xi, E^{\prime\vee}[1])=\left\{ \begin{array}{@{}cl} 1 & \text{if }\gamma^{-1}(\xi)\text{ is curvilinear at }E'\\ 2 & \text{if }\gamma^{-1}(\xi)\text{ is not curvilinear at }E'.\\ \end{array} \right. \end{align*}$$
$$\begin{align*}\hom(\mathcal{I}_\xi, E^{\prime\vee}[1])=\left\{ \begin{array}{@{}cl} 1 & \text{if }\gamma^{-1}(\xi)\text{ is curvilinear at }E'\\ 2 & \text{if }\gamma^{-1}(\xi)\text{ is not curvilinear at }E'.\\ \end{array} \right. \end{align*}$$
In particular, for a given
![]() $E\in \mathcal {M}$
, there exists a unique
$E\in \mathcal {M}$
, there exists a unique
![]() $\xi \in S^{[3]}$
such that
$\xi \in S^{[3]}$
such that
![]() $h^1(E\otimes \mathcal {I}_\xi )=2$
; it is nothing but the image under
$h^1(E\otimes \mathcal {I}_\xi )=2$
; it is nothing but the image under
![]() $\gamma $
of the unique noncurvilinear length 3 subscheme supported at
$\gamma $
of the unique noncurvilinear length 3 subscheme supported at
![]() $E\in \mathcal {M}$
. This concludes the proof of the proposition.
$E\in \mathcal {M}$
. This concludes the proof of the proposition.
5.2 Discarding maps of degree 3 (I)
In view of Corollary 2.3, every degree 3 map ![]() arises from
arises from
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
, where
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
, where
![]() $E\in \mathcal {M}$
and
$E\in \mathcal {M}$
and
![]() $\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=4$
. In this subsection, we discard the case where the schematic intersection
$\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=4$
. In this subsection, we discard the case where the schematic intersection
![]() $\bigcap _{s\in V^\vee }Z(s)$
is of length 4, by means of the following:
$\bigcap _{s\in V^\vee }Z(s)$
is of length 4, by means of the following:
Proposition 5.6. For all
![]() $E\in \mathcal {M}$
and
$E\in \mathcal {M}$
and
![]() $\xi \in S^{[4]}$
, the inequality
$\xi \in S^{[4]}$
, the inequality
![]() $h^0(E\otimes \mathcal {I}_\xi )\leq 2$
holds.
$h^0(E\otimes \mathcal {I}_\xi )\leq 2$
holds.
In order to prove this result, we perform a Bridgeland analysis which has many symmetries with that of the previous subsection. In this case, the numerical wall
![]() $\overline {W}$
defined by
$\overline {W}$
defined by
![]() $E^\vee $
and
$E^\vee $
and
![]() $\mathcal {I}_\xi $
has endpoints
$\mathcal {I}_\xi $
has endpoints
![]() $\beta =\frac {-3}{5}$
and
$\beta =\frac {-3}{5}$
and
![]() $\beta =\frac {-1}{2}$
. Any nonzero morphism
$\beta =\frac {-1}{2}$
. Any nonzero morphism
![]() $E^\vee \to \mathcal {I}_\xi $
is an injection in
$E^\vee \to \mathcal {I}_\xi $
is an injection in
![]() $\operatorname {\mathrm {Coh}}^\beta (S)$
(
$\operatorname {\mathrm {Coh}}^\beta (S)$
(
![]() $\frac {-3}{5}\leq \beta <\frac {-1}{2}$
), which destabilizes
$\frac {-3}{5}\leq \beta <\frac {-1}{2}$
), which destabilizes
![]() $\mathcal {I}_\xi $
along
$\mathcal {I}_\xi $
along
![]() $\overline {W}$
.
$\overline {W}$
.
The wall
![]() $\overline {W}$
has a hole created by the spherical bundle
$\overline {W}$
has a hole created by the spherical bundle
![]() $\overline {G}$
with
$\overline {G}$
with
![]() $v(\overline {G})=(7,-4L,23)$
. Moreover,
$v(\overline {G})=(7,-4L,23)$
. Moreover,
![]() $E^\vee ,\overline {G}[1]\in \operatorname {\mathrm {Coh}}^{\frac {-5}{9}}(S)$
are
$E^\vee ,\overline {G}[1]\in \operatorname {\mathrm {Coh}}^{\frac {-5}{9}}(S)$
are
![]() $\sigma _{\alpha ,\frac {-5}{9}}$
-stable for every
$\sigma _{\alpha ,\frac {-5}{9}}$
-stable for every
![]() $\alpha>0$
; let us write
$\alpha>0$
; let us write
![]() $\overline {\sigma _0}:=\overline {W}\cap \{\beta =\frac {-5}{9}\}$
.
$\overline {\sigma _0}:=\overline {W}\cap \{\beta =\frac {-5}{9}\}$
.
Again, by exploiting the
![]() $\overline {\sigma _0}$
-stability of
$\overline {\sigma _0}$
-stability of
![]() $E^\vee $
and
$E^\vee $
and
![]() $\overline {G}[1]$
and the fact that
$\overline {G}[1]$
and the fact that
![]() $\operatorname {\mathrm {ext}}^1(\overline {G}[1],E^\vee )=1$
, one can construct several isomorphisms of (Hilbert schemes of) moduli spaces:
$\operatorname {\mathrm {ext}}^1(\overline {G}[1],E^\vee )=1$
, one can construct several isomorphisms of (Hilbert schemes of) moduli spaces:
Lemma 5.7. Let
![]() $\sigma '$
be a stability condition above
$\sigma '$
be a stability condition above
![]() $\overline {W}$
, close enough to
$\overline {W}$
, close enough to
![]() $\overline {\sigma _0}$
. Then there are isomorphisms:
$\overline {\sigma _0}$
. Then there are isomorphisms:
-
(1)
 $\mathcal {M}(2,-L,5)\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-5,3L,-18)$
.
$\mathcal {M}(2,-L,5)\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-5,3L,-18)$
. -
(2)
 $\mathcal {M}(2,-L,5)^{[2]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-3,2L,-13)$
.
$\mathcal {M}(2,-L,5)^{[2]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-3,2L,-13)$
. -
(3)
 $\mathcal {M}(2,-L,5)^{[3]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-1,L,-8)$
.
$\mathcal {M}(2,-L,5)^{[3]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(-1,L,-8)$
. -
(4)
 $\overline {\gamma }:\mathcal {M}(2,-L,5)^{[4]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(1,0,-3)=S^{[4]}$
.
$\overline {\gamma }:\mathcal {M}(2,-L,5)^{[4]}\overset {\cong }{\longrightarrow }\mathcal {M}_{\sigma '}(1,0,-3)=S^{[4]}$
.
Proof. The arguments are similar to those of the previous subsection. For instance, in (1) one sends
![]() $M\in \mathcal {M}(2,-L,5)$
to the isomorphism class of the object P sitting in a nontrivial extension
$M\in \mathcal {M}(2,-L,5)$
to the isomorphism class of the object P sitting in a nontrivial extension
![]() $0\to M\to P\to \overline {G}[1]\to 0$
.
$0\to M\to P\to \overline {G}[1]\to 0$
.
Remark 5.8. Let
![]() $(S,L)$
be a polarized
$(S,L)$
be a polarized
![]() $K3$
surface of genus g,
$K3$
surface of genus g,
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. The isomorphisms of Hilbert schemes
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
. The isomorphisms of Hilbert schemes
![]() $S^{[2]}\cong \mathcal {M}(2,L,3)^{[2]}$
(in genus 7) and
$S^{[2]}\cong \mathcal {M}(2,L,3)^{[2]}$
(in genus 7) and
![]() $S^{[3]}\cong \mathcal {M}(2,L,5)^{[3]}$
,
$S^{[3]}\cong \mathcal {M}(2,L,5)^{[3]}$
,
![]() $S^{[4]}\cong \mathcal {M}(2,L,5)^{[4]}$
(in genus 11) can be generalized, with similar arguments, to the following statement: If
$S^{[4]}\cong \mathcal {M}(2,L,5)^{[4]}$
(in genus 11) can be generalized, with similar arguments, to the following statement: If
![]() $g=4n-1$
, then there are isomorphisms
$g=4n-1$
, then there are isomorphisms
![]() $S^{[n]}\cong \mathcal {M}(2,L,2n-1)^{[n]}$
,
$S^{[n]}\cong \mathcal {M}(2,L,2n-1)^{[n]}$
,
![]() $S^{[n+1]}\cong \mathcal {M}(2,L,2n-1)^{[n+1]}$
.
$S^{[n+1]}\cong \mathcal {M}(2,L,2n-1)^{[n+1]}$
.
This can be thought of as a reinterpretation, in terms of Bridgeland stability, of an isomorphism of moduli spaces of sheaves on S and a Fourier–Mukai partner, which is due to Yoshioka and holds in broader generality ([Reference YoshiokaYos01, Theorem 7.6]).
Now, we can prove Proposition 5.6 with similar arguments to those of Proposition 5.1:
Proof of Proposition 5.6.
Given
![]() $\xi \in S^{[4]}$
and
$\xi \in S^{[4]}$
and
![]() $E'\in \mathcal {M}$
, we want to determine the number
$E'\in \mathcal {M}$
, we want to determine the number
![]() $\hom (E^{\prime \vee },\mathcal {I}_\xi )=h^0(E'\otimes \mathcal {I}_\xi )$
. We will use the isomorphism
$\hom (E^{\prime \vee },\mathcal {I}_\xi )=h^0(E'\otimes \mathcal {I}_\xi )$
. We will use the isomorphism
![]() $\overline {\gamma }$
of the previous lemma, together with the fact that
$\overline {\gamma }$
of the previous lemma, together with the fact that
![]() $E^{\prime \vee }\in \mathcal {M}(2,-L,5)$
. Consider the HN filtration
$E^{\prime \vee }\in \mathcal {M}(2,-L,5)$
. Consider the HN filtration
of
![]() $\mathcal {I}_\xi $
for stability conditions just below
$\mathcal {I}_\xi $
for stability conditions just below
![]() $\overline {\sigma _0}$
; the factor
$\overline {\sigma _0}$
; the factor
![]() $\overline {F}$
is determined by
$\overline {F}$
is determined by
![]() $\overline {\gamma }^{-1}(\xi )$
. Indeed, one has
$\overline {\gamma }^{-1}(\xi )$
. Indeed, one has
![]() $\overline {F}=\Phi _{\overline {\mathcal {E}}}(\mathcal {O}_{\overline {\gamma }^{-1}(\xi )})$
, where
$\overline {F}=\Phi _{\overline {\mathcal {E}}}(\mathcal {O}_{\overline {\gamma }^{-1}(\xi )})$
, where
![]() $\overline {\mathcal {E}}$
denotes the universal bundle on
$\overline {\mathcal {E}}$
denotes the universal bundle on
![]() $S\times \mathcal {M}(2,-L,5)$
and
$S\times \mathcal {M}(2,-L,5)$
and
![]() $\Phi _{\overline {\mathcal {E}}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M}(2,-L,5))\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
is the corresponding Fourier–Mukai equivalence.
$\Phi _{\overline {\mathcal {E}}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M}(2,-L,5))\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)$
is the corresponding Fourier–Mukai equivalence.
Due to the vanishing
![]() $\operatorname {\mathrm {Hom}}(E^{\prime \vee },\overline {G}[1])=0$
, we have
$\operatorname {\mathrm {Hom}}(E^{\prime \vee },\overline {G}[1])=0$
, we have
 $$\begin{align*}\begin{aligned} \operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(E^{\prime\vee},\mathcal{I}_\xi)&=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(E^{\prime\vee}, \overline{F})=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\Phi_{\overline{\mathcal{E}}}(k(E^{\prime\vee}), \Phi_{\overline{\mathcal{E}}}(\mathcal{O}_{\overline{\gamma}^{-1}(\xi)}))=\\ &=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(\mathcal{M}(2,-L,5))}(k(E^{\prime\vee}),\mathcal{O}_{\overline{\gamma}^{-1}(\xi)}). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(E^{\prime\vee},\mathcal{I}_\xi)&=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(E^{\prime\vee}, \overline{F})=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(S)}(\Phi_{\overline{\mathcal{E}}}(k(E^{\prime\vee}), \Phi_{\overline{\mathcal{E}}}(\mathcal{O}_{\overline{\gamma}^{-1}(\xi)}))=\\ &=\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{D}^{\mathrm{b}}}\nolimits(\mathcal{M}(2,-L,5))}(k(E^{\prime\vee}),\mathcal{O}_{\overline{\gamma}^{-1}(\xi)}). \end{aligned} \end{align*}$$
If
![]() $E^{\prime \vee }\notin \operatorname {\mathrm {supp}} \overline {\gamma }^{-1}(\xi )$
, the vanishing
$E^{\prime \vee }\notin \operatorname {\mathrm {supp}} \overline {\gamma }^{-1}(\xi )$
, the vanishing
![]() $\hom (E^{\prime \vee },\mathcal {I}_\xi )=0$
follows.
$\hom (E^{\prime \vee },\mathcal {I}_\xi )=0$
follows.
On the other hand, if
![]() $E^{\prime \vee }\in \operatorname {\mathrm {supp}} \overline {\gamma }^{-1}(\xi )$
, we have the equality
$E^{\prime \vee }\in \operatorname {\mathrm {supp}} \overline {\gamma }^{-1}(\xi )$
, we have the equality
(following from
![]() $\operatorname {\mathrm {ext}}^2(k(E^{\prime \vee }),\mathcal {O}_{\overline {\gamma }^{-1}(\xi )})=\hom (\mathcal {O}_{\overline {\gamma }^{-1}(\xi )},k(E^{\prime \vee }))=1$
and
$\operatorname {\mathrm {ext}}^2(k(E^{\prime \vee }),\mathcal {O}_{\overline {\gamma }^{-1}(\xi )})=\hom (\mathcal {O}_{\overline {\gamma }^{-1}(\xi )},k(E^{\prime \vee }))=1$
and
![]() $\chi (k(E^{\prime \vee }), \mathcal {O}_{\overline {\gamma }^{-1}(\xi )})=0$
). Therefore, by applying Lemma 2.6 we deduce that
$\chi (k(E^{\prime \vee }), \mathcal {O}_{\overline {\gamma }^{-1}(\xi )})=0$
). Therefore, by applying Lemma 2.6 we deduce that
 $$\begin{align*}\hom(E^{\prime\vee}, \mathcal{I}_\xi)=\left\{\!\begin{array}{c l} 1 & \text{if }\overline{\gamma}^{-1}(\xi)\text{ is of complete intersection at }E^{\prime\vee}\\ 2 & \text{if }\overline{\gamma}^{-1}(\xi)\text{ is not of complete intersection at }E^{\prime\vee}\\ \end{array} \right. \end{align*}$$
$$\begin{align*}\hom(E^{\prime\vee}, \mathcal{I}_\xi)=\left\{\!\begin{array}{c l} 1 & \text{if }\overline{\gamma}^{-1}(\xi)\text{ is of complete intersection at }E^{\prime\vee}\\ 2 & \text{if }\overline{\gamma}^{-1}(\xi)\text{ is not of complete intersection at }E^{\prime\vee}\\ \end{array} \right. \end{align*}$$
which finishes the proof.
Furthermore, the analysis performed in the proof of Proposition 5.6 yields the following:
Corollary 5.9. Let
![]() $E\in \mathcal {M}$
. Then:
$E\in \mathcal {M}$
. Then:
-
(1) The jump locus
 $\{\xi \in S^{[4]}\;|\;h^0(E\otimes \mathcal {I}_\xi )\ge 2\}$
is isomorphic to
$\{\xi \in S^{[4]}\;|\;h^0(E\otimes \mathcal {I}_\xi )\ge 2\}$
is isomorphic to
 $\mathrm {Bl}_{E}(\mathcal {M})$
.
$\mathrm {Bl}_{E}(\mathcal {M})$
. -
(2) Under this isomorphism, every
 $\xi \in S^{[4]}$
in the exceptional divisor of
$\xi \in S^{[4]}$
in the exceptional divisor of
 $\mathrm{Bl}_{E}(\mathcal{M})$
satisfies
$\mathrm{Bl}_{E}(\mathcal{M})$
satisfies
 $h^0(E'\otimes \mathcal {I}_\xi )=0$
for all
$h^0(E'\otimes \mathcal {I}_\xi )=0$
for all
 $E'\in \mathcal {M}\setminus \{E\}$
.
$E'\in \mathcal {M}\setminus \{E\}$
.
5.3 Discarding maps of degree 3 (II)
In this subsection, we complete the proof of the emptiness of
![]() $W^2_3(S,L)$
. Assume given a map
$W^2_3(S,L)$
. Assume given a map ![]() of degree 3, defined by
of degree 3, defined by
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
for
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
for
![]() $E\in \mathcal {M}$
. The base ideal
$E\in \mathcal {M}$
. The base ideal
![]() $\mathcal {I}$
of the linear system
$\mathcal {I}$
of the linear system
![]() $V\subset H^0(L)$
has colength
$V\subset H^0(L)$
has colength
![]() $L^2-c_2(E)=13$
, and
$L^2-c_2(E)=13$
, and
![]() $\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=4$
; according to Proposition 5.6, the schematic intersection
$\deg \left (\bigcap _{s\in V^\vee }Z_{cycle}(s)\right )=4$
; according to Proposition 5.6, the schematic intersection
![]() $\xi :=\bigcap _{s\in V^\vee }Z(s)$
must be of length
$\xi :=\bigcap _{s\in V^\vee }Z(s)$
must be of length
![]() $\leq 3$
.
$\leq 3$
.
Lemma 5.10. Under these assumptions, the schematic intersection
![]() $\xi $
has length 3.
$\xi $
has length 3.
Proof. If
![]() $\xi $
consists of a reduced point
$\xi $
consists of a reduced point
![]() $p\in S$
, then by Lemma 2.4 there is a local trivialization
$p\in S$
, then by Lemma 2.4 there is a local trivialization
![]() $E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p such that
$E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p such that
![]() $s_p\in m_pe_1+m_p^4 e_2$
for every
$s_p\in m_pe_1+m_p^4 e_2$
for every
![]() $s\in V^\vee $
. This implies
$s\in V^\vee $
. This implies
![]() $\mathcal {I}\subset \mathcal {I}_p^5$
and hence
$\mathcal {I}\subset \mathcal {I}_p^5$
and hence
![]() $\operatorname {\mathrm {colength}}(\mathcal {I})\geq \operatorname {\mathrm {colength}}(\mathcal {I}_p^5)=15$
, which is a contradiction.
$\operatorname {\mathrm {colength}}(\mathcal {I})\geq \operatorname {\mathrm {colength}}(\mathcal {I}_p^5)=15$
, which is a contradiction.
Assume now that
![]() $\xi $
is of length 2, supported at two distinct points p and q. If
$\xi $
is of length 2, supported at two distinct points p and q. If
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p+2q$
, then by Lemma 2.4 one has
$\bigcap _{s\in V^\vee }Z_{cycle}(s)=2p+2q$
, then by Lemma 2.4 one has
![]() $s_p\in m_pe_1+m_p^2e_2$
for all
$s_p\in m_pe_1+m_p^2e_2$
for all
![]() $s\in V^\vee $
, in an appropriate trivialization of E near p; therefore,
$s\in V^\vee $
, in an appropriate trivialization of E near p; therefore,
![]() $\mathcal {I}\subset \mathcal {I}_p^3$
, and since
$\mathcal {I}\subset \mathcal {I}_p^3$
, and since
![]() $\mathcal {I}$
has (at most) three local generators at p, it follows that
$\mathcal {I}$
has (at most) three local generators at p, it follows that
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 7$
. Similarly, we have
$\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 7$
. Similarly, we have
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 7$
, hence
$\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 7$
, hence
![]() $\operatorname {\mathrm {colength}}(\mathcal {I})\geq 14$
which is impossible.
$\operatorname {\mathrm {colength}}(\mathcal {I})\geq 14$
which is impossible.
On the other hand, if
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)=3p+q$
, a similar use of Lemma 2.4 yields
$\bigcap _{s\in V^\vee }Z_{cycle}(s)=3p+q$
, a similar use of Lemma 2.4 yields
![]() $\mathcal {I}\subset \mathcal {I}_p^4\cap \mathcal {I}_q^2$
; since
$\mathcal {I}\subset \mathcal {I}_p^4\cap \mathcal {I}_q^2$
; since
![]() $\mathcal {I}$
has three generators at p, we have
$\mathcal {I}$
has three generators at p, we have
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 12$
and therefore
$\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 12$
and therefore
![]() $\operatorname {\mathrm {colength}}(\mathcal {I})\geq \operatorname {\mathrm {colength}}(\mathcal {I},p)+\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 15$
, contradiction.
$\operatorname {\mathrm {colength}}(\mathcal {I})\geq \operatorname {\mathrm {colength}}(\mathcal {I},p)+\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 15$
, contradiction.
It only remains to discard the situation where
![]() $\xi $
is nonreduced of length 2, supported at a point p. In this case, by Lemma 2.4 we can find (in appropriate local coordinates) generators
$\xi $
is nonreduced of length 2, supported at a point p. In this case, by Lemma 2.4 we can find (in appropriate local coordinates) generators
![]() $e_1,e_2$
of E around p such that
$e_1,e_2$
of E around p such that
![]() $s_p\in (x,y^2)e_1+(x^2,xy^2,y^4)e_2$
for every
$s_p\in (x,y^2)e_1+(x^2,xy^2,y^4)e_2$
for every
![]() $s\in V^\vee $
. Under the isomorphism
$s\in V^\vee $
. Under the isomorphism
![]() $V\cong \bigwedge ^2V^\vee $
, this implies that
$V\cong \bigwedge ^2V^\vee $
, this implies that
![]() $\mathcal {I}\subset (x^3,x^2y^2,xy^4,y^6)$
locally at p; since
$\mathcal {I}\subset (x^3,x^2y^2,xy^4,y^6)$
locally at p; since
![]() $\mathcal {I}$
has at most three generators at p, it follows that
$\mathcal {I}$
has at most three generators at p, it follows that
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 14$
, which gives a contradiction.
$\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 14$
, which gives a contradiction.
Apart from having a schematic intersection
![]() $\xi =\bigcap _{s\in V^\vee }Z(s)$
of length 3, we can reduce to a more concrete situation:
$\xi =\bigcap _{s\in V^\vee }Z(s)$
of length 3, we can reduce to a more concrete situation:
Lemma 5.11. Let
![]() $p\in S$
be the point where
$p\in S$
be the point where
![]() $\mathrm {cycle}(\xi )$
and
$\mathrm {cycle}(\xi )$
and
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
differ. Then
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
differ. Then
![]() $\xi $
is reduced at p.
$\xi $
is reduced at p.
Proof. Let us first show that
![]() $\xi $
is curvilinear. Assume for the sake of a contradiction that
$\xi $
is curvilinear. Assume for the sake of a contradiction that
![]() $\xi $
is not curvilinear, namely
$\xi $
is not curvilinear, namely
![]() $\mathcal {I}_\xi =\mathcal {I}_p^2$
. Since
$\mathcal {I}_\xi =\mathcal {I}_p^2$
. Since
![]() $h^0(E\otimes \mathcal {I}_\xi )\geq 3$
, we have
$h^0(E\otimes \mathcal {I}_\xi )\geq 3$
, we have
![]() $h^1(E\otimes \mathcal {I}_\xi )\geq 2$
and we can consider a stable sheaf F arising as a double extension
$h^1(E\otimes \mathcal {I}_\xi )\geq 2$
and we can consider a stable sheaf F arising as a double extension
Note that
![]() $v(F)=(4,L,1)$
. Since
$v(F)=(4,L,1)$
. Since
![]() $E\otimes \mathcal {I}_p^2\otimes k(p)$
is a six-dimensional (
$E\otimes \mathcal {I}_p^2\otimes k(p)$
is a six-dimensional (
![]() $E\otimes \mathcal {I}_p^2$
has six local generators at p), it follows that the minimal number of generators of F at p is at least six. This implies that the reflexive hull
$E\otimes \mathcal {I}_p^2$
has six local generators at p), it follows that the minimal number of generators of F at p is at least six. This implies that the reflexive hull
![]() $F^{**}$
of F has Mukai vector
$F^{**}$
of F has Mukai vector
![]() $v(F^{**})=(4,L,k)$
with
$v(F^{**})=(4,L,k)$
with
![]() $k\geq 3$
, hence
$k\geq 3$
, hence
![]() $v(F^{**})^2\leq -4$
which contradicts the stability of
$v(F^{**})^2\leq -4$
which contradicts the stability of
![]() $F^{**}$
.
$F^{**}$
.
Now, we only need to rule out the scenario where
![]() $\xi $
is of the form
$\xi $
is of the form
![]() $(x,y^m)$
locally at p for
$(x,y^m)$
locally at p for
![]() $m\in \{2,3\}$
. In that case, by Lemma 2.4 we have
$m\in \{2,3\}$
. In that case, by Lemma 2.4 we have
![]() $s_p\in (x,y^m)\cdot e_1+(x^2,xy,y^{m+1})\cdot e_2$
for all
$s_p\in (x,y^m)\cdot e_1+(x^2,xy,y^{m+1})\cdot e_2$
for all
![]() $s\in V^\vee $
in an appropriate trivialization
$s\in V^\vee $
in an appropriate trivialization
![]() $E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
. In view of the isomorphism
$E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
. In view of the isomorphism
![]() $V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
$V\cong \bigwedge ^2V^\vee $
, it follows that the base ideal
![]() $\mathcal {I}$
satisfies
$\mathcal {I}$
satisfies
![]() $\mathcal {I}\otimes \hat {\mathcal {O}}_{S,p}\subset (x^3,x^2y, xy^{m+1},y^{2m+1})$
locally at p; furthermore, recall that
$\mathcal {I}\otimes \hat {\mathcal {O}}_{S,p}\subset (x^3,x^2y, xy^{m+1},y^{2m+1})$
locally at p; furthermore, recall that
![]() $\mathcal {I}$
has at most three local generators at p.
$\mathcal {I}$
has at most three local generators at p.
For
![]() $m=3$
, this implies that
$m=3$
, this implies that
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 14$
, which is a contradiction.
$\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 14$
, which is a contradiction.
For
![]() $m=2$
, this implies that
$m=2$
, this implies that
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 11$
. If
$\operatorname {\mathrm {colength}}(\mathcal {I},p)\geq 11$
. If
![]() $q\neq p$
is the other point where
$q\neq p$
is the other point where
![]() $\xi $
is supported, then
$\xi $
is supported, then
![]() $\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 3$
; hence,
$\operatorname {\mathrm {colength}}(\mathcal {I},q)\geq 3$
; hence,
![]() $\operatorname {\mathrm {colength}}(\mathcal {I})\geq 14$
, and again we obtain a contradiction.
$\operatorname {\mathrm {colength}}(\mathcal {I})\geq 14$
, and again we obtain a contradiction.
The last ingredient we need to derive a contradiction from this situation is the following lemma:
Lemma 5.12. Let
![]() $\xi \in S^{[3]}$
be a length 3 subscheme, which is reduced at
$\xi \in S^{[3]}$
be a length 3 subscheme, which is reduced at
![]() $p\in S$
. Then the locus
$p\in S$
. Then the locus
describes a curve in the linear system
![]() $|\hat {L}|$
, where
$|\hat {L}|$
, where
![]() $\operatorname {\mathrm {Pic}}(\mathcal {M})= \mathbb {Z}\cdot \hat {L}$
.
$\operatorname {\mathrm {Pic}}(\mathcal {M})= \mathbb {Z}\cdot \hat {L}$
.
Proof. Let us denote by
![]() $\zeta $
the (length 2) residual subscheme of p in
$\zeta $
the (length 2) residual subscheme of p in
![]() $\xi $
. Let
$\xi $
. Let
![]() $\mathcal {E}$
be a universal bundle on
$\mathcal {E}$
be a universal bundle on
![]() $S\times \mathcal {M}$
, defining a Fourier–Mukai equivalence
$S\times \mathcal {M}$
, defining a Fourier–Mukai equivalence
![]() $\widetilde {\Phi _{\mathcal {E}}}:=\Phi _{\mathcal {E}}^{S\to \mathcal {M}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})$
.
$\widetilde {\Phi _{\mathcal {E}}}:=\Phi _{\mathcal {E}}^{S\to \mathcal {M}}:\mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (S)\to \mathop {\mathrm {D}^{\mathrm {b}}}\nolimits (\mathcal {M})$
.
The first observation is that, for an appropriate choice of
![]() $\mathcal {E}$
(obtained by twisting
$\mathcal {E}$
(obtained by twisting
![]() $\mathcal {E}$
with the pullback of a line bundle on
$\mathcal {E}$
with the pullback of a line bundle on
![]() $\mathcal {M}$
), we have
$\mathcal {M}$
), we have
![]() $R^0\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )\cong \mathcal {O}_{\mathcal {M}}$
. This can be deduced from the following facts:
$R^0\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )\cong \mathcal {O}_{\mathcal {M}}$
. This can be deduced from the following facts:
-
•
 $v(\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi ))=(1,0,-2)$
(see, e.g., [Reference YoshiokaYos01, Lemma 7.2] or [Reference MaciociaMac17, Proposition 15]).
$v(\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi ))=(1,0,-2)$
(see, e.g., [Reference YoshiokaYos01, Lemma 7.2] or [Reference MaciociaMac17, Proposition 15]). -
•
 $R^1\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )={\mathcal {E}\mathit {xt}}^2(\mathcal {O}_{\gamma ^{-1}(\xi )},\mathcal {O}_{\mathcal {M}})$
, where
$R^1\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )={\mathcal {E}\mathit {xt}}^2(\mathcal {O}_{\gamma ^{-1}(\xi )},\mathcal {O}_{\mathcal {M}})$
, where
 $\gamma :\mathcal {M}^{[3]}\to S^{[3]}$
is the isomorphism of Lemma 5.5. Indeed, to prove this equality one simply applies the Fourier-Mukai functor
$\gamma :\mathcal {M}^{[3]}\to S^{[3]}$
is the isomorphism of Lemma 5.5. Indeed, to prove this equality one simply applies the Fourier-Mukai functor
 $\widetilde {\Phi _{\mathcal {E}}}$
to the distinguished triangle (see the proof of Proposition 5.1), and uses that
$\widetilde {\Phi _{\mathcal {E}}}$
to the distinguished triangle (see the proof of Proposition 5.1), and uses that $$\begin{align*}0\to G\to \mathcal{I}_\xi\to \Phi^{\mathcal{M}\to S}_{\mathcal{E}}(\mathcal{O}_{\gamma^{-1}(\xi)})^\vee[1]\to 0 \end{align*}$$
$$\begin{align*}0\to G\to \mathcal{I}_\xi\to \Phi^{\mathcal{M}\to S}_{\mathcal{E}}(\mathcal{O}_{\gamma^{-1}(\xi)})^\vee[1]\to 0 \end{align*}$$
 $\Phi ^{\mathcal {M}\to S}_{\mathcal {E}}(\cdot ^\vee )^\vee $
is the quasi-inverse of
$\Phi ^{\mathcal {M}\to S}_{\mathcal {E}}(\cdot ^\vee )^\vee $
is the quasi-inverse of
 $\widetilde {\Phi _{\mathcal {E}}}$
.
$\widetilde {\Phi _{\mathcal {E}}}$
.
The unique (up to constant) global section of
![]() $R^0\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )\cong \mathcal {O}_{\mathcal {M}}$
restricts, at a point
$R^0\widetilde {\Phi _{\mathcal {E}}}(\mathcal {I}_\xi )\cong \mathcal {O}_{\mathcal {M}}$
restricts, at a point
![]() $E'\in \mathcal {M}\setminus \gamma ^{-1}(\xi )$
, to the unique section of
$E'\in \mathcal {M}\setminus \gamma ^{-1}(\xi )$
, to the unique section of
![]() $H^0(S,E'\otimes \mathcal {I}_\xi )$
. We will denote by
$H^0(S,E'\otimes \mathcal {I}_\xi )$
. We will denote by
![]() $\widetilde {s}\in H^0(S\times \mathcal {M},\pi _1^*(\mathcal {I}_\xi )\otimes \mathcal {E})$
the corresponding section, where
$\widetilde {s}\in H^0(S\times \mathcal {M},\pi _1^*(\mathcal {I}_\xi )\otimes \mathcal {E})$
the corresponding section, where
![]() $\pi _1:S\times \mathcal {M}\to S$
is the first projection.
$\pi _1:S\times \mathcal {M}\to S$
is the first projection.
Locally, at a point
![]() $E'\in \mathcal {M}$
, the locus
$E'\in \mathcal {M}$
, the locus
![]() $C_{p,\xi }$
is given as follows. Fix
$C_{p,\xi }$
is given as follows. Fix
![]() $x,y$
local analytic coordinates of S around p,
$x,y$
local analytic coordinates of S around p,
![]() $z,w$
local coordinates of
$z,w$
local coordinates of
![]() $\mathcal {M}$
around
$\mathcal {M}$
around
![]() $E'$
and a local trivialization of
$E'$
and a local trivialization of
![]() $\mathcal {E}$
around
$\mathcal {E}$
around
![]() $(p,E')\in S\times \mathcal {M}$
. Then
$(p,E')\in S\times \mathcal {M}$
. Then
![]() $\tilde s$
has a local expression
$\tilde s$
has a local expression
and
![]() $C_{p,\xi }$
is locally given by the equation
$C_{p,\xi }$
is locally given by the equation
![]() $a_1b_2-a_2b_1=0$
.
$a_1b_2-a_2b_1=0$
.
To determine the class of the curve
![]() $C_{p,\xi }$
, we pick a basis
$C_{p,\xi }$
, we pick a basis
![]() $w_1,w_2$
of the tangent space
$w_1,w_2$
of the tangent space
![]() $T_pS$
at p. For
$T_pS$
at p. For
![]() $i=1,2$
, the section
$i=1,2$
, the section
![]() $\tilde s$
gives rise to a section
$\tilde s$
gives rise to a section
Now, observe that
![]() $\mathcal {I}_{\xi }/(\mathcal {I}_\zeta \otimes \mathcal {I}_{[w_i]})$
is isomorphic (as an
$\mathcal {I}_{\xi }/(\mathcal {I}_\zeta \otimes \mathcal {I}_{[w_i]})$
is isomorphic (as an
![]() $\mathcal {O}_S$
-module) to the skyscraper sheaf
$\mathcal {O}_S$
-module) to the skyscraper sheaf
![]() $k(p)$
; this isomorphism is canonical (up to constant), defined via
$k(p)$
; this isomorphism is canonical (up to constant), defined via
![]() $w_i$
. We obtain an isomorphism
$w_i$
. We obtain an isomorphism
given by
![]() $w_i$
, where
$w_i$
, where
![]() $\mathcal {E}_p\cong \mathcal {E}|_{\{p\}\times \mathcal {M}}$
is the vector bundle on
$\mathcal {E}_p\cong \mathcal {E}|_{\{p\}\times \mathcal {M}}$
is the vector bundle on
![]() $\mathcal {M}$
defined by the point
$\mathcal {M}$
defined by the point
![]() $p\in S$
.
$p\in S$
.
The curve
![]() $C_{p,\xi }$
is then defined as the zero locus of
$C_{p,\xi }$
is then defined as the zero locus of
![]() $\tilde {s_1}\wedge \tilde {s_2}\in H^0(\bigwedge ^2 \mathcal {E}_p)$
. Since
$\tilde {s_1}\wedge \tilde {s_2}\in H^0(\bigwedge ^2 \mathcal {E}_p)$
. Since
![]() $v(\mathcal {E}_p)=(2,\hat {L},5)$
(see again [Reference MaciociaMac17, Proposition 15])), we have
$v(\mathcal {E}_p)=(2,\hat {L},5)$
(see again [Reference MaciociaMac17, Proposition 15])), we have
![]() $\bigwedge ^2 \mathcal {E}_p=\hat {L}$
and the assertion follows.
$\bigwedge ^2 \mathcal {E}_p=\hat {L}$
and the assertion follows.
Now, we can conclude the proof of the nonexistence of degree 3 maps. For this last argument, the assumption
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
is not enough; we will also assume that
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
is not enough; we will also assume that
![]() $(S,L)$
is general among
$(S,L)$
is general among
![]() $K3$
surfaces of Picard rank 1.
$K3$
surfaces of Picard rank 1.
Proposition 5.13. If
![]() $(S,L)$
is general among
$(S,L)$
is general among
![]() $K3$
surfaces of Picard rank 1, then there exists no
$K3$
surfaces of Picard rank 1, then there exists no
![]() $V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
$V^\vee \in \mathrm {Gr}(3,H^0(E))$
such that
![]() $\bigcap _{s\in V^\vee } Z_{cycle}(s)=2p+q+r$
(with
$\bigcap _{s\in V^\vee } Z_{cycle}(s)=2p+q+r$
(with
![]() $p\neq q,r$
) and
$p\neq q,r$
) and
![]() $\bigcap _{s\in V^\vee }Z(s)$
is of length 3 and reduced at p.
$\bigcap _{s\in V^\vee }Z(s)$
is of length 3 and reduced at p.
Proof. We argue by contradiction. As in the proof of Lemma 5.12, we denote by
![]() $\zeta $
the (length 2) residual subscheme of p in
$\zeta $
the (length 2) residual subscheme of p in
![]() $\bigcap _{s\in V^\vee }Z(s)$
; in the notations of the statement, we have
$\bigcap _{s\in V^\vee }Z(s)$
; in the notations of the statement, we have
![]() $\zeta =q+r$
with
$\zeta =q+r$
with
![]() $q,r$
two (possibly infinitely near) points.
$q,r$
two (possibly infinitely near) points.
First, notice that for any length 2 subscheme
![]() $\eta \in \mathbb {P}(T_pS)$
nonreduced at p, the inequality
$\eta \in \mathbb {P}(T_pS)$
nonreduced at p, the inequality
![]() $h^0(E\otimes \mathcal {I}_{\eta \cup \zeta })\ge 2$
holds; this follows from Lemma 2.4. Hence, the subschemes
$h^0(E\otimes \mathcal {I}_{\eta \cup \zeta })\ge 2$
holds; this follows from Lemma 2.4. Hence, the subschemes
![]() $\{\eta \cup \zeta \;|\;\eta \in \mathbb {P}(T_pS)\}$
describe a smooth rational curve in the jump locus
$\{\eta \cup \zeta \;|\;\eta \in \mathbb {P}(T_pS)\}$
describe a smooth rational curve in the jump locus
![]() $\mathrm {Bl}_{E}(\mathcal {M})\subset S^{[4]}$
of Corollary 5.9. We claim that this curve is the exceptional divisor in
$\mathrm {Bl}_{E}(\mathcal {M})\subset S^{[4]}$
of Corollary 5.9. We claim that this curve is the exceptional divisor in
![]() $\mathrm {Bl}_{E}(\mathcal {M})$
; in particular, by Corollary 5.9.(2) this will imply that
$\mathrm {Bl}_{E}(\mathcal {M})$
; in particular, by Corollary 5.9.(2) this will imply that
![]() $h^0(\tilde E \otimes \mathcal {I}_{\eta \cup \zeta })=0$
for any
$h^0(\tilde E \otimes \mathcal {I}_{\eta \cup \zeta })=0$
for any
![]() $\eta \in \mathbb {P}(T_pS)$
and
$\eta \in \mathbb {P}(T_pS)$
and
![]() $\tilde E \in \mathcal {M}\setminus~\{ E\}$
.
$\tilde E \in \mathcal {M}\setminus~\{ E\}$
.
In order to prove the claim, assume that the curve is not the exceptional divisor. Then its image R in
![]() $\mathcal {M}$
is a rational curve, describing a component of the curve
$\mathcal {M}$
is a rational curve, describing a component of the curve
The curve
![]() $C_{p,\xi }$
lies in the primitive linear system
$C_{p,\xi }$
lies in the primitive linear system
![]() $|\hat {L}|$
of
$|\hat {L}|$
of
![]() $\mathcal {M}$
by Lemma 5.12, hence
$\mathcal {M}$
by Lemma 5.12, hence
![]() $R=C_{p,\xi }\in |\hat {L}|$
and
$R=C_{p,\xi }\in |\hat {L}|$
and
![]() $p_a(R)=11$
. This yields a contradiction since on the one hand R can only be singular at
$p_a(R)=11$
. This yields a contradiction since on the one hand R can only be singular at
![]() $E\in \mathcal {M}$
, whereas on the other hand every rational curve in
$E\in \mathcal {M}$
, whereas on the other hand every rational curve in
![]() $|\hat {L}|$
is nodal under our generality assumptions on
$|\hat {L}|$
is nodal under our generality assumptions on
![]() $(S,L)$
(hence on
$(S,L)$
(hence on
![]() $(\mathcal {M},\hat {L})$
) by Chen’s result [Reference ChenChe02].
$(\mathcal {M},\hat {L})$
) by Chen’s result [Reference ChenChe02].
Now, we start the analysis. Under our hypotheses, we get
![]() $V=\bigwedge ^2 V^\vee \subset H^0(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_\zeta ^2)$
. Given
$V=\bigwedge ^2 V^\vee \subset H^0(L\otimes \mathcal {I}_p^3\otimes \mathcal {I}_\zeta ^2)$
. Given
![]() $z,w$
local coordinates at p, consider for every
$z,w$
local coordinates at p, consider for every
![]() $\lambda \in \mathbb {C}$
the colength 4 ideal
$\lambda \in \mathbb {C}$
the colength 4 ideal
![]() $\mathcal {J}_\lambda :=(z(z+\lambda w),w(z+\lambda w),w^3)\supset \mathcal {I}_p^3$
. Since
$\mathcal {J}_\lambda :=(z(z+\lambda w),w(z+\lambda w),w^3)\supset \mathcal {I}_p^3$
. Since
![]() $V\subset H^0(L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2)$
, we get
$V\subset H^0(L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2)$
, we get
![]() $h^1(L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2)\ge 1$
.
$h^1(L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2)\ge 1$
.
Given
![]() $\lambda \in \mathbb {C}$
, we consider any nontrivial extension
$\lambda \in \mathbb {C}$
, we consider any nontrivial extension
![]() $\tilde E_\lambda $
of
$\tilde E_\lambda $
of
![]() $L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2$
by
$L \otimes \mathcal J_\lambda \otimes \mathcal {I}_\zeta ^2$
by
![]() $\mathcal {O}_S$
and complete it to a commutative diagram with exact rows and columns:
$\mathcal {O}_S$
and complete it to a commutative diagram with exact rows and columns:

Here,
![]() $s_\lambda $
denotes the section in
$s_\lambda $
denotes the section in
![]() $H^0(\tilde E_\lambda )$
induced by the extension, and
$H^0(\tilde E_\lambda )$
induced by the extension, and
![]() $s_\lambda '$
is the section corresponding to
$s_\lambda '$
is the section corresponding to
![]() $s_\lambda $
under the inclusion
$s_\lambda $
under the inclusion
![]() $H^0(\tilde E_\lambda )\subset H^0(\tilde E_\lambda ^{**})$
. Now, observe that
$H^0(\tilde E_\lambda )\subset H^0(\tilde E_\lambda ^{**})$
. Now, observe that
![]() $Z(s_\lambda ')$
is of local complete intersection at every point; this implies that
$Z(s_\lambda ')$
is of local complete intersection at every point; this implies that
![]() $Z(s_\lambda ')$
has length
$Z(s_\lambda ')$
has length
![]() $\leq 7$
(here we use that any local complete intersection ideal sheaf containing
$\leq 7$
(here we use that any local complete intersection ideal sheaf containing
![]() $\mathcal {I}_\zeta ^2$
has colength
$\mathcal {I}_\zeta ^2$
has colength
![]() $\leq 4$
). On the other hand, by stability of
$\leq 4$
). On the other hand, by stability of
![]() $E_\lambda ^{**}$
we have
$E_\lambda ^{**}$
we have
![]() $7\leq c_2(E_\lambda ^{**})=\operatorname {\mathrm {length}} Z(s_\lambda ')$
.
$7\leq c_2(E_\lambda ^{**})=\operatorname {\mathrm {length}} Z(s_\lambda ')$
.
Therefore, we deduce that
![]() $Z(s_\lambda ')$
has length
$Z(s_\lambda ')$
has length
![]() $7$
and
$7$
and
![]() $Z_{cycle}(s_\lambda ')=3p+2q+2r$
. In particular,
$Z_{cycle}(s_\lambda ')=3p+2q+2r$
. In particular,
![]() $s_\lambda '$
vanishes at
$s_\lambda '$
vanishes at
![]() $\eta _\lambda \cup \zeta $
for a certain
$\eta _\lambda \cup \zeta $
for a certain
![]() $\eta _\lambda \in \mathbb {P}(T_pS)$
; it follows from the observation in the second paragraph of this proof that
$\eta _\lambda \in \mathbb {P}(T_pS)$
; it follows from the observation in the second paragraph of this proof that
![]() $E_\lambda ^{**}=E$
(and hence
$E_\lambda ^{**}=E$
(and hence
![]() $s_\lambda '\in V^\vee =H^0(E\otimes \mathcal {I}_{p\cup \zeta })$
).
$s_\lambda '\in V^\vee =H^0(E\otimes \mathcal {I}_{p\cup \zeta })$
).
Moreover, for any
![]() $\lambda \neq \mu $
and any choice of extensions, the corresponding sections
$\lambda \neq \mu $
and any choice of extensions, the corresponding sections
![]() $s_\lambda ',s_\mu '$
are not proportional since they vanish at a different subscheme at p. Indeed, any colength 3 complete intersection ideal containing
$s_\lambda ',s_\mu '$
are not proportional since they vanish at a different subscheme at p. Indeed, any colength 3 complete intersection ideal containing
![]() $\mathcal J_\lambda $
must be of the form
$\mathcal J_\lambda $
must be of the form
![]() $(z+\lambda w+\epsilon w^2,w^3)$
for some
$(z+\lambda w+\epsilon w^2,w^3)$
for some
![]() $\epsilon $
.
$\epsilon $
.
Hence, varying
![]() $s_\lambda $
algebraically with
$s_\lambda $
algebraically with
![]() $\lambda $
(and taking closure), we can construct an effective divisor
$\lambda $
(and taking closure), we can construct an effective divisor
![]() $C\subset \mathbb {P}(V^\vee )$
of sections whose zero loci are supported in
$C\subset \mathbb {P}(V^\vee )$
of sections whose zero loci are supported in
![]() $\{p,q,r\}$
.
$\{p,q,r\}$
.
Now, recall that, if T denotes the base locus of the rational map ![]() , then the fiber of
, then the fiber of
![]() $S\setminus T\longrightarrow \mathbb {P}(V^\vee )$
over
$S\setminus T\longrightarrow \mathbb {P}(V^\vee )$
over
![]() $[s]\in \mathbb {P}(V^\vee )$
is given by
$[s]\in \mathbb {P}(V^\vee )$
is given by
![]() $Z(s)\cap (S\setminus T)$
(see Proposition 2.1). It follows that the morphism factors through
$Z(s)\cap (S\setminus T)$
(see Proposition 2.1). It follows that the morphism factors through
in particular, we have a generically finite morphism from S minus a finite set of points to an affine variety, which is a contradiction.
6 Genus 13
In this section, we study a very general polarized
![]() $K3$
surface
$K3$
surface
![]() $(S,L)$
of genus
$(S,L)$
of genus
![]() $13$
(which in particular implies
$13$
(which in particular implies
![]() $\mathrm {Pic}(S)=\mathbb Z\cdot L$
). In [Reference MorettiMor23], it was proven that
$\mathrm {Pic}(S)=\mathbb Z\cdot L$
). In [Reference MorettiMor23], it was proven that
![]() $\mathrm {irr}_L(S)\le 6$
. We are going to improve this bound to
$\mathrm {irr}_L(S)\le 6$
. We are going to improve this bound to
![]() $\mathrm {irr}_L(S)\le 4$
by showing that
$\mathrm {irr}_L(S)\le 4$
by showing that
![]() $W^2_4(S,L)$
has a component of positive dimension.
$W^2_4(S,L)$
has a component of positive dimension.
In this case, the moduli space of vector bundles with minimal
![]() $c_2=8$
is
$c_2=8$
is
![]() $\mathcal {M}=\mathcal {M}(2,L,6)$
and can be endowed with a primitive polarization
$\mathcal {M}=\mathcal {M}(2,L,6)$
and can be endowed with a primitive polarization
![]() $\hat L$
of genus
$\hat L$
of genus
![]() $4$
. Note that, since
$4$
. Note that, since
![]() $(S,L)$
is very general,
$(S,L)$
is very general,
![]() $(\mathcal {M},\hat L)$
is also very general among the
$(\mathcal {M},\hat L)$
is also very general among the
![]() $K3$
surfaces of genus
$K3$
surfaces of genus
![]() $4$
. This enables us to apply a result of Galati–Knutsen ([Reference Galati and KnutsenGK13, Proposition 2.2]), which asserts the existence of (finitely many) curves
$4$
. This enables us to apply a result of Galati–Knutsen ([Reference Galati and KnutsenGK13, Proposition 2.2]), which asserts the existence of (finitely many) curves
![]() $C_1,...,C_N\in |\hat {L}|$
with a triple point.
$C_1,...,C_N\in |\hat {L}|$
with a triple point.
Again, by Chen’s results [Reference ChenChe02] on rational curves, the curves
![]() $C_i$
have geometric genus 1 and have the triple point as only singularity. Let us denote by
$C_i$
have geometric genus 1 and have the triple point as only singularity. Let us denote by
![]() $\nu _i:\tilde C_i\to C_i$
the normalization of
$\nu _i:\tilde C_i\to C_i$
the normalization of
![]() $C_i$
.
$C_i$
.
Proposition 6.1. Let
![]() $(S,L)$
be a very general
$(S,L)$
be a very general
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $13$
, and let
$13$
, and let
![]() $C_1,\dots ,C_N\in |\hat L|$
be the elliptic curves with a triple point. Then there are nonconstant morphisms
$C_1,\dots ,C_N\in |\hat L|$
be the elliptic curves with a triple point. Then there are nonconstant morphisms
(
![]() $i=1,...,N$
) with pairwise disjoint images. In particular,
$i=1,...,N$
) with pairwise disjoint images. In particular,
![]() $\mathrm {irr}_L(S)\le 4$
and
$\mathrm {irr}_L(S)\le 4$
and
![]() $\mathrm {dim}(W^2_4(S,L))\ge 1.$
$\mathrm {dim}(W^2_4(S,L))\ge 1.$
Proof. Let
![]() $E_i\in \mathcal {M}$
be the triple point of the elliptic curve
$E_i\in \mathcal {M}$
be the triple point of the elliptic curve
![]() $C_i$
. The pushforward of any line bundle on
$C_i$
. The pushforward of any line bundle on
![]() $\tilde C_i$
produces a rank 1, torsion-free sheaf on
$\tilde C_i$
produces a rank 1, torsion-free sheaf on
![]() $C_i$
, with three generators at the singular point
$C_i$
, with three generators at the singular point
![]() $E_i\in C_i$
. We thus have a (noncanonical) closed immersion
$E_i\in C_i$
. We thus have a (noncanonical) closed immersion
where
![]() $\overline {JC_i}$
denotes the compactified Jacobian of
$\overline {JC_i}$
denotes the compactified Jacobian of
![]() $C_i$
(see [Reference BeauvilleBea99, Lemma 3.1]) whose image is contained in the locus of torsion-free sheaves with three generators at the triple point.
$C_i$
(see [Reference BeauvilleBea99, Lemma 3.1]) whose image is contained in the locus of torsion-free sheaves with three generators at the triple point.
On the other hand,
![]() $C_i$
is the unique curve with a triple point at
$C_i$
is the unique curve with a triple point at
![]() $E_i$
(indeed one can derive a numerical contradiction from
$E_i$
(indeed one can derive a numerical contradiction from
![]() $h^1(\mathcal {M},\hat {L}\otimes \mathcal {I}_{E_i})\geq 3$
by considering successive stable extensions). Thus, Lemma 2.13 provides an isomorphism
$h^1(\mathcal {M},\hat {L}\otimes \mathcal {I}_{E_i})\geq 3$
by considering successive stable extensions). Thus, Lemma 2.13 provides an isomorphism
All in all, we obtain a morphism
![]() $\tilde C_i \to W^2_4(S,L)$
(after sending
$\tilde C_i \to W^2_4(S,L)$
(after sending
![]() $\xi \mapsto (E_i,H^0(E_i\otimes \mathcal {I}_\xi ))$
). This morphism is not constant (otherwise the sections of
$\xi \mapsto (E_i,H^0(E_i\otimes \mathcal {I}_\xi ))$
). This morphism is not constant (otherwise the sections of
![]() $H^0(E\otimes \mathcal {I}_\xi )$
would vanish at infinitely many points). Finally, since the vector bundles
$H^0(E\otimes \mathcal {I}_\xi )$
would vanish at infinitely many points). Finally, since the vector bundles
![]() $E_i$
are pairwise distinct (recall that there is a unique curve with a triple point at
$E_i$
are pairwise distinct (recall that there is a unique curve with a triple point at
![]() $E_i$
), the images of all these morphisms are pairwise disjoint.
$E_i$
), the images of all these morphisms are pairwise disjoint.
Remark 6.2. If one can prove that
![]() $h^0(E\otimes \mathcal {I}_\zeta )\le 2$
for all
$h^0(E\otimes \mathcal {I}_\zeta )\le 2$
for all
![]() $\zeta \in S^{[5]}$
, then the map
$\zeta \in S^{[5]}$
, then the map
![]() $\tilde C_i\to W^2_4(S,L)$
would be a closed immersion (see also Remark 2.5).
$\tilde C_i\to W^2_4(S,L)$
would be a closed immersion (see also Remark 2.5).
7 Even genera
The goal of this section is to prove Theorem B. This result wants to be a motivation for future work towards a more complete statement. Many proofs are similar (or considerably simpler) to the odd genera case, hence we will provide fewer details.
As usual,
![]() $(S,L)$
will denote a polarized
$(S,L)$
will denote a polarized
![]() $K3$
surface with
$K3$
surface with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
.
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
.
7.1 Genus 8
Assume that the polarization has genus 8 (i.e.,
![]() $L^2=14$
). Then
$L^2=14$
). Then
![]() $\operatorname {\mathrm {irr}}_L(S)\leq 4$
, as proved in [Reference MorettiMor23]. Indeed, let E denote the stable vector bundle with
$\operatorname {\mathrm {irr}}_L(S)\leq 4$
, as proved in [Reference MorettiMor23]. Indeed, let E denote the stable vector bundle with
![]() $v(E)=(2,L,4)$
. It satisfies
$v(E)=(2,L,4)$
. It satisfies
![]() $h^0(E)=6$
and
$h^0(E)=6$
and
![]() $c_2(E)=5$
. Then for every point
$c_2(E)=5$
. Then for every point
![]() $p\in S$
, we have
$p\in S$
, we have
![]() $h^0(E\otimes \mathcal {I}_p)=4$
, and any
$h^0(E\otimes \mathcal {I}_p)=4$
, and any
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E\otimes \mathcal {I}_p))$
defines a rational dominant map
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E\otimes \mathcal {I}_p))$
defines a rational dominant map ![]() of degree
of degree
![]() $\leq 4$
.
$\leq 4$
.
In other words, we obtain an irreducible component of
![]() $W^2_4(S,L)$
as the projectivization of a rank 4 vector bundle on S.
$W^2_4(S,L)$
as the projectivization of a rank 4 vector bundle on S.
In order to determine the equality
![]() $\operatorname {\mathrm {irr}}_L(S)=4$
, we note that according to Corollary 2.3, degree 3 maps correspond to
$\operatorname {\mathrm {irr}}_L(S)=4$
, we note that according to Corollary 2.3, degree 3 maps correspond to
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
such that
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
such that
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
is of degree
![]() $2$
. The case where the schematic intersection
$2$
. The case where the schematic intersection
![]() $\bigcap _{s\in V^\vee }Z(s)$
is of length 2 is discarded by the following:
$\bigcap _{s\in V^\vee }Z(s)$
is of length 2 is discarded by the following:
Lemma 7.1. For every
![]() $\xi \in S^{[2]}$
, the vanishing
$\xi \in S^{[2]}$
, the vanishing
![]() $h^1({E}\otimes \mathcal {I}_\xi )=0$
holds.
$h^1({E}\otimes \mathcal {I}_\xi )=0$
holds.
Proof. We use Bridgeland stability. Both
![]() $\mathcal {I}_\xi $
and
$\mathcal {I}_\xi $
and
![]() $E^\vee [1]$
are
$E^\vee [1]$
are
![]() $\sigma _{\alpha ,-\frac {1}{3}}$
-stable objects for every
$\sigma _{\alpha ,-\frac {1}{3}}$
-stable objects for every
![]() $\alpha>0$
, as a consequence of Lemma 2.11 (and the fact that there are no rank 3 spherical classes). In addition, one easily checks that the numerical wall
$\alpha>0$
, as a consequence of Lemma 2.11 (and the fact that there are no rank 3 spherical classes). In addition, one easily checks that the numerical wall
![]() $W(\mathcal {I}_\xi , E^\vee [1])$
intersects the vertical line
$W(\mathcal {I}_\xi , E^\vee [1])$
intersects the vertical line
![]() $\beta =\frac {-1}{3}$
; for the corresponding stability condition
$\beta =\frac {-1}{3}$
; for the corresponding stability condition
![]() $\sigma _0$
, both
$\sigma _0$
, both
![]() $\mathcal {I}_\xi $
and
$\mathcal {I}_\xi $
and
![]() $E^\vee [1]$
are
$E^\vee [1]$
are
![]() $\sigma _0$
-stable objects of the same slope, hence
$\sigma _0$
-stable objects of the same slope, hence
![]() $0=\hom (\mathcal {I}_\xi , E^\vee [1])=h^1(E\otimes \mathcal {I}_\xi )$
.
$0=\hom (\mathcal {I}_\xi , E^\vee [1])=h^1(E\otimes \mathcal {I}_\xi )$
.
On the other hand, if the schematic intersection is a reduced point, then an argument analogous to that of Lemma 3.3 yields a contradiction again. This proves the equality
![]() $\operatorname {\mathrm {irr}}_L(S)=4$
.
$\operatorname {\mathrm {irr}}_L(S)=4$
.
7.2 Genus 10
Assume now that L is a polarization of genus 10 (i.e.,
![]() $L^2=18$
). Let E denote the stable vector bundle with
$L^2=18$
). Let E denote the stable vector bundle with
![]() $v(E)=(2,L,5)$
(which satisfies
$v(E)=(2,L,5)$
(which satisfies
![]() $h^0(E)=7$
,
$h^0(E)=7$
,
![]() $c_2(E)=6$
).
$c_2(E)=6$
).
The interesting point for this genus is that
![]() $W^2_4(S,L)$
is not irreducible:
$W^2_4(S,L)$
is not irreducible:
Lemma 7.2.
![]() $W^2_4(S,L)$
has a component isomorphic to the Hilbert square
$W^2_4(S,L)$
has a component isomorphic to the Hilbert square
![]() $S^{[2]}$
, and a component isomorphic to
$S^{[2]}$
, and a component isomorphic to
![]() $\mathbb P (E)$
.
$\mathbb P (E)$
.
Proof. The component isomorphic to
![]() $S^{[2]}$
is elementary to construct: For any
$S^{[2]}$
is elementary to construct: For any
![]() $\xi \in S^{[2]}$
, the vector space
$\xi \in S^{[2]}$
, the vector space
![]() $H^0(E\otimes \mathcal {I}_\xi )$
has dimension
$H^0(E\otimes \mathcal {I}_\xi )$
has dimension
![]() $\geq 3$
and hence induces a map of degree
$\geq 3$
and hence induces a map of degree
![]() $\leq 4$
by Proposition 2.1. The fact that the map
$\leq 4$
by Proposition 2.1. The fact that the map
![]() $S^{[2]}\to W^2_4(S,L)$
is an isomorphism onto its image follows from Remark 2.5 together with the remark below the proof of this lemma.
$S^{[2]}\to W^2_4(S,L)$
is an isomorphism onto its image follows from Remark 2.5 together with the remark below the proof of this lemma.
For the second component, pick
![]() $[w]\in \mathbb {P}(E)$
, namely
$[w]\in \mathbb {P}(E)$
, namely
![]() $[w] \in \mathbb {P}(E/E\otimes \mathcal I_p)$
for some
$[w] \in \mathbb {P}(E/E\otimes \mathcal I_p)$
for some
![]() $p\in S$
. Consider the subsheaf
$p\in S$
. Consider the subsheaf
![]() $E_w\subset E$
such that
$E_w\subset E$
such that
![]() $E_w|_{S\setminus p}\cong E|_{S\setminus p}$
, and
$E_w|_{S\setminus p}\cong E|_{S\setminus p}$
, and
![]() $E_w=m_p\cdot w+m_p^2E$
in a neighborhood of p. It is easy to check that
$E_w=m_p\cdot w+m_p^2E$
in a neighborhood of p. It is easy to check that
![]() $h^0(E_w)=3$
and that every section in
$h^0(E_w)=3$
and that every section in
![]() $H^0(E_w)\subset H^0(E)$
vanishes with order
$H^0(E_w)\subset H^0(E)$
vanishes with order
![]() $\geq 2$
at p. Thus, by Proposition 2.1,
$\geq 2$
at p. Thus, by Proposition 2.1,
![]() $H^0(E_w)$
defines a map of degree
$H^0(E_w)$
defines a map of degree
![]() $\leq 4$
.
$\leq 4$
.
Remark 7.3. Any map of degree 3 is given by
![]() $V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
such that
$V^\vee \in \operatorname {\mathrm {Gr}}(3,H^0(E))$
such that
![]() $\bigcap _{s\in V^\vee }Z_{cycle}(s)$
has degree
$\bigcap _{s\in V^\vee }Z_{cycle}(s)$
has degree
![]() $3$
.
$3$
.
-
1. Bridgeland stability easily gives
 $h^1(E\otimes \mathcal {I}_\xi )\le 1$
(hence
$h^1(E\otimes \mathcal {I}_\xi )\le 1$
(hence
 $h^0(E\otimes \mathcal {I}_\xi )\le 2$
) for any
$h^0(E\otimes \mathcal {I}_\xi )\le 2$
) for any
 $\xi \in S^{[3]}$
. Indeed, a nonzero morphism
$\xi \in S^{[3]}$
. Indeed, a nonzero morphism
 $\mathcal {I}_\xi \to E^\vee [1]$
determines the HN filtration of
$\mathcal {I}_\xi \to E^\vee [1]$
determines the HN filtration of
 $\mathcal {I}_\xi $
for suitable stability conditions. This discards the case where
$\mathcal {I}_\xi $
for suitable stability conditions. This discards the case where
 $\bigcap _{s\in V^\vee }Z(s)$
has length 3.
$\bigcap _{s\in V^\vee }Z(s)$
has length 3. -
2. If
 $\bigcap _{s\in V^\vee }Z(s)$
is a reduced point
$\bigcap _{s\in V^\vee }Z(s)$
is a reduced point
 $p\in S$
, then for an appropriate trivialization
$p\in S$
, then for an appropriate trivialization
 $E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p, the subsheaf
$E_p\cong e_1\cdot \mathcal {O}_{S,p}\oplus e_2\cdot \mathcal {O}_{S,p}$
of E near p, the subsheaf
 $E_1\subset E$
defined by
$E_1\subset E$
defined by
 $E_1=m_p\cdot e_1+m_p^3\cdot e_2$
satisfies
$E_1=m_p\cdot e_1+m_p^3\cdot e_2$
satisfies
 $h^0(E_1)\geq 3$
(hence
$h^0(E_1)\geq 3$
(hence
 $h^1(E_1)\geq 3$
). The triple extension is stable of rank 5: Since
$h^1(E_1)\geq 3$
). The triple extension is stable of rank 5: Since $$\begin{align*}0\to\mathcal{O}_S^{\oplus 3}\to F\to E_1\to 0 \end{align*}$$
$$\begin{align*}0\to\mathcal{O}_S^{\oplus 3}\to F\to E_1\to 0 \end{align*}$$
 $E_1$
has six local generators at p, it follows that
$E_1$
has six local generators at p, it follows that
 $v(F^{**})=(5,L,k)$
for some
$v(F^{**})=(5,L,k)$
for some
 $k\geq 2$
.
$k\geq 2$
.
If
 $k\geq 3$
, this contradicts the stability of
$k\geq 3$
, this contradicts the stability of
 $F^{**}$
. For
$F^{**}$
. For
 $k=2$
, we have that F has exactly 6 local generators at p, which implies
$k=2$
, we have that F has exactly 6 local generators at p, which implies
 $h^0(F^{**}\otimes \mathcal {I}_p)\geq 2$
(hence
$h^0(F^{**}\otimes \mathcal {I}_p)\geq 2$
(hence
 $h^1(F^{**}\otimes \mathcal {I}_p)\geq 1$
). This easily contradicts the fact that
$h^1(F^{**}\otimes \mathcal {I}_p)\geq 1$
). This easily contradicts the fact that
 $F^{**}$
is spherical.
$F^{**}$
is spherical.
The configuration that is hard to exclude is that of a length 2 schematic intersection. Such cases are parametrized by a component of the intersection
![]() $\mathbb P(E)\cap S^{[2]}$
of the two loci described in Lemma 7.2 (it coincides with the intersection along the locus of nonreduced subschemes).
$\mathbb P(E)\cap S^{[2]}$
of the two loci described in Lemma 7.2 (it coincides with the intersection along the locus of nonreduced subschemes).
7.3 Genus 12 and 14
In this section, we consider analogous statements for
![]() $K3$
surfaces of genus 12 and 14. In the case of genus 14, the desired component was already described in [Reference MorettiMor23, Theorem 2.4]. For genus 12, the following improves the estimate given in [Reference MorettiMor23]:
$K3$
surfaces of genus 12 and 14. In the case of genus 14, the desired component was already described in [Reference MorettiMor23, Theorem 2.4]. For genus 12, the following improves the estimate given in [Reference MorettiMor23]:
Proposition 7.4. If
![]() $(S,L)$
is a polarized
$(S,L)$
is a polarized
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $12$
with
$12$
with
![]() $\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
, then
$\operatorname {\mathrm {Pic}}(S)=\mathbb {Z}\cdot L$
, then
![]() $W^2_4(S,L)$
has a unirational
$W^2_4(S,L)$
has a unirational
![]() $3$
-dimensional component. In particular,
$3$
-dimensional component. In particular,
![]() $\operatorname {\mathrm {irr}}_L(S)\le 4$
.
$\operatorname {\mathrm {irr}}_L(S)\le 4$
.
Proof. This can be proved via Bridgeland stability, similarly to other genera. Consider the spherical stable vector bundle E with
![]() $v(E)=(2,L,6)$
(so that
$v(E)=(2,L,6)$
(so that
![]() $c_2(E)=7$
and
$c_2(E)=7$
and
![]() $h^0(E)=8$
).
$h^0(E)=8$
).
If
![]() $\xi \in S^{[3]}$
, any nonzero morphism
$\xi \in S^{[3]}$
, any nonzero morphism
![]() $\mathcal {I}_\xi \to E^\vee [1]$
defines a short exact sequence
$\mathcal {I}_\xi \to E^\vee [1]$
defines a short exact sequence
(for F the stable bundle with
![]() $v(F)=(3,-L,4)$
) destabilizing
$v(F)=(3,-L,4)$
) destabilizing
![]() $\mathcal {I}_\xi $
along a certain wall W. This is the HN filtration of
$\mathcal {I}_\xi $
along a certain wall W. This is the HN filtration of
![]() $\mathcal {I}_\xi $
just below
$\mathcal {I}_\xi $
just below
![]() $\sigma _0:=W\cap \{\beta =\frac {-2}{5}\}$
(by
$\sigma _0:=W\cap \{\beta =\frac {-2}{5}\}$
(by
![]() $\sigma _0$
-stability of F and
$\sigma _0$
-stability of F and
![]() $E^\vee [1]$
), hence the morphism
$E^\vee [1]$
), hence the morphism
![]() $\mathcal {I}_\xi \to E^\vee [1]$
is unique (up to constant). It follows that the jump locus
$\mathcal {I}_\xi \to E^\vee [1]$
is unique (up to constant). It follows that the jump locus
![]() $R_3=\{\xi \in S^{[3]}|h^1(E\otimes \mathcal {I}_\xi )=1\}$
equals
$R_3=\{\xi \in S^{[3]}|h^1(E\otimes \mathcal {I}_\xi )=1\}$
equals
![]() $\mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],F))=\mathbb {P}^3$
; for each
$\mathbb {P}(\operatorname {\mathrm {Ext}}^1(E^\vee [1],F))=\mathbb {P}^3$
; for each
![]() $\xi $
in this jump locus,
$\xi $
in this jump locus,
![]() $H^0(E\otimes \mathcal {I}_\xi )$
defines a map of degree
$H^0(E\otimes \mathcal {I}_\xi )$
defines a map of degree
![]() $\leq 4$
. Hence, we get a morphism
$\leq 4$
. Hence, we get a morphism
![]() $\mathbb P^3\to W^2_4(S,L)$
. This map is finite onto its image. Otherwise, we would get
$\mathbb P^3\to W^2_4(S,L)$
. This map is finite onto its image. Otherwise, we would get
![]() $H^0(E\otimes \mathcal {I}_{\xi _t})$
constant for a one-dimensional family of
$H^0(E\otimes \mathcal {I}_{\xi _t})$
constant for a one-dimensional family of
![]() $\xi _t\in R_3$
. This would imply that
$\xi _t\in R_3$
. This would imply that
![]() $3=h^0(E\otimes \bigcap \mathcal {I}_{\xi _t})=h^0(E\otimes \mathcal {I}_\zeta )=3$
for some
$3=h^0(E\otimes \bigcap \mathcal {I}_{\xi _t})=h^0(E\otimes \mathcal {I}_\zeta )=3$
for some
![]() $\zeta \in S^{[4]}$
noncurvilinear, thus inducing a map
$\zeta \in S^{[4]}$
noncurvilinear, thus inducing a map
![]() $S\dashrightarrow \mathbb {P}^2$
of degree
$S\dashrightarrow \mathbb {P}^2$
of degree
![]() $2$
, contradiction.
$2$
, contradiction.
8 Final questions and comments
Throughout this section, we denote by
![]() $(S_g,L)$
a very general polarized
$(S_g,L)$
a very general polarized
![]() $K3$
surface of genus g.
$K3$
surface of genus g.
Even though Theorem A and Theorem B are still far from providing a complete description of the number
![]() $\operatorname {\mathrm {irr}}_L(S_g)$
for arbitrary g, they motivate several questions that may deserve some attention. The first natural question is to complete the picture in even genera:
$\operatorname {\mathrm {irr}}_L(S_g)$
for arbitrary g, they motivate several questions that may deserve some attention. The first natural question is to complete the picture in even genera:
Question 8.1. Is
![]() $\operatorname {\mathrm {irr}}_L(S_g)=4$
for
$\operatorname {\mathrm {irr}}_L(S_g)=4$
for
![]() $g=10,12,13,14$
? Are there genera
$g=10,12,13,14$
? Are there genera
![]() $g\geq 15$
for which the equality
$g\geq 15$
for which the equality
![]() $\operatorname {\mathrm {irr}}_L(S_g)=4$
holds?
$\operatorname {\mathrm {irr}}_L(S_g)=4$
holds?
Aside from the independent interest of the Brill–Noether loci, our description seems to indicate that the locus of maps of minimal degree is an essential invariant to understand how
![]() $\operatorname {\mathrm {irr}}_L(S_g)$
varies with g. It is tempting to propose the following:
$\operatorname {\mathrm {irr}}_L(S_g)$
varies with g. It is tempting to propose the following:
Question 8.2. Is it true that either
![]() $\operatorname {\mathrm {irr}}_L(S_{g+2})=\operatorname {\mathrm {irr}}_L(S_g)+1$
, or
$\operatorname {\mathrm {irr}}_L(S_{g+2})=\operatorname {\mathrm {irr}}_L(S_g)+1$
, or
![]() $\operatorname {\mathrm {irr}}_L(S_{g+2})=\operatorname {\mathrm {irr}}_L(S_g)$
and
$\operatorname {\mathrm {irr}}_L(S_{g+2})=\operatorname {\mathrm {irr}}_L(S_g)$
and
![]() $\dim W^2_{\operatorname {\mathrm {irr}}_L(S_{g+2})}=\dim W^2_{\operatorname {\mathrm {irr}}_L(S_{g})}-1$
?
$\dim W^2_{\operatorname {\mathrm {irr}}_L(S_{g+2})}=\dim W^2_{\operatorname {\mathrm {irr}}_L(S_{g})}-1$
?
An affirmative answer would imply an affirmative answer to the following question, which is nothing but a weak version of a conjecture in [Reference Bastianelli, De Poi, Ein, Lazarsfeld and UlleryBDPE+17]:
Question 8.3. Does one have
![]() $\mathrm {irr}_L(S_g)\to \infty $
as
$\mathrm {irr}_L(S_g)\to \infty $
as
![]() $g\to \infty $
?
$g\to \infty $
?
Actually, [Reference Bastianelli, De Poi, Ein, Lazarsfeld and UlleryBDPE+17, Conjecture 4.2] predicts something stronger:
![]() $\operatorname {\mathrm {irr}}(S_g)\to \infty $
as
$\operatorname {\mathrm {irr}}(S_g)\to \infty $
as
![]() $g\to \infty $
. The degree of irrationality of
$g\to \infty $
. The degree of irrationality of
![]() $K3$
surfaces was indeed our original motivation. Therefore, it is natural to ask:
$K3$
surfaces was indeed our original motivation. Therefore, it is natural to ask:
Question 8.4. Does the equality
![]() $\mathrm {irr}(S_g)=\mathrm {irr}_L(S_g)$
hold for every g?
$\mathrm {irr}(S_g)=\mathrm {irr}_L(S_g)$
hold for every g?
It is worth mentioning that the analogous question is true for hypersurfaces of large degree in projective space ([Reference Bastianelli, De Poi, Ein, Lazarsfeld and UlleryBDPE+17]), and it seems an interesting problem for
![]() $(1,d)$
-polarized abelian surfaces (for suitable d).
$(1,d)$
-polarized abelian surfaces (for suitable d).
All of these questions concern the invariant
![]() $\operatorname {\mathrm {irr}}_L(S_g)$
, but also many questions arise about the Brill–Noether loci, with special focus on
$\operatorname {\mathrm {irr}}_L(S_g)$
, but also many questions arise about the Brill–Noether loci, with special focus on
![]() $W^2_{\operatorname {\mathrm {irr}}_L(S_g)}(S_g,L)$
; apart from their dimension, one could ask about other aspects of their geometry (irreducible components, singular locus), Torelli-type questions (e.g., for which g is
$W^2_{\operatorname {\mathrm {irr}}_L(S_g)}(S_g,L)$
; apart from their dimension, one could ask about other aspects of their geometry (irreducible components, singular locus), Torelli-type questions (e.g., for which g is
![]() $(S_g,L)$
determined by
$(S_g,L)$
determined by
![]() $W^2_{\operatorname {\mathrm {irr}}_L(S_g)}(S_g,L)$
), etc.
$W^2_{\operatorname {\mathrm {irr}}_L(S_g)}(S_g,L)$
), etc.
In particular, in view of Remark 2.5 it is tempting to draw some parallels about the singularities of the Brill–Noether loci for general
![]() $K3$
surfaces with the classical case of curves. As Remark 2.5 suggests, this principle should hold for those components arising as cohomology jump loci. The picture in general seems to be quite complicated to have a comprehensive understanding.
$K3$
surfaces with the classical case of curves. As Remark 2.5 suggests, this principle should hold for those components arising as cohomology jump loci. The picture in general seems to be quite complicated to have a comprehensive understanding.
Acknowledgements
We would like to thank G. Farkas for mentoring, as well as A. Beauville, D. Huybrechts, M. Lahoz, E. Macrì, R. Moschetti, I. Smirnov and P. Stellari for answering some of our questions. We are also grateful to R. Lazarsfeld, Á. Ríos Ortiz and I. Vogt for some interesting conversations and to an anonymous referee for his/her comments and suggestions.
The authors are supported by the ERC Advanced Grant SYZYGY. This project has received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program (grant agreement No. 834172).
Competing interest
The authors have no competing interest to declare.
Data availability statement
Data availability is not applicable to this article as no new data were created or analysed in this study.


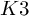
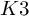
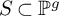
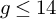
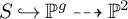 of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most
of minimal degree and their variational structure. In particular, we prove that the degree of irrationality of all such surfaces is at most 
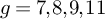
 of degree
of degree