Let  $(W,S)$ be a Coxeter system, and write
$(W,S)$ be a Coxeter system, and write  $S=\{s_i:i\in I\}$, where I is a finite index set. Fix a nonempty convex subset
$S=\{s_i:i\in I\}$, where I is a finite index set. Fix a nonempty convex subset  $\mathscr {L}$ of W. If W is of type A, then
$\mathscr {L}$ of W. If W is of type A, then  $\mathscr {L}$ is the set of linear extensions of a poset, and there are important Bender–Knuth involutions
$\mathscr {L}$ is the set of linear extensions of a poset, and there are important Bender–Knuth involutions  $\mathrm {BK}_i\colon \mathscr {L}\to \mathscr {L}$ indexed by elements of I. For arbitrary W and for each
$\mathrm {BK}_i\colon \mathscr {L}\to \mathscr {L}$ indexed by elements of I. For arbitrary W and for each  $i\in I$, we introduce an operator
$i\in I$, we introduce an operator  $\tau _i\colon W\to W$ (depending on
$\tau _i\colon W\to W$ (depending on  $\mathscr {L}$) that we call a noninvertible Bender–Knuth toggle; this operator restricts to an involution on
$\mathscr {L}$) that we call a noninvertible Bender–Knuth toggle; this operator restricts to an involution on  $\mathscr {L}$ that coincides with
$\mathscr {L}$ that coincides with  $\mathrm {BK}_i$ in type A. Given a Coxeter element
$\mathrm {BK}_i$ in type A. Given a Coxeter element  $c=s_{i_n}\cdots s_{i_1}$, we consider the operator
$c=s_{i_n}\cdots s_{i_1}$, we consider the operator  $\mathrm {Pro}_c=\tau _{i_n}\cdots \tau _{i_1}$. We say W is futuristic if for every nonempty finite convex set
$\mathrm {Pro}_c=\tau _{i_n}\cdots \tau _{i_1}$. We say W is futuristic if for every nonempty finite convex set  $\mathscr {L}$, every Coxeter element c and every
$\mathscr {L}$, every Coxeter element c and every  $u\in W$, there exists an integer
$u\in W$, there exists an integer  $K\geq 0$ such that
$K\geq 0$ such that  $\mathrm {Pro}_c^K(u)\in \mathscr {L}$. We prove that finite Coxeter groups, right-angled Coxeter groups, rank-3 Coxeter groups, affine Coxeter groups of types
$\mathrm {Pro}_c^K(u)\in \mathscr {L}$. We prove that finite Coxeter groups, right-angled Coxeter groups, rank-3 Coxeter groups, affine Coxeter groups of types  $\widetilde A$ and
$\widetilde A$ and  $\widetilde C$, and Coxeter groups whose Coxeter graphs are complete are all futuristic. When W is finite, we actually prove that if
$\widetilde C$, and Coxeter groups whose Coxeter graphs are complete are all futuristic. When W is finite, we actually prove that if  $s_{i_N}\cdots s_{i_1}$ is a reduced expression for the long element of W, then
$s_{i_N}\cdots s_{i_1}$ is a reduced expression for the long element of W, then  $\tau _{i_N}\cdots \tau _{i_1}(W)=\mathscr {L}$; this allows us to determine the smallest integer
$\tau _{i_N}\cdots \tau _{i_1}(W)=\mathscr {L}$; this allows us to determine the smallest integer  $\mathrm {M}(c)$ such that
$\mathrm {M}(c)$ such that  $\mathrm {Pro}_c^{{\mathrm {M}}(c)}(W)=\mathscr {L}$ for all
$\mathrm {Pro}_c^{{\mathrm {M}}(c)}(W)=\mathscr {L}$ for all  $\mathscr {L}$. We also exhibit infinitely many non-futuristic Coxeter groups, including all irreducible affine Coxeter groups that are not of type
$\mathscr {L}$. We also exhibit infinitely many non-futuristic Coxeter groups, including all irreducible affine Coxeter groups that are not of type  $\widetilde A$,
$\widetilde A$,  $\widetilde C$, or
$\widetilde C$, or  $\widetilde G_2$.
$\widetilde G_2$.
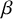 $\beta $E ensemble
$\beta $E ensemble
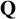 ${\mathbf {Q}}$
${\mathbf {Q}}$