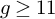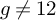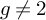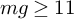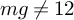1 Introduction
Let
![]() ${\mathcal {F}}_g$
be the moduli stack of primitively polarised K3 surface
${\mathcal {F}}_g$
be the moduli stack of primitively polarised K3 surface
![]() $(X,H)$
with
$(X,H)$
with
![]() $H^2 = 2g-2$
, and let
$H^2 = 2g-2$
, and let
![]() ${\mathcal {P}}_{g_m}$
be the moduli stack of triples
${\mathcal {P}}_{g_m}$
be the moduli stack of triples
![]() $(X,H,C)$
such that
$(X,H,C)$
such that
![]() $(X,H)\in {\mathcal {F}}_g$
and
$(X,H)\in {\mathcal {F}}_g$
and
![]() $C \in |mH|$
a smooth curve of genus
$C \in |mH|$
a smooth curve of genus
![]() $g_m=m^2(g-1)+1$
. There are natural forgetful maps
$g_m=m^2(g-1)+1$
. There are natural forgetful maps

where the fibre of
![]() $\Phi _{g_m}$
over
$\Phi _{g_m}$
over
![]() $(X,H)\in {\mathcal {F}}_g$
is an open subset of the linear system
$(X,H)\in {\mathcal {F}}_g$
is an open subset of the linear system
![]() $|m H|$
. In recent years, there is a series of works studying the rational map
$|m H|$
. In recent years, there is a series of works studying the rational map
![]() ${\Psi }_{{g_{m}}}$
and its rational section. For instance, Mukai has proved in [Reference Mukai16] that the rational map
${\Psi }_{{g_{m}}}$
and its rational section. For instance, Mukai has proved in [Reference Mukai16] that the rational map ![]() is dominant if
is dominant if
![]() $g\leq 11$
and
$g\leq 11$
and
![]() $g \neq 10$
, while Ciliberto–Lopez–Miranda [Reference Ciliberto, Lopez and Miranda8] showed that
$g \neq 10$
, while Ciliberto–Lopez–Miranda [Reference Ciliberto, Lopez and Miranda8] showed that
![]() $\Psi _g $
is generically injective if
$\Psi _g $
is generically injective if
![]() $ g\geq 11$
and
$ g\geq 11$
and
![]() $g\neq 12$
. More generally, due to the results of [Reference Ciliberto, Lopez and Miranda9] and the recent work in Ciliberto–Dedieu–Sernesi [Reference Ciliberto, Dedieu and Sernesi6, Reference Ciliberto and Dedieu5], the map
$g\neq 12$
. More generally, due to the results of [Reference Ciliberto, Lopez and Miranda9] and the recent work in Ciliberto–Dedieu–Sernesi [Reference Ciliberto, Dedieu and Sernesi6, Reference Ciliberto and Dedieu5], the map
![]() ${\Psi }_{{g_{m}}}$
is generically finite when
${\Psi }_{{g_{m}}}$
is generically finite when
![]() $mg\geq 11$
and
$mg\geq 11$
and
![]() $mg\neq 12$
. There are other approaches for the case
$mg\neq 12$
. There are other approaches for the case
![]() $m\geq 2,\,g\geq 8$
or
$m\geq 2,\,g\geq 8$
or
![]() $m\geq 5, g=7$
(cf. [Reference Ciliberto, Flamini, Galati and Knutsen7, Reference Kemeny14]).
$m\geq 5, g=7$
(cf. [Reference Ciliberto, Flamini, Galati and Knutsen7, Reference Kemeny14]).
On the other hand, Mukai has proposed a program in [Reference Mukai18] to find the rational section of
![]() $\Psi _g$
by relating the K3 surface with the Brill–Noether locus of vector bundles on curves. This has been confirmed by Mukai in [Reference Mukai17] when
$\Psi _g$
by relating the K3 surface with the Brill–Noether locus of vector bundles on curves. This has been confirmed by Mukai in [Reference Mukai17] when
![]() $g=11$
and later on Arbarello–Bruno–Sernesi [Reference Arbarello, Bruno and Sernesi1] generalised his result to the case
$g=11$
and later on Arbarello–Bruno–Sernesi [Reference Arbarello, Bruno and Sernesi1] generalised his result to the case
![]() $g=4k+3$
for some k. In recent years, Feyzbakhsh has verified this program in [Reference Feyzbakhsh11, Reference Feyzbakhsh13] for all
$g=4k+3$
for some k. In recent years, Feyzbakhsh has verified this program in [Reference Feyzbakhsh11, Reference Feyzbakhsh13] for all
![]() $g \geq 11$
and
$g \geq 11$
and
![]() $g\neq 12$
by using the Bridgeland stability conditions. In this paper, we would like to investigate the rational section of the map
$g\neq 12$
by using the Bridgeland stability conditions. In this paper, we would like to investigate the rational section of the map
![]() ${\Psi }_{{g_{m}}}$
for arbitrary
${\Psi }_{{g_{m}}}$
for arbitrary
![]() $m\in \mathbb {Z}_{>0}$
via Mukai’s program for curves in nonprimitive classes.
$m\in \mathbb {Z}_{>0}$
via Mukai’s program for curves in nonprimitive classes.
Main results
Let
![]() $(X,H)$
be a primitively polarised K3 surface of genus g with Picard number one. Let
$(X,H)$
be a primitively polarised K3 surface of genus g with Picard number one. Let
![]() ${\mathrm {H}}_{\text {alg}}^{*}(X)\cong {\mathbb {Z}}^{\oplus 3}$
be the algebraic Mukai lattice, and let
${\mathrm {H}}_{\text {alg}}^{*}(X)\cong {\mathbb {Z}}^{\oplus 3}$
be the algebraic Mukai lattice, and let
![]() $\mathbf {M}(v)$
be the moduli space of H-Gieseker semistable coherent sheaves on X with Mukai vector
$\mathbf {M}(v)$
be the moduli space of H-Gieseker semistable coherent sheaves on X with Mukai vector
![]() $v=(r, cH,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
. For
$v=(r, cH,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
. For
![]() $C\in |mH|$
an irreducible curve, let
$C\in |mH|$
an irreducible curve, let
![]() ${\mathbf {BN}}_C(v)$
be the Brill–Noether locus of slope semi-stable vector bundles on C with rank
${\mathbf {BN}}_C(v)$
be the Brill–Noether locus of slope semi-stable vector bundles on C with rank
![]() $r $
, degree
$r $
, degree
![]() $2m c(g-1)$
and
$2m c(g-1)$
and
![]() $h^0\geq r+s$
. The first main result of this paper is:
$h^0\geq r+s$
. The first main result of this paper is:
Theorem 1.1. Assume
![]() $g>2$
. Let
$g>2$
. Let
![]() $C\in |mH|$
be an irreducible curve. Then if
$C\in |mH|$
be an irreducible curve. Then if
![]() $mg\geq 11$
and
$mg\geq 11$
and
![]() $mg\neq 12$
, there exists a primitive Mukai vector
$mg\neq 12$
, there exists a primitive Mukai vector
![]() $v=(r,cH,s)$
with
$v=(r,cH,s)$
with
![]() $v^2=0$
such that the restriction map
$v^2=0$
such that the restriction map
 $$ \begin{align} \begin{aligned} \psi \colon \mathbf{M}(v) &\rightarrow {\mathbf{BN}}_C(v) \\ E &\mapsto E|_C \\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \psi \colon \mathbf{M}(v) &\rightarrow {\mathbf{BN}}_C(v) \\ E &\mapsto E|_C \\ \end{aligned} \end{align} $$
is an isomorphism.
As in [Reference Feyzbakhsh11], one can then reconstruct X as the moduli space of twisted sheaves on
![]() ${\mathbf {BN}}_C(v)$
. Clearly, such reconstruction is unique for K3 surfaces in
${\mathbf {BN}}_C(v)$
. Clearly, such reconstruction is unique for K3 surfaces in
![]() ${\mathcal {F}}_g$
of Picard number one. Due to the results of [Reference Dutta and Huybrechts10], when
${\mathcal {F}}_g$
of Picard number one. Due to the results of [Reference Dutta and Huybrechts10], when
![]() $m>1$
, generic curves in
$m>1$
, generic curves in
![]() $|m H|$
have maximal variation, that is, the rational map
$|m H|$
have maximal variation, that is, the rational map
is generically finite. One can also deduce the generic quasi-finiteness of
![]() ${\Psi }_{g_m}$
from Theorem 1.1 when
${\Psi }_{g_m}$
from Theorem 1.1 when
![]() $m>1, g\geq 3$
,
$m>1, g\geq 3$
,
![]() $mg\geq 11$
and
$mg\geq 11$
and
![]() $mg\neq 12$
. When
$mg\neq 12$
. When
![]() $g_m<11$
, the map
$g_m<11$
, the map
![]() ${\Psi }_{{g_{m}}}$
is not generically quasi-finite and Mukai’s program will fail. We expect that Theorem 1.1 holds whenever
${\Psi }_{{g_{m}}}$
is not generically quasi-finite and Mukai’s program will fail. We expect that Theorem 1.1 holds whenever
![]() $g_m\geq 11$
. So far, the missing values of
$g_m\geq 11$
. So far, the missing values of
![]() $(g,m)$
are
$(g,m)$
are
A mysterious case is when
![]() $g=2$
, where our method fails for any m.
$g=2$
, where our method fails for any m.
More generally, one may consider the restriction map (1.1) for
![]() $v^2=2n>0$
. Most recently, Feyzbakhsh [Reference Feyzbakhsh12] has generalised her construction in [Reference Feyzbakhsh11, Reference Feyzbakhsh13] and showed that for each Mukai vector
$v^2=2n>0$
. Most recently, Feyzbakhsh [Reference Feyzbakhsh12] has generalised her construction in [Reference Feyzbakhsh11, Reference Feyzbakhsh13] and showed that for each Mukai vector
![]() $v=(r,cH,s)$
satisfying
$v=(r,cH,s)$
satisfying
the restriction gives an isomorphism
![]() $\mathbf {M}(v)\cong {\mathbf {BN}}_C(v)$
when g is sufficiently large and the class of C is primitive. As mentioned in [Reference Feyzbakhsh12], the analysis in [Reference Feyzbakhsh12] also works for the nonprimitive case and one can actually show that Feyzbakhsh’s construction still gives an isomorphism for
$\mathbf {M}(v)\cong {\mathbf {BN}}_C(v)$
when g is sufficiently large and the class of C is primitive. As mentioned in [Reference Feyzbakhsh12], the analysis in [Reference Feyzbakhsh12] also works for the nonprimitive case and one can actually show that Feyzbakhsh’s construction still gives an isomorphism for
![]() $ C\in |mH| $
if g is sufficiently large (depending on r and m). This gives many examples of Brill–Noether loci on curves as hyper-Kähler varieties of dimension
$ C\in |mH| $
if g is sufficiently large (depending on r and m). This gives many examples of Brill–Noether loci on curves as hyper-Kähler varieties of dimension
![]() $2g-2r\lfloor \frac {g}{r}\rfloor $
. In this paper, we also improve her result (see Theorem 7.1) and obtain an explicit condition of v for
$2g-2r\lfloor \frac {g}{r}\rfloor $
. In this paper, we also improve her result (see Theorem 7.1) and obtain an explicit condition of v for
![]() $\psi $
being an isomorphism (see Theorem 7.3). As an application, we show that one can construct hyper-Kähler varieties as the Brill–Noether loci of curves in every dimension.
$\psi $
being an isomorphism (see Theorem 7.3). As an application, we show that one can construct hyper-Kähler varieties as the Brill–Noether loci of curves in every dimension.
Theorem 1.2. For any
![]() $n>0\in \mathbb {Z}$
, there exists an integer
$n>0\in \mathbb {Z}$
, there exists an integer
![]() $N=N(n)$
satisfying that if
$N=N(n)$
satisfying that if
![]() $g>N$
, there is a primitive Mukai vector
$g>N$
, there is a primitive Mukai vector
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
with
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
with
![]() $v^2=2n$
such that the restriction map
$v^2=2n$
such that the restriction map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism for all irreducible curves C on X.
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism for all irreducible curves C on X.
In other words, the bound N does not depend on the class of C. This makes use of the boundedness result of prime character nonresidues (See Lemma 8.2). The strategy of our proof is similar to [Reference Feyzbakhsh11, Reference Feyzbakhsh13, Reference Feyzbakhsh12]. Roughly speaking, we prove that
![]() $\psi $
will be a well-defined and injective morphism if the Gieseker chambers for objects with Mukai vector v and
$\psi $
will be a well-defined and injective morphism if the Gieseker chambers for objects with Mukai vector v and ![]() are large enough, and
are large enough, and
![]() $\psi $
is bijective if further the Harder–Narasimhan polygon of
$\psi $
is bijective if further the Harder–Narasimhan polygon of
![]() $i_\ast F$
for
$i_\ast F$
for
![]() $F\in {\mathbf {BN}}_C(v)$
achieves its maximum. The main ingredient is the use of a wall-crossing argument to analyse the existence of walls. There are two crucial improvement in our approach. One is that we find the strongest criterion (Proposition 3.4) to characterise the stability conditions which are not lying on the wall of objects with a given Mukai vector. This leads to a more explicit condition for
$F\in {\mathbf {BN}}_C(v)$
achieves its maximum. The main ingredient is the use of a wall-crossing argument to analyse the existence of walls. There are two crucial improvement in our approach. One is that we find the strongest criterion (Proposition 3.4) to characterise the stability conditions which are not lying on the wall of objects with a given Mukai vector. This leads to a more explicit condition for
![]() $\psi $
being an isomorphism. The other one is that we develop a method in analysing the relative position of HN polygons towards the surjectivity of
$\psi $
being an isomorphism. The other one is that we develop a method in analysing the relative position of HN polygons towards the surjectivity of
![]() $\psi $
. This allows us to get a sharper bound of
$\psi $
. This allows us to get a sharper bound of
![]() $(g,m)$
without using the computer program.
$(g,m)$
without using the computer program.
Organization of this paper
In Section 2, we review the basic knowledge of the Bridgeland stability condition on K3 surfaces and the wall-chamber structure on a section. In Section 3, we introduce the (strictly) destabilising regions
![]() $\Omega ^{(+)}_v(-)$
of a Mukai vector v. They characterise the stability conditions which are not lying on the wall of objects in
$\Omega ^{(+)}_v(-)$
of a Mukai vector v. They characterise the stability conditions which are not lying on the wall of objects in
![]() $\mathrm {D}^b(X)$
with Mukai vector v. This will play a key role in the proof of our main theorems.
$\mathrm {D}^b(X)$
with Mukai vector v. This will play a key role in the proof of our main theorems.
In Section 4, we show that the map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is a well-defined morphism and
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is a well-defined morphism and
![]() $h^0(X,E)=r+s$
for any
$h^0(X,E)=r+s$
for any
![]() $E\in \mathbf {M}(v)$
if the positive integers
$E\in \mathbf {M}(v)$
if the positive integers
![]() $r,c$
and s satisfy
$r,c$
and s satisfy
 $$ \begin{align} \gcd(r,c)=1,\, r>\frac{v^2+2}{2}\,\text{ and } \, g-1\geq \begin{cases} r, & \mbox{if } v^2=0;\\ \max \big\{ \frac{r^2}{c}>r ,\frac{r^2}{mr-c}\big\}, & \mbox{if } v^2>0. \end{cases} \end{align} $$
$$ \begin{align} \gcd(r,c)=1,\, r>\frac{v^2+2}{2}\,\text{ and } \, g-1\geq \begin{cases} r, & \mbox{if } v^2=0;\\ \max \big\{ \frac{r^2}{c}>r ,\frac{r^2}{mr-c}\big\}, & \mbox{if } v^2>0. \end{cases} \end{align} $$
The first two assumptions provide that any stable sheaf in
![]() $\mathbf {M}(v)$
is locally free while the third assumption essentially ensures that there is no wall between the large volume limit and the Brill–Noether wall. As a by-product, we obtain a numerical criterion for the injectivity of
$\mathbf {M}(v)$
is locally free while the third assumption essentially ensures that there is no wall between the large volume limit and the Brill–Noether wall. As a by-product, we obtain a numerical criterion for the injectivity of
![]() $\psi $
.
$\psi $
.
Section 5 and Section 6 are devoted to studying the surjectivity of the restriction map
![]() $\psi $
. They contain the most technical part of this paper. In Section 5, we show that
$\psi $
. They contain the most technical part of this paper. In Section 5, we show that
![]() $\psi $
is surjective if the Harder–Narasimhan polygon of
$\psi $
is surjective if the Harder–Narasimhan polygon of
![]() $i_\ast F$
for arbitrary
$i_\ast F$
for arbitrary
![]() $F\in {\mathbf {BN}}_C(v)$
is maximal when g is relatively large. It involves a dedicated analysis of the slope of destabilising factors of
$F\in {\mathbf {BN}}_C(v)$
is maximal when g is relatively large. It involves a dedicated analysis of the slope of destabilising factors of
![]() $i_*F$
via a geometric vision of the destabilising region. In Section 6, we analyse the sharpness of HN-polygons for special Mukai vectors with zero square. The concept of sharpness is used to detect how far the HN-polygon stays away from the convex polygon given by the critical position of the first wall. This makes the construction valid for small genera.
$i_*F$
via a geometric vision of the destabilising region. In Section 6, we analyse the sharpness of HN-polygons for special Mukai vectors with zero square. The concept of sharpness is used to detect how far the HN-polygon stays away from the convex polygon given by the critical position of the first wall. This makes the construction valid for small genera.
In Section 7, we analyse the surjectivity of the tangent map
![]() $d\psi $
of
$d\psi $
of
![]() $\psi $
and show that it is always surjective if
$\psi $
and show that it is always surjective if
![]() $g-1\geq 4r^2$
. In Section 8, we prove Theorem 1.1 and Theorem 1.2 by showing the existence of Mukai vectors satisfying all conditions. Here, we make use of the bound of prime character nonresidues.
$g-1\geq 4r^2$
. In Section 8, we prove Theorem 1.1 and Theorem 1.2 by showing the existence of Mukai vectors satisfying all conditions. Here, we make use of the bound of prime character nonresidues.
Notation and conventions
Throughout this paper, we always assume
![]() $(X, H)$
is a primitively polarised K3 surface of genus g of Picard number one.
$(X, H)$
is a primitively polarised K3 surface of genus g of Picard number one.
For any two points
![]() $p,q\in \mathbb {R}^n$
, let
$p,q\in \mathbb {R}^n$
, let
![]() ${\mathrm {L}}_{p,q}$
be the line passing through them and let
${\mathrm {L}}_{p,q}$
be the line passing through them and let
![]() ${\mathrm {L}}^+_{p,q}$
be the ray starting from p. We use
${\mathrm {L}}^+_{p,q}$
be the ray starting from p. We use
![]() ${\mathrm {L}}_{[p,q]}$
,
${\mathrm {L}}_{[p,q]}$
,
![]() ${\mathrm {L}}_{(p,q)}$
,
${\mathrm {L}}_{(p,q)}$
,
![]() ${\mathrm {L}}_{(p,q]}$
and
${\mathrm {L}}_{(p,q]}$
and
![]() ${\mathrm {L}}_{[p,q)}$
to denote the closed, open and half open line segment, respectively. For any line segment I, we set
${\mathrm {L}}_{[p,q)}$
to denote the closed, open and half open line segment, respectively. For any line segment I, we set
to be a (half open) triangular region. We denote by
![]() ${\mathbf {P}}_{p_1\dots p_n}$
the polygon with vertices
${\mathbf {P}}_{p_1\dots p_n}$
the polygon with vertices
![]() $p_1,\dots , p_n$
.
$p_1,\dots , p_n$
.
2 Stability condition on K3 surfaces
Let
![]() $\text {D}^{\text {b}}(X)$
be the bounded derived category of coherent sheaves on X. We let
$\text {D}^{\text {b}}(X)$
be the bounded derived category of coherent sheaves on X. We let
![]() $\mathit {K}_{\text {num}}(X)$
be the Grothendieck group of X modulo numerical equivalence. There is an onto map to the (algebraic) Mukai lattice
$\mathit {K}_{\text {num}}(X)$
be the Grothendieck group of X modulo numerical equivalence. There is an onto map to the (algebraic) Mukai lattice ![]() by sending
by sending
As X has Picard number one, we may identify
![]() ${\mathrm {H}}_{\text {alg}}^{*}(X)$
as
${\mathrm {H}}_{\text {alg}}^{*}(X)$
as
![]() ${\mathbb {Z}}^{\oplus 3}$
. So in the sequel of this paper, we shall abuse the notation and simply write
${\mathbb {Z}}^{\oplus 3}$
. So in the sequel of this paper, we shall abuse the notation and simply write
![]() $v(E)=(r,c,s)$
with
$v(E)=(r,c,s)$
with
![]() $r=\operatorname {\mathrm {rk}}(E)$
,
$r=\operatorname {\mathrm {rk}}(E)$
,
![]() $c_1(E)=cH$
and
$c_1(E)=cH$
and
![]() $s=\chi (E)-r$
. Here,
$s=\chi (E)-r$
. Here,
![]() $\chi (E) = \chi ({\mathcal {O}}_X,E)$
is the Euler characteristic. The Mukai pairing
$\chi (E) = \chi ({\mathcal {O}}_X,E)$
is the Euler characteristic. The Mukai pairing
![]() $\left <,\right>$
on
$\left <,\right>$
on
![]() ${\mathrm {H}}_{\text {alg}}^{*}(X)$
defined by
${\mathrm {H}}_{\text {alg}}^{*}(X)$
defined by
![]() $\langle v(E) ,v(F) \rangle =-\chi (E,F)$
can be viewed as an integral quadratic form on
$\langle v(E) ,v(F) \rangle =-\chi (E,F)$
can be viewed as an integral quadratic form on
![]() ${\mathbb {Z}}^{\oplus 3}$
given by
${\mathbb {Z}}^{\oplus 3}$
given by
We may write
![]() $v^2=\left <v,v\right>$
for
$v^2=\left <v,v\right>$
for
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
. Consider the projection map
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
. Consider the projection map
sending a vector
![]() $v=(r,c,s)$
to
$v=(r,c,s)$
to
![]() $(\frac {r}{s},\frac {c}{s} )$
. We write
$(\frac {r}{s},\frac {c}{s} )$
. We write
![]() $\pi _v=\mathrm {pr}(v)$
and
$\pi _v=\mathrm {pr}(v)$
and
![]() $\pi _E=\mathrm {pr}(v(E))$
for
$\pi _E=\mathrm {pr}(v(E))$
for
![]() ${E\in \mathrm {D}^b(X)}$
for simplicity. We let
${E\in \mathrm {D}^b(X)}$
for simplicity. We let
![]() $O=(0,0,0)$
be the origin of
$O=(0,0,0)$
be the origin of
![]() ${\mathrm {H}}_{\text {alg}}^{*}(X)\otimes \mathbb {R}$
and denote by
${\mathrm {H}}_{\text {alg}}^{*}(X)\otimes \mathbb {R}$
and denote by
![]() $o=(0,0)$
the origin of
$o=(0,0)$
the origin of
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
A numerical (Bridgeland) stability condition on X is a pair
![]() $\sigma = ({\mathcal {A}}_\sigma , Z_\sigma )$
consisting a heart
$\sigma = ({\mathcal {A}}_\sigma , Z_\sigma )$
consisting a heart
![]() ${\mathcal {A}}_{\sigma } \subset \text {D}^{\text {b}}(X)$
of a bounded t-structure and an
${\mathcal {A}}_{\sigma } \subset \text {D}^{\text {b}}(X)$
of a bounded t-structure and an
![]() $\mathbb {R}$
-linear map
$\mathbb {R}$
-linear map
satisfying the conditions
-
(i) For any
 $0\neq E\in \mathcal {A}$
, where
$0\neq E\in \mathcal {A}$
, where $$\begin{align*}Z_{\sigma}(E)\in \mathbb{R}_{>0} \exp(i \pi \phi_{\sigma}(E)) \;\text{with} \; 0 < \phi_{\sigma} (E) \leq 1, \end{align*}$$
$$\begin{align*}Z_{\sigma}(E)\in \mathbb{R}_{>0} \exp(i \pi \phi_{\sigma}(E)) \;\text{with} \; 0 < \phi_{\sigma} (E) \leq 1, \end{align*}$$
 $\phi _{\sigma }(E)$
is the phase of
$\phi _{\sigma }(E)$
is the phase of
 $Z_{\sigma }(E) $
in the complex plane.
$Z_{\sigma }(E) $
in the complex plane.
-
(i) The Harder–Narasimhan (HN) property, cf. [Reference Bridgeland3, Definition 2.3].
The
![]() $\sigma $
-slope is defined by
$\sigma $
-slope is defined by
 $$\begin{align*}\mu_{\sigma} (E) = -\frac{\operatorname{{\mathrm{Re}}} Z(E)}{\operatorname{{\mathrm{Im}}} Z(E)}, \end{align*}$$
$$\begin{align*}\mu_{\sigma} (E) = -\frac{\operatorname{{\mathrm{Re}}} Z(E)}{\operatorname{{\mathrm{Im}}} Z(E)}, \end{align*}$$
and we set the
![]() $\sigma $
-phase to be
$\sigma $
-phase to be
An object
![]() $E \in \mathcal {A} $
is called
$E \in \mathcal {A} $
is called
![]() $\sigma $
-(semi)stable if
$\sigma $
-(semi)stable if
![]() $\mu _{\sigma } (F) < (\leq ) \,\mu _{\sigma }(E)$
or equivalently
$\mu _{\sigma } (F) < (\leq ) \,\mu _{\sigma }(E)$
or equivalently
![]() $ \phi _{\sigma }(F) < (\leq ) \, \phi _{\sigma } (E)$
whenever
$ \phi _{\sigma }(F) < (\leq ) \, \phi _{\sigma } (E)$
whenever
![]() $F \subset E$
is a subobject of E in
$F \subset E$
is a subobject of E in
![]() $\mathcal {A}$
. We say an object
$\mathcal {A}$
. We say an object
![]() $E \in \text {D}^{\text {b}}(X)$
is
$E \in \text {D}^{\text {b}}(X)$
is
![]() $\sigma $
-(semi)stable if
$\sigma $
-(semi)stable if
![]() $E[k] \in \mathcal {A}$
for some k, and
$E[k] \in \mathcal {A}$
for some k, and
![]() $E[k]$
is
$E[k]$
is
![]() $\sigma $
-(semi)stable.
$\sigma $
-(semi)stable.
If E is a sheaf with
![]() $v(E) = (r,c,s)$
, we write
$v(E) = (r,c,s)$
, we write
![]() $\mu _H(E)= \frac {c}{r}$
for the H-slope of E and
$\mu _H(E)= \frac {c}{r}$
for the H-slope of E and
![]() $\mu _H^{\pm }(E)$
for the H-slope of the first/last HN factor of E. In [Reference Bridgeland4], Bridgeland has constructed a continuous family of stability conditions on X as follows: For
$\mu _H^{\pm }(E)$
for the H-slope of the first/last HN factor of E. In [Reference Bridgeland4], Bridgeland has constructed a continuous family of stability conditions on X as follows: For
![]() $\alpha ,\beta \in \mathbb {R}$
with
$\alpha ,\beta \in \mathbb {R}$
with
![]() $\alpha> 0$
, for any
$\alpha> 0$
, for any
![]() $\beta \in \mathbb {R}$
, the
$\beta \in \mathbb {R}$
, the
![]() $\beta $
-tilt of
$\beta $
-tilt of
![]() $\operatorname {\mathrm {Coh}}(X)$
is defined by
$\operatorname {\mathrm {Coh}}(X)$
is defined by
which is the heart of a t-structure on
![]() $\text {D}^{\text {b}}(X)$
with
$\text {D}^{\text {b}}(X)$
with
 $$\begin{align*}Z_{\alpha ,\beta}(E) = \left\langle (1,\beta ,\frac{H^2}{2}(\beta^2-\alpha^2)),v(E) \right\rangle + \sqrt{-1}\left\langle (0,\frac{1}{H^2},\beta),v(E) \right\rangle;\end{align*}$$
$$\begin{align*}Z_{\alpha ,\beta}(E) = \left\langle (1,\beta ,\frac{H^2}{2}(\beta^2-\alpha^2)),v(E) \right\rangle + \sqrt{-1}\left\langle (0,\frac{1}{H^2},\beta),v(E) \right\rangle;\end{align*}$$
here,
![]() $\operatorname {{\mathrm {H}}}^i(E)$
is the i-th cohomology of E with respect to the standard heart
$\operatorname {{\mathrm {H}}}^i(E)$
is the i-th cohomology of E with respect to the standard heart
![]() $\operatorname {\mathrm {Coh}}(X)$
of
$\operatorname {\mathrm {Coh}}(X)$
of
![]() $\text {D}^{\text {b}}(X)$
. Let
$\text {D}^{\text {b}}(X)$
. Let
![]() $\mathrm {R}(X)$
be the collection of roots in
$\mathrm {R}(X)$
be the collection of roots in
![]() ${\mathrm {H}}_{\text {alg}}^{*}(X)$
, that is,
${\mathrm {H}}_{\text {alg}}^{*}(X)$
, that is,
Theorem 2.1 [Reference Bridgeland4].
The pair ![]() is a Bridgeland stability condition on
is a Bridgeland stability condition on
![]() $\text {D}^{\text {b}}(X)$
if
$\text {D}^{\text {b}}(X)$
if
![]() $\operatorname {{\mathrm {Re}}} Z_{\alpha ,\beta }(\delta )>0$
for all roots
$\operatorname {{\mathrm {Re}}} Z_{\alpha ,\beta }(\delta )>0$
for all roots
![]() $\delta \in \mathrm {R}(X)$
with
$\delta \in \mathrm {R}(X)$
with
![]() $\operatorname {\mathrm {rk}}(\delta )>0$
and
$\operatorname {\mathrm {rk}}(\delta )>0$
and
![]() $\operatorname {{\mathrm {Im}}} Z_{\alpha ,\beta }(\delta ) =0$
.
$\operatorname {{\mathrm {Im}}} Z_{\alpha ,\beta }(\delta ) =0$
.
The stability condition
![]() $\sigma _{\alpha ,\beta }$
is uniquely characterised by its kernel
$\sigma _{\alpha ,\beta }$
is uniquely characterised by its kernel
 $$\begin{align*}\ker Z_{\alpha,\beta} = \left\{ (r,c, s)\in {\mathrm{H}}_{\text{alg}}^{*}(X) \,\middle|\, c=r\beta, s = \frac{r H^2}{2}(\alpha^2+\beta^2) \right\}. \end{align*}$$
$$\begin{align*}\ker Z_{\alpha,\beta} = \left\{ (r,c, s)\in {\mathrm{H}}_{\text{alg}}^{*}(X) \,\middle|\, c=r\beta, s = \frac{r H^2}{2}(\alpha^2+\beta^2) \right\}. \end{align*}$$
According to [Reference Feyzbakhsh11, Lemma 2.4], if we set
![]() $ k(\alpha ,\beta )= \mathrm {pr}(\ker Z_{\alpha , \beta }) \in \mathbb {R}^2$
, then
$ k(\alpha ,\beta )= \mathrm {pr}(\ker Z_{\alpha , \beta }) \in \mathbb {R}^2$
, then
![]() $k(\alpha ,\beta )$
are parameterised by the space
$k(\alpha ,\beta )$
are parameterised by the space
 $$ \begin{align} V(X) = \left\{ (x,y)\in \mathbb{R}^2 \,\middle|\, x>\frac{H^2 y^2}{2} \right\} \setminus \bigcup_{\delta \in \mathrm{R}(X)} {\mathrm{L}}_{(\pi^{\prime}_\delta, \pi_\delta]}, \end{align} $$
$$ \begin{align} V(X) = \left\{ (x,y)\in \mathbb{R}^2 \,\middle|\, x>\frac{H^2 y^2}{2} \right\} \setminus \bigcup_{\delta \in \mathrm{R}(X)} {\mathrm{L}}_{(\pi^{\prime}_\delta, \pi_\delta]}, \end{align} $$
where
![]() $\pi ^{\prime }_\delta $
is the intersection point of the parabola
$\pi ^{\prime }_\delta $
is the intersection point of the parabola
![]() $\Big \{x=\frac {H^2 y^2}{2}\Big \}$
and the line
$\Big \{x=\frac {H^2 y^2}{2}\Big \}$
and the line
![]() ${\mathrm {L}}_{o, \pi _\delta } $
. See Figure 1 for a picture of
${\mathrm {L}}_{o, \pi _\delta } $
. See Figure 1 for a picture of
![]() $V(X)$
. Therefore, we may view the stability condition
$V(X)$
. Therefore, we may view the stability condition
![]() $\sigma _{\alpha ,\beta }$
as the point
$\sigma _{\alpha ,\beta }$
as the point
![]() $k(\alpha ,\beta ) $
in
$k(\alpha ,\beta ) $
in
![]() $V(X)$
.
$V(X)$
.

Figure 1 Visualization of
![]() $V(X)$
.
$V(X)$
.
The following are some simple observations that will be frequently used in this paper:
-
(A) If
 $\sigma \in V(X)$
, then the line segment
$\sigma \in V(X)$
, then the line segment
 ${\mathrm {L}}_{( o, \sigma ]}$
is contained in
${\mathrm {L}}_{( o, \sigma ]}$
is contained in
 $V(X)$
.
$V(X)$
. -
(B) If
 $\gcd (r,c)=1$
and
$\gcd (r,c)=1$
and
 $r>0$
, the line
$r>0$
, the line
 $ry=cx$
contains a (unique) projection of root if and only if
$ry=cx$
contains a (unique) projection of root if and only if
 $r \mid c^2(g-1)+1$
(cf. [Reference Yoshioka20]). In particular, the unique projection of root on the x-axis is
$r \mid c^2(g-1)+1$
(cf. [Reference Yoshioka20]). In particular, the unique projection of root on the x-axis is
 $(1,0)$
, which we denote by
$(1,0)$
, which we denote by
 $o'$
.
$o'$
.
A simple observation is, for elements in the same heart, we can read their phases from the plane.
Proposition 2.2 (Phase reading, see Figure 2).
Fix
![]() $\sigma _{\alpha ,\beta } \in V(X)$
. For
$\sigma _{\alpha ,\beta } \in V(X)$
. For
![]() $E\in \operatorname {\mathrm {Coh}}^\beta (X)$
, let
$E\in \operatorname {\mathrm {Coh}}^\beta (X)$
, let
![]() $0<\theta _\sigma \leq \unicode{x3c0} $
be the directed angle from
$0<\theta _\sigma \leq \unicode{x3c0} $
be the directed angle from
![]() $\overrightarrow {\sigma \pi _E}$
to
$\overrightarrow {\sigma \pi _E}$
to
![]() $\overrightarrow {o\sigma }$
modulo
$\overrightarrow {o\sigma }$
modulo
![]() $\unicode{x3c0} $
. Then,
$\unicode{x3c0} $
. Then,
![]() $\phi _\sigma $
is a strictly increasing function of
$\phi _\sigma $
is a strictly increasing function of
![]() $\theta _\sigma $
.
$\theta _\sigma $
.

Figure 2 An example of
![]() $\theta _\sigma (E)$
.
$\theta _\sigma (E)$
.
Proof. Note that
![]() $\phi _\sigma (E_1)=\phi _\sigma (E_2)$
if and only if
$\phi _\sigma (E_1)=\phi _\sigma (E_2)$
if and only if
for some
![]() $\lambda \in \mathbb {R}^*$
, which is equivalent to
$\lambda \in \mathbb {R}^*$
, which is equivalent to
![]() $\sigma ,\pi _{v(E_1)},\pi _{v(E_2)}$
being colinear, as
$\sigma ,\pi _{v(E_1)},\pi _{v(E_2)}$
being colinear, as
![]() $\sigma \in V(X)$
is precisely the projection of the kernel of
$\sigma \in V(X)$
is precisely the projection of the kernel of
![]() $Z_\sigma $
. This already proves
$Z_\sigma $
. This already proves
![]() $\phi _\sigma $
is a strictly monotonic function of
$\phi _\sigma $
is a strictly monotonic function of
![]() $\theta _\sigma $
due to continuity. It is increasing since
$\theta _\sigma $
due to continuity. It is increasing since
![]() $ \phi _{\sigma }(0+)< \phi _{\sigma }(\pi )$
. The interchange phase
$ \phi _{\sigma }(0+)< \phi _{\sigma }(\pi )$
. The interchange phase
![]() $\phi _\sigma =1$
corresponds to the line
$\phi _\sigma =1$
corresponds to the line
![]() ${\mathrm {L}}_{o, \sigma }$
.
${\mathrm {L}}_{o, \sigma }$
.
Wall and chamber structure
For any object
![]() $E\in \text {D}^{\text {b}}(X)$
, there is a wall and chamber structure of
$E\in \text {D}^{\text {b}}(X)$
, there is a wall and chamber structure of
![]() $V(X)$
described as follows.
$V(X)$
described as follows.
Proposition 2.3 (cf. [Reference Feyzbakhsh11, Proposition 2.6]).
Given an object
![]() $E\in \text {D}^{\text {b}}(X)$
, there exists a locally finite set of walls (line segments) in
$E\in \text {D}^{\text {b}}(X)$
, there exists a locally finite set of walls (line segments) in
![]() $V(X)$
with the following properties:
$V(X)$
with the following properties:
-
(a) The
 $\sigma _{\alpha ,\beta }$
-(semi)stability of E is independent of the choice of the stability condition
$\sigma _{\alpha ,\beta }$
-(semi)stability of E is independent of the choice of the stability condition
 $\sigma _{\alpha ,\beta }$
in any chamber.
$\sigma _{\alpha ,\beta }$
in any chamber. -
(b) If
 $\sigma _{\alpha _0, \beta _0}$
is on a wall
$\sigma _{\alpha _0, \beta _0}$
is on a wall
 ${\mathcal {W}}_E$
, that is, the point
${\mathcal {W}}_E$
, that is, the point
 $k(\alpha _0, \beta _0)\in {\mathcal {W}}_E$
, E is strictly
$k(\alpha _0, \beta _0)\in {\mathcal {W}}_E$
, E is strictly
 $\sigma _{\alpha _0, \beta _0}$
-semistable.
$\sigma _{\alpha _0, \beta _0}$
-semistable. -
(c) If E is semistable in one of the adjacent chambers to a wall, then it is unstable in other adjacent chambers.
-
(d) Any wall
 ${\mathcal {W}}_E$
is a connected component of
${\mathcal {W}}_E$
is a connected component of
 $\mathrm {L} \cap V (X)$
, where
$\mathrm {L} \cap V (X)$
, where
 $\mathrm {L}$
is a line passing through the point
$\mathrm {L}$
is a line passing through the point
 $\pi _E$
if
$\pi _E$
if
 $\chi (E)\neq \operatorname {\mathrm {rk}}(E) $
or with slope
$\chi (E)\neq \operatorname {\mathrm {rk}}(E) $
or with slope
 $\operatorname {\mathrm {rk}}(E)/c_H(E)$
if
$\operatorname {\mathrm {rk}}(E)/c_H(E)$
if
 $\chi (E) = \operatorname {\mathrm {rk}}(E)$
.
$\chi (E) = \operatorname {\mathrm {rk}}(E)$
.
By definition, if
![]() $E\in \operatorname {\mathrm {Coh}}^\beta (X)$
is
$E\in \operatorname {\mathrm {Coh}}^\beta (X)$
is
![]() $\sigma _{\alpha ,\beta }$
-semistable, then
$\sigma _{\alpha ,\beta }$
-semistable, then
![]() $\pi _E\neq \sigma _{\alpha ,\beta }$
since
$\pi _E\neq \sigma _{\alpha ,\beta }$
since
![]() $Z_{\alpha ,\beta }(E) \neq 0$
(recall that in Section 2 we identify a stability
$Z_{\alpha ,\beta }(E) \neq 0$
(recall that in Section 2 we identify a stability
![]() $\sigma _{\alpha ,\beta }$
with the projection of kernel
$\sigma _{\alpha ,\beta }$
with the projection of kernel ![]() by abuse of notation). Combined with Proposition 2.3, one can see that for any line segment
by abuse of notation). Combined with Proposition 2.3, one can see that for any line segment
![]() ${\mathrm {L}}_{[ \sigma _1, \sigma _2 ]}\subseteq V(X)$
containing
${\mathrm {L}}_{[ \sigma _1, \sigma _2 ]}\subseteq V(X)$
containing
![]() $\sigma _{\alpha ,\beta }$
with
$\sigma _{\alpha ,\beta }$
with
![]() $\sigma _1, \sigma _2$
, and
$\sigma _1, \sigma _2$
, and
![]() $\pi _E$
colinear, we have
$\pi _E$
colinear, we have
that is,
![]() $v(E)$
cannot lie in the kernel of any stability condition in
$v(E)$
cannot lie in the kernel of any stability condition in
![]() $V(X)$
. (In the case where E is stable, this follows directly from the
$V(X)$
. (In the case where E is stable, this follows directly from the
![]() $v(E)^2\geq -2$
and hence
$v(E)^2\geq -2$
and hence
![]() $\pi _E \notin V(X)$
.) This will be used in later sections.
$\pi _E \notin V(X)$
.) This will be used in later sections.
3 The destabilising regions
In this section, we characterize the stability conditions which are not lying on the walls of an object
![]() $E\in \mathrm {D}^b(X)$
. As a warm-up, we first assume
$E\in \mathrm {D}^b(X)$
. As a warm-up, we first assume
![]() $\pi _E\in \partial V(X)$
and hence
$\pi _E\in \partial V(X)$
and hence
![]() $v(E)^2=0$
or
$v(E)^2=0$
or
![]() $-2$
. Then we have
$-2$
. Then we have
Proposition 3.1 (Triangle rule, see Figure 3).
Let
![]() $E\in \text {D}^{\text {b}}(X)$
, and let
$E\in \text {D}^{\text {b}}(X)$
, and let
![]() $I \subseteq V(X)$
be a line segment. Assume
$I \subseteq V(X)$
be a line segment. Assume
Then any point in I is not on a wall. In particular, if
![]() $I={\mathrm {L}}_{[ \sigma _1,\sigma _2]}$
, then E is
$I={\mathrm {L}}_{[ \sigma _1,\sigma _2]}$
, then E is
![]() $\sigma _1$
-stable if and only if it is
$\sigma _1$
-stable if and only if it is
![]() $\sigma _2$
-stable.
$\sigma _2$
-stable.

Figure 3 An example of triangle rule: if any point in the colored region is a stability condition, then there is no wall between
![]() $\sigma_1$
and
$\sigma_1$
and
![]() $\sigma_2$
.
$\sigma_2$
.
Proof. Assume on the contrary, that is, there is a wall
![]() ${\mathcal {W}}_E\subseteq \mathrm {L}\cap V(X)$
where L passes through
${\mathcal {W}}_E\subseteq \mathrm {L}\cap V(X)$
where L passes through
![]() $\pi _E$
and intersects with I. Let
$\pi _E$
and intersects with I. Let
![]() $\sigma _0=I \cap {\mathcal {W}}_E$
. By our assumption, one has
$\sigma _0=I \cap {\mathcal {W}}_E$
. By our assumption, one has
By Proposition 2.3 (b), E is strictly
![]() $\sigma $
-semistable for any
$\sigma $
-semistable for any
![]() $\sigma \in {\mathrm {L}}_{(\pi _E , \sigma _0 ]}$
. Up to a shift, one may assume that
$\sigma \in {\mathrm {L}}_{(\pi _E , \sigma _0 ]}$
. Up to a shift, one may assume that
![]() $E\in \operatorname {\mathrm {Coh}}^{\beta (\sigma _0)}(X)$
. Since
$E\in \operatorname {\mathrm {Coh}}^{\beta (\sigma _0)}(X)$
. Since
![]() $\sigma _0$
is on a wall, there exists some semistable factor
$\sigma _0$
is on a wall, there exists some semistable factor
![]() $F\subset E$
in
$F\subset E$
in
![]() $\operatorname {\mathrm {Coh}}^{\beta (\sigma _0)}(X)$
such that
$\operatorname {\mathrm {Coh}}^{\beta (\sigma _0)}(X)$
such that
![]() $\phi _{\sigma _0}(F)=\phi _{\sigma _0}(E)$
and
$\phi _{\sigma _0}(F)=\phi _{\sigma _0}(E)$
and
![]() $\phi _{\sigma }(F)>\phi _{\sigma }(E)$
for
$\phi _{\sigma }(F)>\phi _{\sigma }(E)$
for
![]() $\sigma $
in an adjacent chamber. In particular,
$\sigma $
in an adjacent chamber. In particular,
![]() $\pi _F \neq \pi _E$
. Applying Proposition 2.3(b) to E, F, and
$\pi _F \neq \pi _E$
. Applying Proposition 2.3(b) to E, F, and
![]() $\operatorname {\mathrm {cok}}(F \to E)$
, respectively, we know that they remain in the heart for any
$\operatorname {\mathrm {cok}}(F \to E)$
, respectively, we know that they remain in the heart for any
![]() $\sigma \in {\mathrm {L}}_{( \pi _E,\sigma _0]}$
. Hence,
$\sigma \in {\mathrm {L}}_{( \pi _E,\sigma _0]}$
. Hence,
![]() $F\subset E$
is a proper subobject in the corresponding
$F\subset E$
is a proper subobject in the corresponding
![]() $\operatorname {\mathrm {Coh}}^\beta (X)$
. As a consequence, we get
$\operatorname {\mathrm {Coh}}^\beta (X)$
. As a consequence, we get
Now, if we tend
![]() $\sigma $
to
$\sigma $
to
![]() $\pi _E$
, then
$\pi _E$
, then
![]() $| Z_\sigma (E)| \to 0$
while
$| Z_\sigma (E)| \to 0$
while
![]() $| Z_\sigma (F)|\to \epsilon>0$
since
$| Z_\sigma (F)|\to \epsilon>0$
since
![]() $\pi _F \neq \pi _E$
. This is a contradiction.
$\pi _F \neq \pi _E$
. This is a contradiction.
Destabilising regions
The proposition above only works for
![]() $\pi _E\in \partial V(X)$
due to Equation (2.2). For the case
$\pi _E\in \partial V(X)$
due to Equation (2.2). For the case
![]() $v(E)^2\geq 0$
, we need to make use of the three-dimensional region defined as below: For any
$v(E)^2\geq 0$
, we need to make use of the three-dimensional region defined as below: For any
![]() $\sigma \in V(X)$
and
$\sigma \in V(X)$
and
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
, let
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
, let
![]() ${\mathrm {L}}_{( \sigma ',\sigma ")} \subseteq {\mathrm {L}}_{\sigma , \pi _v} \cap \, V(X)$
be the connected component containing
${\mathrm {L}}_{( \sigma ',\sigma ")} \subseteq {\mathrm {L}}_{\sigma , \pi _v} \cap \, V(X)$
be the connected component containing
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $[\sigma ]\subseteq \mathbb {R}^3$
be the preimage of
$[\sigma ]\subseteq \mathbb {R}^3$
be the preimage of
![]() $\sigma $
via the projection
$\sigma $
via the projection
![]() $\mathrm {pr}:\mathbb {R}^3\dashrightarrow \mathbb {R}^2$
. Consider the plane
$\mathrm {pr}:\mathbb {R}^3\dashrightarrow \mathbb {R}^2$
. Consider the plane
![]() $\Pi $
spanned by
$\Pi $
spanned by
![]() $[\sigma ]$
and
$[\sigma ]$
and
![]() $v(E)$
. Then
$v(E)$
. Then
![]() $[\sigma _0] \subset \Pi $
for any
$[\sigma _0] \subset \Pi $
for any
![]() $\sigma _0 \in {\mathrm {L}}_{(\sigma ',\sigma ")}$
. We define the destabilising region of v with respect to
$\sigma _0 \in {\mathrm {L}}_{(\sigma ',\sigma ")}$
. We define the destabilising region of v with respect to
![]() $\sigma $
as
$\sigma $
as
where
![]() $ v^+_\sigma = [\sigma '] \cap ( [ \sigma "]+v) $
and
$ v^+_\sigma = [\sigma '] \cap ( [ \sigma "]+v) $
and
![]() $v^-_\sigma =[\sigma "] \cap ( [\sigma ']+v)$
. Note that for any
$v^-_\sigma =[\sigma "] \cap ( [\sigma ']+v)$
. Note that for any
![]() $\sigma \in V(X)$
, we have
$\sigma \in V(X)$
, we have
![]() $x\cdot z \geq 0$
for any
$x\cdot z \geq 0$
for any
![]() $(x,y,z)\in [\sigma ]$
. Consider the (open) shadow area in Figure 4 which is bounded by the two lines and consists of nonzero
$(x,y,z)\in [\sigma ]$
. Consider the (open) shadow area in Figure 4 which is bounded by the two lines and consists of nonzero
![]() $(x,y,z)\in [\sigma ]$
for some
$(x,y,z)\in [\sigma ]$
for some
![]() $\sigma $
. Since
$\sigma $
. Since
![]() $v^2 \geq 0$
,
$v^2 \geq 0$
,
![]() $\pi _E \notin V(X)$
and hence v is not in this shadow area. Therefore, the x-coordinates of
$\pi _E \notin V(X)$
and hence v is not in this shadow area. Therefore, the x-coordinates of
![]() $v_{\sigma }^+$
and
$v_{\sigma }^+$
and
![]() $v_{\sigma }^{-}$
have opposite sign. We may simply put
$v_{\sigma }^{-}$
have opposite sign. We may simply put
up to switching
![]() $\sigma '$
and
$\sigma '$
and
![]() $\sigma "$
.
$\sigma "$
.

Figure 4 The (open) shawdow area is covered by kernel of stability conditions.
There is a natural decomposition
where
![]() $\Omega ^\pm _v(\sigma )=\Omega _v(\sigma )\cap {\mathbf {P}}_{Ov^{\!\pm }_{\sigma } v} \setminus {\mathrm {L}}_{(O,v)}$
. We call
$\Omega ^\pm _v(\sigma )=\Omega _v(\sigma )\cap {\mathbf {P}}_{Ov^{\!\pm }_{\sigma } v} \setminus {\mathrm {L}}_{(O,v)}$
. We call
![]() $\Omega ^+_v(\sigma )$
the strictly destabilising region of v with respect to
$\Omega ^+_v(\sigma )$
the strictly destabilising region of v with respect to
![]() $\sigma $
. A key result is:
$\sigma $
. A key result is:
Lemma 3.2. For
![]() $E\in \text {D}^{\text {b}}(X)$
with
$E\in \text {D}^{\text {b}}(X)$
with
![]() $v(E)^2 \geq 0$
and
$v(E)^2 \geq 0$
and
![]() $\sigma \in V(X) $
, if
$\sigma \in V(X) $
, if
![]() $\sigma $
is lying on a wall of E, then there exists an integer point in
$\sigma $
is lying on a wall of E, then there exists an integer point in
![]() $ \Omega ^+_{v(E)} (\sigma ) .$
$ \Omega ^+_{v(E)} (\sigma ) .$
Proof. Set
![]() $v=v(E)$
for temporary notation. Firstly, for any
$v=v(E)$
for temporary notation. Firstly, for any
![]() $G\subseteq F \subseteq E$
in
$G\subseteq F \subseteq E$
in
![]() $\operatorname {\mathrm {Coh}}^{\beta (\sigma )}(X)$
satisfying that
$\operatorname {\mathrm {Coh}}^{\beta (\sigma )}(X)$
satisfying that
![]() $E,F,G$
have the same
$E,F,G$
have the same
![]() $\sigma $
-phase, we always have that
$\sigma $
-phase, we always have that
![]() $v(F/G)$
is lying in the parallelogram
$v(F/G)$
is lying in the parallelogram
![]() $ {\mathbf {P}}_{Ov^{\!+}_{\sigma } v v^{\!-}_{\sigma }}$
. This is because there are inclusions
$ {\mathbf {P}}_{Ov^{\!+}_{\sigma } v v^{\!-}_{\sigma }}$
. This is because there are inclusions
for any
![]() $\tau \in {\mathrm {L}}_{(\sigma ',\sigma " )}$
, which yields that
$\tau \in {\mathrm {L}}_{(\sigma ',\sigma " )}$
, which yields that
 $$ \begin{align*} v(F/G) \in \bigcap_{\tau \in {\mathrm{L}}_{( \sigma', \sigma" )}} Z_\tau^{-1}({\mathrm{L}}_{[ 0,Z_\tau(v)]})={\mathbf{P}}_{Ov^+_{\sigma} v v^-_{\sigma}}. \end{align*} $$
$$ \begin{align*} v(F/G) \in \bigcap_{\tau \in {\mathrm{L}}_{( \sigma', \sigma" )}} Z_\tau^{-1}({\mathrm{L}}_{[ 0,Z_\tau(v)]})={\mathbf{P}}_{Ov^+_{\sigma} v v^-_{\sigma}}. \end{align*} $$
In particular, if
![]() $0=\widetilde {E}_0 \subset \dots \subset \widetilde {E}_k=E$
is a
$0=\widetilde {E}_0 \subset \dots \subset \widetilde {E}_k=E$
is a
![]() $\sigma $
-Jordan–Holder filtration of E with
$\sigma $
-Jordan–Holder filtration of E with
![]() $E_i = \widetilde {E}_i / \widetilde {E}_{i-1}$
its JH-factors, then any
$E_i = \widetilde {E}_i / \widetilde {E}_{i-1}$
its JH-factors, then any
![]() $v(E_i)$
and also
$v(E_i)$
and also
![]() $v-v(E_i)$
is lying
$v-v(E_i)$
is lying
![]() ${\mathbf {P}}_{Ov^+_{\sigma } v v^-_{\sigma }}$
.
${\mathbf {P}}_{Ov^+_{\sigma } v v^-_{\sigma }}$
.
If necessary, reordering these factors
![]() $E_i$
such that the angles between
$E_i$
such that the angles between
![]() ${\mathrm {L}}^+_{O,v(E_i)}$
and
${\mathrm {L}}^+_{O,v(E_i)}$
and
![]() ${\mathrm {L}}_{O,v_\sigma ^+}^+$
increase with respect to i. And we get a polygon with vertexes
${\mathrm {L}}_{O,v_\sigma ^+}^+$
increase with respect to i. And we get a polygon with vertexes
![]() $\sum _{i=1}^j v(E_i)$
(
$\sum _{i=1}^j v(E_i)$
(
![]() $0\leq j\leq k$
). Since
$0\leq j\leq k$
). Since
![]() $v(E_1)$
and
$v(E_1)$
and
![]() $v-v(E_k)$
lie in
$v-v(E_k)$
lie in
![]() $\mathbf {P}^+_{Ov^+_\sigma v}$
, one sees that
$\mathbf {P}^+_{Ov^+_\sigma v}$
, one sees that
 $\sum \limits _{i=1}^{j} v(E_i)$
is an integer point in
$\sum \limits _{i=1}^{j} v(E_i)$
is an integer point in
![]() ${\mathbf {P}}_{O v_\sigma ^+ v}\setminus {\mathrm {L}}_{(O,v)} $
for any j. We claim that either
${\mathbf {P}}_{O v_\sigma ^+ v}\setminus {\mathrm {L}}_{(O,v)} $
for any j. We claim that either
![]() $v(E_1)$
or
$v(E_1)$
or
 $\sum \limits _{i=1}^{k-1} v(E_i)$
is lying in
$\sum \limits _{i=1}^{k-1} v(E_i)$
is lying in
![]() $\Omega _v(\sigma )$
. This can be proved by using purely Euclidean geometry. Suppose this fails, then we have
$\Omega _v(\sigma )$
. This can be proved by using purely Euclidean geometry. Suppose this fails, then we have
 $$ \begin{align} \begin{aligned} v(E_1)^2\geq -2 \quad \mbox{and}\quad (v(E_1)-v)^2 <-2 , \\ (\sum\limits_{i=1}^{k-1} v(E_i) -v)^2\geq -2 \quad \mbox{and}\quad (\sum\limits_{i=1}^{k-1} v(E_i) )^2<-2, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} v(E_1)^2\geq -2 \quad \mbox{and}\quad (v(E_1)-v)^2 <-2 , \\ (\sum\limits_{i=1}^{k-1} v(E_i) -v)^2\geq -2 \quad \mbox{and}\quad (\sum\limits_{i=1}^{k-1} v(E_i) )^2<-2, \end{aligned} \end{align} $$
as
![]() $E_i$
is stable. If we restrict the quadratic equation
$E_i$
is stable. If we restrict the quadratic equation
![]() $u^2=-2$
to the plane of
$u^2=-2$
to the plane of
![]() ${\mathbf {P}}_{ovv_\sigma ^+}$
, we can obtain a hyperbola whose center is O. The edge
${\mathbf {P}}_{ovv_\sigma ^+}$
, we can obtain a hyperbola whose center is O. The edge
![]() ${\mathrm {L}}_{[O,\, v_\sigma ^+]}$
can meet the connected component of this hyperbola at most one point. Similarly,
${\mathrm {L}}_{[O,\, v_\sigma ^+]}$
can meet the connected component of this hyperbola at most one point. Similarly,
![]() ${\mathrm {L}}_{[v,\, v_\sigma ^+]} $
can intersect with the connected component of the hyperbola defined by
${\mathrm {L}}_{[v,\, v_\sigma ^+]} $
can intersect with the connected component of the hyperbola defined by
![]() $(u-v)^2=-2 $
at most one point. Note that the edge
$(u-v)^2=-2 $
at most one point. Note that the edge
![]() ${\mathrm {L}}_{[O,v]}$
is lying outside the area
${\mathrm {L}}_{[O,v]}$
is lying outside the area
See the shadow part in Figure 5. By Equation (3.2),
![]() $v_\sigma ^+$
has to lie in the region (3.3). Moreover, as one can see from the picture, there is a point
$v_\sigma ^+$
has to lie in the region (3.3). Moreover, as one can see from the picture, there is a point
![]() $w\in {\mathbf {P}}_{Ov^+_\sigma v}^\circ $
lying on the intersection of two hyperboloids
$w\in {\mathbf {P}}_{Ov^+_\sigma v}^\circ $
lying on the intersection of two hyperboloids
and the line
![]() ${\mathrm {L}}_{w,v^+_\sigma }$
will intersect the edge
${\mathrm {L}}_{w,v^+_\sigma }$
will intersect the edge
![]() ${\mathrm {L}}_{[O,v]}$
at a point, denoted by q. Thus, we get that the point
${\mathrm {L}}_{[O,v]}$
at a point, denoted by q. Thus, we get that the point
![]() $v(E_1)$
is contained in the triangle
$v(E_1)$
is contained in the triangle
![]() ${\mathbf {P}}_{qv v^+_\sigma }$
, while the point
${\mathbf {P}}_{qv v^+_\sigma }$
, while the point
![]() $\sum _{i=1}^{k-1} v(E_i)$
is contained in the triangle
$\sum _{i=1}^{k-1} v(E_i)$
is contained in the triangle
![]() $ {\mathbf {P}}_{Oq v^+_\sigma }$
. If we define
$ {\mathbf {P}}_{Oq v^+_\sigma }$
. If we define
![]() ${\mathrm {L}}_u$
to be the line passing through
${\mathrm {L}}_u$
to be the line passing through
![]() $u\in \mathbb {R}^3$
and parallel to the line
$u\in \mathbb {R}^3$
and parallel to the line
![]() ${\mathrm {L}}_{w, v^+_{\sigma } }$
, the discussion above exactly means
${\mathrm {L}}_{w, v^+_{\sigma } }$
, the discussion above exactly means
where
![]() $p_1={\mathrm {L}}_{\sum _{i=1}^{k-1} v(E_i)}\cap {\mathrm {L}}_{[O,\,v]} $
and
$p_1={\mathrm {L}}_{\sum _{i=1}^{k-1} v(E_i)}\cap {\mathrm {L}}_{[O,\,v]} $
and
![]() $p_2={\mathrm {L}}_{v(E_1)}\cap {\mathrm {L}}_{[O,\,v]}$
; see Figure 5.
$p_2={\mathrm {L}}_{v(E_1)}\cap {\mathrm {L}}_{[O,\,v]}$
; see Figure 5.

Figure 5 If this plane corresponds to a wall, there must be some integer point inside this triangle and below these two hyperbolas.
Next, one can regard
![]() ${\mathrm {L}}_{w,v^+_\sigma }$
as a stability condition in a natural way. Consider the line
${\mathrm {L}}_{w,v^+_\sigma }$
as a stability condition in a natural way. Consider the line
![]() $\ell $
passing through the origin O on the plane
$\ell $
passing through the origin O on the plane
![]() $\Pi $
, which is parallel to the line passing through w and
$\Pi $
, which is parallel to the line passing through w and
![]() $v_{\sigma }^+$
. By construction, the line
$v_{\sigma }^+$
. By construction, the line
![]() $\ell $
lies between
$\ell $
lies between
![]() $[\sigma ']$
and
$[\sigma ']$
and
![]() $[\sigma "]$
. Thus, there is a stability condition
$[\sigma "]$
. Thus, there is a stability condition
![]() $\tau \in (\sigma ', \sigma ") $
such that
$\tau \in (\sigma ', \sigma ") $
such that
![]() $[\tau ]$
corresponds to the line
$[\tau ]$
corresponds to the line
![]() $\ell $
. Since
$\ell $
. Since
![]() $Z_\tau (\ell ) = 0$
, we obtain
$Z_\tau (\ell ) = 0$
, we obtain
![]() $Z_\tau (E_1) = Z_\tau (p_2)$
, and the same holds for
$Z_\tau (E_1) = Z_\tau (p_2)$
, and the same holds for
![]() $p_1$
.
$p_1$
.
Using the inclusions (3.5), we obtain the inequality
 $$ \begin{align} \frac{\big\lvert Z_{\tau}(v(E_1)) \big\rvert}{\big\lvert Z_{\tau}(\sum_{i=1}^{k-1} v(E_i))\big\rvert }=\frac{\big\lvert Z_{\tau}(p_2)\big\rvert }{ \big\lvert Z_{\tau}(p_1) \big\rvert } = \frac{\|{\mathrm{L}}_{[O,\,p_2]}\|}{\|{\mathrm{L}}_{[O,\,p_1]}\|}>1. \end{align} $$
$$ \begin{align} \frac{\big\lvert Z_{\tau}(v(E_1)) \big\rvert}{\big\lvert Z_{\tau}(\sum_{i=1}^{k-1} v(E_i))\big\rvert }=\frac{\big\lvert Z_{\tau}(p_2)\big\rvert }{ \big\lvert Z_{\tau}(p_1) \big\rvert } = \frac{\|{\mathrm{L}}_{[O,\,p_2]}\|}{\|{\mathrm{L}}_{[O,\,p_1]}\|}>1. \end{align} $$
However, this contradicts to the relation
![]() $ \sum _{i=1}^{k-1}\big \lvert Z_{\tau }(v(E_i)) \big \rvert = \big |Z_{\tau } \left (\sum _{i=1}^{k-1} v(E_i) \right )\big |$
which finishes the proof.
$ \sum _{i=1}^{k-1}\big \lvert Z_{\tau }(v(E_i)) \big \rvert = \big |Z_{\tau } \left (\sum _{i=1}^{k-1} v(E_i) \right )\big |$
which finishes the proof.
Remark 3.3. If
![]() $v(\widetilde E_i)$
already lies in
$v(\widetilde E_i)$
already lies in
![]() ${\mathbf {P}}_{O v v_\sigma ^+} \setminus {\mathrm {L}}_{(O, v )}$
for all i, then our argument actually implies that we can always take a destabilising sequence
${\mathbf {P}}_{O v v_\sigma ^+} \setminus {\mathrm {L}}_{(O, v )}$
for all i, then our argument actually implies that we can always take a destabilising sequence
such that
![]() $v(F) \in \Omega ^+_{v(E)}(\sigma )$
and
$v(F) \in \Omega ^+_{v(E)}(\sigma )$
and
![]() $v(Q) \in \Omega ^-_{v(E)}(\sigma )$
. This will happen, for instance, if
$v(Q) \in \Omega ^-_{v(E)}(\sigma )$
. This will happen, for instance, if
![]() $E=i_* G$
for some slope stable vector bundle G on C. Indeed, as any subobject A of the sheaf E (in the heart
$E=i_* G$
for some slope stable vector bundle G on C. Indeed, as any subobject A of the sheaf E (in the heart
![]() $\operatorname {\mathrm {Coh}}^{\beta (\sigma )}(X)$
) is also a sheaf (cf., for example, [Reference Bayer2, Proposition 2.4]), we have
$\operatorname {\mathrm {Coh}}^{\beta (\sigma )}(X)$
) is also a sheaf (cf., for example, [Reference Bayer2, Proposition 2.4]), we have
![]() $v(A)\in {\mathbf {P}}_{O v_\sigma ^+ v }\setminus {\mathrm {L}}_{(O,v)}$
(since
$v(A)\in {\mathbf {P}}_{O v_\sigma ^+ v }\setminus {\mathrm {L}}_{(O,v)}$
(since
![]() $r(A) \geq 0$
and the case
$r(A) \geq 0$
and the case
![]() $r(A)=0$
cannot happen as it is on a wall). In particular, this holds for
$r(A)=0$
cannot happen as it is on a wall). In particular, this holds for
![]() $v(\widetilde {E}_i)$
.
$v(\widetilde {E}_i)$
.
Then we can obtain a generalisation of Proposition 3.1.
Proposition 3.4. Given
![]() $v^2\geq 0$
and a region
$v^2\geq 0$
and a region
![]() $\mathcal {I}\subseteq V(X)$
, we define
$\mathcal {I}\subseteq V(X)$
, we define
Then any
![]() $\sigma \in \mathcal {I}$
is not lying on a wall of any E with
$\sigma \in \mathcal {I}$
is not lying on a wall of any E with
![]() $v(E) = v$
if and only if
$v(E) = v$
if and only if
Similarly, any E with
![]() $v(E) = v$
cannot be strictly
$v(E) = v$
cannot be strictly
![]() $\sigma $
-semistable for any
$\sigma $
-semistable for any
![]() $\sigma \in \mathcal {I}$
if and only if
$\sigma \in \mathcal {I}$
if and only if
Proof. The ‘if’ part follows directly from Lemma 3.2. For the ‘only if’ part, suppose there exists some stability condition
![]() $\sigma $
and an integer point
$\sigma $
and an integer point
![]() $w \in \Omega _v(\sigma )$
. Then, we can find
$w \in \Omega _v(\sigma )$
. Then, we can find
![]() $\sigma $
-stable objects
$\sigma $
-stable objects
![]() $F_1$
and
$F_1$
and
![]() $F_2$
such that
$F_2$
such that
![]() $v(F_1)=w$
and
$v(F_1)=w$
and
![]() $v(F_2)=v-w$
, and
$v(F_2)=v-w$
, and
![]() $\sigma $
will be lying on a wall of
$\sigma $
will be lying on a wall of ![]() from the construction. For the strictly semistable case, one just notes that the Mukai vectors of all the factors are lying on
from the construction. For the strictly semistable case, one just notes that the Mukai vectors of all the factors are lying on
![]() ${\mathrm {L}}_{(O,v)}$
.
${\mathrm {L}}_{(O,v)}$
.
According to Proposition 3.4, we will say a Mukai vector
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
admits no wall in
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
admits no wall in
![]() $\mathcal {I}$
if Equation (3.7) holds and admits no strictly semistable condition if Equation (3.8) holds.
$\mathcal {I}$
if Equation (3.7) holds and admits no strictly semistable condition if Equation (3.8) holds.
Note that from the definition, one automatically has
![]() $\Omega _v(\sigma )=\Omega _v({\mathrm {L}}_{(\sigma ',\sigma ")})$
. This motivates us to find a subregion of
$\Omega _v(\sigma )=\Omega _v({\mathrm {L}}_{(\sigma ',\sigma ")})$
. This motivates us to find a subregion of
![]() $V(X)$
with regular boundary. A candidate is
$V(X)$
with regular boundary. A candidate is
which is used in [Reference Feyzbakhsh12]. As a consequence, if v admits no wall in
![]() $I\subseteq {\mathrm {L}}_{(o,o')}$
, then it admits no wall in
$I\subseteq {\mathrm {L}}_{(o,o')}$
, then it admits no wall in
![]() ${\pmb {\triangle }}_{\pi _v}(I) \cap \Gamma $
as well.
${\pmb {\triangle }}_{\pi _v}(I) \cap \Gamma $
as well.
Remark 3.5. Comparing Proposition 3.1 with Proposition 3.4, one can conclude that for
![]() $v^2=0$
and
$v^2=0$
and
![]() $\mathcal {I}$
being a line segment, the condition (3.1) implies Equation (3.7). Actually, if
$\mathcal {I}$
being a line segment, the condition (3.1) implies Equation (3.7). Actually, if
![]() $\Omega ^+_v(\sigma )$
contains any integer point
$\Omega ^+_v(\sigma )$
contains any integer point
![]() $\delta $
, then
$\delta $
, then
![]() $\pi _\delta $
is a root lying in
$\pi _\delta $
is a root lying in
![]() ${\mathrm {L}}_{(\pi _v,\sigma ]}$
. This suggests that the condition (3.1) can be replaced by
${\mathrm {L}}_{(\pi _v,\sigma ]}$
. This suggests that the condition (3.1) can be replaced by
![]() ${\pmb {\triangle }}_{\pi _v}(I) \subseteq V'(X)$
, where
${\pmb {\triangle }}_{\pi _v}(I) \subseteq V'(X)$
, where
 $$ \begin{align*} V'(X) = \left\{ (x,y)\in \mathbb{R}^2 \,\middle|\, x>\frac{H^2 y^2}{2} \right\} \setminus \bigcup_{\delta \in \mathrm{R}(X)} \{\pi_\delta\}. \end{align*} $$
$$ \begin{align*} V'(X) = \left\{ (x,y)\in \mathbb{R}^2 \,\middle|\, x>\frac{H^2 y^2}{2} \right\} \setminus \bigcup_{\delta \in \mathrm{R}(X)} \{\pi_\delta\}. \end{align*} $$
4 The restriction map to Brill–Noether locus
Given a positive primitive vector
![]() $v= (r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
, let
$v= (r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
, let
![]() $\mathbf {M}(v)$
be the moduli space of H-Gieseker semistable sheaves on the surface X with Mukai vector v. In this section, we always assume
$\mathbf {M}(v)$
be the moduli space of H-Gieseker semistable sheaves on the surface X with Mukai vector v. In this section, we always assume
![]() $r,c,s>0$
and
$r,c,s>0$
and
Then
![]() $\mathbf {M}(v)$
is a smooth variety consisting of
$\mathbf {M}(v)$
is a smooth variety consisting of
![]() $\mu _H$
-stable locally free sheaves (cf. [Reference Yoshioka21, Remark 3.2]). The main result is:
$\mu _H$
-stable locally free sheaves (cf. [Reference Yoshioka21, Remark 3.2]). The main result is:
Theorem 4.1. For any irreducible curve
![]() $C\in |mH|$
, the restriction map is an injective morphism
$C\in |mH|$
, the restriction map is an injective morphism
 $$ \begin{align*} \begin{aligned} \psi: \mathbf{M}(v) &\to {\mathbf{BN}}_C(v) ,\\ E &\mapsto E|_C \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi: \mathbf{M}(v) &\to {\mathbf{BN}}_C(v) ,\\ E &\mapsto E|_C \end{aligned} \end{align*} $$
with stable image (i.e.,
![]() $E|_C$
is stable) if the following conditions hold
$E|_C$
is stable) if the following conditions hold
-
(i)
 $(mr-c)s>rc$
;
$(mr-c)s>rc$
; -
(ii) v admits no wall in
 ${\mathrm {L}}_{(o, \sigma _v]}$
, where
${\mathrm {L}}_{(o, \sigma _v]}$
, where
 $\sigma _v=(\frac {rc}{(mr-c)s},0)$
;
$\sigma _v=(\frac {rc}{(mr-c)s},0)$
; -
(iii)
 $v(-m)=\big (r, c-mr, s+ (g-1)m(mr-2c) \big )$
admits no wall in
$v(-m)=\big (r, c-mr, s+ (g-1)m(mr-2c) \big )$
admits no wall in
 ${\pmb {\triangle }}_{\pi _{v(-m)}}({\mathrm {L}}_{(o, o']}) \cap \Gamma $
, where
${\pmb {\triangle }}_{\pi _{v(-m)}}({\mathrm {L}}_{(o, o']}) \cap \Gamma $
, where
 $\Gamma $
is defined in Equation (3.9).
$\Gamma $
is defined in Equation (3.9).
Proof. It suffices to prove that for any
![]() $E\in \mathbf {M}(v)$
, the restriction
$E\in \mathbf {M}(v)$
, the restriction
![]() $E|_C$
is slope stable with
$E|_C$
is slope stable with
![]() $h^0(C, E|_C)\geq r+s$
and
$h^0(C, E|_C)\geq r+s$
and
![]() $E|_C$
uniquely determines E.
$E|_C$
uniquely determines E.
Firstly, we show that
![]() $E|_C$
is slope semistable. Note that condition (i) ensures that
$E|_C$
is slope semistable. Note that condition (i) ensures that
![]() $\sigma _v$
lies in
$\sigma _v$
lies in
![]() ${\mathrm {L}}_{(o, o')}$
. By [Reference Feyzbakhsh11, Lemma 2.13 (b)], it suffices to show that
${\mathrm {L}}_{(o, o')}$
. By [Reference Feyzbakhsh11, Lemma 2.13 (b)], it suffices to show that
![]() $i_*(E|_C)$
is
$i_*(E|_C)$
is
![]() $\sigma _v$
-semistable. Consider the exact sequence
$\sigma _v$
-semistable. Consider the exact sequence
we have
![]() $\pi _{i_\ast (E|_C)}= (\frac {r}{(g-1)(2c-mr)},0)$
is lying on
$\pi _{i_\ast (E|_C)}= (\frac {r}{(g-1)(2c-mr)},0)$
is lying on
![]() ${\mathrm {L}}_{\pi _{E}, \pi _{E(-C)}}$
. Since E is slope stable, according to [Reference Feyzbakhsh11, Lemma 2.15], E is
${\mathrm {L}}_{\pi _{E}, \pi _{E(-C)}}$
. Since E is slope stable, according to [Reference Feyzbakhsh11, Lemma 2.15], E is
![]() $\sigma $
-stable for any
$\sigma $
-stable for any
![]() $\sigma \in {\mathrm {L}}_{(o, \pi _v)} \cap V(X) $
. Choose
$\sigma \in {\mathrm {L}}_{(o, \pi _v)} \cap V(X) $
. Choose
![]() ${\sigma _1 \in {\mathrm {L}}_{ ( o, \pi _v)}}$
sufficiently close to o. We have
${\sigma _1 \in {\mathrm {L}}_{ ( o, \pi _v)}}$
sufficiently close to o. We have
as in Figure 6. Note that for any line
![]() $\mathrm {L}$
passing through
$\mathrm {L}$
passing through
![]() $\pi _E$
, the intersection
$\pi _E$
, the intersection
![]() ${\mathbf {P}}_{o\sigma _v\sigma _1}\setminus \{o\} \cap \mathrm {L}$
is connected. By our assumption 4.1, v admits no wall in
${\mathbf {P}}_{o\sigma _v\sigma _1}\setminus \{o\} \cap \mathrm {L}$
is connected. By our assumption 4.1, v admits no wall in
![]() ${\mathrm {L}}_{(o,\sigma _v]}$
. This implies it also admits no wall in
${\mathrm {L}}_{(o,\sigma _v]}$
. This implies it also admits no wall in
![]() ${\mathbf {P}}_{o\sigma _v\sigma _1}\setminus \{o\}$
. Hence, E is
${\mathbf {P}}_{o\sigma _v\sigma _1}\setminus \{o\}$
. Hence, E is
![]() $\sigma _v$
-stable as E is
$\sigma _v$
-stable as E is
![]() $\sigma _1$
-stable. Similarly, we have
$\sigma _1$
-stable. Similarly, we have
![]() $E(-C)$
is also
$E(-C)$
is also
![]() $\sigma _v$
-stable by using the assumption (iii). As in the proof of Proposition 2.2, E and
$\sigma _v$
-stable by using the assumption (iii). As in the proof of Proposition 2.2, E and
![]() $E(-C)$
are of the same
$E(-C)$
are of the same
![]() $\sigma _v$
-phase since
$\sigma _v$
-phase since
![]() $\sigma _v \in {\mathrm {L}}_{\pi _{E},\pi _{E(-C)}} $
. Hence, the restriction
$\sigma _v \in {\mathrm {L}}_{\pi _{E},\pi _{E(-C)}} $
. Hence, the restriction
![]() $i_*(E|_C)$
is
$i_*(E|_C)$
is
![]() $\sigma _v$
-semistable with E and
$\sigma _v$
-semistable with E and
![]() $E(-C)[1]$
as its JH-factors.
$E(-C)[1]$
as its JH-factors.

Figure 6 Any point in the colored region is a stability condition.
Secondly, we show that
![]() $E|_C$
is slope stable. By using [Reference Feyzbakhsh11, Lemma 2.13 (b)], we are reduced to prove
$E|_C$
is slope stable. By using [Reference Feyzbakhsh11, Lemma 2.13 (b)], we are reduced to prove
![]() $i_*(E|_C)$
is
$i_*(E|_C)$
is
![]() $\sigma $
-stable for some
$\sigma $
-stable for some
![]() $\sigma \in {\mathrm {L}}_{ (o,\sigma _v)} $
. Moreover, due to [Reference Feyzbakhsh11, Lemma 2.13 (a)],
$\sigma \in {\mathrm {L}}_{ (o,\sigma _v)} $
. Moreover, due to [Reference Feyzbakhsh11, Lemma 2.13 (a)],
![]() $i_*(E|_C)$
is semistable for any stability condition lying in a line segment
$i_*(E|_C)$
is semistable for any stability condition lying in a line segment
![]() $ {\mathrm {L}}_{( o,a)}\subseteq {\mathrm {L}}_{( o,\sigma _v)} $
. Suppose that
$ {\mathrm {L}}_{( o,a)}\subseteq {\mathrm {L}}_{( o,\sigma _v)} $
. Suppose that
![]() $i_*(E|_C)$
is strictly semistable for all stability conditions in
$i_*(E|_C)$
is strictly semistable for all stability conditions in
![]() ${\mathrm {L}}_{(o,a)} $
. Then for any
${\mathrm {L}}_{(o,a)} $
. Then for any
![]() $\sigma _0 \in {\mathrm {L}}_{(o, a)}$
and any destabilising sequence
$\sigma _0 \in {\mathrm {L}}_{(o, a)}$
and any destabilising sequence
such that
![]() $F_1,F_2$
are
$F_1,F_2$
are
![]() $\sigma _{0}$
-semistable with the same
$\sigma _{0}$
-semistable with the same
![]() $\sigma _0$
-phase as
$\sigma _0$
-phase as
![]() $i_*(E|_C)$
, we have
$i_*(E|_C)$
, we have
![]() ${\pi _{F_1}=\pi _{i_*(E|_C)}}$
. This gives
${\pi _{F_1}=\pi _{i_*(E|_C)}}$
. This gives
![]() $\phi _{\sigma _v}(F_{1})=\phi _{\sigma _v}(i_\ast (E|_C))$
, which implies that
$\phi _{\sigma _v}(F_{1})=\phi _{\sigma _v}(i_\ast (E|_C))$
, which implies that
![]() $F_1$
is
$F_1$
is
![]() $\sigma _v$
-semistable. However, this contradicts to the uniqueness of JH-factors of
$\sigma _v$
-semistable. However, this contradicts to the uniqueness of JH-factors of
![]() $i_\ast (E|_C)$
with respect to
$i_\ast (E|_C)$
with respect to
![]() $\sigma _v$
. Thus,
$\sigma _v$
. Thus,
![]() $i_*(E|_C)$
is
$i_*(E|_C)$
is
![]() $\sigma $
-stable for some
$\sigma $
-stable for some
![]() $\sigma \in {\mathrm {L}}_{(o,a)}$
.
$\sigma \in {\mathrm {L}}_{(o,a)}$
.
Next, we show that
![]() $h^0(C, E|_C)=h^0(X,E)\geq r+s$
. Let us consider the long exact sequence of cohomology induced by (4.1)
$h^0(C, E|_C)=h^0(X,E)\geq r+s$
. Let us consider the long exact sequence of cohomology induced by (4.1)
As
![]() $E(-C)$
is
$E(-C)$
is
![]() $\mu _H$
-stable and
$\mu _H$
-stable and
![]() $ \mu _H (E(-C))<0$
, we have
$ \mu _H (E(-C))<0$
, we have
Then we choose
![]() $\sigma _2 \in {\mathrm {L}}_{(\pi _{v(-m)} , o)}$
sufficiently close to o and
$\sigma _2 \in {\mathrm {L}}_{(\pi _{v(-m)} , o)}$
sufficiently close to o and
![]() $\sigma _3 \in {\mathrm {L}}_{(\pi _{v(-m)} , o')}$
sufficiently close to
$\sigma _3 \in {\mathrm {L}}_{(\pi _{v(-m)} , o')}$
sufficiently close to
![]() $o'$
so that
$o'$
so that
![]() ${\mathbf {P}}_{o\sigma _2\sigma _3o'} \setminus \left \{ o,o' \right \} \subseteq \Gamma $
; see Figure 6. As shown above,
${\mathbf {P}}_{o\sigma _2\sigma _3o'} \setminus \left \{ o,o' \right \} \subseteq \Gamma $
; see Figure 6. As shown above,
![]() $E(-C)$
is
$E(-C)$
is
![]() $\sigma $
-stable for any
$\sigma $
-stable for any
![]() $\sigma \in {\mathbf {P}}_{o\sigma _2\sigma _3 o'} \setminus \left \{ o,o' \right \} $
. In particular,
$\sigma \in {\mathbf {P}}_{o\sigma _2\sigma _3 o'} \setminus \left \{ o,o' \right \} $
. In particular,
![]() $E(-C)$
is
$E(-C)$
is
![]() $\sigma _3$
-stable. According to [Reference Feyzbakhsh11, Lemma 2.15], we have
$\sigma _3$
-stable. According to [Reference Feyzbakhsh11, Lemma 2.15], we have
and
![]() ${\mathcal {O}}_X$
is also
${\mathcal {O}}_X$
is also
![]() $\sigma _v$
-stable. Note that
$\sigma _v$
-stable. Note that
![]() $\pi _{{\mathcal {O}}_X} = o'$
. By Proposition 3.1 and Proposition 2.2, we know that
$\pi _{{\mathcal {O}}_X} = o'$
. By Proposition 3.1 and Proposition 2.2, we know that
![]() ${\mathcal {O}}_X$
is
${\mathcal {O}}_X$
is
![]() $\sigma _3$
-stable and
$\sigma _3$
-stable and
![]() $\phi _{\sigma _3}(E(-C))=\phi _{\sigma _3}({\mathcal {O}}_X)$
. Then we have
$\phi _{\sigma _3}(E(-C))=\phi _{\sigma _3}({\mathcal {O}}_X)$
. Then we have
where
![]() $\mathcal {A} = \operatorname {\mathrm {Coh}}^{\beta (\sigma _3)}(X)$
. Therefore, we get an isomorphism
$\mathcal {A} = \operatorname {\mathrm {Coh}}^{\beta (\sigma _3)}(X)$
. Therefore, we get an isomorphism ![]() . By Serre duality and the stability of E, we have
. By Serre duality and the stability of E, we have
![]() ${\mathrm {H}}^2(X,E) \cong \operatorname {\mathrm {Hom}}_X(E,\omega _X) \cong \operatorname {\mathrm {Hom}}_X(E,{\mathcal {O}}_X) =0 $
. It follows that
${\mathrm {H}}^2(X,E) \cong \operatorname {\mathrm {Hom}}_X(E,\omega _X) \cong \operatorname {\mathrm {Hom}}_X(E,{\mathcal {O}}_X) =0 $
. It follows that
This proves our claim.
In the end, the uniqueness of E follows from the fact that the JH factors of
![]() $i_*(E|_C)$
are unique with respect to
$i_*(E|_C)$
are unique with respect to
![]() $\sigma _v$
.
$\sigma _v$
.

Figure 7
![]() $\pi _\delta $
in the interior of
$\pi _\delta $
in the interior of
![]() $\mathbf {P}^\circ _{o\pi _v\infty }$
(colored area).
$\mathbf {P}^\circ _{o\pi _v\infty }$
(colored area).
A numerical criterion
As in [Reference Feyzbakhsh11], we would like to find a purely numerical condition for Theorem 4.1 to hold. An elementary result is
Lemma 4.2. Let
![]() ${\mathbf {P}}_{o\pi _v \infty }$
be the trapezoidal region bounded by
${\mathbf {P}}_{o\pi _v \infty }$
be the trapezoidal region bounded by
![]() ${\mathrm {L}}_{[o,\pi _v]}$
, the (positive) half x-axis
${\mathrm {L}}_{[o,\pi _v]}$
, the (positive) half x-axis
![]() ${\mathrm {L}}_{[o,\infty )}$
and the vertical ray
${\mathrm {L}}_{[o,\infty )}$
and the vertical ray
![]() ${\mathrm {L}}_{[\pi _v,\infty )}$
in Figure 7. Then v admits no wall in
${\mathrm {L}}_{[\pi _v,\infty )}$
in Figure 7. Then v admits no wall in
![]() ${\mathbf {P}}_{o\pi _v \infty } \cap \Gamma $
if one of the following conditions holds
${\mathbf {P}}_{o\pi _v \infty } \cap \Gamma $
if one of the following conditions holds
-
(i)
 $v^2=0 \,$
and
$v^2=0 \,$
and
 $\, r/\gcd (r,c) \leq g-1$
.
$\, r/\gcd (r,c) \leq g-1$
. -
(ii)
 $ s=\lfloor \frac {(g-1)c^2+1}{r} \rfloor $
and
$ s=\lfloor \frac {(g-1)c^2+1}{r} \rfloor $
and
 $\, g-1 \geq \max \{ \frac {r^2}{c}, r+1\}.$
$\, g-1 \geq \max \{ \frac {r^2}{c}, r+1\}.$
Proof. (i). By Proposition 3.1, it will be sufficient to show that
Due to the explicit description of
![]() $V(X)$
in (2.1), this is equivalent to showing that there is no projection of root lying in
$V(X)$
in (2.1), this is equivalent to showing that there is no projection of root lying in
![]() $\mathbf {P}^\circ _{o\pi _v\infty }$
. Suppose there exists a root
$\mathbf {P}^\circ _{o\pi _v\infty }$
. Suppose there exists a root
![]() $\delta =(r',c',s')\in \mathrm {R}(X)$
with
$\delta =(r',c',s')\in \mathrm {R}(X)$
with
![]() $\pi _\delta \in \mathbf {P}^\circ _{o\pi _v\infty }$
. Then we have
$\pi _\delta \in \mathbf {P}^\circ _{o\pi _v\infty }$
. Then we have
see Figure 7. Note that
![]() $2rs=c^2(2g-2)$
and
$2rs=c^2(2g-2)$
and
![]() $2r's'=(c')^2(2g-2) +2$
, one can plug into (4.3) to get
$2r's'=(c')^2(2g-2) +2$
, one can plug into (4.3) to get
which is not possible.
(ii). According to Proposition 3.4, we just need to show that
![]() $ \Omega ^+_{v}(\sigma )\cap {\mathrm {H}}_{\text {alg}}^{*}(X) =\emptyset $
for any
$ \Omega ^+_{v}(\sigma )\cap {\mathrm {H}}_{\text {alg}}^{*}(X) =\emptyset $
for any
![]() $\sigma \in {\mathbf {P}}_{o\pi _v \infty } \cap \Gamma $
. Suppose there is an integer point
$\sigma \in {\mathbf {P}}_{o\pi _v \infty } \cap \Gamma $
. Suppose there is an integer point
![]() $(x,y,z)\in \Omega ^+_v( \sigma _0) $
for some
$(x,y,z)\in \Omega ^+_v( \sigma _0) $
for some
![]() $\sigma _0\in {\mathbf {P}}_{o\pi _v \infty } $
. By the construction of
$\sigma _0\in {\mathbf {P}}_{o\pi _v \infty } $
. By the construction of
![]() $\Omega ^+_{v}({\mathbf {P}}_{o\pi _v \infty } \cap \Gamma )$
, we have
$\Omega ^+_{v}({\mathbf {P}}_{o\pi _v \infty } \cap \Gamma )$
, we have
![]() $0<y\leq c$
and the point
$0<y\leq c$
and the point
![]() $(x,y,z)$
is lying in the interior of the triangle
$(x,y,z)$
is lying in the interior of the triangle
![]() ${\mathbf {P}}_{u_1 u_2 u_3}$
with vertices
${\mathbf {P}}_{u_1 u_2 u_3}$
with vertices
As
![]() $ y^2(g-1)+1\geq xz$
and
$ y^2(g-1)+1\geq xz$
and
![]() $z\geq \frac {sy}{c}$
, one has
$z\geq \frac {sy}{c}$
, one has
 $$ \begin{align*}\frac{ry}{c}<x< \frac{y^2(g-1)+1}{sy/c}.\end{align*} $$
$$ \begin{align*}\frac{ry}{c}<x< \frac{y^2(g-1)+1}{sy/c}.\end{align*} $$
Note that
![]() $c^2(g-1)-\frac {v^2}{2}=rs$
, the condition
$c^2(g-1)-\frac {v^2}{2}=rs$
, the condition
![]() $s=\lfloor \frac {(g-1)c^2+1}{r} \rfloor $
is equivalent to
$s=\lfloor \frac {(g-1)c^2+1}{r} \rfloor $
is equivalent to
![]() $r>\frac {v^2}{2}+1$
. Then we have
$r>\frac {v^2}{2}+1$
. Then we have
 $$ \begin{align} \begin{aligned} 0< \frac{y^2(g-1)+1}{sy/c}- \frac{ry}{c} &< \max\left\{\frac{gc}{s}-\frac{r}{c}, \frac{c^2(g-1)+1}{s}-r\right\} \\ & = \max\left\{\frac{r(c^2+\frac{v^2}{2})}{c(c^2(g-1)-\frac{v^2}{2})}, \frac{r(\frac{v^2}{2}+1)}{c^2(g-1)-\frac{v^2}{2}}\right\}\\ &\leq \max\left\{\frac{r(c^2+r-2)}{c(c^2(g-1)-r+2)}, \frac{r^2-r}{c^2(g-1)-r+2}\right\} \\& \leq \frac{1}{c}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0< \frac{y^2(g-1)+1}{sy/c}- \frac{ry}{c} &< \max\left\{\frac{gc}{s}-\frac{r}{c}, \frac{c^2(g-1)+1}{s}-r\right\} \\ & = \max\left\{\frac{r(c^2+\frac{v^2}{2})}{c(c^2(g-1)-\frac{v^2}{2})}, \frac{r(\frac{v^2}{2}+1)}{c^2(g-1)-\frac{v^2}{2}}\right\}\\ &\leq \max\left\{\frac{r(c^2+r-2)}{c(c^2(g-1)-r+2)}, \frac{r^2-r}{c^2(g-1)-r+2}\right\} \\& \leq \frac{1}{c}. \end{aligned} \end{align} $$
Here, the last inequality follows from our assumption
![]() $g-1\geq \max \{\frac {r^2}{c},r+1\}$
. This means
$g-1\geq \max \{\frac {r^2}{c},r+1\}$
. This means
![]() $0<x-\frac {ry}{c}<\frac {1}{c}$
which contradicts to the fact x is an integer.
$0<x-\frac {ry}{c}<\frac {1}{c}$
which contradicts to the fact x is an integer.
Injectivity condition
Let us summarise our numerical criterion in short. We may say
![]() $v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying the injectivity condition
$v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying the injectivity condition ![]() if the following inequalities holds
if the following inequalities holds
 $$ \begin{align} \begin{aligned} r>\max\left\{\frac{v^2}{2}+1,\frac{c}{m}\right\}, \quad c>0, \quad s>\frac{rc}{mr-c}, \quad \gcd(r,c)=1\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} r>\max\left\{\frac{v^2}{2}+1,\frac{c}{m}\right\}, \quad c>0, \quad s>\frac{rc}{mr-c}, \quad \gcd(r,c)=1\\ \end{aligned} \end{align} $$
and
 $$ \begin{align} g-1\geq \begin{cases} r, & \mbox{if } v^2=0\\ \max \{ \frac{r^2}{c} ,\frac{r^2}{mr-c},r+1\}, & \mbox{if } v^2>0. \end{cases} \end{align} $$
$$ \begin{align} g-1\geq \begin{cases} r, & \mbox{if } v^2=0\\ \max \{ \frac{r^2}{c} ,\frac{r^2}{mr-c},r+1\}, & \mbox{if } v^2>0. \end{cases} \end{align} $$
Then we have
Corollary 4.3. The restriction map
![]() $\psi : \mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an injective morphism with stable image if v satisfies the condition:
$\psi : \mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an injective morphism with stable image if v satisfies the condition:
Proof. The condition
![]() $mr>c>0$
ensures
$mr>c>0$
ensures
![]() $\pi _v$
lies in the first quadrant while
$\pi _v$
lies in the first quadrant while
![]() $\pi _{v(-m)}$
lies in the second quadrant, and the condition
$\pi _{v(-m)}$
lies in the second quadrant, and the condition
![]() $s(mr-c)>rc$
ensures
$s(mr-c)>rc$
ensures
![]() $\sigma _v$
is below
$\sigma _v$
is below
![]() $o'$
. The assertion then follows from the direct computation that
$o'$
. The assertion then follows from the direct computation that
![]() ${\mathrm {L}}_{(o,\sigma _v]} \subseteq {\pmb {\triangle }}_{\pi _w}({\mathrm {L}}_{[o, o']}) \cap \Gamma \subseteq {\mathbf {P}}_{o\pi _w \infty } \cap \Gamma $
for
${\mathrm {L}}_{(o,\sigma _v]} \subseteq {\pmb {\triangle }}_{\pi _w}({\mathrm {L}}_{[o, o']}) \cap \Gamma \subseteq {\mathbf {P}}_{o\pi _w \infty } \cap \Gamma $
for
![]() $w = v$
or
$w = v$
or
![]() $v(-m)$
.
$v(-m)$
.
5 Surjectivity of the restriction map
Throughout this section, we let
![]() $v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a positive vector satisfying the injectivity condition (✶). Due to Corollary 4.3, the restriction map
$v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a positive vector satisfying the injectivity condition (✶). Due to Corollary 4.3, the restriction map
is an injective morphism with stable image. Following the ideas in [Reference Feyzbakhsh11, Reference Feyzbakhsh13], we give sufficient conditions such that
![]() $\psi $
is surjective.
$\psi $
is surjective.
The first wall
As in [Reference Feyzbakhsh11], we first describe the wall that bounds the Gieseker chamber of
![]() $i_\ast F$
for
$i_\ast F$
for
![]() ${F\in {\mathbf {BN}}_C(v)}$
. The following result is an extension of [Reference Feyzbakhsh11, Proposition 4.2].
${F\in {\mathbf {BN}}_C(v)}$
. The following result is an extension of [Reference Feyzbakhsh11, Proposition 4.2].
Theorem 5.1. For any
![]() $F\in {\mathbf {BN}}_C(v)$
, the wall that bounds the Gieseker chamber of
$F\in {\mathbf {BN}}_C(v)$
, the wall that bounds the Gieseker chamber of
![]() $i_*F$
is not below the line
$i_*F$
is not below the line
![]() ${\mathrm {L}}_{\pi _v, \pi _{v(-m)}}$
, and they coincide if and only if
${\mathrm {L}}_{\pi _v, \pi _{v(-m)}}$
, and they coincide if and only if
![]() $F=E|_C$
for some
$F=E|_C$
for some
![]() $E\in \mathbf {M}(v)$
.
$E\in \mathbf {M}(v)$
.
Proof. The argument is essentially the same as the primitive case proved in [Reference Feyzbakhsh11, Proposition 4.2]. Here, we provide the details for completeness.
We first show that for any v satisfying Equation (✶−1), if both v and
![]() $v(-m)$
admit no wall in
$v(-m)$
admit no wall in
![]() $(o, \sigma _v ]$
, then so does
$(o, \sigma _v ]$
, then so does
Let
![]() ${\mathcal {W}}_{i_*F}$
be the first wall, and let
${\mathcal {W}}_{i_*F}$
be the first wall, and let
![]() $\sigma _{\alpha ',0}\in {\mathcal {W}}_{i_*F} $
be a stability condition. Suppose
$\sigma _{\alpha ',0}\in {\mathcal {W}}_{i_*F} $
be a stability condition. Suppose
![]() ${\mathcal {W}}_{i_\ast F}$
is below or on the line
${\mathcal {W}}_{i_\ast F}$
is below or on the line
![]() ${\mathrm {L}}_{\pi _v, \pi _{v(-m)}}$
. Then for any destabilising sequence
${\mathrm {L}}_{\pi _v, \pi _{v(-m)}}$
. Then for any destabilising sequence
in
![]() $\operatorname {\mathrm {Coh}}^{\beta =0}(X)$
such that
$\operatorname {\mathrm {Coh}}^{\beta =0}(X)$
such that
![]() $F_1,F_2$
are
$F_1,F_2$
are
![]() $\sigma _{\alpha ',0}$
-semistable, and
$\sigma _{\alpha ',0}$
-semistable, and
Taking the cohomology of Equation (5.1) gives a long exact sequence of sheaves
Set
![]() $v(F_1)=(r',c',s')$
, then we have
$v(F_1)=(r',c',s')$
, then we have
![]() $r'>0$
by Equation (5.2). Let T be the maximal torsion subsheaf of
$r'>0$
by Equation (5.2). Let T be the maximal torsion subsheaf of
![]() $F_1$
, and we can write
$F_1$
, and we can write
![]() $v(T)=(0, \hat c, \hat s)$
for some
$v(T)=(0, \hat c, \hat s)$
for some
![]() $\hat c, \hat s\in \mathbb {Z}$
. Consider the inclusions
$\hat c, \hat s\in \mathbb {Z}$
. Consider the inclusions
![]() $T \hookrightarrow F_1 \hookrightarrow i_*F$
and take the cohomology, one can get
$T \hookrightarrow F_1 \hookrightarrow i_*F$
and take the cohomology, one can get
Since
![]() $\operatorname {{\mathrm {H}}}^{-1}(\operatorname {\mathrm {cok}})$
is torsion-free, it must be zero. It follows that T is a subsheaf of
$\operatorname {{\mathrm {H}}}^{-1}(\operatorname {\mathrm {cok}})$
is torsion-free, it must be zero. It follows that T is a subsheaf of
![]() $i_*F$
and
$i_*F$
and
![]() $\operatorname {\mathrm {rk}} (i^* T)= \frac {\hat c}{m}$
. If we let
$\operatorname {\mathrm {rk}} (i^* T)= \frac {\hat c}{m}$
. If we let
![]() $v({\mathrm {H}}^0(F_2))=(0,c",s")$
, by restricting (5.3) to the curve C, one can get
$v({\mathrm {H}}^0(F_2))=(0,c",s")$
, by restricting (5.3) to the curve C, one can get
 $$ \begin{align*} \begin{aligned} r'+\frac{\hat c}{m} &=\operatorname{\mathrm{rk}}(F_1 / T) + \operatorname{\mathrm{rk}}(i^*T ) \geq \operatorname{\mathrm{rk}}(i^*F_1)\\ &\geq \operatorname{\mathrm{rk}}(i^*\ker d_1) \geq \operatorname{\mathrm{rk}}(i^*F) - \operatorname{\mathrm{rk}} (i^*\operatorname{{\mathrm{H}}}^0(F_2)) = r -\frac{c"}{m}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} r'+\frac{\hat c}{m} &=\operatorname{\mathrm{rk}}(F_1 / T) + \operatorname{\mathrm{rk}}(i^*T ) \geq \operatorname{\mathrm{rk}}(i^*F_1)\\ &\geq \operatorname{\mathrm{rk}}(i^*\ker d_1) \geq \operatorname{\mathrm{rk}}(i^*F) - \operatorname{\mathrm{rk}} (i^*\operatorname{{\mathrm{H}}}^0(F_2)) = r -\frac{c"}{m}. \end{aligned} \end{align*} $$
In other words,
Using Lemma 5.2 below, we can take the destabilising sequence (5.1) satisfying
This gives
Combining Equations (5.4) and (5.6), we get
![]() $mr-c"-\hat {c}= mr'$
, thus
$mr-c"-\hat {c}= mr'$
, thus
 $$\begin{align*}\mu_H(F_1/T) = \frac{c'-\hat{c}}{r'} = \frac{c'-\hat{c}}{r - \frac{c"+\hat{c}}{m} } = \frac{c}{r}, \end{align*}$$
$$\begin{align*}\mu_H(F_1/T) = \frac{c'-\hat{c}}{r'} = \frac{c'-\hat{c}}{r - \frac{c"+\hat{c}}{m} } = \frac{c}{r}, \end{align*}$$
and both
![]() $F_1/T$
and
$F_1/T$
and
![]() $ \operatorname {{\mathrm {H}}}^{-1}(F_2)$
are
$ \operatorname {{\mathrm {H}}}^{-1}(F_2)$
are
![]() $\mu _H$
-semistable. Since
$\mu _H$
-semistable. Since
![]() $\gcd (r,c)=1$
and
$\gcd (r,c)=1$
and
![]() $i_*F$
does not contain any skyscraper sheaf, we have
$i_*F$
does not contain any skyscraper sheaf, we have
![]() $\hat {c}= c" =0$
and
$\hat {c}= c" =0$
and
![]() $\hat {s}=0$
. This shows
$\hat {s}=0$
. This shows
![]() $T =0$
, and hence
$T =0$
, and hence
![]() $v(F_1)=(r, c, s')$
. Note that by our assumption, we have
$v(F_1)=(r, c, s')$
. Note that by our assumption, we have
![]() $\pi _{v(F_1)}\in {\mathrm {L}}_{(o,\pi _v)}$
, which means
$\pi _{v(F_1)}\in {\mathrm {L}}_{(o,\pi _v)}$
, which means
![]() $s \leq s'$
. If
$s \leq s'$
. If
![]() $s<s'$
; however, as
$s<s'$
; however, as
![]() $v^2 < 2r-2$
by Equation (✶-1), this gives
$v^2 < 2r-2$
by Equation (✶-1), this gives
 $$\begin{align*}\begin{aligned} v(F_1)^2&=c^2(2g-2) -2rs'\\ &=v^2+2r(s-s')\\ &< 2r(s-s'+1)-2 \leq -2 \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} v(F_1)^2&=c^2(2g-2) -2rs'\\ &=v^2+2r(s-s')\\ &< 2r(s-s'+1)-2 \leq -2 \end{aligned} \end{align*}$$
which contradicts to the fact that
![]() $F_1$
is
$F_1$
is
![]() $\mu _H$
-stable. This forces
$\mu _H$
-stable. This forces
![]() $s=s'$
and
$s=s'$
and
![]() ${\mathcal {W}}_{i_\ast \mathcal {F}}\subseteq {\mathrm {L}}_{\pi _v,\pi _{v(-m)}}$
.
${\mathcal {W}}_{i_\ast \mathcal {F}}\subseteq {\mathrm {L}}_{\pi _v,\pi _{v(-m)}}$
.
In the case that
![]() ${\mathcal {W}}_{i_\ast \mathcal {F}}\subseteq {\mathrm {L}}_{\pi _v,\pi _{v(-m)}}$
, we have
${\mathcal {W}}_{i_\ast \mathcal {F}}\subseteq {\mathrm {L}}_{\pi _v,\pi _{v(-m)}}$
, we have
and
![]() $F_1$
is a stable sheaf. Note that the map
$F_1$
is a stable sheaf. Note that the map
![]() $d_0:F_1 \rightarrow i_* F$
factors through
$d_0:F_1 \rightarrow i_* F$
factors through
![]() $d_0'\colon i_* (F_1|_C) \to i_*F$
and
$d_0'\colon i_* (F_1|_C) \to i_*F$
and
![]() $\mu _H(i_* (F_1|_C))=\mu _H(i_\ast F)$
. Applying Theorem 4.1 to
$\mu _H(i_* (F_1|_C))=\mu _H(i_\ast F)$
. Applying Theorem 4.1 to
![]() $F_1$
, we know that
$F_1$
, we know that
![]() $i_*(F_1|_C)$
is stable as well. It follows that
$i_*(F_1|_C)$
is stable as well. It follows that
![]() $d_0'$
is an isomorphism.
$d_0'$
is an isomorphism.
Lemma 5.2. With notations and assumptions as above, one can find a destabilising sequence (5.1) such that
![]() $F_i$
satisfies
$F_i$
satisfies
Proof. Denote
![]() $\sigma _1 = {\mathcal {W}}_{i_*F} \cap {\mathrm {L}}_{(o,\sigma _v]}$
. By Remark 3.3, we can take the destabilising sequence
$\sigma _1 = {\mathcal {W}}_{i_*F} \cap {\mathrm {L}}_{(o,\sigma _v]}$
. By Remark 3.3, we can take the destabilising sequence
satisfying
![]() $v(F_1) \in \Omega ^+_{v|_C}(\sigma _1) \subseteq \Omega ^+_{v|_C} ({\mathrm {L}}_{( o, \sigma _v]})$
and
$v(F_1) \in \Omega ^+_{v|_C}(\sigma _1) \subseteq \Omega ^+_{v|_C} ({\mathrm {L}}_{( o, \sigma _v]})$
and
![]() $v(F_2) \in \Omega ^-_{v|_C}(\sigma _1) \subseteq \Omega ^-_{v|_C} ({\mathrm {L}}_{( o, \sigma _v]})$
. We divide the proof into three steps.
$v(F_2) \in \Omega ^-_{v|_C}(\sigma _1) \subseteq \Omega ^-_{v|_C} ({\mathrm {L}}_{( o, \sigma _v]})$
. We divide the proof into three steps.
Step 1
We show that for any point
![]() $u=(x_0,y_0,z_0)$
with
$u=(x_0,y_0,z_0)$
with
![]() $u^2 \geq -2$
and
$u^2 \geq -2$
and
![]() $x_0>0$
, u is lying in
$x_0>0$
, u is lying in
![]() $\Omega _{v}^+({\mathrm {L}}_{(o,\sigma _v]})$
if
$\Omega _{v}^+({\mathrm {L}}_{(o,\sigma _v]})$
if
![]() $x_0\leq r$
or
$x_0\leq r$
or
![]() $z_0\leq s$
, and
$z_0\leq s$
, and
![]() $\pi _u\in \mathbf {P}^\circ _{o\sigma _v\pi _v}$
. By its definition, we know that
$\pi _u\in \mathbf {P}^\circ _{o\sigma _v\pi _v}$
. By its definition, we know that
![]() $u\in \Omega _v^+({\mathrm {L}}_{(o,\sigma _v]})$
if
$u\in \Omega _v^+({\mathrm {L}}_{(o,\sigma _v]})$
if
for some
![]() $\sigma \in {\mathrm {L}}_{(o,\sigma _v]}$
.
$\sigma \in {\mathrm {L}}_{(o,\sigma _v]}$
.
As
![]() $\pi _u=(\frac {x_0}{z_0}, \frac {y_0}{z_0})$
is lying in the interior of the triangle
$\pi _u=(\frac {x_0}{z_0}, \frac {y_0}{z_0})$
is lying in the interior of the triangle
![]() ${\mathbf {P}}_{o\sigma _v\pi _v}$
, we have
${\mathbf {P}}_{o\sigma _v\pi _v}$
, we have
 $$ \begin{align} \frac{y_0}{z_0}< \frac{c}{s}\quad \text{and} \quad \frac{x_0/z_0}{y_0/z_0}=\frac{x_0}{y_0}>\frac{r}{c}. \end{align} $$
$$ \begin{align} \frac{y_0}{z_0}< \frac{c}{s}\quad \text{and} \quad \frac{x_0/z_0}{y_0/z_0}=\frac{x_0}{y_0}>\frac{r}{c}. \end{align} $$
The line
![]() ${\mathrm {L}}_{\pi _u, \pi _v}$
will meet the open edge
${\mathrm {L}}_{\pi _u, \pi _v}$
will meet the open edge
![]() ${\mathrm {L}}_{(o,\sigma _v)}$
. Denote by
${\mathrm {L}}_{(o,\sigma _v)}$
. Denote by
![]() $\sigma $
the intersection point
$\sigma $
the intersection point
![]() ${\mathrm {L}}_{(o,\sigma _v]}\cap {\mathrm {L}}^+_{\pi _v,\pi _u}$
. From the construction, we know that u is coplanar to v,
${\mathrm {L}}_{(o,\sigma _v]}\cap {\mathrm {L}}^+_{\pi _v,\pi _u}$
. From the construction, we know that u is coplanar to v,
![]() $v_\sigma ^+$
and O. Indeed, it is lying in the planar cone bounded by the two rays
$v_\sigma ^+$
and O. Indeed, it is lying in the planar cone bounded by the two rays
![]() ${\mathrm {L}}^+_{O,v}$
and
${\mathrm {L}}^+_{O,v}$
and
![]() ${\mathrm {L}}^+_{O, v^+_{\sigma }}$
. The condition
${\mathrm {L}}^+_{O, v^+_{\sigma }}$
. The condition
![]() $ x_0 \leq r$
or
$ x_0 \leq r$
or
![]() $z_0 \leq s$
will ensure that
$z_0 \leq s$
will ensure that
![]() $u\in \mathbf {P}^\circ _{Ov v_{\sigma }^+}$
.
$u\in \mathbf {P}^\circ _{Ov v_{\sigma }^+}$
.
Moreover, when
![]() $x_0\leq r, z_0\geq s$
or
$x_0\leq r, z_0\geq s$
or
![]() $x_0\geq r, z_0\leq s$
, we have
$x_0\geq r, z_0\leq s$
, we have
![]() $(u-v)^2\geq (g-1)(y_0-c)^2>0$
. When
$(u-v)^2\geq (g-1)(y_0-c)^2>0$
. When
![]() $x_0\leq r$
and
$x_0\leq r$
and
![]() $z_0\leq s$
, then we have
$z_0\leq s$
, then we have
by Equation (5.9).
Step 2
Set
![]() $v(F_1)=(r',c', s')$
and
$v(F_1)=(r',c', s')$
and
![]() $v(F_2)=(-r', mr-c', s-\tilde s-s')$
with
$v(F_2)=(-r', mr-c', s-\tilde s-s')$
with
![]() $0<c'<m r$
and
$0<c'<m r$
and
![]() $ r'>0$
. We claim that
$ r'>0$
. We claim that
Firstly, we must have either
![]() $r'\leq r$
or
$r'\leq r$
or
![]() $s'\leq s$
. Otherwise, one will have
$s'\leq s$
. Otherwise, one will have
or
Both of them are impossible as
![]() $v(F_1)\in \Omega _{v|_C}^+({\mathrm {L}}_{(o,\sigma _v]})$
.
$v(F_1)\in \Omega _{v|_C}^+({\mathrm {L}}_{(o,\sigma _v]})$
.
Now, suppose
![]() $\mu _H(F_1) < \frac {c}{r}$
. Then we have
$\mu _H(F_1) < \frac {c}{r}$
. Then we have
![]() $v(F_1)\in \mathbf {P}^\circ _{o \sigma _v \pi _v} $
as
$v(F_1)\in \mathbf {P}^\circ _{o \sigma _v \pi _v} $
as
![]() $\phi _{\sigma _v}(F_1) \geq \phi _{\sigma _v}(v)$
. According to Step 1, we get
$\phi _{\sigma _v}(F_1) \geq \phi _{\sigma _v}(v)$
. According to Step 1, we get
which contradicts to the assumption
![]() $\Omega _{v}^+ ({\mathrm {L}}_{(o, \sigma _v]})\cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
. Similarly, we have
$\Omega _{v}^+ ({\mathrm {L}}_{(o, \sigma _v]})\cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
. Similarly, we have
![]() $\mu _H(F_2) \leq \frac {c-mr}{r} $
as there is no integer point in
$\mu _H(F_2) \leq \frac {c-mr}{r} $
as there is no integer point in
![]() $\Omega _{v(-m)}^+({\mathrm {L}}_{(o,\sigma _v]})$
. This proves the claim. As a consequence, we get
$\Omega _{v(-m)}^+({\mathrm {L}}_{(o,\sigma _v]})$
. This proves the claim. As a consequence, we get
which implies
![]() $r'\leq r$
.
$r'\leq r$
.
Step 3
Let
![]() $(F_1)_{\min }$
be the last
$(F_1)_{\min }$
be the last
![]() $\mu _H$
-HN factor of
$\mu _H$
-HN factor of
![]() $F_1$
, hence also of
$F_1$
, hence also of
![]() $F_1/T$
. According to [Reference Bridgeland4, Proposition 14.2], for
$F_1/T$
. According to [Reference Bridgeland4, Proposition 14.2], for
![]() $\sigma $
sufficiently close to o, we always have
$\sigma $
sufficiently close to o, we always have
-
•
 $(F_1)_{\min }$
is
$(F_1)_{\min }$
is
 $\sigma $
-semistable,
$\sigma $
-semistable, -
•
 $v(G)$
is proportional to
$v(G)$
is proportional to
 $v((F_1)_{\min })$
for any
$v((F_1)_{\min })$
for any
 $\sigma $
-stable factor G of
$\sigma $
-stable factor G of
 $(F_1)_{\min }$
.
$(F_1)_{\min }$
.
As
![]() $(F_1)_{\min } $
is a quotient sheaf of
$(F_1)_{\min } $
is a quotient sheaf of
![]() $F_1$
, it is also a quotient of
$F_1$
, it is also a quotient of
![]() $F_1$
in
$F_1$
in
![]() $\operatorname {\mathrm {Coh}}^{\beta =0}(X)$
. Since
$\operatorname {\mathrm {Coh}}^{\beta =0}(X)$
. Since
![]() $F_1$
is
$F_1$
is
![]() $\sigma _1$
-semistable, we have
$\sigma _1$
-semistable, we have
Combined with the fact
![]() $\mu _H (F_1) \geq \mu _H((F_1)_{\min })$
, we have
$\mu _H (F_1) \geq \mu _H((F_1)_{\min })$
, we have
![]() $\pi _{G} = \pi _{(F_1)_{\min } } \in {\mathbf {P}}_{o\sigma _1 \pi _{F_1}}$
. As the triangle
$\pi _{G} = \pi _{(F_1)_{\min } } \in {\mathbf {P}}_{o\sigma _1 \pi _{F_1}}$
. As the triangle
![]() ${\mathbf {P}}_{o\sigma _1 \pi _{F_1} }$
is lying below the ray
${\mathbf {P}}_{o\sigma _1 \pi _{F_1} }$
is lying below the ray
![]() ${\mathrm {L}}^+_{\sigma _v,\pi _v}$
, we get
${\mathrm {L}}^+_{\sigma _v,\pi _v}$
, we get
![]() $\pi _G \in {\mathbf {P}}_{o\sigma _v \pi _v}^\circ $
if
$\pi _G \in {\mathbf {P}}_{o\sigma _v \pi _v}^\circ $
if
![]() $\mu _H(G) < \frac {c}{r}$
. Note that
$\mu _H(G) < \frac {c}{r}$
. Note that
![]() $\operatorname {\mathrm {rk}}(G)\leq \operatorname {\mathrm {rk}}(F_1)=r$
. We must have
$\operatorname {\mathrm {rk}}(G)\leq \operatorname {\mathrm {rk}}(F_1)=r$
. We must have
![]() $\mu _H(G)\geq \frac {c}{r}$
otherwise one will get
$\mu _H(G)\geq \frac {c}{r}$
otherwise one will get
![]() $\pi _G\in \Omega _v^+({\mathrm {L}}_{(o,\sigma _v]})$
by the same argument in Step 2. It follows that
$\pi _G\in \Omega _v^+({\mathrm {L}}_{(o,\sigma _v]})$
by the same argument in Step 2. It follows that
A similar argument shows
![]() $\mu _H^+({\mathrm {H}}^{-1}(F_2)) \leq \frac {c-mr}{r}$
. This finishes the proof.
$\mu _H^+({\mathrm {H}}^{-1}(F_2)) \leq \frac {c-mr}{r}$
. This finishes the proof.
HN-polygon
Let
![]() $\sigma _{\alpha ,0}$
be a stability condition with
$\sigma _{\alpha ,0}$
be a stability condition with
![]() $\alpha $
close to
$\alpha $
close to
![]() $\sqrt {2/H^2}$
. By [Reference Feyzbakhsh11, Proposition 3.4], for fixed E, the HN filtration of
$\sqrt {2/H^2}$
. By [Reference Feyzbakhsh11, Proposition 3.4], for fixed E, the HN filtration of
![]() $\sigma _{\alpha ,0}$
will stay the same for
$\sigma _{\alpha ,0}$
will stay the same for
![]() $\sqrt {2/H^2}+\epsilon>\alpha >\sqrt {2/H^2}$
. Denote by
$\sqrt {2/H^2}+\epsilon>\alpha >\sqrt {2/H^2}$
. Denote by
![]() $\overline \sigma $
the limit of
$\overline \sigma $
the limit of
![]() $\sigma _{\alpha , 0}$
. The ‘stability function’ can be written as
$\sigma _{\alpha , 0}$
. The ‘stability function’ can be written as
if
![]() $v(E)=(r,c,s)$
. Let
$v(E)=(r,c,s)$
. Let
![]() ${\mathbf {P}}_{i_*F}$
be the HN polygon (Here, our definition of HN polygon is slightly different from [Reference Feyzbakhsh11, Definition 3.3]. We drop off the part on the right-hand side of the line segment
${\mathbf {P}}_{i_*F}$
be the HN polygon (Here, our definition of HN polygon is slightly different from [Reference Feyzbakhsh11, Definition 3.3]. We drop off the part on the right-hand side of the line segment
![]() ${\mathrm {L}}_{[0,\overline {Z}(i_*F)]}$
) for
${\mathrm {L}}_{[0,\overline {Z}(i_*F)]}$
) for
![]() $i_*F$
with respect to
$i_*F$
with respect to
![]() $\overline \sigma $
. For
$\overline \sigma $
. For
![]() $E\in \mathbf {M}(v)$
, we have
$E\in \mathbf {M}(v)$
, we have
![]() ${\mathbf {P}}_{i_*(E|_C)}={\mathbf {P}}_{0z_1z_2}$
, where
${\mathbf {P}}_{i_*(E|_C)}={\mathbf {P}}_{0z_1z_2}$
, where
As the polygon
![]() ${\mathbf {P}}_{i_\ast (E|_C)}$
only depends on v, we may simply write it as
${\mathbf {P}}_{i_\ast (E|_C)}$
only depends on v, we may simply write it as
![]() ${\mathbf {P}}_v$
.
${\mathbf {P}}_v$
.
Theorem 5.3. For any
![]() $F\in {\mathbf {BN}}_C(v)$
, we have
$F\in {\mathbf {BN}}_C(v)$
, we have
![]() ${\mathbf {P}}_{i_*F} \subseteq {\mathbf {P}}_v$
. Moreover, they coincide if and only if
${\mathbf {P}}_{i_*F} \subseteq {\mathbf {P}}_v$
. Moreover, they coincide if and only if
![]() $F=E|_C$
for some
$F=E|_C$
for some
![]() $E\in \mathbf {M}(v)$
.
$E\in \mathbf {M}(v)$
.
Proof. When
![]() $v^2=0$
, this is essentially proved in [Reference Feyzbakhsh11, Lemma 4.3]. Let us give a slightly different argument which also works for
$v^2=0$
, this is essentially proved in [Reference Feyzbakhsh11, Lemma 4.3]. Let us give a slightly different argument which also works for
![]() $v^2>0$
. Suppose the HN-filtration of
$v^2>0$
. Suppose the HN-filtration of
![]() $i_*F$
for
$i_*F$
for
![]() $\bar {\sigma }=(\operatorname {\mathrm {Coh}}^{\beta =0}(X), \overline {Z})$
is given by
$\bar {\sigma }=(\operatorname {\mathrm {Coh}}^{\beta =0}(X), \overline {Z})$
is given by
with ![]() the semistable HN-factors. To show
the semistable HN-factors. To show
![]() ${\mathbf {P}}_{i_\ast F}\subseteq {\mathbf {P}}_v$
, it suffices to show that
${\mathbf {P}}_{i_\ast F}\subseteq {\mathbf {P}}_v$
, it suffices to show that
(see Figure 8b) since
![]() $ {\mathbf {P}}_{i_*F}$
is convex. According to the proof of Proposition 2.2, for any object in
$ {\mathbf {P}}_{i_*F}$
is convex. According to the proof of Proposition 2.2, for any object in
![]() $\operatorname {\mathrm {Coh}}^0(X) $
, the angle
$\operatorname {\mathrm {Coh}}^0(X) $
, the angle
![]() $\phi _{\bar {\sigma }}$
in Figure 8b is an increasing function of the angle
$\phi _{\bar {\sigma }}$
in Figure 8b is an increasing function of the angle
![]() $\theta _{o'}$
in Figure 8a. (They are actually equal in this case, as
$\theta _{o'}$
in Figure 8a. (They are actually equal in this case, as
![]() $\cot \theta _{o'} = \frac {y-1}{x}=\frac {r-s}{c}=\frac {\operatorname {{\mathrm {Re}}} \overline Z}{\operatorname {{\mathrm {Im}}} \overline Z} = \cot \phi _{\bar {\sigma }}$
). Therefore, it is equivalent to show
$\cot \theta _{o'} = \frac {y-1}{x}=\frac {r-s}{c}=\frac {\operatorname {{\mathrm {Re}}} \overline Z}{\operatorname {{\mathrm {Im}}} \overline Z} = \cot \phi _{\bar {\sigma }}$
). Therefore, it is equivalent to show
in Figure 8a.

Figure 8 The angle
![]() $\theta _{o'}$
is equal to the angle
$\theta _{o'}$
is equal to the angle
![]() $\phi _{\bar {\sigma }}$
.
$\phi _{\bar {\sigma }}$
.
To prove Equation (5.13), consider the sequence
for each
![]() $\widetilde {E}_n$
. Since the first wall is not below
$\widetilde {E}_n$
. Since the first wall is not below
![]() ${\mathrm {L}}_{\pi _{i_* F}, \pi _v}$
, we have
${\mathrm {L}}_{\pi _{i_* F}, \pi _v}$
, we have
![]() $\phi _{\sigma _v}(\widetilde {E}_n)\leq \phi _{\sigma _v}(i_*F)$
. As
$\phi _{\sigma _v}(\widetilde {E}_n)\leq \phi _{\sigma _v}(i_*F)$
. As
![]() $\phi _{\bar \sigma }(\widetilde {E}_n) \geq \phi _{\bar \sigma }(i_*F)$
, there exists some stability condition
$\phi _{\bar \sigma }(\widetilde {E}_n) \geq \phi _{\bar \sigma }(i_*F)$
, there exists some stability condition
![]() $\sigma \in {\mathrm {L}}_{(o', \sigma _v]}$
such that the objects in Equation (5.14) have the same
$\sigma \in {\mathrm {L}}_{(o', \sigma _v]}$
such that the objects in Equation (5.14) have the same
![]() $\sigma $
-phase. As a consequence, we have
$\sigma $
-phase. As a consequence, we have
 $$ \begin{align} \pi_{\widetilde E_i} \in \bigcup_{\sigma\in{\mathrm{L}}_{[\sigma_v, o')}} {\mathrm{L}}_{\pi_{i_*F, \sigma}}.\end{align} $$
$$ \begin{align} \pi_{\widetilde E_i} \in \bigcup_{\sigma\in{\mathrm{L}}_{[\sigma_v, o')}} {\mathrm{L}}_{\pi_{i_*F, \sigma}}.\end{align} $$
Take
![]() $n=1$
, and set
$n=1$
, and set
![]() $v(E_1) = (r',c',s')$
. We claim that
$v(E_1) = (r',c',s')$
. We claim that
![]() $\pi _{E_1} \notin {\mathbf {P}}_{o' \pi _v \sigma _v} \setminus \left \{ \pi _v \right \} $
which yields
$\pi _{E_1} \notin {\mathbf {P}}_{o' \pi _v \sigma _v} \setminus \left \{ \pi _v \right \} $
which yields
![]() $ \theta _{o'}(\pi _{E_1}) \leq \theta _{o'}(\pi _v)$
. This can be proved by cases as follows:
$ \theta _{o'}(\pi _{E_1}) \leq \theta _{o'}(\pi _v)$
. This can be proved by cases as follows:
-
Case (1) If
 $v^2 =0$
,
$v^2 =0$
,
 $\pi _{E_1} \notin {\mathbf {P}}_{o' \pi _v \sigma _v}\setminus \{ \pi _v\}$
automatically holds. This is because
$\pi _{E_1} \notin {\mathbf {P}}_{o' \pi _v \sigma _v}\setminus \{ \pi _v\}$
automatically holds. This is because
 ${\mathbf {P}}_{o' \pi _v \sigma _v}\setminus \{ \pi _v,o'\} \subseteq V(X)$
and Equation (2.2).
${\mathbf {P}}_{o' \pi _v \sigma _v}\setminus \{ \pi _v,o'\} \subseteq V(X)$
and Equation (2.2). -
Case (2) If
 $v^2>0$
and
$v^2>0$
and
 $r' \leq r$
or
$r' \leq r$
or
 $s' \leq s$
, as
$s' \leq s$
, as
 $E_1$
is
$E_1$
is
 $\bar {\sigma }$
-semistable, we may assume
$\bar {\sigma }$
-semistable, we may assume
 $v(E_1)^2 \geq -2$
otherwise we may replace
$v(E_1)^2 \geq -2$
otherwise we may replace
 $E_1$
by its first JH-factor. According to Step 1 in Lemma 5.2, we have which contradicts to the assumption
$E_1$
by its first JH-factor. According to Step 1 in Lemma 5.2, we have which contradicts to the assumption $$ \begin{align*}v(E_1) \in \Omega_v^+({\mathrm{L}}_{(o,\,o')})\end{align*} $$
$$ \begin{align*}v(E_1) \in \Omega_v^+({\mathrm{L}}_{(o,\,o')})\end{align*} $$
 $\Omega _v^+({\mathrm {L}}_{(o,\,o')})\cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
.
$\Omega _v^+({\mathrm {L}}_{(o,\,o')})\cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
.
-
Case (3) If
 $r'> r$
and
$r'> r$
and
 $s'>s$
, we claim that
$s'>s$
, we claim that
 $r' < r+1$
. Choose a stability condition
$r' < r+1$
. Choose a stability condition
 $\sigma \in {\mathrm {L}}_{[\sigma _v, o')}$
such that
$\sigma \in {\mathrm {L}}_{[\sigma _v, o')}$
such that
 $\phi _{\sigma }(i_*F) = \phi _{\sigma }(E_1)$
. Then
$\phi _{\sigma }(i_*F) = \phi _{\sigma }(E_1)$
. Then
 $v(E_1)\notin \{ O, v|_c\}$
is lying in the triangle
$v(E_1)\notin \{ O, v|_c\}$
is lying in the triangle
 ${\mathbf {P}}_{Ov|_c (v|_c)^+_{\sigma }}$
. This means we have
${\mathbf {P}}_{Ov|_c (v|_c)^+_{\sigma }}$
. This means we have
 $0< c' < mr$
and
$0< c' < mr$
and  $$\begin{align*}g(c')^2 - r's' \geq 0, \quad g(c'-mr)^2 -r'(s'+(g-1)m(mr-2c)) \geq 0. \end{align*}$$
$$\begin{align*}g(c')^2 - r's' \geq 0, \quad g(c'-mr)^2 -r'(s'+(g-1)m(mr-2c)) \geq 0. \end{align*}$$
After reduction, we know that
 $r'<r+1$
as
$r'<r+1$
as
 $g c^2 -(r+1)s \leq 0 $
and
$g c^2 -(r+1)s \leq 0 $
and
 $ g (c-mr)^2 -(r+1)\tilde {s} \leq 0$
by (✶-2).
$ g (c-mr)^2 -(r+1)\tilde {s} \leq 0$
by (✶-2).
Similarly, take
![]() $n=l-1$
and use the
$n=l-1$
and use the
![]() $\bar {\sigma }$
-semistability of
$\bar {\sigma }$
-semistability of
![]() $\operatorname {\mathrm {cok}}(f_{l-1})=E_l$
, one can prove the second inequality of Equation (5.13).
$\operatorname {\mathrm {cok}}(f_{l-1})=E_l$
, one can prove the second inequality of Equation (5.13).
Finally, if
![]() ${\mathbf {P}}_{i_*F} = {\mathbf {P}}_v$
, the first wall will coincide with the line
${\mathbf {P}}_{i_*F} = {\mathbf {P}}_v$
, the first wall will coincide with the line
![]() ${\mathrm {L}}_{\pi _{v(-m)},\pi _v}$
and the last assertion follows from Theorem 5.1.
${\mathrm {L}}_{\pi _{v(-m)},\pi _v}$
and the last assertion follows from Theorem 5.1.
Remark 5.4. The discussion above can be much more simplified if the following is true: For any
![]() $\sigma $
on a wall of
$\sigma $
on a wall of
![]() $i_*F$
, there exists a JH-filtration of
$i_*F$
, there exists a JH-filtration of
![]() $i_*F$
which is convex (i.e., the polygon with vertices
$i_*F$
which is convex (i.e., the polygon with vertices
![]() $v(\widetilde E_i)$
is convex in the plane of
$v(\widetilde E_i)$
is convex in the plane of
![]() ${\mathbf {P}}_{O v v^+_\sigma }$
).
${\mathbf {P}}_{O v v^+_\sigma }$
).
Now, we provide a numerical criterion for verifying
![]() ${\mathbf {P}}_v={\mathbf {P}}_{i_\ast F}$
via Euclidean geometry. The key ingredient is the upper bound on the number of global sections of an object
${\mathbf {P}}_v={\mathbf {P}}_{i_\ast F}$
via Euclidean geometry. The key ingredient is the upper bound on the number of global sections of an object
![]() $E\in \mathrm {D}^b(X)$
established by Feyzbakhsh in [Reference Feyzbakhsh11, Reference Feyzbakhsh13]. Recall that for any
$E\in \mathrm {D}^b(X)$
established by Feyzbakhsh in [Reference Feyzbakhsh11, Reference Feyzbakhsh13]. Recall that for any
![]() $x,y \in \mathbb {Z}$
, there is a function
$x,y \in \mathbb {Z}$
, there is a function
and one can define ![]() , where
, where
![]() $E_i$
’s are the
$E_i$
’s are the
![]() $\overline {\sigma }$
-semistable factors of E. Moreover, we have a metric function given by
$\overline {\sigma }$
-semistable factors of E. Moreover, we have a metric function given by
and we set ![]() . Clearly, one has
. Clearly, one has
![]() $\|E\| \geq \ell (E)$
once the y-coordinates are nonzero.
$\|E\| \geq \ell (E)$
once the y-coordinates are nonzero.
Proposition 5.5 [Reference Feyzbakhsh13, Proposition 3.3 and Remark 3.4].
Suppose
![]() $E\in \operatorname {\mathrm {Coh}}^0(X)$
which has no subobject
$E\in \operatorname {\mathrm {Coh}}^0(X)$
which has no subobject
![]() $F\subseteq E$
in
$F\subseteq E$
in
![]() $\operatorname {\mathrm {Coh}}^0(X)$
with
$\operatorname {\mathrm {Coh}}^0(X)$
with
![]() $c_1(F)=0$
, we have
$c_1(F)=0$
, we have
 $$ \begin{align} h^0(X,E)\leq \sum_i \left\lfloor \frac{\ell(E_i) + \chi(E_i)}{2} \right\rfloor = \sum_i \left\lfloor \frac{\ell(E_i)-\operatorname{{\mathrm{Re}}} \overline Z(E_i)}{2}\right\rfloor, \end{align} $$
$$ \begin{align} h^0(X,E)\leq \sum_i \left\lfloor \frac{\ell(E_i) + \chi(E_i)}{2} \right\rfloor = \sum_i \left\lfloor \frac{\ell(E_i)-\operatorname{{\mathrm{Re}}} \overline Z(E_i)}{2}\right\rfloor, \end{align} $$
where
![]() $E_i$
’s are semistable factors with respect to
$E_i$
’s are semistable factors with respect to
![]() $\overline \sigma $
. In particular,
$\overline \sigma $
. In particular,
Following [Reference Feyzbakhsh11], we can give a criterion for the surjectivity of
![]() $\psi $
.
$\psi $
.
Theorem 5.6. With the notation as in §5.2: Let
![]() $z_1^{+1}=r-s+1+c\sqrt {-1}$
,
$z_1^{+1}=r-s+1+c\sqrt {-1}$
,
![]() $z^{\prime }_1=r-s-\frac {r-s}{c}+(c-1)\sqrt {-1}$
and
$z^{\prime }_1=r-s-\frac {r-s}{c}+(c-1)\sqrt {-1}$
and
![]() $z^{\prime }_2=r-s-\frac {r-\gamma ^2s}{\gamma c}+(c+1)\sqrt {-1}$
, where
$z^{\prime }_2=r-s-\frac {r-\gamma ^2s}{\gamma c}+(c+1)\sqrt {-1}$
, where
![]() $\gamma =\frac {mr}{c}-1$
. Assume that
$\gamma =\frac {mr}{c}-1$
. Assume that
-
(i)
 $\frac {s-r}{c}+\frac {s-r-\chi }{m r-c}\geq 2$
$\frac {s-r}{c}+\frac {s-r-\chi }{m r-c}\geq 2$
-
(ii)
 $ \|z_1- z^{\prime }_1\|-\|z^{\prime }_1 -z_1^{+1}\|+ \|z_1 -z^{\prime }_2\|-\|z^{\prime }_2 -z_1^{+1}\|\geq \frac {2c^2}{r+s}+\frac {2(mr-c)^2}{r+s-\chi }, $
$ \|z_1- z^{\prime }_1\|-\|z^{\prime }_1 -z_1^{+1}\|+ \|z_1 -z^{\prime }_2\|-\|z^{\prime }_2 -z_1^{+1}\|\geq \frac {2c^2}{r+s}+\frac {2(mr-c)^2}{r+s-\chi }, $
where
![]() $\chi =\chi (i_\ast F) = m(g-1)(2c-mr)$
. Then the restriction map
$\chi =\chi (i_\ast F) = m(g-1)(2c-mr)$
. Then the restriction map
![]() $\psi $
will be surjective.
$\psi $
will be surjective.
Proof. Suppose we have
![]() ${\mathbf {P}}_v\neq {\mathbf {P}}_{i_\ast F}$
for some
${\mathbf {P}}_v\neq {\mathbf {P}}_{i_\ast F}$
for some
![]() $F\in {\mathbf {BN}}_C(v)$
. By Proposition 5.5 and the convexity, we have
$F\in {\mathbf {BN}}_C(v)$
. By Proposition 5.5 and the convexity, we have
where
![]() $ \hbar =\sqrt {(r+s-\chi )^2+4(mr-c)^2}+ \sqrt {(r+s)^2+4c^2}.$
Then we get
$ \hbar =\sqrt {(r+s-\chi )^2+4(mr-c)^2}+ \sqrt {(r+s)^2+4c^2}.$
Then we get
However, note that the polygon
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+1}z_2'z_2}$
is convex under the assumption (i), we have
${\mathbf {P}}_{0z^{\prime }_1z_1^{+1}z_2'z_2}$
is convex under the assumption (i), we have
Combined with assumption (ii), we get
 $$ \begin{align} {\hbar+ \chi} - 2(r+s) &= \sqrt{(r+s)^2+4c^2}-(r+s) \nonumber\\ & \mathrel{\phantom{=}}+ \sqrt{(r+s-\chi)^2+4(mr-c)^2}-(r+s-\chi) \nonumber \\ &< \frac{2c^2}{r+s}+\frac{2(mr-c)^2}{r+s-\chi}. \end{align} $$
$$ \begin{align} {\hbar+ \chi} - 2(r+s) &= \sqrt{(r+s)^2+4c^2}-(r+s) \nonumber\\ & \mathrel{\phantom{=}}+ \sqrt{(r+s-\chi)^2+4(mr-c)^2}-(r+s-\chi) \nonumber \\ &< \frac{2c^2}{r+s}+\frac{2(mr-c)^2}{r+s-\chi}. \end{align} $$
which contradicts Equation (5.18). This proves the assertion.
Surjectivity condition
As an application, we get an explicit criterion for
![]() $\psi $
being surjective for
$\psi $
being surjective for
![]() $v^2\geq 0$
.
$v^2\geq 0$
.
Corollary 5.7. The restriction map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is bijective if we further have the inequality
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is bijective if we further have the inequality
We may call it a surjectivity condition.
Proof. As
![]() $r>1+\frac {v^2}{2}$
, we have
$r>1+\frac {v^2}{2}$
, we have
This gives
 $$ \begin{align} \begin{aligned} s-r&\geq 4rc^2-r\geq 3c\\ s-r-\chi & =\frac{(g-1)(mr-c)^2}{r}-\frac{v^2}{2r}-r \geq 4r(mr-c)^2-r \geq 3(mr-c), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} s-r&\geq 4rc^2-r\geq 3c\\ s-r-\chi & =\frac{(g-1)(mr-c)^2}{r}-\frac{v^2}{2r}-r \geq 4r(mr-c)^2-r \geq 3(mr-c), \end{aligned} \end{align} $$
as
![]() $mr-c>0$
. Moreover, one can compute that
$mr-c>0$
. Moreover, one can compute that
It follows that
 $$ \begin{align*} \|z_1- z^{\prime}_1\|-\|z^{\prime}_1 -z_1^{+1}\| &= \sqrt{(\frac{s-r}{c})^2+4g}-\sqrt{(\frac{s-r}{c}-1)^2+4g} \\ &> \frac{\frac{s-r}{c}-\frac{1}{2}}{\sqrt{(\frac{s+r}{c})^2+4(1+\frac{n}{c^2})}} \\ &> \frac{2s-2r-c}{2s+2r+c}> \frac{2c^2}{s}+\frac{2c^2}{r+s} \end{align*} $$
$$ \begin{align*} \|z_1- z^{\prime}_1\|-\|z^{\prime}_1 -z_1^{+1}\| &= \sqrt{(\frac{s-r}{c})^2+4g}-\sqrt{(\frac{s-r}{c}-1)^2+4g} \\ &> \frac{\frac{s-r}{c}-\frac{1}{2}}{\sqrt{(\frac{s+r}{c})^2+4(1+\frac{n}{c^2})}} \\ &> \frac{2s-2r-c}{2s+2r+c}> \frac{2c^2}{s}+\frac{2c^2}{r+s} \end{align*} $$
and
![]() $\|z_1 -z^{\prime }_2\|-\|z^{\prime }_2- z_1^{+1}\| = \sqrt {(\frac {s-r-\chi }{mr-c})^2+4g} - \sqrt {(\frac {s-r-\chi }{mr-c}-1)^2+4g} \geq 0$
. The assertion can be concluded from Theorem 5.6.
$\|z_1 -z^{\prime }_2\|-\|z^{\prime }_2- z_1^{+1}\| = \sqrt {(\frac {s-r-\chi }{mr-c})^2+4g} - \sqrt {(\frac {s-r-\chi }{mr-c}-1)^2+4g} \geq 0$
. The assertion can be concluded from Theorem 5.6.
Remark 5.8. For g sufficiently large, it is not hard to find Mukai vectors satisfying the conditions in Theorem 5.6. For instance, when
![]() $v^2=0$
and
$v^2=0$
and
![]() $g>84$
, the Mukai vectors given in [Reference Feyzbakhsh11] and [Reference Feyzbakhsh13] will automatically satisfy the conditions for any
$g>84$
, the Mukai vectors given in [Reference Feyzbakhsh11] and [Reference Feyzbakhsh13] will automatically satisfy the conditions for any
![]() $m\geq 1$
. However, when g is small, it becomes impossible to find such Mukai vectors.
$m\geq 1$
. However, when g is small, it becomes impossible to find such Mukai vectors.
6 Surjectivity for special Mukai vectors
According to Remark 5.8, Theorem 5.6 does not work well for small g. In this section, we develop a way to improve the estimate in §5 for special Mukai vectors of square zero. Let us first introduce the sharpness of the polygon
![]() ${\mathbf {P}}_v$
.
${\mathbf {P}}_v$
.
Definition 6.1. Denote by
![]() $z_1^{+d}$
the point
$z_1^{+d}$
the point
![]() $r-s+d+c\sqrt {-1}$
. Let
$r-s+d+c\sqrt {-1}$
. Let
![]() $z_1', z_2'$
be the points as in the Theorem 5.6. We say the polygon
$z_1', z_2'$
be the points as in the Theorem 5.6. We say the polygon
![]() ${\mathbf {P}}_v$
is d-sharp if for any
${\mathbf {P}}_v$
is d-sharp if for any
![]() ${\mathbf {P}}_{i_*F}\neq {\mathbf {P}}_v$
, one of the following is true:
${\mathbf {P}}_{i_*F}\neq {\mathbf {P}}_v$
, one of the following is true:
-
(i)
 ${\mathbf {P}}_{i_*F}$
is contained in the polygon
${\mathbf {P}}_{i_*F}$
is contained in the polygon
 ${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
.
${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
. -
(ii)
 $z_1^{+j}$
is a vertex of
$z_1^{+j}$
is a vertex of
 ${\mathbf {P}}_{i_*F}$
for some
${\mathbf {P}}_{i_*F}$
for some
 $1 \leq j \leq d-1$
.
$1 \leq j \leq d-1$
.
There is a simple numerical criterion for the d-sharpness of
![]() ${\mathbf {P}}_v$
.
${\mathbf {P}}_v$
.
Lemma 6.2. With the notations as before, suppose that
 $$ \begin{align} \frac{s-r}{c}+\frac{\gamma^2 s-r}{\gamma c}\geq 2d, \end{align} $$
$$ \begin{align} \frac{s-r}{c}+\frac{\gamma^2 s-r}{\gamma c}\geq 2d, \end{align} $$
where
![]() $\gamma =\frac {mr}{c}-1$
, the polygon
$\gamma =\frac {mr}{c}-1$
, the polygon
![]() ${\mathbf {P}}_{v}$
will be d-sharp.
${\mathbf {P}}_{v}$
will be d-sharp.
Proof. From the definition of two polygons, one observes that the interior of
![]() ${{\mathbf {P}}_{v}-{\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}}$
only contains
${{\mathbf {P}}_{v}-{\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}}$
only contains
![]() $z_1^{+j} ~ (1\leq j\leq d-1)$
as integer points. If
$z_1^{+j} ~ (1\leq j\leq d-1)$
as integer points. If
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
is convex, then either
${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
is convex, then either
![]() ${\mathbf {P}}_{i_\ast F}$
is contained in
${\mathbf {P}}_{i_\ast F}$
is contained in
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
or
${\mathbf {P}}_{0z^{\prime }_1z_1^{+d} z_2' z_2}$
or
![]() $z_1^{+j}$
is a vertex of
$z_1^{+j}$
is a vertex of
![]() ${\mathbf {P}}_{i_\ast F}$
. A little writing reveals the convexity of this polygon literally means Equation (6.1).
${\mathbf {P}}_{i_\ast F}$
. A little writing reveals the convexity of this polygon literally means Equation (6.1).
Surjectivity condition for special Mukai vectors
The following is an enhancement of Theorem 5.6 for special Mukai vectors.
Theorem 6.3. Suppose
![]() $g\geq 3$
. Let
$g\geq 3$
. Let
![]() $v=(g-1,k,k^2)\in {\mathrm {H}}_{\operatorname {\mathrm {alg}}}^\ast (X)$
be a primitive Mukai vector with
$v=(g-1,k,k^2)\in {\mathrm {H}}_{\operatorname {\mathrm {alg}}}^\ast (X)$
be a primitive Mukai vector with
![]() $\gcd (g-1,k)=1$
. Assume that
$\gcd (g-1,k)=1$
. Assume that
![]() $(m,k)$
satisfies the conditions
$(m,k)$
satisfies the conditions
 $$\begin{align} &g<\min\Big\{2k, 2(mg-m-k)\Big\},~g\neq k~\mbox{and} ~g\neq m(g-1)-k,\\& \mbox{either } k\nmid g+1 \text{ or } m(g-1)-k \nmid g+1.\nonumber \end{align} $$
$$\begin{align} &g<\min\Big\{2k, 2(mg-m-k)\Big\},~g\neq k~\mbox{and} ~g\neq m(g-1)-k,\\& \mbox{either } k\nmid g+1 \text{ or } m(g-1)-k \nmid g+1.\nonumber \end{align} $$
Then the restriction map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is surjective.
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is surjective.
Proof. By Lemma 6.2, if there is
![]() ${\mathbf {P}}_{i_\ast F}\neq {\mathbf {P}}_v$
for some F, the polygon
${\mathbf {P}}_{i_\ast F}\neq {\mathbf {P}}_v$
for some F, the polygon
![]() ${\mathbf {P}}_{v}$
will be at least
${\mathbf {P}}_{v}$
will be at least
![]() $3$
-sharp. Therefore, one of the following is true:
$3$
-sharp. Therefore, one of the following is true:
-
(i)
 ${\mathbf {P}}_{i_*F}$
is contained in the polygon
${\mathbf {P}}_{i_*F}$
is contained in the polygon
 ${\mathbf {P}}_{0z^{\prime }_1z_1^{+3} z_2' z_2}$
.
${\mathbf {P}}_{0z^{\prime }_1z_1^{+3} z_2' z_2}$
. -
(ii)
 $z_1^{+1}=g-k^2+k\sqrt {-1}$
is a vertex of
$z_1^{+1}=g-k^2+k\sqrt {-1}$
is a vertex of
 ${\mathbf {P}}_{i_*F}$
${\mathbf {P}}_{i_*F}$
-
(iii)
 $z_1^{+2}=g+1-k^2+k\sqrt {-1}$
is a vertex of
$z_1^{+2}=g+1-k^2+k\sqrt {-1}$
is a vertex of
 ${\mathbf {P}}_{i_*F}$
${\mathbf {P}}_{i_*F}$
We will analyse them by cases. Let us first show that case (i) is impossible if
![]() $(g,k,m)\neq (5,3,3)$
. By Equation (5.18), it suffices to show that
$(g,k,m)\neq (5,3,3)$
. By Equation (5.18), it suffices to show that
when
![]() ${\mathbf {P}}_{i_*F}\subseteq {\mathbf {P}}_{0z^{\prime }_1z_1^{+3} z_2' z_2}$
. Set
${\mathbf {P}}_{i_*F}\subseteq {\mathbf {P}}_{0z^{\prime }_1z_1^{+3} z_2' z_2}$
. Set
![]() $\tilde {k} = m(g-1)-k$
. As in the proof of Theorem 5.6, from the convexity and a direct computation, one can get
$\tilde {k} = m(g-1)-k$
. As in the proof of Theorem 5.6, from the convexity and a direct computation, one can get
 $$ \begin{align} \begin{aligned} \hbar- \|i_\ast F\|&> \|z_1 -z^{\prime}_1\|-\|z^{\prime}_1 -z_1^{+3}\|+ \|z_1 -z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+3}\|\\[5pt] & = \sqrt{(\frac{k^2-g+1}{k})^2+4g} - \sqrt{(\frac{k^2-g+1}{k}-3)^2+4g} \\[5pt] & \mathrel{\phantom{>}} + \sqrt{(\frac{\tilde k^2-g+1}{\tilde k})^2+4g} - \sqrt{(\frac{\tilde k^2-g+1}{\tilde k}-3)^2+4g}\\[5pt] & \geq \frac{4k^2}{\sqrt{(g-1+k^2)^2+4k^2}+(g-1+k^2)} +\frac{4\tilde k^2}{\sqrt{(g-1+\tilde k^2)^2+4\tilde k^2}+(g-1+\tilde k^2)} \\[5pt] &=\hbar+\chi-2(g-1+k^2) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \hbar- \|i_\ast F\|&> \|z_1 -z^{\prime}_1\|-\|z^{\prime}_1 -z_1^{+3}\|+ \|z_1 -z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+3}\|\\[5pt] & = \sqrt{(\frac{k^2-g+1}{k})^2+4g} - \sqrt{(\frac{k^2-g+1}{k}-3)^2+4g} \\[5pt] & \mathrel{\phantom{>}} + \sqrt{(\frac{\tilde k^2-g+1}{\tilde k})^2+4g} - \sqrt{(\frac{\tilde k^2-g+1}{\tilde k}-3)^2+4g}\\[5pt] & \geq \frac{4k^2}{\sqrt{(g-1+k^2)^2+4k^2}+(g-1+k^2)} +\frac{4\tilde k^2}{\sqrt{(g-1+\tilde k^2)^2+4\tilde k^2}+(g-1+\tilde k^2)} \\[5pt] &=\hbar+\chi-2(g-1+k^2) \end{aligned} \end{align} $$
whenever
![]() $(g,k,m)\notin \Big \{(5,3,m), (6,4,3), (8,5,2)\Big \}$
satisfies our assumption.
$(g,k,m)\notin \Big \{(5,3,m), (6,4,3), (8,5,2)\Big \}$
satisfies our assumption.
In the case
![]() $(g, k,m)=(6,4,3)$
,
$(g, k,m)=(6,4,3)$
,
![]() $(8,5,2)$
or
$(8,5,2)$
or
![]() $(5,3,m)$
with
$(5,3,m)$
with
![]() $m\geq 4$
, though the inequality (6.3) fails, one can give an improvement of the estimate (6.3) by considering the convex hull of integer points in
$m\geq 4$
, though the inequality (6.3) fails, one can give an improvement of the estimate (6.3) by considering the convex hull of integer points in
![]() ${\mathbf {P}}_{0z_1'z_1^{+3}z_2'z_2}$
. In those cases, the convex hull is a convex polygon with vertices
${\mathbf {P}}_{0z_1'z_1^{+3}z_2'z_2}$
. In those cases, the convex hull is a convex polygon with vertices
![]() $z_1, z_1^{+3}, z_1', z_2'$
and
$z_1, z_1^{+3}, z_1', z_2'$
and
![]() $z_3$
, where
$z_3$
, where
![]() $z_3$
is given as below:
$z_3$
is given as below:
-
•
 $(g, k,m)=(5,3,m)$
,
$(g, k,m)=(5,3,m)$
,
 $z_3=-3+2\sqrt {-1}$
;
$z_3=-3+2\sqrt {-1}$
; -
•
 $(g, k,m)=(6,4,3)$
,
$(g, k,m)=(6,4,3)$
,
 $z_3=-8+3\sqrt {-1}$
;
$z_3=-8+3\sqrt {-1}$
; -
•
 $(g, k,m)=(8,5,2)$
,
$(g, k,m)=(8,5,2)$
,
 $z_3=-14+4\sqrt {-1}$
.
$z_3=-14+4\sqrt {-1}$
.
Then one can get
A computer calculation of their values shows that Equation (6.2) still holds.
In case (ii) and (iii), if
![]() $z_1^{+1}$
or
$z_1^{+1}$
or
![]() $z_1^{+2}$
is a vertex of
$z_1^{+2}$
is a vertex of
![]() ${\mathbf {P}}_{i_*F}$
, there exists
${\mathbf {P}}_{i_*F}$
, there exists
![]() $\widetilde {E}_j \subset i_*F$
in the HN-filtration (5.11) such that
$\widetilde {E}_j \subset i_*F$
in the HN-filtration (5.11) such that
![]() $\overline Z(\widetilde {E}_j)=z_1^{+1}$
(respectively,
$\overline Z(\widetilde {E}_j)=z_1^{+1}$
(respectively,
![]() $z_1^{+2}$
). Then we have
$z_1^{+2}$
). Then we have
 $$ \begin{align*} \begin{aligned} h^0(X,i_*F) &\leq \sum_i \left\lfloor \frac{ l (E_i)+\chi(E_i)}{2}\right\rfloor \\[5pt] &\leq \sum_{i\leq j} (\left\lfloor \frac{l (E_i)+\chi(E_i)}{2}\right\rfloor -\frac{\chi(E_i)}{2}) + \sum_{i> j} (\left\lfloor \frac{l (E_i)+\chi(E_i)}{2}\right\rfloor-\frac{\chi(E_i)}{2} ) +\frac{\chi}{2}\\[5pt] & \leq \frac{\hbar+\chi}{2}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} h^0(X,i_*F) &\leq \sum_i \left\lfloor \frac{ l (E_i)+\chi(E_i)}{2}\right\rfloor \\[5pt] &\leq \sum_{i\leq j} (\left\lfloor \frac{l (E_i)+\chi(E_i)}{2}\right\rfloor -\frac{\chi(E_i)}{2}) + \sum_{i> j} (\left\lfloor \frac{l (E_i)+\chi(E_i)}{2}\right\rfloor-\frac{\chi(E_i)}{2} ) +\frac{\chi}{2}\\[5pt] & \leq \frac{\hbar+\chi}{2}. \end{aligned} \end{align*} $$
For simplicity, we may use
![]() $\frac {\hbar _1}{2}$
and
$\frac {\hbar _1}{2}$
and
![]() $\frac {\hbar _2}{2}$
to denote the first two terms in the second row. As
$\frac {\hbar _2}{2}$
to denote the first two terms in the second row. As
![]() $h^0(X,i_\ast F)\geq g-1+k^2$
, following the argument in Theorem 5.6, it suffices to prove the inequality
$h^0(X,i_\ast F)\geq g-1+k^2$
, following the argument in Theorem 5.6, it suffices to prove the inequality
or equivalently,
For case ii), a direct computation shows
 $$ \begin{align} \hspace{-120pt}\|z_1^{+1}\|-\hbar_1& = \sum_{i\leq j} \|E_i\|-\hbar_1-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \nonumber\\[5pt] & \geq \sum\limits_{i\leq j} (\|E_i\|- \ell(E_i))-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \nonumber \\[5pt] &\geq (\|E_1\|- \ell(E_1))-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|)\nonumber \\[5pt] & \geq \frac{3}{\sqrt{k^2+4g-3}}-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \end{align} $$
$$ \begin{align} \hspace{-120pt}\|z_1^{+1}\|-\hbar_1& = \sum_{i\leq j} \|E_i\|-\hbar_1-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \nonumber\\[5pt] & \geq \sum\limits_{i\leq j} (\|E_i\|- \ell(E_i))-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \nonumber \\[5pt] &\geq (\|E_1\|- \ell(E_1))-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|)\nonumber \\[5pt] & \geq \frac{3}{\sqrt{k^2+4g-3}}-(\sum_{i\leq j}\|E_i\|-\|z_1^{+1}\|) \end{align} $$
 $$ \begin{align} &\qquad\geq \frac{3}{\sqrt{k^2+4g-3}}-(\|z^{\prime}_1\| + \|z^{\prime}_1-z_1^{+1}\|-\| z_1^{+1}\| ) \end{align} $$
$$ \begin{align} &\qquad\geq \frac{3}{\sqrt{k^2+4g-3}}-(\|z^{\prime}_1\| + \|z^{\prime}_1-z_1^{+1}\|-\| z_1^{+1}\| ) \end{align} $$
Let us explain why the inequality (6.6) holds. Note that
![]() $\overline {Z}(E_1)=x+y\sqrt {-1}$
satisfies
$\overline {Z}(E_1)=x+y\sqrt {-1}$
satisfies
Then we have
![]() $-x< ky$
and
$-x< ky$
and
![]() $y \nmid x$
by our assumption
$y \nmid x$
by our assumption
![]() $g-1\neq k$
,
$g-1\neq k$
,
![]() $g\neq k$
, and
$g\neq k$
, and
![]() $g<2k$
. This will give
$g<2k$
. This will give
 $$ \begin{align*} \|E_1\|- \ell(E_1) &\geq \sqrt{x^2 +4g y^2}- \sqrt{x^2+4(g-1)y^2+y^2} \quad (\textrm{since } y\nmid x)\\ & \geq \frac{3y^2}{2 \sqrt{x^2+(4g-3)y^2}} \\ & \geq \frac{3y^2}{2 \sqrt{k^2y^2+(4g-3)y^2}} \\ &> \frac{3}{\sqrt{k^2+4g-3}} \quad (\textrm{since } y \geq 2, \text{ which is a consequence of } y\nmid x). \end{align*} $$
$$ \begin{align*} \|E_1\|- \ell(E_1) &\geq \sqrt{x^2 +4g y^2}- \sqrt{x^2+4(g-1)y^2+y^2} \quad (\textrm{since } y\nmid x)\\ & \geq \frac{3y^2}{2 \sqrt{x^2+(4g-3)y^2}} \\ & \geq \frac{3y^2}{2 \sqrt{k^2y^2+(4g-3)y^2}} \\ &> \frac{3}{\sqrt{k^2+4g-3}} \quad (\textrm{since } y \geq 2, \text{ which is a consequence of } y\nmid x). \end{align*} $$
The inequality (6.8) holds because
 $$ \begin{align*} \|z_1^{+1} -z^{\prime}_1 \|+\|z^{\prime}_1 \| -\|z_1^{+1}\|&= \sqrt{(\frac{k^2-(g-1)}{k}-1)^2+4g} + (k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g } -(k^2 +g) \\ &=\sqrt{(\frac{k^2-(g-1)}{k}-1)^2+4g}- \left(k-1+\frac{g+1}{k}\right)\\ &\mathrel{\phantom{=}}+(k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g } -\left((k^2 +g)-(k-1+\frac{g+1}{k})\right)\\ &< \frac{2g(k-1)}{k^3-k^2+(g+1)k} + \frac{-2 g (k-1)^2}{k^4-k^3+(g+1)k^2-(g+1)k}\\ &= \frac{2g(k-1)}{(k^2+g+1)(k^2-k+g+1)} \\ & \leq \frac{3}{\sqrt{k^2+4g-3}} \end{align*} $$
$$ \begin{align*} \|z_1^{+1} -z^{\prime}_1 \|+\|z^{\prime}_1 \| -\|z_1^{+1}\|&= \sqrt{(\frac{k^2-(g-1)}{k}-1)^2+4g} + (k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g } -(k^2 +g) \\ &=\sqrt{(\frac{k^2-(g-1)}{k}-1)^2+4g}- \left(k-1+\frac{g+1}{k}\right)\\ &\mathrel{\phantom{=}}+(k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g } -\left((k^2 +g)-(k-1+\frac{g+1}{k})\right)\\ &< \frac{2g(k-1)}{k^3-k^2+(g+1)k} + \frac{-2 g (k-1)^2}{k^4-k^3+(g+1)k^2-(g+1)k}\\ &= \frac{2g(k-1)}{(k^2+g+1)(k^2-k+g+1)} \\ & \leq \frac{3}{\sqrt{k^2+4g-3}} \end{align*} $$
when
![]() $k\geq \frac {g+1}{2}\geq 2$
. Note that
$k\geq \frac {g+1}{2}\geq 2$
. Note that
![]() $ \|z_1^{+1}\|-\hbar _1=k^2+g- 2\sum \limits _{i\leq j} \left \lfloor \frac {l (E_i)+\chi (E_i)}{2}\right \rfloor -\sum \limits _{i\leq j} \chi (E_i)$
is an even number, this yields
$ \|z_1^{+1}\|-\hbar _1=k^2+g- 2\sum \limits _{i\leq j} \left \lfloor \frac {l (E_i)+\chi (E_i)}{2}\right \rfloor -\sum \limits _{i\leq j} \chi (E_i)$
is an even number, this yields
![]() $ \|z_1^{+1}\|-\hbar _1 \geq 2.$
$ \|z_1^{+1}\|-\hbar _1 \geq 2.$
Next, recall that
![]() $\widetilde {E}_l=i_\ast F$
in the HN filtration (5.11), we can get
$\widetilde {E}_l=i_\ast F$
in the HN filtration (5.11), we can get
 $$ \begin{align*} \|z_1^{+1} -z_2\|-\hbar_2 & \geq \sum\limits_{i>j} (\|E_i\|- \ell(E_i))-(\sum_{i> j}\|E_i\|-\|z_1^{+1}- z_2\|) \\ &\geq (\|E_l\|- \ell(E_l))-(\|z_1^{+1}-z^{\prime}_2\| + \|z^{\prime}_2- z_2\|-\|z_1^{+1} - z_2\| ) \\ &> \frac{3}{\sqrt{\tilde k^2+4g-3}} - \frac{2g(\tilde k-1)}{(\tilde k^2+g+1)(\tilde k^2-\tilde k+g+1)}>0 \end{align*} $$
$$ \begin{align*} \|z_1^{+1} -z_2\|-\hbar_2 & \geq \sum\limits_{i>j} (\|E_i\|- \ell(E_i))-(\sum_{i> j}\|E_i\|-\|z_1^{+1}- z_2\|) \\ &\geq (\|E_l\|- \ell(E_l))-(\|z_1^{+1}-z^{\prime}_2\| + \|z^{\prime}_2- z_2\|-\|z_1^{+1} - z_2\| ) \\ &> \frac{3}{\sqrt{\tilde k^2+4g-3}} - \frac{2g(\tilde k-1)}{(\tilde k^2+g+1)(\tilde k^2-\tilde k+g+1)}>0 \end{align*} $$
as
![]() $\tilde {k}>\frac {g+1}{2}$
. Combining them together, we can obtain (6.5).
$\tilde {k}>\frac {g+1}{2}$
. Combining them together, we can obtain (6.5).
For case (iii), if
![]() $k\nmid g+1$
, we have
$k\nmid g+1$
, we have
 $$ \begin{align} \|z_1^{+1}\|-\hbar_1& = \sum_{i\leq j}\|E_i\|-\hbar_1+\|z_1^{+1}\|-\sum_{i\leq j}\|E_i\| \nonumber \\ &\geq \|E_1\|-\ell(E_1) +\|z_1^{+1}\|-\|z^{\prime}_1\|-\|z^{\prime}_1-z_1^{+2}\| \nonumber \\ &\geq \frac{3}{\sqrt{k^2+4g-3}} + \|z_1^{+1}\|-\|z^{\prime}_1\|-\|z^{\prime}_1-z_1^{+2}\| \end{align} $$
$$ \begin{align} \|z_1^{+1}\|-\hbar_1& = \sum_{i\leq j}\|E_i\|-\hbar_1+\|z_1^{+1}\|-\sum_{i\leq j}\|E_i\| \nonumber \\ &\geq \|E_1\|-\ell(E_1) +\|z_1^{+1}\|-\|z^{\prime}_1\|-\|z^{\prime}_1-z_1^{+2}\| \nonumber \\ &\geq \frac{3}{\sqrt{k^2+4g-3}} + \|z_1^{+1}\|-\|z^{\prime}_1\|-\|z^{\prime}_1-z_1^{+2}\| \end{align} $$
Here, the inequality (6.10) holds because
 $$ \begin{align*} \|z_1^{+2}-z^{\prime}_1 \|+\|z^{\prime}_1\| -\|z_1^{+1}\| &=\sqrt{(\frac{k^2-(g-1)}{k}-2)^2+4g}+(k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g} -(k^2+g)\\ &=\sqrt{(\frac{k^2-(g-1)}{k}-2)^2+4g}-(k-2+\frac{g+1}{k})\\ &\mathrel{\phantom{\geq}} + (k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g}-(k^2-k+(g+1)-\frac{g+1}{k})-1 \\ &\leq \frac{2 g (2 k-1)}{k \left(g+(k-1)^2\right)}-\frac{2 g (k-1)}{k \left(g+k^2+1\right)}-1\\ &= \frac{2 g \left(k^2+2k+g-1\right)}{\left(k^2+g+1\right)\left(k^2-2k+g+1\right)} -1\\ &< \frac{3}{\sqrt{k^2+4g-3}}-1. \end{align*} $$
$$ \begin{align*} \|z_1^{+2}-z^{\prime}_1 \|+\|z^{\prime}_1\| -\|z_1^{+1}\| &=\sqrt{(\frac{k^2-(g-1)}{k}-2)^2+4g}+(k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g} -(k^2+g)\\ &=\sqrt{(\frac{k^2-(g-1)}{k}-2)^2+4g}-(k-2+\frac{g+1}{k})\\ &\mathrel{\phantom{\geq}} + (k-1)\sqrt{(\frac{k^2-(g-1)}{k})^2+4g}-(k^2-k+(g+1)-\frac{g+1}{k})-1 \\ &\leq \frac{2 g (2 k-1)}{k \left(g+(k-1)^2\right)}-\frac{2 g (k-1)}{k \left(g+k^2+1\right)}-1\\ &= \frac{2 g \left(k^2+2k+g-1\right)}{\left(k^2+g+1\right)\left(k^2-2k+g+1\right)} -1\\ &< \frac{3}{\sqrt{k^2+4g-3}}-1. \end{align*} $$
Note that
![]() $\|z_1^{+1}\|-\hbar _1$
is an odd number, this yields
$\|z_1^{+1}\|-\hbar _1$
is an odd number, this yields
![]() $\|z_1^{+1}\|-\hbar _1 \geq 3$
. Similarly, one can get
$\|z_1^{+1}\|-\hbar _1 \geq 3$
. Similarly, one can get
under the assumption
![]() $m(g-1)-k \nmid g+1 $
. Since both of them are at least positive under our assumption, we get Equation (6.5) as well. This finishes the proof for
$m(g-1)-k \nmid g+1 $
. Since both of them are at least positive under our assumption, we get Equation (6.5) as well. This finishes the proof for
![]() $(g,k,m)\neq (5,3,3)$
.
$(g,k,m)\neq (5,3,3)$
.
For the remaining case
![]() $(g,k,m)=(5,3,3)$
, we have to make use of the
$(g,k,m)=(5,3,3)$
, we have to make use of the
![]() $4$
-sharpness of
$4$
-sharpness of
![]() ${\mathbf {P}}_v$
. We just need to verify
${\mathbf {P}}_v$
. We just need to verify
![]() ${\mathbf {P}}_{i_*F}$
is not contained in
${\mathbf {P}}_{i_*F}$
is not contained in
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
and
${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
and
![]() $z_1^{+3}=-2+3\sqrt {-1}$
is not a vertex of
$z_1^{+3}=-2+3\sqrt {-1}$
is not a vertex of
![]() ${\mathbf {P}}_{i_\ast F}$
. As above, by using the convex hull of integer points in
${\mathbf {P}}_{i_\ast F}$
. As above, by using the convex hull of integer points in
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
, we have
${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
, we have
 $$ \begin{align*} \begin{aligned} \hbar- \|i_\ast F\| \geq & \|z_1\|-\|-3+2\sqrt{-1}\|- \|-3+2\sqrt{-1}-z_1^{+4}\| + \|z_1 -z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+4}\|\\ &=-2 \sqrt{6}-\sqrt{89}+\sqrt{205}+\frac{\sqrt{7549}}{9}-\frac{\sqrt{3301}}{9} \\ &>\hbar+\chi-2(g-1+k^2) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \hbar- \|i_\ast F\| \geq & \|z_1\|-\|-3+2\sqrt{-1}\|- \|-3+2\sqrt{-1}-z_1^{+4}\| + \|z_1 -z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+4}\|\\ &=-2 \sqrt{6}-\sqrt{89}+\sqrt{205}+\frac{\sqrt{7549}}{9}-\frac{\sqrt{3301}}{9} \\ &>\hbar+\chi-2(g-1+k^2) \end{aligned} \end{align*} $$
which show that
![]() ${\mathbf {P}}_{i_*F}$
cannot lie in
${\mathbf {P}}_{i_*F}$
cannot lie in
![]() ${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
. Moreover, a similar estimate of
${\mathbf {P}}_{0z^{\prime }_1z_1^{+4} z_2' z_2}$
. Moreover, a similar estimate of
![]() ${\|E_1\|-\ell (E_1)}$
and
${\|E_1\|-\ell (E_1)}$
and
![]() $\|E_l\|-\ell (E_l)$
in (ii) and (iii) shows that
$\|E_l\|-\ell (E_l)$
in (ii) and (iii) shows that
![]() $z_1^{+3}$
is not a vertex of
$z_1^{+3}$
is not a vertex of
![]() ${\mathbf {P}}_{i_\ast F}$
.
${\mathbf {P}}_{i_\ast F}$
.
Remark 6.4. One can also directly check the small genera cases by running the computer program in [Reference Feyzbakhsh13, Section 4] .
7 Surjectivity of the tangent map
In this section, we adapt Feyzbakhsh’s approach to study the surjectivity of the tangent map and obtain a sufficient condition for
![]() $\psi $
being an isomorphism.
$\psi $
being an isomorphism.
Theorem 7.1. Let
![]() $v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a Mukai vector satisfying the injectivity condition (✶). The morphism
$v=(r,c,s)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a Mukai vector satisfying the injectivity condition (✶). The morphism
is an isomorphism whenever the following conditions hold
-
(i)
 $\psi $
is surjective;
$\psi $
is surjective; -
(ii)
 $h^0(X,E) = r+s$
for any
$h^0(X,E) = r+s$
for any
 $E \in \mathbf {M}(v)$
;
$E \in \mathbf {M}(v)$
; -
(iii) there exists
 $\sigma \in {\mathrm {L}}_{(\pi _{v(-m)},\pi _{v_K})}\cap V(X)$
such that (7.1)where
$\sigma \in {\mathrm {L}}_{(\pi _{v(-m)},\pi _{v_K})}\cap V(X)$
such that (7.1)where $$ \begin{align} \Omega^+_{v(-m)}({\mathrm{L}}_{(o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X) = \Omega^+_{v_K}({\mathrm{L}}_{(o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X)=\emptyset, \end{align} $$
$$ \begin{align} \Omega^+_{v(-m)}({\mathrm{L}}_{(o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X) = \Omega^+_{v_K}({\mathrm{L}}_{(o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X)=\emptyset, \end{align} $$
 $v_K = (s,-c,r)$
;
$v_K = (s,-c,r)$
;
-
(iv)
 $2s>v^2+2c^2$
, or
$2s>v^2+2c^2$
, or
 $2s>v^2+2$
and
$2s>v^2+2$
and
 $\gcd (c,s)=1$
.
$\gcd (c,s)=1$
.
Proof. As
![]() $\psi $
is bijective, it suffices to show the tangent map
$\psi $
is bijective, it suffices to show the tangent map
![]() $\mathrm {d}\psi $
is surjective. The argument is similar as [Reference Feyzbakhsh11, §6]. For the convenience of readers, we sketch the proof as below. For any
$\mathrm {d}\psi $
is surjective. The argument is similar as [Reference Feyzbakhsh11, §6]. For the convenience of readers, we sketch the proof as below. For any
![]() $E\in \mathbf {M}(v)$
, the differential map
$E\in \mathbf {M}(v)$
, the differential map
![]() $\mathrm {d}\psi : T_{[E]} \mathbf {M}(v) \to T_{[E|_C]}{\mathbf {BN}}_C(v)$
at
$\mathrm {d}\psi : T_{[E]} \mathbf {M}(v) \to T_{[E|_C]}{\mathbf {BN}}_C(v)$
at
![]() $[E]$
can be identified as the map
$[E]$
can be identified as the map
sending
![]() $(E\to E[1])$
to
$(E\to E[1])$
to
![]() $(E|_C \to E|_C[1]) $
.
$(E|_C \to E|_C[1]) $
.
Let
![]() $\xi \colon E|_C\to E|_C[1]$
be a tangent vector in
$\xi \colon E|_C\to E|_C[1]$
be a tangent vector in
![]() $ T_{[E|_C]}{\mathbf {BN}}_C(v)$
. Then Feyzbakhsh has shown in [Reference Feyzbakhsh11, §6] that there exist morphisms
$ T_{[E|_C]}{\mathbf {BN}}_C(v)$
. Then Feyzbakhsh has shown in [Reference Feyzbakhsh11, §6] that there exist morphisms
![]() $\xi ' $
and
$\xi ' $
and
![]() $\xi " $
such that the following commutative diagram holds
$\xi " $
such that the following commutative diagram holds

provided that
where
![]() $K_E$
is the cone of the evaluation map
$K_E$
is the cone of the evaluation map
![]() ${\mathcal {O}}_X^{h^0(X,E)} \rightarrow E \rightarrow K_E$
in
${\mathcal {O}}_X^{h^0(X,E)} \rightarrow E \rightarrow K_E$
in
![]() $\text {D}^{\text {b}}(X)$
. Note that
$\text {D}^{\text {b}}(X)$
. Note that
![]() $\mathrm {d}\psi (\xi ') = \xi $
, we are therefore reduced to check (7.2) holds for every E.
$\mathrm {d}\psi (\xi ') = \xi $
, we are therefore reduced to check (7.2) holds for every E.
Note that
![]() $v(K_E) = -v_K$
and
$v(K_E) = -v_K$
and
![]() $\pi _{v_K} = \pi _{K_E}$
. We can choose the stability condition
$\pi _{v_K} = \pi _{K_E}$
. We can choose the stability condition
![]() ${\sigma _1\in {\mathrm {L}}_{( \pi _{v_K}, o')}}$
sufficiently close to
${\sigma _1\in {\mathrm {L}}_{( \pi _{v_K}, o')}}$
sufficiently close to
![]() $o'$
and
$o'$
and
![]() $\sigma _2 \in {\mathrm {L}}_{(\pi _{K},o)} $
sufficiently close to o so that
$\sigma _2 \in {\mathrm {L}}_{(\pi _{K},o)} $
sufficiently close to o so that
see Figure 9. As in the proof of Theorem 4.1, we have
![]() ${\mathcal {O}}_X$
and E are
${\mathcal {O}}_X$
and E are
![]() $\sigma _1$
-semistable of the same phase. Then as the quotient of E by
$\sigma _1$
-semistable of the same phase. Then as the quotient of E by
![]() ${\mathcal {O}}_X^{h^0(X,E)}$
,
${\mathcal {O}}_X^{h^0(X,E)}$
,
![]() $K_E$
is also
$K_E$
is also
![]() $\sigma _1$
-semistable of the same
$\sigma _1$
-semistable of the same
![]() $\sigma _1$
-phase. Note that Lemma 4.2 still holds if we exchange r and s in Mukai vector v. Then we get
$\sigma _1$
-phase. Note that Lemma 4.2 still holds if we exchange r and s in Mukai vector v. Then we get
Since
![]() $v_K$
is primitive, we have
$v_K$
is primitive, we have
![]() $ \Omega _{v_K}({\mathbf {P}}_{o\pi _{v_K} \infty } \cap \Gamma ) \cap {\mathrm {H}}_{\text {alg}}^{*}(X) = \emptyset $
. By Proposition 3.4,
$ \Omega _{v_K}({\mathbf {P}}_{o\pi _{v_K} \infty } \cap \Gamma ) \cap {\mathrm {H}}_{\text {alg}}^{*}(X) = \emptyset $
. By Proposition 3.4,
![]() $v_K$
admits no strictly semistable stability conditions in
$v_K$
admits no strictly semistable stability conditions in
![]() ${\mathbf {P}}_{o\sigma _2 \sigma _1 o'}\setminus \{o,o'\}$
. Therefore,
${\mathbf {P}}_{o\sigma _2 \sigma _1 o'}\setminus \{o,o'\}$
. Therefore,
![]() $K_E$
is stable for any
$K_E$
is stable for any
![]() $\tau \in {\mathbf {P}}_{o\sigma _2 \sigma _1 o'}\setminus \{o,o'\}$
. This implies that
$\tau \in {\mathbf {P}}_{o\sigma _2 \sigma _1 o'}\setminus \{o,o'\}$
. This implies that
![]() $K_E$
is
$K_E$
is
![]() $\sigma _{\alpha ,0}$
-stable for
$\sigma _{\alpha ,0}$
-stable for
![]() $\alpha> \sqrt {\frac {2}{H^2}}$
. By [Reference Macrì and Schmidt15, Lemma 6.18], we have
$\alpha> \sqrt {\frac {2}{H^2}}$
. By [Reference Macrì and Schmidt15, Lemma 6.18], we have
![]() $\operatorname {{\mathrm {H}}}^{-1}(K_E)$
is a
$\operatorname {{\mathrm {H}}}^{-1}(K_E)$
is a
![]() $\mu _H$
-semistable torsion-free sheaf and
$\mu _H$
-semistable torsion-free sheaf and
![]() $\operatorname {{\mathrm {H}}}^0(K_E) $
is a torsion sheaf supported in dimension zero. So we can set
$\operatorname {{\mathrm {H}}}^0(K_E) $
is a torsion sheaf supported in dimension zero. So we can set
![]() $v(\operatorname {{\mathrm {H}}}^0(K_E)) = (0,0,a)$
and
$v(\operatorname {{\mathrm {H}}}^0(K_E)) = (0,0,a)$
and
![]() $v(\operatorname {{\mathrm {H}}}^{-1}(K_E)) = (s,-c,r+a)$
for some
$v(\operatorname {{\mathrm {H}}}^{-1}(K_E)) = (s,-c,r+a)$
for some
![]() $a\geq 0$
. By [Reference Feyzbakhsh11, Lemma 3.1], we have
$a\geq 0$
. By [Reference Feyzbakhsh11, Lemma 3.1], we have
When
![]() $\gcd (c,s)=1$
, we have
$\gcd (c,s)=1$
, we have
![]() $\operatorname {{\mathrm {H}}}^{-1}(K_E)$
is slope stable and
$\operatorname {{\mathrm {H}}}^{-1}(K_E)$
is slope stable and
![]() $v(\operatorname {{\mathrm {H}}}^{-1}(K_E))^2\geq -2$
. Then by condition (iv), we have
$v(\operatorname {{\mathrm {H}}}^{-1}(K_E))^2\geq -2$
. Then by condition (iv), we have
![]() $a=0$
and
$a=0$
and
![]() $\operatorname {{\mathrm {H}}}^0(K_E)=0$
. So we obtain
$\operatorname {{\mathrm {H}}}^0(K_E)=0$
. So we obtain
![]() $K_E =M[1]$
, where
$K_E =M[1]$
, where
![]() $M = \operatorname {{\mathrm {H}}}^{-1}(K_E)$
is a
$M = \operatorname {{\mathrm {H}}}^{-1}(K_E)$
is a
![]() $\mu _H$
-semistable torsion-free sheaf.
$\mu _H$
-semistable torsion-free sheaf.

Figure 9 Any point in the colored region is a stability condition.
Since
![]() $\Omega ^+_{v_K}({\mathrm {L}}_{(o,\sigma ]}) \cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset ,$
$\Omega ^+_{v_K}({\mathrm {L}}_{(o,\sigma ]}) \cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset ,$
![]() $v(M)$
admits no strictly semistable condition in
$v(M)$
admits no strictly semistable condition in
![]() ${\mathrm {L}}_{(o,\sigma ]}$
. It follows that M is
${\mathrm {L}}_{(o,\sigma ]}$
. It follows that M is
![]() $\sigma $
-stable as it is
$\sigma $
-stable as it is
![]() $\sigma _2$
-stable. Similarly, we have
$\sigma _2$
-stable. Similarly, we have
![]() $E(-C)[1]$
is also
$E(-C)[1]$
is also
![]() $\sigma $
-stable. Since M and
$\sigma $
-stable. Since M and
![]() $E(-C)[1]$
are
$E(-C)[1]$
are
![]() $\sigma $
-stable of the same phase, one must have
$\sigma $
-stable of the same phase, one must have
![]() $\operatorname {\mathrm {Hom}}_X(M,E(-C)[1])=0$
. This proves the assertion.
$\operatorname {\mathrm {Hom}}_X(M,E(-C)[1])=0$
. This proves the assertion.
Conditions for reconstructing K3 surfaces
As a first application, we obtain a numerical criterion for Mukai’s program of reconstructing K3 surfaces, that is, the case
![]() $v^2=0$
.
$v^2=0$
.
Theorem 7.2. Assume
![]() $g>2$
. Let
$g>2$
. Let
![]() $v=(r,c,ck)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a primitive Mukai vector with
$v=(r,c,ck)\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
be a primitive Mukai vector with
![]() $v^2=0$
. Suppose it satisfies the condition
$v^2=0$
. Suppose it satisfies the condition
 $$ \begin{align} r \mid g-1,\,\, k\nmid g,\,\, 0<k\leq 3g-3 \text{~and~} m>1+\frac{ck}{r(k-1)}. \end{align} $$
$$ \begin{align} r \mid g-1,\,\, k\nmid g,\,\, 0<k\leq 3g-3 \text{~and~} m>1+\frac{ck}{r(k-1)}. \end{align} $$
The restriction map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism if it is a surjective morphism.
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism if it is a surjective morphism.
Proof. Let us check that the conditions (ii)–(iv) in Theorem 7.1 are satisfied. By our assumption, we know that
![]() $\gcd (r-s,c)=1$
. According to [Reference Feyzbakhsh13, Lemma 3.1], one has
$\gcd (r-s,c)=1$
. According to [Reference Feyzbakhsh13, Lemma 3.1], one has
which forces
![]() $h^0(X,E)= r+s $
by Equation (4.2). This verifies the condition (ii).
$h^0(X,E)= r+s $
by Equation (4.2). This verifies the condition (ii).
For the condition (iv), note that we have
![]() $s=\frac {c^2(g-1)}{r}\geq c^2$
where the equality holds when
$s=\frac {c^2(g-1)}{r}\geq c^2$
where the equality holds when
![]() $r= g-1$
. If
$r= g-1$
. If
![]() $r=g-1$
, the inequality in Equation (7.3) will be equality. By [Reference Feyzbakhsh11, lemma 3.1], we have
$r=g-1$
, the inequality in Equation (7.3) will be equality. By [Reference Feyzbakhsh11, lemma 3.1], we have
![]() $c\mid (g-1)$
which is a contradiction. Thus, we only need to verify the condition (iii). By Remark 3.5, it suffices to show
$c\mid (g-1)$
which is a contradiction. Thus, we only need to verify the condition (iii). By Remark 3.5, it suffices to show
To make the computation easier, we may consider the action of tensoring the invertible sheaf
![]() ${\mathcal {O}}_X(H)$
which sends the triangle
${\mathcal {O}}_X(H)$
which sends the triangle
![]() ${\mathbf {P}}_{o \pi _{v_K} \pi _{v(-m)}}$
to the triangle
${\mathbf {P}}_{o \pi _{v_K} \pi _{v(-m)}}$
to the triangle
![]() ${\mathbf {P}}_{op_1p_2}$
, where
${\mathbf {P}}_{op_1p_2}$
, where
![]() $p_1=\pi _{v_K(1)}$
and
$p_1=\pi _{v_K(1)}$
and
![]() $p_2=\pi _{v(1-m)}$
. Then it is equivalent to show there are no projection of roots in
$p_2=\pi _{v(1-m)}$
. Then it is equivalent to show there are no projection of roots in
![]() ${\mathbf {P}}_{op_1p_2}-\{\text {vertices}\}$
.
${\mathbf {P}}_{op_1p_2}-\{\text {vertices}\}$
.
Firstly, we show that there is no projection of root on the two edges joining o. By definition, we have
 $$ \begin{align*}p_1=(\frac{kc}{(k-1)^2 r},\frac{c}{(k-1)r}) \text{ and } p_2=(\frac{cr}{k((m-1)r-c)^2}, \frac{c}{k(c-(m-1)r)}). \end{align*} $$
$$ \begin{align*}p_1=(\frac{kc}{(k-1)^2 r},\frac{c}{(k-1)r}) \text{ and } p_2=(\frac{cr}{k((m-1)r-c)^2}, \frac{c}{k(c-(m-1)r)}). \end{align*} $$
Then two open edges
![]() ${\mathrm {L}}_{(o,p_1)}$
and
${\mathrm {L}}_{(o,p_1)}$
and
![]() ${\mathrm {L}}_{(o,p_2)}$
do not contain any projection of roots by Observation (B).
${\mathrm {L}}_{(o,p_2)}$
do not contain any projection of roots by Observation (B).
Next, since
![]() $(m-1)r>\frac {ck}{(k-1)}>c$
, we know that
$(m-1)r>\frac {ck}{(k-1)}>c$
, we know that
![]() $p_1$
is lying in the first quadrant while projection
$p_1$
is lying in the first quadrant while projection
![]() $p_2$
is lying in the second quadrant. So the region
$p_2$
is lying in the second quadrant. So the region
is contained in the union of two trapezoidal regions
![]() ${\mathbf {P}}_{o p_1 \infty }^\circ $
,
${\mathbf {P}}_{o p_1 \infty }^\circ $
,
![]() ${\mathbf {P}}_{o p_2\infty }^\circ $
and the x-axis. As
${\mathbf {P}}_{o p_2\infty }^\circ $
and the x-axis. As
![]() $r|(g-1)$
and
$r|(g-1)$
and
![]() $\gcd (r,c)=1$
, we have an inclusion
$\gcd (r,c)=1$
, we have an inclusion
from Lemma 4.2 (i). Moreover, if there is a root
![]() $\delta =(r',c',s')\in \mathrm {R}(X)$
with
$\delta =(r',c',s')\in \mathrm {R}(X)$
with
![]() $r'>0$
whose projection
$r'>0$
whose projection
![]() $\pi _\delta $
is lying in
$\pi _\delta $
is lying in
![]() ${\mathbf {P}}_{o p_1 \infty }^\circ $
, one can follow the computation in Lemma 4.2 to get inequalities
${\mathbf {P}}_{o p_1 \infty }^\circ $
, one can follow the computation in Lemma 4.2 to get inequalities
 $$ \begin{align} k c' < (k-1) r' < k c' +\frac{k}{(g-1)c'}. \end{align} $$
$$ \begin{align} k c' < (k-1) r' < k c' +\frac{k}{(g-1)c'}. \end{align} $$
However, one can directly check that there are no such integers
![]() $(r',c',s')$
satisfying Equation (7.4) under the assumption
$(r',c',s')$
satisfying Equation (7.4) under the assumption
![]() $k\leq g-1$
or
$k\leq g-1$
or
![]() $3<k\leq 3g-3$
.
$3<k\leq 3g-3$
.
It remains to show that
![]() ${\mathbf {P}}_{op_1p_2} \cap y\text {-axis}\subseteq V(X)$
. Note that
${\mathbf {P}}_{op_1p_2} \cap y\text {-axis}\subseteq V(X)$
. Note that
 $$ \begin{align*}{\mathrm{L}}_{[p_1, p_2]} \cap x\text{-axis}=( \frac{c/(k-1)}{(m-1)r-c},0)\end{align*} $$
$$ \begin{align*}{\mathrm{L}}_{[p_1, p_2]} \cap x\text{-axis}=( \frac{c/(k-1)}{(m-1)r-c},0)\end{align*} $$
which is below
![]() $o'$
. It follows that
$o'$
. It follows that
![]() ${\mathbf {P}}_{op_1p_2} \cap y\text {-axis}\subseteq {\mathrm {L}}_{(o, o')}\subseteq V(X)$
.
${\mathbf {P}}_{op_1p_2} \cap y\text {-axis}\subseteq {\mathrm {L}}_{(o, o')}\subseteq V(X)$
.
Conditions for reconstructing hyper-Kähler
Now, we reconstruct hyper-Kähler varieties as Brill–Noether locus for Mukai vectors given in Corollary 5.7.
Theorem 7.3. Assume
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying conditions (✶) and (✶✶). The restriction map
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying conditions (✶) and (✶✶). The restriction map
![]() $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism.
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is an isomorphism.
Proof. By Corollary 5.7,
![]() $\psi $
is a bijective morphism. We only need to verify the conditions (ii)–(iv) in Theorem 7.1. We will check them one by one.
$\psi $
is a bijective morphism. We only need to verify the conditions (ii)–(iv) in Theorem 7.1. We will check them one by one.
-
(1) Let us first verify that
 $h^0(X,E) =r+s$
for any
$h^0(X,E) =r+s$
for any
 $E\in \mathbf {M}(v)$
. By [Reference Feyzbakhsh13, Proposition 3.1], it suffices to show that (7.5)
$E\in \mathbf {M}(v)$
. By [Reference Feyzbakhsh13, Proposition 3.1], it suffices to show that (7.5) $$ \begin{align} \frac{\sqrt{(r-s)^2+ (2g+2)c^2}}{2} < \frac{r+s}{2} +1. \end{align} $$
$$ \begin{align} \frac{\sqrt{(r-s)^2+ (2g+2)c^2}}{2} < \frac{r+s}{2} +1. \end{align} $$
After simplification, one can find that Equation (7.5) is equivalent to
 $$\begin{align*}\frac{(g+1)c^2-1}{2r+2}-1 <s. \end{align*}$$
$$\begin{align*}\frac{(g+1)c^2-1}{2r+2}-1 <s. \end{align*}$$
This holds when
 $(g-1)c^2 -rs <r$
and
$(g-1)c^2 -rs <r$
and
 $g> 4r^2+1$
.
$g> 4r^2+1$
. -
(2) For condition (ii), we claim that
and hence $$ \begin{align*}{\mathrm{L}}_{(\pi_{v(-m)},\pi_{v_K})}\cap \Gamma \neq \emptyset,\end{align*} $$
$$ \begin{align*}{\mathrm{L}}_{(\pi_{v(-m)},\pi_{v_K})}\cap \Gamma \neq \emptyset,\end{align*} $$
 ${\mathrm {L}}_{(\pi _{v(-m)},\pi _{v_K})}\cap V(X)\neq \emptyset $
. Let us write
${\mathrm {L}}_{(\pi _{v(-m)},\pi _{v_K})}\cap V(X)\neq \emptyset $
. Let us write
 $v(-m)=(r, \tilde {c},\tilde {s} )$
and
$v(-m)=(r, \tilde {c},\tilde {s} )$
and
 $v_K=(s,-c,r)$
with
$v_K=(s,-c,r)$
with
 $\tilde {c}=c-mr$
and
$\tilde {c}=c-mr$
and
 $ \tilde s=\lfloor \frac {(g-1)\tilde c^2 +1}{r}\rfloor ~ $
. Then we only need to show that the quadratic equation (7.6)has roots for
$ \tilde s=\lfloor \frac {(g-1)\tilde c^2 +1}{r}\rfloor ~ $
. Then we only need to show that the quadratic equation (7.6)has roots for $$ \begin{align} g((1-t)t\tilde{c}+t(-c))^2 = ((1-t)r+ t s)((1-t)\tilde{s}+ t r) \end{align} $$
$$ \begin{align} g((1-t)t\tilde{c}+t(-c))^2 = ((1-t)r+ t s)((1-t)\tilde{s}+ t r) \end{align} $$
 $0<t<1$
. By calculating the discriminant of (7.6), we know it has a solution
$0<t<1$
. By calculating the discriminant of (7.6), we know it has a solution
 $t_0$
satisfying (7.7)
$t_0$
satisfying (7.7) $$ \begin{align} 0<t_0 < \frac{\tilde{c}^2 g -r\tilde{s}}{s\tilde{s}+r^2 +2\tilde c cg+2(\tilde c^2 g-r\tilde s)}<1. \end{align} $$
$$ \begin{align} 0<t_0 < \frac{\tilde{c}^2 g -r\tilde{s}}{s\tilde{s}+r^2 +2\tilde c cg+2(\tilde c^2 g-r\tilde s)}<1. \end{align} $$
-
(3) Choose
 $\sigma \in {\mathrm {L}}_{(\pi _{v(-m)}, \pi _{v_K})} \cap \Gamma $
. We first verify that
$\sigma \in {\mathrm {L}}_{(\pi _{v(-m)}, \pi _{v_K})} \cap \Gamma $
. We first verify that  $$ \begin{align*}\Omega^+_{v(-m)}({\mathrm{L}}_{ (o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X)= \emptyset.\end{align*} $$
$$ \begin{align*}\Omega^+_{v(-m)}({\mathrm{L}}_{ (o,\sigma]}) \cap {\mathrm{H}}_{\text{alg}}^{*}(X)= \emptyset.\end{align*} $$
Suppose there is an integer point
 $p_0=(x_0,y_0,z_0) \in \Omega ^+_{v(-m)}({\mathrm {L}}_{[ \sigma , o)})$
. By Lemma 7.4 below, we have
$p_0=(x_0,y_0,z_0) \in \Omega ^+_{v(-m)}({\mathrm {L}}_{[ \sigma , o)})$
. By Lemma 7.4 below, we have  $$ \begin{align*}\tilde{c}-1 < y_0< 0.\end{align*} $$
$$ \begin{align*}\tilde{c}-1 < y_0< 0.\end{align*} $$
Moreover, one may observe that
 $p_0$
is lying in a (closed) planer region enclosed by the conic and two lines
$p_0$
is lying in a (closed) planer region enclosed by the conic and two lines $$ \begin{align*} Q= \left\{ y = y_0 ,\; (g-1)y^2+1= xz \right\} \end{align*} $$
$$ \begin{align*} Q= \left\{ y = y_0 ,\; (g-1)y^2+1= xz \right\} \end{align*} $$
 $$ \begin{align*}L_1=\left\{y = y_0,\; z=\frac{y_0 \tilde s}{\tilde{c}} \right\};~ L_2 =\left\{ (1-t)\frac{y_0}{\tilde{c}}(r,\tilde{c},\tilde{s} )-\frac{ty_0}{c}(s,-c,r) ,t\in \mathbb{R} \right\}.\end{align*} $$
$$ \begin{align*}L_1=\left\{y = y_0,\; z=\frac{y_0 \tilde s}{\tilde{c}} \right\};~ L_2 =\left\{ (1-t)\frac{y_0}{\tilde{c}}(r,\tilde{c},\tilde{s} )-\frac{ty_0}{c}(s,-c,r) ,t\in \mathbb{R} \right\}.\end{align*} $$
It has three vertices given by the intersection points
 $L_1\cap L_2$
,
$L_1\cap L_2$
,
 $L_1\cap Q$
and
$L_1\cap Q$
and
 $L_2\cap Q$
. This yields (7.8)where
$L_2\cap Q$
. This yields (7.8)where $$ \begin{align} \begin{aligned} \frac{y_0 r}{\tilde c} \leq x_0 \leq (1-t') \frac{y_0r}{\tilde c} -\frac{t'y_0 s}{c}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \frac{y_0 r}{\tilde c} \leq x_0 \leq (1-t') \frac{y_0r}{\tilde c} -\frac{t'y_0 s}{c}, \end{aligned} \end{align} $$
 $t'$
is the smaller root of the quadratic equation
$t'$
is the smaller root of the quadratic equation  $$ \begin{align*}(g-1)y_0^2+1= [(1-t) \frac{y_0r}{\tilde c} -\frac{ty_0 s}{c} ] [(1-t) \frac{y_0\tilde s}{\tilde c} -\frac{ty_0 r}{c}].\end{align*} $$
$$ \begin{align*}(g-1)y_0^2+1= [(1-t) \frac{y_0r}{\tilde c} -\frac{ty_0 s}{c} ] [(1-t) \frac{y_0\tilde s}{\tilde c} -\frac{ty_0 r}{c}].\end{align*} $$
Solving the equation, one can get
(7.9)as $$ \begin{align} \begin{aligned} t' \leq 2 \frac{(g-1) y_0^2+1-\frac{r\tilde s y_0^2}{\tilde c^2}}{-\frac{\tilde c \tilde s s}{c} -2r\tilde s} \leq \frac{2c(y_0^2r+\tilde c^2)}{ (-\tilde c\tilde s s-2r c\tilde s)\tilde c^2} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} t' \leq 2 \frac{(g-1) y_0^2+1-\frac{r\tilde s y_0^2}{\tilde c^2}}{-\frac{\tilde c \tilde s s}{c} -2r\tilde s} \leq \frac{2c(y_0^2r+\tilde c^2)}{ (-\tilde c\tilde s s-2r c\tilde s)\tilde c^2} \end{aligned} \end{align} $$
 $(g-1)\tilde c^2-r\tilde s< r$
. Plugging Equation (7.9) into (7.8), we get where the last inequality holds because
$(g-1)\tilde c^2-r\tilde s< r$
. Plugging Equation (7.9) into (7.8), we get where the last inequality holds because $$ \begin{align*} \begin{aligned} 0< x_0 -\frac{y_0r}{\tilde c}&\leq \frac{2cy_0(y_0^2r+\tilde c^2)}{ (\tilde c\tilde s s+2r c\tilde s)\tilde c^2} (\frac{s\tilde c+rc}{c\tilde c}) \\&= (\frac{y_0}{\tilde c})(\frac{y_0^2r+\tilde c^2}{\tilde s\tilde c^2}) (\frac{s\tilde c+rc}{s\tilde c+2rc}) \\ &\leq \frac{3(r+1)}{\tilde s } \\ & < \frac{3r(r+1)}{(g-1)\tilde{c}^2-r} \\ &< -\frac{1}{\tilde c}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} 0< x_0 -\frac{y_0r}{\tilde c}&\leq \frac{2cy_0(y_0^2r+\tilde c^2)}{ (\tilde c\tilde s s+2r c\tilde s)\tilde c^2} (\frac{s\tilde c+rc}{c\tilde c}) \\&= (\frac{y_0}{\tilde c})(\frac{y_0^2r+\tilde c^2}{\tilde s\tilde c^2}) (\frac{s\tilde c+rc}{s\tilde c+2rc}) \\ &\leq \frac{3(r+1)}{\tilde s } \\ & < \frac{3r(r+1)}{(g-1)\tilde{c}^2-r} \\ &< -\frac{1}{\tilde c}, \end{aligned} \end{align*} $$
 $g-1\geq 4r^2$
. This contradicts to
$g-1\geq 4r^2$
. This contradicts to
 $x_0,y_0\in \mathbb {Z}$
. A similar computation shows that
$x_0,y_0\in \mathbb {Z}$
. A similar computation shows that
 $\Omega ^+_{v_K}({\mathrm {L}}_{(o, \sigma ]}) \cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
as well.
$\Omega ^+_{v_K}({\mathrm {L}}_{(o, \sigma ]}) \cap {\mathrm {H}}_{\text {alg}}^{*}(X)=\emptyset $
as well.
-
(4) Condition (iv) holds since our assumption
 $g>4r^2+1 $
ensures that
$g>4r^2+1 $
ensures that  $$\begin{align*}2s> 2r-2 +2c^2 >v^2 + 2c^2.\\[-37pt] \end{align*}$$
$$\begin{align*}2s> 2r-2 +2c^2 >v^2 + 2c^2.\\[-37pt] \end{align*}$$
Lemma 7.4. For any integer point
![]() $(x_0,\ y_0,\ z_0) \in \Omega ^+_{v(-m)}({\mathrm {L}}_{(o,\sigma ]})$
in Theorem 7.3, we have
$(x_0,\ y_0,\ z_0) \in \Omega ^+_{v(-m)}({\mathrm {L}}_{(o,\sigma ]})$
in Theorem 7.3, we have
Proof. Set
![]() $v_{t} = (1-t) v(-m) + t v_K$
. Let
$v_{t} = (1-t) v(-m) + t v_K$
. Let
![]() $0<t_0<t_1<1 $
be the roots of Equation (7.6). We set
$0<t_0<t_1<1 $
be the roots of Equation (7.6). We set
Then
![]() $\Omega ^+_{v(-m)}({\mathrm {L}}_{(o,\sigma ]})$
is contained in the tetrahedron
$\Omega ^+_{v(-m)}({\mathrm {L}}_{(o,\sigma ]})$
is contained in the tetrahedron
![]() $ \mathbf {T}_{Ov(-m)\varpi w}$
with four vertices
$ \mathbf {T}_{Ov(-m)\varpi w}$
with four vertices
![]() $O, v(-m), w $
and
$O, v(-m), w $
and
![]() $\varpi = (r, \tilde {c}, \frac {g\tilde {c}^2}{r})$
. This gives
$\varpi = (r, \tilde {c}, \frac {g\tilde {c}^2}{r})$
. This gives
![]() $y'<y_0<0 $
. Hence, we only need to estimate the lower bound of
$y'<y_0<0 $
. Hence, we only need to estimate the lower bound of
![]() $y'$
.
$y'$
.
Set
![]() $v_{t_0}=(r_{t_0},c_{t_0}, s_{t_0})$
, then we have
$v_{t_0}=(r_{t_0},c_{t_0}, s_{t_0})$
, then we have
![]() $w=\frac {y'}{c_{t_0}}v_{t_0}\in {\mathrm {L}}_{o,v_{t_0}}$
. Note that
$w=\frac {y'}{c_{t_0}}v_{t_0}\in {\mathrm {L}}_{o,v_{t_0}}$
. Note that
![]() $w - v(-m)\in {\mathrm {L}}_{O, \, v_{t_1}}$
is lying on the hyperboloid
$w - v(-m)\in {\mathrm {L}}_{O, \, v_{t_1}}$
is lying on the hyperboloid
Then one can see that
![]() $y'<\tilde c-1$
if
$y'<\tilde c-1$
if
that is,
Plugging the coordinates of
![]() $v_{t_0}$
into Equation (7.11) and simplify all the terms, one can obtain a quadratic inequality of
$v_{t_0}$
into Equation (7.11) and simplify all the terms, one can obtain a quadratic inequality of
![]() $t_0$
and one can easily see that Equation (7.11) holds if
$t_0$
and one can easily see that Equation (7.11) holds if
 $$\begin{align*}t_0 < \frac{(2-\tilde{c})(\tilde{c}^2 g -r\tilde{s})}{ \tilde{c}[r\tilde{s}-r^2-s\tilde{s}+(2-\tilde{c})g(c+\tilde{c}) ] + r^2+s\tilde{s} -(c+2) r\tilde{s}}. \end{align*}$$
$$\begin{align*}t_0 < \frac{(2-\tilde{c})(\tilde{c}^2 g -r\tilde{s})}{ \tilde{c}[r\tilde{s}-r^2-s\tilde{s}+(2-\tilde{c})g(c+\tilde{c}) ] + r^2+s\tilde{s} -(c+2) r\tilde{s}}. \end{align*}$$
Using the upper bound of
![]() $t_0$
given in Equation (7.7), we are reduced to check
$t_0$
given in Equation (7.7), we are reduced to check
After further simplification and reduction, the inequality above becomes
The right-hand side can be estimated as below
 $$ \begin{align} \begin{aligned} \mathrm{RHS}&> r^2+ s\tilde s+2\tilde c g-(\tilde c+c-2)(\tilde c^2 g-r\tilde s)\\ &= r^2+ s\tilde s +2\tilde c g+(mr+2-2c) (\tilde c^2+\frac{v^2}{2})\\ & > r^2+s\tilde s +2\tilde c g-r (\tilde c^2+r)\\ &\geq (\frac{(g-1)c^2}{r}-1)(\frac{(g-1)\tilde{c}^2}{r}-1) +2\tilde c g-r\tilde c^2 \\ &>0.\\[-16pt] \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathrm{RHS}&> r^2+ s\tilde s+2\tilde c g-(\tilde c+c-2)(\tilde c^2 g-r\tilde s)\\ &= r^2+ s\tilde s +2\tilde c g+(mr+2-2c) (\tilde c^2+\frac{v^2}{2})\\ & > r^2+s\tilde s +2\tilde c g-r (\tilde c^2+r)\\ &\geq (\frac{(g-1)c^2}{r}-1)(\frac{(g-1)\tilde{c}^2}{r}-1) +2\tilde c g-r\tilde c^2 \\ &>0.\\[-16pt] \end{aligned} \end{align} $$
8 Proof of the main theorems
We now prove our main theorems by finding suitable Mukai vectors
![]() $v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying the conditions in Theorem 7.2 and Theorem 7.3, respectively.
$v\in {\mathrm {H}}_{\text {alg}}^{*}(X)$
satisfying the conditions in Theorem 7.2 and Theorem 7.3, respectively.
Proof of Theorem 1.1
As the case of
![]() $m=1$
is already known, we may always assume
$m=1$
is already known, we may always assume
![]() $m>1$
. There will be two cases:
$m>1$
. There will be two cases:
-
(i) If
 $(g,m)\neq (7,2)$
, we can choose the Mukai vector
$(g,m)\neq (7,2)$
, we can choose the Mukai vector
 $v=(g-1, k,k^2)$
with k given in the Table 1.
$v=(g-1, k,k^2)$
with k given in the Table 1.Table 1 Choices of Mukai vectors.

Note that when
 $g\geq 8$
, we have
$g\geq 8$
, we have  $$ \begin{align*}k=\min\left\{k_0~ |~k_0>\frac{g}{2},\gcd(g-1,k_0)=1\right\} < g-2.\end{align*} $$
$$ \begin{align*}k=\min\left\{k_0~ |~k_0>\frac{g}{2},\gcd(g-1,k_0)=1\right\} < g-2.\end{align*} $$
By a direct computation, one can easily see that the values of k and m in Table 1 satisfy the special surjectivity condition (✶✶†) given in Theorem 6.3. This ensure the restriction map
 $\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is surjective. The assertion follows from Theorem 7.2 as it satisfies the condition (✶✶✶). Indeed, the only nontrivial condition one needs to check is
$\psi :\mathbf {M}(v)\to {\mathbf {BN}}_C(v)$
is surjective. The assertion follows from Theorem 7.2 as it satisfies the condition (✶✶✶). Indeed, the only nontrivial condition one needs to check is  $$ \begin{align*}m>1+\frac{k^2}{(g-1)(k-1)}.\end{align*} $$
$$ \begin{align*}m>1+\frac{k^2}{(g-1)(k-1)}.\end{align*} $$
-
(ii) If
 $(g,m)=(7,2)$
, Theorem 6.3 cannot be applied because primitive Mukai vectors of the form
$(g,m)=(7,2)$
, Theorem 6.3 cannot be applied because primitive Mukai vectors of the form
 $(6,k,k^2)$
do not satisfy the assumptions in Theorem 6.3. However, we can choose
$(6,k,k^2)$
do not satisfy the assumptions in Theorem 6.3. However, we can choose
 $v=(2,1,3)$
, and the assertion can be concluded by the following result.
$v=(2,1,3)$
, and the assertion can be concluded by the following result.
Proposition 8.1. Suppose
![]() $g=7$
. The restriction map
$g=7$
. The restriction map
![]() $\psi :\mathbf {M}(2,1,3)\to {\mathbf {BN}}_C(2,1,3)$
is an isomorphism for any irreducible curve
$\psi :\mathbf {M}(2,1,3)\to {\mathbf {BN}}_C(2,1,3)$
is an isomorphism for any irreducible curve
![]() $C\in |2H|$
.
$C\in |2H|$
.
Proof. Note that v satisfies the injectivity condition (✶),
![]() $\psi $
is an injective morphism with stable image. It also satisfies the condition (✶✶✶). Due to Theorem 7.2, it suffices to show that
$\psi $
is an injective morphism with stable image. It also satisfies the condition (✶✶✶). Due to Theorem 7.2, it suffices to show that
![]() $\psi $
is surjective. The idea is to use Theorem 5.3. Suppose one has
$\psi $
is surjective. The idea is to use Theorem 5.3. Suppose one has
for some
![]() $F\in {\mathbf {BN}}_C(v)$
. A direct computation shows
$F\in {\mathbf {BN}}_C(v)$
. A direct computation shows
![]() ${\mathbf {P}}_v$
is at least
${\mathbf {P}}_v$
is at least
![]() $2$
-sharp. Then either
$2$
-sharp. Then either
![]() ${\mathbf {P}}_{i_*F}$
lies inside the polygon
${\mathbf {P}}_{i_*F}$
lies inside the polygon
![]() ${\mathbf {P}}_{0 z_1^{+2} z^{\prime }_2 z_2}$
, or it has
${\mathbf {P}}_{0 z_1^{+2} z^{\prime }_2 z_2}$
, or it has
![]() $z_1^{+1}$
as a vertex. For the first case, one has
$z_1^{+1}$
as a vertex. For the first case, one has
 $$ \begin{align*} \hbar- \|i_\ast F\| &> \|z_1- z^{\prime}_1\|-\|z^{\prime}_1- z_1^{+2}\|+ \|z_1- z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+2}\| \\ &=\frac{\sqrt{877}}{3}-\frac{\sqrt{613}}{3} \\&> \sqrt{29}+\sqrt{877}-34 ={\hbar+ \chi} - 10 \end{align*} $$
$$ \begin{align*} \hbar- \|i_\ast F\| &> \|z_1- z^{\prime}_1\|-\|z^{\prime}_1- z_1^{+2}\|+ \|z_1- z^{\prime}_2\|-\|z^{\prime}_2- z_1^{+2}\| \\ &=\frac{\sqrt{877}}{3}-\frac{\sqrt{613}}{3} \\&> \sqrt{29}+\sqrt{877}-34 ={\hbar+ \chi} - 10 \end{align*} $$
which contradicts Equation (5.18). For the second case, it forces
![]() $\overline Z(\widetilde {E}_1)=z_1^{+1}$
and hence
$\overline Z(\widetilde {E}_1)=z_1^{+1}$
and hence
However, we have
 $$ \begin{align*} \begin{aligned} \frac{\hbar-(\|z_1^{+1} -z^{\prime}_2\|+\|z^{\prime}_2- z_2\|)}{2}-\lfloor \frac{\ell( z_1^{+1})}{2} \rfloor&= \frac{1}{6} \left(\sqrt{877}-4 \sqrt{46}\right)+\frac{\sqrt{7}}{2}-1 \\&> \frac{1}{2} \left(\sqrt{29}+\sqrt{877}-34\right)\\&= \frac{\hbar+\chi}{2}-5 \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{\hbar-(\|z_1^{+1} -z^{\prime}_2\|+\|z^{\prime}_2- z_2\|)}{2}-\lfloor \frac{\ell( z_1^{+1})}{2} \rfloor&= \frac{1}{6} \left(\sqrt{877}-4 \sqrt{46}\right)+\frac{\sqrt{7}}{2}-1 \\&> \frac{1}{2} \left(\sqrt{29}+\sqrt{877}-34\right)\\&= \frac{\hbar+\chi}{2}-5 \end{aligned} \end{align*} $$
which is impossible. It follows from Theorem 5.3 that
![]() $\psi $
is surjective.
$\psi $
is surjective.
Proof of Theorem 1.2
By Corollary 5.7, for each
![]() $n>0$
, we need to find a positive Mukai vectors
$n>0$
, we need to find a positive Mukai vectors
![]() $v=(r,c,s)$
with
$v=(r,c,s)$
with
![]() $v^2=c^2(2g-2)-2rs=2n$
satisfying conditions (✶) and (✶✶), that is,
$v^2=c^2(2g-2)-2rs=2n$
satisfying conditions (✶) and (✶✶), that is,
A key tool is
Lemma 8.2. For each n, there is an integer
![]() $N=N(n)$
such that for
$N=N(n)$
such that for
![]() $g>N$
, one can find a prime number p satisfying that
$g>N$
, one can find a prime number p satisfying that
-
(i)
 $n+1<p<\frac {\sqrt {g-1}}{2}$
and
$n+1<p<\frac {\sqrt {g-1}}{2}$
and
 $\gcd (p, 8(g-1)n)=1$
,
$\gcd (p, 8(g-1)n)=1$
, -
(ii) the equation
 $x^2\equiv (g-1)n\ \mod p$
has a solution.
$x^2\equiv (g-1)n\ \mod p$
has a solution.
Proof. The idea is to use the bound for prime character nonresidues. In [Reference Pollack19, Theorem 1.3], it has been proved that there exists an integer
![]() $m_0$
with the property: if
$m_0$
with the property: if
![]() $j> j_0$
and
$j> j_0$
and
![]() $\chi $
is a quadratic character modulo j, there are at least
$\chi $
is a quadratic character modulo j, there are at least
![]() $\log (j)$
primes
$\log (j)$
primes
![]() $\ell \leq \sqrt [3]{j}$
with
$\ell \leq \sqrt [3]{j}$
with
![]() $\chi (\ell )= 1$
. Choose N to be the minimal integer satisfying
$\chi (\ell )= 1$
. Choose N to be the minimal integer satisfying
-
•
 $8(N-1)n\geq j_0$
,
$8(N-1)n\geq j_0$
, -
• the
 $\lfloor \log (8(N-1)n)\rfloor $
-th prime number
$\lfloor \log (8(N-1)n)\rfloor $
-th prime number
 $>n+1$
,
$>n+1$
, -
•
 $\sqrt [3]{8(N-1)n}\leq \frac {\sqrt {N-1}}{2}$
.
$\sqrt [3]{8(N-1)n}\leq \frac {\sqrt {N-1}}{2}$
.
Clearly, N only depends on n. For
![]() $g>N$
, we write
$g>N$
, we write
 $$ \begin{align*}(g-1)n=a^2\prod_{i=1}^k q_i ,\end{align*} $$
$$ \begin{align*}(g-1)n=a^2\prod_{i=1}^k q_i ,\end{align*} $$
where
![]() $q_i$
are distinct primes. Let
$q_i$
are distinct primes. Let
![]() $\chi _i$
be the character defined by
$\chi _i$
be the character defined by
 $$ \begin{align*}\chi_i(d)= \left( \frac{d }{q_i}\right)(-1)^{\frac{(d-1)(q_i-1)}{4}}\end{align*} $$
$$ \begin{align*}\chi_i(d)= \left( \frac{d }{q_i}\right)(-1)^{\frac{(d-1)(q_i-1)}{4}}\end{align*} $$
if
![]() $q_i$
is odd and
$q_i$
is odd and
![]() $\chi _i(d)=(-1)^{\frac {d^2-1}{8}}$
if
$\chi _i(d)=(-1)^{\frac {d^2-1}{8}}$
if
![]() $q_i=2$
. Consider the quadratic character
$q_i=2$
. Consider the quadratic character
 $$ \begin{align*}\chi(d)=\prod_{i=1}^k \chi_i(d)\end{align*} $$
$$ \begin{align*}\chi(d)=\prod_{i=1}^k \chi_i(d)\end{align*} $$
modulo
![]() $8(g-1)n$
. As
$8(g-1)n$
. As
![]() $8(g-1)n>N\geq j_0$
, there exists a prime p such that
$8(g-1)n>N\geq j_0$
, there exists a prime p such that
![]() $\chi (p)=1$
and
$\chi (p)=1$
and
Moreover, one can compute the Jacobi symbol
 $$ \begin{align*}\left( \frac{n(g-1)}{p}\right)=\prod_{i=1}^k \left( \frac{q_i }{p}\right)=\prod_{i=1}^k \chi_i(p) =\chi(p)=1\end{align*} $$
$$ \begin{align*}\left( \frac{n(g-1)}{p}\right)=\prod_{i=1}^k \left( \frac{q_i }{p}\right)=\prod_{i=1}^k \chi_i(p) =\chi(p)=1\end{align*} $$
by the law of reciprocity. It follows that
![]() $x^2=(g-1)n\ \mod p$
has a solution.
$x^2=(g-1)n\ \mod p$
has a solution.
Due to Lemma 8.2, when
![]() $g>N(n)$
, we can find an odd prime p and an integer
$g>N(n)$
, we can find an odd prime p and an integer
![]() $0<c<p$
satisfying
$0<c<p$
satisfying
Here,
![]() $c(g-1)$
is actually a solution of the equation of
$c(g-1)$
is actually a solution of the equation of
![]() $x^2\equiv (g-1)n\ \mod p$
. Choose the Mukai vector
$x^2\equiv (g-1)n\ \mod p$
. Choose the Mukai vector
![]() $v=(p,c, \frac {c^2(g-1)-n}{p})$
, then we have
$v=(p,c, \frac {c^2(g-1)-n}{p})$
, then we have
and
 $$ \begin{align*}\frac{c^2(g-1)-n}{p}>\frac{4c^2p^2-p}{p}=4c^2p-1> pc,\end{align*} $$
$$ \begin{align*}\frac{c^2(g-1)-n}{p}>\frac{4c^2p^2-p}{p}=4c^2p-1> pc,\end{align*} $$
by Lemma 8.2 (i). The assertion then follows immediately.
Acknowledgements
The authors want to thank Yifeng Liu for very helpful discussions. The authors were supported by NSFC Grant (No. 12121001, 12171090 and 12425105) and Shanghai Pilot Program for Basic Research (No. 21TQ00). The first author was also supported by NKRD Program of China (No. 2020YFA0713200) and LNMS. This project was initiated from the workshop ‘Curves on K3 surfaces’ in June 2021 supported by NSFC General Program (No. 12171090).