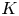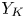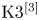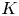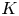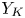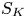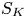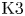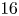1. Introduction
Together with manifolds of ![]() $\mathrm {K}3^{[n]}$ type, deformations of generalized Kummer varieties constitute the most well-studied hyper-Kähler manifolds. We refer to this deformation type in dimension
$\mathrm {K}3^{[n]}$ type, deformations of generalized Kummer varieties constitute the most well-studied hyper-Kähler manifolds. We refer to this deformation type in dimension ![]() $2n$ as to the
$2n$ as to the ![]() $\mathrm {Kum}^n$ type. After Beauville [Reference BeauvilleBea83] gave the first examples of such hyper-Kähler manifolds, many more have been constructed from moduli spaces of stable sheaves on abelian surfaces, see [Reference YoshiokaYos01]. However, the varieties so obtained always have Picard rank at least
$\mathrm {Kum}^n$ type. After Beauville [Reference BeauvilleBea83] gave the first examples of such hyper-Kähler manifolds, many more have been constructed from moduli spaces of stable sheaves on abelian surfaces, see [Reference YoshiokaYos01]. However, the varieties so obtained always have Picard rank at least ![]() $2$, and our understanding of a general projective variety of
$2$, and our understanding of a general projective variety of ![]() $\mathrm {Kum}^n$ type remains poor. In fact, for the time being, no construction of such variety is known (but see [Reference O'GradyO'Gr22] for some recent ideas).
$\mathrm {Kum}^n$ type remains poor. In fact, for the time being, no construction of such variety is known (but see [Reference O'GradyO'Gr22] for some recent ideas).
In the present article we partially remedy this for hyper-Kähler sixfolds of generalized Kummer type, by associating to any ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type a hyper-Kähler manifold
$\mathrm {Kum}^3$ type a hyper-Kähler manifold ![]() $Y_K$ of
$Y_K$ of ![]() $\mathrm {K}3^{[3]}$ type. They are related by a dominant rational map
$\mathrm {K}3^{[3]}$ type. They are related by a dominant rational map
of degree ![]() $2^5$, described as follows.
$2^5$, described as follows.
Any ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type admits an action of the group
$\mathrm {Kum}^3$ type admits an action of the group ![]() $( {\mathbb {Z}}/4 {\mathbb {Z}})^4\rtimes {\mathbb {Z}}/2 {\mathbb {Z}}$ by symplectic automorphisms, where
$( {\mathbb {Z}}/4 {\mathbb {Z}})^4\rtimes {\mathbb {Z}}/2 {\mathbb {Z}}$ by symplectic automorphisms, where ![]() $ {\mathbb {Z}}/2 {\mathbb {Z}}$ acts on the first factor as
$ {\mathbb {Z}}/2 {\mathbb {Z}}$ acts on the first factor as ![]() $-1$. In fact, this is the group
$-1$. In fact, this is the group ![]() $\operatorname {Aut}_0(K)$ of automorphisms of
$\operatorname {Aut}_0(K)$ of automorphisms of ![]() $K$ which act trivially on its second cohomology, which is deformation invariant by [Reference Hassett and TschinkelHT13]. It has been computed in [Reference Boissière, Nieper-Wißkirchen and SartiBNS11] for the generalized Kummer variety associated to an abelian surface. We let
$K$ which act trivially on its second cohomology, which is deformation invariant by [Reference Hassett and TschinkelHT13]. It has been computed in [Reference Boissière, Nieper-Wißkirchen and SartiBNS11] for the generalized Kummer variety associated to an abelian surface. We let ![]() $G\subset \operatorname {Aut}_0(K)$ be the subgroup generated by the automorphisms whose fixed locus contains a
$G\subset \operatorname {Aut}_0(K)$ be the subgroup generated by the automorphisms whose fixed locus contains a ![]() $4$-dimensional component. We will show in Lemma 2.4 that
$4$-dimensional component. We will show in Lemma 2.4 that
Theorem 1.1 Let ![]() $K$ be a manifold of
$K$ be a manifold of ![]() $\mathrm {Kum}^3$ type. The quotient
$\mathrm {Kum}^3$ type. The quotient ![]() $K/G$ admits a resolution
$K/G$ admits a resolution ![]() $Y_K\to K/G$ with
$Y_K\to K/G$ with ![]() $Y_K$ a manifold of
$Y_K$ a manifold of ![]() $\mathrm {K}3^{[3]}$ type.
$\mathrm {K}3^{[3]}$ type.
The resolution ![]() $Y_K\to K/G$ is obtained via a single blow-up of the reduced singular locus. It can also be described as the quotient by
$Y_K\to K/G$ is obtained via a single blow-up of the reduced singular locus. It can also be described as the quotient by ![]() $G$ of the blow-up of
$G$ of the blow-up of ![]() $K$ at the union of the fixed loci of all non-trivial automorphisms in
$K$ at the union of the fixed loci of all non-trivial automorphisms in ![]() $G$. We show that there is an isometry of transcendental Hodge structures
$G$. We show that there is an isometry of transcendental Hodge structures
where on the right-hand side the form is multiplied by ![]() $2$. This parallels the classical construction of the Kummer
$2$. This parallels the classical construction of the Kummer ![]() $\mathrm {K}3$ surface
$\mathrm {K}3$ surface ![]() $\operatorname {\mathrm {Km}}(A)$ associated to an abelian surface
$\operatorname {\mathrm {Km}}(A)$ associated to an abelian surface ![]() $A$, where
$A$, where ![]() $H^2_{\mathrm {tr}}(\operatorname {\mathrm {Km}}(A), {\mathbb {Z}})$ is Hodge isometric to
$H^2_{\mathrm {tr}}(\operatorname {\mathrm {Km}}(A), {\mathbb {Z}})$ is Hodge isometric to ![]() $H^2_{\mathrm {tr}}(A, {\mathbb {Z}})(2)$. The study of the integral transcendental lattices of the manifolds
$H^2_{\mathrm {tr}}(A, {\mathbb {Z}})(2)$. The study of the integral transcendental lattices of the manifolds ![]() $Y_K$ will be the subject of future work.
$Y_K$ will be the subject of future work.
As a consequence, we obtain a well-defined ![]() $\mathrm {K}3$ surface associated to any projective sixfold of generalized Kummer type.
$\mathrm {K}3$ surface associated to any projective sixfold of generalized Kummer type.
Theorem 1.2 Let ![]() $K$ be a projective variety of
$K$ be a projective variety of ![]() $\mathrm {Kum}^3$ type. There exists a unique (up to isomorphism) projective
$\mathrm {Kum}^3$ type. There exists a unique (up to isomorphism) projective ![]() $\mathrm {K}3$ surface
$\mathrm {K}3$ surface ![]() $S_K$ such that the variety
$S_K$ such that the variety ![]() $Y_K$ of
$Y_K$ of ![]() $\mathrm {K}3^{[3]}$ type given by Theorem 1.1 is birational to a moduli space
$\mathrm {K}3^{[3]}$ type given by Theorem 1.1 is birational to a moduli space ![]() $M_{S_K, H}(v)$ of stable sheaves on
$M_{S_K, H}(v)$ of stable sheaves on ![]() $S_K$, for some primitive Mukai vector
$S_K$, for some primitive Mukai vector ![]() $v$ and a
$v$ and a ![]() $v$-generic polarization
$v$-generic polarization ![]() $H$.
$H$.
We call ![]() $S_K$ the
$S_K$ the ![]() $\mathrm {K}3$ surface associated to the sixfold
$\mathrm {K}3$ surface associated to the sixfold ![]() $K$. It is characterized by the existence of a Hodge isometry
$K$. It is characterized by the existence of a Hodge isometry ![]() $H^2_{\mathrm {tr}}(S_K, {\mathbb {Z}})\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. These surfaces come in countably many
$H^2_{\mathrm {tr}}(S_K, {\mathbb {Z}})\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. These surfaces come in countably many ![]() $4$-dimensional families of general Picard rank
$4$-dimensional families of general Picard rank ![]() $16$; up to isogeny, they are the K3 surfaces
$16$; up to isogeny, they are the K3 surfaces ![]() $S$ admitting an isometric embedding
$S$ admitting an isometric embedding ![]() $H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\hookrightarrow \Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ of rational quadratic spaces. Here,
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\hookrightarrow \Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ of rational quadratic spaces. Here, ![]() $\Lambda _{\mathrm {Kum}^3}$ is the lattice which is the second cohomology of manifolds of
$\Lambda _{\mathrm {Kum}^3}$ is the lattice which is the second cohomology of manifolds of ![]() $\mathrm {Kum}^3$ type; it was computed in [Reference BeauvilleBea83] that
$\mathrm {Kum}^3$ type; it was computed in [Reference BeauvilleBea83] that ![]() $\Lambda _{\mathrm {Kum}^3}=U^{\oplus 3}\oplus \langle -8 \rangle$, where we denote by
$\Lambda _{\mathrm {Kum}^3}=U^{\oplus 3}\oplus \langle -8 \rangle$, where we denote by ![]() $U$ the hyperbolic plane.
$U$ the hyperbolic plane.
Applications
In a series of papers [Reference MarkmanMar20, Reference MarkmanMar22, Reference MarkmanMar23], Markman has proven striking results on the Hodge conjecture for hyper-Kähler varieties of ![]() $\mathrm {Kum}^n$ and
$\mathrm {Kum}^n$ and ![]() $\mathrm {K}3^{[n]}$ type. He uses Verbitsky's theory of hyperholomorphic sheaves [Reference VerbitskyVer96] to produce very interesting algebraic cycles on general projective hyper-Kähler varieties via deformation. Through our construction, we are able to deduce more cases of the Hodge conjecture from his results.
$\mathrm {K}3^{[n]}$ type. He uses Verbitsky's theory of hyperholomorphic sheaves [Reference VerbitskyVer96] to produce very interesting algebraic cycles on general projective hyper-Kähler varieties via deformation. Through our construction, we are able to deduce more cases of the Hodge conjecture from his results.
Our main application is to the Kuga–Satake Hodge conjecture for ![]() $\mathrm {K}3$ surfaces [Reference van GeemenvGe00]. The Kuga–Satake construction [Reference DeligneDel71] associates via Hodge theory an abelian variety
$\mathrm {K}3$ surfaces [Reference van GeemenvGe00]. The Kuga–Satake construction [Reference DeligneDel71] associates via Hodge theory an abelian variety ![]() $\mathrm {KS}(S)$ to any projective K3 surface
$\mathrm {KS}(S)$ to any projective K3 surface ![]() $S$, and the conjecture predicts the existence of an algebraic cycle inducing an embedding of the transcendental Hodge structure of the surface into the second cohomology of
$S$, and the conjecture predicts the existence of an algebraic cycle inducing an embedding of the transcendental Hodge structure of the surface into the second cohomology of ![]() $\mathrm {KS}(S)\times \mathrm {KS}(S)$. It is known to hold in many cases for
$\mathrm {KS}(S)\times \mathrm {KS}(S)$. It is known to hold in many cases for ![]() $\mathrm {K}3$ surfaces of Picard number at least
$\mathrm {K}3$ surfaces of Picard number at least ![]() $17$ (see [Reference MorrisonMor85]), but it is wide open otherwise. There are a couple of families of
$17$ (see [Reference MorrisonMor85]), but it is wide open otherwise. There are a couple of families of ![]() $\mathrm {K}3$ surfaces of general Picard rank
$\mathrm {K}3$ surfaces of general Picard rank ![]() $16$ for which the conjecture is known, namely, the family of double covers of the plane branched at six lines [Reference ParanjapePar88] and the family of K3 surfaces with
$16$ for which the conjecture is known, namely, the family of double covers of the plane branched at six lines [Reference ParanjapePar88] and the family of K3 surfaces with ![]() $15$ nodes in
$15$ nodes in ![]() $ {\mathbb {P}}^4$ (see [Reference Ingalls, Logan and PatashnickILP22]).
$ {\mathbb {P}}^4$ (see [Reference Ingalls, Logan and PatashnickILP22]).
Theorem 1.3 gives infinitely many new families of K3 surfaces of general Picard rank ![]() $16$ for which the Kuga–Satake Hodge conjecture holds true.
$16$ for which the Kuga–Satake Hodge conjecture holds true.
Theorem 1.3 Let ![]() $S$ be a projective
$S$ be a projective ![]() $\mathrm {K}3$ surface such that there exists an isometric embedding of
$\mathrm {K}3$ surface such that there exists an isometric embedding of ![]() $H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ into
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ into ![]() $\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$, where
$\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$, where ![]() $(2)$ indicates that the form is multiplied by
$(2)$ indicates that the form is multiplied by ![]() $2$. Then, there exists an algebraic cycle
$2$. Then, there exists an algebraic cycle ![]() $\gamma$ on
$\gamma$ on ![]() $S\times \mathrm {KS}(S)\times \mathrm {KS}(S)$ inducing an embedding
$S\times \mathrm {KS}(S)\times \mathrm {KS}(S)$ inducing an embedding ![]() $\gamma _*\colon H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\hookrightarrow H^2(\mathrm {KS}(S)\times \mathrm {KS}(S), {\mathbb {Q}})$ of rational Hodge structures.
$\gamma _*\colon H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\hookrightarrow H^2(\mathrm {KS}(S)\times \mathrm {KS}(S), {\mathbb {Q}})$ of rational Hodge structures.
Via Theorem 1.2, we deduce this statement from the validity of the Kuga–Satake Hodge conjecture for varieties of ![]() $\mathrm {Kum}^n$ type, established by Voisin [Reference VoisinVoi22] as a consequence of results of O'Grady [Reference O'GradyO'Gr21] and Markman [Reference MarkmanMar23]. Once Theorem 1.3 is proven, a result of Varesco [Reference VarescoVar22] implies that the Hodge conjecture holds for all powers of any K3 surface satisfying the assumption of the above theorem, see Corollary 5.8.
$\mathrm {Kum}^n$ type, established by Voisin [Reference VoisinVoi22] as a consequence of results of O'Grady [Reference O'GradyO'Gr21] and Markman [Reference MarkmanMar23]. Once Theorem 1.3 is proven, a result of Varesco [Reference VarescoVar22] implies that the Hodge conjecture holds for all powers of any K3 surface satisfying the assumption of the above theorem, see Corollary 5.8.
In the recent preprint [Reference MarkmanMar22], Markman proves that any rational Hodge isometry ![]() $H^2(X, {\mathbb {Q}})\xrightarrow { \ \sim \ } H^2(X', {\mathbb {Q}})$ between varieties of
$H^2(X, {\mathbb {Q}})\xrightarrow { \ \sim \ } H^2(X', {\mathbb {Q}})$ between varieties of ![]() $\mathrm {K}3^{[n]}$ type is algebraic. He expects that an extension of his argument will lead to the analogous result for varieties of
$\mathrm {K}3^{[n]}$ type is algebraic. He expects that an extension of his argument will lead to the analogous result for varieties of ![]() $\mathrm {Kum}^n$ type. In dimension
$\mathrm {Kum}^n$ type. In dimension ![]() $6$, we can obtain it from the
$6$, we can obtain it from the ![]() $\mathrm {K}3^{[3]}$ case via Theorem 1.1.
$\mathrm {K}3^{[3]}$ case via Theorem 1.1.
Theorem 1.4 Let ![]() $K, K'$ be projective varieties of deformation type
$K, K'$ be projective varieties of deformation type ![]() $\mathrm {Kum}^3$. Let
$\mathrm {Kum}^3$. Let
be a Hodge isometry. Then ![]() $f$ is induced by an algebraic correspondence.
$f$ is induced by an algebraic correspondence.
Overview of the contents
We sketch the proof of Theorem 1.1. First, we calculate the fixed loci ![]() $K^g$ of all the automorphisms
$K^g$ of all the automorphisms ![]() $g\in G$: we show that
$g\in G$: we show that ![]() $\bigcup _{g\neq 1 \in G} K^g$ is the union of
$\bigcup _{g\neq 1 \in G} K^g$ is the union of ![]() $16$ hyper-Kähler manifolds of
$16$ hyper-Kähler manifolds of ![]() $\mathrm {K}3^{[2]}$ type, and we determine the various intersections of these components. Thanks to the deformation invariance of
$\mathrm {K}3^{[2]}$ type, and we determine the various intersections of these components. Thanks to the deformation invariance of ![]() $G$, it is in fact enough to calculate these loci in the special case of the generalized Kummer sixfold on an abelian surface.
$G$, it is in fact enough to calculate these loci in the special case of the generalized Kummer sixfold on an abelian surface.
We then describe explicitly the singularities of ![]() $K/G$. It turns out that these are of a particular simple nature, modeled on products of ordinary double points on surfaces. A resolution
$K/G$. It turns out that these are of a particular simple nature, modeled on products of ordinary double points on surfaces. A resolution ![]() $Y_K$ of
$Y_K$ of ![]() $K/G$ is obtained via a single blow-up of the singular locus. The quotient
$K/G$ is obtained via a single blow-up of the singular locus. The quotient ![]() $K/G$ is a primitive symplectic orbifold as studied by Fujiki [Reference FujikiFuj83] and Menet [Reference MenetMen20], and we use a criterion due to Fujiki to prove that
$K/G$ is a primitive symplectic orbifold as studied by Fujiki [Reference FujikiFuj83] and Menet [Reference MenetMen20], and we use a criterion due to Fujiki to prove that ![]() $Y_K$ is a hyper-Kähler manifold. Moreover, the resolution can be performed in families, so that the
$Y_K$ is a hyper-Kähler manifold. Moreover, the resolution can be performed in families, so that the ![]() $Y_K$ are deformation equivalent to each other. To complete the proof of Theorem 1.1 it is therefore sufficient to find a single
$Y_K$ are deformation equivalent to each other. To complete the proof of Theorem 1.1 it is therefore sufficient to find a single ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type such that
$\mathrm {Kum}^3$ type such that ![]() $Y_K$ is of
$Y_K$ is of ![]() $\mathrm {K}3^{[3]}$ type.
$\mathrm {K}3^{[3]}$ type.
The specific example we study is a Beauville–Mukai system ![]() $K_J(v_3)$ on a general principally polarized abelian surface
$K_J(v_3)$ on a general principally polarized abelian surface ![]() $\Theta \subset J$. It admits a Lagrangian fibration to the linear system
$\Theta \subset J$. It admits a Lagrangian fibration to the linear system ![]() $|2\Theta |= {\mathbb {P}}^3$, whose general fibres parametrize certain degree-
$|2\Theta |= {\mathbb {P}}^3$, whose general fibres parametrize certain degree-![]() $3$ line bundles supported on curves in the linear system. We show that the norm map for line bundles induces a dominant rational map of degree
$3$ line bundles supported on curves in the linear system. We show that the norm map for line bundles induces a dominant rational map of degree ![]() $2^5$ from
$2^5$ from ![]() $K_J(v_3)$ onto a Beauville–Mukai system
$K_J(v_3)$ onto a Beauville–Mukai system ![]() $M_{\operatorname {\mathrm {Km}}(J)}(w_3)$, a moduli space of sheaves on the Kummer
$M_{\operatorname {\mathrm {Km}}(J)}(w_3)$, a moduli space of sheaves on the Kummer ![]() $\mathrm {K}3$ surface
$\mathrm {K}3$ surface ![]() $\operatorname {\mathrm {Km}}(J)$ associated to
$\operatorname {\mathrm {Km}}(J)$ associated to ![]() $J$; the hyper-Kähler variety
$J$; the hyper-Kähler variety ![]() $M_{\operatorname {\mathrm {Km}}(J)}(w_3)$ is birational to
$M_{\operatorname {\mathrm {Km}}(J)}(w_3)$ is birational to ![]() ${\operatorname {\mathrm {Km}}(J)}^{[3]}$. We next prove that the norm map descends to a birational map
${\operatorname {\mathrm {Km}}(J)}^{[3]}$. We next prove that the norm map descends to a birational map
It follows that the hyper-Kähler manifold ![]() $Y_{K_J(v_3)}$ is birational to
$Y_{K_J(v_3)}$ is birational to ![]() $\mathrm {Km}(J)^{[3]}$, and hence
$\mathrm {Km}(J)^{[3]}$, and hence ![]() $Y_{K_J(v_3)}$ is of
$Y_{K_J(v_3)}$ is of ![]() $\mathrm {K}3^{[3]}$ type by Huybrechts’ theorem [Reference HuybrechtsHuy99] that birational hyper-Kähler manifolds are deformation equivalent.
$\mathrm {K}3^{[3]}$ type by Huybrechts’ theorem [Reference HuybrechtsHuy99] that birational hyper-Kähler manifolds are deformation equivalent.
Once Theorem 1.1 is proven, the other results follow from it. When ![]() $K$ is projective, we define the associated
$K$ is projective, we define the associated ![]() $\mathrm {K}3$ surface
$\mathrm {K}3$ surface ![]() $S_K$ as the unique (up to isomorphism)
$S_K$ as the unique (up to isomorphism) ![]() $\mathrm {K}3$ surface whose transcendental lattice is Hodge isometric to
$\mathrm {K}3$ surface whose transcendental lattice is Hodge isometric to ![]() $H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. This is justified by the fact that
$H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. This is justified by the fact that ![]() $H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ has rank at most
$H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ has rank at most ![]() $6$ and, hence, it appears as transcendental lattice of some
$6$ and, hence, it appears as transcendental lattice of some ![]() $\mathrm {K}3$ surface of Picard rank at least
$\mathrm {K}3$ surface of Picard rank at least ![]() $16$. Moreover, for such Picard numbers, two
$16$. Moreover, for such Picard numbers, two ![]() $\mathrm {K}3$ surfaces with Hodge isometric transcendental lattices are isomorphic; therefore,
$\mathrm {K}3$ surfaces with Hodge isometric transcendental lattices are isomorphic; therefore, ![]() $S_K$ is determined up to isomorphism. To prove our applications, we exploit the algebraic cycle in
$S_K$ is determined up to isomorphism. To prove our applications, we exploit the algebraic cycle in ![]() $K\times Y_K$ given by the rational map
$K\times Y_K$ given by the rational map ![]() $K\dashrightarrow Y_K$.
$K\dashrightarrow Y_K$.
The organization of this text is as follows. In § 2 we calculate the fixed loci of the automorphisms of ![]() $G$. In § 3 we study in detail the case of
$G$. In § 3 we study in detail the case of ![]() $K_J(v_3)$ as outlined above. In § 4 we prove Theorems 1.1 and 1.2. Finally, in § 5 we use our construction to prove Theorems 1.3 and 1.4.
$K_J(v_3)$ as outlined above. In § 4 we prove Theorems 1.1 and 1.2. Finally, in § 5 we use our construction to prove Theorems 1.3 and 1.4.
2. Automorphisms trivial on the second cohomology
Let ![]() $K$ be a manifold of
$K$ be a manifold of ![]() $\mathrm {Kum}^3$ type and let
$\mathrm {Kum}^3$ type and let ![]() $\operatorname {Aut}_0(K)$ be the group of automorphisms of
$\operatorname {Aut}_0(K)$ be the group of automorphisms of ![]() $K$ which act trivially on
$K$ which act trivially on ![]() $H^2(K, {\mathbb {Z}})$. We let
$H^2(K, {\mathbb {Z}})$. We let ![]() $K^h$ denote the fixed locus of an automorphism
$K^h$ denote the fixed locus of an automorphism ![]() $h$ of
$h$ of ![]() $K$.
$K$.
Definition 2.1 We denote by ![]() $G$ the subgroup of
$G$ the subgroup of ![]() $\operatorname {Aut}_0(K)$ generated by the automorphisms
$\operatorname {Aut}_0(K)$ generated by the automorphisms ![]() $g\in \operatorname {Aut}_0(K)$ such that
$g\in \operatorname {Aut}_0(K)$ such that ![]() $K^g$ has a
$K^g$ has a ![]() $4$-dimensional component.
$4$-dimensional component.
We will see in Lemma 2.4 that ![]() $G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$. The main result proven in this section is then the following.
$G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$. The main result proven in this section is then the following.
Theorem 2.2 Let ![]() $Z\subset K$ be defined as
$Z\subset K$ be defined as ![]() $Z:= \bigcup _{g\neq 1\in G} K^{g}$. Then
$Z:= \bigcup _{g\neq 1\in G} K^{g}$. Then ![]() $Z$ is the union of
$Z$ is the union of ![]() $16$ fourfolds
$16$ fourfolds ![]() $Z_j$, each of which is a smooth hyper-Kähler manifold of
$Z_j$, each of which is a smooth hyper-Kähler manifold of ![]() $\mathrm {K}3^{[2]}$ type. Moreover, two distinct components intersect in a K3 surface, three distinct components intersect in four points, and four or more distinct components do not intersect.
$\mathrm {K}3^{[2]}$ type. Moreover, two distinct components intersect in a K3 surface, three distinct components intersect in four points, and four or more distinct components do not intersect.
In order to prove this, we will compute the fixed loci of all automorphisms in ![]() $G$. Thanks to the deformation invariance of automorphisms trivial on the second cohomology it will be sufficient to treat the case of the generalized Kummer variety associated to an abelian surface
$G$. Thanks to the deformation invariance of automorphisms trivial on the second cohomology it will be sufficient to treat the case of the generalized Kummer variety associated to an abelian surface ![]() $A$, i.e.
$A$, i.e. ![]() $K$ is the fibre over
$K$ is the fibre over ![]() $0$ of the composition
$0$ of the composition
of the Hilbert–Chow morphism with the summation map. We denote by ![]() $A^{(4)}_0\subset A^{(4)}$ the fibre over
$A^{(4)}_0\subset A^{(4)}$ the fibre over ![]() $0$ of
$0$ of ![]() $\sum$. The restriction
$\sum$. The restriction ![]() $\nu \colon K\to A^{(4)}_0$ is a crepant resolution.
$\nu \colon K\to A^{(4)}_0$ is a crepant resolution.
In this case the group of automorphisms of ![]() $K$ acting trivially on the second cohomology has the natural description
$K$ acting trivially on the second cohomology has the natural description ![]() $\operatorname {Aut}_0(K) = A_4 \rtimes \langle -1 \rangle,$ and the action on
$\operatorname {Aut}_0(K) = A_4 \rtimes \langle -1 \rangle,$ and the action on ![]() $K$ and
$K$ and ![]() $A^{[4]}$ is induced by that on
$A^{[4]}$ is induced by that on ![]() $A$, see [Reference Boissière, Nieper-Wißkirchen and SartiBNS11].
$A$, see [Reference Boissière, Nieper-Wißkirchen and SartiBNS11].
2.3 Notation
We let ![]() $A_n$ be the group of points of order
$A_n$ be the group of points of order ![]() $n$ of
$n$ of ![]() $A$. Via the isomorphism above, we write the elements of
$A$. Via the isomorphism above, we write the elements of ![]() $\operatorname {Aut}_0(K^3(A))$ as
$\operatorname {Aut}_0(K^3(A))$ as ![]() $(\epsilon, \pm 1)$ for
$(\epsilon, \pm 1)$ for ![]() $\epsilon \in A_4$. For
$\epsilon \in A_4$. For ![]() $\tau \in A_2$, we denote by
$\tau \in A_2$, we denote by ![]() $A_{2,\tau }$ the set
$A_{2,\tau }$ the set ![]() $\{a\in A \ | \ 2a=\tau \}$, which consists of
$\{a\in A \ | \ 2a=\tau \}$, which consists of ![]() $16$ points. The quotient surface
$16$ points. The quotient surface ![]() $A/\langle (\tau, -1) \rangle$ has
$A/\langle (\tau, -1) \rangle$ has ![]() $16$ nodes corresponding to points in
$16$ nodes corresponding to points in ![]() $A_{2,\tau }$; its minimal resolution
$A_{2,\tau }$; its minimal resolution ![]() $\operatorname {\mathrm {Km}}^{\tau }(A)$ is isomorphic to the Kummer
$\operatorname {\mathrm {Km}}^{\tau }(A)$ is isomorphic to the Kummer ![]() $\mathrm {K}3$ surface associated to
$\mathrm {K}3$ surface associated to ![]() $A$.
$A$.
Lemma 2.4 Let ![]() $K$ be any manifold of
$K$ be any manifold of ![]() $\mathrm {Kum}^3$ type. Then
$\mathrm {Kum}^3$ type. Then ![]() $G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$.
$G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$.
Proof. Since automorphisms in ![]() $\operatorname {Aut}_0(K)$ deform with
$\operatorname {Aut}_0(K)$ deform with ![]() $K$, their fixed loci deform as well. Therefore, it suffices to prove the lemma for the generalized Kummer variety
$K$, their fixed loci deform as well. Therefore, it suffices to prove the lemma for the generalized Kummer variety ![]() $K=K^3(A)$ on an abelian surface
$K=K^3(A)$ on an abelian surface ![]() $A$. In this case we show that
$A$. In this case we show that
We have ![]() $\operatorname {Aut}_0(K^3(A))= A_4\rtimes \langle -1\rangle$. If
$\operatorname {Aut}_0(K^3(A))= A_4\rtimes \langle -1\rangle$. If ![]() $h\in \operatorname {Aut}_0(K^3(A))$ is induced by translation by
$h\in \operatorname {Aut}_0(K^3(A))$ is induced by translation by ![]() $0\neq \epsilon \in A_4$, then, by [Reference OguisoOgu20, Lemma 3.5], the fixed locus
$0\neq \epsilon \in A_4$, then, by [Reference OguisoOgu20, Lemma 3.5], the fixed locus ![]() $(K^3(A))^h$ is a union of K3 surfaces if
$(K^3(A))^h$ is a union of K3 surfaces if ![]() $2\epsilon =0$ and consists of isolated point if
$2\epsilon =0$ and consists of isolated point if ![]() $2\epsilon \neq 0$. Consider now
$2\epsilon \neq 0$. Consider now ![]() $h=(\epsilon, -1)$. The fixed locus of
$h=(\epsilon, -1)$. The fixed locus of ![]() $h=(\epsilon, -1)$ on
$h=(\epsilon, -1)$ on ![]() $A^{(4)}$ consists of
$A^{(4)}$ consists of
and subvarieties of lower dimension. If ![]() $\epsilon \in A_2$, then
$\epsilon \in A_2$, then ![]() $W_{\epsilon }$ is contained in
$W_{\epsilon }$ is contained in ![]() $A^{(4)}_0$ and, hence,
$A^{(4)}_0$ and, hence, ![]() ${(\epsilon, -1)\in G}$. If
${(\epsilon, -1)\in G}$. If ![]() $\epsilon \notin A_2$, then
$\epsilon \notin A_2$, then ![]() $W_{\epsilon }$ has empty intersection with
$W_{\epsilon }$ has empty intersection with ![]() $A^{(4)}_0$; the action of
$A^{(4)}_0$; the action of ![]() $h$ on
$h$ on ![]() $A^{(4)}_0$ fixes isolated points and the surfaces
$A^{(4)}_0$ fixes isolated points and the surfaces ![]() $\{ (\alpha, b, -b-\epsilon, - \alpha + \epsilon ),\ b\in A\}$, where
$\{ (\alpha, b, -b-\epsilon, - \alpha + \epsilon ),\ b\in A\}$, where ![]() $\alpha \in A$ satisfies
$\alpha \in A$ satisfies ![]() $\alpha =-\alpha -\epsilon$. The general point of such a surface is supported on four distinct points. Therefore, the fixed locus
$\alpha =-\alpha -\epsilon$. The general point of such a surface is supported on four distinct points. Therefore, the fixed locus ![]() $(K^3(A))^h$ consists of surfaces and isolated points, because it is a union of symplectic varieties and the fibres of
$(K^3(A))^h$ consists of surfaces and isolated points, because it is a union of symplectic varieties and the fibres of ![]() $\nu$ have dimension at most
$\nu$ have dimension at most ![]() $3$. We conclude that
$3$. We conclude that ![]() $G$ is generated by the
$G$ is generated by the ![]() $16$ involutions
$16$ involutions ![]() $(\tau,-1)$ with
$(\tau,-1)$ with ![]() $\tau \in A_2$ and, hence,
$\tau \in A_2$ and, hence, ![]() $G=A_2\times \langle -1\rangle$.
$G=A_2\times \langle -1\rangle$.
2.5 Relevant subvarieties
In what follows we let ![]() $K=K^3(A)$ be the generalized Kummer variety on an abelian surface
$K=K^3(A)$ be the generalized Kummer variety on an abelian surface ![]() $A$. We will calculate the fixed loci of automorphisms in
$A$. We will calculate the fixed loci of automorphisms in ![]() $G=A_2\times \langle -1\rangle$ acting on
$G=A_2\times \langle -1\rangle$ acting on ![]() $K$. The next definition introduces the relevant subvarieties. We denote by
$K$. The next definition introduces the relevant subvarieties. We denote by ![]() $\xi =(a,b,c,d)$ a point of
$\xi =(a,b,c,d)$ a point of ![]() $A_0^{(4)}$, and refer to
$A_0^{(4)}$, and refer to ![]() $\{a,b,c,d\}$ as the support of
$\{a,b,c,d\}$ as the support of ![]() $\xi$.
$\xi$.
Definition 2.6 We define the following subvarieties of ![]() $A_0^{(4)}$:
$A_0^{(4)}$:
– for any
 $\tau \in A_{2}$, we let
$\tau \in A_{2}$, we let
 \[ W_{\tau}:= \{(a, b, -a+\tau, -b+\tau), \ \text{for } \ a,b\in A \}; \]
\[ W_{\tau}:= \{(a, b, -a+\tau, -b+\tau), \ \text{for } \ a,b\in A \}; \]
– for a pair
 $(\tau, \theta )\in A_2 \times A_2$ with
$(\tau, \theta )\in A_2 \times A_2$ with  $\tau \neq 0$, we let
$\tau \neq 0$, we let
 \[ V_{\tau, \theta} := \{ (a, a+\tau, -a+\theta , -a+\tau+\theta), \ \text{for } \ a\in A\}. \]
\[ V_{\tau, \theta} := \{ (a, a+\tau, -a+\theta , -a+\tau+\theta), \ \text{for } \ a\in A\}. \]
We denote by ![]() $\overline {W_{\tau }}$ and
$\overline {W_{\tau }}$ and ![]() $\overline {V_{\tau, \theta }}$ the subvarieties of
$\overline {V_{\tau, \theta }}$ the subvarieties of ![]() $K$ obtained as strict transform of
$K$ obtained as strict transform of ![]() $W_{\tau }$ and
$W_{\tau }$ and ![]() $V_{\tau, \theta }$ under the Hilbert–Chow morphism, respectively.
$V_{\tau, \theta }$ under the Hilbert–Chow morphism, respectively.
Note that none among the ![]() $W_{\tau }$ and
$W_{\tau }$ and ![]() $V_{\tau, \theta }$ is contained in the exceptional locus of
$V_{\tau, \theta }$ is contained in the exceptional locus of ![]() $\nu \colon K\to A^{(4)}_0$, so that
$\nu \colon K\to A^{(4)}_0$, so that ![]() $\overline {W_{\tau }}$ and
$\overline {W_{\tau }}$ and ![]() $\overline {V_{\tau,\theta }}$ are well-defined. We will show in Lemma 2.9 that the
$\overline {V_{\tau,\theta }}$ are well-defined. We will show in Lemma 2.9 that the ![]() $\overline {W_{\tau }}$ are hyper-Kähler varieties of
$\overline {W_{\tau }}$ are hyper-Kähler varieties of ![]() $\mathrm {K}3^{[2]}$ type and that the
$\mathrm {K}3^{[2]}$ type and that the ![]() $\overline {V_{\tau,\theta }}$ are K3 surfaces.
$\overline {V_{\tau,\theta }}$ are K3 surfaces.
Remark 2.7 (i) For ![]() $\tau \in A_2$, the
$\tau \in A_2$, the ![]() $G$-equivariant morphism
$G$-equivariant morphism ![]() $\psi _{\tau }\colon A\times A\to A^{(4)}$ such that
$\psi _{\tau }\colon A\times A\to A^{(4)}$ such that ![]() $(a,b)\mapsto (a, b, -a+\tau, -b+\tau )$ has degree
$(a,b)\mapsto (a, b, -a+\tau, -b+\tau )$ has degree ![]() $8$ and induces an isomorphism
$8$ and induces an isomorphism
Moreover, ![]() $W_{\tau }\neq W_{\tau '}$ unless
$W_{\tau }\neq W_{\tau '}$ unless ![]() $\tau =\tau '$, as can be seen considering a point
$\tau =\tau '$, as can be seen considering a point ![]() $(\epsilon, \epsilon, \epsilon, \epsilon )$ for some
$(\epsilon, \epsilon, \epsilon, \epsilon )$ for some ![]() $\epsilon \in A_{2,\tau }$.
$\epsilon \in A_{2,\tau }$.
(ii) Given ![]() $0\neq \tau \in A_2$ and
$0\neq \tau \in A_2$ and ![]() $\theta \in A_2$, the
$\theta \in A_2$, the ![]() $G$-equivariant morphism
$G$-equivariant morphism ![]() $\psi _{\tau, \theta }\colon A\to A^{(4)}$ defined by
$\psi _{\tau, \theta }\colon A\to A^{(4)}$ defined by ![]() $a \mapsto (a, a+\tau, -a+\theta, -a+\tau +\theta )$ induces an isomorphism
$a \mapsto (a, a+\tau, -a+\theta, -a+\tau +\theta )$ induces an isomorphism
For a given ![]() $\tau \in A_2$, the union
$\tau \in A_2$, the union ![]() $\bigcup _{\theta \in A_2} V_{\tau, \theta }$ has eight irreducible components. In fact,
$\bigcup _{\theta \in A_2} V_{\tau, \theta }$ has eight irreducible components. In fact, ![]() $V_{\tau, \theta }=V_{\tau, \theta '}$ if and only if
$V_{\tau, \theta }=V_{\tau, \theta '}$ if and only if ![]() $\theta ' \in \{\theta, \theta +\tau \}$, which can be seen considering a point
$\theta ' \in \{\theta, \theta +\tau \}$, which can be seen considering a point ![]() $(a, a+\tau, a, a+\tau )$: it belongs to
$(a, a+\tau, a, a+\tau )$: it belongs to ![]() $V_{\tau, \theta }$ if and only if
$V_{\tau, \theta }$ if and only if ![]() $a\in A_{2, \theta }$ or
$a\in A_{2, \theta }$ or ![]() $a\in A_{2,\theta +\tau }$. Moreover, it can be easily checked that
$a\in A_{2,\theta +\tau }$. Moreover, it can be easily checked that ![]() $V_{\tau, \theta }\neq V_{\tau ', \theta '}$ for
$V_{\tau, \theta }\neq V_{\tau ', \theta '}$ for ![]() $\tau \neq \tau '$. In total, we therefore have
$\tau \neq \tau '$. In total, we therefore have ![]() $120$ distinct surfaces
$120$ distinct surfaces ![]() $V_{\tau, \theta }$.
$V_{\tau, \theta }$.
We recall a result of Kamenova, Mongardi and Oblomonkov which will be used in the sequel.
Proposition 2.8 [Reference Kamenova, Mongardi and OblomkovKMO22, Lemma B.1]
Let ![]() $\iota \colon {\mathbb {C}}^2\to {\mathbb {C}}^2$ be the involution given by
$\iota \colon {\mathbb {C}}^2\to {\mathbb {C}}^2$ be the involution given by ![]() $(x,y)\mapsto (-x, -y)$. Consider the rational map
$(x,y)\mapsto (-x, -y)$. Consider the rational map
which maps a general ![]() $\zeta ={(P_1, \ldots, P_{n})}$ to
$\zeta ={(P_1, \ldots, P_{n})}$ to ![]() $\xi ={(P_1, \iota (P_1), \ldots, P_n, \iota (P_n))}$. Then
$\xi ={(P_1, \iota (P_1), \ldots, P_n, \iota (P_n))}$. Then ![]() $\Phi$ extends to a closed embedding, with image the fixed locus for the action of
$\Phi$ extends to a closed embedding, with image the fixed locus for the action of ![]() $\iota$ on
$\iota$ on ![]() $( {\mathbb {C}}^2)^{[2n]}$.
$( {\mathbb {C}}^2)^{[2n]}$.
The next lemma describes the varieties ![]() $\overline {V_{\tau, \theta }}$ and
$\overline {V_{\tau, \theta }}$ and ![]() $\overline {W_{\tau }}$ introduced above.
$\overline {W_{\tau }}$ introduced above.
Lemma 2.9
(i) For
 $\tau \neq 0$,
$\tau \neq 0$,  $\theta \in A_2$, the rational map
$\theta \in A_2$, the rational map  $\phi _{\tau,\theta }$ defined by the commutative diagram
where
$\phi _{\tau,\theta }$ defined by the commutative diagram
where
 $q$ is the natural map, extends to a regular morphism, which is an isomorphism onto its image
$q$ is the natural map, extends to a regular morphism, which is an isomorphism onto its image  $\overline {V_{\tau, \theta }}$.
$\overline {V_{\tau, \theta }}$.(ii) For
 $\tau \in A_2$, the rational map
$\tau \in A_2$, the rational map  $\phi _{\tau }$ defined by the commutative diagram
where
$\phi _{\tau }$ defined by the commutative diagram
where
 $q$ is the composition of the Hilbert–Chow morphism with the natural map
$q$ is the composition of the Hilbert–Chow morphism with the natural map  $(\operatorname {\mathrm {Km}}^{\tau }(A))^{(2)} \to (A/\langle (\tau, -1)\rangle )^{(2)}$, extends to a regular morphism, which is an isomorphism onto its image
$(\operatorname {\mathrm {Km}}^{\tau }(A))^{(2)} \to (A/\langle (\tau, -1)\rangle )^{(2)}$, extends to a regular morphism, which is an isomorphism onto its image  $\overline {W_{\tau }}$.
$\overline {W_{\tau }}$.
Proof. We prove part (i). As translations are fixed point free, for any ![]() $\alpha \in A/\langle \tau, (\theta, -1)\rangle$ the support of
$\alpha \in A/\langle \tau, (\theta, -1)\rangle$ the support of ![]() $\psi _{\tau, \theta } (\alpha )\in V_{\tau, \theta }$ consists of either two or four distinct points, according to whether
$\psi _{\tau, \theta } (\alpha )\in V_{\tau, \theta }$ consists of either two or four distinct points, according to whether ![]() $\alpha$ is a node or not. If
$\alpha$ is a node or not. If ![]() $\alpha$ is not a node
$\alpha$ is not a node ![]() $q^{-1}(\alpha )$ is a single point at which
$q^{-1}(\alpha )$ is a single point at which ![]() $\phi _{\tau, \theta }$ is well-defined. Otherwise,
$\phi _{\tau, \theta }$ is well-defined. Otherwise, ![]() $\psi _{\tau, \theta } (\alpha ) =(a, a+\tau, a, a+\tau )$ for some
$\psi _{\tau, \theta } (\alpha ) =(a, a+\tau, a, a+\tau )$ for some ![]() $a$ in
$a$ in ![]() $A_{2, \theta }$ or
$A_{2, \theta }$ or ![]() $A_{2,\tau +\theta }$. Then, there is a canonical identification
$A_{2,\tau +\theta }$. Then, there is a canonical identification ![]() $\nu ^{-1}(\psi _{\tau, \theta } (\alpha ))= {\mathbb {P}}(T_aA) \times {\mathbb {P}}(T_{a+\tau } A)$. The exceptional divisor in
$\nu ^{-1}(\psi _{\tau, \theta } (\alpha ))= {\mathbb {P}}(T_aA) \times {\mathbb {P}}(T_{a+\tau } A)$. The exceptional divisor in ![]() $\operatorname {\mathrm {Km}}^{\theta }(A/\langle \tau \rangle )$ corresponding to the node
$\operatorname {\mathrm {Km}}^{\theta }(A/\langle \tau \rangle )$ corresponding to the node ![]() $\alpha$ is identified with
$\alpha$ is identified with ![]() $ {\mathbb {P}}(T_a A)$. Translation by
$ {\mathbb {P}}(T_a A)$. Translation by ![]() $\tau$ gives an isomorphism
$\tau$ gives an isomorphism ![]() $ {\mathbb {P}}(T_aA)\xrightarrow {\ \sim \ } {\mathbb {P}}(T_{a+\tau}A)$, and the morphism
$ {\mathbb {P}}(T_aA)\xrightarrow {\ \sim \ } {\mathbb {P}}(T_{a+\tau}A)$, and the morphism ![]() $\phi _{\tau, \theta }$ is extended via
$\phi _{\tau, \theta }$ is extended via ![]() $\phi _{\tau, \theta } (t):= (t, \tau (t))$ for
$\phi _{\tau, \theta } (t):= (t, \tau (t))$ for ![]() $t\in {\mathbb {P}}(T_aA)$.
$t\in {\mathbb {P}}(T_aA)$.
The proof of part (ii) is similar. If ![]() $\psi _{\tau } (\alpha, \beta )$ consists of four distinct points, then
$\psi _{\tau } (\alpha, \beta )$ consists of four distinct points, then ![]() $q^{-1}(\alpha, \beta )$ is a single point at which
$q^{-1}(\alpha, \beta )$ is a single point at which ![]() $\phi _{\tau }$ is well-defined. If the support of
$\phi _{\tau }$ is well-defined. If the support of ![]() $\psi _{\tau }(\alpha, \beta )$ consists of three distinct points, then exactly one between
$\psi _{\tau }(\alpha, \beta )$ consists of three distinct points, then exactly one between ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ is a node of
$\beta$ is a node of ![]() $A/\langle (\tau, -1) \rangle$, and
$A/\langle (\tau, -1) \rangle$, and ![]() $\psi _{\tau }(\alpha, \beta )=(a, \epsilon, -a+\tau, \epsilon )$ for some
$\psi _{\tau }(\alpha, \beta )=(a, \epsilon, -a+\tau, \epsilon )$ for some ![]() $a\in A\setminus A_{2,\tau }$ and
$a\in A\setminus A_{2,\tau }$ and ![]() $\epsilon \in A_{2,\tau }$; we extend
$\epsilon \in A_{2,\tau }$; we extend ![]() $\phi _{\tau }$ via the canonical identifications
$\phi _{\tau }$ via the canonical identifications ![]() $q^{-1}(\alpha, \beta ) = {\mathbb {P}}(T_{\epsilon }A)=\nu ^{-1}(\psi _{\tau }(\alpha,\beta ))$. If the support of
$q^{-1}(\alpha, \beta ) = {\mathbb {P}}(T_{\epsilon }A)=\nu ^{-1}(\psi _{\tau }(\alpha,\beta ))$. If the support of ![]() $\psi _{\tau }(\alpha, \beta )$ consists of two distinct points then either
$\psi _{\tau }(\alpha, \beta )$ consists of two distinct points then either ![]() $\alpha =\beta$ for some smooth point or
$\alpha =\beta$ for some smooth point or ![]() $\alpha \neq \beta$ with both
$\alpha \neq \beta$ with both ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ nodes of
$\beta$ nodes of ![]() $A/\langle (\tau,-1)\rangle$. In the first case there exists
$A/\langle (\tau,-1)\rangle$. In the first case there exists ![]() $a\in A\setminus A_{2,\tau }$ such that
$a\in A\setminus A_{2,\tau }$ such that ![]() $\psi _{\tau }(\alpha,\beta )=(a, a, -a+\tau, -a+\tau )$. Then
$\psi _{\tau }(\alpha,\beta )=(a, a, -a+\tau, -a+\tau )$. Then ![]() $q^{-1}(\alpha, \beta ) = \mathbb {P}(T_a A)$ and
$q^{-1}(\alpha, \beta ) = \mathbb {P}(T_a A)$ and ![]() $\nu ^{-1}(\psi _{\tau } (\alpha, \beta ))= {\mathbb {P}}(T_{a}A)\times {\mathbb {P}}(T_{-a+\tau } A)$, and we define
$\nu ^{-1}(\psi _{\tau } (\alpha, \beta ))= {\mathbb {P}}(T_{a}A)\times {\mathbb {P}}(T_{-a+\tau } A)$, and we define ![]() $\phi _{\tau }$ by
$\phi _{\tau }$ by ![]() $t\mapsto (t, (\tau, -1)(t))$. In the second case
$t\mapsto (t, (\tau, -1)(t))$. In the second case ![]() $\psi _{\tau }(\alpha, \beta )= (\epsilon _1, \epsilon _2, \epsilon _1, \epsilon _2)$ for some
$\psi _{\tau }(\alpha, \beta )= (\epsilon _1, \epsilon _2, \epsilon _1, \epsilon _2)$ for some ![]() $\epsilon _1\neq \epsilon _2$ both in
$\epsilon _1\neq \epsilon _2$ both in ![]() $A_{2,\tau }$, and we extend
$A_{2,\tau }$, and we extend ![]() $\phi _{\tau }$ via the canonical isomorphisms
$\phi _{\tau }$ via the canonical isomorphisms ![]() $q^{-1}(\alpha, \beta ) = {\mathbb {P}}(T_{\epsilon _1}A)\times {\mathbb {P}}(T_{\epsilon _2}A) = \nu ^{-1}(\psi _{\tau }(\alpha,\beta ))$. Finally, consider the case when
$q^{-1}(\alpha, \beta ) = {\mathbb {P}}(T_{\epsilon _1}A)\times {\mathbb {P}}(T_{\epsilon _2}A) = \nu ^{-1}(\psi _{\tau }(\alpha,\beta ))$. Finally, consider the case when ![]() $\alpha =\beta$ and
$\alpha =\beta$ and ![]() $\alpha$ is a node. Locally analytically around the node
$\alpha$ is a node. Locally analytically around the node ![]() $\alpha$ of
$\alpha$ of ![]() $A/\langle (\tau, -1)\rangle$, the morphism
$A/\langle (\tau, -1)\rangle$, the morphism ![]() $q$ is isomorphic to the composition
$q$ is isomorphic to the composition
where ![]() $\iota (x,y)=(-x,-y)$ is the restriction of the involution
$\iota (x,y)=(-x,-y)$ is the restriction of the involution ![]() $(\tau, -1)$. The rational map
$(\tau, -1)$. The rational map ![]() $\phi _{\tau }$ is identified with
$\phi _{\tau }$ is identified with ![]() $\Phi \colon (\mathrm {Bl}_0( {\mathbb {C}}^2/\iota ))^{[2]} \dashrightarrow ( {\mathbb {C}}^2)^{[4]}$ which maps a general
$\Phi \colon (\mathrm {Bl}_0( {\mathbb {C}}^2/\iota ))^{[2]} \dashrightarrow ( {\mathbb {C}}^2)^{[4]}$ which maps a general ![]() $\zeta =(\alpha,\beta )$ to the subscheme
$\zeta =(\alpha,\beta )$ to the subscheme ![]() $\xi =(\alpha,\iota (\alpha ), \beta, \iota (\beta ))$. Then Proposition 2.8 implies that
$\xi =(\alpha,\iota (\alpha ), \beta, \iota (\beta ))$. Then Proposition 2.8 implies that ![]() $\phi _\tau$ extends to a closed embedding
$\phi _\tau$ extends to a closed embedding ![]() $(\mathrm {Bl}_0( {\mathbb {C}}^2/\iota ))^{[2]}\hookrightarrow ( {\mathbb {C}}^2)^{[4]}$, completing the proof.
$(\mathrm {Bl}_0( {\mathbb {C}}^2/\iota ))^{[2]}\hookrightarrow ( {\mathbb {C}}^2)^{[4]}$, completing the proof.
The various intersections of the submanifolds ![]() $\overline {W_{\tau }}\subset K$ are as follows.
$\overline {W_{\tau }}\subset K$ are as follows.
Lemma 2.10
(i) For
 $\tau _1 \neq \tau _2$ in
$\tau _1 \neq \tau _2$ in  $A_2$ we have
$A_2$ we have  $\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}=\overline {V_{\tau _1+\tau _2, \tau _1}}$.
$\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}=\overline {V_{\tau _1+\tau _2, \tau _1}}$.(ii) For pairwise distinct
 $\tau _1$,
$\tau _1$,  $\tau _2$,
$\tau _2$,  $\tau _3$ in
$\tau _3$ in  $A_2$, the intersection
$A_2$, the intersection  $\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}\cap \overline {W_{\tau _3}}$ consists of the four distinct points of the set
$\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}\cap \overline {W_{\tau _3}}$ consists of the four distinct points of the set
 \[ \nu^{-1}( \{ (a, a+\tau_1+\tau_2, -a+\tau_1, -a+\tau_2) \in A_0^{(4)}, \ a\in A_{2, \tau_1+\tau_2+\tau_3}\}) \subset K. \]
\[ \nu^{-1}( \{ (a, a+\tau_1+\tau_2, -a+\tau_1, -a+\tau_2) \in A_0^{(4)}, \ a\in A_{2, \tau_1+\tau_2+\tau_3}\}) \subset K. \]
(iii) The intersection of four or more distinct submanifolds
 $\overline {W_{\tau }}$ is empty.
$\overline {W_{\tau }}$ is empty.
Proof. (i) A point ![]() $\xi \in A_0^{(4)}$ belongs to
$\xi \in A_0^{(4)}$ belongs to ![]() ${W_{\tau _1}}\cap {W_{\tau _2}}$ if and only if it can be written as
${W_{\tau _1}}\cap {W_{\tau _2}}$ if and only if it can be written as ![]() $\xi =(a,b,-a+\tau _1, -b+\tau _1)$ as well as
$\xi =(a,b,-a+\tau _1, -b+\tau _1)$ as well as ![]() $\xi =(a', b' , -a'+\tau _2, -b'+\tau _2)$, for some
$\xi =(a', b' , -a'+\tau _2, -b'+\tau _2)$, for some ![]() $a,b,a',b'$ in
$a,b,a',b'$ in ![]() $A$. Then, we may assume that
$A$. Then, we may assume that ![]() $a'=a$; since
$a'=a$; since ![]() $\tau _1\neq \tau _2$, it follows that
$\tau _1\neq \tau _2$, it follows that ![]() $-a+\tau _1 \neq -a'+\tau _2$. This forces either
$-a+\tau _1 \neq -a'+\tau _2$. This forces either ![]() $b' =-a+\tau _1$ or
$b' =-a+\tau _1$ or ![]() $-b'+\tau _2= -a +\tau _1$; in both cases, we can write
$-b'+\tau _2= -a +\tau _1$; in both cases, we can write
i.e. ![]() $\xi \in V_{\tau _1+\tau _2, \tau _1}$. Thus,
$\xi \in V_{\tau _1+\tau _2, \tau _1}$. Thus, ![]() ${W_{\tau _1}}\cap {W_{\tau _2}}=V_{\tau _1+\tau _2, \tau _1}$ and, hence, for their strict transforms we have
${W_{\tau _1}}\cap {W_{\tau _2}}=V_{\tau _1+\tau _2, \tau _1}$ and, hence, for their strict transforms we have ![]() $\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}=\overline {V_{\tau _1+\tau _2, \tau _1}}$.
$\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}=\overline {V_{\tau _1+\tau _2, \tau _1}}$.
(ii) By part (i), a point ![]() $\xi$ lies in the intersection
$\xi$ lies in the intersection ![]() $W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _2}$ if and only if it can be written as
$W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _2}$ if and only if it can be written as ![]() $\xi = (a, a+\tau _1+\tau _2, -a+\tau _1, -a+\tau _2)$ as well as
$\xi = (a, a+\tau _1+\tau _2, -a+\tau _1, -a+\tau _2)$ as well as ![]() $\xi =(a'',b'', -a''+\tau _3, -b''+\tau _3)$. Again, we may assume
$\xi =(a'',b'', -a''+\tau _3, -b''+\tau _3)$. Again, we may assume ![]() $a''= a$. Then we must have
$a''= a$. Then we must have ![]() $-a+\tau _3= a+\tau _1+\tau _2$; equivalently,
$-a+\tau _3= a+\tau _1+\tau _2$; equivalently, ![]() $a\in A_{2,\tau _1+\tau _2+\tau _3}$. Moreover, either we have
$a\in A_{2,\tau _1+\tau _2+\tau _3}$. Moreover, either we have ![]() $b''=-a+\tau _1$ or
$b''=-a+\tau _1$ or ![]() $b''=-a+\tau _2$. Note that, since
$b''=-a+\tau _2$. Note that, since ![]() $a\in A_{2, \tau _1+\tau _2+\tau _3}$, in the first case
$a\in A_{2, \tau _1+\tau _2+\tau _3}$, in the first case ![]() $-b''+\tau _3= -a+\tau _2$, while in the second case
$-b''+\tau _3= -a+\tau _2$, while in the second case ![]() $-b''+\tau _3= - a+\tau _1$. This shows that
$-b''+\tau _3= - a+\tau _1$. This shows that
This set consists of four distinct points. Indeed, ![]() $G$ acts transitively on it and the subgroup of
$G$ acts transitively on it and the subgroup of ![]() $G$ generated by the
$G$ generated by the ![]() $(\tau _i, -1)$,
$(\tau _i, -1)$, ![]() $i=1,2,3$ acts trivially. Moreover, it is easy to see that if
$i=1,2,3$ acts trivially. Moreover, it is easy to see that if ![]() $g\in G$ is not an element of this subgroup, then it has no fixed points in the above set. Hence, the intersection
$g\in G$ is not an element of this subgroup, then it has no fixed points in the above set. Hence, the intersection ![]() $W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}$ is in bijection with
$W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}$ is in bijection with ![]() $( {\mathbb {Z}}/2 {\mathbb {Z}})^2$. No point of this set belongs to the exceptional locus of the Hilbert–Chow morphism, so that
$( {\mathbb {Z}}/2 {\mathbb {Z}})^2$. No point of this set belongs to the exceptional locus of the Hilbert–Chow morphism, so that ![]() $\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}\cap \overline {W_{\tau _3}}$ consists of four distinct points.
$\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}}\cap \overline {W_{\tau _3}}$ consists of four distinct points.
(iii) Note that ![]() $W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}\cap W_{\tau _1+\tau _2+\tau _3}$ is empty. We have seen above that if
$W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}\cap W_{\tau _1+\tau _2+\tau _3}$ is empty. We have seen above that if ![]() $\theta \in A_2\setminus \{\tau _1, \tau _2, \tau _3, \tau _1+\tau _2+\tau _3\}$, the action of
$\theta \in A_2\setminus \{\tau _1, \tau _2, \tau _3, \tau _1+\tau _2+\tau _3\}$, the action of ![]() $(\theta, -1)$ on
$(\theta, -1)$ on ![]() $W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}$ is free; as
$W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}$ is free; as ![]() ${W_{\theta }}$ is clearly fixed by
${W_{\theta }}$ is clearly fixed by ![]() $(\theta, -1)$, it follows that
$(\theta, -1)$, it follows that ![]() $W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}\cap W_{\theta } =\emptyset$.
$W_{\tau _1}\cap W_{\tau _2}\cap W_{\tau _3}\cap W_{\theta } =\emptyset$.
2.11 Fixed loci
We calculate the fixed locus of the automorphisms ![]() $g\in G$. Our results confirm those of Oguiso [Reference OguisoOgu20] and Kamenova, Mongardi and Oblomkov [Reference Kamenova, Mongardi and OblomkovKMO22].
$g\in G$. Our results confirm those of Oguiso [Reference OguisoOgu20] and Kamenova, Mongardi and Oblomkov [Reference Kamenova, Mongardi and OblomkovKMO22].
Proposition 2.12 Let ![]() $g\neq 1\in G$. Then:
$g\neq 1\in G$. Then:
– if
 $g=(\tau, 1)$, with
$g=(\tau, 1)$, with  $\tau \neq 0\in A_2$, the fixed locus
$\tau \neq 0\in A_2$, the fixed locus  $K^g$ is the disjoint union of the eight
$K^g$ is the disjoint union of the eight  $\mathrm {K}3$ surfaces
$\mathrm {K}3$ surfaces  $\overline {V_{\tau, \theta }}$, for
$\overline {V_{\tau, \theta }}$, for  $\theta$ varying in
$\theta$ varying in  $A_2$;
$A_2$;– if
 $g=(\tau, -1)$ with
$g=(\tau, -1)$ with  $\tau \in A_2$, the fixed locus
$\tau \in A_2$, the fixed locus  $K^g$ is the union of the
$K^g$ is the union of the  $\mathrm {K}3^{[2]}$ type variety
$\mathrm {K}3^{[2]}$ type variety  $\overline {W_{\tau }}$ and
$\overline {W_{\tau }}$ and  $140$ isolated points; the isolated points are given by the set
$140$ isolated points; the isolated points are given by the set
 \[ \biggl\{(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4) , \ \epsilon_i \in A_{2,\tau} \text{ pairwise distinct and such that } \sum_{i=1}^4 \epsilon_i =0 \in A \biggr\}. \]
\[ \biggl\{(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4) , \ \epsilon_i \in A_{2,\tau} \text{ pairwise distinct and such that } \sum_{i=1}^4 \epsilon_i =0 \in A \biggr\}. \]
Proof. Let ![]() $g=(\tau, 1)$ with
$g=(\tau, 1)$ with ![]() $\tau \neq 0\in A_2$. The action of
$\tau \neq 0\in A_2$. The action of ![]() $g$ on
$g$ on ![]() $\xi =(a,b,c,d)\in A^{(4)}$ is given by
$\xi =(a,b,c,d)\in A^{(4)}$ is given by ![]() $\xi \mapsto (a+\tau, b+\tau, c+\tau, d+\tau )$. We see immediately that the surfaces
$\xi \mapsto (a+\tau, b+\tau, c+\tau, d+\tau )$. We see immediately that the surfaces ![]() $V_{\tau, \theta }$ are fixed by
$V_{\tau, \theta }$ are fixed by ![]() $g$. Conversely, if
$g$. Conversely, if ![]() $\xi$ is fixed and
$\xi$ is fixed and ![]() $a$ belongs to its support, then also
$a$ belongs to its support, then also ![]() $a+\tau$ must be in the support. Therefore,
$a+\tau$ must be in the support. Therefore, ![]() $\xi =(a, a+\tau, b, b+\tau )$; if
$\xi =(a, a+\tau, b, b+\tau )$; if ![]() $\xi \in A^{(4)}_0$, then
$\xi \in A^{(4)}_0$, then ![]() $2a+2b=0$, so that
$2a+2b=0$, so that ![]() $\theta := a+b$ belongs to
$\theta := a+b$ belongs to ![]() $A_2$ and
$A_2$ and ![]() $\xi \in V_{\tau, \theta }$. By the description of
$\xi \in V_{\tau, \theta }$. By the description of ![]() $\overline {V_{\tau, \theta }}$ given in Lemma 2.9(i), the fixed locus of
$\overline {V_{\tau, \theta }}$ given in Lemma 2.9(i), the fixed locus of ![]() $g$ in
$g$ in ![]() $\nu ^{-1}(V_{\tau, \theta })$ is precisely
$\nu ^{-1}(V_{\tau, \theta })$ is precisely ![]() $\overline {V_{\tau, \theta }}$. Since the fixed locus is smooth,
$\overline {V_{\tau, \theta }}$. Since the fixed locus is smooth, ![]() $K^g$ is the disjoint union of the eight K
$K^g$ is the disjoint union of the eight K![]() $3$ surfaces
$3$ surfaces ![]() $\overline {V_{\tau, \theta }}$, for
$\overline {V_{\tau, \theta }}$, for ![]() $\theta \in A_2$.
$\theta \in A_2$.
Assume now that ![]() $g=(\tau, -1)$. If
$g=(\tau, -1)$. If ![]() $\xi =(a,b,c,d) \in A^{(4)}$, the action of
$\xi =(a,b,c,d) \in A^{(4)}$, the action of ![]() $g$ is given by
$g$ is given by ![]() $\xi \mapsto (-a+\tau, -b+\tau, -c+\tau, -d+\tau )$. Note that
$\xi \mapsto (-a+\tau, -b+\tau, -c+\tau, -d+\tau )$. Note that ![]() $W_{\tau }$ is contained in the fixed locus of
$W_{\tau }$ is contained in the fixed locus of ![]() $g$ on
$g$ on ![]() $A^{(4)}_0$. Moreover any
$A^{(4)}_0$. Moreover any ![]() $\xi$ entirely supported at points of
$\xi$ entirely supported at points of ![]() $A_{2,\tau }$ is fixed by
$A_{2,\tau }$ is fixed by ![]() $g$. Conversely, let
$g$. Conversely, let ![]() $\xi \in A_0^{(4)}$ be fixed. Then we have the following possibilities. If the support of
$\xi \in A_0^{(4)}$ be fixed. Then we have the following possibilities. If the support of ![]() $\xi$ does not intersect
$\xi$ does not intersect ![]() $A_{2, \tau }$, we have
$A_{2, \tau }$, we have ![]() $\xi = (a, -a+\tau, b, -b+\tau )$ for some
$\xi = (a, -a+\tau, b, -b+\tau )$ for some ![]() $a,b\in A\setminus A_{2, \tau }$ and
$a,b\in A\setminus A_{2, \tau }$ and ![]() $\xi$ belongs to
$\xi$ belongs to ![]() $W_{\tau }$. If the support of
$W_{\tau }$. If the support of ![]() $\xi$ contains some
$\xi$ contains some ![]() $\epsilon \in A_{2,\tau }$ and some
$\epsilon \in A_{2,\tau }$ and some ![]() $a\notin A_{2,\tau }$, then
$a\notin A_{2,\tau }$, then ![]() $\xi = (a, -a+\tau, \epsilon, b)$ for some
$\xi = (a, -a+\tau, \epsilon, b)$ for some ![]() $b\in A$; as
$b\in A$; as ![]() $\xi \in A_0^{(4)}$, we must have
$\xi \in A_0^{(4)}$, we must have ![]() $b=\epsilon$, and hence
$b=\epsilon$, and hence ![]() $\xi$ belongs to
$\xi$ belongs to ![]() $W_{\tau }$. Finally, assume that
$W_{\tau }$. Finally, assume that ![]() $\xi =( \epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ is entirely supported at
$\xi =( \epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ is entirely supported at ![]() $A_{2,\tau }$. As
$A_{2,\tau }$. As ![]() $\xi$ belongs to
$\xi$ belongs to ![]() $A^{(4)}_0$ we have
$A^{(4)}_0$ we have ![]() $\sum _i \epsilon _i =0$ in
$\sum _i \epsilon _i =0$ in ![]() $A$. If the support of
$A$. If the support of ![]() $\xi$ consists of four distinct points, then
$\xi$ consists of four distinct points, then ![]() $\xi \notin W_{\tau }$. Otherwise,
$\xi \notin W_{\tau }$. Otherwise, ![]() $\xi =(\epsilon _1, \epsilon _1, \epsilon _2, \epsilon _2)$ lies in
$\xi =(\epsilon _1, \epsilon _1, \epsilon _2, \epsilon _2)$ lies in ![]() $W_{\tau }$.
$W_{\tau }$.
We conclude that the fixed locus of ![]() $g$ acting on
$g$ acting on ![]() $A^{(4)}_0$ consists of
$A^{(4)}_0$ consists of ![]() $W_{\tau }$ and the isolated points in the set
$W_{\tau }$ and the isolated points in the set
 \[ \biggl\{(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4) , \ \epsilon_i \in A_{2,\tau} \text{ pairwise distinct and such that } \sum_{i=1}^4 \epsilon_i =0 \in A \biggr\}. \]
\[ \biggl\{(\epsilon_1, \epsilon_2, \epsilon_3, \epsilon_4) , \ \epsilon_i \in A_{2,\tau} \text{ pairwise distinct and such that } \sum_{i=1}^4 \epsilon_i =0 \in A \biggr\}. \]
There are ![]() $140$ isolated fixed points. Indeed, the total number of ordered sequences
$140$ isolated fixed points. Indeed, the total number of ordered sequences ![]() $(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ such that
$(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ such that ![]() $\sum _i \epsilon _i = 0$ is
$\sum _i \epsilon _i = 0$ is ![]() $16^3$. There are
$16^3$. There are ![]() $16$ such sequences with support a single point, and
$16$ such sequences with support a single point, and ![]() $6\binom{16}{2}=16 \cdot 45$ with support two distinct points. The number of ordered sequences as above supported on four distinct points is
$6\binom{16}{2}=16 \cdot 45$ with support two distinct points. The number of ordered sequences as above supported on four distinct points is ![]() $16^3-16-16\cdot 45=16\cdot 210$; under the symmetric group, each of them has an orbit of cardinality
$16^3-16-16\cdot 45=16\cdot 210$; under the symmetric group, each of them has an orbit of cardinality ![]() $24$. Hence, the number of isolated fixed points is
$24$. Hence, the number of isolated fixed points is ![]() $\tfrac {210\cdot 16}{24} = 140$.
$\tfrac {210\cdot 16}{24} = 140$.
Therefore, ![]() $K^g$ consists of
$K^g$ consists of ![]() $140$ isolated fixed points and the fixed locus of
$140$ isolated fixed points and the fixed locus of ![]() $g$ acting on
$g$ acting on ![]() $\nu ^{-1}(W_\tau )$. To conclude we have to check that the latter coincides with
$\nu ^{-1}(W_\tau )$. To conclude we have to check that the latter coincides with ![]() $\overline {W_{\tau }}$. Using the description of
$\overline {W_{\tau }}$. Using the description of ![]() $\overline {W_{\tau }}$ given in the proof of Lemma 2.9(ii) and the second assertion of Proposition 2.8 it is readily seen that
$\overline {W_{\tau }}$ given in the proof of Lemma 2.9(ii) and the second assertion of Proposition 2.8 it is readily seen that ![]() $\nu ^{-1}(\xi ) \cap K^g = \nu ^{-1}(\xi ) \cap \overline {W_{\tau }}$ for any
$\nu ^{-1}(\xi ) \cap K^g = \nu ^{-1}(\xi ) \cap \overline {W_{\tau }}$ for any ![]() $\xi \in W_{\tau }$.
$\xi \in W_{\tau }$.
Remark 2.13 Let ![]() $h=(\epsilon, \pm 1)$ be an automorphism in
$h=(\epsilon, \pm 1)$ be an automorphism in ![]() $\operatorname {Aut}_0(K^3(A))=A_4\rtimes \langle -1\rangle$. One can see directly from Definition 2.6 that
$\operatorname {Aut}_0(K^3(A))=A_4\rtimes \langle -1\rangle$. One can see directly from Definition 2.6 that ![]() $h$ maps
$h$ maps ![]() $\overline {W_{\tau }}$ to
$\overline {W_{\tau }}$ to ![]() $\overline {W_{\tau +2\epsilon }}$, for any
$\overline {W_{\tau +2\epsilon }}$, for any ![]() $\tau \in A_2$.
$\tau \in A_2$.
We can finally give the proof of the main result of this section.
Proof of Theorem 2.2 Let us first assume that ![]() $K$ is the generalized Kummer variety associated to an abelian surface
$K$ is the generalized Kummer variety associated to an abelian surface ![]() $A$. Let
$A$. Let ![]() $g= (\tau, 1)\in G$, with
$g= (\tau, 1)\in G$, with ![]() $\tau \neq 0\in A_2$. Consider a component
$\tau \neq 0\in A_2$. Consider a component ![]() $\overline {V_{\tau, \theta }}$ of
$\overline {V_{\tau, \theta }}$ of ![]() $K^g$. The surface
$K^g$. The surface ![]() $V_{\tau, \theta }$ is clearly contained in
$V_{\tau, \theta }$ is clearly contained in ![]() $W_{\theta }$ and, hence, the same holds for their strict transforms. Now let
$W_{\theta }$ and, hence, the same holds for their strict transforms. Now let ![]() $g= (\tau, -1)\in G$. Let
$g= (\tau, -1)\in G$. Let ![]() $P$ be an isolated fixed point in
$P$ be an isolated fixed point in ![]() $K^{g}$. Then we have
$K^{g}$. Then we have ![]() $P=(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ for some pairwise distinct
$P=(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4)$ for some pairwise distinct ![]() $\epsilon _i \in A_{2,\tau }$ summing up to
$\epsilon _i \in A_{2,\tau }$ summing up to ![]() $0$ in
$0$ in ![]() $A$. The last condition implies that we can write
$A$. The last condition implies that we can write ![]() $P=(\epsilon _1, \epsilon _2, \epsilon _1+\theta, \epsilon _2+\theta )$ for some
$P=(\epsilon _1, \epsilon _2, \epsilon _1+\theta, \epsilon _2+\theta )$ for some ![]() $0\neq \theta \in A_{2}$. This is the same as
$0\neq \theta \in A_{2}$. This is the same as
which lies in ![]() $\overline {W_{\tau +\theta }}$. By Lemma 2.12 we conclude that for a generalized Kummer variety the union of the fixed loci
$\overline {W_{\tau +\theta }}$. By Lemma 2.12 we conclude that for a generalized Kummer variety the union of the fixed loci ![]() $K^g$ consists of the
$K^g$ consists of the ![]() $16$ varieties
$16$ varieties ![]() $\overline {W_{\tau }}$ of
$\overline {W_{\tau }}$ of ![]() $\mathrm {K}3^{[2]}$ type. The intersections of these components were computed in Lemma 2.10.
$\mathrm {K}3^{[2]}$ type. The intersections of these components were computed in Lemma 2.10.
Now let ![]() $f\colon \mathcal {K}\to B$ be a smooth and proper family of
$f\colon \mathcal {K}\to B$ be a smooth and proper family of ![]() $\mathrm {Kum}^3$ manifolds over a connected base
$\mathrm {Kum}^3$ manifolds over a connected base ![]() $B$, with a fibre
$B$, with a fibre ![]() $\mathcal {K}_0$ isomorphic to the generalized Kummer variety on an abelian surface
$\mathcal {K}_0$ isomorphic to the generalized Kummer variety on an abelian surface ![]() $A$. By the result of Hassett and Tschinkel [Reference Hassett and TschinkelHT13, Theorem 2.1], up to a finite étale base change, there is a fibrewise action of
$A$. By the result of Hassett and Tschinkel [Reference Hassett and TschinkelHT13, Theorem 2.1], up to a finite étale base change, there is a fibrewise action of ![]() $G=A_2\times \langle -1 \rangle$ on
$G=A_2\times \langle -1 \rangle$ on ![]() $\mathcal {K}$. By [Reference FujikiFuj83, Lemma 3.10], this action is locally trivial with respect to
$\mathcal {K}$. By [Reference FujikiFuj83, Lemma 3.10], this action is locally trivial with respect to ![]() $f$, i.e. any
$f$, i.e. any ![]() $x\in \mathcal {K}$ has a neighborhood
$x\in \mathcal {K}$ has a neighborhood ![]() $U_x=(f^{-1}f(U_x)\cap \mathcal {K}_{f(x)} )\times f(U_x)$ such that the action on
$U_x=(f^{-1}f(U_x)\cap \mathcal {K}_{f(x)} )\times f(U_x)$ such that the action on ![]() $U_x$ of the stabilizer subgroup of
$U_x$ of the stabilizer subgroup of ![]() $x$ is induced by that on the fibre
$x$ is induced by that on the fibre ![]() $\mathcal {K}_{f(x)}$. Therefore, for any
$\mathcal {K}_{f(x)}$. Therefore, for any ![]() $\tau \in A_{2}$ the fixed locus
$\tau \in A_{2}$ the fixed locus ![]() $\mathcal {K}^g$ of
$\mathcal {K}^g$ of ![]() $g=(\tau, -1)$ contains a smooth family
$g=(\tau, -1)$ contains a smooth family ![]() $\overline {\mathcal {W}_{\tau }}\to B$ of manifolds of
$\overline {\mathcal {W}_{\tau }}\to B$ of manifolds of ![]() $\mathrm {K}3^{[2]}$ type as the unique component of
$\mathrm {K}3^{[2]}$ type as the unique component of ![]() $\mathcal {K}^g$ with positive-dimensional intersection with the fibres of
$\mathcal {K}^g$ with positive-dimensional intersection with the fibres of ![]() $f$. We conclude that for any
$f$. We conclude that for any ![]() $b\in B$ we have
$b\in B$ we have
and that the components ![]() $\overline {\mathcal {W}_{\tau }}_{\lvert _{\mathcal {K}_b}}$ intersect as claimed.
$\overline {\mathcal {W}_{\tau }}_{\lvert _{\mathcal {K}_b}}$ intersect as claimed.
3. A Lagrangian fibration
Throughout this section, ![]() $J$ denotes a general principally polarized abelian surface. We fix a symmetric theta divisor
$J$ denotes a general principally polarized abelian surface. We fix a symmetric theta divisor ![]() $\Theta \subset J$, which is unique up to translation by a point of
$\Theta \subset J$, which is unique up to translation by a point of ![]() $J_2$. For any integer
$J_2$. For any integer ![]() $d$, we consider the Mukai vector
$d$, we consider the Mukai vector ![]() $v_d:= (0, 2\Theta, d-4)$ on
$v_d:= (0, 2\Theta, d-4)$ on ![]() $J$ and the moduli space
$J$ and the moduli space ![]() $M_J(v_d)$ of
$M_J(v_d)$ of ![]() $\Theta$-semistable sheaves with Mukai vector
$\Theta$-semistable sheaves with Mukai vector ![]() $v_d$ ([Reference Huybrechts and LehnHL10]). The Albanese fibration
$v_d$ ([Reference Huybrechts and LehnHL10]). The Albanese fibration
is isotrivial [Reference YoshiokaYos01]. We denote the fibre of ![]() $\mathrm {alb}$ over
$\mathrm {alb}$ over ![]() $(\mathcal {O}_J, 0 )$ by
$(\mathcal {O}_J, 0 )$ by ![]() $K_J(v_d)$. For
$K_J(v_d)$. For ![]() $d$ even,
$d$ even, ![]() $K_J(v_d)$ is singular and admits a crepant resolution of
$K_J(v_d)$ is singular and admits a crepant resolution of ![]() $\mathrm {OG}6$ type, by [Reference O'GradyO'Gr03] and [Reference Lehn and SorgerLS06]. When
$\mathrm {OG}6$ type, by [Reference O'GradyO'Gr03] and [Reference Lehn and SorgerLS06]. When ![]() $d$ is odd,
$d$ is odd, ![]() $K_J(v_d)$ is smooth, and it is a hyper-Kähler sixfold of
$K_J(v_d)$ is smooth, and it is a hyper-Kähler sixfold of ![]() $\mathrm {Kum}^3$ type [Reference YoshiokaYos01]. In this case, we consider the group
$\mathrm {Kum}^3$ type [Reference YoshiokaYos01]. In this case, we consider the group ![]() $G \subset \operatorname {Aut}_0(K_{J}(v_d))$ introduced in Definition 2.1.
$G \subset \operatorname {Aut}_0(K_{J}(v_d))$ introduced in Definition 2.1.
The main result of this section is the following.
Theorem 3.1 The quotient ![]() $K_J(v_3)/ G$ is birational to
$K_J(v_3)/ G$ is birational to ![]() $\operatorname {\mathrm {Km}}(J)^{[3]}$.
$\operatorname {\mathrm {Km}}(J)^{[3]}$.
We will, in fact, show that for any odd ![]() $d$ the quotient
$d$ the quotient ![]() $K_J(v_d)/G$ is birational to a variety of
$K_J(v_d)/G$ is birational to a variety of ![]() $\mathrm {K}3^{[3]}$ type. Before proceeding with the proof we need to fix some notation.
$\mathrm {K}3^{[3]}$ type. Before proceeding with the proof we need to fix some notation.
3.2 Preliminaries
Let ![]() $C$ be a smooth projective curve of genus
$C$ be a smooth projective curve of genus ![]() $g$. Its Picard variety
$g$. Its Picard variety ![]() $\operatorname {\mathrm {Pic}}^{\bullet }(C)=\bigsqcup _d \operatorname {\mathrm {Pic}}^d(C)$ is the group of line bundles modulo isomorphism. Tensor product gives multiplication maps
$\operatorname {\mathrm {Pic}}^{\bullet }(C)=\bigsqcup _d \operatorname {\mathrm {Pic}}^d(C)$ is the group of line bundles modulo isomorphism. Tensor product gives multiplication maps ![]() $m\colon \operatorname {\mathrm {Pic}}^{a}(C) \times \operatorname {\mathrm {Pic}}^{b}(C) \to \operatorname {\mathrm {Pic}}^{a+b}(C)$. We denote by
$m\colon \operatorname {\mathrm {Pic}}^{a}(C) \times \operatorname {\mathrm {Pic}}^{b}(C) \to \operatorname {\mathrm {Pic}}^{a+b}(C)$. We denote by ![]() $[n]\colon \operatorname {\mathrm {Pic}}^d(C)\to \operatorname {\mathrm {Pic}}^{nd}(C)$ the
$[n]\colon \operatorname {\mathrm {Pic}}^d(C)\to \operatorname {\mathrm {Pic}}^{nd}(C)$ the ![]() $n$th power map. The Jacobian of
$n$th power map. The Jacobian of ![]() $C$ is the abelian variety
$C$ is the abelian variety ![]() $\operatorname {\mathrm {Pic}}^0(C)$; for
$\operatorname {\mathrm {Pic}}^0(C)$; for ![]() $d\neq 0$, the variety
$d\neq 0$, the variety ![]() $\operatorname {\mathrm {Pic}}^d(C)$ is a torsor under
$\operatorname {\mathrm {Pic}}^d(C)$ is a torsor under ![]() $\operatorname {\mathrm {Pic}}^0(C)$.
$\operatorname {\mathrm {Pic}}^0(C)$.
Assume now that ![]() $\pi \colon \tilde {C}\to C$ is an étale double cover, so that
$\pi \colon \tilde {C}\to C$ is an étale double cover, so that ![]() $\tilde {C}$ is of genus
$\tilde {C}$ is of genus ![]() $2g-1$. In this situation, for each integer
$2g-1$. In this situation, for each integer ![]() $d$, we have:
$d$, we have:
– the pull-back map
 $\pi ^*\colon \operatorname {\mathrm {Pic}}^{d}(C)\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$;
$\pi ^*\colon \operatorname {\mathrm {Pic}}^{d}(C)\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$;– the norm map
 $\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^d({C})$;
$\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^d({C})$;– the covering involution
 $\sigma \colon \tilde {C}\to \tilde {C}$, inducing
$\sigma \colon \tilde {C}\to \tilde {C}$, inducing  $\sigma ^*\colon \operatorname {\mathrm {Pic}}^{d}(\tilde {C})\to \operatorname {\mathrm {Pic}}^d(\tilde {C})$.
$\sigma ^*\colon \operatorname {\mathrm {Pic}}^{d}(\tilde {C})\to \operatorname {\mathrm {Pic}}^d(\tilde {C})$.
The composition ![]() $\mathrm {Nm}_\pi \circ \pi ^*\colon \operatorname {\mathrm {Pic}}^d(C)\to \operatorname {\mathrm {Pic}}^{2d}(C)$ coincides with multiplication by
$\mathrm {Nm}_\pi \circ \pi ^*\colon \operatorname {\mathrm {Pic}}^d(C)\to \operatorname {\mathrm {Pic}}^{2d}(C)$ coincides with multiplication by ![]() $2$, while
$2$, while ![]() $\pi ^*\circ \mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$ is given by
$\pi ^*\circ \mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$ is given by ![]() $L\mapsto L\otimes \sigma ^*(L)$.
$L\mapsto L\otimes \sigma ^*(L)$.
We refer to Mumford's paper [Reference MumfordMum74] for the following. The étale double cover ![]() $\pi$ is uniquely determined by a
$\pi$ is uniquely determined by a ![]() $2$-torsion line bundle
$2$-torsion line bundle ![]() $\eta$ on
$\eta$ on ![]() $C$, which is the only non-trivial element in
$C$, which is the only non-trivial element in ![]() $\ker (\pi ^*\colon \operatorname {\mathrm {Pic}}^{0}(C)\to \operatorname {\mathrm {Pic}}^0(\tilde {C}))$. Moreover, the image of the pull-back map
$\ker (\pi ^*\colon \operatorname {\mathrm {Pic}}^{0}(C)\to \operatorname {\mathrm {Pic}}^0(\tilde {C}))$. Moreover, the image of the pull-back map ![]() $\pi ^*\colon \operatorname {\mathrm {Pic}}^{d}(C)\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$ is precisely the fixed locus of
$\pi ^*\colon \operatorname {\mathrm {Pic}}^{d}(C)\to \operatorname {\mathrm {Pic}}^{2d}(\tilde {C})$ is precisely the fixed locus of ![]() $\sigma ^*$. The involution
$\sigma ^*$. The involution ![]() $\sigma ^*$ acts as the inverse
$\sigma ^*$ acts as the inverse ![]() $L\mapsto L^{\vee }$ on the kernel of the norm map
$L\mapsto L^{\vee }$ on the kernel of the norm map ![]() $\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^0(\tilde {C})\to \operatorname {\mathrm {Pic}}^0(C)$. This kernel has two connected components; the one containing the neutral element is the Prym variety
$\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^0(\tilde {C})\to \operatorname {\mathrm {Pic}}^0(C)$. This kernel has two connected components; the one containing the neutral element is the Prym variety ![]() $P(\pi )$ of the cover, an abelian variety of dimension
$P(\pi )$ of the cover, an abelian variety of dimension ![]() $g-1$. The fibres of
$g-1$. The fibres of ![]() $\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^d(C)$ are torsors under
$\mathrm {Nm}_\pi \colon \operatorname {\mathrm {Pic}}^d(\tilde {C})\to \operatorname {\mathrm {Pic}}^d(C)$ are torsors under ![]() $P(\pi )\times {\mathbb {Z}}/2 {\mathbb {Z}}$.
$P(\pi )\times {\mathbb {Z}}/2 {\mathbb {Z}}$.
3.3 Geometric set-up
Let ![]() $\Theta \subset J$ be the general principally polarized abelian surface of Picard rank
$\Theta \subset J$ be the general principally polarized abelian surface of Picard rank ![]() $1$, with
$1$, with ![]() $\Theta$ a symmetric theta divisor. By Riemann–Roch
$\Theta$ a symmetric theta divisor. By Riemann–Roch ![]() $H^0(J, \mathcal {O}_J(2\Theta ))=4$; we will identify the complete linear system
$H^0(J, \mathcal {O}_J(2\Theta ))=4$; we will identify the complete linear system ![]() $\lvert 2\Theta \rvert$ with
$\lvert 2\Theta \rvert$ with ![]() $ {\mathbb {P}}^3$. It is classically known that this linear system is base-point free and induces an embedding of
$ {\mathbb {P}}^3$. It is classically known that this linear system is base-point free and induces an embedding of ![]() $J/\pm 1$ into
$J/\pm 1$ into ![]() $ {\mathbb {P}}^{3,\vee }$ as a quartic surface with
$ {\mathbb {P}}^{3,\vee }$ as a quartic surface with ![]() $16$ nodes. Blowing-up the nodes of this quartic surface one obtains the Kummer K3 surface
$16$ nodes. Blowing-up the nodes of this quartic surface one obtains the Kummer K3 surface ![]() $\operatorname {\mathrm {Km}}(J)$ associated to
$\operatorname {\mathrm {Km}}(J)$ associated to ![]() $J$. We denote by
$J$. We denote by ![]() $H$ the divisor on
$H$ the divisor on ![]() $\operatorname {\mathrm {Km}}(J)$ obtained as pull-back of a hyperplane section of
$\operatorname {\mathrm {Km}}(J)$ obtained as pull-back of a hyperplane section of ![]() $J/\pm 1\subset {\mathbb {P}}^{3,\vee }$. The linear system
$J/\pm 1\subset {\mathbb {P}}^{3,\vee }$. The linear system ![]() $|H|$ is naturally identified with
$|H|$ is naturally identified with ![]() $\lvert 2\Theta \rvert = {\mathbb {P}}^3$.
$\lvert 2\Theta \rvert = {\mathbb {P}}^3$.
Consider the universal family of genus-![]() $5$ curves
$5$ curves ![]() $\tilde {\mathcal {C}}\to \lvert 2\Theta \rvert$. The involution
$\tilde {\mathcal {C}}\to \lvert 2\Theta \rvert$. The involution ![]() $-1$ of
$-1$ of ![]() $J$ acts trivially on
$J$ acts trivially on ![]() $\lvert 2\Theta \rvert$, and we consider the quotient family
$\lvert 2\Theta \rvert$, and we consider the quotient family ![]() $\mathcal {C}\to {\mathbb {P}}^3$, which is identified with the hyperplane linear system on
$\mathcal {C}\to {\mathbb {P}}^3$, which is identified with the hyperplane linear system on ![]() $J/\pm 1\subset {\mathbb {P}}^{3,\vee }$. There is a degree
$J/\pm 1\subset {\mathbb {P}}^{3,\vee }$. There is a degree ![]() $2$ morphism
$2$ morphism ![]() $\pi \colon \tilde {\mathcal {C}}\to \mathcal {C}$ over
$\pi \colon \tilde {\mathcal {C}}\to \mathcal {C}$ over ![]() $ {\mathbb {P}}^3$. We denote by
$ {\mathbb {P}}^3$. We denote by ![]() $\mathcal {D}\to \lvert H\rvert$ the universal family of curves over the linear system
$\mathcal {D}\to \lvert H\rvert$ the universal family of curves over the linear system ![]() $\lvert H\rvert$ on
$\lvert H\rvert$ on ![]() $\operatorname {\mathrm {Km}}(J)$; clearly,
$\operatorname {\mathrm {Km}}(J)$; clearly, ![]() $\mathcal {C}_b=\mathcal {D}_b$ if and only if
$\mathcal {C}_b=\mathcal {D}_b$ if and only if ![]() $\mathcal {C}_b$ does not pass through any of the nodes of
$\mathcal {C}_b$ does not pass through any of the nodes of ![]() $J/\pm 1$.
$J/\pm 1$.
A detailed study of the linear system ![]() $\lvert 2\Theta \rvert$ and the map
$\lvert 2\Theta \rvert$ and the map ![]() $\pi \colon \tilde {\mathcal {C}}\to \mathcal {C}$ can be found in Verra's article [Reference VerraVer87]. In particular, he shows that, for any
$\pi \colon \tilde {\mathcal {C}}\to \mathcal {C}$ can be found in Verra's article [Reference VerraVer87]. In particular, he shows that, for any ![]() $b\in {\mathbb {P}}^3$, the curve
$b\in {\mathbb {P}}^3$, the curve ![]() $\tilde {\mathcal {C}}_b$ is smooth if and only if
$\tilde {\mathcal {C}}_b$ is smooth if and only if ![]() $\mathcal {C}_b$ is so, and in this case the Prym variety of the étale double cover
$\mathcal {C}_b$ is so, and in this case the Prym variety of the étale double cover ![]() $\pi _b \colon \tilde {\mathcal {C}}_b \to \mathcal {C}_b$ is the abelian surface
$\pi _b \colon \tilde {\mathcal {C}}_b \to \mathcal {C}_b$ is the abelian surface ![]() $J$. Moreover,
$J$. Moreover, ![]() $\mathcal {C}_b$ is smooth if and only if it does not contain any node of
$\mathcal {C}_b$ is smooth if and only if it does not contain any node of ![]() $J/\pm 1$ and it does not lie on a tangent hyperplane.
$J/\pm 1$ and it does not lie on a tangent hyperplane.
3.4 Beauville–Mukai systems
Taking the Jacobian of the smooth curves in the families introduced above yields families of abelian varieties over a Zariski open subvariety of ![]() $ {\mathbb {P}}^3$. The total space of these families can be compactified considering suitable moduli spaces of stable sheaves on
$ {\mathbb {P}}^3$. The total space of these families can be compactified considering suitable moduli spaces of stable sheaves on ![]() $J$ and
$J$ and ![]() $\mathrm {Km}(J)$. The construction leads to certain hyper-Kähler varieties equipped with Lagrangians fibrations, called Beauville–Mukai systems [Reference BeauvilleBea91, Reference MukaiMuk84].
$\mathrm {Km}(J)$. The construction leads to certain hyper-Kähler varieties equipped with Lagrangians fibrations, called Beauville–Mukai systems [Reference BeauvilleBea91, Reference MukaiMuk84].
Consider the Mukai vector ![]() $v_d=(0, 2\Theta, d-4)$ on
$v_d=(0, 2\Theta, d-4)$ on ![]() $J$, for an integer
$J$, for an integer ![]() $d$. The moduli space
$d$. The moduli space ![]() $M_J(v_d)$ parametrizes pure dimension
$M_J(v_d)$ parametrizes pure dimension ![]() $1$ sheaves on
$1$ sheaves on ![]() $J$ which are push-forward of semistable and torsion-free sheaves of rank
$J$ which are push-forward of semistable and torsion-free sheaves of rank ![]() $1$ and degree
$1$ and degree ![]() $d$ supported on curves algebraically equivalent to
$d$ supported on curves algebraically equivalent to ![]() $2\Theta$. Mapping a sheaf to its support [Reference Le PotierLeP93] gives a morphism
$2\Theta$. Mapping a sheaf to its support [Reference Le PotierLeP93] gives a morphism
We define the degree-![]() $d$ relative compactified Jacobian as
$d$ relative compactified Jacobian as
If ![]() $b\in {\mathbb {P}}^3$ corresponds to a smooth curve in
$b\in {\mathbb {P}}^3$ corresponds to a smooth curve in ![]() $|2\Theta |$, the fibre over
$|2\Theta |$, the fibre over ![]() $b$ of the support morphism
$b$ of the support morphism ![]() $\mathrm {supp}\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \to {\mathbb {P}}^3$ is the degree-
$\mathrm {supp}\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \to {\mathbb {P}}^3$ is the degree-![]() $d$ Picard variety of the curve. The Albanese morphism
$d$ Picard variety of the curve. The Albanese morphism ![]() $\mathrm {alb}\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \to J$ is an isotrivial fibration with fibre
$\mathrm {alb}\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \to J$ is an isotrivial fibration with fibre ![]() $K_J(v_d)$, and it maps a sheaf
$K_J(v_d)$, and it maps a sheaf ![]() $F\in K_J(v_d)$ to the sum
$F\in K_J(v_d)$ to the sum ![]() $\sum c_2(F)\in J$, see [Reference WieneckWie18, § 6].
$\sum c_2(F)\in J$, see [Reference WieneckWie18, § 6].
A similar construction can be done for the family of curves ![]() $\mathcal {D}$ on
$\mathcal {D}$ on ![]() $\operatorname {\mathrm {Km}}(J)$. Given an integer
$\operatorname {\mathrm {Km}}(J)$. Given an integer ![]() $d$, we consider the Mukai vector
$d$, we consider the Mukai vector ![]() $w_d= (0, H, d-2)$ on
$w_d= (0, H, d-2)$ on ![]() $\operatorname {\mathrm {Km}}(J)$. The degree
$\operatorname {\mathrm {Km}}(J)$. The degree ![]() $d$ relative compactified Jacobian of curves in
$d$ relative compactified Jacobian of curves in ![]() $|H|$ is the moduli space
$|H|$ is the moduli space
of semistable sheaves with Mukai vector ![]() $w_d$, with respect to a fixed
$w_d$, with respect to a fixed ![]() $w_d$-generic polarization. It is a hyper-Kähler variety of
$w_d$-generic polarization. It is a hyper-Kähler variety of ![]() $\mathrm {K}3^{[3]}$ type by [Reference O'GradyO'Gr97] and [Reference YoshiokaYos99]. The moduli space
$\mathrm {K}3^{[3]}$ type by [Reference O'GradyO'Gr97] and [Reference YoshiokaYos99]. The moduli space ![]() $M_{\operatorname {\mathrm {Km}}(J)}(w_d)$ parametrizes pure dimension-
$M_{\operatorname {\mathrm {Km}}(J)}(w_d)$ parametrizes pure dimension-![]() $1$ sheaves on
$1$ sheaves on ![]() $\operatorname {\mathrm {Km}}(J)$ which are push-forward of torsion-free sheaves of rank
$\operatorname {\mathrm {Km}}(J)$ which are push-forward of torsion-free sheaves of rank ![]() $1$ and degree
$1$ and degree ![]() $d$ on curves in the linear system
$d$ on curves in the linear system ![]() $\lvert H \rvert$. There is a morphism
$\lvert H \rvert$. There is a morphism ![]() $\mathrm {supp} \colon \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)\to {\mathbb {P}}^3$ which is a Lagrangian fibration, whose general fibres are the degree-
$\mathrm {supp} \colon \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)\to {\mathbb {P}}^3$ which is a Lagrangian fibration, whose general fibres are the degree-![]() $d$ Picard varieties of the smooth curves in
$d$ Picard varieties of the smooth curves in ![]() $\lvert H \rvert$.
$\lvert H \rvert$.
3.5 The relative norm map
We denote by ![]() $B\subset {\mathbb {P}}^3$ the locus parametrizing smooth curves. The maps introduced in § 3.2 give morphisms over
$B\subset {\mathbb {P}}^3$ the locus parametrizing smooth curves. The maps introduced in § 3.2 give morphisms over ![]() $B$. Hence, we obtain rational maps
$B$. Hence, we obtain rational maps
 \begin{align*} \mathrm{Nm}_\pi & \colon \overline{\operatorname{\mathrm{Pic}}}^d(\tilde{\mathcal{C}}/{\mathbb{P}}^3) \dashrightarrow \overline{\operatorname{\mathrm{Pic}}}^{d}({\mathcal{D}}/{\mathbb{P}}^3);\\ \pi^* & \colon \overline{\operatorname{\mathrm{Pic}}}^d(\mathcal{D}/{\mathbb{P}}^3) \dashrightarrow \overline{\operatorname{\mathrm{Pic}}}^{2d}(\tilde{\mathcal{C}}/{\mathbb{P}}^3). \end{align*}
\begin{align*} \mathrm{Nm}_\pi & \colon \overline{\operatorname{\mathrm{Pic}}}^d(\tilde{\mathcal{C}}/{\mathbb{P}}^3) \dashrightarrow \overline{\operatorname{\mathrm{Pic}}}^{d}({\mathcal{D}}/{\mathbb{P}}^3);\\ \pi^* & \colon \overline{\operatorname{\mathrm{Pic}}}^d(\mathcal{D}/{\mathbb{P}}^3) \dashrightarrow \overline{\operatorname{\mathrm{Pic}}}^{2d}(\tilde{\mathcal{C}}/{\mathbb{P}}^3). \end{align*}
The pull-back ![]() $\pi ^*$ has been studied by Rapagnetta [Reference RapagnettaRap07] and by Mongardi, Rapagnetta and Saccà [Reference Mongardi, Rapagnetta and SaccàMRS18]. They show that it gives a degree-
$\pi ^*$ has been studied by Rapagnetta [Reference RapagnettaRap07] and by Mongardi, Rapagnetta and Saccà [Reference Mongardi, Rapagnetta and SaccàMRS18]. They show that it gives a degree-![]() $2$ dominant rational map
$2$ dominant rational map
exhibiting a variety of OG6 type as the quotient of a variety of ![]() $\mathrm {K}3^{[3]}$ type by a birational symplectic involution. We consider instead the norm map
$\mathrm {K}3^{[3]}$ type by a birational symplectic involution. We consider instead the norm map ![]() $\mathrm {Nm}_{\pi }$.
$\mathrm {Nm}_{\pi }$.
Lemma 3.6 For each ![]() $d$, the restriction
$d$, the restriction ![]() $\mathrm {Nm}_\pi \colon K_J(v_d) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{d}({\mathcal {D}}/ {\mathbb {P}}^3)$ is dominant and generically finite of degree
$\mathrm {Nm}_\pi \colon K_J(v_d) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{d}({\mathcal {D}}/ {\mathbb {P}}^3)$ is dominant and generically finite of degree ![]() $2^5$.
$2^5$.
Proof. For each ![]() $k$, the
$k$, the ![]() $k$th power map
$k$th power map ![]() $[k]\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{kd}(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)$ restricts to a rational map
$[k]\colon \overline {\operatorname {\mathrm {Pic}}}^d(\tilde {\mathcal {C}}/ {\mathbb {P}}^3) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{kd}(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)$ restricts to a rational map ![]() $[k]\colon K_J(v_d) \dashrightarrow K_J(v_{kd})$. This can be easily checked at smooth curves
$[k]\colon K_J(v_d) \dashrightarrow K_J(v_{kd})$. This can be easily checked at smooth curves ![]() $\tilde {\mathcal {C}_b}$ in the family using the description of the Albanese map
$\tilde {\mathcal {C}_b}$ in the family using the description of the Albanese map ![]() $L\mapsto \sum c_2(L)$.
$L\mapsto \sum c_2(L)$.
Consider the following commutative diagram.

Both the horizontal maps are dominant and generically finite of the same degree ![]() $2^6$. Indeed, they preserve the fibres of the respective support morphisms, which, generically, are torsors under abelian threefolds. Hence, the degree of
$2^6$. Indeed, they preserve the fibres of the respective support morphisms, which, generically, are torsors under abelian threefolds. Hence, the degree of ![]() $[2]$ is the number of points of order
$[2]$ is the number of points of order ![]() $2$ on an abelian threefold.
$2$ on an abelian threefold.
It thus suffices to prove the lemma for ![]() $\mathrm {Nm}_\pi \colon K_J(v_{2d}) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{2d}({\mathcal {D}}/ {\mathbb {P}}^3)$. Since
$\mathrm {Nm}_\pi \colon K_J(v_{2d}) \dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^{2d}({\mathcal {D}}/ {\mathbb {P}}^3)$. Since ![]() $K_J(v_{2d})$ is the closure of the image of
$K_J(v_{2d})$ is the closure of the image of ![]() $\pi ^*$, the involution
$\pi ^*$, the involution ![]() $\sigma ^*$ is the identity on
$\sigma ^*$ is the identity on ![]() $K_J(v_{2d})$. Hence, the rational map
$K_J(v_{2d})$. Hence, the rational map
coincides with multiplication by ![]() $[2]$; this composition is therefore dominant and generically finite of degree
$[2]$; this composition is therefore dominant and generically finite of degree ![]() $2^6$. Since
$2^6$. Since ![]() $\pi ^*\colon \overline {\operatorname {\mathrm {Pic}}}^{2d}({\mathcal {D}}/ {\mathbb {P}}^3)\dashrightarrow K_J(v_{4d})$ is generically finite of degree
$\pi ^*\colon \overline {\operatorname {\mathrm {Pic}}}^{2d}({\mathcal {D}}/ {\mathbb {P}}^3)\dashrightarrow K_J(v_{4d})$ is generically finite of degree ![]() $2$, it follows that
$2$, it follows that ![]() $\mathrm {Nm}_\pi$ is dominant and it has degree
$\mathrm {Nm}_\pi$ is dominant and it has degree ![]() $2^5$.
$2^5$.
3.7 The action of  $G$
$G$
Assume now that ![]() $d$ is odd, so that
$d$ is odd, so that ![]() $K_J(v_d)$ is a smooth variety of
$K_J(v_d)$ is a smooth variety of ![]() $\mathrm {Kum}^3$ type and the support map gives a Lagrangian fibration on it. In this case the group
$\mathrm {Kum}^3$ type and the support map gives a Lagrangian fibration on it. In this case the group ![]() $\operatorname {Aut}_0(K_J(v_d))$ has been explicitly identified by Kim in [Reference KimKim21].
$\operatorname {Aut}_0(K_J(v_d))$ has been explicitly identified by Kim in [Reference KimKim21].
Proposition 3.8 Let ![]() $d$ be odd. Then
$d$ be odd. Then ![]() $G=\operatorname {\mathrm {Pic}}^0(J)_2 \times \langle -1\rangle$, where
$G=\operatorname {\mathrm {Pic}}^0(J)_2 \times \langle -1\rangle$, where ![]() $-1$ acts on
$-1$ acts on ![]() $K_J(v_d)$ via the pull-back
$K_J(v_d)$ via the pull-back ![]() $F\mapsto (-1)^*(F)$ of sheaves, and the action of
$F\mapsto (-1)^*(F)$ of sheaves, and the action of ![]() $L\in \operatorname {\mathrm {Pic}}^0(J)_2$ is given by
$L\in \operatorname {\mathrm {Pic}}^0(J)_2$ is given by ![]() $F\mapsto F\otimes L$. Any element of
$F\mapsto F\otimes L$. Any element of ![]() $G$ preserves the fibres of the support fibration.
$G$ preserves the fibres of the support fibration.
Proof. We first show that ![]() $\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle$ acts on
$\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle$ acts on ![]() $K_J(v_d)$ via automorphisms trivial on the second cohomology and which preserve the Lagrangian fibration given by the support morphism.
$K_J(v_d)$ via automorphisms trivial on the second cohomology and which preserve the Lagrangian fibration given by the support morphism.
Since ![]() $-1\colon J\to J$ acts trivially on the cohomology of
$-1\colon J\to J$ acts trivially on the cohomology of ![]() $J$ in even degrees, the pull-back of sheaves defines an automorphism
$J$ in even degrees, the pull-back of sheaves defines an automorphism ![]() $(-1)^*$ of
$(-1)^*$ of ![]() $K_J(v_d)$; this automorphism is trivial for
$K_J(v_d)$; this automorphism is trivial for ![]() $d$ even but not for
$d$ even but not for ![]() $d$ odd. By [Reference Mongardi and WandelMW15, Lemma 2.34], the action of
$d$ odd. By [Reference Mongardi and WandelMW15, Lemma 2.34], the action of ![]() $(-1)^*$ is symplectic, i.e. the induced action on the transcendental cohomology
$(-1)^*$ is symplectic, i.e. the induced action on the transcendental cohomology ![]() $H^2_{\mathrm {tr}}(K_J(v_d), {\mathbb {Z}})$ is the identity. Since all curves in
$H^2_{\mathrm {tr}}(K_J(v_d), {\mathbb {Z}})$ is the identity. Since all curves in ![]() $\lvert 2\Theta \rvert$ are stable under
$\lvert 2\Theta \rvert$ are stable under ![]() $-1$, the automorphism
$-1$, the automorphism ![]() $(-1)^*$ preserves all fibres of the support fibration. The Picard rank of
$(-1)^*$ preserves all fibres of the support fibration. The Picard rank of ![]() $K_J(v_d)$ is
$K_J(v_d)$ is ![]() $2$, because
$2$, because ![]() $J$ is a general abelian surface by assumption (see [Reference YoshiokaYos01]). Hence, by Lemma 3.10, the induced action of
$J$ is a general abelian surface by assumption (see [Reference YoshiokaYos01]). Hence, by Lemma 3.10, the induced action of ![]() $(-1)^*$ on
$(-1)^*$ on ![]() $\operatorname {\mathrm {NS}}(K_J(v_d))$ is also the identity. Since
$\operatorname {\mathrm {NS}}(K_J(v_d))$ is also the identity. Since ![]() $H^2(K_J(v_d), {\mathbb {Z}})$ is torsion free, we conclude that
$H^2(K_J(v_d), {\mathbb {Z}})$ is torsion free, we conclude that ![]() $(-1)^*$ acts trivially on the second cohomology.
$(-1)^*$ acts trivially on the second cohomology.
Now let ![]() $L\in \operatorname {\mathrm {Pic}}^0(J)_2$. Let
$L\in \operatorname {\mathrm {Pic}}^0(J)_2$. Let ![]() $B\subset \lvert 2\Theta \rvert$ be the locus of smooth curves, and consider the universal curve
$B\subset \lvert 2\Theta \rvert$ be the locus of smooth curves, and consider the universal curve ![]() $j\colon \tilde {\mathcal {C}}_B\hookrightarrow J\times B$. By [Reference WieneckWie18, Lemma 6.9], the corresponding pull-back
$j\colon \tilde {\mathcal {C}}_B\hookrightarrow J\times B$. By [Reference WieneckWie18, Lemma 6.9], the corresponding pull-back ![]() $j^*\colon \operatorname {\mathrm {Pic}}^0(J)\times B \to \overline {\operatorname {\mathrm {Pic}}}^0(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)_B$ is an injection of abelian schemes. Note that the covering involution
$j^*\colon \operatorname {\mathrm {Pic}}^0(J)\times B \to \overline {\operatorname {\mathrm {Pic}}}^0(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)_B$ is an injection of abelian schemes. Note that the covering involution ![]() $\sigma$ for the cover
$\sigma$ for the cover ![]() $\pi \colon \tilde {\mathcal {C}}_B\to {\mathcal {C}}_B$ is the restriction of
$\pi \colon \tilde {\mathcal {C}}_B\to {\mathcal {C}}_B$ is the restriction of ![]() $-1\times \mathrm {id}_B$. Hence, the induced involution
$-1\times \mathrm {id}_B$. Hence, the induced involution ![]() $\sigma ^*$ on
$\sigma ^*$ on ![]() $\overline {\operatorname {\mathrm {Pic}}}^0(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)_B$ is the inverse map on
$\overline {\operatorname {\mathrm {Pic}}}^0(\tilde {\mathcal {C}}/ {\mathbb {P}}^3)_B$ is the inverse map on ![]() $j^*_b(\operatorname {\mathrm {Pic}}^0(J))$, for each
$j^*_b(\operatorname {\mathrm {Pic}}^0(J))$, for each ![]() $b\in B$. As
$b\in B$. As ![]() $K_J(v_0)$ is the fixed locus of this involution, the
$K_J(v_0)$ is the fixed locus of this involution, the ![]() $2$-torsion line bundle
$2$-torsion line bundle ![]() $L$ on
$L$ on ![]() $J$ corresponds uniquely to a
$J$ corresponds uniquely to a ![]() $2$-torsion section
$2$-torsion section ![]() $s_L$ of
$s_L$ of ![]() $K_J(v_0)_B\to B$. For any
$K_J(v_0)_B\to B$. For any ![]() $d$, the variety
$d$, the variety ![]() $K_J(v_d)_B$ is a torsor under
$K_J(v_d)_B$ is a torsor under ![]() $K_J(v_0)_B$ and, hence,
$K_J(v_0)_B$ and, hence, ![]() $F\mapsto F\otimes L$ induces a birational automorphism
$F\mapsto F\otimes L$ induces a birational automorphism ![]() $g_L$ of
$g_L$ of ![]() $K_J(v_d)$, which restricts to a translation on the smooth fibres of the support morphism. This implies that
$K_J(v_d)$, which restricts to a translation on the smooth fibres of the support morphism. This implies that ![]() $g_L$ is symplectic. We deduce from Lemma 3.10 that
$g_L$ is symplectic. We deduce from Lemma 3.10 that ![]() $g_L$ extends to a regular automorphism of
$g_L$ extends to a regular automorphism of ![]() $K_J(v_d)$, whose induced action is trivial on
$K_J(v_d)$, whose induced action is trivial on ![]() $\operatorname {\mathrm {NS}}(K_J(v_d))$ as well.
$\operatorname {\mathrm {NS}}(K_J(v_d))$ as well.
According to [Reference KimKim21, Theorem 5.1] we have described all automorphisms in ![]() $\operatorname {Aut}_0(K_J(v_d))$ preserving the fibration
$\operatorname {Aut}_0(K_J(v_d))$ preserving the fibration ![]() $\mathrm {supp}\colon K_J(v_d)\to {\mathbb {P}}^3$. We claim now that an automorphism in
$\mathrm {supp}\colon K_J(v_d)\to {\mathbb {P}}^3$. We claim now that an automorphism in ![]() $\operatorname {Aut}_0(K_J(v_d))$ which does not preserve the fibration cannot fix a component of dimension
$\operatorname {Aut}_0(K_J(v_d))$ which does not preserve the fibration cannot fix a component of dimension ![]() $4$ on
$4$ on ![]() $K_J(v_d)$; this will show that
$K_J(v_d)$; this will show that ![]() $G=\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle$.
$G=\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle$.
Let ![]() $D = \mathrm {supp}^* (\mathcal {O}_{ {\mathbb {P}}^n}(1)) \in \operatorname {\mathrm {Pic}}(K_J(v_d))$ be the line bundle inducing the fibration. Since
$D = \mathrm {supp}^* (\mathcal {O}_{ {\mathbb {P}}^n}(1)) \in \operatorname {\mathrm {Pic}}(K_J(v_d))$ be the line bundle inducing the fibration. Since ![]() $\operatorname {Aut}_0(K_J(v_d))$ acts trivially on
$\operatorname {Aut}_0(K_J(v_d))$ acts trivially on ![]() $H^2(K_J(v_d), {\mathbb {Z}})$, it acts on
$H^2(K_J(v_d), {\mathbb {Z}})$, it acts on ![]() $|D|= {\mathbb {P}}^3=|2\Theta |$. We obtain an action of
$|D|= {\mathbb {P}}^3=|2\Theta |$. We obtain an action of ![]() $\operatorname {Aut}_0(K_J(v_d))/(\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle ) \cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^4$ on
$\operatorname {Aut}_0(K_J(v_d))/(\operatorname {\mathrm {Pic}}^0(J)_2\times \langle -1\rangle ) \cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^4$ on ![]() $|2\Theta |$, which, up to conjugation by an automorphism of
$|2\Theta |$, which, up to conjugation by an automorphism of ![]() $ {\mathbb {P}}^3$, is identified with the action generated by
$ {\mathbb {P}}^3$, is identified with the action generated by
see [Reference Gonzalez-DorregoGon94, Lemma 1.52, Note 1.4]. Thus, ![]() $h\in \operatorname {Aut}_0(K_J(v_d))$ either acts trivially on
$h\in \operatorname {Aut}_0(K_J(v_d))$ either acts trivially on ![]() $|2\Theta |$ or it fixes a pair of skew lines. Assume by contradiction that
$|2\Theta |$ or it fixes a pair of skew lines. Assume by contradiction that ![]() $h\in \operatorname {Aut}_0(K_J(v_d))$ fixes a fourfold but does not preserve the support fibration. Then
$h\in \operatorname {Aut}_0(K_J(v_d))$ fixes a fourfold but does not preserve the support fibration. Then ![]() $(K_J(v_d))^h$ contains one of the varieties
$(K_J(v_d))^h$ contains one of the varieties ![]() ${Z_{j}}$ of
${Z_{j}}$ of ![]() $\mathrm {K}3^{[2]}$ type from Theorem 2.2, and the image of
$\mathrm {K}3^{[2]}$ type from Theorem 2.2, and the image of ![]() $Z_j$ via the fibration must be a line
$Z_j$ via the fibration must be a line ![]() $R \subset |2\Theta |$ fixed by
$R \subset |2\Theta |$ fixed by ![]() $h$. But, by a theorem of Matsushita [Reference MatsushitaMat99], the
$h$. But, by a theorem of Matsushita [Reference MatsushitaMat99], the ![]() $\mathrm {K}3^{[2]}$ variety
$\mathrm {K}3^{[2]}$ variety ![]() $Z_j$ does not admit any non-constant morphism to
$Z_j$ does not admit any non-constant morphism to ![]() $ {\mathbb {P}}^1$.
$ {\mathbb {P}}^1$.
Remark 3.9 By [Reference VerraVer87], the relative Prym variety ![]() $\mathcal {P}\to B$ of the double cover
$\mathcal {P}\to B$ of the double cover ![]() $\pi \colon \tilde {\mathcal {C}}_B\to \mathcal {C}_B$ is an isotrivial family over
$\pi \colon \tilde {\mathcal {C}}_B\to \mathcal {C}_B$ is an isotrivial family over ![]() $B$ with fibre
$B$ with fibre ![]() $J$. Since the involution
$J$. Since the involution ![]() $\sigma ^*$ acts as the inverse on the image of the pull-back
$\sigma ^*$ acts as the inverse on the image of the pull-back ![]() $j^*$, the constant abelian scheme
$j^*$, the constant abelian scheme ![]() $j^*(\operatorname {\mathrm {Pic}}^0(J)\times B)$ is contained into, and hence equal to, the relative Prym variety.
$j^*(\operatorname {\mathrm {Pic}}^0(J)\times B)$ is contained into, and hence equal to, the relative Prym variety.
Lemma 3.10 Let ![]() $f\colon X\to {\mathbb {P}}^n$ be a Lagrangian fibration, where
$f\colon X\to {\mathbb {P}}^n$ be a Lagrangian fibration, where ![]() $X$ is a
$X$ is a ![]() $2n$-dimensional projective hyper-Kähler variety of Picard rank
$2n$-dimensional projective hyper-Kähler variety of Picard rank ![]() $2$. Let
$2$. Let ![]() $g\colon X\dashrightarrow X$ be a birational automorphism such that
$g\colon X\dashrightarrow X$ be a birational automorphism such that ![]() $f\circ g = f$. Then
$f\circ g = f$. Then ![]() $g$ extends to a regular automorphism of
$g$ extends to a regular automorphism of ![]() $X$, and
$X$, and ![]() $g^*_{\lvert _{ \operatorname {\mathrm {NS}}(X)}}\colon \operatorname {\mathrm {NS}}(X)\to \operatorname {\mathrm {NS}}(X)$ is the identity.
$g^*_{\lvert _{ \operatorname {\mathrm {NS}}(X)}}\colon \operatorname {\mathrm {NS}}(X)\to \operatorname {\mathrm {NS}}(X)$ is the identity.
Proof. The Néron–Severi group ![]() $\operatorname {\mathrm {NS}}(X)$ is a rank
$\operatorname {\mathrm {NS}}(X)$ is a rank ![]() $2$ lattice of signature
$2$ lattice of signature ![]() $(1,1)$. Any birational automorphism
$(1,1)$. Any birational automorphism ![]() $g$ induces an isometry
$g$ induces an isometry ![]() $g^*$ of
$g^*$ of ![]() $H^2(X, {\mathbb {Z}})$ which restricts to an isometry of
$H^2(X, {\mathbb {Z}})$ which restricts to an isometry of ![]() $\operatorname {\mathrm {NS}}(X)$. Denote by
$\operatorname {\mathrm {NS}}(X)$. Denote by ![]() $D\in \operatorname {\mathrm {NS}}(X)$ the class of the line bundle
$D\in \operatorname {\mathrm {NS}}(X)$ the class of the line bundle ![]() $f^*(\mathcal {O}_{ {\mathbb {P}}^n}(1))$, and pick
$f^*(\mathcal {O}_{ {\mathbb {P}}^n}(1))$, and pick ![]() $E\in \operatorname {\mathrm {NS}}(X)$ such that
$E\in \operatorname {\mathrm {NS}}(X)$ such that ![]() $D$ and
$D$ and ![]() $E$ generate
$E$ generate ![]() $\operatorname {\mathrm {NS}}(X)\otimes {\mathbb {Q}}$. Since
$\operatorname {\mathrm {NS}}(X)\otimes {\mathbb {Q}}$. Since ![]() $f\circ g=f$, we have
$f\circ g=f$, we have ![]() $g^*(D)=D$. Using that
$g^*(D)=D$. Using that ![]() $D$ is isotropic one sees that this forces
$D$ is isotropic one sees that this forces ![]() $g^*(E)=E$ as well, so that
$g^*(E)=E$ as well, so that ![]() $g^*$ is the identity on
$g^*$ is the identity on ![]() $\operatorname {\mathrm {NS}}(X)$; by [Reference FujikiFuj81],
$\operatorname {\mathrm {NS}}(X)$; by [Reference FujikiFuj81], ![]() $g$ extends to an automorphism of
$g$ extends to an automorphism of ![]() $X$.
$X$.
We can now complete the proof of the main result of this section.
Proof of Theorem 3.1 Using the identification of ![]() $G$ given in Proposition 3.8 we will show that the norm map descends to a birational map
$G$ given in Proposition 3.8 we will show that the norm map descends to a birational map ![]() $K_J(v_d)/G\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$, for any odd
$K_J(v_d)/G\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$, for any odd ![]() $d$. The varieties
$d$. The varieties ![]() $\overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ are of
$\overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ are of ![]() $\mathrm {K}3^{[3]}$ type, and
$\mathrm {K}3^{[3]}$ type, and ![]() $\overline {\operatorname {\mathrm {Pic}}}^3(\mathcal {D}/ {\mathbb {P}}^3)$ is birational to
$\overline {\operatorname {\mathrm {Pic}}}^3(\mathcal {D}/ {\mathbb {P}}^3)$ is birational to ![]() $\operatorname {\mathrm {Km}}(J)^{[3]}$, see [Reference BeauvilleBea99, Proposition 1.3].
$\operatorname {\mathrm {Km}}(J)^{[3]}$, see [Reference BeauvilleBea99, Proposition 1.3].
For a smooth curve ![]() $\tilde {\mathcal {C}}_b \in \lvert 2\Theta \rvert$ the norm map is induced by the map of divisors which sends
$\tilde {\mathcal {C}}_b \in \lvert 2\Theta \rvert$ the norm map is induced by the map of divisors which sends ![]() $\sum _i a_i[P_i]$ to
$\sum _i a_i[P_i]$ to ![]() $\sum _i a_i [\pi (P_i)]$. It is then clear that
$\sum _i a_i [\pi (P_i)]$. It is then clear that ![]() $\mathrm {Nm}_\pi ((-1)^*(F))= \mathrm {Nm}_\pi (F)$ for any
$\mathrm {Nm}_\pi ((-1)^*(F))= \mathrm {Nm}_\pi (F)$ for any ![]() $F\in K_J(v_d)_B$. Instead let
$F\in K_J(v_d)_B$. Instead let ![]() $L\in \operatorname {\mathrm {Pic}}^0(J)_2$, and let
$L\in \operatorname {\mathrm {Pic}}^0(J)_2$, and let ![]() $s_L\colon {\mathbb {P}}^3 \dashrightarrow K_J(v_0)$ be the rational section defined by
$s_L\colon {\mathbb {P}}^3 \dashrightarrow K_J(v_0)$ be the rational section defined by ![]() $s_L(b)= j_b^*(L)$, where
$s_L(b)= j_b^*(L)$, where ![]() $j\colon \tilde {\mathcal {C}}_B\hookrightarrow J\times B$ denotes the natural inclusion. By Remark 3.9, the section
$j\colon \tilde {\mathcal {C}}_B\hookrightarrow J\times B$ denotes the natural inclusion. By Remark 3.9, the section ![]() $s_L$ is contained in the relative Prym variety; in particular, the composition
$s_L$ is contained in the relative Prym variety; in particular, the composition ![]() $\mathrm {Nm}_\pi \circ s_L$ gives the zero section of
$\mathrm {Nm}_\pi \circ s_L$ gives the zero section of ![]() $\overline {\operatorname {\mathrm {Pic}}}^0(\mathcal {D}/ {\mathbb {P}}^3)_B\to {\mathbb {P}}^3$.
$\overline {\operatorname {\mathrm {Pic}}}^0(\mathcal {D}/ {\mathbb {P}}^3)_B\to {\mathbb {P}}^3$.
Therefore, for any ![]() $g\in G$ and
$g\in G$ and ![]() $y\in K_J(v_d)_B$ we have
$y\in K_J(v_d)_B$ we have ![]() $\mathrm {Nm}_\pi (g(y))= \mathrm {Nm}_\pi (y)$, which means that
$\mathrm {Nm}_\pi (g(y))= \mathrm {Nm}_\pi (y)$, which means that ![]() $\mathrm {Nm}_\pi \colon K_J(v_d)\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ descends to a rational map
$\mathrm {Nm}_\pi \colon K_J(v_d)\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ descends to a rational map
This map is, in fact, birational, because ![]() $\mathrm {Nm}_\pi \colon K_J(v_d)\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ is generically finite of degree
$\mathrm {Nm}_\pi \colon K_J(v_d)\dashrightarrow \overline {\operatorname {\mathrm {Pic}}}^d(\mathcal {D}/ {\mathbb {P}}^3)$ is generically finite of degree ![]() $2^5$ by Lemma 3.6, and
$2^5$ by Lemma 3.6, and ![]() $G$ has also order
$G$ has also order ![]() $2^5$.
$2^5$.
4. The K3 surface associated to a  $\mathrm {Kum}^3$ variety
$\mathrm {Kum}^3$ variety
In this section we give the proof of Theorems 1.1 and 1.2. We let ![]() $K$ be a manifold of
$K$ be a manifold of ![]() $\mathrm {Kum}^3$ type and consider the quotient
$\mathrm {Kum}^3$ type and consider the quotient ![]() $K/G$ by the group
$K/G$ by the group ![]() $G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$ of Definition 2.1. We will show that the blow-up of the singular locus of
$G\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^5$ of Definition 2.1. We will show that the blow-up of the singular locus of ![]() $K/G$ yields a hyper-Kähler manifold
$K/G$ yields a hyper-Kähler manifold ![]() $Y_K$ of
$Y_K$ of ![]() $\mathrm {K}3^{[3]}$ type.
$\mathrm {K}3^{[3]}$ type.
4.1 The singularities of  $K/G$
$K/G$
By Theorem 2.2, the locus ![]() $Z=\bigcup _{1\neq g\in G} K^g$ is the union of
$Z=\bigcup _{1\neq g\in G} K^g$ is the union of ![]() $16$ irreducible components
$16$ irreducible components ![]() $Z_i$, for
$Z_i$, for ![]() $i=1,\ldots, 16$. Denote by
$i=1,\ldots, 16$. Denote by ![]() $X_i \subset K/G$, the image of
$X_i \subset K/G$, the image of ![]() $Z_i$ via the quotient map
$Z_i$ via the quotient map ![]() $q\colon K\to K/G$. We introduce the following stratification of
$q\colon K\to K/G$. We introduce the following stratification of ![]() $K/G$ into closed subspaces:
$K/G$ into closed subspaces:
clearly, ![]() $X^0=K/G$.
$X^0=K/G$.
Proposition 4.2 The subspace ![]() $X^j$ is empty for
$X^j$ is empty for ![]() $j\geqslant 4$. For
$j\geqslant 4$. For ![]() $j<4$, a point
$j<4$, a point ![]() $x\in X^j\setminus X^{j+1}$ has a neighborhood
$x\in X^j\setminus X^{j+1}$ has a neighborhood ![]() $U_x\subset K/G$ analytically isomorphic to
$U_x\subset K/G$ analytically isomorphic to
where ![]() $\iota$ is the involution
$\iota$ is the involution ![]() $(x,y)\mapsto (-x,-y)$.
$(x,y)\mapsto (-x,-y)$.
Proof. Theorem 2.2 implies immediately that ![]() $X^j$ is empty for
$X^j$ is empty for ![]() $j\geqslant 4$. The group
$j\geqslant 4$. The group ![]() $G$ acts freely on
$G$ acts freely on ![]() $q^{-1}(X^0\setminus X^1)$ and, hence,
$q^{-1}(X^0\setminus X^1)$ and, hence, ![]() $X^0\setminus X^1$ is smooth.
$X^0\setminus X^1$ is smooth.
If ![]() $\mathcal {K}\to B$ is a smooth proper family of
$\mathcal {K}\to B$ is a smooth proper family of ![]() $\mathrm {Kum}^3$ manifolds, the quotient
$\mathrm {Kum}^3$ manifolds, the quotient ![]() $\mathcal {K}/G \to B$ is a locally trivial family (see [Reference FujikiFuj83, Lemma 3.10]): any point
$\mathcal {K}/G \to B$ is a locally trivial family (see [Reference FujikiFuj83, Lemma 3.10]): any point ![]() $x\in \mathcal {K}/G$ has a neighborhood
$x\in \mathcal {K}/G$ has a neighborhood ![]() $U_x$ of the form to
$U_x$ of the form to ![]() $f(U_x)\times (f^{-1}(f(x))\cap U_x)$. Therefore, to prove the proposition we may assume that
$f(U_x)\times (f^{-1}(f(x))\cap U_x)$. Therefore, to prove the proposition we may assume that ![]() $K$ is the generalized Kummer sixfold on an abelian surface
$K$ is the generalized Kummer sixfold on an abelian surface ![]() $A$.
$A$.
In this case the components ![]() $Z_{i}$ are the explicit
$Z_{i}$ are the explicit ![]() $\overline {W_{\tau }}$, for
$\overline {W_{\tau }}$, for ![]() $\tau \in A_2$ (see Definition 2.6). Recall that
$\tau \in A_2$ (see Definition 2.6). Recall that ![]() $\overline {W_{\tau }}\subset K$ is the unique positive-dimensional component of the fixed locus of
$\overline {W_{\tau }}\subset K$ is the unique positive-dimensional component of the fixed locus of ![]() $(\tau, -1)\in G$, and that the induced action of
$(\tau, -1)\in G$, and that the induced action of ![]() $G/\langle (\tau,-1) \rangle$ on
$G/\langle (\tau,-1) \rangle$ on ![]() $\overline {W_{\tau }}$ is faithful. For any
$\overline {W_{\tau }}$ is faithful. For any ![]() $z\in \overline {W_{\tau }}$ there is a decomposition
$z\in \overline {W_{\tau }}$ there is a decomposition ![]() $T_z(K)=N_{\overline {W_{\tau }}\vert K, z}\oplus T_z(\overline {W_{\tau }})$, where the first factor is the normal space. The action of
$T_z(K)=N_{\overline {W_{\tau }}\vert K, z}\oplus T_z(\overline {W_{\tau }})$, where the first factor is the normal space. The action of ![]() $(\tau, -1)$ on
$(\tau, -1)$ on ![]() $T_z(K)$ is
$T_z(K)$ is ![]() $(-1, 1)$. Now let
$(-1, 1)$. Now let ![]() $x\in X^1 \setminus X^2$, and let
$x\in X^1 \setminus X^2$, and let ![]() $z\in K$ be a preimage of
$z\in K$ be a preimage of ![]() $x$. By definition,
$x$. By definition, ![]() $z$ belongs to exactly one component
$z$ belongs to exactly one component ![]() $\overline {W_{\tau }}$. The stabilizer is
$\overline {W_{\tau }}$. The stabilizer is ![]() $G_z=\langle (\tau,-1) \rangle$. By the above, there exists a neighborhood
$G_z=\langle (\tau,-1) \rangle$. By the above, there exists a neighborhood ![]() $V_z$ of
$V_z$ of ![]() $z\in K$ such that
$z\in K$ such that ![]() $g(V_z)\cap V_z$ is empty for any
$g(V_z)\cap V_z$ is empty for any ![]() $g \notin G_z$, and
$g \notin G_z$, and ![]() $V_z=( {\mathbb {C}}^2)^3$ with
$V_z=( {\mathbb {C}}^2)^3$ with ![]() $(\tau, -1)_{\vert _{V_z}} =(\iota, \mathrm {id}, \mathrm {id})$. The image of
$(\tau, -1)_{\vert _{V_z}} =(\iota, \mathrm {id}, \mathrm {id})$. The image of ![]() $V_z$ under the quotient map is thus a neighborhood
$V_z$ under the quotient map is thus a neighborhood ![]() $U_x=( {\mathbb {C}}^2/\iota )\times ( {\mathbb {C}}^2)^2$ of
$U_x=( {\mathbb {C}}^2/\iota )\times ( {\mathbb {C}}^2)^2$ of ![]() $x$ in
$x$ in ![]() $K/G$.
$K/G$.
In the other cases we proceed similarly. Let ![]() $x\in X^2\setminus X^3$, and let
$x\in X^2\setminus X^3$, and let ![]() $z\in K$ be one of its preimages. Then
$z\in K$ be one of its preimages. Then ![]() $z$ belongs to two distinct components
$z$ belongs to two distinct components ![]() $\overline {W_{\tau _1}}$ and
$\overline {W_{\tau _1}}$ and ![]() $\overline {W_{\tau _2}}$. The stabilizer
$\overline {W_{\tau _2}}$. The stabilizer ![]() $G_z\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^2$ is the subgroup
$G_z\cong ( {\mathbb {Z}}/2 {\mathbb {Z}})^2$ is the subgroup ![]() $\langle (\tau _1,-1), (\tau _2,-1)\rangle$ of
$\langle (\tau _1,-1), (\tau _2,-1)\rangle$ of ![]() $G$. There is a decomposition
$G$. There is a decomposition ![]() $T_z(K) = N_{\overline {W_{\tau _1}}\vert K, z} \oplus N_{\overline {W_{\tau _2}}\vert K, z} \oplus T_z(\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}})$, and the action of
$T_z(K) = N_{\overline {W_{\tau _1}}\vert K, z} \oplus N_{\overline {W_{\tau _2}}\vert K, z} \oplus T_z(\overline {W_{\tau _1}}\cap \overline {W_{\tau _2}})$, and the action of ![]() $G_z$ is generated by
$G_z$ is generated by ![]() $(-1, 1, 1)$ and
$(-1, 1, 1)$ and ![]() $(1, -1, 1)$. This implies that the image in
$(1, -1, 1)$. This implies that the image in ![]() $K/G$ of a sufficiently small neighborhood of
$K/G$ of a sufficiently small neighborhood of ![]() $z$ in
$z$ in ![]() $K$ is isomorphic to
$K$ is isomorphic to ![]() $( {\mathbb {C}}^2/\iota )^2\times ( {\mathbb {C}}^2)$.
$( {\mathbb {C}}^2/\iota )^2\times ( {\mathbb {C}}^2)$.
Finally, let ![]() $x\in X^3$ and
$x\in X^3$ and ![]() $z\in K$ a preimage of it. Then
$z\in K$ a preimage of it. Then ![]() $z$ belongs to exactly three components
$z$ belongs to exactly three components ![]() $\overline {W_{\tau _i}}$, for
$\overline {W_{\tau _i}}$, for ![]() $i=1,2,3$. The stabilizer
$i=1,2,3$. The stabilizer ![]() $G_z$ is the subgroup generated by the involutions
$G_z$ is the subgroup generated by the involutions ![]() $(\tau _i, -1)$, for
$(\tau _i, -1)$, for ![]() $i=1,2,3$, and there is a decomposition
$i=1,2,3$, and there is a decomposition ![]() $T_z(K)=\bigoplus _{i=1}^3 N_{\overline {W_{\tau _i}}\vert K,z}$ of the tangent space. The action of
$T_z(K)=\bigoplus _{i=1}^3 N_{\overline {W_{\tau _i}}\vert K,z}$ of the tangent space. The action of ![]() $(\tau _i,-1)$ on
$(\tau _i,-1)$ on ![]() $T_{z}(K)$ is
$T_{z}(K)$ is ![]() $-1$ on the
$-1$ on the ![]() $i$th summand and the identity on the complement. We conclude that there exists a neighborhood
$i$th summand and the identity on the complement. We conclude that there exists a neighborhood ![]() $V_z$ of
$V_z$ of ![]() $z$ in
$z$ in ![]() $K$ whose image in
$K$ whose image in ![]() $K/G$ is isomorphic to
$K/G$ is isomorphic to ![]() $( {\mathbb {C}}^2/\iota )^3$.
$( {\mathbb {C}}^2/\iota )^3$.
4.3 The symplectic resolution of  $K/G$
$K/G$
We will now conclude the proof of Theorem 1.1 in several steps. First we show that the blow-up of the singular locus of ![]() $K/G$ resolves the singularities.
$K/G$ resolves the singularities.
Proposition 4.4 Let ![]() $Y_K:= \mathrm {Bl}_{X^1}(K/G)$ be the blow-up of the singular locus with reduced structure. Then
$Y_K:= \mathrm {Bl}_{X^1}(K/G)$ be the blow-up of the singular locus with reduced structure. Then ![]() $Y_K$ is a smooth manifold. It is identified with the quotient by
$Y_K$ is a smooth manifold. It is identified with the quotient by ![]() $G$ of the blow-up of
$G$ of the blow-up of ![]() $K$ at
$K$ at ![]() $Z=\bigcup _{1\neq g\in G} K^g$.
$Z=\bigcup _{1\neq g\in G} K^g$.
The proposition will be reduced to the following elementary statement.
Lemma 4.5 Let ![]() $\iota \colon {\mathbb {C}}^2 \to {\mathbb {C}}^2$ be the involution
$\iota \colon {\mathbb {C}}^2 \to {\mathbb {C}}^2$ be the involution ![]() $(x,y)\mapsto (-x, -y)$, let
$(x,y)\mapsto (-x, -y)$, let ![]() $j,k$ be positive integers. Then the blow-up of
$j,k$ be positive integers. Then the blow-up of ![]() $( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$ along its singular locus is isomorphic to
$( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$ along its singular locus is isomorphic to ![]() ${( \mathrm {Bl}_0 ( {\mathbb {C}}^2/\iota ) )^j\times ( {\mathbb {C}}^2)^k}$. It is thus smooth, and identified with the quotient
${( \mathrm {Bl}_0 ( {\mathbb {C}}^2/\iota ) )^j\times ( {\mathbb {C}}^2)^k}$. It is thus smooth, and identified with the quotient ![]() $(\mathrm {Bl}_0( {\mathbb {C}}^2)/\iota )^j\times ( {\mathbb {C}}^2)^k$ of
$(\mathrm {Bl}_0( {\mathbb {C}}^2)/\iota )^j\times ( {\mathbb {C}}^2)^k$ of ![]() $(\mathrm {Bl}_0( {\mathbb {C}}^2))^j\times ( {\mathbb {C}}^2)^k$.
$(\mathrm {Bl}_0( {\mathbb {C}}^2))^j\times ( {\mathbb {C}}^2)^k$.
Proof. Given noetherian schemes ![]() $T_1$ and
$T_1$ and ![]() $T_2$ and closed subschemes
$T_2$ and closed subschemes ![]() $V_1\subsetneq T_1$ and
$V_1\subsetneq T_1$ and ![]() $V_2\subsetneq T_2$, we have
$V_2\subsetneq T_2$, we have
It is easy to see this when ![]() $T_1$ and
$T_1$ and ![]() $T_2$ are affine schemes, using the definition of blowing-up via the Proj construction [Reference HartshorneHar77, II, § 7]. The singular locus of
$T_2$ are affine schemes, using the definition of blowing-up via the Proj construction [Reference HartshorneHar77, II, § 7]. The singular locus of ![]() $( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$ is the union of
$( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$ is the union of ![]() $\operatorname {pr}_i^{-1}(\{0\})$ for
$\operatorname {pr}_i^{-1}(\{0\})$ for ![]() $i$ from
$i$ from ![]() $1$ to
$1$ to ![]() $j$, where
$j$, where ![]() $\operatorname {pr}_i\colon ( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k \to ( {\mathbb {C}}^2/\iota )$ is the projection onto the
$\operatorname {pr}_i\colon ( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k \to ( {\mathbb {C}}^2/\iota )$ is the projection onto the ![]() $i$th factor. Via the above observation, the statement is reduced to the case
$i$th factor. Via the above observation, the statement is reduced to the case ![]() $j=1$,
$j=1$, ![]() $k=0$, which is the well-known minimal resolution of an isolated
$k=0$, which is the well-known minimal resolution of an isolated ![]() $A_1$-singularity of a surface.
$A_1$-singularity of a surface.
Proof of Proposition 4.4 By Proposition 4.2, any point ![]() $x\in K/G$ has a neighborhood of the form
$x\in K/G$ has a neighborhood of the form ![]() $( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$. Therefore, Lemma 4.5 immediately implies that the blow-up
$( {\mathbb {C}}^2/\iota )^j\times ( {\mathbb {C}}^2)^k$. Therefore, Lemma 4.5 immediately implies that the blow-up ![]() $Y_K$ of the singular locus is smooth. It also implies that the natural birational map
$Y_K$ of the singular locus is smooth. It also implies that the natural birational map ![]() $\mathrm {Bl}_Z(K)/G\dashrightarrow Y_K$ extends to an isomorphism.
$\mathrm {Bl}_Z(K)/G\dashrightarrow Y_K$ extends to an isomorphism.
We will now use a criterion due to Fujiki [Reference FujikiFuj83] to show that ![]() $Y_K$ is symplectic, i.e. that it admits a nowhere degenerate holomorphic
$Y_K$ is symplectic, i.e. that it admits a nowhere degenerate holomorphic ![]() $2$-form.
$2$-form.
Proposition 4.6 The manifold ![]() $Y_K$ is hyper-Kähler.
$Y_K$ is hyper-Kähler.
Proof. The singular space ![]() $K/G$ is a primitively symplectic V-manifold in the sense of Fujiki. According to his [Reference FujikiFuj83, Proposition 2.9], to show that
$K/G$ is a primitively symplectic V-manifold in the sense of Fujiki. According to his [Reference FujikiFuj83, Proposition 2.9], to show that ![]() $Y_K$ admits a symplectic form it suffices to check that the following two conditions are satisfied:
$Y_K$ admits a symplectic form it suffices to check that the following two conditions are satisfied:
(i) for each component
 $X_j$ of the singular locus of
$X_j$ of the singular locus of  $K/G$, a general point
$K/G$, a general point  $x\in X_j$ has a neighborhood
$x\in X_j$ has a neighborhood  $U_x = A \times V_x$ in
$U_x = A \times V_x$ in  $K/G$, where
$K/G$, where  $A$ is a surface and
$A$ is a surface and  $V_x=U_x\cap X_j$ is a smooth neighborhood of
$V_x=U_x\cap X_j$ is a smooth neighborhood of  $x$ in
$x$ in  $X_j$;
$X_j$;(ii) the restriction of
 $p\colon Y_K\to K/G$ to the preimage of
$p\colon Y_K\to K/G$ to the preimage of  $U_x$ is the product
where
$U_x$ is the product
where \[ p'\times \mathrm{id}\colon \tilde{A}\times V_x \to A\times V_x, \]
\[ p'\times \mathrm{id}\colon \tilde{A}\times V_x \to A\times V_x, \]
 $p'$ is the minimal resolution of
$p'$ is the minimal resolution of  $A$.
$A$.
We have already shown in the course of proof of Propositions 4.2 and 4.4 that these conditions hold, with ![]() $A$ a neighborhood of the ordinary node
$A$ a neighborhood of the ordinary node ![]() $0\in {\mathbb {C}}^2/\iota$, whose minimal resolution is the blow-up of the singular point.
$0\in {\mathbb {C}}^2/\iota$, whose minimal resolution is the blow-up of the singular point.
Hence, ![]() $Y_K$ is symplectic. From its description as the quotient
$Y_K$ is symplectic. From its description as the quotient ![]() $\mathrm {Bl}_Z(K)/G$ we obtain
$\mathrm {Bl}_Z(K)/G$ we obtain ![]() ${h^{2,0}(Y_K)=1}$ (see also § 4.7). Finally,
${h^{2,0}(Y_K)=1}$ (see also § 4.7). Finally, ![]() $Y_K$ is simply connected by [Reference FujikiFuj83, Lemma 1.2].
$Y_K$ is simply connected by [Reference FujikiFuj83, Lemma 1.2].
We can now complete the proof of our main result.
Proof of Theorem 1.1 Let ![]() $\mathcal {K}\to B$ be a smooth proper family of manifolds of
$\mathcal {K}\to B$ be a smooth proper family of manifolds of ![]() $\mathrm {Kum}^3$ type. Up to a finite étale base-change,
$\mathrm {Kum}^3$ type. Up to a finite étale base-change, ![]() $G$ acts fibrewise on
$G$ acts fibrewise on ![]() $\mathcal {K}$, and the fixed loci of automorphisms in
$\mathcal {K}$, and the fixed loci of automorphisms in ![]() $G$ are smooth families over
$G$ are smooth families over ![]() $B$. By Theorem 2.2, the union
$B$. By Theorem 2.2, the union ![]() $\mathcal {Z}$ of
$\mathcal {Z}$ of ![]() $\mathcal {K}^g$ for
$\mathcal {K}^g$ for ![]() $1\neq g\in G$ has
$1\neq g\in G$ has ![]() $16$ components
$16$ components ![]() $\mathcal {Z}_i$, each of which is a smooth family of manifolds of
$\mathcal {Z}_i$, each of which is a smooth family of manifolds of ![]() $\mathrm {K}3^{[2]}$ type over
$\mathrm {K}3^{[2]}$ type over ![]() $B$. The blow-up of
$B$. The blow-up of ![]() $\mathcal {K}$ along
$\mathcal {K}$ along ![]() $\mathcal {Z}$ is a smooth family
$\mathcal {Z}$ is a smooth family ![]() $\widetilde {\mathcal {K}}$ over
$\widetilde {\mathcal {K}}$ over ![]() $B$, and the action of
$B$, and the action of ![]() $G$ extends to a fibrewise action on
$G$ extends to a fibrewise action on ![]() $\widetilde {\mathcal {K}}$. By Propositions 4.4 and 4.6, the quotient
$\widetilde {\mathcal {K}}$. By Propositions 4.4 and 4.6, the quotient ![]() $\mathcal {Y}=\widetilde {\mathcal {K}}/G$ is a smooth proper family of hyper-Kähler manifolds over
$\mathcal {Y}=\widetilde {\mathcal {K}}/G$ is a smooth proper family of hyper-Kähler manifolds over ![]() $B$, with fibre over the point
$B$, with fibre over the point ![]() $b\in B$ the manifold
$b\in B$ the manifold ![]() $Y_{\mathcal {K}_b}$. It thus suffices to find a single
$Y_{\mathcal {K}_b}$. It thus suffices to find a single ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type such that
$\mathrm {Kum}^3$ type such that ![]() $Y_K$ is hyper-Kähler of
$Y_K$ is hyper-Kähler of ![]() $\mathrm {K}3^{[3]}$ type.
$\mathrm {K}3^{[3]}$ type.
Consider the sixfold ![]() $K_J(v_3)$ introduced in § 3, which is constructed from a Beauville–Mukai system on a principally polarized abelian surface
$K_J(v_3)$ introduced in § 3, which is constructed from a Beauville–Mukai system on a principally polarized abelian surface ![]() $J$. By Theorem 3.1, in this case
$J$. By Theorem 3.1, in this case ![]() $Y_{K_J(v_3)}$ is birational to the Hilbert scheme
$Y_{K_J(v_3)}$ is birational to the Hilbert scheme ![]() $\operatorname {\mathrm {Km}}(J)^{[3]}$ on the Kummer K3 surface associated to
$\operatorname {\mathrm {Km}}(J)^{[3]}$ on the Kummer K3 surface associated to ![]() $J$. By [Reference HuybrechtsHuy99, Theorem 4.6], birational hyper-Kähler manifolds are deformation equivalent, and therefore
$J$. By [Reference HuybrechtsHuy99, Theorem 4.6], birational hyper-Kähler manifolds are deformation equivalent, and therefore ![]() $Y_{K_J(v_3)}$ is of
$Y_{K_J(v_3)}$ is of ![]() $\mathrm {K}3^{[3]}$ type.
$\mathrm {K}3^{[3]}$ type.
4.7 The associated  $\mathrm {K}3$ surface
$\mathrm {K}3$ surface
The following computation is entirely analogous to [Reference FloccariFlo23, § 3]. If ![]() $Z$ is a compact Kähler manifold, we let
$Z$ is a compact Kähler manifold, we let ![]() $H^2_{\mathrm {tr}}(Z, {\mathbb {Z}})$ denote the smallest sub-Hodge structure of
$H^2_{\mathrm {tr}}(Z, {\mathbb {Z}})$ denote the smallest sub-Hodge structure of ![]() $H^2(Z, {\mathbb {Z}})$ whose complexification contains
$H^2(Z, {\mathbb {Z}})$ whose complexification contains ![]() $H^{2, 0}(Z)$. Let
$H^{2, 0}(Z)$. Let ![]() $K$ be a manifold of
$K$ be a manifold of ![]() $\mathrm {Kum}^3$ type, and denote by
$\mathrm {Kum}^3$ type, and denote by ![]() $\widetilde {K}$ the blow-up of
$\widetilde {K}$ the blow-up of ![]() $K$ along
$K$ along ![]() $\bigcup _{1\neq g\in G} K^g$. By Proposition 4.4 we have a commutative diagram
$\bigcup _{1\neq g\in G} K^g$. By Proposition 4.4 we have a commutative diagram

where ![]() $p, p'$ are blow-up maps and
$p, p'$ are blow-up maps and ![]() $q, q'$ are the quotient maps for the action of
$q, q'$ are the quotient maps for the action of ![]() $G$.
$G$.
The pull-back gives an isomorphism ![]() ${p'}^*\colon H^2_{\mathrm {tr}}(K, {\mathbb {Z}}) \to H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})$. Since
${p'}^*\colon H^2_{\mathrm {tr}}(K, {\mathbb {Z}}) \to H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})$. Since ![]() $G$ acts trivially on
$G$ acts trivially on ![]() $H^2(K, {\mathbb {Z}})$, the push-forward
$H^2(K, {\mathbb {Z}})$, the push-forward ![]() $q'_*\colon H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})\to H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ is injective, and
$q'_*\colon H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})\to H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ is injective, and ![]() ${q'}^*q'_*$ is multiplication by
${q'}^*q'_*$ is multiplication by ![]() $2^5$ on
$2^5$ on ![]() $H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})$. It follows that
$H^2_{\mathrm {tr}}(\widetilde {K}, {\mathbb {Z}})$. It follows that
becomes an isomorphism of Hodge structures after tensoring with ![]() $ {\mathbb {Q}}$. Denote by
$ {\mathbb {Q}}$. Denote by ![]() $q_K$ and
$q_K$ and ![]() $q_{Y_K}$ the Beauville–Bogomolov forms on
$q_{Y_K}$ the Beauville–Bogomolov forms on ![]() $H^2(K, {\mathbb {Z}})$ and
$H^2(K, {\mathbb {Z}})$ and ![]() $H^2(Y_K, {\mathbb {Z}})$, respectively.
$H^2(Y_K, {\mathbb {Z}})$, respectively.
Lemma 4.8 For any ![]() $x\in H_{\mathrm {tr}}^2(K, {\mathbb {Z}})$ we have
$x\in H_{\mathrm {tr}}^2(K, {\mathbb {Z}})$ we have ![]() $q_{Y_K} (r_*(x), r_*(x)) = 2^9 q_K(x, x)$. Therefore,
$q_{Y_K} (r_*(x), r_*(x)) = 2^9 q_K(x, x)$. Therefore,
is a rational Hodge isometry, where ![]() $(2)$ indicates that the form is multiplied by
$(2)$ indicates that the form is multiplied by ![]() $2$.
$2$.
Proof. Let ![]() $c_K$ and
$c_K$ and ![]() $c_Y$ be the Fujiki constants of
$c_Y$ be the Fujiki constants of ![]() $K$ and
$K$ and ![]() $Y$, respectively [Reference FujikiFuj87]. This means that we have
$Y$, respectively [Reference FujikiFuj87]. This means that we have ![]() $\int _K x^6 = c_K q_K(x,x)^3$ for any
$\int _K x^6 = c_K q_K(x,x)^3$ for any ![]() $x\in H^2(K, {\mathbb {Z}})$, and similarly for
$x\in H^2(K, {\mathbb {Z}})$, and similarly for ![]() $Y_K$. Let
$Y_K$. Let ![]() $x\in H_{\mathrm {tr}}^2(K, {\mathbb {Z}})$; since
$x\in H_{\mathrm {tr}}^2(K, {\mathbb {Z}})$; since ![]() $x$ is
$x$ is ![]() $G$-invariant, we have
$G$-invariant, we have ![]() $r^*(r_* x) = 2^5 x$. We compute
$r^*(r_* x) = 2^5 x$. We compute
 \begin{align*} q_{Y_K}(r_*x, r_*x)^3 & = \frac{1}{c_{Y_K}}\int_{Y_K} (r_*x)^6 \\ &= \frac{1}{2^5 c_{Y_K}} \int_K (r^*r_* x)^6\\ & = \frac{1}{2^5 c_{Y_K}} \int_K (2^5 x)^6 \\ & =\frac{2^{25}c_K }{c_{Y_K}} q_K(x,x)^3. \end{align*}
\begin{align*} q_{Y_K}(r_*x, r_*x)^3 & = \frac{1}{c_{Y_K}}\int_{Y_K} (r_*x)^6 \\ &= \frac{1}{2^5 c_{Y_K}} \int_K (r^*r_* x)^6\\ & = \frac{1}{2^5 c_{Y_K}} \int_K (2^5 x)^6 \\ & =\frac{2^{25}c_K }{c_{Y_K}} q_K(x,x)^3. \end{align*}
By [Reference RapagnettaRap08], we have ![]() $c_{Y_K}= 15$ and
$c_{Y_K}= 15$ and ![]() $c_K=60$. Hence,
$c_K=60$. Hence, ![]() $q_{Y_K}(r_*x, r_*x)=2^{9} q_K(x,x)$, so
$q_{Y_K}(r_*x, r_*x)=2^{9} q_K(x,x)$, so ![]() $r_*/2^4$ multiplies the form by
$r_*/2^4$ multiplies the form by ![]() $2$ and yields the claimed rational Hodge isometry.
$2$ and yields the claimed rational Hodge isometry.
We now prove that every projective ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type has a naturally associated K3 surface.
$\mathrm {Kum}^3$ type has a naturally associated K3 surface.
Proof of Theorem 1.2 Let ![]() $K$ be a projective variety of
$K$ be a projective variety of ![]() $\mathrm {Kum}^3$ type and let
$\mathrm {Kum}^3$ type and let ![]() $Y_K$ be the crepant resolution of
$Y_K$ be the crepant resolution of ![]() $K/G$. By the above lemma, the transcendental lattice
$K/G$. By the above lemma, the transcendental lattice ![]() $H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ is an even lattice of signature
$H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$ is an even lattice of signature ![]() $(2, k)$, and rank at most
$(2, k)$, and rank at most ![]() $6$. By [Reference MorrisonMor84, Corollary 2.10], there exists a
$6$. By [Reference MorrisonMor84, Corollary 2.10], there exists a ![]() $\mathrm {K}3$ surface
$\mathrm {K}3$ surface ![]() $S_K$ such that
$S_K$ such that ![]() $H^2_{\mathrm {tr}}(S_K, {\mathbb {Z}})$ is Hodge isometric to
$H^2_{\mathrm {tr}}(S_K, {\mathbb {Z}})$ is Hodge isometric to ![]() $H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. A criterion independently due to Mongardi and Wandel [Reference Mongardi and WandelMW15] and Addington [Reference AddingtonAdd16, Proposition 4] ensures that
$H^2_{\mathrm {tr}}(Y_K, {\mathbb {Z}})$. A criterion independently due to Mongardi and Wandel [Reference Mongardi and WandelMW15] and Addington [Reference AddingtonAdd16, Proposition 4] ensures that ![]() $Y_K$ is birational to
$Y_K$ is birational to ![]() $M_{S_{K},H}(v)$, for some primitive Mukai vector
$M_{S_{K},H}(v)$, for some primitive Mukai vector ![]() $v$ and a
$v$ and a ![]() $v$-generic polarization
$v$-generic polarization ![]() $H$ on
$H$ on ![]() $S_K$. The surface
$S_K$. The surface ![]() $S_K$ is uniquely determined up to isomorphism, because two
$S_K$ is uniquely determined up to isomorphism, because two ![]() $\mathrm {K}3$ surfaces of Picard rank at least
$\mathrm {K}3$ surfaces of Picard rank at least ![]() $12$ with Hodge isometric transcendental lattices are isomorphic, see [Reference HuybrechtsHuy16, Chapter 16, Corollary 3.8]
$12$ with Hodge isometric transcendental lattices are isomorphic, see [Reference HuybrechtsHuy16, Chapter 16, Corollary 3.8]
Remark 4.9 The K3 surfaces ![]() $S_K$ come in countably many
$S_K$ come in countably many ![]() $4$-dimensional families. A projective
$4$-dimensional families. A projective ![]() $K_0$ of
$K_0$ of ![]() $\mathrm {Kum}^3$ type with Picard rank
$\mathrm {Kum}^3$ type with Picard rank ![]() $1$ gives such a family, consisting of the K3 surfaces
$1$ gives such a family, consisting of the K3 surfaces ![]() $S$ such that
$S$ such that ![]() $H^2_{\mathrm {tr}}(S, {\mathbb {Z}})$ is a sublattice of
$H^2_{\mathrm {tr}}(S, {\mathbb {Z}})$ is a sublattice of ![]() $H^2_{\mathrm {tr}}(S_{K_0}, {\mathbb {Z}})$.
$H^2_{\mathrm {tr}}(S_{K_0}, {\mathbb {Z}})$.
Up to isogeny, the K3 surfaces obtained are easily characterized as follows. Recall that ![]() $\Lambda _{\mathrm {Kum}^3}=U^{\oplus 3}\oplus \langle -8\rangle$ is the lattice
$\Lambda _{\mathrm {Kum}^3}=U^{\oplus 3}\oplus \langle -8\rangle$ is the lattice ![]() $H^2(K, {\mathbb {Z}})$ for
$H^2(K, {\mathbb {Z}})$ for ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type.
$\mathrm {Kum}^3$ type.
Lemma 4.10 Let ![]() $S$ be a projective
$S$ be a projective ![]() $\mathrm {K}3$ surface. The following are equivalent:
$\mathrm {K}3$ surface. The following are equivalent:
– there exists an isometric embedding of
 $H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ into
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ into  $\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$;
$\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$;– there exist a projective variety
 $K$ of
$K$ of  $\mathrm {Kum}^3$ type with associated
$\mathrm {Kum}^3$ type with associated  $\mathrm {K}3$ surface
$\mathrm {K}3$ surface  $S_K$ and a rational Hodge isometry
$S_K$ and a rational Hodge isometry  $H^2_{\mathrm {tr}}(S, {\mathbb {Q}}) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K, {\mathbb {Q}})$.
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}}) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K, {\mathbb {Q}})$.
Proof. The second assertion implies the first thanks to Lemma 4.8. Conversely, let ![]() $\Phi \colon H^2_{\mathrm {tr}}(S, {\mathbb {Q}}) \hookrightarrow \Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ be an isometric embedding. Choose a primitive sublattice
$\Phi \colon H^2_{\mathrm {tr}}(S, {\mathbb {Q}}) \hookrightarrow \Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ be an isometric embedding. Choose a primitive sublattice ![]() $T\subset \Lambda _{\mathrm {Kum}^3}$ such that
$T\subset \Lambda _{\mathrm {Kum}^3}$ such that ![]() $T(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ coincides with the image of
$T(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$ coincides with the image of ![]() $\Phi$. Equip
$\Phi$. Equip ![]() $T$ with the Hodge structure induced by that on
$T$ with the Hodge structure induced by that on ![]() $H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ via
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}})$ via ![]() $\Phi$. By the surjectivity of the period map [Reference HuybrechtsHuy99], there exists a manifold
$\Phi$. By the surjectivity of the period map [Reference HuybrechtsHuy99], there exists a manifold ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type such that
$\mathrm {Kum}^3$ type such that ![]() $H^2_{\mathrm {tr}}(K, {\mathbb {Z}})$ is Hodge isometric to
$H^2_{\mathrm {tr}}(K, {\mathbb {Z}})$ is Hodge isometric to ![]() $T$, and Lemma 4.8 gives a Hodge isometry
$T$, and Lemma 4.8 gives a Hodge isometry ![]() $H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K, {\mathbb {Q}})$. Since the signature of
$H^2_{\mathrm {tr}}(S, {\mathbb {Q}})\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K, {\mathbb {Q}})$. Since the signature of ![]() $T$ is necessarily
$T$ is necessarily ![]() $(2, k)$ with
$(2, k)$ with ![]() $k\leqslant 4$, Huybrechts’ projectivity criterion [Reference HuybrechtsHuy99] implies that
$k\leqslant 4$, Huybrechts’ projectivity criterion [Reference HuybrechtsHuy99] implies that ![]() $K$ is projective.
$K$ is projective.
5. Applications to the Hodge conjecture
In this section we prove Theorems 1.3 and 1.4. Throughout, all cohomology groups are taken with rational coefficients, which are thus suppressed from the notation.
We start with a simple observation. Let ![]() $X, Y$ be smooth projective varieties and let
$X, Y$ be smooth projective varieties and let ![]() $\phi \colon H^2(X)\to H^2(Y)$ be a morphism of Hodge structures.
$\phi \colon H^2(X)\to H^2(Y)$ be a morphism of Hodge structures.
Lemma 5.1 The morphism ![]() $\phi$ is induced by an algebraic correspondence if and only if its restriction to
$\phi$ is induced by an algebraic correspondence if and only if its restriction to ![]() $H^{2}_{\mathrm {tr}}(X)$ is so.
$H^{2}_{\mathrm {tr}}(X)$ is so.
Proof. There is a decomposition ![]() $H^2(X)=H^2_{\mathrm {tr}}(X) \oplus H^2_{\mathrm {alg}}(X)$, where
$H^2(X)=H^2_{\mathrm {tr}}(X) \oplus H^2_{\mathrm {alg}}(X)$, where ![]() $H^2_{\mathrm {alg}}(X)$ is spanned by cycle classes of divisors. Similarly,
$H^2_{\mathrm {alg}}(X)$ is spanned by cycle classes of divisors. Similarly, ![]() $H^2(Y)= H^2_{\mathrm {tr}}(Y) \oplus H^2_{\mathrm {alg}}(Y)$. Any morphism
$H^2(Y)= H^2_{\mathrm {tr}}(Y) \oplus H^2_{\mathrm {alg}}(Y)$. Any morphism ![]() $H^2_{\mathrm {tr}}(X)\to H^2_{\mathrm {alg}}(Y)$ or
$H^2_{\mathrm {tr}}(X)\to H^2_{\mathrm {alg}}(Y)$ or ![]() $H^2_{\mathrm {alg}}(X)\to H^2_{\mathrm {tr}}(Y)$ of Hodge structures is trivial. Hence,
$H^2_{\mathrm {alg}}(X)\to H^2_{\mathrm {tr}}(Y)$ of Hodge structures is trivial. Hence, ![]() $\phi$ gives a Hodge class
$\phi$ gives a Hodge class
The lemma follows because the second summand consists of algebraic classes.
Proof of Theorem 1.4 Let ![]() $K$ and
$K$ and ![]() $K'$ be projective varieties of
$K'$ be projective varieties of ![]() $\mathrm {Kum}^3$ type and assume that
$\mathrm {Kum}^3$ type and assume that ![]() $f\colon H^2(K) \xrightarrow { \ \sim \ } H^2(K')$ is a rational Hodge isometry. By the above lemma, it suffices to show that the component
$f\colon H^2(K) \xrightarrow { \ \sim \ } H^2(K')$ is a rational Hodge isometry. By the above lemma, it suffices to show that the component ![]() $f_{\mathrm {tr}}\colon H_{\mathrm {tr}}^2(K) \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(K')$ is algebraic.
$f_{\mathrm {tr}}\colon H_{\mathrm {tr}}^2(K) \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(K')$ is algebraic.
Let ![]() $Y$,
$Y$, ![]() $Y'$ be the varieties of
$Y'$ be the varieties of ![]() $\mathrm {K}3^{[3]}$ type given by Theorem 1.1 applied to
$\mathrm {K}3^{[3]}$ type given by Theorem 1.1 applied to ![]() $K$ and
$K$ and ![]() $K'$, respectively, and let
$K'$, respectively, and let ![]() $r\colon K\dashrightarrow Y$ and
$r\colon K\dashrightarrow Y$ and ![]() $r'\colon K'\dashrightarrow Y'$ be the corresponding rational maps. They induce isomorphisms of Hodge structures
$r'\colon K'\dashrightarrow Y'$ be the corresponding rational maps. They induce isomorphisms of Hodge structures ![]() $r_*\colon H^2_{\mathrm {tr}}(K) \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(Y)$ and
$r_*\colon H^2_{\mathrm {tr}}(K) \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(Y)$ and ![]() $r'_*\colon H^2_{\mathrm {tr}}(K') \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(Y')$. Let
$r'_*\colon H^2_{\mathrm {tr}}(K') \xrightarrow {\ \sim \ } H_{\mathrm {tr}}^2(Y')$. Let ![]() $\bar {f}_{\mathrm {tr}}$ be defined as
$\bar {f}_{\mathrm {tr}}$ be defined as
The inverse of ![]() $r_*$ is
$r_*$ is ![]() $r^*/2^5$, and similarly for
$r^*/2^5$, and similarly for ![]() $r'$. It follows that
$r'$. It follows that ![]() $f_{\mathrm {tr}}$ is algebraic if and only if
$f_{\mathrm {tr}}$ is algebraic if and only if ![]() $\bar {f}_{\mathrm {tr}}$ is so. By Lemma 4.8, the map
$\bar {f}_{\mathrm {tr}}$ is so. By Lemma 4.8, the map ![]() $\bar {f}_{\mathrm {tr}}$ is a rational Hodge isometry and, hence, it is algebraic by Markman's theorem in [Reference MarkmanMar22].
$\bar {f}_{\mathrm {tr}}$ is a rational Hodge isometry and, hence, it is algebraic by Markman's theorem in [Reference MarkmanMar22].
5.2 The Kuga–Satake correspondence
The Kuga–Satake construction associates an abelian variety to any polarized Hodge structure of ![]() $\mathrm {K}3$ type. We briefly recall this construction, referring to [Reference van GeemenvGe00] and [Reference HuybrechtsHuy16, Chapter 4] for more details.
$\mathrm {K}3$ type. We briefly recall this construction, referring to [Reference van GeemenvGe00] and [Reference HuybrechtsHuy16, Chapter 4] for more details.
Let ![]() $(V, q)$ be an effective polarized
$(V, q)$ be an effective polarized ![]() $ {\mathbb {Q}}$-Hodge structure of weight
$ {\mathbb {Q}}$-Hodge structure of weight ![]() $2$ with
$2$ with ![]() $h^{2,0}(V)=1$. The Clifford algebra
$h^{2,0}(V)=1$. The Clifford algebra ![]() $C(V)$ is defined as the quotient
$C(V)$ is defined as the quotient
As a ![]() $ {\mathbb {Q}}$-vector space,
$ {\mathbb {Q}}$-vector space, ![]() $C(V)\cong \bigwedge ^{\bullet }(V)$; hence,
$C(V)\cong \bigwedge ^{\bullet }(V)$; hence, ![]() $\dim (C(V))=2^{\mathrm {rk}(V)}$. The Clifford algebra is
$\dim (C(V))=2^{\mathrm {rk}(V)}$. The Clifford algebra is ![]() $ {\mathbb {Z}}/2 {\mathbb {Z}}$-graded,
$ {\mathbb {Z}}/2 {\mathbb {Z}}$-graded, ![]() $C(V)=C^+(V)\oplus C^-(V)$. In [Reference DeligneDel71], Deligne shows that the Hodge structure of
$C(V)=C^+(V)\oplus C^-(V)$. In [Reference DeligneDel71], Deligne shows that the Hodge structure of ![]() $V$ induces a Hodge structure of weight
$V$ induces a Hodge structure of weight ![]() $1$ on
$1$ on ![]() $C^+(V)$ of type
$C^+(V)$ of type ![]() $(1,0), (0,1)$, which admits a polarization and, hence, defines an abelian variety
$(1,0), (0,1)$, which admits a polarization and, hence, defines an abelian variety ![]() $\mathrm {KS}(V)$ up to isogeny. This
$\mathrm {KS}(V)$ up to isogeny. This ![]() $2^{\mathrm {rk}(V)-2}$-dimensional abelian variety is called the Kuga–Satake variety of
$2^{\mathrm {rk}(V)-2}$-dimensional abelian variety is called the Kuga–Satake variety of ![]() $V$. Upon fixing some
$V$. Upon fixing some ![]() $v_0\in V$, the action of
$v_0\in V$, the action of ![]() $V$ on
$V$ on ![]() $C(V)$ via left multiplication induces an embedding of weight
$C(V)$ via left multiplication induces an embedding of weight ![]() $0$ rational Hodge structures
$0$ rational Hodge structures
which maps ![]() $v$ to the endomorphism
$v$ to the endomorphism ![]() $w\mapsto vwv_0$.
$w\mapsto vwv_0$.
Remark 5.3 If ![]() $V'\subset V$ is a sub-Hodge structure such that
$V'\subset V$ is a sub-Hodge structure such that ![]() ${V'}^{\bot }$ consists of Hodge classes, then
${V'}^{\bot }$ consists of Hodge classes, then ![]() $\mathrm {KS}(V)$ is isogenous to a power of
$\mathrm {KS}(V)$ is isogenous to a power of ![]() $\mathrm {KS}(V')$. Replacing the form
$\mathrm {KS}(V')$. Replacing the form ![]() $q$ with a non-zero rational multiple results in isogenous Kuga–Satake varieties. See [Reference HuybrechtsHuy16, Chapter 4, Example 2.4 and Proof of Proposition 3.3]
$q$ with a non-zero rational multiple results in isogenous Kuga–Satake varieties. See [Reference HuybrechtsHuy16, Chapter 4, Example 2.4 and Proof of Proposition 3.3]
Let ![]() $X$ be a projective hyper-Kähler variety of dimension
$X$ be a projective hyper-Kähler variety of dimension ![]() $2n$. The Kuga–Satake variety
$2n$. The Kuga–Satake variety ![]() $\mathrm {KS}(X)$ of
$\mathrm {KS}(X)$ of ![]() $X$ is the abelian variety obtained from
$X$ is the abelian variety obtained from ![]() $(H^2_{\mathrm {tr}}(X), q_X)$ via the Kuga–Satake construction, where
$(H^2_{\mathrm {tr}}(X), q_X)$ via the Kuga–Satake construction, where ![]() $q_X$ is the restriction of the Beauville–Bogomolov form. Identifying
$q_X$ is the restriction of the Beauville–Bogomolov form. Identifying ![]() $H^1(\mathrm {KS}(X))$ with its dual, there exists an embedding of Hodge structures of
$H^1(\mathrm {KS}(X))$ with its dual, there exists an embedding of Hodge structures of ![]() $H^2_{\mathrm {tr}}(X)$ into
$H^2_{\mathrm {tr}}(X)$ into ![]() $H^2(\mathrm {KS}(X)\times \mathrm {KS}(X) )$. According to the Hodge conjecture this embedding should be induced by an algebraic cycle.
$H^2(\mathrm {KS}(X)\times \mathrm {KS}(X) )$. According to the Hodge conjecture this embedding should be induced by an algebraic cycle.
Conjecture 5.4 (Kuga–Satake Hodge conjecture)
Let ![]() $X$ be a projective hyper-Kähler variety. There exists an algebraic cycle
$X$ be a projective hyper-Kähler variety. There exists an algebraic cycle ![]() $\zeta$ on
$\zeta$ on ![]() $X\times \mathrm {KS}(X) \times \mathrm {KS}(X)$ such that the associated correspondence induces an embedding of Hodge structures
$X\times \mathrm {KS}(X) \times \mathrm {KS}(X)$ such that the associated correspondence induces an embedding of Hodge structures
Remark 5.5 For a K3 surface ![]() $X$, the above form of the conjecture is equivalent to [Reference van GeemenvGe00, § 10.2]. To see this, let
$X$, the above form of the conjecture is equivalent to [Reference van GeemenvGe00, § 10.2]. To see this, let ![]() $\mathsf {Mot}$ be the category of Grothendieck motives over
$\mathsf {Mot}$ be the category of Grothendieck motives over ![]() $ {\mathbb {C}}$, in which morphisms are given by algebraic cycles modulo homological equivalence, see [Reference AndréAnd04]. The motive
$ {\mathbb {C}}$, in which morphisms are given by algebraic cycles modulo homological equivalence, see [Reference AndréAnd04]. The motive ![]() $\operatorname {\mathfrak {h}}(X)\in \mathsf {Mot}$ of
$\operatorname {\mathfrak {h}}(X)\in \mathsf {Mot}$ of ![]() $X$ decomposes as the sum of its transcendental part
$X$ decomposes as the sum of its transcendental part ![]() $\operatorname {\mathfrak {h}}_{\mathrm {tr}}(X)$ and some motives of Hodge–Tate type. Since the standard conjectures hold for
$\operatorname {\mathfrak {h}}_{\mathrm {tr}}(X)$ and some motives of Hodge–Tate type. Since the standard conjectures hold for ![]() $X$ and
$X$ and ![]() $\mathrm {KS}(X)$, the tensor subcategory of
$\mathrm {KS}(X)$, the tensor subcategory of ![]() $\mathsf {Mot}$ generated by their motives is abelian and semisimple [Reference ArapuraAra06, Theorem 4.1]. Therefore, Conjecture 5.4 and the formulation of van Geemen [Reference van GeemenvGe00, § 10.2] are both equivalent to
$\mathsf {Mot}$ generated by their motives is abelian and semisimple [Reference ArapuraAra06, Theorem 4.1]. Therefore, Conjecture 5.4 and the formulation of van Geemen [Reference van GeemenvGe00, § 10.2] are both equivalent to ![]() $\operatorname {\mathfrak {h}}^2_{\mathrm {tr}}(X)$ being a direct summand of
$\operatorname {\mathfrak {h}}^2_{\mathrm {tr}}(X)$ being a direct summand of ![]() $\operatorname {\mathfrak {h}}^2(\mathrm {KS}(X)\times \mathrm {KS}(X))$ in the category
$\operatorname {\mathfrak {h}}^2(\mathrm {KS}(X)\times \mathrm {KS}(X))$ in the category ![]() $\mathsf {Mot}$.
$\mathsf {Mot}$.
We will use the following easy lemma.
Lemma 5.6 Let ![]() $X$ and
$X$ and ![]() $Z$ be projective hyper-Kähler varieties. Assume that there exists an algebraic cycle
$Z$ be projective hyper-Kähler varieties. Assume that there exists an algebraic cycle ![]() $\gamma$ on
$\gamma$ on ![]() $Z\times X$ which induces a rational Hodge isometry
$Z\times X$ which induces a rational Hodge isometry
for some non-zero ![]() $k\in {\mathbb {Q}}$. Then, if Conjecture 5.4 holds for
$k\in {\mathbb {Q}}$. Then, if Conjecture 5.4 holds for ![]() $X$, it holds for
$X$, it holds for ![]() $Z$ as well.
$Z$ as well.
Proof. By Remark 5.3 there exists an isogeny ![]() $\phi \colon \mathrm {KS}(X)\to \mathrm {KS}(Z)$ of Kuga–Satake varieties. It induces an isomorphism
$\phi \colon \mathrm {KS}(X)\to \mathrm {KS}(Z)$ of Kuga–Satake varieties. It induces an isomorphism
of rational Hodge structures. If Conjecture 5.4 holds for ![]() $X$, there exists an algebraic cycle
$X$, there exists an algebraic cycle ![]() $\zeta$ on
$\zeta$ on ![]() $X\times \mathrm {KS}(X) \times \mathrm {KS}(X)$ giving an embedding of Hodge structures
$X\times \mathrm {KS}(X) \times \mathrm {KS}(X)$ giving an embedding of Hodge structures
It follows that the embedding of Hodge structure given by the composition
is induced by an algebraic cycle on ![]() $Z\times \mathrm {KS}(Z)\times \mathrm {KS}(Z)$.
$Z\times \mathrm {KS}(Z)\times \mathrm {KS}(Z)$.
For convenience of the reader we restate Theorem 1.3.
Theorem 5.7 Let ![]() $S$ be a projective
$S$ be a projective ![]() $\mathrm {K}3$ surface such that there exists an isometric embedding of
$\mathrm {K}3$ surface such that there exists an isometric embedding of ![]() $H^2_{\mathrm {tr}}(S)$ into
$H^2_{\mathrm {tr}}(S)$ into ![]() $\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$. Then Conjecture 5.4 holds for
$\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$. Then Conjecture 5.4 holds for ![]() $S$.
$S$.
Proof. By Lemma 4.10, there exists a projective variety ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type with associated K3 surface
$\mathrm {Kum}^3$ type with associated K3 surface ![]() $S_K$ and a rational Hodge isometry
$S_K$ and a rational Hodge isometry ![]() $t_0\colon H^2_{\mathrm {tr}}(S)\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K)$. Denote by
$t_0\colon H^2_{\mathrm {tr}}(S)\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(S_K)$. Denote by ![]() $Y_K$ the crepant resolution of
$Y_K$ the crepant resolution of ![]() $K/G$ given by Theorem 1.1 and let
$K/G$ given by Theorem 1.1 and let ![]() $v, H$ be given by Theorem 1.2, so that
$v, H$ be given by Theorem 1.2, so that ![]() $Y_K$ is birational to the moduli space
$Y_K$ is birational to the moduli space ![]() $M_{S_K,H}(v)$. Denote by
$M_{S_K,H}(v)$. Denote by ![]() $r\colon K\dashrightarrow Y_K$ the natural rational map of degree
$r\colon K\dashrightarrow Y_K$ the natural rational map of degree ![]() $2^5$.
$2^5$.
By [Reference BuskinBus19, Reference HuybrechtsHuy19], the isometry ![]() $t_0$ is algebraic. Next, by [Reference MukaiMuk87], there exists a quasi-tautological sheaf
$t_0$ is algebraic. Next, by [Reference MukaiMuk87], there exists a quasi-tautological sheaf ![]() $U$ over
$U$ over ![]() $S_K \times M_{S_K,H}(v)$, which means that there exists an integer
$S_K \times M_{S_K,H}(v)$, which means that there exists an integer ![]() $\rho$ such that for any
$\rho$ such that for any ![]() $F\in M_{S_K,H}(v)$ the restriction of
$F\in M_{S_K,H}(v)$ the restriction of ![]() $U$ to
$U$ to ![]() $S_K\times \{F\}$ is
$S_K\times \{F\}$ is ![]() $F^{\oplus \rho }$. Consider the algebraic class
$F^{\oplus \rho }$. Consider the algebraic class
where ![]() $\mathrm {pr}\colon S_K\times M_{S_K, H}(v) \to S_K$ is the projection. By [Reference O'GradyO'Gr97], its Künneth component
$\mathrm {pr}\colon S_K\times M_{S_K, H}(v) \to S_K$ is the projection. By [Reference O'GradyO'Gr97], its Künneth component ![]() $\gamma _3\in H^6 (S_K\times M_{S_K, H}(v))$ induces a Hodge isometry
$\gamma _3\in H^6 (S_K\times M_{S_K, H}(v))$ induces a Hodge isometry
By [Reference Charles and MarkmanCM13], the standard conjectures holds for ![]() $M_{S_K, H}(v)$ (this also follows from [Reference BüllesBül20] via the arguments of [Reference ArapuraAra06]). Hence, all Künneth components of
$M_{S_K, H}(v)$ (this also follows from [Reference BüllesBül20] via the arguments of [Reference ArapuraAra06]). Hence, all Künneth components of ![]() $\gamma$ are algebraic. Now let
$\gamma$ are algebraic. Now let ![]() $f\colon M_{S_K, H}(v)\dashrightarrow Y_K$ be a birational map. Then the push-forward
$f\colon M_{S_K, H}(v)\dashrightarrow Y_K$ be a birational map. Then the push-forward ![]() $f_*\colon H^2_{\mathrm {tr}}(M_{S_K, H}(v))\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(Y_K)$ is a Hodge isometry. By Lemma 4.8, a multiple of the composition
$f_*\colon H^2_{\mathrm {tr}}(M_{S_K, H}(v))\xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(Y_K)$ is a Hodge isometry. By Lemma 4.8, a multiple of the composition ![]() $r^* \circ f_*$ gives a Hodge isometry
$r^* \circ f_*$ gives a Hodge isometry ![]() $t_2\colon H^2_{\mathrm {tr}}(M_{S_K, H}(v)) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(K)(2)$.
$t_2\colon H^2_{\mathrm {tr}}(M_{S_K, H}(v)) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(K)(2)$.
It follows that the Hodge isometry
is induced by an algebraic cycle on ![]() $S\times K$. The Kuga–Satake Hodge conjecture holds for
$S\times K$. The Kuga–Satake Hodge conjecture holds for ![]() $K$ by [Reference VoisinVoi22]. By Lemma 5.6, Conjecture 5.4 holds for the K3 surface
$K$ by [Reference VoisinVoi22]. By Lemma 5.6, Conjecture 5.4 holds for the K3 surface ![]() $S$ as well.
$S$ as well.
For the general projective variety ![]() $K$ of
$K$ of ![]() $\mathrm {Kum}^3$ type,
$\mathrm {Kum}^3$ type, ![]() $H^2_{\mathrm {tr}}(K, {\mathbb {Q}})$ is a rank-
$H^2_{\mathrm {tr}}(K, {\mathbb {Q}})$ is a rank-![]() $6$ Hodge structure with Hodge numbers
$6$ Hodge structure with Hodge numbers ![]() $(1, 4, 1)$ and the explicit knowledge of the quadratic form allows one to show that the Kuga–Satake variety is
$(1, 4, 1)$ and the explicit knowledge of the quadratic form allows one to show that the Kuga–Satake variety is ![]() $A^4$, where
$A^4$, where ![]() $A$ is an abelian fourfold of Weil type (cf. [Reference van GeemenvGe00, Theorem 9.2]). O'Grady moreover shows in [Reference O'GradyO'Gr21] that
$A$ is an abelian fourfold of Weil type (cf. [Reference van GeemenvGe00, Theorem 9.2]). O'Grady moreover shows in [Reference O'GradyO'Gr21] that ![]() $H^1(A, {\mathbb {Q}})\cong H^3(K, {\mathbb {Q}})$. This is a crucial ingredient in the subsequent work of Markman [Reference MarkmanMar23] and Voisin [Reference VoisinVoi22]. O'Grady's theorem further allows us to apply a result of Varesco [Reference VarescoVar22] to prove the Hodge conjecture for all powers of the K3 surfaces appearing in Theorem 1.3.
$H^1(A, {\mathbb {Q}})\cong H^3(K, {\mathbb {Q}})$. This is a crucial ingredient in the subsequent work of Markman [Reference MarkmanMar23] and Voisin [Reference VoisinVoi22]. O'Grady's theorem further allows us to apply a result of Varesco [Reference VarescoVar22] to prove the Hodge conjecture for all powers of the K3 surfaces appearing in Theorem 1.3.
Corollary 5.8 Let ![]() $S$ be a projective
$S$ be a projective ![]() $\mathrm {K}3$ surface such that there exists an isometric embedding of
$\mathrm {K}3$ surface such that there exists an isometric embedding of ![]() $H^2_{\mathrm {tr}}(S)$ into
$H^2_{\mathrm {tr}}(S)$ into ![]() $\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$. Then the Hodge conjecture holds for all powers of
$\Lambda _{\mathrm {Kum}^3}(2)\otimes _{ {\mathbb {Z}}} {\mathbb {Q}}$. Then the Hodge conjecture holds for all powers of ![]() $S$.
$S$.
Proof. By Remark 4.9, there exists a ![]() $4$-dimensional family
$4$-dimensional family ![]() $\mathcal {S}\to B$ of projective K3 surfaces of general Picard rank
$\mathcal {S}\to B$ of projective K3 surfaces of general Picard rank ![]() $16$ such that: for each
$16$ such that: for each ![]() $b\in B$ the fibre
$b\in B$ the fibre ![]() $\mathcal {S}_b$ is of the form
$\mathcal {S}_b$ is of the form ![]() $S_{K_b}$ for some
$S_{K_b}$ for some ![]() $K_b$ of
$K_b$ of ![]() $\mathrm {Kum}^3$ type and for some
$\mathrm {Kum}^3$ type and for some ![]() $0\in B$ there exists a rational Hodge isometry
$0\in B$ there exists a rational Hodge isometry ![]() $H^2_{\mathrm {tr}}(S) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(\mathcal {S}_0)$. By [Reference HuybrechtsHuy19], it is sufficient to prove the Hodge conjecture for all powers of
$H^2_{\mathrm {tr}}(S) \xrightarrow {\ \sim \ } H^2_{\mathrm {tr}}(\mathcal {S}_0)$. By [Reference HuybrechtsHuy19], it is sufficient to prove the Hodge conjecture for all powers of ![]() $\mathcal {S}_0$.
$\mathcal {S}_0$.
To this end, it will be enough to check that ![]() $\mathcal {S}\to B$ satisfies the two assumptions of [Reference VarescoVar22, Theorem 0.2]. As explained in [Reference VarescoVar22, Theorem 4.1], the first of these assumptions is that the Kuga–Satake variety of a general K3 surface in the family is isogenous to
$\mathcal {S}\to B$ satisfies the two assumptions of [Reference VarescoVar22, Theorem 0.2]. As explained in [Reference VarescoVar22, Theorem 4.1], the first of these assumptions is that the Kuga–Satake variety of a general K3 surface in the family is isogenous to ![]() $A^4$ for an abelian fourfold
$A^4$ for an abelian fourfold ![]() $A$ of Weil type with trivial discriminant. This holds by O'Grady's theorem in [Reference O'GradyO'Gr21] as already mentioned. The other assumption is that the Kuga–Satake Hodge conjecture holds for the surfaces
$A$ of Weil type with trivial discriminant. This holds by O'Grady's theorem in [Reference O'GradyO'Gr21] as already mentioned. The other assumption is that the Kuga–Satake Hodge conjecture holds for the surfaces ![]() $\mathcal {S}_b$ for all
$\mathcal {S}_b$ for all ![]() $b\in B$, which is the content of Theorem 5.7.
$b\in B$, which is the content of Theorem 5.7.
Remark 5.9 The conclusions of Theorem 5.7 and Corollary 5.8 were known for the two ![]() $4$-dimensional families of K3 surfaces studied in [Reference ParanjapePar88] and [Reference Ingalls, Logan and PatashnickILP22]. The general fibre has transcendental lattice
$4$-dimensional families of K3 surfaces studied in [Reference ParanjapePar88] and [Reference Ingalls, Logan and PatashnickILP22]. The general fibre has transcendental lattice ![]() $U^{\oplus 2}\oplus \langle -2\rangle ^{\oplus 2}$ in the first case and
$U^{\oplus 2}\oplus \langle -2\rangle ^{\oplus 2}$ in the first case and ![]() $U^{\oplus 2} \oplus \langle -6\rangle \oplus \langle -2\rangle$ in the second. The reader may check that the K3 surfaces studied in [Reference ParanjapePar88] satisfy the assumption of our Theorem 5.7, while those appearing in [Reference Ingalls, Logan and PatashnickILP22] do not.
$U^{\oplus 2} \oplus \langle -6\rangle \oplus \langle -2\rangle$ in the second. The reader may check that the K3 surfaces studied in [Reference ParanjapePar88] satisfy the assumption of our Theorem 5.7, while those appearing in [Reference Ingalls, Logan and PatashnickILP22] do not.
Acknowledgements
It is a pleasure to thank Ben Moonen, Kieran O'Grady, Claudio Pedrini and Stefan Schreieder for their interest in this project. I am grateful to Lie Fu and Giovanni Mongardi for their comments on a first version of this article, and to Grégoire Menet for useful discussions. I thank Mauro Varesco for suggesting to me Corollary 5.8. I thank Giacomo Mezzedimi and Domenico Valloni for many conversations related to these topics, and the anonymous referee for his/her comments.
Conflicts of Interest
None.