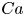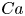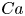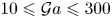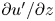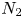doi:10.1017/jfm.2024.269 Gai & Wachs On the dynamics and wakes of a freely settling Platonic polyhedron in a quiescent Newtonian fluid
JFM Rapids
Aeroacoustics of a ducted fan ingesting an adverse pressure gradient boundary layer
-
- Published online by Cambridge University Press:
- 15 April 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steady water waves with arbitrary surface pressure: their recovery from bottom-pressure measurements
-
- Published online by Cambridge University Press:
- 19 April 2024, R2
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Peeling fingers in an elastic Hele-Shaw channel
-
- Published online by Cambridge University Press:
- 16 April 2024, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evolution of wind-induced wave groups in water of finite depth
-
- Published online by Cambridge University Press:
- 12 April 2024, A2
-
- Article
-
- You have access
- HTML
- Export citation
On the dynamics and wakes of a freely settling Platonic polyhedron in a quiescent Newtonian fluid
-
- Published online by Cambridge University Press:
- 15 April 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Low-order modelling of three-dimensional surface waves in liquid film flow on a rotating disk
-
- Published online by Cambridge University Press:
- 15 April 2024, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of turbulence in unsteady flow over urban canopies
-
- Published online by Cambridge University Press:
- 16 April 2024, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interplay of scales during the spatial evolution of energy-containing motions in wall-bounded turbulent flows
-
- Published online by Cambridge University Press:
- 16 April 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterization of partial wetting by CMAS droplets using multiphase many-body dissipative particle dynamics and data-driven discovery based on PINNs
-
- Published online by Cambridge University Press:
- 16 April 2024, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mechanism for axial pattern formation of concentrated suspension in a horizontal rotating cylinder
-
- Published online by Cambridge University Press:
- 16 April 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reactive control of velocity fluctuations using an active deformable surface and real-time PIV
-
- Published online by Cambridge University Press:
- 16 April 2024, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cylinder flow and noise control by active base blowing
-
- Published online by Cambridge University Press:
- 16 April 2024, A10
-
- Article
-
- You have access
- HTML
- Export citation
Langmuir turbulence in suspended kelp farms
-
- Published online by Cambridge University Press:
- 16 April 2024, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimensional homogeneity constrained gene expression programming for discovering governing equations
-
- Published online by Cambridge University Press:
- 18 April 2024, A12
-
- Article
-
- You have access
- HTML
- Export citation
Excitation and evolution of radiating modes in supersonic boundary layers. Part 1. Fundamental resonance with impinging sound waves
-
- Published online by Cambridge University Press:
- 18 April 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Excitation and evolution of radiating modes in supersonic boundary layers. Part 2. Back effect of spontaneously radiated Mach waves
-
- Published online by Cambridge University Press:
- 18 April 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics and active mixing of a droplet in a Stokes trap
-
- Published online by Cambridge University Press:
- 22 April 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium distributions under advection–diffusion in laminar channel flow with partially absorbing boundaries
-
- Published online by Cambridge University Press:
- 18 April 2024, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Viscoelastic wetting: Cox–Voinov theory with normal stress effects
-
- Published online by Cambridge University Press:
- 18 April 2024, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of a viscous gravity current beneath a granular mush
-
- Published online by Cambridge University Press:
- 18 April 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation