2.1. Flow set-up

The experiments were carried out within the test section of a water flume, which measures 5.2 m in length and 0.64 m in width. The flume was filled with water such that the depth in the test section was 0.32 m. Two centrifugal pumps operated in parallel to generate a free stream velocity of U _∞ = 5.3 cm s⁻¹. The flat plate apparatus, shown in figure 1, was positioned horizontally at zero angle of attack and with the bottom surface at a depth of 0.12 m below the free surface of the water. The leading edge of the flat plate was located 2.9 m downstream of the flume entrance. The flat plate had dimensions of 1.18 m × 0.62 m × 15.9 mm in the streamwise, spanwise and wall-normal directions, respectively. The optimized leading-edge profile developed by Hanson & Buckley (Reference Hanson and Buckley2012) was used for the flat plate to ensure a laminar boundary layer would form on the bottom surface. Additionally, the trailing edge of the flat plate tapers down to prevent large-scale vortex shedding. A rectangular cut-out in the plate begins 0.27 m downstream of the leading edge and allows for an insert containing the actively deformable surface and a spherical cap element to be added to the apparatus. The purpose of the spherical cap was to disturb the laminar boundary layer and generate the periodic velocity fluctuations that were subsequently targeted by reactive control.

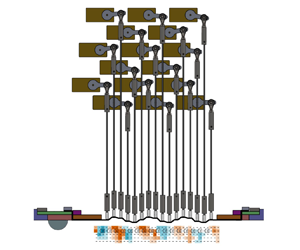
Figure 1. Schematic of flat plate apparatus showing the spherical cap and the active surface used for reactive control experimentation.

With consideration of the work of Acarlar & Smith (Reference Acarlar and Smith1987) on similar wake flows, a spherical cap with a height of h = 12 mm and a base diameter of 28 mm was selected. The Reynolds number of the spherical cap based on its height is Re_h = 635. From Acarlar & Smith (Reference Acarlar and Smith1987), this spherical cap was anticipated to have a Strouhal number in the range of St_u ≈ 0.2–0.25. The spherical cap was centred at a distance of l = 285 mm downstream of the plate's leading edge. At this location, the Reynolds number of the flow, based on length l, is Re_l ≈ 15 000. This indicates that the flow should be laminar leading up to the spherical cap. As well, the momentum thickness (θ) of the boundary layer at l and in the absence of the spherical cap is θ = 1.5 mm. As such, the Re_θ value is Re_θ = 81.

As is visible in figure 1, a Cartesian coordinate system for the flow is defined at the centre of the spherical cap and at the wall. The streamwise, wall-normal and spanwise directions of the flow are specified by x, y and z, respectively. The corresponding flow velocity components are given by U, V and W, and the fluctuating velocity components are given by u, v and w. This coordinate system will be used for the remainder of this paper. Prior to the completion of any reactive experiments, the flow on the bottom surface of the flat plate in the absence of the spherical cap was evaluated using PIV. Good agreement was observed between the measured boundary layer profile and the Blasius boundary layer profile.

2.2. Active deformable surface

An active deformable surface composed of 16 independent actuation locations that can be displaced in the wall-normal direction was developed. For readability, it will be referred to as the ‘active surface’ from this point forward. As is visible in figure 2(a), the active surface that is in contact with the flow is composed of a 1.6-mm-thick silicone rubber sheet (Δx × Δz = 245 × 60 mm²) that has been stretched flush with the bottom surface of the flat plate. Adhered to the topside of the rubber surface are 16 actuator feet that each control one of the independent actuation locations. The actuator feet have dimensions of Δx × Δz = 4 × 10 mm² and are centred about z = 0. The first actuator foot is centred at x/h = 5.3 and subsequent feet are placed with a centre-to-centre spacing of 10 mm (0.83h). Consequently, the 16th and final actuator is centred at x/h = 17.8. Each actuator foot is connected by a 2-mm-diameter stainless-steel pushrod to a 20-mm-long servo arm mounted on a high-speed digital servo motor (Savox SH-1290MG). Each servo motor is capable of oscillating the connected actuator foot at frequencies of up to 10 Hz, depending on the amplitude selected. This corresponds to a normalized frequency of f × h/U _∞ = 2.3. As well, the maximum amplitude of the surface deformation was limited to ±7.2 mm for all experiments.

Figure 2. (a) Schematic of the active surface mounted flush to the lower surface of the flat plate. The FOV of the offline PIV and RT-PIV systems are indicated as FOV1 and FOV2, respectively. (b) A photograph of the active surface assembly showing the mounting plate and nylon guides that hold the servo motors and support the flexible pushrods, respectively.

As is visible in figure 2(b), the pushrods each pass through holes in two nylon guide plates. These guide plates provide additional support to the flexible pushrods and constrain the bottoms of the pushrods to only allow movement of the actuator feet in the y direction. As is also shown by figure 2(b), an aluminium mounting plate acts as the primary structural element of the active surface assembly. The rotational displacement of the servo arms was converted to linear displacement of the actuator feet using the relation y_a = r sin⁻¹(β), where y_a is the actuator foot displacement, r is the servo arm length and β is the angle of the servo arm relative to the x axis.

Control of the servo motors was achieved using a Speedgoat real-time target machine (Performance model) with a 16-bit input/output module (model IO135). This system generates and feeds an analogue voltage signal for each of the 16 servo motors to two Teensy 3.2 boards. The Teensy boards read the voltages of the analogue signals and output pulse width modulation (PWM) signals to control each of the servo motors. Direct control of the servos from the IO135 module was not possible as it could not produce 16 independent PWM signals with sufficient resolution to smoothly control the servo motors. In the supplementary movies available at https://doi.org/10.1017/jfm.2024.292, movie 1 shows the upper portion of the assembly including the servo motors and pushrods, while movie 2 shows the underside of the active surface that is placed in contact with the flow during experiments. In these movies, the active surface is programmed to generate a travelling sine wave.

The displacement amplitude and response time of the active surface was evaluated by comparing the actual displacement of the surface with the displacement specified by the control signal as shown in figure 3. The actual displacements were extracted from images of the active surface captured by the offline PIV system. As negative displacements were not fully visible in the PIV images due to camera view blockage, a control signal with positive displacements was evaluated. As is demonstrated by figure 3, the actuator follows the control signal well. However, the peak actuator displacements are slightly damped relative to those specified by the control signal. This level of damping is consistent across different actuators of the active surface and is primarily attributed to resistance applied by the stretched rubber surface. Additionally, the actuators lagged their control signal by approximately 40 ms. This delay is mainly attributed to the reaction time of the actuators.

Figure 3. Time series comparison of an actuator tracking a sample control signal. The actuator location is obtained from off-line PIV images.

2.3. Offline PIV

During all reactive control experiments, the velocity field was measured using a standard planar PIV system and subsequently analysed for evaluating the performance of the control system. Two cameras (LaVision GmbH ImagerProX4M) were used with their imaging domain combined together into FOV1 shown in figure 2(a). Each camera features a 2048 × 2048-pixel monochrome charge-coupled device (CCD) sensor with 7.4 × 7.4 μm² pixels and 14-bit resolution. To increase the camera frame rate and eliminate excess data, the camera sensors were cropped to a size of 2048 × 625-pixels for all sets. Each camera was fitted with a 60-mm lens (Nikon AF Micro Nikkor) with an aperture setting of f/4. The resulting combined FOV had dimensions of (Δx, Δy) = 259 mm × 39 mm and a spatial resolution of 65.5-μm pixel⁻¹. The leading edge of FOV1 was located at x/h = 2.7. The seeding particles added to the water flow were 2-μm silver-coated glass spheres (Potters Industries Conduct-O-Fil SG02S40).

The FOV1 was illuminated by a dual cavity Nd: YAG laser (New Wave Research Gemini PIV). Each cavity operates independently and can produce laser pulses with an energy of up to 90 mJ per pulse and at a maximum rate of 30 Hz. The laser beam was shaped into a ~1-mm-thick laser sheet projected upwards through the bottom of the water flume and aligned with the x–y plane at the spanwise centre of the deformable surface (z = 0).

The offline PIV system was triggered externally using a delay/pulse generator (Berkeley Nucleonics Corporation model 575). The frame-straddling technique with a laser pulse delay of 16 ms was used to record double-frame images at a rate of 7.35 Hz. The offline PIV system was used to capture 1500 image pairs for each reactive control case which corresponds to 204 s of data collection. Processing of the acquired images was completed using DaVis 8.4.0 (La Vision GmbH). A multipass algorithm was used to compute the PIV vector fields. The final processing pass used 32 × 32-pixel (2.1 × 2.1 mm²) Gaussian-weighted interrogation windows (IWs) with 75 % overlap. Lastly, the vector fields from each camera were then stitched together into a single field.

2.4. Real-time PIV

The camera for the RT-PIV system was placed on the opposite spanwise side of the water flume from the two cameras for the offline PIV system. Consequently, the RT-PIV and offline PIV cameras imaged opposite sides of the same laser sheet. A Sony XCL-5005 monochrome camera was used for the RT-PIV system. This camera features a 2448 × 2050-pixel CCD sensor with 3.45 × 3.45 μm² pixels and 8-bit resolution. The camera was fitted with a 35 mm lens (Nikon AF Nikkor) with an aperture setting of f/2.8. The digital resolution of the camera was set to 78 μm pixel⁻¹. During experiments, the sensor was cropped to the desired size of 2368 × 320-pixels (185 × 25 mm²), imaging FOV2 shown in figure 2(a). The FOV2 spanned a range from y/h = 0.46–2.54 in the wall-normal direction, and a streamwise range of x/h = 4.1–19.5.

The same delay/pulse generator was used to trigger the RT-PIV and synchronize it with the offline PIV system. However, the Sony XCL-5005 camera recorded sequences of single-frame images with each image having an equal exposure time of 67 ms with an interframe time of 1 ms. Therefore, this camera was triggered at a rate of 14.7 Hz in a single-frame mode, which is twice the 7.35 Hz acquisition rate of the double-frame offline system. Similar to the offline PIV, the RT-PIV system was operated in a frame-straddling mode by considering successive image pairs within the single-frame image sequence. More specifically, the RT-PIV camera was triggered such that the laser pulse for the first image of an image pair occurred 1 ms before the end of the image's exposure time. The second laser pulse, occurring 16 ms later, therefore, occurred 14 ms into the exposure time of the second image. Through this, image pairs with the appropriate timing were produced at the same 7.35 Hz frequency similar to the offline PIV system.

Images were transmitted as they were captured to a frame grabber (Speedgoat GmbH model IO811) via a Base Camera Link connection. The images were then fed immediately into a PIV algorithm implemented in Simulink Real-Time (MathWorks) and run on the Speedgoat target machine. The RT-PIV algorithm was a basic single-pass PIV algorithm which analysed 64 × 64 pixel IWs with no overlap (one vector per 5 × 5 mm²). Cross-correlation of the IW pairs was conducted by multiplying the Fourier transform of the one IW with the complex conjugate of the Fourier transform of the other IW. Taking the inverse Fourier transform of the resulting array then produces the cross-correlation map of the two IWs. The peak value of the cross-correlation map for each IW pair was identified and then refined using three-point Gaussian subpixel interpolation. Lastly, the refined peak location was converted to U and V velocities using the known time delay between laser pulses and the digital resolution of images. The final output of the PIV algorithm was a vector field composed of 37 × 5 velocity vectors in the x and y directions.

The performance of the RT-PIV system is evaluated here by comparing snapshots of the instantaneous velocity field from RT-PIV in with those from the offline PIV system in figure 4. Figure 4(a,b) show the U component while figure 4(c,d) show the V component obtained from RT-PIV and offline PIV systems, respectively. As both systems were imaging similar FOVs at the same time instances, this comparison provided a clear indication of the performance of the RT-PIV system versus a standard PIV system. Note that the y-axis in figure 4 and all subsequent plots has been flipped relative to the orientation shown in figures 1 and 2 so the positive y is in the upward direction. As can be seen in figure 4, the RT-PIV measurements have a lower spatial resolution than those from the offline PIV system. This is a result of the RT-PIV employing 5 × 5 mm² IWs with no overlap, whereas the offline PIV system used 2.1 × 2.1 mm² IWs with 75 % overlap. Despite this, there is strong agreement between the streamwise and wall-normal velocity fields measured by the two systems. Figure 4(a,b) show similar uplifted regions of low-speed fluid that characterize the streamwise velocity field of the periodic flow. As well, figure 4(c,d) show similar pairs of wall-normal motions towards and away from the wall.

Figure 4. Snapshot of streamwise and wall-normal velocity fields measured by (a,c) the RT-PIV system and (b,d) the offline PIV systems for the same time instant. Panels (a,b) show the streamwise velocity component, while the panels (c,d) show the wall-normal velocity component.

Figure 5 provides an additional comparison of the time series of U and V velocities measured by the two systems within a 5 × 5 mm² region of space centred at (x, y) = (11.2h, 1.1h). This region corresponds to a single velocity vector measured by the RT-PIV system. For the offline PIV system, the velocity vectors that fell within the selected region were spatially averaged for the comparison. Figure 5 shows some minor discrepancies between the RT-PIV and offline PIV measurements. There appear to be two primary factors contributing to the observed differences in data between the RT-PIV and offline PIV systems. Firstly, the cameras employed by the RT-PIV system have a lower bit depth of 8 bits, while the offline PIV system uses 14-bit cameras. Additionally, the RT-PIV system only utilized a single pass of PIV processing, whereas the offline PIV system utilized three passes. As a result, the RT-PIV system has a lower signal-to-noise ratio than the offline PIV system, leading to slightly higher errors in the data. Despite the discrepancies, both systems show good agreement in figure 5. Overall, figures 4 and 5 provide confidence that accurate flow measurements were produced by the RT-PIV system. Figure 5 also highlights the periodic nature of the flow. A dominant frequency of ~1 Hz is apparent in the time series of both the streamwise and wall-normal flows.

Figure 5. Time series of velocity measurements from the offline PIV and RT-PIV systems for a 5 × 5 mm² area centred at (x, y) = (11.2h, 1.1h). Due to the higher spatial resolution of the offline PIV system, the vectors within the noted area were spatially averaged.

The latency of the RT-PIV system, Δt_l, is defined as the time between the measurement instant and when the velocity field computation is completed. The measurement instant, t ₀, is defined as the midpoint between the first and second laser pulses. Therefore, Δt_l consists of the remaining exposure time of the second image frame, read-out time of the camera and the time required for PIV computations. Based on the time instants of the laser pulses, t ₀ occurs 6 ms into the exposure time of the second image. The remaining exposure time for the second image is 61 ms. Based on the specifications for a Base Camera Link connection and the RT-PIV camera, the image readout time was estimated as ~60 ms. Lastly, from the execution time of the real-time Simulink model containing the PIV algorithm, the PIV processing time was found to approximately equal 44 ms. As such, Δt_l was found to be 165 ms. Over this latency period, the flow structures can have a maximum advection of 0.73h (8.7 mm) based on the free stream velocity.

As is described in more detail in § 2.5, each of the 16 actuators of the active surface reacted to velocity measurements from a single grid point of the RT-PIV field that is referred to as a ‘sensor IW’ here. Figure 6 shows a schematic of FOV2 relative to the active surface with the 16 sensor IWs indicated with dotted lines. To counteract the latencies of the active surface and RT-PIV system (40 and 165 ms, respectively), the sensor IW for each actuator was offset upstream of the corresponding actuator foot by a value of Δx_s, as shown in figure 6. Considering the combined latency of the active surface and RT-PIV system and the free stream velocity of the flow, three values of Δx_s/h of −0.6, −0.9 and −1.2 were chosen to investigate. For a structure advecting at the free stream velocity of the flow, these three offsets correspond to actuations that, respectively, lag, coincide with and precede the velocity detected by the upstream sensor IW. As well, two wall-normal positions of the sensor IWs (y_s) were also investigated. Values of y_s/h = 1.1 and 1.5 were chosen as these encompassed a range within which strong streamwise and wall-normal velocity fluctuations were observed for the unforced flow.

Figure 6. Schematic of the active surface relative to FOV2. The velocity field shows contours of wall-normal velocity overlaid with vectors of velocity fluctuations. The dimensions of y_s and Δx_s noted in the figure correspond to the wall-normal and streamwise offsets of sensor IWs relative to their respective actuator feet.

2.5. Reactive flow control

In the reactive control schemes, each of the 16 actuators respond to velocity measurements from a ‘sensor IW’ of the RT-PIV. The v- and u-control schemes used here are adaptation of the v- and u-control strategies of Choi et al. (Reference Choi, Moin and Kim1994). The v-control strategy involves measuring the wall-normal velocity close to the wall and deforming the wall at proportional wall-normal velocities. In contrast, the u-control strategy involves measuring streamwise velocity fluctuations and targeting them by deforming the wall.

2.5.1. Control based on wall-normal velocity (v-control)

Figure 7 shows sample time series of input, intermediate and output signals of the v-control algorithm to demonstrate the algorithm. The first step of v-control is the application of a simple threshold filter to remove any erroneous measurement of wall-normal velocity (V) that does not satisfy |V| < 0.5U _∞. Two erroneous measurements are seen at 2.7 and 5.4 s of the sample V signal shown in figure 7. The outliers were replaced with a value of zero as this keeps the actuators static until the next valid measurement becomes available. Following this, the mean component of the V velocity signal was removed by subtracting a running average calculated over a period of 1088 ms (approximately one shedding cycle). This kept the mean value of the input V signal close to zero. The ‘filtered V’ in figure 7 shows the input V signal after the application of the threshold filter and running average subtraction. The filtered V signal was next converted to the angular velocity that the servo arm must be moved at to achieve the desired wall velocity. This was done using the relation between the angle of the servo arm and the displacement of the actuator foot noted in § 2.2.

Figure 7. Sample time series outlining the steps within the v-control algorithm for a gain of +1. Here ‘V’ is the wall-normal velocity measurement from the RT-PIV system that is input to the v-control algorithm; ‘filtered V’ shows V after application of the threshold filter and subtraction of a sliding average; dy_a/dt is the time-derivative of the output signal obtained from the v-control algorithm.

The angular velocity signal was then up-sampled by a factor of 10 to allow for microstepping of the servo motors in a manner that approximates motion at the desired velocity. The signal was next multiplied by a gain value. Six gain values of ±0.5, ±1 and ±1.5 were used. The sign of the gain value specifies whether actuators move in the same or an opposing direction to the measured fluid motion. Negative gain values correspond to opposing actuations similar to the v-control scheme proposed by Choi et al. (Reference Choi, Moin and Kim1994). The positive gain cases were included in this investigation to evaluate how compliant actuations impact the flow. A gain magnitude of one corresponds to v-control that attempts to move the active surface at speeds equal to the measured wall-normal flow speed and gain magnitudes of 0.5 and 1.5 correspond to actuation speeds that were slower and faster than the measured wall-normal velocities, respectively. The signal was next sent through a discrete time integrator. This step converts the angular velocity signal to the angular position signal of the servo arm. The discrete time integrator was the reason for inclusion of the running average subtraction from the input V signal. If this was not done, the mean component of the V signal would quickly accumulate during integration of the velocity signal and result in actuators becoming saturated. To directly compare the output signal of the v-control algorithm with respect to the input V signal from the real-time PIV, the time-derivative of the v-control output, i.e. dy_a/dt, is shown in figure 7. The ‘sample and hold’ appearance of the signal is due to each actuator maintaining a constant velocity in the time period between velocity measurements. Lastly, the integrated velocity signal was converted to a PWM signal for controlling the actuators using a manufacturer provided calibration for the servo motors.

2.5.2. Control based on streamwise velocity (u-control)

The intent of the u-control algorithm is to displace the active surface in the wall-normal direction for generating the desired streamwise velocity fluctuations. Figure 8 shows sample time series of input, intermediate and output signals of the u-control algorithm. The first step of the u-control algorithm involved converting the real-time U measurements from the RT-PIV system to fluctuating u values by subtracting the average velocity of the unforced flow. The average velocity, $\langle U\rangle$, was calculated from 2000 velocity field measurements of the unforced flow collected at a rate of 7.35 Hz using the RT-PIV system. The subtraction of a premeasured average was used because the u-control algorithm did not require a discrete time integrator and, as such, there was no risk of the actuators becoming saturated due to accumulation of mean components in the u signal. Following the mean subtraction, a threshold filter was applied to detect values of |u| > 0.5U _∞. The outliers were set equal to the most recent valid u value because this kept actuators stationary until the next valid u measurement. The U signal in figure 8 shows the input signal to the algorithm and u_f shows the signal that results after subtraction of the premeasured average and application of the threshold filter. It is evident that the threshold filter removed an outlier from the input U signal at 8.7 s in figure 8.

Figure 8. Sample time series outlining the signal processing within the u-control algorithm with a gain of −1. The U signal is the streamwise velocity measurement from the RT-PIV system that is input to the u-control algorithm; u_f is the threshold filtered fluctuating streamwise velocity signal; y_a is the displacement of the active surface at the corresponding actuation location.

The u_f values were then multiplied by a gain value and converted to the desired surface displacement using a linear relation: y_a = kG × u_f. Here, k is a constant equal to −0.118 s, and G is the gain for the control case. The constant k was determined from open-loop operation of the active surface in the absence of the spherical cap. The experiments indicated that the strength of streamwise velocity fluctuations produced by the open-loop actuations are linearly proportional to the displacement of the active surface. Based on the measurements, the value of k was chosen such that the amplitude of actuator displacement was comparable to that seen for v-control. The direct conversion from velocity to displacement using a linear relation allowed the u-control algorithm to be designed without requiring the use of a discrete time integrator.

As with v-control, six gain values of ±0.5, ±1 and ±1.5 are investigated. Negative and positive gains correspond to control where streamwise velocity fluctuations induced at the wall are opposing and compliant to the streamwise velocity fluctuations measured in the flow, respectively. Figure 8 shows the output y_a signal of the u-control algorithm. The displacements shown by y_a lag u_f by one sampling period (136 ms). This occurs because actuators were controlled to move to the desired displacement over the time period between velocity measurements. This ensured that actuators moved smoothly to new displacements. Consequently, as is demonstrated by figure 8, the u-control algorithm was successful at moving the active surface to displacements that were proportional to measured streamwise velocity fluctuations.

3.1. Instantaneous flow

Figure 9(a,b) show contours of the instantaneous U_u and V_u fields overlaid with vectors of velocity fluctuations (u_u, v_u). As well, movie 3 in the supplemental material shows a movie of the unforced flow to illustrate its periodicity and development across the measurement domain. The vector fields in figure 9 show several spanwise vortices. The vortices occur with a streamwise spacing of ~4h (the shedding wavelength) fitting approximately four actuator feet between them. Consequently, the active surface has sufficient spatial resolution to target individual coherent motions within the flow. Additionally, inspection of the frequency spectrum of the unforced flow, highlights that the shedding frequency is f_u = 0.9 Hz. When normalized by U _∞ and h, the Strouhal number of the flow is St_u = 0.2. Consequently, St_u is much lower than the maximum Strouhal number for the active surface which is 2.3. As such, the active surface will be operated well below its maximum capabilities when responding to the periodic motions within the flow.

Figure 9. Instantaneous (a) streamwise and (b) wall-normal velocity contours in the wake of the spherical cap without actuation. The vectors show the fluctuating velocity components.

The U_u field shows that each vortex results in a region of uplifted low-speed fluid at its upstream edge. As well, in the V_u field the vortex core is located between an upstream ejection and a downstream sweep motion. The zones of ejection motion in the near-wake region of figure 9(b) take a U-shape and are accompanied by smaller zones of sweep motion located above them. Farther downstream, both motions form zones that are inclined with respect to the wall. The degree of inclination of these zones varies along the wall-normal direction with the inclination increasing closer to the wall. This inclination presents some additional challenges to the proper timing of actuations based on measurements away from the wall. An instance of this occurs when a sweep motion is detected at a particular streamwise position at y/h = 1.5, while there might be an ejection motion in the near-wall region. As such, the effect of different sensor locations should be investigated.

The figure also shows that the height of the vortices with respect to the wall gradually increases from y/h ≈ 1 to 2.5. As a result, ejection and sweep zones stretch gradually away from the wall and attenuate as they advect downstream. However, when comparing the streamwise and wall-normal velocity fluctuations along the horizontal lines y_s/h = 1.1 and 1.5, it was observed that these fluctuations closely resemble those along a straight line that follows the inclined trajectory of the ejection and sweep zones. This similarity is primarily due to the gradual movement of the ejection and sweep zones, shifting approximately 1h over a streamwise range of 20h. Based on investigations by Acarlar & Smith (Reference Acarlar and Smith1987) into similar wake flows, the unforced flow field is the result of a series of hairpin vortices being shed from the spherical cap. Consequently, the spanwise vortices evident in figure 9 represent the heads of individual hairpin vortices. As well, the inclined shape of the ejection and sweep zones may be explained as a result of the legs of each hairpin vortex extending upstream of the hairpin head. Hairpin vortices are a common coherent structure observed in turbulent wall-bounded flows (Adrian Reference Adrian2007). As such, this flow field allows for investigation of reactive control techniques on coherent structures similar to those found in turbulent wall-bounded flows but with reduced complexity due to their periodicity and coherence.

3.2. Time-averaged flow

The average streamwise velocity of the unforced flow in figure 10(a) shows a small region of reverse flow in the near-wake up to x/h ≈ 4, as shown by the black contour line on the left-hand side of the figure. Therefore, the first actuator foot centred at x/h = 5.3 is outside of the reverse flow region. The average streamwise flow field shows fast recovery of the velocity deficit up to x/h ≈ 8. Beyond this, there is a gradual recovery of the velocity deficit.

Figure 10. (a) Average streamwise velocity, (b) average wall-normal velocity and (c) Reynolds shear stress contours of the unforced flow. Panel (a) is also overlaid with average velocity vectors and the black line indicating the $\langle {U_u}\rangle = 0$ contour.

The average wall-normal flow field shown by figure 10(b) exhibits three key regions. There is a small negative region at the upstream edge of figure 10(b). This region is associated with fluid being drawn consistently downwards in the near wake of the spherical cap. Beneath this negative region, there is an intense positive region that gradually tapers from the upstream edge of figure 14(b) until approximately x/h = 8. This region is a result of the spanwise vortices that generate strong ejection motions. As can be observed in figure 9 and movie 3, the region close to the wall up to x/h ≈ 8 is dominated by a series of interconnected ejection motions. Past x/h ≈ 8, stretching of the ejection motions away from the wall and penetration of sweep motions towards the wall ends this initial intense upward motion. The final region consists of weak upward motion that extends diagonally in a wide band from the top of the intense region of upward motion to the upper right-hand corner of figure 10(b). This region is the cumulative result of the passage of periodic ejection and sweep motions. The positive sign of this region demonstrates that the ejection motions are generally stronger than sweep motions. Additionally, the inclination of this positive region with respect to the flow direction demonstrates the stretching of the hairpin vortices as they advect downstream.

The Reynolds shear stress contour, shown by figure 10(c), has two notable regions. The first is the positive region that extends across the entire streamwise range. This positive region is associated with the passage of ejection and sweep motions. The attenuation of this region along its streamwise dimension and its inclination with respect to the flow direction further highlights the weakening and stretching of vortices as they are advected downstream. Additionally, this positive region indicates strong production of turbulent kinetic energy (TKE). The second notable region in figure 10(c) is the narrow region of negative Reynolds shear stress below the positive region. For x/h > 6, the gradient $\textrm{d}\langle {U_u}\rangle /\textrm{d}y$ is positive across the measurement domain, as seen in the overlaid velocity vectors in figure 10(a). As such, this negative Reynolds stress region contributes to negative production of TKE.

5.1. Instantaneous flow

The impacts of the v- and u-control on the instantaneous flow was significant in many of the investigated control cases; however, trends were not easily inferred simply by viewing the instantaneous fields. Consequently, only a few general conclusions will be discussed here based on the instantaneous flow fields. A statistical analysis of the effects of v- and u-control are presented in subsequent sections.

Figure 13 shows contours of the instantaneous flow fields for v-control with a gain of −1.5. As well, the sensor IWs are centred at (Δx_s, y_s)/h = (−0.6, 1.1) with respect to the actuators. To better outline the temporal impacts of the reactive control, movie 4 in the supplemental material shows a movie of the corresponding flow field. Note that data close to the wall (y/h < 0.5) is excluded from figure 13 and all subsequent plots derived from the reactive control cases because surface protrusion into FOV1 did not allow for accurate measurements in this region.

Figure 13. Instantaneous (a) streamwise and (b) wall-normal velocity contours overlaid with velocity fluctuation vectors during v-control with a gain of G = −1.5 and sensor locations of (Δx_s, y_s) = (−0.9, 1.1).

Figure 14. Instantaneous (a) streamwise and (b) wall-normal velocity contours overlaid with velocity fluctuations vectors during u-control with a gain of G = −1.5 and sensor locations of (Δx_s, y_s) = (−0.9, 1.1).

As is evident in figure 13 and movie 4, the periodicity of the flow field is interrupted, and the flow consists of smaller and irregular structures. Relative to the unforced flow, the shape and organization of the ejection and sweep motions is significantly altered as they appear random. As well, the shedding frequency likewise becomes less consistent. This is evident in the closely spaced vortices visible at x/h ≈ 11.5–13.5 in figure 13. However, a chaotic pattern of alternating ejections and sweeps persists in the controlled flow. For all v-control cases, similar effects on the spatial organization of the ejection and sweep motions remained visible, although the extent of these effects decreases at smaller gain values.

Regarding u-control, figure 14 and movie 5 in the supplemental material show contours of the instantaneous flow fields for a gain of −1.5 (opposing actuations) and a sensor location of (Δx_s, y_s) = (−0.6, 1.1). Figure 14 and movie 5 show that the applied u-control is less disruptive to the periodic flow than the v-control case shown by figure 13. The flow structures exhibit a similar pattern of paired ejection and sweep motions visible in the unforced flow. However, clear changes to the shapes of the coherent motions could be observed in all the investigated u-control cases. As with v-control, the extent of effects on the flow decreases along with gain magnitude. The controlled flow appears to generally show less lift up of low-speed fluid relative to the unforced flow. In addition, many of the ejection and sweep motions in the flow during u-control have significantly larger inclination with respect to the wall; the ejection and sweep zones are approximately perpendicular to the wall. This suggests that the applied u-control affects the flow field, but it does not produce the same degree of disruption of the periodic flow seen in some of the v-control cases.

5.2. Impact of varying gain on mean flow

Figure 15 shows contour plots of the average streamwise velocity during reactive control relative to the unforced case (i.e. $\langle U\rangle - \langle {U_u}\rangle$). Six tested gains are considered here while the sensors are located at (Δx_s, y_s)/h = (−0.6, 1.1) relative to their respective actuator feet. As previously outlined, negative gains correspond to control intended to oppose the natural fluid motions, while positive gain values indicate control intended to apply actuations that comply with the fluid motions. By subtracting the $\langle {U_u}\rangle$ field, the impacts of the reactive control cases were made more evident. In figure 15, positive regions within the plots indicate areas where the average streamwise velocity was greater than that of the unforced flow, shown in figure 10(a), and vice versa for negative regions. As well, to supplement the contour plots discussed in this section corresponding velocity profiles for several streamwise locations in each contour plot are presented in Appendix A. These velocity profiles provide a more detailed comparison of the effects of the reactive control.

Figure 15. Average streamwise velocity relative to the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δx_s, y_s)/h = (−0.6, 1.1). The gain value is noted at the upper left-hand corner of each panel.

As evident in figure 15, the general features of the relative streamwise velocity fields for the different reactive control cases are similar between v- and u-control and across the different gain values. A positive region extends diagonally from the most upstream region near the wall to the most downstream region away from the wall in all plots. This positive region indicates a weaker wake deficit in the controlled flow and, therefore, an enhancement of the wake recovery. The positive region is most intense and attached to the bottom of the plots in the range of approximately 3 < x/h < 8, though there is significant variation between cases. Downstream of x/h = 8, the positive region is less intense and separated from the bottom of each plot. Consequently, the applied control generally induces an increase in the rate of recovery of the velocity deficit across this positive region. Additionally, the plots in figure 15 all feature negative regions encapsulated underneath the positive regions. These negative regions are indicative of larger velocity deficits in the near wall region as a result of the applied control.

The positive and negative regions are both interesting from a flow control perspective. The positive regions are encouraging as they indicate that the controlled wake flows are regaining momentum faster in the positive areas than observed in the unforced flow. Therefore, recovery of the velocity deficit is accelerated through greater turbulent mixing. The negative regions may indicate that sweep motions, which transport high-speed fluid towards the wall, have been somewhat hindered from penetrating towards the wall by the reactive control. Preventing high-speed fluid from reaching the wall and causing high-shear-rate regions is a key drag reduction mechanism of opposition v-control (Choi et al. Reference Choi, Moin and Kim1994). As such, the negative regions may indicate that the reactive control produces this drag reduction mechanism.

The negative gain cases of v-control, figure 15(a–c) show a consistent trend of increasing magnitude of the positive regions with increasingly negative gains. The increased magnitude of the positive regions is predominantly observed for x/h < 8. Consequently, this highlights that v-control with increasing negative gains is associated with a steady increase in the recovery rate of the velocity deficit. The increase in the rate of velocity deficit recovery can be explained as a result of increasing magnitude of actuations, which destabilizes the shear layer and allows wall-normal transport of momentum earlier in the wake. As such, at higher gain magnitudes the flow was able to regain momentum faster as the earlier formation of sweep motions in the wake promoted entrance of high-speed fluid. Additionally, increasing negative gains for v-control are associated with a steady increase in magnitude of the negative regions close to the wall. This suggests that the opposing actuations are increasingly inhibiting the penetration of high-speed fluid towards the wall.

The positive gain cases of v-control also show a relatively large increase in the magnitude of the positive region from a gain of 0.5 to 1, (figure 15d,e). However, the cases with gains of 1 and 1.5 (figure 15e, f), show relatively similar positive regions. Therefore, only within a certain range, increasing positive gains lead to increases in the rate of velocity deficit recovery. Similarly, there is also less of a consistent trend in the negative regions with increasing gain magnitude. From a gain of 0.5 to 1, there is a decrease in the size and magnitude of the negative region close to the wall. For the case with a gain of 1.5, (figure 15f), the magnitude of the negative region significantly increases again. These observations indicate that the compliant v-control actuations were less capable at inhibiting the motion of high-speed fluid towards the wall relative to the opposition v-control.

The u-control cases in figure 15(g–l), while showing the same general features as in the v-control cases, demonstrate some notable differences. As with v-control, increasing gain magnitude for u-control corresponds with significant increases to the magnitude of the positive regions. This may be explained to some degree by the explanation provided for this trend in the v-control cases. As well, increasing gain magnitudes are associated with decreasing size and magnitude of the negative regions close to the wall. Consequently, for u-control, increasing gain magnitude enhances the wake recovery and minimizes the reduction of streamwise velocity close to the wall. The latter of these effects may indicate that u-control with larger gain magnitudes is less capable of impeding the motion of high-speed fluid towards the wall.

Comparing the positive and negative gains for u-control, we observe that the figure 15(g–i) with negative gains exhibit positive regions attached to the plot bottoms over a considerably larger streamwise range than the figure 15( j–l) with equivalent positive gains. As well, the negative gain cases have negative regions close to the wall that are significantly reduced in size and magnitude in comparison with the equivalent positive gain cases. Consequently, u-control cases with negative gains induced recovery of the velocity deficit over a larger streamwise range while also exhibiting less reduction of the streamwise velocity close to the wall. The greater magnitude of the near-wall negative region for the positive gain cases seems to agree with the suggestion of Rebbeck & Choi (Reference Rebbeck and Choi2006) that compliant streamwise velocity fluctuations induced near the wall aid at inhibiting the penetration of sweep motions towards the wall. The differences between u-control cases with equivalent positive and negative gains are less evident than those between v-control cases with equivalent positive and negative gains.

A similar analysis is conducted for the average wall-normal velocity fields of the reactive control cases. Figure 16 shows contour plots of the average wall-normal velocity relative to the average wall-normal velocity of the unforced flow during reactive control at the six tested gains and with (Δx_s, y_s)/h = (−0.6, 1.1). As is shown by figure 10(b), the $\langle {V_u}\rangle$ field of the unforced flow is predominantly positive except for a small negative region attached at the upstream edge of the plot. As such, in the subsequent discussion, negative regions in figure 16 indicate areas where the average wall-normal velocity away from the wall is reduced in comparison with the unforced flow, and vice versa for positive regions.

Figure 16. Average wall-normal velocity field relative to that of the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δx_s, y_s)/h = (−0.6, 1.1) and at all tested gain values.

There are several common features that exist across all the subplots in figure 16, although with some variation in their presentation. One of these common features is the negative regions near the wall and attached to the upstream edge of each plot in figure 16. These regions indicate a reduction in wall-normal motions resulting from an upstream shift in the flow field due to the earlier occurrence of wall-normal momentum transport in the wake. This is consistent with the conclusion that the increased velocity deficit recovery seen in the plots in figure 15 was also somewhat due to sweep and ejection motions forming earlier in the wake. A second common feature of all the plots in figure 16 is a negative region extended in the streamwise dimension and roughly at the centre of each plot. These negative regions, which will be referred to as the primary negative regions from this point forward, indicate a reduction to the region of positive $\langle V\rangle$ in figure 10(b) that was associated with the stretching of vortices and the corresponding ejection and sweep motions away from the wall. Adrian (Reference Adrian2007) noted that the stretching of hairpin vortices away from the wall is associated with an intensification of the vortices. Consequently, the primary negative regions are attributed to weaker vortices because of the applied reactive control. As well, there are two positive regions common to all of the plots in figure 16. The first is a positive region approximately at x/h = 5. As with the upstream negative regions, these positive regions are partially due to the upstream shift of the average wall-normal flow. Additionally, the plots exhibit positive regions close to the wall, often over a significant streamwise range. These are attributed in part to decreased penetration of sweep motions towards the wall because of the applied control. Some portion of the near-wall positive regions may also be due to the outward deformations of the wall.

With regard to the v-control cases, there are some clear trends that are visible between cases with gains of the same sign. The negative gain (opposing actuation) cases of v-control (figure 16a–c), show a trend of decreasing size and magnitude of the primary negative region with increasing gain magnitude. This indicates that at larger negative gains, v-control is not affecting the strength of the vortices as much as at lower negative gains. As well, there is an increase in the size and magnitude of the near-wall positive regions for increasing negative gain values. This indicates that the penetration of sweep events towards the wall is inhibited to a greater degree at larger negative gains. This is consistent with the conclusions drawn from the corresponding average streamwise plots shown in figure 15.

For the positive gain (compliant actuation) cases (figure 16d–f), there is a trend of increasing size and magnitude of the primary negative region with increasing gain magnitude. This indicates that v-control cases with larger positive gains had a greater weakening effect on vortices. As well, the positive gain v-control cases all exhibit multiple distinct positive regions close to the wall. The cause of this is partially attributed to individual actuators being biased towards outwards or inwards deformations during the v-control case. This resulted due to imperfect removal of the mean component of the wall-normal velocity in the v-control algorithm. Overall, however, the intermittency and weaker magnitudes of the near-wall positive regions for the positive gain cases of v-control indicates that these cases were less successful at inhibiting the progress of sweep motions towards the wall.

With regards to u-control, the negative gain cases (figure 16g–i) show slightly increasing magnitudes of the primary negative regions with increasing gain magnitude. This indicates that cases of u-control with larger negative gains weakened vortices more than cases with smaller negative gains. Additionally, figure 16(g–i) all show similar near-wall positive regions. This indicates that all the negative gain values for u-control similarly inhibited the progress of sweep motions towards the wall. The positive gain cases of u-control (figure 16j–l) likewise demonstrate slightly increasing magnitudes of the primary negative regions with increasing gain magnitude. As well, there is a reduction of the near-wall positive region with increasing positive gain. As such, larger positive gains led to slightly weaker vortices and slightly less inhibition of the penetration of sweep motions towards the wall. These observations are consistent with those from the average streamwise flow fields in figure 15.

Comparing cases of u-control with equivalent positive and negative gain magnitudes, the negative gain cases have primary negative regions that are larger and have a higher magnitude. Therefore, the opposing actuation cases had a relatively stronger effect towards weakening the vortices compared with the compliant actuation cases. Additionally, the positive gain cases of u-control have near-wall positive regions that are moderately larger and higher in magnitude. This indicates that u-control cases with positive gains are relatively more effective at inhibiting the progress of sweep motions towards the wall.

Lastly, the effect of different gain values on Reynolds shear stress ($- \langle uv\rangle$) was characterized in figure 17. Referring back to figure 10(c), the Reynolds shear stress contour for the unforced flow was characterized by a negative region close to the wall and a positive region above this that spanned the entire streamwise range. All the plots in figure 17 have a positive region attached to the upstream edge. This region is attributed to greater wall-normal momentum transport early in the wake of the spherical cap. As well, all the plots show a negative region inclined with respect to the flow direction that extends across most of the streamwise range. This region indicates that the reactive control generally reduced the positive region of Reynolds shear stress seen in the unforced flow. This reduction of positive Reynolds shear stress was interpreted as a weakening of the ejection and sweep motions relative to the unforced flow. This, in turn, indicates that the vortices which induce the ejection and sweep motions have been weakened. Lastly, the plots in figure 17 all have positive regions below the large negative region. These near-wall positive regions demonstrate that the reactive control reduced, and even eliminated in some cases, the negative region of Reynolds shear stress seen close to the wall in the unforced flow.

Figure 17. Reynolds shear stress field relative to that of the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δx_s, y_s)/h = (−0.6, 1.1) and at all tested gain values.

For both v- and u-control, increasing gain magnitudes lead to larger positive regions in figure 17, which means greater reduction of the negative regions of Reynolds stress close to the wall. A second common trend across both control strategies in figure 17 is the increase in magnitude of the negative regions with increasing gain magnitude. This trend indicates that increasing actuation amplitudes generally reduces the strength of vortices. These negative regions indicate areas where the production of TKE is reduced relative to the unforced flow.

Regarding the v-control cases (figure 17a–f), the trends exhibited are relatively consistent with those shown by figures 15 and 16. The negative gain cases show a steady increase in the magnitude of the negative and positive regions with increasing gain magnitude. For the positive gain cases there is a relatively large increase in the magnitudes of the positive and negative regions when the gain increases from 0.5 to 1. From a gain of 1 to 1.5, however, there is relatively little change in the Reynolds stress field. As well, the negative gain cases of v-control appear to have a larger impact on the Reynolds stresses close to the wall compared with the positive gain cases.

The u-control cases likewise show increasing magnitude of the positive and negative regions with increasing gain. Consequently, vortices are weakened, and the near-wall flow is more disrupted by larger amplitudes of both opposing and compliant actuations. The negative gain cases (figure 17g–i) have positive and negative regions that are relatively lower in magnitude than those of the positive gain cases in figure 17( j–l). This indicates that the positive gain cases had an overall larger impact on the Reynolds stress field.

From the above discussion of figures 15–17, it is evident that there are notable differences between v- and u-control, and both are sensitive to changes in gain magnitude and sign. The differences observed between cases of each control strategies for gains of opposite sign are particularly encouraging as this indicates that the opposing and compliant actuations are impacting the flow in different ways. The negative gain cases of v-control present some of the most compelling results in that the mean flow fields indicate that sweep motions were increasingly inhibited from penetrating towards the wall with increasing strength of opposing actuations. This is a key drag reduction mechanism of the v-control strategy numerically investigated by Choi et al. (Reference Choi, Moin and Kim1994). As such, the observation of this effect indicates that the v-control applied in this work was behaving to some extent as was predicted by numerical works.

5.3. Impact of varying sensor location on mean flow

We have so far characterized the impact of gain sign and magnitude on the average flow fields during the application of v- and u-control for a single location of sensor IWs. The remaining discussion in this section describes the impact of sensor location on the two control schemes when applying opposing and compliant actuations. As previously outlined, sensors were offset from their respective actuators by (Δx_s, y_s). Here, Δx_s/h values of −0.6, −0.9 and −1.2 are evaluated along with y_s/h values of 1.1 and 1.5. Only the average streamwise velocity fields are considered in this section for brevity.

Figure 18 shows the average streamwise flow fields relative to that of the unforced flow for v- and u-control with a gain of −1 (opposing actuations) and for each of the six different sensor locations. Regarding the two y_s values tested, a general result across almost all the subplots is that the positive regions have a reduced magnitude for y_s/h = 1.5 as compared with cases with y_s/h = 1.1. As highlighted by § 4, for y_s/h = 1.5 the active surface saw lower actuation amplitudes in comparison with the cases with y_s/h = 1.1. As such, the weaker positive regions shown by cases with y_s/h = 1.5 are attributed to this weaker actuation. The near-wall negative regions show less of a consistent effect of y_s. For v-control there appears to be relatively minimal effect of the y_s value on the negative near-wall regions. However, for u-control the near-wall negative regions are larger in size and magnitude for cases with y_s/h = 1.5.

Figure 18. Average streamwise velocity fields relative to that of the unforced flow for reactive control cases with a gain of −1 and at the six tested sensor locations. Text in the upper left-hand corner of each panel shows (Δx_s, y_s)/h for each case.

Changes to the Δx_s value likewise demonstrate some notable impacts on the effects of v-control applying opposing actuations in figure 18(a–f). For cases with y_s/h = 1.1, moving the sensors farther upstream, i.e. Δx_s/h goes from −0.6 to −1.2, results in slight increases to the recovery rate in the near-wake while also decreasing the extent of flow speed reductions close to the wall. The cases with y_s/h = 1.5 show a decrease in both the near-wake velocity deficit recovery rate and in the reduction of the near-wall flow speed when the sensors are moved farther upstream. The weaker reduction of the near-wall flow speed for more upstream sensor locations could indicate that sweep motions penetrate towards the wall to a greater extent for these cases.

The opposing actuation u-control cases show similar trends across the different Δx_s values at both y_s values. Comparing cases with Δx_s/h = −0.6 and −0.9, the more upstream sensor position (Δx_s/h = −0.9) leads to a lower near-wake velocity deficit recovery rate and greater reduction of the near-wall flow speed. From Δx_s/h = −0.9 to −1.2, however, the opposite occurs. The cases with Δx_s/h = −1.2 show greater near-wake velocity deficit recovery rates and less reduction of the near-wall flow speed in comparison with cases with Δx_s/h = −0.9.

Figure 19 shows the average streamwise flow fields relative to that of the unforced flow for v- and u-control with a gain of one (compliant actuations) and for each of the six different sensor locations. The two y_s values appear to affect the strength of the positive regions. Cases with y_s/h = 1.5 generally have weaker positive regions compared with cases with y_s/h = 1.1. As with the opposing actuation cases in figure 18, this is attributed primarily to weaker actuation of the surface for cases with y_s/h = 1.5. As well, for both v- and u-control, cases with y_s/h = 1.1 predominantly show stronger reductions of the near-wall flow speed.

Figure 19. Average streamwise velocity fields relative to the unforced flow for reactive control cases for (a–f) v-control and (g–l) u-control with a gain of +1 and at the six tested sensor locations. Text in the upper left-hand corner of each panel indicates (Δx_s, y_s)/h for each case.

The impact of Δx_s on v-control applying compliant actuations as seen in figure 19(a–f) is significant and differs at the two y_s values. Cases with y_s/h = 1.1 show a small decrease in the near-wake velocity deficit recovery rate with increasing upstream sensor positions. As well, there is a significant increase in the reduction of the near-wall flow speed as Δx_s/h goes from −0.6 to −0.9. As such, the opposition of sweep motions penetrating towards the wall is increased by the more upstream sensor position. For the compliant actuation v-control cases with y_s/h = 1.5 (figure 19d–f), the cases with Δx_s/h = −0.6 and −1.2 are relatively similar and show near-wake velocity deficit recovery rates and near-wall flow speed reductions of moderate strength compared with the other plots in figure 19. The case with Δx_s/h = −0.6 (figure 19e) has a significantly increased near-wake velocity deficit recovery rate and shows quite minimal reduction of the near-wall flow speed. Consequently, this case appears to have induced relatively little opposition to sweep motions.

The effect of Δx_s on compliant actuation cases of u-control is similar to the effect it had for opposing actuation cases of u-control. The cases with Δx_s/h = −0.9 have slightly lower near-wake velocity deficit recovery rates and greater reductions of the near-wall flow speed compared with cases with the other two streamwise sensor locations. As such, the cases with Δx_s/h = −0.9 appear to have most strongly opposed the advance of sweep motions towards the wall.

Considering figures 18 and 19 together, it is evident that v- and u-control were sensitive to sensor location when applying opposing and compliant actuations. The effects of sensor location differed significantly for v-control applying opposing actuations compared with v-control applying compliant actuations. The greatest reduction of the near-wall flow speed is achieved with Δx_s/h = −0.6 for opposing actuations and with Δx_s/h = −1.2 for compliant actuations. As well, the opposing actuations cases show consistent changes in the positive and negative regions with changing streamwise sensor position. This is not observed for the compliant actuation cases. Regarding u-control, there is greater similarity between the effects of sensor location between cases applying opposing and compliant actuations. The primary difference is that, for opposing actuations, the greatest reduction of the near-wall flow speed occurs with y_s/h = 1.5, while for compliant actuations, it occurs with y_s/h = 1.1.