1. Introduction
Active control of turbulence presents enormous potential for improving the efficiency and efficacy of innumerable real-world systems. Consequently, a growing focus has been applied to the development of active flow control techniques over the past several decades (Gad-el-Hak Reference Gad-el-Hak2000; Brunton & Noack Reference Brunton and Noack2015; Duriez, Brunton & Noack Reference Duriez, Brunton and Noack2016). A major driver of the increasing attention towards active flow control has been a result of improvements in electronics and computing over the past few decades. This has led to the development of better sensors, actuators and systems for real-time control that make the investigation of active flow control a more attainable venture.
Among the numerous potential applications of active flow control, the control of wall-bounded turbulent flows is of great interest due to the prevalence of these flows in various systems. Coherent structures such as hairpin and streamwise vortices, high- and low-speed streaks and ejection and sweep motions are known to play critical roles in the self-sustained mechanism of turbulence in wall-bounded flows (Robinson Reference Robinson1991; Adrian Reference Adrian2007). Consequently, rather than considering all the highly nonlinear characteristics of turbulent boundary layers, the targeted manipulation of one or multiple types of coherent structures in these flows could potentially allow for a simplified approach to the active control of these complex turbulent flows. This type of control, where sensors detect oncoming coherent motions and actuators attempt to favourably influence them is referred to as reactive control (Gad-el-Hak, Pollard & Bonnet Reference Gad-el-Hak, Pollard and Bonnet1998).
While reactive control simplifies the problem of turbulence control somewhat, it is still a difficult task given that detecting coherent structures is not trivial and the optimal approach for manipulating different coherent structures is likewise unclear. Choi, Moin & Kim (Reference Choi, Moin and Kim1994) investigated reactive control using the direct numerical simulation of a turbulent channel flow on a course grid with 32 × 65 × 32 grid points (streamwise, wall-normal and spanwise, respectively). A finer grid with 128 × 129 × 128 grid points was used for verification of a select number of cases. At each time instant of the simulation, reactive control was realized by setting the boundary condition for each grid point of the wall to a velocity that was proportional to one detected at a grid point above the wall. Of the control strategies that Choi et al. (Reference Choi, Moin and Kim1994) investigated, we will specifically focus on control strategies based on streamwise and wall-normal velocity components as these strategies are most relevant to those investigated in this work. These were so called u-control and v-control, where u and v denote streamwise and wall-normal velocity fluctuations, respectively.
Choi et al. (Reference Choi, Moin and Kim1994) defined u-control as inducing streamwise fluid motions at the wall that were proportional to streamwise velocity fluctuations measured away from the wall. Both compliant and opposing actuations were investigated. Compliant actuations indicate that the streamwise velocity induced at the wall had the same sign as those measured in the flow and vice versa for opposing actuations. Choi et al. (Reference Choi, Moin and Kim1994) observed a 10 % drag reduction when applying compliant actuations and a drag increase when applying opposing actuations. They indicate that compliant actuations led to a reduction of the wall-normal gradient of streamwise velocity (i.e. ∂u/∂y) close to the wall while opposing actuations increased this gradient in the near-wall region. It is worth noting that u-control received minimal attention in Choi et al. (Reference Choi, Moin and Kim1994) and has likewise seen almost no further subsequent investigation. This is attributed to the fact that Choi et al. (Reference Choi, Moin and Kim1994) found it was less effective at reducing skin friction drag in comparison with other reactive control schemes they investigated.
The v-control strategy, as Choi et al. (Reference Choi, Moin and Kim1994) defined it, involved detecting ejection and sweep motions based on their wall-normal velocity at a location away from the wall, and targeting them with proportional wall-normal fluid motions induced at the wall. It should be noted that Choi et al. (Reference Choi, Moin and Kim1994) and most subsequent works on v-control have only investigated opposing actuation, where wall-normal fluid motions induced at the wall have an opposite sign to those measured in the flow. Choi et al. (Reference Choi, Moin and Kim1994) found that v-control produced a 25 % drag reduction in part through opposing of sweep motions. This v-control pushes high-shear-rate regions away the wall where they contribute less to skin friction drag. As well, through investigating the effect of v-control on an isolated vortex pair, Choi et al. (Reference Choi, Moin and Kim1994) also observed that v-control prevents the lift-up of near-wall vorticity. This decreases the formation of streamwise vortices to some extent which, in turn, reduces skin friction drag. A similar numerical investigation of v-control by Wang, Huang & Xu (Reference Wang, Huang and Xu2016) further supports these conclusions. Wang et al. (Reference Wang, Huang and Xu2016) characterized the circulation of vortices in a direct numerical simulation of turbulent channel flow during v-control. They found that v-control caused weaker and relatively fewer vortices to occur in the flow.
It is noted in Choi et al. (Reference Choi, Moin and Kim1994) and many subsequent works on v-control, that the wall-normal location of sensors, ![]() $y_s^ +$, is critical to the effectiveness of v-control. Here, the superscript ‘+’ indicates that the distance is normalized using inner scaling. Choi et al. (Reference Choi, Moin and Kim1994) investigated four
$y_s^ +$, is critical to the effectiveness of v-control. Here, the superscript ‘+’ indicates that the distance is normalized using inner scaling. Choi et al. (Reference Choi, Moin and Kim1994) investigated four ![]() $y_s^ +$ values of 5, 10, 20 and 26 and determined that
$y_s^ +$ values of 5, 10, 20 and 26 and determined that ![]() $y_s^ += 10$ produced the greatest drag reduction. Furthermore, for
$y_s^ += 10$ produced the greatest drag reduction. Furthermore, for ![]() $y_s^ += 26$, they observed a steep increase in drag. Several other numerical studies also found drag reductions were achieved by v-control with approximately
$y_s^ += 26$, they observed a steep increase in drag. Several other numerical studies also found drag reductions were achieved by v-control with approximately ![]() $y_s^ + < 20$; however, for
$y_s^ + < 20$; however, for ![]() $y_s^ + > 20$, the effect of v-control becomes unstable, and there is a substantial drag increase (Hammond, Bewley & Moin Reference Hammond, Bewley and Moin1998; Lim & Kim Reference Lim and Kim2004; Chung & Talha Reference Chung and Talha2011; Deng & Xu Reference Deng and Xu2012). Deng & Xu (Reference Deng and Xu2012) used the streak transient growth (STG) mechanism proposed by Schoppa & Hussain (Reference Schoppa and Hussain2002) to explain the change in the behaviour of v-control based on variation in
$y_s^ + > 20$, the effect of v-control becomes unstable, and there is a substantial drag increase (Hammond, Bewley & Moin Reference Hammond, Bewley and Moin1998; Lim & Kim Reference Lim and Kim2004; Chung & Talha Reference Chung and Talha2011; Deng & Xu Reference Deng and Xu2012). Deng & Xu (Reference Deng and Xu2012) used the streak transient growth (STG) mechanism proposed by Schoppa & Hussain (Reference Schoppa and Hussain2002) to explain the change in the behaviour of v-control based on variation in ![]() $y_s^ +$. They note that in the STG stage of streamwise vortex development, wall-normal velocity fluctuations change in sign at y + ≈ 20. As such, they indicate that for v-control with
$y_s^ +$. They note that in the STG stage of streamwise vortex development, wall-normal velocity fluctuations change in sign at y + ≈ 20. As such, they indicate that for v-control with ![]() $y_s^ + < 20$, the desired opposition of wall-normal velocity fluctuations occurs; however, for
$y_s^ + < 20$, the desired opposition of wall-normal velocity fluctuations occurs; however, for ![]() $y_s^ + > 20$, fluid motions induced at the wall are compliant with the wall-normal velocity fluctuations closest to the wall.
$y_s^ + > 20$, fluid motions induced at the wall are compliant with the wall-normal velocity fluctuations closest to the wall.
Additionally, several numerical simulations have investigated the impact of different amplitudes of opposing actuation. Chung & Talha (Reference Chung and Talha2011) found that applying actuations greater in strength than those measured at the detection location led to v-control becoming unstable and inducing significant drag increases for all detection locations (![]() $5 < y_s^ + < 30$). Deng et al. (Reference Deng, Xu, Huang and Cui2014) likewise investigated strengthened v-control; however, they added what they refer to as ‘time relaxation’ to their adapted v-control scheme. The time relaxation was essentially a form of low-pass filtering and considered the velocity induced at the wall at a previous time step in calculating the velocity that would be induced at the current time step. The time relaxation was successful at stabilizing strengthened v-control, and they were able to achieve a maximum drag reduction of 33 % using
$5 < y_s^ + < 30$). Deng et al. (Reference Deng, Xu, Huang and Cui2014) likewise investigated strengthened v-control; however, they added what they refer to as ‘time relaxation’ to their adapted v-control scheme. The time relaxation was essentially a form of low-pass filtering and considered the velocity induced at the wall at a previous time step in calculating the velocity that would be induced at the current time step. The time relaxation was successful at stabilizing strengthened v-control, and they were able to achieve a maximum drag reduction of 33 % using ![]() $y_s^ += 15.4$ and wall-normal suction and blowing significantly larger in amplitude than the wall-normal velocities measured at the sensor plane.
$y_s^ += 15.4$ and wall-normal suction and blowing significantly larger in amplitude than the wall-normal velocities measured at the sensor plane.
Beyond the investigation of variables such as sensor location and actuation amplitude, different actuation techniques have also been explored as an alternative to suction and blowing. Endo, Kasagi & Yuji (Reference Endo, Kasagi and Yuji2000), Kang & Choi (Reference Kang and Choi2000) and Pamiès et al. (Reference Pamiès, Garnier, Merlen and Sagaut2011) numerically investigated adaptations of v-control that used active wall deformation in the wall-normal direction. As such, the wall was moved at opposing velocities to wall-normal fluid velocities measured at the sensor location. Both Endo et al. (Reference Endo, Kasagi and Yuji2000) and Kang & Choi (Reference Kang and Choi2000) investigated cases with complete control of the deformation of all grid points of the wall. With this full control of surface deformation, they were able to achieve drag reductions in the range of 12 %–17 %. The root-mean-square of wall deformation was in the range of 1–3.2 wall units for these investigations. As well, Endo et al. (Reference Endo, Kasagi and Yuji2000) and Pamiès et al. (Reference Pamiès, Garnier, Merlen and Sagaut2011) numerically investigated semirealistic scenarios where active wall-deformation was achieved using an array of finite size actuators that were elongated in the streamwise direction to target streamwise vortices. Endo et al. (Reference Endo, Kasagi and Yuji2000) achieved a drag reduction similar to that of their case with full control of wall deformation. Pamiès et al. (Reference Pamiès, Garnier, Merlen and Sagaut2011), however, noted a negligible drag reduction in their simulation. The actuator design and specific reactive control employed by these two works does differ somewhat and, as such, this likely explains their opposing results. This highlights the significant difficulty of developing active turbulence control in that two works applying seemingly similar control strategies can have much different levels of efficacy.
Despite the many promising numerical results of reactive control and associated v-control strategies highlighted so far, there has been very little experimental investigation related to v-control and reactive control in general. Breuer, Haritonidis & Landahl (Reference Breuer, Haritonidis and Landahl1989) represents one of the earliest examples of an experimental implementation of reactive control. They employed a series of pneumatically driven flexible membranes embedded in the wall to oppose disturbances generated in a laminar boundary layer. Their work indicated that the active wall deformation was successful at delaying the growth of the artificial disturbance. As well, Rebbeck & Choi (Reference Rebbeck and Choi2006) represents one of the only experimental investigations of real-time control meant to mimic v-control. They applied intermittent wall-normal blowing at a single location in a turbulent boundary layer to oppose sweep motions detected by an upstream hot-wire anemometer. They demonstrated that the penetration of sweep motions towards the wall can be blocked by an opposing blowing actuation induced at the wall. Lastly, the investigation by Goldin et al. (Reference Goldin, King, Patzold, Nitsche, Haller and Woias2013) into the damping of Tollmien–Schlichting (TS) waves in a laminar boundary layer is another tangential example of an experimental implementation of reactive control. Goldin et al. (Reference Goldin, King, Patzold, Nitsche, Haller and Woias2013) used hot-wire anemometers to detect TS waves and then controlled a streamwise cascade of bars that could be actuated in the wall-normal direction to induce a ‘counter wave’. They were able to reduce the root-mean-square amplitude of TS waves by up to 85 % with this strategy. The results of Breuer et al. (Reference Breuer, Haritonidis and Landahl1989), Rebbeck & Choi (Reference Rebbeck and Choi2006) and Goldin et al. (Reference Goldin, King, Patzold, Nitsche, Haller and Woias2013) are positive indications that reactive control can be achieved in experimental settings. However, significant development is needed to advance experimental implementations of reactive control towards more complex and applicable states.
Two aspects that contribute significantly to the difficulty of experimental implementation are the development of (a) actuation and (b) sensor systems. The number of actuators employed for experimental implementations of reactive control is limited by the physical dimensions of the actuators themselves and by the number of sensors that are used. In numerical works, it is possible to assume that actuators do not have any physical dimension. Consequently, the majority of numerical investigations assume full actuation across all the grid points of the wall. In addition, numerical investigations have complete knowledge of flow parameters in a three-dimensional domain, while experimental investigations are limited to certain flow parameters at selected locations. In Rebbeck & Choi (Reference Rebbeck and Choi2006), it is evident that applying reactive control with just a single actuator and sensor is a significant limitation. One of the goals of the current investigation is to begin approaching the extent of actuation and sensing seen in numerical works by harnessing multiple actuators and sensors for the experimental implementation of reactive control schemes.
A few investigations have demonstrated the potential of active wall-normal surface deformation for controlling wall-bounded flows. As previously mentioned, Breuer et al. (Reference Breuer, Haritonidis and Landahl1989) successfully employed wall-deformation to delay the growth of an artificial disturbance in a laminar boundary layer. As well, the numerical work of Carlson & Lumley (Reference Carlson and Lumley1996) evaluated the effects of an outward Gaussian wall deformation on a pair of high- and low-speed streaks in the near-wall region. The wall-normal deformation was found to lift the streaks, causing the adjacent, opposing streaks to expand. The lifting of high- and low-speed streaks was associated with drag reduction and increase, respectively. Additionally, the investigations of Kim et al. (Reference Kim, Jeon, Park and Choi2003) and Gibeau & Ghaemi (Reference Gibeau and Ghaemi2022, Reference Gibeau and Ghaemi2023) used a circular membrane to replace a section of the wall and deformed the membrane at various frequencies using an electromagnetic actuator. They observed that high- and low-speed streamwise motions were produced by the downward and upward wall motions, respectively, in both laminar and turbulent boundary layers. Gibeau & Ghaemi (Reference Gibeau and Ghaemi2023) notes that the active wall motions induce streamwise velocity fluctuations that are stronger than the corresponding wall-normal velocity fluctuations. This suggests that the wall-normal actuators are also suitable for u-control strategies. Cattafesta & Sheplak (Reference Cattafesta and Sheplak2011) note that wall deformation is becoming a more viable actuation technique with advances in the areas of piezoelectric actuators and microelectromechanical systems. Consequently, given the numerical and experimental demonstrations of the abilities of active wall deformation and the growing viability of these actuators, this type of actuation was chosen for the current investigation.
The required real-time flow sensing away from the wall is also a limiting factor for the experimental implementation of reactive control. This limitation was highlighted in many numerical works on v-control (Choi et al. Reference Choi, Moin and Kim1994; Endo et al. Reference Endo, Kasagi and Yuji2000; Deng et al. Reference Deng, Xu, Huang and Cui2014). Consequently, a significant step in the current investigation involved utilizing a real-time particle image velocimetry (RT-PIV) system capable of measuring velocity field over a two-dimensional domain. The major benefits of an RT-PIV system are that it is non-invasive, highly adaptable to a variety of flow set-ups, and can provide velocity measurements at many locations. Early RT-PIV systems required complex and custom hardware systems to handle the large amounts of data and computational requirements of particle image velocimetry (PIV) algorithms (Maruyama, Yamaguchi & Kawase Reference Maruyama, Yamaguchi and Kawase2001; Fujiwara, Fujimoto & Maruyama Reference Fujiwara, Fujimoto and Maruyama2003; Siegel & Cohen Reference Siegel and Cohen2003; Aubert, Bochard & Fresse Reference Aubert, Bochard and Fresse2006; Yu et al. Reference Yu, Leeser, Tadmor and Siegel2006; Muñoz et al. Reference Muñoz, Dellavale, Sonnaillon and Bonetto2009). In recent years, the improvement of computing technologies and the commonality of machine vision applications in the industry has greatly improved the feasibility of RT-PIV systems. Willert, Munson & Gharib (Reference Willert, Munson and Gharib2010) demonstrated the first use of RT-PIV as a sensor for active flow control. They used an RT-PIV system producing 15 vector fields per second to conduct control of vortex formation on an airfoil immersed in an oil tunnel facility. More recently, Gautier & Aider (Reference Gautier and Aider2015) demonstrated a ground-breaking RT-PIV system that leveraged graphics processing unit architecture and an optical flow algorithm developed by Le Besnerais & Champagnat (Reference Le Besnerais and Champagnat2005) to obtain dense velocity vector fields from 2-megapixel images at a rate of several hundred velocity fields per second. The RT-PIV system described by Gautier & Aider (Reference Gautier and Aider2015) was used to control the flow downstream of a backward-facing step (Gautier & Aider Reference Gautier and Aider2014; Gautier et al. Reference Gautier, Aider, Duriez, Noack, Segond and Abel2015), and bimodal wake flow from a bluff body (Varon et al. Reference Varon, Aider, Eulalie, Edmige and Gilotte2019). Consequently, these examples provided confidence that the development of an RT-PIV system was a reasonable approach for conducting reactive control.
The current investigation enhances our understanding of the control strategies investigated by Choi et al. (Reference Choi, Moin and Kim1994) and advances our experimental capabilities for the realization of reactive control. The reactive control for the current investigation was applied to a periodic flow downstream of a wall-mounted spherical cap immersed in a laminar boundary layer. The coherence and periodicity of the structures in this flow were desirable as it was hypothesized that this would allow for clearer observation of the effects and underlying mechanisms of the reactive control. More specifically, this experimental investigation addresses the following aspects.
i. Development of an active deformable surface using an array of multiple actuators placed in a streamwise arrangement. Each actuator is controlled independently allowing the surface to generate complex on-demand surface deformations.
ii. Development of an RT-PIV system for fast non-intrusive sensing of velocity fluctuations above the actuators. Several sensor locations are investigated to understand the effects of streamwise and wall-normal distance between sensor and actuator locations.
iii. Understanding the efficacy of v- and u-control using compliant and opposing strategies for controlling velocity fluctuations. The results compare the impact of v- and u-control using compliant and opposing strategies and provide guidance for the future development of flow control techniques.
In the upcoming section, the experimental methodology is described in detail, including a comprehensive account of the procedures utilized for the reactive control of streamwise and wall-normal velocity fluctuations. Following that, the results of the experiments are discussed in depth. Lastly, the conclusions drawn from the investigation are summarized.
2. Experimental methodology
Experiments were conducted on the underside of a flat plate apparatus mounted in a water flume at the University of Alberta. This flow facility is described in § 2.1. An actively deformable surface with 16 independent actuators was developed for the reactive control and is described in § 2.2. Flow measurements were carried out using a standard PIV for a posteriori analysis of the reactive control as outlined in § 2.3. To provide clear distinction, this standard PIV system will be referred to as the ‘offline PIV’ system. The RT-PIV that provided real-time flow measurements for the reactive control system is described in § 2.4. The two PIV systems were synchronized to enable using a single laser for illuminating the field of view (FOV) of both systems. Lastly, the two reactive control algorithms investigated in this work are described in § 2.5.
2.1. Flow set-up
The experiments were carried out within the test section of a water flume, which measures 5.2 m in length and 0.64 m in width. The flume was filled with water such that the depth in the test section was 0.32 m. Two centrifugal pumps operated in parallel to generate a free stream velocity of U ∞ = 5.3 cm s−1. The flat plate apparatus, shown in figure 1, was positioned horizontally at zero angle of attack and with the bottom surface at a depth of 0.12 m below the free surface of the water. The leading edge of the flat plate was located 2.9 m downstream of the flume entrance. The flat plate had dimensions of 1.18 m × 0.62 m × 15.9 mm in the streamwise, spanwise and wall-normal directions, respectively. The optimized leading-edge profile developed by Hanson & Buckley (Reference Hanson and Buckley2012) was used for the flat plate to ensure a laminar boundary layer would form on the bottom surface. Additionally, the trailing edge of the flat plate tapers down to prevent large-scale vortex shedding. A rectangular cut-out in the plate begins 0.27 m downstream of the leading edge and allows for an insert containing the actively deformable surface and a spherical cap element to be added to the apparatus. The purpose of the spherical cap was to disturb the laminar boundary layer and generate the periodic velocity fluctuations that were subsequently targeted by reactive control.

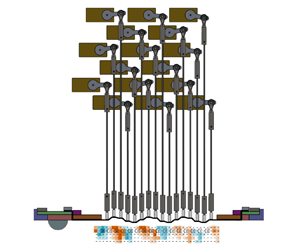
Figure 1. Schematic of flat plate apparatus showing the spherical cap and the active surface used for reactive control experimentation.
With consideration of the work of Acarlar & Smith (Reference Acarlar and Smith1987) on similar wake flows, a spherical cap with a height of h = 12 mm and a base diameter of 28 mm was selected. The Reynolds number of the spherical cap based on its height is Reh = 635. From Acarlar & Smith (Reference Acarlar and Smith1987), this spherical cap was anticipated to have a Strouhal number in the range of Stu ≈ 0.2–0.25. The spherical cap was centred at a distance of l = 285 mm downstream of the plate's leading edge. At this location, the Reynolds number of the flow, based on length l, is Rel ≈ 15 000. This indicates that the flow should be laminar leading up to the spherical cap. As well, the momentum thickness (θ) of the boundary layer at l and in the absence of the spherical cap is θ = 1.5 mm. As such, the Reθ value is Reθ = 81.
As is visible in figure 1, a Cartesian coordinate system for the flow is defined at the centre of the spherical cap and at the wall. The streamwise, wall-normal and spanwise directions of the flow are specified by x, y and z, respectively. The corresponding flow velocity components are given by U, V and W, and the fluctuating velocity components are given by u, v and w. This coordinate system will be used for the remainder of this paper. Prior to the completion of any reactive experiments, the flow on the bottom surface of the flat plate in the absence of the spherical cap was evaluated using PIV. Good agreement was observed between the measured boundary layer profile and the Blasius boundary layer profile.
2.2. Active deformable surface
An active deformable surface composed of 16 independent actuation locations that can be displaced in the wall-normal direction was developed. For readability, it will be referred to as the ‘active surface’ from this point forward. As is visible in figure 2(a), the active surface that is in contact with the flow is composed of a 1.6-mm-thick silicone rubber sheet (Δx × Δz = 245 × 60 mm2) that has been stretched flush with the bottom surface of the flat plate. Adhered to the topside of the rubber surface are 16 actuator feet that each control one of the independent actuation locations. The actuator feet have dimensions of Δx × Δz = 4 × 10 mm2 and are centred about z = 0. The first actuator foot is centred at x/h = 5.3 and subsequent feet are placed with a centre-to-centre spacing of 10 mm (0.83h). Consequently, the 16th and final actuator is centred at x/h = 17.8. Each actuator foot is connected by a 2-mm-diameter stainless-steel pushrod to a 20-mm-long servo arm mounted on a high-speed digital servo motor (Savox SH-1290MG). Each servo motor is capable of oscillating the connected actuator foot at frequencies of up to 10 Hz, depending on the amplitude selected. This corresponds to a normalized frequency of f × h/U ∞ = 2.3. As well, the maximum amplitude of the surface deformation was limited to ±7.2 mm for all experiments.

Figure 2. (a) Schematic of the active surface mounted flush to the lower surface of the flat plate. The FOV of the offline PIV and RT-PIV systems are indicated as FOV1 and FOV2, respectively. (b) A photograph of the active surface assembly showing the mounting plate and nylon guides that hold the servo motors and support the flexible pushrods, respectively.
As is visible in figure 2(b), the pushrods each pass through holes in two nylon guide plates. These guide plates provide additional support to the flexible pushrods and constrain the bottoms of the pushrods to only allow movement of the actuator feet in the y direction. As is also shown by figure 2(b), an aluminium mounting plate acts as the primary structural element of the active surface assembly. The rotational displacement of the servo arms was converted to linear displacement of the actuator feet using the relation ya = r sin−1(β), where ya is the actuator foot displacement, r is the servo arm length and β is the angle of the servo arm relative to the x axis.
Control of the servo motors was achieved using a Speedgoat real-time target machine (Performance model) with a 16-bit input/output module (model IO135). This system generates and feeds an analogue voltage signal for each of the 16 servo motors to two Teensy 3.2 boards. The Teensy boards read the voltages of the analogue signals and output pulse width modulation (PWM) signals to control each of the servo motors. Direct control of the servos from the IO135 module was not possible as it could not produce 16 independent PWM signals with sufficient resolution to smoothly control the servo motors. In the supplementary movies available at https://doi.org/10.1017/jfm.2024.292, movie 1 shows the upper portion of the assembly including the servo motors and pushrods, while movie 2 shows the underside of the active surface that is placed in contact with the flow during experiments. In these movies, the active surface is programmed to generate a travelling sine wave.
The displacement amplitude and response time of the active surface was evaluated by comparing the actual displacement of the surface with the displacement specified by the control signal as shown in figure 3. The actual displacements were extracted from images of the active surface captured by the offline PIV system. As negative displacements were not fully visible in the PIV images due to camera view blockage, a control signal with positive displacements was evaluated. As is demonstrated by figure 3, the actuator follows the control signal well. However, the peak actuator displacements are slightly damped relative to those specified by the control signal. This level of damping is consistent across different actuators of the active surface and is primarily attributed to resistance applied by the stretched rubber surface. Additionally, the actuators lagged their control signal by approximately 40 ms. This delay is mainly attributed to the reaction time of the actuators.

Figure 3. Time series comparison of an actuator tracking a sample control signal. The actuator location is obtained from off-line PIV images.
2.3. Offline PIV
During all reactive control experiments, the velocity field was measured using a standard planar PIV system and subsequently analysed for evaluating the performance of the control system. Two cameras (LaVision GmbH ImagerProX4M) were used with their imaging domain combined together into FOV1 shown in figure 2(a). Each camera features a 2048 × 2048-pixel monochrome charge-coupled device (CCD) sensor with 7.4 × 7.4 μm2 pixels and 14-bit resolution. To increase the camera frame rate and eliminate excess data, the camera sensors were cropped to a size of 2048 × 625-pixels for all sets. Each camera was fitted with a 60-mm lens (Nikon AF Micro Nikkor) with an aperture setting of f/4. The resulting combined FOV had dimensions of (Δx, Δy) = 259 mm × 39 mm and a spatial resolution of 65.5-μm pixel−1. The leading edge of FOV1 was located at x/h = 2.7. The seeding particles added to the water flow were 2-μm silver-coated glass spheres (Potters Industries Conduct-O-Fil SG02S40).
The FOV1 was illuminated by a dual cavity Nd: YAG laser (New Wave Research Gemini PIV). Each cavity operates independently and can produce laser pulses with an energy of up to 90 mJ per pulse and at a maximum rate of 30 Hz. The laser beam was shaped into a ~1-mm-thick laser sheet projected upwards through the bottom of the water flume and aligned with the x–y plane at the spanwise centre of the deformable surface (z = 0).
The offline PIV system was triggered externally using a delay/pulse generator (Berkeley Nucleonics Corporation model 575). The frame-straddling technique with a laser pulse delay of 16 ms was used to record double-frame images at a rate of 7.35 Hz. The offline PIV system was used to capture 1500 image pairs for each reactive control case which corresponds to 204 s of data collection. Processing of the acquired images was completed using DaVis 8.4.0 (La Vision GmbH). A multipass algorithm was used to compute the PIV vector fields. The final processing pass used 32 × 32-pixel (2.1 × 2.1 mm2) Gaussian-weighted interrogation windows (IWs) with 75 % overlap. Lastly, the vector fields from each camera were then stitched together into a single field.
2.4. Real-time PIV
The camera for the RT-PIV system was placed on the opposite spanwise side of the water flume from the two cameras for the offline PIV system. Consequently, the RT-PIV and offline PIV cameras imaged opposite sides of the same laser sheet. A Sony XCL-5005 monochrome camera was used for the RT-PIV system. This camera features a 2448 × 2050-pixel CCD sensor with 3.45 × 3.45 μm2 pixels and 8-bit resolution. The camera was fitted with a 35 mm lens (Nikon AF Nikkor) with an aperture setting of f/2.8. The digital resolution of the camera was set to 78 μm pixel−1. During experiments, the sensor was cropped to the desired size of 2368 × 320-pixels (185 × 25 mm2), imaging FOV2 shown in figure 2(a). The FOV2 spanned a range from y/h = 0.46–2.54 in the wall-normal direction, and a streamwise range of x/h = 4.1–19.5.
The same delay/pulse generator was used to trigger the RT-PIV and synchronize it with the offline PIV system. However, the Sony XCL-5005 camera recorded sequences of single-frame images with each image having an equal exposure time of 67 ms with an interframe time of 1 ms. Therefore, this camera was triggered at a rate of 14.7 Hz in a single-frame mode, which is twice the 7.35 Hz acquisition rate of the double-frame offline system. Similar to the offline PIV, the RT-PIV system was operated in a frame-straddling mode by considering successive image pairs within the single-frame image sequence. More specifically, the RT-PIV camera was triggered such that the laser pulse for the first image of an image pair occurred 1 ms before the end of the image's exposure time. The second laser pulse, occurring 16 ms later, therefore, occurred 14 ms into the exposure time of the second image. Through this, image pairs with the appropriate timing were produced at the same 7.35 Hz frequency similar to the offline PIV system.
Images were transmitted as they were captured to a frame grabber (Speedgoat GmbH model IO811) via a Base Camera Link connection. The images were then fed immediately into a PIV algorithm implemented in Simulink Real-Time (MathWorks) and run on the Speedgoat target machine. The RT-PIV algorithm was a basic single-pass PIV algorithm which analysed 64 × 64 pixel IWs with no overlap (one vector per 5 × 5 mm2). Cross-correlation of the IW pairs was conducted by multiplying the Fourier transform of the one IW with the complex conjugate of the Fourier transform of the other IW. Taking the inverse Fourier transform of the resulting array then produces the cross-correlation map of the two IWs. The peak value of the cross-correlation map for each IW pair was identified and then refined using three-point Gaussian subpixel interpolation. Lastly, the refined peak location was converted to U and V velocities using the known time delay between laser pulses and the digital resolution of images. The final output of the PIV algorithm was a vector field composed of 37 × 5 velocity vectors in the x and y directions.
The performance of the RT-PIV system is evaluated here by comparing snapshots of the instantaneous velocity field from RT-PIV in with those from the offline PIV system in figure 4. Figure 4(a,b) show the U component while figure 4(c,d) show the V component obtained from RT-PIV and offline PIV systems, respectively. As both systems were imaging similar FOVs at the same time instances, this comparison provided a clear indication of the performance of the RT-PIV system versus a standard PIV system. Note that the y-axis in figure 4 and all subsequent plots has been flipped relative to the orientation shown in figures 1 and 2 so the positive y is in the upward direction. As can be seen in figure 4, the RT-PIV measurements have a lower spatial resolution than those from the offline PIV system. This is a result of the RT-PIV employing 5 × 5 mm2 IWs with no overlap, whereas the offline PIV system used 2.1 × 2.1 mm2 IWs with 75 % overlap. Despite this, there is strong agreement between the streamwise and wall-normal velocity fields measured by the two systems. Figure 4(a,b) show similar uplifted regions of low-speed fluid that characterize the streamwise velocity field of the periodic flow. As well, figure 4(c,d) show similar pairs of wall-normal motions towards and away from the wall.

Figure 4. Snapshot of streamwise and wall-normal velocity fields measured by (a,c) the RT-PIV system and (b,d) the offline PIV systems for the same time instant. Panels (a,b) show the streamwise velocity component, while the panels (c,d) show the wall-normal velocity component.
Figure 5 provides an additional comparison of the time series of U and V velocities measured by the two systems within a 5 × 5 mm2 region of space centred at (x, y) = (11.2h, 1.1h). This region corresponds to a single velocity vector measured by the RT-PIV system. For the offline PIV system, the velocity vectors that fell within the selected region were spatially averaged for the comparison. Figure 5 shows some minor discrepancies between the RT-PIV and offline PIV measurements. There appear to be two primary factors contributing to the observed differences in data between the RT-PIV and offline PIV systems. Firstly, the cameras employed by the RT-PIV system have a lower bit depth of 8 bits, while the offline PIV system uses 14-bit cameras. Additionally, the RT-PIV system only utilized a single pass of PIV processing, whereas the offline PIV system utilized three passes. As a result, the RT-PIV system has a lower signal-to-noise ratio than the offline PIV system, leading to slightly higher errors in the data. Despite the discrepancies, both systems show good agreement in figure 5. Overall, figures 4 and 5 provide confidence that accurate flow measurements were produced by the RT-PIV system. Figure 5 also highlights the periodic nature of the flow. A dominant frequency of ~1 Hz is apparent in the time series of both the streamwise and wall-normal flows.

Figure 5. Time series of velocity measurements from the offline PIV and RT-PIV systems for a 5 × 5 mm2 area centred at (x, y) = (11.2h, 1.1h). Due to the higher spatial resolution of the offline PIV system, the vectors within the noted area were spatially averaged.
The latency of the RT-PIV system, Δtl, is defined as the time between the measurement instant and when the velocity field computation is completed. The measurement instant, t 0, is defined as the midpoint between the first and second laser pulses. Therefore, Δtl consists of the remaining exposure time of the second image frame, read-out time of the camera and the time required for PIV computations. Based on the time instants of the laser pulses, t 0 occurs 6 ms into the exposure time of the second image. The remaining exposure time for the second image is 61 ms. Based on the specifications for a Base Camera Link connection and the RT-PIV camera, the image readout time was estimated as ~60 ms. Lastly, from the execution time of the real-time Simulink model containing the PIV algorithm, the PIV processing time was found to approximately equal 44 ms. As such, Δtl was found to be 165 ms. Over this latency period, the flow structures can have a maximum advection of 0.73h (8.7 mm) based on the free stream velocity.
As is described in more detail in § 2.5, each of the 16 actuators of the active surface reacted to velocity measurements from a single grid point of the RT-PIV field that is referred to as a ‘sensor IW’ here. Figure 6 shows a schematic of FOV2 relative to the active surface with the 16 sensor IWs indicated with dotted lines. To counteract the latencies of the active surface and RT-PIV system (40 and 165 ms, respectively), the sensor IW for each actuator was offset upstream of the corresponding actuator foot by a value of Δxs, as shown in figure 6. Considering the combined latency of the active surface and RT-PIV system and the free stream velocity of the flow, three values of Δxs/h of −0.6, −0.9 and −1.2 were chosen to investigate. For a structure advecting at the free stream velocity of the flow, these three offsets correspond to actuations that, respectively, lag, coincide with and precede the velocity detected by the upstream sensor IW. As well, two wall-normal positions of the sensor IWs (ys) were also investigated. Values of ys/h = 1.1 and 1.5 were chosen as these encompassed a range within which strong streamwise and wall-normal velocity fluctuations were observed for the unforced flow.

Figure 6. Schematic of the active surface relative to FOV2. The velocity field shows contours of wall-normal velocity overlaid with vectors of velocity fluctuations. The dimensions of ys and Δxs noted in the figure correspond to the wall-normal and streamwise offsets of sensor IWs relative to their respective actuator feet.
2.5. Reactive flow control
In the reactive control schemes, each of the 16 actuators respond to velocity measurements from a ‘sensor IW’ of the RT-PIV. The v- and u-control schemes used here are adaptation of the v- and u-control strategies of Choi et al. (Reference Choi, Moin and Kim1994). The v-control strategy involves measuring the wall-normal velocity close to the wall and deforming the wall at proportional wall-normal velocities. In contrast, the u-control strategy involves measuring streamwise velocity fluctuations and targeting them by deforming the wall.
2.5.1. Control based on wall-normal velocity (v-control)
Figure 7 shows sample time series of input, intermediate and output signals of the v-control algorithm to demonstrate the algorithm. The first step of v-control is the application of a simple threshold filter to remove any erroneous measurement of wall-normal velocity (V) that does not satisfy |V| < 0.5U ∞. Two erroneous measurements are seen at 2.7 and 5.4 s of the sample V signal shown in figure 7. The outliers were replaced with a value of zero as this keeps the actuators static until the next valid measurement becomes available. Following this, the mean component of the V velocity signal was removed by subtracting a running average calculated over a period of 1088 ms (approximately one shedding cycle). This kept the mean value of the input V signal close to zero. The ‘filtered V’ in figure 7 shows the input V signal after the application of the threshold filter and running average subtraction. The filtered V signal was next converted to the angular velocity that the servo arm must be moved at to achieve the desired wall velocity. This was done using the relation between the angle of the servo arm and the displacement of the actuator foot noted in § 2.2.

Figure 7. Sample time series outlining the steps within the v-control algorithm for a gain of +1. Here ‘V’ is the wall-normal velocity measurement from the RT-PIV system that is input to the v-control algorithm; ‘filtered V’ shows V after application of the threshold filter and subtraction of a sliding average; dya/dt is the time-derivative of the output signal obtained from the v-control algorithm.
The angular velocity signal was then up-sampled by a factor of 10 to allow for microstepping of the servo motors in a manner that approximates motion at the desired velocity. The signal was next multiplied by a gain value. Six gain values of ±0.5, ±1 and ±1.5 were used. The sign of the gain value specifies whether actuators move in the same or an opposing direction to the measured fluid motion. Negative gain values correspond to opposing actuations similar to the v-control scheme proposed by Choi et al. (Reference Choi, Moin and Kim1994). The positive gain cases were included in this investigation to evaluate how compliant actuations impact the flow. A gain magnitude of one corresponds to v-control that attempts to move the active surface at speeds equal to the measured wall-normal flow speed and gain magnitudes of 0.5 and 1.5 correspond to actuation speeds that were slower and faster than the measured wall-normal velocities, respectively. The signal was next sent through a discrete time integrator. This step converts the angular velocity signal to the angular position signal of the servo arm. The discrete time integrator was the reason for inclusion of the running average subtraction from the input V signal. If this was not done, the mean component of the V signal would quickly accumulate during integration of the velocity signal and result in actuators becoming saturated. To directly compare the output signal of the v-control algorithm with respect to the input V signal from the real-time PIV, the time-derivative of the v-control output, i.e. dya/dt, is shown in figure 7. The ‘sample and hold’ appearance of the signal is due to each actuator maintaining a constant velocity in the time period between velocity measurements. Lastly, the integrated velocity signal was converted to a PWM signal for controlling the actuators using a manufacturer provided calibration for the servo motors.
2.5.2. Control based on streamwise velocity (u-control)
The intent of the u-control algorithm is to displace the active surface in the wall-normal direction for generating the desired streamwise velocity fluctuations. Figure 8 shows sample time series of input, intermediate and output signals of the u-control algorithm. The first step of the u-control algorithm involved converting the real-time U measurements from the RT-PIV system to fluctuating u values by subtracting the average velocity of the unforced flow. The average velocity, ![]() $\langle U\rangle$, was calculated from 2000 velocity field measurements of the unforced flow collected at a rate of 7.35 Hz using the RT-PIV system. The subtraction of a premeasured average was used because the u-control algorithm did not require a discrete time integrator and, as such, there was no risk of the actuators becoming saturated due to accumulation of mean components in the u signal. Following the mean subtraction, a threshold filter was applied to detect values of |u| > 0.5U ∞. The outliers were set equal to the most recent valid u value because this kept actuators stationary until the next valid u measurement. The U signal in figure 8 shows the input signal to the algorithm and uf shows the signal that results after subtraction of the premeasured average and application of the threshold filter. It is evident that the threshold filter removed an outlier from the input U signal at 8.7 s in figure 8.
$\langle U\rangle$, was calculated from 2000 velocity field measurements of the unforced flow collected at a rate of 7.35 Hz using the RT-PIV system. The subtraction of a premeasured average was used because the u-control algorithm did not require a discrete time integrator and, as such, there was no risk of the actuators becoming saturated due to accumulation of mean components in the u signal. Following the mean subtraction, a threshold filter was applied to detect values of |u| > 0.5U ∞. The outliers were set equal to the most recent valid u value because this kept actuators stationary until the next valid u measurement. The U signal in figure 8 shows the input signal to the algorithm and uf shows the signal that results after subtraction of the premeasured average and application of the threshold filter. It is evident that the threshold filter removed an outlier from the input U signal at 8.7 s in figure 8.

Figure 8. Sample time series outlining the signal processing within the u-control algorithm with a gain of −1. The U signal is the streamwise velocity measurement from the RT-PIV system that is input to the u-control algorithm; uf is the threshold filtered fluctuating streamwise velocity signal; ya is the displacement of the active surface at the corresponding actuation location.
The uf values were then multiplied by a gain value and converted to the desired surface displacement using a linear relation: ya = kG × uf. Here, k is a constant equal to −0.118 s, and G is the gain for the control case. The constant k was determined from open-loop operation of the active surface in the absence of the spherical cap. The experiments indicated that the strength of streamwise velocity fluctuations produced by the open-loop actuations are linearly proportional to the displacement of the active surface. Based on the measurements, the value of k was chosen such that the amplitude of actuator displacement was comparable to that seen for v-control. The direct conversion from velocity to displacement using a linear relation allowed the u-control algorithm to be designed without requiring the use of a discrete time integrator.
As with v-control, six gain values of ±0.5, ±1 and ±1.5 are investigated. Negative and positive gains correspond to control where streamwise velocity fluctuations induced at the wall are opposing and compliant to the streamwise velocity fluctuations measured in the flow, respectively. Figure 8 shows the output ya signal of the u-control algorithm. The displacements shown by ya lag uf by one sampling period (136 ms). This occurs because actuators were controlled to move to the desired displacement over the time period between velocity measurements. This ensured that actuators moved smoothly to new displacements. Consequently, as is demonstrated by figure 8, the u-control algorithm was successful at moving the active surface to displacements that were proportional to measured streamwise velocity fluctuations.
3. Unforced flow
The wake flow behind the spherical cap without any surface deformation is defined as the unforced flow in the current investigation. The instantaneous and time-averaged characteristics of the unforced flow are outlined in §§ 3.1 and 3.2, respectively, using measurements collected by the offline PIV system. Note that throughout this and subsequent sections, quantities denoted by a subscript ‘u’ refer to flow variables of the unforced flow (no actuation). As well, in § 3.2 and later discussions, ![]() $\langle \cdots \rangle $ denotes a time-average of the variable within the angle brackets.
$\langle \cdots \rangle $ denotes a time-average of the variable within the angle brackets.
3.1. Instantaneous flow
Figure 9(a,b) show contours of the instantaneous Uu and Vu fields overlaid with vectors of velocity fluctuations (uu, vu). As well, movie 3 in the supplemental material shows a movie of the unforced flow to illustrate its periodicity and development across the measurement domain. The vector fields in figure 9 show several spanwise vortices. The vortices occur with a streamwise spacing of ~4h (the shedding wavelength) fitting approximately four actuator feet between them. Consequently, the active surface has sufficient spatial resolution to target individual coherent motions within the flow. Additionally, inspection of the frequency spectrum of the unforced flow, highlights that the shedding frequency is fu = 0.9 Hz. When normalized by U ∞ and h, the Strouhal number of the flow is Stu = 0.2. Consequently, Stu is much lower than the maximum Strouhal number for the active surface which is 2.3. As such, the active surface will be operated well below its maximum capabilities when responding to the periodic motions within the flow.

Figure 9. Instantaneous (a) streamwise and (b) wall-normal velocity contours in the wake of the spherical cap without actuation. The vectors show the fluctuating velocity components.
The Uu field shows that each vortex results in a region of uplifted low-speed fluid at its upstream edge. As well, in the Vu field the vortex core is located between an upstream ejection and a downstream sweep motion. The zones of ejection motion in the near-wake region of figure 9(b) take a U-shape and are accompanied by smaller zones of sweep motion located above them. Farther downstream, both motions form zones that are inclined with respect to the wall. The degree of inclination of these zones varies along the wall-normal direction with the inclination increasing closer to the wall. This inclination presents some additional challenges to the proper timing of actuations based on measurements away from the wall. An instance of this occurs when a sweep motion is detected at a particular streamwise position at y/h = 1.5, while there might be an ejection motion in the near-wall region. As such, the effect of different sensor locations should be investigated.
The figure also shows that the height of the vortices with respect to the wall gradually increases from y/h ≈ 1 to 2.5. As a result, ejection and sweep zones stretch gradually away from the wall and attenuate as they advect downstream. However, when comparing the streamwise and wall-normal velocity fluctuations along the horizontal lines ys/h = 1.1 and 1.5, it was observed that these fluctuations closely resemble those along a straight line that follows the inclined trajectory of the ejection and sweep zones. This similarity is primarily due to the gradual movement of the ejection and sweep zones, shifting approximately 1h over a streamwise range of 20h. Based on investigations by Acarlar & Smith (Reference Acarlar and Smith1987) into similar wake flows, the unforced flow field is the result of a series of hairpin vortices being shed from the spherical cap. Consequently, the spanwise vortices evident in figure 9 represent the heads of individual hairpin vortices. As well, the inclined shape of the ejection and sweep zones may be explained as a result of the legs of each hairpin vortex extending upstream of the hairpin head. Hairpin vortices are a common coherent structure observed in turbulent wall-bounded flows (Adrian Reference Adrian2007). As such, this flow field allows for investigation of reactive control techniques on coherent structures similar to those found in turbulent wall-bounded flows but with reduced complexity due to their periodicity and coherence.
3.2. Time-averaged flow
The average streamwise velocity of the unforced flow in figure 10(a) shows a small region of reverse flow in the near-wake up to x/h ≈ 4, as shown by the black contour line on the left-hand side of the figure. Therefore, the first actuator foot centred at x/h = 5.3 is outside of the reverse flow region. The average streamwise flow field shows fast recovery of the velocity deficit up to x/h ≈ 8. Beyond this, there is a gradual recovery of the velocity deficit.

Figure 10. (a) Average streamwise velocity, (b) average wall-normal velocity and (c) Reynolds shear stress contours of the unforced flow. Panel (a) is also overlaid with average velocity vectors and the black line indicating the ![]() $\langle {U_u}\rangle = 0$ contour.
$\langle {U_u}\rangle = 0$ contour.
The average wall-normal flow field shown by figure 10(b) exhibits three key regions. There is a small negative region at the upstream edge of figure 10(b). This region is associated with fluid being drawn consistently downwards in the near wake of the spherical cap. Beneath this negative region, there is an intense positive region that gradually tapers from the upstream edge of figure 14(b) until approximately x/h = 8. This region is a result of the spanwise vortices that generate strong ejection motions. As can be observed in figure 9 and movie 3, the region close to the wall up to x/h ≈ 8 is dominated by a series of interconnected ejection motions. Past x/h ≈ 8, stretching of the ejection motions away from the wall and penetration of sweep motions towards the wall ends this initial intense upward motion. The final region consists of weak upward motion that extends diagonally in a wide band from the top of the intense region of upward motion to the upper right-hand corner of figure 10(b). This region is the cumulative result of the passage of periodic ejection and sweep motions. The positive sign of this region demonstrates that the ejection motions are generally stronger than sweep motions. Additionally, the inclination of this positive region with respect to the flow direction demonstrates the stretching of the hairpin vortices as they advect downstream.
The Reynolds shear stress contour, shown by figure 10(c), has two notable regions. The first is the positive region that extends across the entire streamwise range. This positive region is associated with the passage of ejection and sweep motions. The attenuation of this region along its streamwise dimension and its inclination with respect to the flow direction further highlights the weakening and stretching of vortices as they are advected downstream. Additionally, this positive region indicates strong production of turbulent kinetic energy (TKE). The second notable region in figure 10(c) is the narrow region of negative Reynolds shear stress below the positive region. For x/h > 6, the gradient ![]() $\textrm{d}\langle {U_u}\rangle /\textrm{d}y$ is positive across the measurement domain, as seen in the overlaid velocity vectors in figure 10(a). As such, this negative Reynolds stress region contributes to negative production of TKE.
$\textrm{d}\langle {U_u}\rangle /\textrm{d}y$ is positive across the measurement domain, as seen in the overlaid velocity vectors in figure 10(a). As such, this negative Reynolds stress region contributes to negative production of TKE.
4. Actuation and flow energy
This section begins by presenting the standard deviation of the actuation amplitudes during reactive control for different gain values and sensor locations. Following that, the impact of reactive control on the TKE of the flow is investigated to determine energy variations with gain values and sensor locations. Lastly, we compare the trends in actuation amplitudes with those in TKE to establish their correlation.
Figure 11 presents the standard deviation of the active surface displacement (σy), which was calculated by averaging the standard deviation of control signals sent to the 16 actuators. The figure shows σy values for v- and u-control cases with the three gain values and six sensor locations. In general, σy values varies from 4 % to 18 % of h for different cases. It is also seen that both v- and u-control roughly exhibit similar actuation amplitudes at the different gain magnitudes. This was done intentionally during the design of the u-control algorithm to allow for easier comparison between the two control strategies. As should be expected, gain magnitude appears to have a relatively monotonic impact on σy. However, the effect is larger for the v-control relative to the u-control. The average slope of σy versus gain magnitude for v-control is 1.18 mm while the slope is 1.06 mm for the u-control, indicating a faster increase of surface deformations with increasing the gain for v-control.

Figure 11. Standard deviation of actuator displacement averaged across the active surface (σy) for (a) v-control and (b) u-control with different gains and sensor locations. The numbers in brackets in the legend indicate (Δxs, ys)/h for each case.
A notable trend visible in figure 11 is the effect of the two ys values of 1.1 and 1.5 on both v- and u-control. Control cases with ys/h = 1.1 generally show larger σy values compared with cases with ys/h = 1.5. This is primarily a result of the peak velocity fluctuations passing through the sensor IWs positioned at ys/h = 1.1. As well, it is observed that the value of σy has less dependence on Δxs for cases with ys/h = 1.5. There are some small differences within v- and u-control cases for the same gain magnitude but opposite gain signs. These differences suggest that the opposing and compliant actuations for v- and u-control impact the flow in different manners.
Figure 12 demonstrates the impact of reactive control on the TKE of the flow (Et) for the reactive control cases. Here, Et is calculated by summing up ![]() $\langle {u^2}\rangle + \langle {v^2}\rangle$ over the measurement domain of the offline PIV data and is then normalized by the total kinetic energy of the unforced flow (Et ,u). Consequently, cases in figure 12 with Et/Et ,u < 1 indicate that the reactive control has resulted in reducing the total kinetic energy of the flow relative to the unforced flow. Reducing the energy of the flow is desirable as it suggests that the reactive control successfully attenuated energetic motions in the flow without adding excess turbulent energy. In contrast, cases with Et/Et ,u > 1 indicate that actuations have added to the TKE of the flow. However, figure 10 does not provide evidence as to whether the excess energy is added to the energetic motions of the unforced flow or if the energetic motions of the unforced flow are dampened while new turbulent motions are generated. In general, figure 10 shows that an increase in gain magnitude is associated with an increase in Et, and in some cases resulting in Et/Et ,u > 1.
$\langle {u^2}\rangle + \langle {v^2}\rangle$ over the measurement domain of the offline PIV data and is then normalized by the total kinetic energy of the unforced flow (Et ,u). Consequently, cases in figure 12 with Et/Et ,u < 1 indicate that the reactive control has resulted in reducing the total kinetic energy of the flow relative to the unforced flow. Reducing the energy of the flow is desirable as it suggests that the reactive control successfully attenuated energetic motions in the flow without adding excess turbulent energy. In contrast, cases with Et/Et ,u > 1 indicate that actuations have added to the TKE of the flow. However, figure 10 does not provide evidence as to whether the excess energy is added to the energetic motions of the unforced flow or if the energetic motions of the unforced flow are dampened while new turbulent motions are generated. In general, figure 10 shows that an increase in gain magnitude is associated with an increase in Et, and in some cases resulting in Et/Et ,u > 1.

Figure 12. Total kinetic energy (Et) for (a) v-control and (b) u-control cases determined from POD analysis. The numbers in brackets in the legend indicate (Δxs, ys)/h for each case.
With regards to v-control, most cases with negative gain values have a value of Et/Et ,u close to or less than one. As a result, these actuations have either led to a decrease in the kinetic energy of the flow or have had little effect on it. The v-control cases with gains of −1.5 and ys/h = 1.1 are the exception with total kinetic energies well above that of the unforced flow. This result agrees with Chung & Talha (Reference Chung and Talha2011) who found that applying actuations stronger than measured wall-normal velocity fluctuations led to poorer performance of opposing v-control. The positive gain cases of v-control demonstrate trends in Et that appear monotonic with increasing the gain value. As such, for these cases the value of Et seems closely related to the amplitude of actuations seen in figure 11. Comparing v-control cases with positive and negative gains demonstrates that the opposing actuations generally resulted in lower values of Et compared with compliant actuations. The lowest Et value for v-control is 0.87Et ,u and occurs for a case with a gain of −0.5 and (Δxs, ys)/h = (−0.9, 1.5).
The u-control cases with opposing actuation demonstrate trends in Et that appear similar to those of σy shown by figure 11. This implies that larger Et values correspond with higher σy values. The positive gain cases of u-control also appear to show similar trends in Et that correlate with actuation amplitude, although to a lesser extent than the negative gain cases. The exceptions to this are the three positive gain cases with ys/h = 1.5. These cases converge on a value of Et/Et ,u ≈ 1 for a gain of 1.5. Additionally, several cases of u-control, both with positive and negative gains, lowered the total kinetic energy of the flow below that of the unforced flow. A minimum Et value of 0.88Et ,u is achieved for u-control with a gain of −0.5 and (Δxs, ys)/h = (−0.6, 1.5).
Comparing between the plots for v- and u-control, there is some similarity between trends in Et for v-control cases with negative gains and u-control cases with positive gains. This may indicate that the opposing actuation cases of v-control have some similar effects to the compliant actuation cases of u-control. This would agree with Choi et al. (Reference Choi, Moin and Kim1994) who found that drag reductions were achieved with opposing wall-normal actuations and compliant streamwise actuations.
Considering figures 11 and 12 together, the value of Et seems to correlate strongly with σy for compliant actuation cases of v-control and opposing actuation cases of u-control. This indicates that the actuation may be generally exciting the flow for these cases. For opposing actuation cases of v-control and compliant actuation cases of u-control, the impact of the reactive control is less dependent on σy.
5. Impacts of reactive control
The impacts of the reactive control techniques on the flow motions are investigated from the offline PIV measurements. Section 5.1 first outlines the impacts of reactive control on the instantaneous flow. Following this, § 5.2 provides analyses of the impacts of reactive control at the various tested gain values on the mean properties of the flow. Lastly, § 5.3 provides a discussion of the impacts of reactive control with varying sensor locations on the mean properties of the flow.
5.1. Instantaneous flow
The impacts of the v- and u-control on the instantaneous flow was significant in many of the investigated control cases; however, trends were not easily inferred simply by viewing the instantaneous fields. Consequently, only a few general conclusions will be discussed here based on the instantaneous flow fields. A statistical analysis of the effects of v- and u-control are presented in subsequent sections.
Figure 13 shows contours of the instantaneous flow fields for v-control with a gain of −1.5. As well, the sensor IWs are centred at (Δxs, ys)/h = (−0.6, 1.1) with respect to the actuators. To better outline the temporal impacts of the reactive control, movie 4 in the supplemental material shows a movie of the corresponding flow field. Note that data close to the wall (y/h < 0.5) is excluded from figure 13 and all subsequent plots derived from the reactive control cases because surface protrusion into FOV1 did not allow for accurate measurements in this region.

Figure 13. Instantaneous (a) streamwise and (b) wall-normal velocity contours overlaid with velocity fluctuation vectors during v-control with a gain of G = −1.5 and sensor locations of (Δxs, ys) = (−0.9, 1.1).

Figure 14. Instantaneous (a) streamwise and (b) wall-normal velocity contours overlaid with velocity fluctuations vectors during u-control with a gain of G = −1.5 and sensor locations of (Δxs, ys) = (−0.9, 1.1).
As is evident in figure 13 and movie 4, the periodicity of the flow field is interrupted, and the flow consists of smaller and irregular structures. Relative to the unforced flow, the shape and organization of the ejection and sweep motions is significantly altered as they appear random. As well, the shedding frequency likewise becomes less consistent. This is evident in the closely spaced vortices visible at x/h ≈ 11.5–13.5 in figure 13. However, a chaotic pattern of alternating ejections and sweeps persists in the controlled flow. For all v-control cases, similar effects on the spatial organization of the ejection and sweep motions remained visible, although the extent of these effects decreases at smaller gain values.
Regarding u-control, figure 14 and movie 5 in the supplemental material show contours of the instantaneous flow fields for a gain of −1.5 (opposing actuations) and a sensor location of (Δxs, ys) = (−0.6, 1.1). Figure 14 and movie 5 show that the applied u-control is less disruptive to the periodic flow than the v-control case shown by figure 13. The flow structures exhibit a similar pattern of paired ejection and sweep motions visible in the unforced flow. However, clear changes to the shapes of the coherent motions could be observed in all the investigated u-control cases. As with v-control, the extent of effects on the flow decreases along with gain magnitude. The controlled flow appears to generally show less lift up of low-speed fluid relative to the unforced flow. In addition, many of the ejection and sweep motions in the flow during u-control have significantly larger inclination with respect to the wall; the ejection and sweep zones are approximately perpendicular to the wall. This suggests that the applied u-control affects the flow field, but it does not produce the same degree of disruption of the periodic flow seen in some of the v-control cases.
5.2. Impact of varying gain on mean flow
Figure 15 shows contour plots of the average streamwise velocity during reactive control relative to the unforced case (i.e. ![]() $\langle U\rangle - \langle {U_u}\rangle$). Six tested gains are considered here while the sensors are located at (Δxs, ys)/h = (−0.6, 1.1) relative to their respective actuator feet. As previously outlined, negative gains correspond to control intended to oppose the natural fluid motions, while positive gain values indicate control intended to apply actuations that comply with the fluid motions. By subtracting the
$\langle U\rangle - \langle {U_u}\rangle$). Six tested gains are considered here while the sensors are located at (Δxs, ys)/h = (−0.6, 1.1) relative to their respective actuator feet. As previously outlined, negative gains correspond to control intended to oppose the natural fluid motions, while positive gain values indicate control intended to apply actuations that comply with the fluid motions. By subtracting the ![]() $\langle {U_u}\rangle$ field, the impacts of the reactive control cases were made more evident. In figure 15, positive regions within the plots indicate areas where the average streamwise velocity was greater than that of the unforced flow, shown in figure 10(a), and vice versa for negative regions. As well, to supplement the contour plots discussed in this section corresponding velocity profiles for several streamwise locations in each contour plot are presented in Appendix A. These velocity profiles provide a more detailed comparison of the effects of the reactive control.
$\langle {U_u}\rangle$ field, the impacts of the reactive control cases were made more evident. In figure 15, positive regions within the plots indicate areas where the average streamwise velocity was greater than that of the unforced flow, shown in figure 10(a), and vice versa for negative regions. As well, to supplement the contour plots discussed in this section corresponding velocity profiles for several streamwise locations in each contour plot are presented in Appendix A. These velocity profiles provide a more detailed comparison of the effects of the reactive control.

Figure 15. Average streamwise velocity relative to the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δxs, ys)/h = (−0.6, 1.1). The gain value is noted at the upper left-hand corner of each panel.
As evident in figure 15, the general features of the relative streamwise velocity fields for the different reactive control cases are similar between v- and u-control and across the different gain values. A positive region extends diagonally from the most upstream region near the wall to the most downstream region away from the wall in all plots. This positive region indicates a weaker wake deficit in the controlled flow and, therefore, an enhancement of the wake recovery. The positive region is most intense and attached to the bottom of the plots in the range of approximately 3 < x/h < 8, though there is significant variation between cases. Downstream of x/h = 8, the positive region is less intense and separated from the bottom of each plot. Consequently, the applied control generally induces an increase in the rate of recovery of the velocity deficit across this positive region. Additionally, the plots in figure 15 all feature negative regions encapsulated underneath the positive regions. These negative regions are indicative of larger velocity deficits in the near wall region as a result of the applied control.
The positive and negative regions are both interesting from a flow control perspective. The positive regions are encouraging as they indicate that the controlled wake flows are regaining momentum faster in the positive areas than observed in the unforced flow. Therefore, recovery of the velocity deficit is accelerated through greater turbulent mixing. The negative regions may indicate that sweep motions, which transport high-speed fluid towards the wall, have been somewhat hindered from penetrating towards the wall by the reactive control. Preventing high-speed fluid from reaching the wall and causing high-shear-rate regions is a key drag reduction mechanism of opposition v-control (Choi et al. Reference Choi, Moin and Kim1994). As such, the negative regions may indicate that the reactive control produces this drag reduction mechanism.
The negative gain cases of v-control, figure 15(a–c) show a consistent trend of increasing magnitude of the positive regions with increasingly negative gains. The increased magnitude of the positive regions is predominantly observed for x/h < 8. Consequently, this highlights that v-control with increasing negative gains is associated with a steady increase in the recovery rate of the velocity deficit. The increase in the rate of velocity deficit recovery can be explained as a result of increasing magnitude of actuations, which destabilizes the shear layer and allows wall-normal transport of momentum earlier in the wake. As such, at higher gain magnitudes the flow was able to regain momentum faster as the earlier formation of sweep motions in the wake promoted entrance of high-speed fluid. Additionally, increasing negative gains for v-control are associated with a steady increase in magnitude of the negative regions close to the wall. This suggests that the opposing actuations are increasingly inhibiting the penetration of high-speed fluid towards the wall.
The positive gain cases of v-control also show a relatively large increase in the magnitude of the positive region from a gain of 0.5 to 1, (figure 15d,e). However, the cases with gains of 1 and 1.5 (figure 15e, f), show relatively similar positive regions. Therefore, only within a certain range, increasing positive gains lead to increases in the rate of velocity deficit recovery. Similarly, there is also less of a consistent trend in the negative regions with increasing gain magnitude. From a gain of 0.5 to 1, there is a decrease in the size and magnitude of the negative region close to the wall. For the case with a gain of 1.5, (figure 15f), the magnitude of the negative region significantly increases again. These observations indicate that the compliant v-control actuations were less capable at inhibiting the motion of high-speed fluid towards the wall relative to the opposition v-control.
The u-control cases in figure 15(g–l), while showing the same general features as in the v-control cases, demonstrate some notable differences. As with v-control, increasing gain magnitude for u-control corresponds with significant increases to the magnitude of the positive regions. This may be explained to some degree by the explanation provided for this trend in the v-control cases. As well, increasing gain magnitudes are associated with decreasing size and magnitude of the negative regions close to the wall. Consequently, for u-control, increasing gain magnitude enhances the wake recovery and minimizes the reduction of streamwise velocity close to the wall. The latter of these effects may indicate that u-control with larger gain magnitudes is less capable of impeding the motion of high-speed fluid towards the wall.
Comparing the positive and negative gains for u-control, we observe that the figure 15(g–i) with negative gains exhibit positive regions attached to the plot bottoms over a considerably larger streamwise range than the figure 15( j–l) with equivalent positive gains. As well, the negative gain cases have negative regions close to the wall that are significantly reduced in size and magnitude in comparison with the equivalent positive gain cases. Consequently, u-control cases with negative gains induced recovery of the velocity deficit over a larger streamwise range while also exhibiting less reduction of the streamwise velocity close to the wall. The greater magnitude of the near-wall negative region for the positive gain cases seems to agree with the suggestion of Rebbeck & Choi (Reference Rebbeck and Choi2006) that compliant streamwise velocity fluctuations induced near the wall aid at inhibiting the penetration of sweep motions towards the wall. The differences between u-control cases with equivalent positive and negative gains are less evident than those between v-control cases with equivalent positive and negative gains.
A similar analysis is conducted for the average wall-normal velocity fields of the reactive control cases. Figure 16 shows contour plots of the average wall-normal velocity relative to the average wall-normal velocity of the unforced flow during reactive control at the six tested gains and with (Δxs, ys)/h = (−0.6, 1.1). As is shown by figure 10(b), the ![]() $\langle {V_u}\rangle$ field of the unforced flow is predominantly positive except for a small negative region attached at the upstream edge of the plot. As such, in the subsequent discussion, negative regions in figure 16 indicate areas where the average wall-normal velocity away from the wall is reduced in comparison with the unforced flow, and vice versa for positive regions.
$\langle {V_u}\rangle$ field of the unforced flow is predominantly positive except for a small negative region attached at the upstream edge of the plot. As such, in the subsequent discussion, negative regions in figure 16 indicate areas where the average wall-normal velocity away from the wall is reduced in comparison with the unforced flow, and vice versa for positive regions.

Figure 16. Average wall-normal velocity field relative to that of the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values.
There are several common features that exist across all the subplots in figure 16, although with some variation in their presentation. One of these common features is the negative regions near the wall and attached to the upstream edge of each plot in figure 16. These regions indicate a reduction in wall-normal motions resulting from an upstream shift in the flow field due to the earlier occurrence of wall-normal momentum transport in the wake. This is consistent with the conclusion that the increased velocity deficit recovery seen in the plots in figure 15 was also somewhat due to sweep and ejection motions forming earlier in the wake. A second common feature of all the plots in figure 16 is a negative region extended in the streamwise dimension and roughly at the centre of each plot. These negative regions, which will be referred to as the primary negative regions from this point forward, indicate a reduction to the region of positive ![]() $\langle V\rangle$ in figure 10(b) that was associated with the stretching of vortices and the corresponding ejection and sweep motions away from the wall. Adrian (Reference Adrian2007) noted that the stretching of hairpin vortices away from the wall is associated with an intensification of the vortices. Consequently, the primary negative regions are attributed to weaker vortices because of the applied reactive control. As well, there are two positive regions common to all of the plots in figure 16. The first is a positive region approximately at x/h = 5. As with the upstream negative regions, these positive regions are partially due to the upstream shift of the average wall-normal flow. Additionally, the plots exhibit positive regions close to the wall, often over a significant streamwise range. These are attributed in part to decreased penetration of sweep motions towards the wall because of the applied control. Some portion of the near-wall positive regions may also be due to the outward deformations of the wall.
$\langle V\rangle$ in figure 10(b) that was associated with the stretching of vortices and the corresponding ejection and sweep motions away from the wall. Adrian (Reference Adrian2007) noted that the stretching of hairpin vortices away from the wall is associated with an intensification of the vortices. Consequently, the primary negative regions are attributed to weaker vortices because of the applied reactive control. As well, there are two positive regions common to all of the plots in figure 16. The first is a positive region approximately at x/h = 5. As with the upstream negative regions, these positive regions are partially due to the upstream shift of the average wall-normal flow. Additionally, the plots exhibit positive regions close to the wall, often over a significant streamwise range. These are attributed in part to decreased penetration of sweep motions towards the wall because of the applied control. Some portion of the near-wall positive regions may also be due to the outward deformations of the wall.
With regard to the v-control cases, there are some clear trends that are visible between cases with gains of the same sign. The negative gain (opposing actuation) cases of v-control (figure 16a–c), show a trend of decreasing size and magnitude of the primary negative region with increasing gain magnitude. This indicates that at larger negative gains, v-control is not affecting the strength of the vortices as much as at lower negative gains. As well, there is an increase in the size and magnitude of the near-wall positive regions for increasing negative gain values. This indicates that the penetration of sweep events towards the wall is inhibited to a greater degree at larger negative gains. This is consistent with the conclusions drawn from the corresponding average streamwise plots shown in figure 15.
For the positive gain (compliant actuation) cases (figure 16d–f), there is a trend of increasing size and magnitude of the primary negative region with increasing gain magnitude. This indicates that v-control cases with larger positive gains had a greater weakening effect on vortices. As well, the positive gain v-control cases all exhibit multiple distinct positive regions close to the wall. The cause of this is partially attributed to individual actuators being biased towards outwards or inwards deformations during the v-control case. This resulted due to imperfect removal of the mean component of the wall-normal velocity in the v-control algorithm. Overall, however, the intermittency and weaker magnitudes of the near-wall positive regions for the positive gain cases of v-control indicates that these cases were less successful at inhibiting the progress of sweep motions towards the wall.
With regards to u-control, the negative gain cases (figure 16g–i) show slightly increasing magnitudes of the primary negative regions with increasing gain magnitude. This indicates that cases of u-control with larger negative gains weakened vortices more than cases with smaller negative gains. Additionally, figure 16(g–i) all show similar near-wall positive regions. This indicates that all the negative gain values for u-control similarly inhibited the progress of sweep motions towards the wall. The positive gain cases of u-control (figure 16j–l) likewise demonstrate slightly increasing magnitudes of the primary negative regions with increasing gain magnitude. As well, there is a reduction of the near-wall positive region with increasing positive gain. As such, larger positive gains led to slightly weaker vortices and slightly less inhibition of the penetration of sweep motions towards the wall. These observations are consistent with those from the average streamwise flow fields in figure 15.
Comparing cases of u-control with equivalent positive and negative gain magnitudes, the negative gain cases have primary negative regions that are larger and have a higher magnitude. Therefore, the opposing actuation cases had a relatively stronger effect towards weakening the vortices compared with the compliant actuation cases. Additionally, the positive gain cases of u-control have near-wall positive regions that are moderately larger and higher in magnitude. This indicates that u-control cases with positive gains are relatively more effective at inhibiting the progress of sweep motions towards the wall.
Lastly, the effect of different gain values on Reynolds shear stress (![]() $- \langle uv\rangle$) was characterized in figure 17. Referring back to figure 10(c), the Reynolds shear stress contour for the unforced flow was characterized by a negative region close to the wall and a positive region above this that spanned the entire streamwise range. All the plots in figure 17 have a positive region attached to the upstream edge. This region is attributed to greater wall-normal momentum transport early in the wake of the spherical cap. As well, all the plots show a negative region inclined with respect to the flow direction that extends across most of the streamwise range. This region indicates that the reactive control generally reduced the positive region of Reynolds shear stress seen in the unforced flow. This reduction of positive Reynolds shear stress was interpreted as a weakening of the ejection and sweep motions relative to the unforced flow. This, in turn, indicates that the vortices which induce the ejection and sweep motions have been weakened. Lastly, the plots in figure 17 all have positive regions below the large negative region. These near-wall positive regions demonstrate that the reactive control reduced, and even eliminated in some cases, the negative region of Reynolds shear stress seen close to the wall in the unforced flow.
$- \langle uv\rangle$) was characterized in figure 17. Referring back to figure 10(c), the Reynolds shear stress contour for the unforced flow was characterized by a negative region close to the wall and a positive region above this that spanned the entire streamwise range. All the plots in figure 17 have a positive region attached to the upstream edge. This region is attributed to greater wall-normal momentum transport early in the wake of the spherical cap. As well, all the plots show a negative region inclined with respect to the flow direction that extends across most of the streamwise range. This region indicates that the reactive control generally reduced the positive region of Reynolds shear stress seen in the unforced flow. This reduction of positive Reynolds shear stress was interpreted as a weakening of the ejection and sweep motions relative to the unforced flow. This, in turn, indicates that the vortices which induce the ejection and sweep motions have been weakened. Lastly, the plots in figure 17 all have positive regions below the large negative region. These near-wall positive regions demonstrate that the reactive control reduced, and even eliminated in some cases, the negative region of Reynolds shear stress seen close to the wall in the unforced flow.

Figure 17. Reynolds shear stress field relative to that of the unforced flow for (a–f) v-control and (g–l) u-control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values.
For both v- and u-control, increasing gain magnitudes lead to larger positive regions in figure 17, which means greater reduction of the negative regions of Reynolds stress close to the wall. A second common trend across both control strategies in figure 17 is the increase in magnitude of the negative regions with increasing gain magnitude. This trend indicates that increasing actuation amplitudes generally reduces the strength of vortices. These negative regions indicate areas where the production of TKE is reduced relative to the unforced flow.
Regarding the v-control cases (figure 17a–f), the trends exhibited are relatively consistent with those shown by figures 15 and 16. The negative gain cases show a steady increase in the magnitude of the negative and positive regions with increasing gain magnitude. For the positive gain cases there is a relatively large increase in the magnitudes of the positive and negative regions when the gain increases from 0.5 to 1. From a gain of 1 to 1.5, however, there is relatively little change in the Reynolds stress field. As well, the negative gain cases of v-control appear to have a larger impact on the Reynolds stresses close to the wall compared with the positive gain cases.
The u-control cases likewise show increasing magnitude of the positive and negative regions with increasing gain. Consequently, vortices are weakened, and the near-wall flow is more disrupted by larger amplitudes of both opposing and compliant actuations. The negative gain cases (figure 17g–i) have positive and negative regions that are relatively lower in magnitude than those of the positive gain cases in figure 17( j–l). This indicates that the positive gain cases had an overall larger impact on the Reynolds stress field.
From the above discussion of figures 15–17, it is evident that there are notable differences between v- and u-control, and both are sensitive to changes in gain magnitude and sign. The differences observed between cases of each control strategies for gains of opposite sign are particularly encouraging as this indicates that the opposing and compliant actuations are impacting the flow in different ways. The negative gain cases of v-control present some of the most compelling results in that the mean flow fields indicate that sweep motions were increasingly inhibited from penetrating towards the wall with increasing strength of opposing actuations. This is a key drag reduction mechanism of the v-control strategy numerically investigated by Choi et al. (Reference Choi, Moin and Kim1994). As such, the observation of this effect indicates that the v-control applied in this work was behaving to some extent as was predicted by numerical works.
5.3. Impact of varying sensor location on mean flow
We have so far characterized the impact of gain sign and magnitude on the average flow fields during the application of v- and u-control for a single location of sensor IWs. The remaining discussion in this section describes the impact of sensor location on the two control schemes when applying opposing and compliant actuations. As previously outlined, sensors were offset from their respective actuators by (Δxs, ys). Here, Δxs/h values of −0.6, −0.9 and −1.2 are evaluated along with ys/h values of 1.1 and 1.5. Only the average streamwise velocity fields are considered in this section for brevity.
Figure 18 shows the average streamwise flow fields relative to that of the unforced flow for v- and u-control with a gain of −1 (opposing actuations) and for each of the six different sensor locations. Regarding the two ys values tested, a general result across almost all the subplots is that the positive regions have a reduced magnitude for ys/h = 1.5 as compared with cases with ys/h = 1.1. As highlighted by § 4, for ys/h = 1.5 the active surface saw lower actuation amplitudes in comparison with the cases with ys/h = 1.1. As such, the weaker positive regions shown by cases with ys/h = 1.5 are attributed to this weaker actuation. The near-wall negative regions show less of a consistent effect of ys. For v-control there appears to be relatively minimal effect of the ys value on the negative near-wall regions. However, for u-control the near-wall negative regions are larger in size and magnitude for cases with ys/h = 1.5.

Figure 18. Average streamwise velocity fields relative to that of the unforced flow for reactive control cases with a gain of −1 and at the six tested sensor locations. Text in the upper left-hand corner of each panel shows (Δxs, ys)/h for each case.
Changes to the Δxs value likewise demonstrate some notable impacts on the effects of v-control applying opposing actuations in figure 18(a–f). For cases with ys/h = 1.1, moving the sensors farther upstream, i.e. Δxs/h goes from −0.6 to −1.2, results in slight increases to the recovery rate in the near-wake while also decreasing the extent of flow speed reductions close to the wall. The cases with ys/h = 1.5 show a decrease in both the near-wake velocity deficit recovery rate and in the reduction of the near-wall flow speed when the sensors are moved farther upstream. The weaker reduction of the near-wall flow speed for more upstream sensor locations could indicate that sweep motions penetrate towards the wall to a greater extent for these cases.
The opposing actuation u-control cases show similar trends across the different Δxs values at both ys values. Comparing cases with Δxs/h = −0.6 and −0.9, the more upstream sensor position (Δxs/h = −0.9) leads to a lower near-wake velocity deficit recovery rate and greater reduction of the near-wall flow speed. From Δxs/h = −0.9 to −1.2, however, the opposite occurs. The cases with Δxs/h = −1.2 show greater near-wake velocity deficit recovery rates and less reduction of the near-wall flow speed in comparison with cases with Δxs/h = −0.9.
Figure 19 shows the average streamwise flow fields relative to that of the unforced flow for v- and u-control with a gain of one (compliant actuations) and for each of the six different sensor locations. The two ys values appear to affect the strength of the positive regions. Cases with ys/h = 1.5 generally have weaker positive regions compared with cases with ys/h = 1.1. As with the opposing actuation cases in figure 18, this is attributed primarily to weaker actuation of the surface for cases with ys/h = 1.5. As well, for both v- and u-control, cases with ys/h = 1.1 predominantly show stronger reductions of the near-wall flow speed.

Figure 19. Average streamwise velocity fields relative to the unforced flow for reactive control cases for (a–f) v-control and (g–l) u-control with a gain of +1 and at the six tested sensor locations. Text in the upper left-hand corner of each panel indicates (Δxs, ys)/h for each case.
The impact of Δxs on v-control applying compliant actuations as seen in figure 19(a–f) is significant and differs at the two ys values. Cases with ys/h = 1.1 show a small decrease in the near-wake velocity deficit recovery rate with increasing upstream sensor positions. As well, there is a significant increase in the reduction of the near-wall flow speed as Δxs/h goes from −0.6 to −0.9. As such, the opposition of sweep motions penetrating towards the wall is increased by the more upstream sensor position. For the compliant actuation v-control cases with ys/h = 1.5 (figure 19d–f), the cases with Δxs/h = −0.6 and −1.2 are relatively similar and show near-wake velocity deficit recovery rates and near-wall flow speed reductions of moderate strength compared with the other plots in figure 19. The case with Δxs/h = −0.6 (figure 19e) has a significantly increased near-wake velocity deficit recovery rate and shows quite minimal reduction of the near-wall flow speed. Consequently, this case appears to have induced relatively little opposition to sweep motions.
The effect of Δxs on compliant actuation cases of u-control is similar to the effect it had for opposing actuation cases of u-control. The cases with Δxs/h = −0.9 have slightly lower near-wake velocity deficit recovery rates and greater reductions of the near-wall flow speed compared with cases with the other two streamwise sensor locations. As such, the cases with Δxs/h = −0.9 appear to have most strongly opposed the advance of sweep motions towards the wall.
Considering figures 18 and 19 together, it is evident that v- and u-control were sensitive to sensor location when applying opposing and compliant actuations. The effects of sensor location differed significantly for v-control applying opposing actuations compared with v-control applying compliant actuations. The greatest reduction of the near-wall flow speed is achieved with Δxs/h = −0.6 for opposing actuations and with Δxs/h = −1.2 for compliant actuations. As well, the opposing actuations cases show consistent changes in the positive and negative regions with changing streamwise sensor position. This is not observed for the compliant actuation cases. Regarding u-control, there is greater similarity between the effects of sensor location between cases applying opposing and compliant actuations. The primary difference is that, for opposing actuations, the greatest reduction of the near-wall flow speed occurs with ys/h = 1.5, while for compliant actuations, it occurs with ys/h = 1.1.
6. Drag coefficient
In this section, we provide an estimate of the drag coefficient (Cd) for the combination of the spherical cap and actuated surface. The calculation of Cd is based on estimating the momentum loss of the incoming boundary layer in the streamwise-wall-normal plane crossing the spanwise centre of the wake. It is important to note that due to the two-dimensional limitation of the measurements, this analysis does not yield the exact Cd value but rather provides an indicative Cd to facilitate comparisons between various reactive control cases.
To calculate the momentum loss, the integral momentum theorem is applied to a rectangular control volume, following a procedure described by Bohl & Koochesfahani (Reference Bohl and Koochesfahani2009). The control volume encompasses an inlet boundary situated upstream of the spherical cap, where the laminar boundary layer remains undisturbed and adheres to a Blasius laminar boundary layer profile. The downstream boundary layer is positioned at x/h = 18.3, just downstream of the final actuator of the active surface. The wall-normal extent of the control volume ranges from y/h = 0 to 3.3, aligning with the wall-normal range of the offline PIV. After simplifying the integral momentum equation and accounting for the impact of flow unsteadiness and pressure variation at the boundaries, Cd is computed following
 \begin{gather}
{C_d} = \frac{2}{{hU_\infty
^2}}\left[\int_0^{3.0h} {\left( {\langle U_i\rangle^2 - \langle U_e\rangle^2 + \langle v _e^2\rangle -
\langle u_e^2\rangle + \frac{1}{2}(\langle U_c\rangle^2 - U_\infty^2)}
\right)\textrm{d}y}\right.\nonumber\\
+ \left.\int_{2.7h}^{18.3h} {(\langle U\rangle \langle V\rangle + \langle uv\rangle)\,\textrm{d}\kern0.7pt
x}\right]\!,\end{gather}
\begin{gather}
{C_d} = \frac{2}{{hU_\infty
^2}}\left[\int_0^{3.0h} {\left( {\langle U_i\rangle^2 - \langle U_e\rangle^2 + \langle v _e^2\rangle -
\langle u_e^2\rangle + \frac{1}{2}(\langle U_c\rangle^2 - U_\infty^2)}
\right)\textrm{d}y}\right.\nonumber\\
+ \left.\int_{2.7h}^{18.3h} {(\langle U\rangle \langle V\rangle + \langle uv\rangle)\,\textrm{d}\kern0.7pt
x}\right]\!,\end{gather}where subscript ‘i’ indicates variables at the inlet, subscript ‘e’ indicates variables at the exit and UC is the mean streamwise velocity at (x/h, y/h) = (18.3, 3.0). The offline PIV data is utilized in the Cd calculation here. The use of streamwise integration from x/h = 2.7 to 18.3 along the upper boundary is due to the limited domain of the offline PIV system. However, the structures generated by the spherical cap do not reach the upper boundary approximately until x/h = 15, and therefore this assumption does not affect the Cd calculations.
Figure 20 shows the Cd values that were calculated for all the investigated reactive control cases normalized by the drag coefficient of the unforced flow (Cd ,u). Considering the v-control cases shown by figure 20(a), it is evident that Cd is sensitive to both the streamwise and wall-normal sensor locations. As well, there is a general trend of increasing Cd value with increasing gain magnitude. This latter observation agrees with the expectation that larger displacements of the surface into the flow should lead to greater pressure drag. Additionally, 11 of the v-control cases exhibit Cd values below that of the unforced flow. This observation is encouraging as it demonstrates that there is potential for achieving drag reductions using active deformation of the wall. The lowest Cd values observed were 0.84Cd ,u for the v-control case with a gain of one and (Δxs, ys)/h = (−0.9, 1.5). The v-control cases with Cd/Cd ,u<1 have gain magnitudes of 0.5 or 1 with three having negative gains and eight having positive gains. The greater number of positive gain v-control cases can be partially attributed to the lesser reduction of the streamwise velocity near the wall by positive gain cases, as noted in the previous section.

Figure 20. Drag coefficient of the spherical cap (Cd) during the application of (a) v-control and (b) u-control. Cd is normalized in all cases by the drag coefficient of the spherical cap for the unforced flow (Cd ,u).
For u-control cases shown by figure 20(b), the negative gain cases show sensitivity to the wall-normal sensor position while the positive gain cases appear to be sensitive to both the streamwise and wall-normal sensor positions. As well, there is a slight trend of increasing Cd value for some of the positive and negative gain cases. As such, relative to v-control, larger actuations of the surface for u-control have a relatively small impact on Cd. There are 15 cases of u-control that have Cd/Cd ,u < 1. A minimum Cd value of 0.86 Cd ,u is achieved by the u-control case with a gain of −0.5 and (Δxs, ys)/h = (−0.9, 1.1). The higher average Cd value for the positive gain u-control cases can again be explained because of the tendency of these cases to induce a greater reduction of the streamwise velocity close to the wall in comparison with the negative gain u-control cases.
7. Suppression of vortex shedding
The disruption of the periodic flow is investigated here using proper orthogonal decomposition (POD) implemented based on the snapshot method of Sirovich (Reference Sirovich1987). The spatial modes produced by POD are sorted by their TKE and, as such, can provide information on the importance of different structures. For this work, data within the region of x/h = 5–18.3 and y/h = 0.5–3.3 was analysed. The streamwise range extends from just upstream of the first actuator to slightly downstream of the final actuator. Additionally, the lower wall-normal limit of y/h = 0.5 was applied to exclude data close to the wall that may have been corrupted by active wall deformations. The upper wall-normal limit of y/h = 3.3 simply represents the upper spatial limit of the data.
Figure 21 shows the energy content of the first six POD modes for the unforced flow and v- and u-control with (Δxs, ys)/h = (−0.9, 1.1). Note that in figure 21, all of the mode energies are normalized by the total kinetic energy of the unforced flow (Et ,u) as opposed to the total kinetic energy of the corresponding reactive control case. This allowed for a clearer comparison of the relative energy of the spatial modes for different cases. The unforced flow shows two dominant modes that account for 65 % of the total kinetic energy contained within the unforced flow. These dominant modes for the unforced flow correspond to the vortex shedding process. Likewise, the first two modes of the reactive control cases also correspond to the vortex shedding process. As outlined in Appendix B, this was verified through inspection of the spatial pattern of the modes, the phase plots of the corresponding time-varying coefficients and the power spectral density (PSD) of the time varying coefficient of the first POD mode. The energy of the first two modes is significantly lower for all the reactive control cases compared with the unforced flow. As such, although the vortex shedding process continues to contribute a significant proportion of the TKE of the flow for the reactive control cases, the energy of the vortex shedding process is significantly reduced compared with that of the unforced flow.

Figure 21. Energies of first six POD modes for (a) v-control and (b) u-control at different gains (G) with (Δxs, ys)/h = (−0.9, 1.1). Mode energies (En) are normalized by the total kinetic energy of the unforced flow (Et ,u).
Regarding the impacts of varying gain, it is evident in figure 21 that increasing gain magnitude leads to further reductions in the energy content of the first two POD modes. Therefore, larger gain magnitudes, which correspond to larger actuation amplitudes, result in weaker vortex shedding. This agrees with observations previously drawn from the analyses of the mean flow fields. Two of the u-control cases shown in figure 21(b) have third POD modes with energies above 10 % of Et ,u. Inspection of other u-control cases with different sensor locations and predominantly with negative gains also showed third POD modes with energies above 10 % of Et ,u. This third high energy mode is attributed to periodic structures generated by the actuation of the active surface as it is moved to target the periodic vortices in the flow.
As illustrated by figure 21, the energy content of the first two POD modes is descriptive of the overall impact of each of the tested reactive control schemes on the vortex shedding. As such, figure 22 was created showing the sum of the energy contributions from the first two POD modes, Es = E 1 + E 2, for all the investigated reactive control cases. The cumulative energies shown by figure 22 are all normalized by vortex shedding energy of the unforced flow (Es ,u). Figure 22 reinforces the conclusions previously drawn regarding the influences of varying gain. Except for a few reactive control cases, increasing gain magnitude is predominantly associated with greater reduction of the energy of the first two POD modes and, consequently, the energy of the vortex shedding process. Furthermore, figure 22 highlights that the lowest Es values for both v- and u-control are achieved by cases with negative gains. For opposing actuation (negative gain) cases, v-control has a minimum Es value of 0.31Es ,u with a gain of −1.5 and (Δxs, ys)/h = (−1.2, 1.1), while for u-control a minimum Es value 0.41Es ,u with a gain of −1.5 and (Δxs, ys)/h = (−0.6, 1.1). For compliant actuations (positive gain) cases, the minimum Es values are, respectively, 0.42Es ,u and 0.52Es ,u for v- and u-control with a gain of 1.5 and (Δxs, ys)/h = (−1.2, 1.1). This indicates that opposition control for both reactive control strategies has a greater ability to disrupt the vortex shedding.

Figure 22. Sum of energy of first two POD modes (Es) for (a) v-control and (b) u-control cases. Here Es is normalized by the vortex shedding energy of the unforced flow (Es ,u). The numbers in brackets in the legend indicate (Δxs, ys)/h for each case.
Figure 22 also demonstrates a complete picture of the effects of different sensor locations. For v-control the effect of the varied sensor locations differs between the cases with positive and negative gains. For cases with negative gains, there is a separation between cases with the two different ys values. Those cases with ys/h = 1.1 have lower Es values than the cases with ys/h = 1.5. This observation may in part be attributed to the larger actuation amplitudes for cases with ys/h = 1.1, as highlighted by figure 11. For positive gains there is more overlap of cases with both ys values. This suggests that the negative gain v-control cases are more sensitive to changes in the ys value than those with positive gains.
For v-control with negative gains and ys/h = 1.5, there is a relatively consistent trend of decreasing Es values with moving the sensor location from Δxs/h = −0.6 to −1.2. This trend can likewise be observed for v-control cases with positive gains and ys/h = 1.1. This indicates that, for these two groups, changes in v-control at different Δxs values can likely be attributed to the changes in timing that the different streamwise sensor positions induce. For negative gain v-control cases with ys/h = 1.1 and positive gain cases with ys/h = 1.5, the energy of the first two POD modes does not vary consistently according to the streamwise position of the sensors. As such, for these two groups the change in energy of the first two POD modes depends on both the gain and the streamwise sensor position.
The u-control cases in figure 22(b) show significant effects of different sensor location on Es. With regards to the negative gain cases, those with ys/h = 1.5 show larger changes in Es as the gain magnitude increases in comparison with cases with ys/h = 1.1. The positive gain u-control cases with both ys values overlap significantly. As such, this indicates the ys value has a relatively smaller impact on the positive gain cases than it does on the negative gain cases. As well, for the negative gain cases with ys/h = 1.1 and positive gain cases with ys/h = 1.5, the value of Es decreases consistently with moving the sensors from Δxs/h = −1.2 to −0.6. For the positive gain cases with ys/h = 1.1 and negative gain cases with ys/h = 1.5, the opposite relation is observed. These cases show an increase in Es with moving the sensors from Δxs/h = −1.2 to −0.6. The inversion of trends in Es between cases with the same gain sign and different ys values may be attributed to the shapes of fluid motions in the flow. Positive u regions extend farther downstream at y/h = 1.1 compared with y/h = 1.5. As such, cases with ys/h = 1.1 will detect positive u regions slightly earlier than cases with ys/h = 1.5. Consequently, more upstream positioning of sensors for cases with ys/h = 1.5 results in similar timing of actuations to cases with ys/h = 1.1 and fewer upstream sensor positions.
8. Overall performance
The overall performance of the reactive control cases is evaluated by calculating a coefficient of performance (COP) for each case following
The first term in square brackets is the ratio between the vortex shedding energy in the unforced flow (Es ,u) and the vortex shedding energy in the controlled flow (Es). As discussed in the previous section, the vortex shedding energy is captured by the first two POD modes. A higher Es ,u/Es ratio indicates a more effective reactive control strategy in reducing the vortex shedding energy. The second term indicates the ratio of the energy of non-shedding motions for the unforced and reactive cases. This term comprises of the energy of all POD modes except modes one and two. Similarly to the first term, a larger ratio indicates a reduction in the energy of non-shedding motions. Multiplying the two terms together provides an assessment of the overall control performance. Larger values of COP indicate superior performance in terms of reducing both vortex shedding energy and the energy associated with other flow motions. As an example, in a reactive control case where vortex shedding energy is halved but the energy of other motions is doubled, the resulting COP value is 1.
Figure 23 shows the COP values for all the reactive control cases. The opposing actuation v-control cases clearly have the highest COP values on average with a large proportion of cases having a value greater than one. A maximum COP of 1.21 is seen for the opposing v-control with a gain value of −0.5 and senor IW of (Δxs, ys)/h = (−0.9, 1.5). As such, this indicates that this reactive control scheme was the most successful at attenuating the energy of vortex shedding relative to the turbulent energy added in the form of other flow structures. The compliant actuation v-control cases show a trend of decreasing COP values with increasing gain magnitudes with only four cases having COP values greater than one. A similar observation can be made for the opposing actuation u-control cases and the compliant actuation u-control cases. Consequently, the performance of these reactive control schemes generally decreases with increasing gain magnitude. On average the compliant actuation u-control cases have higher COP values than the opposing actuation u-control cases. The highest COP value for opposing actuation u-control cases is 1.20 for the case with a gain of −0.5 and (Δxs, ys)/h = (−0.6, 1.5). As such, although opposing actuation u-control has a greater maximum COP value, compliant actuation u-control performed better on average. Additionally, figure 23 illustrates that, across all reactive control cases, those with gain magnitudes of 0.5 consistently show some of the highest COP values.

Figure 23. The COP for reactive control cases for (a) v-control and (b) u-control.
It should be highlighted that the active surface deformation utilized for forcing the flow in the current investigation cannot induce u and v fluctuations independently. Upward motions of the wall will induce +v and −u fluctuations, and vice versa for downward motions. In addition, the coupling between u and v is also seen in the unforced wake flow. The flow field investigated here consists of successive ejection and sweep zones. Therefore, +u and –v fluctuations occur approximately together within sweep zones and –u and +v occur together within ejection zones. If the real-time PIV detects an ejection motion (–u and +v), the u-control strategy with positive gain results in +ya displacement to generate a –u fluctuation. However, the positive gain u-control strategy in this scenario also induces a +v fluctuation and, thus, acts similarly to the positive gain v-control strategy. This highlights that there is some mutual resemblance between v- and u-control strategies with gains of the same sign.
Despite this similarity between v- and u-control strategies with gains of the same sign, their performance is significantly different as seen in figure 23. Therefore, although actuation of the surface produces a certain coupling of u and v fluctuations, the overall performance of either u and v-control strategy is not completely governed by this coupling. A factor that contributed to the differences observed between cases of v- and u-control with gains of the same sign is the accuracy of the input velocity signal. The V signal utilized for v-control is inherently noisier than the U signal due to its smaller magnitude. As well, the v-control algorithm utilizes a running average to calculate v and integrates the desired velocity of each actuator to specify its displacement, while the u-control algorithm uses a predetermined average to calculate u and then explicitly sets the displacement of actuators according to it. These differences at the level of the control algorithm mean that v-control is somewhat less reliable than u-control and produces greater variation in the shape and motion of the active surface. As such, this would have played some role in the differences observed between v- and u-control.
The performance of the v- and u-control cases was also compared using COP with predetermined actuations applied through travelling and standing sinusoidal waveforms. The travelling sine wave had an amplitude of 0.33h, a frequency of 0.9 Hz (similar to the vortex shedding frequency) and a wave speed of U ∞. The standing sine wave actuation employed a 0.33h amplitude and a 0.9 Hz frequency, with a wavelength of 4.9h. The results showed that the COP values for the travelling and standing sine wave actuation cases were 1.01 and 0.84, respectively. These values would place the travelling and standing sine wave actuations among the bottom half of reactive control cases in terms of overall performance. Therefore, the reactive control strategy can outperform predetermined control when the control parameters are appropriately set.
9. Summary and conclusions
The objective of the current investigation was to experimentally implement reactive control in a simple wall-bounded flow using novel actuation and real-time measurement systems. The actuation system developed for forcing the flow was an active deformable surface. It was composed of a streamwise array of 16 actuation points capable of deforming the wall in the wall-normal direction. As well, the inputs to the reactive control strategies were velocity measurements captured by a RT-PIV system. The flow that reactive control was applied to was the wake flow behind a spherical cap immersed in a laminar boundary layer. This flow demonstrated periodic shedding of hairpin vortices that generate ejection and sweep motions. As such, the impact of the reactive control strategies on these structures is informative for the eventual control of more complex turbulent flows.
The reactive control strategies investigated through this work were so called v-control and u-control and were inspired in part by similar strategies proposed and numerically investigated by Choi et al. (Reference Choi, Moin and Kim1994). The v-control algorithm involved moving the active surface at velocities proportional to wall-normal velocity fluctuations measured upstream of each actuation location by the RT-PIV system. Similarly, the u-control algorithm applied wall-normal deformations of the active surface to induce streamwise velocity fluctuations that were proportional to upstream streamwise velocity fluctuations measured by the RT-PIV system. The control strategies were used to apply opposing and compliant actuations of different strengths. As well, six different sensing locations extracted from the RT-PIV domain were investigated to evaluate the effects of changes in streamwise and wall-normal distance between sensing and actuation locations.
The reactive control cases investigated through this work demonstrated a few overall impacts on the flow, although with significant variation in the extent of these effects for different gains and sensor locations. One of the general effects was the inhibited penetration of sweep motions towards the wall. This conclusion was drawn primarily from evaluation of the time-averaged flow fields. This analysis highlighted that, close to the active surface, the average streamwise velocity was reduced relative to the unforced flow. As well, the region of average upward flow seen for the unforced flow was held closer to the wall for many reactive control cases. A second overall effect of the reactive control was that it had a general disruptive effect on the periodic vortex shedding. The level of disruption was closely tied to the amplitude of actuations in most cases. However, for some cases, disruption of the periodic vortex shedding occurred along with an increase of the TKE of the flow. For these cases, although the primary energetic structures of the flow were weakened, significant turbulent energy was introduced by the reactive control in the form of other flow motions.
The opposition v-control scheme showed some of the strongest impediment towards the wall-ward advance of sweep motions. Furthermore, there appeared to be a consistent increase in the opposition of sweep motions with increasing gain magnitudes and decreasing the streamwise distance from the sensing location. The significant opposition against sweep motions by these cases contributed to them having the highest Cd values on average due to the reduction of flow speed close to the wall. These cases also showed the greatest disruption of the periodic vortex shedding with a minimum cumulative energy of the first two POD modes equal to 31 % of the value for the unforced flow. As well, these cases generally had total kinetic energies that were close to or below that of the unforced flow. This led to the opposing actuation v-control cases consistently having relatively high COP values. A maximum COP value of 1.21 was achieve by opposing actuation v-control with a gain of −0.5 and (Δxs, ys)/h = (−0.9, 1.5). This was the highest COP value achieved across all the reactive control cases. These results highlight that opposing v-control was able to attenuate the energetic vortex shedding motions while adding relatively less turbulent energy in the form of other flow motions.
The results demonstrated that v-control with compliant actuation did not oppose the wall-ward penetration of sweep motions to the extent seen with opposing v-control cases. The extent of opposition to sweep events also did not follow a clear trend based on gain magnitude or sensor location. As well, the level of disruption of vortex shedding was less for compliant v-control cases compared with opposing actuation cases. The minimum value for the cumulative energy of the first two POD modes was 42 % of the value for the unforced flow. The TKE of the flow for these cases correlated strongly with actuation amplitude and was higher on average than that for the opposing actuation v-control cases. This contributed to the compliant v-control cases having lower COP values on average than the opposing v-control cases. As such, v-control applying compliant actuations caused relatively less disruption of the vortex shedding and more excitation of other motions.
The cases of u-control with opposing actuation showed relatively weak opposition of sweep motions. The opposition to the wall-ward penetration of sweep motions decreased with increasing gain magnitudes and was consistently strongest for cases with streamwise sensor offsets of Δxs/h = −0.9. This weaker opposition of sweep motions contributed to these cases having the lowest Cd values on average. The level of disruption of vortex shedding and the TKE of the flow also correlated with actuation amplitude. Larger actuation amplitudes corresponded to greater disruption of vortex shedding and higher TKE values. It is interesting to note that the level of disruption increased with the gain value while the opposition of sweep motions decreased. This suggests that disruption of the periodic flow did not necessarily correspond to greater opposition to the penetration of sweep motions towards the wall. The highest COP value for opposing actuation u-control cases was 1.20 for the case with a gain of −0.5 and (Δxs, ys)/h = (−0.6, 1.5). This was the second highest COP value achieved across all the reactive control cases. Overall, the COP values for the opposing actuation u-control cases tended to decrease with increasing gain magnitude.
The final subset of cases considered was u-control applying compliant actuations. This group showed relatively strong opposition against sweep motions. The extent of the opposition decreased with increasing gain magnitude and was strongest for cases with Δxs/h = −0.9. The maximum level of disruption of the vortex shedding was relatively smaller compared with the other control schemes. The minimum value for the cumulative energy of the first two POD modes was 52 % of the value for the unforced flow. Regarding TKE, this scheme resulted in lower values on average compared with u-control with opposing actuation. The compliant u-control had a maximum TKE value of 113 % of the value for the unforced flow, which was 9 %–13 % lower than the maximum values of the other three groups of cases. Overall, the compliant actuation u-control significantly diminished the penetration of sweep motions towards the wall while having a relatively smaller impact on the energy and periodicity of the flow. The Cd and COP values for compliant u-control indicate that its performance was less sensitive to changes in gain magnitude than opposing u-control.
In summary, the opposition v-control and compliant u-control cases were the most compelling as they showed the greatest opposition against sweep motions penetrating towards the wall and had the highest COP values on average. As well, the stronger opposition against sweep motions shown by u-control cases with lower actuation amplitudes is intriguing and supports the idea that small actuations can efficiently control wall-bounded flows. The consistent observation of high COP and relatively low Cd values for reactive control cases with smaller gain magnitudes further supports this conclusion.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.292.
Funding
We acknowledge the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) (Alexander Graham Bell Canada Graduate Scholarship-Master's; Discovery Grant RGPIN-2020-07231 Ghaemi, Smart skin for control of wall-bounded turbulent flows).
Declaration of interests
The authors report no conflict of interest.
Appendix A
This appendix contains velocity profiles for more detailed comparison of the effects of different reactive control cases. The discussion is kept relatively brief as the conclusions are consistent with those derived from contour plots in § 5.2.
Figure 24 shows profiles of the average streamwise velocity in the wall-normal direction for reactive control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values. Figure 24(a,b) illustrate that, at the beginning of the active surface, v- and u-control generally cause the average streamwise velocity to increase relative to the unforced flow between y/h = 0.5 to 1.3. The extent of the increase in the average streamwise velocity correlates with gain magnitude with smaller gains corresponding to lesser increases in the average streamwise velocity. As discussed in § 5.2, the increase in average streamwise velocity is attributed to the reactive control promoting wall-normal momentum transport earlier in the wake.

Figure 24. Average streamwise velocity profiles for (a,c,e) v-control and (b,d, f) u-control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values. Panels (a,b), (c,d) and (e, f) show the velocity profiles for the streamwise locations of x/h = 5.3, 11.6 and 17.8, respectively.
At the middle of the active surface, figure 24(c) shows that v-control, particularly the negative gain cases, cause significant reductions to the average streamwise velocity over y/h = 0.5 to 1.3. Figure 24(d), however, demonstrates that the u-control cases have relatively little impact on the average streamwise velocity over y/h = 0.5 to 1.3. This indicates that, at the middle of the active surface, the opposing actuation v-control cases were particularly effective at inhibiting the penetration of sweep motions towards the wall. Additionally, figure 24(c,d) show that the v- and u-control cause some smoothing of the dip in the streamwise velocity profile of the unforced flow between y/h = 1.2 to 2.3. This dip in the streamwise velocity profile of the unforced flow is attributed to the passage of ejection motions carrying low speed fluid out from the wall. The smoothing of this dip can be attributed to a combination of inhibiting the advancement of sweep motions towards the wall and reduction of the stretching of ejection motions away from the wall by the reactive control.
Figure 24(e, f), showing velocity profiles at the end of the active surface, highlight similar results as figure 24(c,d). The v-control cases, and particularly the negative gain cases, show significant reduction of the average streamwise velocity from y/h = 0.5 to 1.7. Both v- and u-control cases show greater average streamwise velocities relative to the unforced flow from approximately y/h = 1.8 to 2.6. The increase in streamwise velocity over this wall-normal range can again be described as a result of the reactive control inhibiting the advance of sweep motions towards the wall and the stretching of ejection motions away from the wall.
Figure 25 shows the wall-normal velocity profiles for reactive control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values. At the start of the active surface, figure 25(a) demonstrates that, close to the wall (approximately y/h < 0.7), v-control generally caused a reduction of the average flow away from the wall relative to the unforced flow. At a farther distance from the wall, the v-control cases show increases in the average flow away from the wall. These effects are attributed to an upstream shift of the wall-normal flow field due to wall-normal momentum transport occurring earlier in the wake when reactive control is applied. As well, figure 25(a) shows that the positive gain cases of v-control cause particularly strong increases in the average flow away from the wall. This indicates that v-control applying compliant actuations induces greater disruption of the flow upstream of the active surface than the opposing actuation cases. Figure 25(b) indicates that, at the start of the active surface, the u-control cases with positive gains show similar effects as the v-control cases. The profiles for the negative gain cases of u-control show slightly different effects in that there is no reduction of the wall-normal flow away from the wall at any point.

Figure 25. Average wall-normal velocity profiles for (a,c,e) v-control and (b,d, f) u-control cases with (Δxs, ys)/h = (−0.6, 1.1) and at all tested gain values. Panels (a,b), (c,d) and (e, f) show the velocity profiles for the streamwise locations of x/h = 5.3, 11.6 and 17.8, respectively.
At the middle of the active surface, figure 25(c,d) illustrate that v- and u-control generally induce an increase in average flow away from the wall, below y/h ≈ 0.9. As well, both reactive control schemes caused reduction to the peak average wall-normal flow of the unforced flow at y/h = 1.3. Both of these effects can be explained as a result of inhibiting both the advance of sweep motions towards the wall and the stretching of ejection motions away from the wall.
Lastly, at the end of the active surface, figure 25(e, f) illustrate that both reactive control strategies cause increases in the average flow away from the wall up to y/h ≈ 1.5 for v-control and y/h ≈ 1.3 for u-control. Again, this can be attributed to the reactive control inhibiting sweep and ejection motions from, respectively, penetrating towards and stretching away from the wall. As well, it is evident that the negative gain v-control cases and positive gain u-control cases show relatively larger increases in the average flow away from the wall. This indicates that opposing actuation v-control and compliant actuation u-control were the most successful at affecting the ejection and sweep motions.
Appendix B
This appendix contains figures and discussion to support the conclusion in § 6 that the first two POD modes of the flow with and without reactive control are associated with the vortex shedding process. Figure 26 shows the first two spatial POD modes of the unforced flow and the flow during the application of v- and u-control with (Δxs, ys)/h = (−0.9, 1.1) and a gain of −1.5. Both spatial modes for the unforced flow show structures that are consistent with the ejection and sweep structures of the periodic vortex shedding. Furthermore, the spatial modes for the highlighted v- and u-control cases likewise exhibit structures that are consistent with the periodic vortex shedding that characterizes the flow. Notably, figure 26(c,d) highlight that the amplitude of spatial POD modes 1 and 2 is significantly attenuated relative to the unforced flow for x/h > 10. This indicates that the highlighted v-control caused significant disruption to the periodic structures of the flow downstream of x/h > 10.

Figure 26. First and second spatial POD modes of (a,b) the unforced flow, (c,d) v-control and (e, f) u-control with (Δxs, ys)/h = (−0.9, 1.1) and a gain of G = −1.5.
As well, figure 27 shows phase plots of the coefficients of the first two POD modes (a 1 and a 2, respectively) normalized by their corresponding eigenvalues (λ 1 and λ 2) for the unforced flow and v- and u-control cases with (Δxs, ys)/h = (−0.9, 1.1) and G = −1.5. As detailed by van Oudheusden et al. (Reference van Oudheusden, Scarano, van Hinsberg and Watt2005), a phase plot of the normalized coefficients of two POD modes associated with a vortex shedding process should yield a plot that approximates a unit circle. This behaviour is exhibited to varying extents by the phase plots in figure 27. Consequently, this indicates that the first two POD modes are associated with a vortex shedding process for the unforced flow and the reactive control cases. The greater deviations from the unit circle shown by the phase plots for the reactive control cases demonstrate the occurrence of greater turbulent fluctuations in the flow.

Figure 27. Phase plots of coefficients for first two POD modes (a 1 and a 2) of (a) the unforced flow, (b) v-control and (c) u-control with (Δxs, ys)/h = (−0.9, 1.1) and G = −1.5. The coefficients are normalized by their corresponding eigenvalues (λ 1 and λ 2).
Lastly, figure 28 shows PSD plots of the time varying coefficient of the a 1 for the unforced flow and v- and u-control cases with (Δxs, ys)/h = (−0.9, 1.1) and G = −1.5. Considering the PSD plot of the unforced flow, the peak Strouhal number of 0.20 agrees with the shedding Strouhal number found for the unforced flow. Figure 28 demonstrates that the negative gain v-control case has a higher peak Strouhal number for a 1 of 0.27. As well, the u-control case had little effect on the peak Strouhal number as it is nearly the same as shown by the unforced flow. As such, this indicates that the applied reactive control can change the shedding frequency.

Figure 28. The PSD plots of the time varying coefficient of the first POD mode (a 1) of the unforced flow and v-control and u-control cases with (Δxs, ys)/h = (−0.9, 1.1) and G = −1.5.