1. Introduction
There has been considerable interest in laminar–turbulent transition of super- and hypersonic boundary-layer flows due to their key role in the development of high-speed vehicles (Kimmel Reference Kimmel2003). An adequate understanding of this physical process is crucial to their design as aerodynamic drag and thermal loading differ drastically depending on whether the flow is laminar or turbulent (Fedorov Reference Fedorov2011; Zhong & Wang Reference Zhong and Wang2012).
Transition is characterised by a high degree of spatial and temporal complexity (Kachanov Reference Kachanov1994). It often starts with amplification of small-amplitude instability waves, which are triggered, via the so-called receptivity (Morkovin Reference Morkovin1969; Goldstein & Hultgren Reference Goldstein and Hultgren1989), by external perturbations, including acoustic, vortical or entropy waves in the free stream and local imperfections on the surface. The instability modes excited first grow exponentially, which is well predicted by linear stability theory. Once the disturbances become sufficiently strong, nonlinear inter-modal interactions take place, leading to final breakdown to turbulence. In many situations, ambient disturbances may further influence the linear and nonlinear development of the instability waves and thereby affect transition location. This scenario has only received limited attention and it will be studied in this paper. Specifically, we will focus on the evolution of such instability waves in a supersonic boundary layer under the influence of impinging acoustic waves.
1.1. Intrinsic instabilities in compressible boundary layers
Theoretical studies of compressible boundary-layer instability as well as extensive computations, performed at different conditions (e.g. Mach number, Reynolds number and wall temperature) have identified a multitude of instability modes, which are now termed the first and second Mack modes, etc. (Mack Reference Mack1975, Reference Mack1984) . Lower-branch first modes that are sufficiently oblique are the continuation of the viscous Tollmien–Schlichting (T-S) instability into the supersonic regime, and they are governed by the compressible version of the triple-deck structure (Smith Reference Smith1989). The remaining first modes and second modes are of inviscid nature, and their existence is associated with a generalised inflection point (Lees & Lin Reference Lees and Lin1946). For insulated walls, the first modes represent dominant instability up to a Mach number of approximately 4, beyond which the second modes prevail. For cooled walls, the second modes can dominate at lower Mach numbers (Mack Reference Mack1993).
Instability modes can be categorised based on their propagation speeds relative to the free stream. A mode travelling relative to the free stream at a velocity smaller than the sound speed is referred to as a subsonic mode. Its eigenfunction decays exponentially away from the boundary layer. In contrast, a mode propagating supersonically relative to the free stream is referred to as a supersonic or radiating mode because its eigenfunction is oscillatory while attenuating, or remains bounded in the far field when the mode is neutral. Both neutral subsonic and supersonic modes have a critical level (i.e. the position where the base-flow velocity is equal to the phase velocity). The critical level of the former coincides with the generalised inflection point, but that of the latter does not. It is well known that the supersonic modes are present in supersonic jets, and radiate Mach waves; see Tam (Reference Tam1995) and references therein.
The present paper is concerned with the supersonic mode, whose existence in compressible boundary layers is also well known (Mack Reference Mack1984). Such modes may exist if the wall is cooled sufficiently below the adiabatic temperature (Chuvakhov & Fedorov Reference Chuvakhov and Fedorov2016) or the free-stream enthalpy is high (Salemi & Fasel Reference Salemi and Fasel2018). They have been reported for flows over flat plates (Mack Reference Mack1987; Bitter & Shepherd Reference Bitter and Shepherd2015), wedges (Chang, Malik & Hussaini Reference Chang, Malik and Hussaini1990; Chang, Vinh & Malik Reference Chang, Vinh and Malik1997) and cones (Knisely & Zhong Reference Knisely and Zhong2017; Mortensen Reference Mortensen2018). Sound radiation by unstable supersonic modes in a hypersonic blunt-cone boundary layer was studied numerically by Knisely & Zhong (Reference Knisely and Zhong2019a,Reference Knisely and Zhongb).
While proven to be rather successful in describing the dispersion relationship and growth rates of small-amplitude instability waves, linear stability theory fails to predict the course of evolution when the magnitude of the instability mode is no longer small enough. A typical evolution path is that the instability wave goes through almost the entire linear amplification regime, acquiring a sufficiently large amplitude near its neutral position. At high Reynolds numbers, a critical layer emerges, where nonlinear interaction first takes place, and usually other physical factors such as viscous and non-equilibrium effects (associated with the slow modulation of the modal amplitude), although remaining negligible in the main bulk, also come into play (Goldstein & Hultgren Reference Goldstein and Hultgren1988; Goldstein & Leib Reference Goldstein and Leib1988). The continued development of the disturbance under the combined influence of these factors is described by the well-developed nonlinear non-equilibrium critical-layer theory, a review of which is given by Wu (Reference Wu2019). In this theory, the nonlinear dynamics is determined by the composition of modes and the singular nature of the inviscid solution in the outer layer. Once a singularity is removed by introducing viscous and/or non-equilibrium effects in the critical layer, the regularised solution represents a locally large disturbance, which contributes dominant nonlinear effects. The dynamics may take a weakly or strongly nonlinear form.
Nonlinear and non-equilibrium critical layers were considered for externally forced waves in shear flows in the late 1970s, but for free instability modes the study of such critical-layer dynamics started with Hickernell (Reference Hickernell1984), who considered temporal evolution of a non-inflectional planar Rossby mode on a rotating free shear layer. The interactions in the critical layer turned out to be of weakly nonlinear nature, the analysis of which led to a novel amplitude equation containing a non-local nonlinear term. Goldstein & Leib (Reference Goldstein and Leib1988) and Goldstein & Hultgren (Reference Goldstein and Hultgren1988) considered a regular Rayleigh instability mode in a free shear layer. They showed that the critical-layer dynamics is strongly nonlinear, and the evolution is governed by an amplitude equation coupled with the vorticity equation, in which the unknown amplitude appears as a coefficient. Goldstein & Leib (Reference Goldstein and Leib1989) studied the nonlinear evolution of a subsonic mode in a supersonic shear layer, for which the inviscid solution of the temperature fluctuation exhibits a simple-pole singularity, which dictates that the interactions are of weakly nonlinear type. An evolution equation was derived, to which the singularity contributes a signature non-local nonlinear term. Leib (Reference Leib1991) extended the analysis to a supersonic mode, which is non-inflectional. The additional logarithmic singularity in the streamwise velocity gives rise to an extra history-dependent nonlinear term. The above studies were the first to solve the non-local nonlinear equations numerically, showing that the amplitude exhibits rather complex behaviours, including finite-distance blow-up and oscillatory saturation. Their analyses are closely related to the present study. Gajjar (Reference Gajjar1995, Reference Gajjar1996) considered the nonlinear development of stationary and travelling vortices in three-dimensional boundary layers. An amplitude equation was derived in each case, with the non-local nonlinearity associated with the three-dimensional nature of the perturbation, and for travelling vortices in the compressible regime with the simple-pole and logarithmic singularities in the temperature and streamwise velocity as well.
There has been a large number of studies of inter-modal interactions within non-equilibrium critical layers (Goldstein Reference Goldstein1995; Wu Reference Wu2019). Important forms of modal composition include pairs of oblique modes with equal frequency but opposite spanwise wavenumbers (Goldstein & Choi Reference Goldstein and Choi1989; Wu, Lee & Cowley Reference Wu, Lee and Cowley1993; Leib & Lee Reference Leib and Lee1995), resonant triads of inviscid Rayleigh waves (Wu Reference Wu1992, Reference Wu1995) and more generally phase-locked modes (i.e. modes having nearly the same phase speed) (Wu & Stewart Reference Wu and Stewart1996; Wu, Stewart & Cowley Reference Wu, Stewart and Cowley2007).
1.2. Effects of external disturbances on transition
External disturbances, including surface roughness elements and free-stream disturbances, may affect the transition route and location through different mechanisms, depending on their position as well as length and time scales. One of the important mechanisms is receptivity, which refers to the process by which external disturbances excite instability modes, and thus determine the initial amplitudes of the latter (Morkovin Reference Morkovin1969). It is now well recognised that excitation in general requires a mechanism of length scale conversion or tuning, which is, in the incompressible or subsonic regime, provided by the adjustment in the leading-edge region (Goldstein Reference Goldstein1983) and/or scattering of free-stream acoustic waves (Ruban Reference Ruban1984; Goldstein Reference Goldstein1985) or vortical disturbances (Duck, Ruban & Zhikharev Reference Duck, Ruban and Zhikharev1996; Wu Reference Wu2001a,Reference Wub) by surface roughness.
The receptivity mechanisms identified for incompressible, or compressible subsonic, boundary layers remain operational in super- and hyper-sonic regimes, but may take on significantly different characteristics. On the other hand, new mechanisms may arise due to the nature of the instabilities. The excitation of first and second modes by impinging sound waves through the leading-edge mechanism was considered by Fedorov & Khokhlov (Reference Fedorov and Khokhlov1991, Reference Fedorov and Khokhlov2001) and Fedorov (Reference Fedorov2003a). Their analysis showed that there exist the so-called fast and slow modes, whose phase velocities in the leading-edge region approach those of the oncoming fast and slow acoustic waves, respectively. Both modes are thus excited. As they undergo no or only marginal decay, the leading-edge adjustment mechanism is much more efficient than its counterpart in the subsonic regime, and has been the subject of a series of direct numerical simulations (DNS) (Ma & Zhong Reference Ma and Zhong2003, Reference Ma and Zhong2005; Balakumar Reference Balakumar2005, Reference Balakumar2009). Vortical disturbances may generate highly oblique modes (Ricco & Wu Reference Ricco and Wu2007), which may be particularly effective for a small specific range of obliqueness angle (Goldstein & Ricco Reference Goldstein and Ricco2018). The mechanism of the acoustic–roughness interaction carries over to the supersonic regime, generating first and second modes in much the same manner as exciting the T-S mode in the subsonic regime when the theory was formulated in a finite-Reynolds-number framework (Fedorov Reference Fedorov2003b). The (improved) large-Reynolds-number asymptotic analyses showed that, among all possible acoustic waves, those on the triple-deck scales and with incident angles close to ![]() $\cos ^{-1}(1/M)$ (
$\cos ^{-1}(1/M)$ (![]() $M$ being the free-stream Mach number) are particularly effective in generating the viscous first mode (Liu, Dong & Wu Reference Liu, Dong and Wu2020), while generation of the second mode was due to a pure surface geometry effect at leading order (Dong, Liu & Wu Reference Dong, Liu and Wu2020).
$M$ being the free-stream Mach number) are particularly effective in generating the viscous first mode (Liu, Dong & Wu Reference Liu, Dong and Wu2020), while generation of the second mode was due to a pure surface geometry effect at leading order (Dong, Liu & Wu Reference Dong, Liu and Wu2020).
New receptivity mechanisms operate for supersonic boundary layers and have been described theoretically. One of these is the sound–gust interaction (Wu Reference Wu1999), in which sound and vortical disturbances with suitable wavenumbers and frequencies interact to generate a forcing that is in resonance with and thereby excites the viscous first mode. Sound–sound interaction also generates the viscous first mode, and this mechanism becomes particularly efficient for sound waves on the triple-deck scales (Hernández & Wu Reference Hernández and Wu2019). Another distinct mechanism operates in the hypersonic flow past a wedge, where, due to the presence of an oblique shock, there exist viscous instability modes confined in the region below the shock (Cowley & Hall Reference Cowley and Hall1990). Qin & Wu (Reference Qin and Wu2016) showed that any of the oncoming acoustic, vortical and entropy disturbances interacts with the shock to generate a slow acoustic wave downstream, and with suitable frequency the latter may resonate with and thereby excite the instability. The above three mechanisms do not resort to any surface roughness, and hence operate in supersonic boundary layers over nominally smooth walls, providing possible explanations for the unstable modes observed.
When external disturbances of sufficient magnitude are present in the main unstable region, they may influence instability characteristics. Surface roughness has received most attention, and is found to play a destabilising role, in most cases causing earlier transition (Klebanoff & Tidstrom Reference Klebanoff and Tidstrom1972; Corke, Barsever & Morkovin Reference Corke, Barsever and Morkovin1986). When roughness elements have a length scale much longer than that of the instability, their impact can be accounted for by local linear stability analysis of the altered base flow. Analyses of this kind have been performed for two-dimensional (Nayfeh, Ragab & Al-Maaitah Reference Nayfeh, Ragab and Al-Maaitah1988; Masad & Iyer Reference Masad and Iyer1994) and three-dimensional roughness (Piot, Casalis & Rist Reference Piot, Casalis and Rist2008; Choudhari et al. Reference Choudhari, Li, Chang, Edwards, Kegerise and King2010; De Tullio et al. Reference De Tullio, Paredes, Sandham and Theofilis2013; Groskopf & Kloker Reference Groskopf and Kloker2016). However, when the length scale of the roughness is comparable to, or shorter than, that of the instability, local stability analysis is no longer tenable, and DNS have been performed instead (Marxen, Iaccarino & Shaqfeh Reference Marxen, Iaccarino and Shaqfeh2010; Edelmann & Rist Reference Edelmann and Rist2013). The physical mechanism is local scattering: the roughness-induced local mean-flow distortion scatters an oncoming instability wave, changing its amplitude over a short length. A transmission coefficient, defined as the ratio of the amplitude of the transmitted wave downstream to that of the oncoming wave, is a natural measure of the overall effect of the roughness (Wu & Dong Reference Wu and Dong2016; Xu et al. Reference Xu, Sherwin, Hall and Wu2016). Another mechanism is modal interaction, where the roughness-induced signature interacts resonantly with instability modes so that the growth rate of the latter is changed substantially (Goldstein & Wundrow Reference Goldstein and Wundrow1995; He, Butler & Wu Reference He, Butler and Wu2019; Xu & Wu Reference Xu and Wu2022).
Acoustic waves are dominant external disturbances affecting supersonic boundary-layer transition, especially in conventional wind tunnel experiments (Pate & Schueler Reference Pate and Schueler1969; Schneider Reference Schneider2001), as intense noise is emitted from the turbulent boundary layers on the tunnel walls and/or radiated due to turbulence being scattered by wall inhomogeneities such as roughness (Laufer Reference Laufer1961, Reference Laufer1964). Wind tunnel experiments were carried out to establish the relationship between the noise level and transition location. Acoustic waves with particular frequencies lead to considerably earlier transition (Spangler & Wells Reference Spangler and Wells1968). By relaminarising the boundary layers on the tunnel walls to reduce the facility-produced acoustic waves, transition was delayed significantly (Kendall Reference Kendall1971).
Because of intense acoustic disturbances to which the test model is exposed, transition in conventional wind tunnels is notably different from that in quiet ones (Beckwith & Miller Reference Beckwith and Miller1990; King Reference King1992; Schneider Reference Schneider2008). Modern hypersonic quiet wind tunnel technology strives to reproduce flight conditions (Schneider Reference Schneider2015). However, even in the latter acoustic waves are radiated from either the engine or the turbulent boundary layers over neighbouring surfaces of the aircraft, and they are likely to have a significant effect on transition. In view of this, conventional tunnels share some similarities with the flight condition, and experimental data obtained in them on instability and transition may still be useful (Duan, Choudhari & Wu Reference Duan, Choudhari and Wu2014).
1.3. The aim of the present work
For either purpose of describing transition scenarios in the presence of impinging acoustic waves and extrapolating wind tunnel data to flight conditions, it is necessary to investigate how they influence the inherent boundary-layer instability and the ensuing transition. Despite its potential importance, there have been few investigations of this aspect, in contrast to extensive studies devoted to receptivity. In this paper, we identify and describe mathematically a mechanism, through which impinging sound waves affect the linear and nonlinear development of instability waves. Specifically, we consider radiating modes, and demonstrate that, while emitting a sound wave to the far field, a radiating mode is also extremely sensitive to an incident acoustic wave with the same frequency and wavenumber due to a fundamental resonance between them with the incident sound acting as the forcing. This mechanism involves both receptivity and nonlinear modal interaction. While receptivity normally refers to excitation of instability modes near the lower branch, the present resonance takes place near the upper branch, in the vicinity of which an incident wave of small intensity excites a radiating mode of much larger amplitude. When the intensity is of a distinguished order of magnitude but still very low, nonlinearity affects the excitation, and moreover the incident sound influences significantly the linear and nonlinear evolution of the locally excited mode as well as of the oncoming pre-existing mode.
The rest of the paper is organised as follows. In § 2, we formulate the problem pertinent to a free-stream acoustic wave impinging upon the boundary layer. The distinguished asymptotic scalings are deduced under which the incident sound wave affects the excitation and evolution of the radiating mode. Two distinct, the non-equilibrium and the equilibrium non-parallel, regimes are considered. In § 3, we investigate the reflection of an impinging sound wave by the boundary layer. The boundary-layer response and reflection coefficient are determined. A systematic numerical study is performed to show, inter alia, that the reflection coefficient becomes infinite for a particular pair of frequency and wavenumber, coinciding with those of the neutral radiating mode. This signals a fundamental resonance between the incident wave and the radiating mode. In § 4, we focus on this particular acoustic wave. Dominant interactions affecting the excitation and evolution take place in the critical layer, and are analysed to derive the amplitude equations in the two regimes mentioned above. These equations are solved numerically to demonstrate the role of the incident sound and nonlinearity in the excitation and evolution of the radiating mode. In order to take into account effects of both non-equilibrium and non-parallelism, we construct a composite amplitude equation in § 5. In § 6, the spontaneously radiated sound wave under the influence of the incident sound is computed. Finally, a summary and conclusions are given in § 7.
2. Formulation
We consider a supersonic boundary-layer flow that forms over a semi-infinite flat plate underneath a uniform free stream, where the density, velocity, shear viscosity and sound speed are denoted by ![]() $\rho _\infty$,
$\rho _\infty$, ![]() $U_\infty$,
$U_\infty$, ![]() $\mu _\infty$ and
$\mu _\infty$ and ![]() $a_\infty$, respectively. Based upon these quantities, the Reynolds number
$a_\infty$, respectively. Based upon these quantities, the Reynolds number ![]() $R$ and the Mach number
$R$ and the Mach number ![]() $M$ are defined as
$M$ are defined as
where the reference length ![]() $\delta ^*$ is the boundary-layer thickness at the location of interest (which is the neutral position of the radiating mode to be considered). To adopt an asymptotic approach and focus on the supersonic regime, we take
$\delta ^*$ is the boundary-layer thickness at the location of interest (which is the neutral position of the radiating mode to be considered). To adopt an asymptotic approach and focus on the supersonic regime, we take ![]() $R\gg 1$ and
$R\gg 1$ and ![]() $1< M=O(1)$.
$1< M=O(1)$.
The flow will be described in a Cartesian coordinate system ![]() $(x,y,z)$, where
$(x,y,z)$, where ![]() $x$ and
$x$ and ![]() $y$ are along and normal to the wall, respectively, and
$y$ are along and normal to the wall, respectively, and ![]() $z$ is in the spanwise direction, all non-dimensionalised by
$z$ is in the spanwise direction, all non-dimensionalised by ![]() $\delta ^*$. The time variable
$\delta ^*$. The time variable ![]() $t$ is normalised by
$t$ is normalised by ![]() $\delta ^*/{U}_\infty$. The density
$\delta ^*/{U}_\infty$. The density ![]() $\rho$, velocity
$\rho$, velocity ![]() $\boldsymbol {u}=(u,v,w)$, pressure
$\boldsymbol {u}=(u,v,w)$, pressure ![]() $p$, temperature
$p$, temperature ![]() $T$ and shear and bulk viscosities
$T$ and shear and bulk viscosities ![]() $\mu$ and
$\mu$ and ![]() $\mu ^\prime$ are non-dimensionalised by
$\mu ^\prime$ are non-dimensionalised by ![]() $\rho _\infty$,
$\rho _\infty$, ![]() ${U}_\infty$,
${U}_\infty$, ![]() $\rho _\infty {U}_\infty ^2$,
$\rho _\infty {U}_\infty ^2$, ![]() ${T}_\infty$ and
${T}_\infty$ and ![]() $\mu _\infty$, respectively. The flow is governed by the compressible Navier–Stokes (N-S) equations (e.g. Stewartson Reference Stewartson1964),
$\mu _\infty$, respectively. The flow is governed by the compressible Navier–Stokes (N-S) equations (e.g. Stewartson Reference Stewartson1964),
where ![]() $\boldsymbol {e}$ and
$\boldsymbol {e}$ and ![]() $\varPhi$ denote the strain-rate tensor and dissipation function, respectively,
$\varPhi$ denote the strain-rate tensor and dissipation function, respectively,
![]() $Pr$ is the Prandtl number and
$Pr$ is the Prandtl number and ![]() $\gamma$ the ratio of specific heats. Furthermore, the conventional assumption of vanishing bulk viscosity,
$\gamma$ the ratio of specific heats. Furthermore, the conventional assumption of vanishing bulk viscosity, ![]() $\mu ^\prime =0$, is invoked.
$\mu ^\prime =0$, is invoked.
2.1. The base flow
The boundary layer develops on a long length scale, and can be described by introducing the slow variable
The base-flow density ![]() $R_B$, velocity field
$R_B$, velocity field ![]() $(U_B, V_B)$, pressure
$(U_B, V_B)$, pressure ![]() $P_B$ and temperature
$P_B$ and temperature ![]() $T_B$ can be expressed as
$T_B$ can be expressed as
The steady boundary-layer equations admit the similarity solution (Stewartson Reference Stewartson1964)
where ![]() $\eta$ is the similarity variable defined, via the Dorodnitsyn–Howarth coordinate transformation, by
$\eta$ is the similarity variable defined, via the Dorodnitsyn–Howarth coordinate transformation, by
In terms of ![]() $\eta$,
$\eta$, ![]() $F$ and
$F$ and ![]() $\bar {T}$, the steady boundary-layer equations reduce to
$\bar {T}$, the steady boundary-layer equations reduce to
 \begin{equation} \left.\begin{gathered} \frac{1}{2}FF^{\prime\prime}+(\bar{K} F^{\prime\prime})^\prime =0, \\ \bar{T}^{\prime\prime}+\frac{PrF+2\bar{K}^\prime}{2\bar{K}}\bar{T}^\prime+Pr(\gamma-1)M^2(F^{\prime\prime})^2 =0, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} \frac{1}{2}FF^{\prime\prime}+(\bar{K} F^{\prime\prime})^\prime =0, \\ \bar{T}^{\prime\prime}+\frac{PrF+2\bar{K}^\prime}{2\bar{K}}\bar{T}^\prime+Pr(\gamma-1)M^2(F^{\prime\prime})^2 =0, \end{gathered}\right\} \end{equation}
where we have put ![]() $\bar {K}(\bar {T})=\bar \mu (\bar {T})/\bar {T}$. For Sutherland's law,
$\bar {K}(\bar {T})=\bar \mu (\bar {T})/\bar {T}$. For Sutherland's law, ![]() $\bar {K}$ is given by
$\bar {K}$ is given by
where ![]() $C_0=110.4\,\mathrm {K}/T_\infty$ with
$C_0=110.4\,\mathrm {K}/T_\infty$ with ![]() $T_\infty$ being the free-stream temperature in Kelvin. The corresponding boundary conditions are
$T_\infty$ being the free-stream temperature in Kelvin. The corresponding boundary conditions are
and
if the wall is isothermal with a prescribed temperature ![]() $\bar {T}_w$.
$\bar {T}_w$.
We consider a perfect gas with ratio of specific heats ![]() $\gamma =1.4$ and Prandtl number
$\gamma =1.4$ and Prandtl number ![]() $Pr=0.72$. The free-stream temperature is taken to be
$Pr=0.72$. The free-stream temperature is taken to be ![]() $T_\infty =300\,\mathrm {K}$, and the Mach number
$T_\infty =300\,\mathrm {K}$, and the Mach number ![]() $M=6$. The above chosen parameters are representative of flight conditions (Chuvakhov & Fedorov Reference Chuvakhov and Fedorov2016). The base-flow equations (2.8) are solved by using a shooting method based on a fourth-order Runge–Kutta integrator. The streamwise velocity and temperature for various cooling ratios, defined by the wall temperature over the adiabatic wall temperature, are shown in figure 1. In particular, the base-flow quantities with the cooling ratio
$M=6$. The above chosen parameters are representative of flight conditions (Chuvakhov & Fedorov Reference Chuvakhov and Fedorov2016). The base-flow equations (2.8) are solved by using a shooting method based on a fourth-order Runge–Kutta integrator. The streamwise velocity and temperature for various cooling ratios, defined by the wall temperature over the adiabatic wall temperature, are shown in figure 1. In particular, the base-flow quantities with the cooling ratio ![]() $r_c=0.427$ (
$r_c=0.427$ (![]() $\bar {T}_w=3$) will be used in the ensuing analysis. As will be shown later, a radiating mode exists only for
$\bar {T}_w=3$) will be used in the ensuing analysis. As will be shown later, a radiating mode exists only for ![]() $r_c$ below a certain value less than unity.
$r_c$ below a certain value less than unity.

Figure 1. The profiles of the base-flow streamwise velocity (a) and temperature (b) for different ![]() $r_c$.
$r_c$.
2.2. Free-stream acoustic waves
Acoustic waves are one type of elementary disturbances in the free stream, where the base flow is uniform. The density, velocity and pressure components of a two-dimensional acoustic wave, ![]() ${\epsilon _s}(\tilde {r}_s, \tilde {u}_s, \tilde {v}_s, \tilde {p}_s)$, where
${\epsilon _s}(\tilde {r}_s, \tilde {u}_s, \tilde {v}_s, \tilde {p}_s)$, where ![]() $\epsilon _s\ll 1$ is the magnitude, are governed by the linearised Euler equations about the uniform background field. Eliminating
$\epsilon _s\ll 1$ is the magnitude, are governed by the linearised Euler equations about the uniform background field. Eliminating ![]() $\tilde {r}_s$,
$\tilde {r}_s$, ![]() $\tilde {u}_s$ and
$\tilde {u}_s$ and ![]() $\tilde {v}_s$ from these equations leads to the equation for pressure
$\tilde {v}_s$ from these equations leads to the equation for pressure ![]() $\tilde {p}_s$
$\tilde {p}_s$
The solution takes the form
where ![]() $\alpha _{s}$ and
$\alpha _{s}$ and ![]() $\gamma _{s}$ are the streamwise and normal wavenumbers, respectively, and
$\gamma _{s}$ are the streamwise and normal wavenumbers, respectively, and ![]() $\omega _{s}$ is the frequency; here,
$\omega _{s}$ is the frequency; here, ![]() $\gamma _{s}$ is taken to be positive so that the group velocity in the wall-normal direction is negative, i.e. the disturbance represents an incoming wave.
$\gamma _{s}$ is taken to be positive so that the group velocity in the wall-normal direction is negative, i.e. the disturbance represents an incoming wave.
Substitution of (2.13) into (2.12) yields the dispersion relation for slow acoustic waves
where ![]() $c_s$ is the phase velocity. We define an incident angle
$c_s$ is the phase velocity. We define an incident angle ![]() $\theta _s$ by
$\theta _s$ by ![]() $\cos \theta _s=\alpha _{s}/\sqrt {\alpha _{s}^2+\gamma _{s}^2}$. Use of the dispersion relation (2.14) shows that
$\cos \theta _s=\alpha _{s}/\sqrt {\alpha _{s}^2+\gamma _{s}^2}$. Use of the dispersion relation (2.14) shows that
A sound wave in the free stream is characterised by its frequency and incident angle.
2.3. Asymptotic scaling
We are interested in slow acoustic waves and instability modes whose wavelengths are comparable to the boundary-layer thickness (i.e. ![]() $\alpha _{s}=O(1)$). Only slow acoustic waves are considered as they have a critical layer, which is crucial for acoustic waves of moderate amplitude to be able to impact the radiating mode. When such a slow acoustic wave impinges on the boundary layer, the response of the latter is in the form of an absorbed disturbance and a reflected wave. For a sound wave with a particular frequency and a specific incident angle, the reflection coefficient becomes infinite, indicating a fundamental resonance between the impinging sound and the intrinsic radiating mode, through which the latter is excited and its evolution influenced. We will investigate these in the non-equilibrium parallel and equilibrium non-parallel regimes.
$\alpha _{s}=O(1)$). Only slow acoustic waves are considered as they have a critical layer, which is crucial for acoustic waves of moderate amplitude to be able to impact the radiating mode. When such a slow acoustic wave impinges on the boundary layer, the response of the latter is in the form of an absorbed disturbance and a reflected wave. For a sound wave with a particular frequency and a specific incident angle, the reflection coefficient becomes infinite, indicating a fundamental resonance between the impinging sound and the intrinsic radiating mode, through which the latter is excited and its evolution influenced. We will investigate these in the non-equilibrium parallel and equilibrium non-parallel regimes.
2.3.1. Non-equilibrium parallel regime
As an inviscid Rayleigh instability mode propagates downstream, its magnitude amplifies exponentially until it reaches a neutral position, ![]() $x_{3,n}$ say. Due to the accumulated growth, the mode is likely to enter a nonlinear stage in the vicinity of the neutral position (Goldstein & Leib Reference Goldstein and Leib1989; Wu Reference Wu2019). This region is represented as
$x_{3,n}$ say. Due to the accumulated growth, the mode is likely to enter a nonlinear stage in the vicinity of the neutral position (Goldstein & Leib Reference Goldstein and Leib1989; Wu Reference Wu2019). This region is represented as
where ![]() $\tilde \mu \ll 1$ and
$\tilde \mu \ll 1$ and ![]() $\bar {x}_1=O(1)$ is negative. The local base-flow velocity and temperature profiles are expanded as
$\bar {x}_1=O(1)$ is negative. The local base-flow velocity and temperature profiles are expanded as
In this region, the growth rate of the mode is ![]() $O(\tilde \mu )$, correspondingly, the amplitude develops over the length scale of
$O(\tilde \mu )$, correspondingly, the amplitude develops over the length scale of ![]() $O(\tilde {\mu }^{-1})$, and so we introduce the slow variable
$O(\tilde {\mu }^{-1})$, and so we introduce the slow variable
The instability mode is of the travelling-wave form, and in the main layer it can be expressed, to leading order, as
where ![]() $E=\exp ({\mathrm {i}\alpha \zeta })$,
$E=\exp ({\mathrm {i}\alpha \zeta })$, ![]() $\zeta =x-ct$ is the coordinate moving at the phase speed, with
$\zeta =x-ct$ is the coordinate moving at the phase speed, with ![]() $\alpha$ and
$\alpha$ and ![]() $c$ being the streamwise wavenumber and phase speed, respectively, and
$c$ being the streamwise wavenumber and phase speed, respectively, and ![]() $A(\tilde {x})$ is the amplitude function describing the evolution. The derivative with respect to
$A(\tilde {x})$ is the amplitude function describing the evolution. The derivative with respect to ![]() $x$ then becomes
$x$ then becomes
In order to derive the scaling, let us first write down the streamwise momentum equation (of the incompressible N-S equations for convenience) for the perturbation
 \begin{align} & \Big[(\bar{U}-c)\frac{\partial}{\partial\zeta}
+\underbrace{\tilde\mu\bar{U}\frac{\partial}{\partial\tilde{x}}\Big]\tilde{u}}_{non\text{-}equilibrium} \nonumber\\
&\quad +\bar{U}^\prime\tilde{v}-\underbrace{R^{-1}\frac{\partial^2\tilde{u}}{\partial\tilde{y}^2}}_{{viscous}}
=-\frac{\partial\tilde{p}}{\partial\zeta}
-\tilde{u}\frac{\partial\tilde{u}}{\partial\zeta}-\tilde{v}\frac{\partial\tilde{u}}{\partial y}
-\tilde\mu\tilde{u}\frac{\partial\tilde{u}}{\partial\tilde{x}}+\cdots.
\end{align}
\begin{align} & \Big[(\bar{U}-c)\frac{\partial}{\partial\zeta}
+\underbrace{\tilde\mu\bar{U}\frac{\partial}{\partial\tilde{x}}\Big]\tilde{u}}_{non\text{-}equilibrium} \nonumber\\
&\quad +\bar{U}^\prime\tilde{v}-\underbrace{R^{-1}\frac{\partial^2\tilde{u}}{\partial\tilde{y}^2}}_{{viscous}}
=-\frac{\partial\tilde{p}}{\partial\zeta}
-\tilde{u}\frac{\partial\tilde{u}}{\partial\zeta}-\tilde{v}\frac{\partial\tilde{u}}{\partial y}
-\tilde\mu\tilde{u}\frac{\partial\tilde{u}}{\partial\tilde{x}}+\cdots.
\end{align}
The scaling is fixed by considering the main and critical layers. In the main layer, the disturbance is linear and inviscid, and its streamwise velocity exhibits a jump of ![]() $O(\tilde {\epsilon }\tilde \mu )$, which is to be determined by analysis of the critical layer. Suppose that the critical-layer width is
$O(\tilde {\epsilon }\tilde \mu )$, which is to be determined by analysis of the critical layer. Suppose that the critical-layer width is ![]() $O(\delta _c)$. The advection term in (2.21) is
$O(\delta _c)$. The advection term in (2.21) is ![]() $O(\delta _c)$, whereas the terms associated with the non-equilibrium and viscous effects are
$O(\delta _c)$, whereas the terms associated with the non-equilibrium and viscous effects are ![]() $O(\tilde \mu )$ and
$O(\tilde \mu )$ and ![]() $O(R^{-1}/\delta _c^2)$, respectively. The requirement that these terms are all balanced leads to
$O(R^{-1}/\delta _c^2)$, respectively. The requirement that these terms are all balanced leads to
In the critical layer, the vertical velocity of the perturbation ![]() $\tilde {v}$ is
$\tilde {v}$ is ![]() $O(\tilde {\epsilon })$, but the logarithmic singularity
$O(\tilde {\epsilon })$, but the logarithmic singularity ![]() $\ln (y-y_c)$ of the inviscid solution for the streamwise velocity suggests that the vorticity, or
$\ln (y-y_c)$ of the inviscid solution for the streamwise velocity suggests that the vorticity, or ![]() $\tilde {u}_y$, is
$\tilde {u}_y$, is ![]() $O(\tilde {\epsilon }\delta _c^{-1})$. The forcing proportional to the product of these two is thus
$O(\tilde {\epsilon }\delta _c^{-1})$. The forcing proportional to the product of these two is thus ![]() $O(\tilde {\epsilon }^2\delta _c^{-1})$. It then induces a mean-flow distortion as well as a second harmonic; their streamwise velocity is
$O(\tilde {\epsilon }^2\delta _c^{-1})$. It then induces a mean-flow distortion as well as a second harmonic; their streamwise velocity is ![]() $O(\tilde {\epsilon }^2\delta _c^{-2})$ as is deduced by balancing the forcing and the non-equilibrium term in (2.21). The fundamental wave interacts with them to produce a forcing of
$O(\tilde {\epsilon }^2\delta _c^{-2})$ as is deduced by balancing the forcing and the non-equilibrium term in (2.21). The fundamental wave interacts with them to produce a forcing of ![]() $O(\tilde {\epsilon }^3\delta _c^{-3})$ at cubic level, which regenerates an
$O(\tilde {\epsilon }^3\delta _c^{-3})$ at cubic level, which regenerates an ![]() $O(\tilde {\epsilon }^3\delta _c^{-4})$ streamwise velocity of the fundamental. If the latter is comparable to the
$O(\tilde {\epsilon }^3\delta _c^{-4})$ streamwise velocity of the fundamental. If the latter is comparable to the ![]() $O(\tilde {\epsilon }\tilde \mu )$ jump in the main layer, i.e. if
$O(\tilde {\epsilon }\tilde \mu )$ jump in the main layer, i.e. if ![]() $\tilde \mu =O(\tilde {\epsilon }^{2/5})$, the nonlinear effect enters the amplitude equation (Leib Reference Leib1991; Wu & Cowley Reference Wu and Cowley1995). Under this scaling the temperature fluctuation also contributes a nonlinear effect (Goldstein & Leib Reference Goldstein and Leib1989). Due to the resonant nature of the forcing, the
$\tilde \mu =O(\tilde {\epsilon }^{2/5})$, the nonlinear effect enters the amplitude equation (Leib Reference Leib1991; Wu & Cowley Reference Wu and Cowley1995). Under this scaling the temperature fluctuation also contributes a nonlinear effect (Goldstein & Leib Reference Goldstein and Leib1989). Due to the resonant nature of the forcing, the ![]() $O(\tilde \epsilon )$ radiating mode can be excited by a much weaker incident wave with the magnitude
$O(\tilde \epsilon )$ radiating mode can be excited by a much weaker incident wave with the magnitude
We then write
where ![]() $\lambda$ is the
$\lambda$ is the ![]() $O(1)$ Haberman parameter measuring the importance of the viscosity. The above relations form the basis of non-equilibrium critical-layer theory describing the interaction between the incident sound and the radiating mode.
$O(1)$ Haberman parameter measuring the importance of the viscosity. The above relations form the basis of non-equilibrium critical-layer theory describing the interaction between the incident sound and the radiating mode.
2.3.2. Equilibrium non-parallel regime
The equilibrium non-parallel regime is pertinent to the region where the length scale over which the growth rate varies is comparable to the length scale over which the amplitude evolves (Wu Reference Wu2005). This region is represented by
We take ![]() $\delta ^*$ to be the boundary-layer thickness at the neutral position, and with the latter being chosen to be origin of the coordinate we can set
$\delta ^*$ to be the boundary-layer thickness at the neutral position, and with the latter being chosen to be origin of the coordinate we can set ![]() $x_{3,n}=0$. Inspection of (2.21) shows that in this region the non-equilibrium effect,
$x_{3,n}=0$. Inspection of (2.21) shows that in this region the non-equilibrium effect, ![]() $\bar \mu =O(R^{-1/2})$, is much smaller than the viscous effect. The critical layer is thus of equilibrium type and viscosity dominated, having a width
$\bar \mu =O(R^{-1/2})$, is much smaller than the viscous effect. The critical layer is thus of equilibrium type and viscosity dominated, having a width ![]() $\delta _c=O(R^{-1/3})$. A similar scaling argument shows that the balance between the outer and inner jumps leads to
$\delta _c=O(R^{-1/3})$. A similar scaling argument shows that the balance between the outer and inner jumps leads to
Again noting the resonant nature of the forcing, we can infer that the radiating mode of ![]() $O(\bar \epsilon )$ can be excited by an incident sound wave with a much smaller magnitude
$O(\bar \epsilon )$ can be excited by an incident sound wave with a much smaller magnitude
The local mean velocity and temperature profiles can be approximated by
to the required order. With the key scalings identified, the effects of sound waves on the evolution of the radiating mode will be analysed in a self-consistent manner.
2.4. Existence of the radiating mode
For inviscid instability, the linearised Euler equations for instability modes can be reduced to the Rayleigh equation for the pressure
For a neutral radiating mode, the boundary condition consists of the impermeability condition at the wall and a finite amplitude at the infinity, namely, ![]() $\hat {p}_0^\prime (0)=0$ and
$\hat {p}_0^\prime (0)=0$ and ![]() $\hat {p}_0$ is bounded as
$\hat {p}_0$ is bounded as ![]() $y\rightarrow \infty$.
$y\rightarrow \infty$.
In order to find eigenvalues of the Rayleigh equation, it is convenient to write equation (2.29) in terms of the similarity valuable ![]() $\eta$ defined by (2.7) (in which
$\eta$ defined by (2.7) (in which ![]() $x_3=x_{3,n}=1$). The Rayleigh equation (2.29) becomes
$x_3=x_{3,n}=1$). The Rayleigh equation (2.29) becomes
where the derivative is with respect to ![]() $\eta$, and the boundary condition becomes
$\eta$, and the boundary condition becomes
More precisely, the wavenumber and phase velocity of the eigenmode must satisfy the condition, ![]() $\alpha ^2[1-M^2(1-c)^2]<0$, or equivalently,
$\alpha ^2[1-M^2(1-c)^2]<0$, or equivalently, ![]() $c<1-1/M$, so that the far-field behaviour of the mode takes the form of an outgoing wave
$c<1-1/M$, so that the far-field behaviour of the mode takes the form of an outgoing wave
where ![]() $\mathscr {C}_{\infty }$ is the normalisation factor, and
$\mathscr {C}_{\infty }$ is the normalisation factor, and ![]() $q=\sqrt {M^2(1-c)^2-1}$.
$q=\sqrt {M^2(1-c)^2-1}$.
Near the critical level ![]() $\eta _c$, where
$\eta _c$, where ![]() $\bar {U}(\eta _c)-c=0$, we seek solutions of Frobenius type to the Rayleigh equation. It can be shown that, as
$\bar {U}(\eta _c)-c=0$, we seek solutions of Frobenius type to the Rayleigh equation. It can be shown that, as ![]() $\bar {\eta }\equiv \eta -\eta _c\rightarrow 0$,
$\bar {\eta }\equiv \eta -\eta _c\rightarrow 0$,
where the constants ![]() ${\bar a}^\pm$ take different values above and below the critical level, and
${\bar a}^\pm$ take different values above and below the critical level, and
 \begin{gather} \bar\phi_a=\bar{\eta}^3+\frac{3}{4}\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\bar{\eta}^4+\frac{1}{10} \left[\frac{2\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}+\frac{3}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 +\alpha^2\bar{T}_c^2\right]\bar{\eta}^5+\cdots, \end{gather}
\begin{gather} \bar\phi_a=\bar{\eta}^3+\frac{3}{4}\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\bar{\eta}^4+\frac{1}{10} \left[\frac{2\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}+\frac{3}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 +\alpha^2\bar{T}_c^2\right]\bar{\eta}^5+\cdots, \end{gather}with
 \begin{align} \bar\chi &= \frac{\alpha^2\bar{T}_c^2}{4}\left[\frac{1}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -\frac{2}{3}\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}-\frac{\alpha^2}{2}\bar{T}_c^2 +\frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}+\left( \frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2\right] \nonumber\\ &\quad -\frac{M^2\alpha^2}{4}(\bar{U}_c^\prime)^2\bar{T}_c-\frac{11}{48}\alpha^2\bar{T}_c^2\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \left(\frac{2\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right). \end{align}
\begin{align} \bar\chi &= \frac{\alpha^2\bar{T}_c^2}{4}\left[\frac{1}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -\frac{2}{3}\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}-\frac{\alpha^2}{2}\bar{T}_c^2 +\frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}+\left( \frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2\right] \nonumber\\ &\quad -\frac{M^2\alpha^2}{4}(\bar{U}_c^\prime)^2\bar{T}_c-\frac{11}{48}\alpha^2\bar{T}_c^2\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \left(\frac{2\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right). \end{align}The analytical formula above supplements the numerical method to solve the eigenvalue problem, the details of which are relegated to Appendix A.1.
For the base-flow condition considered, we find a radiating mode with
and plot the corresponding eigenfunction in figure 2. As is shown, the radiating (supersonic) mode exhibits a wavy structure in the far field, in contrast to the subsonic mode which decays exponentially outside the boundary layer. This feature is closely related to the Mach wave radiation (Wu Reference Wu2005). The dependence of the radiating mode on the base-flow parameters is studied. The variation of the streamwise wavenumber and phase velocity of the neutral radiating mode with the Mach number ![]() $M$ for a fixed wall temperature
$M$ for a fixed wall temperature ![]() $\bar {T}_w=3$ is shown in figure 3. A radiating mode exists only in a small range of Mach number. Similarly, for a fixed Mach number (
$\bar {T}_w=3$ is shown in figure 3. A radiating mode exists only in a small range of Mach number. Similarly, for a fixed Mach number (![]() $M=6$), a radiating mode could only be found in a small range of the cooling ratio, as is shown in figure 4.
$M=6$), a radiating mode could only be found in a small range of the cooling ratio, as is shown in figure 4.

Figure 2. The eigenfunction of a two-dimensional supersonic mode: (a) ![]() $\hat {p}_0$ and (b)
$\hat {p}_0$ and (b) ![]() $\hat {p}_0^{\prime }$.
$\hat {p}_0^{\prime }$.

Figure 3. Variation of the wavenumber ![]() $\alpha$ (a) and the phase speed
$\alpha$ (a) and the phase speed ![]() $c$ (b) of the neutral radiating mode with the Mach number
$c$ (b) of the neutral radiating mode with the Mach number ![]() $M$ for a fixed wall temperature
$M$ for a fixed wall temperature ![]() $\bar {T}_w=3$ (
$\bar {T}_w=3$ (![]() $r_c=0.427$).
$r_c=0.427$).

Figure 4. Variation of the wavenumber ![]() $\alpha$ (a) and the phase speed
$\alpha$ (a) and the phase speed ![]() $c$ (b) of the neutral radiating mode with the cooling ratio
$c$ (b) of the neutral radiating mode with the cooling ratio ![]() $r_c$ for a fixed Mach number
$r_c$ for a fixed Mach number ![]() $M=6$.
$M=6$.
3. Reflection of impinging sound waves
In this section, we consider the reflection of an impinging slow acoustic wave by a supersonic boundary layer. The ensuing response is described by a double-layered structure consisting of the main layer and a critical layer, as is shown in figure 5.

Figure 5. A sketch of the reflection of sound waves by the boundary layer.
3.1. Main layer
In the main layer, where ![]() $y=O(1)$, the disturbance expands as
$y=O(1)$, the disturbance expands as
where ![]() $E_s=\exp ({\mathrm {i}\alpha _{s}(x-c_s t)})$, and the dependence on
$E_s=\exp ({\mathrm {i}\alpha _{s}(x-c_s t)})$, and the dependence on ![]() $x_3$ is parametric. Substitution of (3.1) into (2.2) followed by linearisation yields the equations
$x_3$ is parametric. Substitution of (3.1) into (2.2) followed by linearisation yields the equations
where the prime ‘![]() $\prime$’ in the base-flow quantities denotes the partial differentiation with respect to
$\prime$’ in the base-flow quantities denotes the partial differentiation with respect to ![]() $y$. Elimination of
$y$. Elimination of ![]() $\check \rho _s$,
$\check \rho _s$, ![]() $\check {u}_s$,
$\check {u}_s$, ![]() $\check {v}_s$ and
$\check {v}_s$ and ![]() $\check \theta _s$ leads to the compressible Rayleigh equation for pressure
$\check \theta _s$ leads to the compressible Rayleigh equation for pressure ![]() $\check {p}_s$
$\check {p}_s$
The above equation must be solved subject to the impermeability condition, ![]() $\check {p}_{s,y}(0)=0$, as implied by (3.2c). In the far field, the pressure takes the form
$\check {p}_{s,y}(0)=0$, as implied by (3.2c). In the far field, the pressure takes the form
which represents an incident wave and a reflected wave; here, ![]() $\gamma _{s}=\alpha _{s}\sqrt {M^2(1-c_s)^2-1}$, and
$\gamma _{s}=\alpha _{s}\sqrt {M^2(1-c_s)^2-1}$, and ![]() $\mathscr {R}$ is the reflection coefficient. The solution exhibits a singularity at the critical level
$\mathscr {R}$ is the reflection coefficient. The solution exhibits a singularity at the critical level ![]() $y_c(x_3)$, at which
$y_c(x_3)$, at which ![]() $\bar {U}(x_3, y_c)=c_s$. As
$\bar {U}(x_3, y_c)=c_s$. As ![]() $\tilde \eta \equiv y-y_c\rightarrow 0$, the local solution to (3.3) is constructed by using the Frobenius method as
$\tilde \eta \equiv y-y_c\rightarrow 0$, the local solution to (3.3) is constructed by using the Frobenius method as
where
 \begin{align} \phi_{sa} &=\tilde\eta^3+\chi_{sa}\tilde\eta^4 +\frac{1}{10}\left[3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 -\frac{3}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 \right. \nonumber\\ &\quad + \left.\frac{2\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime} -\frac{3\bar{T}_c^{\prime\prime}}{\bar{T}_c}+3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}\right)^2+\alpha_{s}^2\right]\tilde\eta^5+\cdots, \end{align}
\begin{align} \phi_{sa} &=\tilde\eta^3+\chi_{sa}\tilde\eta^4 +\frac{1}{10}\left[3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 -\frac{3}{2}\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 \right. \nonumber\\ &\quad + \left.\frac{2\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime} -\frac{3\bar{T}_c^{\prime\prime}}{\bar{T}_c}+3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}\right)^2+\alpha_{s}^2\right]\tilde\eta^5+\cdots, \end{align}with
 \begin{gather}\chi_{sb}=\frac{\alpha_{s}^2}{4}\left[ \frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}-\left( \frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2 +\frac{1}{2}\left( \frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -\frac{2}{3}\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}-\frac{M^2(\bar{U}_c^\prime)^2}{\bar{T}_c} -\frac{\alpha_{s}^2}{2}+\frac{11}{12}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2\right]. \end{gather}
\begin{gather}\chi_{sb}=\frac{\alpha_{s}^2}{4}\left[ \frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}-\left( \frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2 +\frac{1}{2}\left( \frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -\frac{2}{3}\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime}-\frac{M^2(\bar{U}_c^\prime)^2}{\bar{T}_c} -\frac{\alpha_{s}^2}{2}+\frac{11}{12}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2\right]. \end{gather}The pressure, velocities and temperature of the disturbance have the expressions
 \begin{align} \check{v}_s &=-\mathrm{i}\alpha_{s} b_s^\pm\frac{\bar{T}_c}{\bar{U}_c^\prime}\left[ 1- \left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\tilde\eta\ln|\tilde\eta| \right.\nonumber\\ &\quad \left.+\left(\frac{2}{3}\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{1}{6}\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} -\frac{3a_s^\pm}{\alpha_{s}^2b_s^\pm} \right)\tilde\eta \right]+O(\tilde\eta^2\ln|\tilde\eta|), \end{align}
\begin{align} \check{v}_s &=-\mathrm{i}\alpha_{s} b_s^\pm\frac{\bar{T}_c}{\bar{U}_c^\prime}\left[ 1- \left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\tilde\eta\ln|\tilde\eta| \right.\nonumber\\ &\quad \left.+\left(\frac{2}{3}\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{1}{6}\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} -\frac{3a_s^\pm}{\alpha_{s}^2b_s^\pm} \right)\tilde\eta \right]+O(\tilde\eta^2\ln|\tilde\eta|), \end{align}
Clearly, the temperature perturbation ![]() $\check \theta _s$ has a simple-pole singularity, while the streamwise velocity
$\check \theta _s$ has a simple-pole singularity, while the streamwise velocity ![]() $\check {u}_s$ exhibits a logarithmic singularity, indicating that the main-layer solution breaks down as
$\check {u}_s$ exhibits a logarithmic singularity, indicating that the main-layer solution breaks down as ![]() $\tilde \eta \rightarrow 0$. Thus we need to analyse the critical layer.
$\tilde \eta \rightarrow 0$. Thus we need to analyse the critical layer.
3.2. Critical layer
By balancing the advection and viscous terms in the momentum or energy equation, we find the critical-layer thickness ![]() $\delta =O(R^{-1/3})$. Then taking
$\delta =O(R^{-1/3})$. Then taking ![]() $\delta =R^{-1/3}$, we introduce an inner variable
$\delta =R^{-1/3}$, we introduce an inner variable
In view of the inner limit of the outer expansion (3.10a)–(3.10d), the inner expansion takes the form
At leading order, the ![]() $y$-momentum equation gives
$y$-momentum equation gives ![]() $P_{s0,Y}=0$, which implies
$P_{s0,Y}=0$, which implies ![]() $P_{s0}=P_{s0}(x_3)$. Matching with the main-layer solution leads to
$P_{s0}=P_{s0}(x_3)$. Matching with the main-layer solution leads to
The continuity, ![]() $x$-momentum and energy equations for the leading-order terms read
$x$-momentum and energy equations for the leading-order terms read ![]() $V_{s0,Y}=0$, and
$V_{s0,Y}=0$, and
respectively. The solution is found to be
It is found that the logarithm terms match their counterparts in the outer solution automatically. At the next order, the continuity and ![]() $x$-momentum equations yield
$x$-momentum equations yield
where ![]() $\bar {\mu }_c^\prime =(\textrm {d}\bar \mu /\textrm {d}\bar {T})|_{y=y_c}$, and the operator
$\bar {\mu }_c^\prime =(\textrm {d}\bar \mu /\textrm {d}\bar {T})|_{y=y_c}$, and the operator ![]() $\mathscr {L}_s$ is defined by
$\mathscr {L}_s$ is defined by
Eliminating ![]() $V_{s1}$ in the above two equations, and solving the resulting equation, the solution is found to be
$V_{s1}$ in the above two equations, and solving the resulting equation, the solution is found to be
 \begin{align} U_{s1,Y} &= \mathrm{i}\alpha_{s}\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{\mu}_c(1-Pr^{-1})}b_s\! \int_{0}^{\infty}\! [1-\exp(-(s_{sp}-s_s)\xi^3)]\nonumber\\ &\quad \times\exp(-s_s\xi^3-\mathrm{i}\alpha_{s}\bar{U}_c^\prime Y\xi)\,{\rm d}\xi \nonumber\\ &\quad -\mathrm{i}\alpha_{s}\bar{T}_c\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)b_s\! \int_{0}^{\infty} \!\exp(-s_s\xi^3-\mathrm{i}\alpha_{s}\bar{U}_c^\prime Y\xi)\,{\rm d}\xi, \end{align}
\begin{align} U_{s1,Y} &= \mathrm{i}\alpha_{s}\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{\mu}_c(1-Pr^{-1})}b_s\! \int_{0}^{\infty}\! [1-\exp(-(s_{sp}-s_s)\xi^3)]\nonumber\\ &\quad \times\exp(-s_s\xi^3-\mathrm{i}\alpha_{s}\bar{U}_c^\prime Y\xi)\,{\rm d}\xi \nonumber\\ &\quad -\mathrm{i}\alpha_{s}\bar{T}_c\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)b_s\! \int_{0}^{\infty} \!\exp(-s_s\xi^3-\mathrm{i}\alpha_{s}\bar{U}_c^\prime Y\xi)\,{\rm d}\xi, \end{align}
where ![]() $s_s={\frac {1}{3}}(\alpha _{s}\bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c$. Matching
$s_s={\frac {1}{3}}(\alpha _{s}\bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c$. Matching ![]() $U_{s1}$ with its outer counterpart (3.10c) determines the jump
$U_{s1}$ with its outer counterpart (3.10c) determines the jump
This jump is used together with the numerical method to obtain the reflection coefficient and boundary-layer response; the details are described in Appendix A.2.
3.3. The reflection coefficient and boundary-layer response
For each incident wave, we compute ![]() $\mathscr {R}$ and
$\mathscr {R}$ and ![]() $\tilde {b}$, where
$\tilde {b}$, where ![]() $\tilde {b}$, introduced in (A16) as the ratio of the pressure amplitude in the critical layer to the amplitude of the incident wave, is a measure of the boundary-layer response. For the particular incident wave satisfying the resonant condition,
$\tilde {b}$, introduced in (A16) as the ratio of the pressure amplitude in the critical layer to the amplitude of the incident wave, is a measure of the boundary-layer response. For the particular incident wave satisfying the resonant condition, ![]() $(\alpha _{s},c_s)=(0.355,0.723)$, it is found that
$(\alpha _{s},c_s)=(0.355,0.723)$, it is found that ![]() $\mathscr {R}=1.299\times 10^{7}+5.140\times 10^{7}\mathrm {i}$ and
$\mathscr {R}=1.299\times 10^{7}+5.140\times 10^{7}\mathrm {i}$ and ![]() $\tilde {b}=5.725\times 10^{7}-7.032\times 10^{6}\mathrm {i}$. They are numerically large, indeed practically infinite, indicating that the resonant over-reflection coincides with the onset of a neutral radiating mode.
$\tilde {b}=5.725\times 10^{7}-7.032\times 10^{6}\mathrm {i}$. They are numerically large, indeed practically infinite, indicating that the resonant over-reflection coincides with the onset of a neutral radiating mode.
Recalling that ![]() $\omega _s=\alpha _{s} c_s$ and (2.15), we can regard
$\omega _s=\alpha _{s} c_s$ and (2.15), we can regard ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ as functions of
$|\tilde {b}|$ as functions of ![]() $\theta _s$ and
$\theta _s$ and ![]() $\omega _s$. Figure 6(a,b) shows contours of
$\omega _s$. Figure 6(a,b) shows contours of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ in the
$|\tilde {b}|$ in the ![]() $\theta _s$–
$\theta _s$–![]() $\omega _s$ plane with increments
$\omega _s$ plane with increments ![]() ${\rm \Delta} \theta _s=0.1$ and
${\rm \Delta} \theta _s=0.1$ and ![]() ${\rm \Delta} \omega _s=10^{-3}$. For most frequencies and incident angles, the boundary-layer response
${\rm \Delta} \omega _s=10^{-3}$. For most frequencies and incident angles, the boundary-layer response ![]() $|\tilde {b}|$ is finite and indeed rather small, while the reflection coefficient remains almost unchanged around the value of unity, indicating that these reflected acoustic waves have roughly the same magnitude as that of incident ones, and the boundary layer does not play a role in the reflection process. A prominent feature is that there appear two long strips indicating a very steep gradient, one of which passes through the resonant point (52.987, 0.257), where the response becomes infinite. The reflection coefficient increases rapidly when approaching either of the two strips. To show further details of the strips, we compute contours of two small regions in the lower strip using a smaller increment, and the results are displayed in figure 6(c,e). The reflection coefficient soars to very large values for a narrow frequency band, resulting in elongated contours enclosing the resonant point. Strong over-reflection occurs for
$|\tilde {b}|$ is finite and indeed rather small, while the reflection coefficient remains almost unchanged around the value of unity, indicating that these reflected acoustic waves have roughly the same magnitude as that of incident ones, and the boundary layer does not play a role in the reflection process. A prominent feature is that there appear two long strips indicating a very steep gradient, one of which passes through the resonant point (52.987, 0.257), where the response becomes infinite. The reflection coefficient increases rapidly when approaching either of the two strips. To show further details of the strips, we compute contours of two small regions in the lower strip using a smaller increment, and the results are displayed in figure 6(c,e). The reflection coefficient soars to very large values for a narrow frequency band, resulting in elongated contours enclosing the resonant point. Strong over-reflection occurs for ![]() $(\theta _s,\omega _s)$ in the strips. Similarly,
$(\theta _s,\omega _s)$ in the strips. Similarly, ![]() $|\tilde {b}|$ acquires large values in the strips, as is shown by figure 6(b) and the enlarged views of the two selected zones (figure 6d,f). These imply that the incident wave facilitates transfer of a considerable amount of energy from the shear flow while the reflected wave absorbs a significant amount from it.
$|\tilde {b}|$ acquires large values in the strips, as is shown by figure 6(b) and the enlarged views of the two selected zones (figure 6d,f). These imply that the incident wave facilitates transfer of a considerable amount of energy from the shear flow while the reflected wave absorbs a significant amount from it.

Figure 6. Contours of ![]() $|\mathscr {R}|$ (a) and
$|\mathscr {R}|$ (a) and ![]() $|\tilde {b}|$ (b) in the
$|\tilde {b}|$ (b) in the ![]() $\theta _s$–
$\theta _s$–![]() $\omega _s$ plane. The resonant point is located at (52.987, 0.257). (c,d) Zoom into the range
$\omega _s$ plane. The resonant point is located at (52.987, 0.257). (c,d) Zoom into the range ![]() $39<\theta _s<41$. (e,f) Zoom into the range
$39<\theta _s<41$. (e,f) Zoom into the range ![]() $61.2<\theta _s<61.6$.
$61.2<\theta _s<61.6$.
To show further the dependence of the boundary-layer response on the parameters, we plot the variations of the reflection coefficient ![]() $|\mathscr {R}|$ and response
$|\mathscr {R}|$ and response ![]() $|\tilde {b}|$ with frequency
$|\tilde {b}|$ with frequency ![]() $\omega _s$ at different incident angles. Figure 7(a,b) depicts the variations of
$\omega _s$ at different incident angles. Figure 7(a,b) depicts the variations of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ with
$|\tilde {b}|$ with ![]() $\omega _s$ at
$\omega _s$ at ![]() $\theta _s=40^{\circ }$, respectively. Two sharp peaks appear at
$\theta _s=40^{\circ }$, respectively. Two sharp peaks appear at ![]() $\omega _s=0.233$ and
$\omega _s=0.233$ and ![]() $0.614$, which lie in the strips in the contours. In order to determine the nature of these peak values, calculations of the variations near the peaks are performed. The panels in figure 7(a,b) zoom into the range near
$0.614$, which lie in the strips in the contours. In order to determine the nature of these peak values, calculations of the variations near the peaks are performed. The panels in figure 7(a,b) zoom into the range near ![]() $\omega _s=0.233$ and
$\omega _s=0.233$ and ![]() $0.614$. The sharp peaks turn out to be finite in these ranges. The peak values in the upper strip (the zoomed views near
$0.614$. The sharp peaks turn out to be finite in these ranges. The peak values in the upper strip (the zoomed views near ![]() $\omega _s=0.614$) are markedly smaller than those in the lower strip (the zoomed views near
$\omega _s=0.614$) are markedly smaller than those in the lower strip (the zoomed views near ![]() $\omega _s=0.233$). Notably, the frequency range over which the peak varies in the upper strip is of
$\omega _s=0.233$). Notably, the frequency range over which the peak varies in the upper strip is of ![]() $O(10^{-4})$, which is much smaller than
$O(10^{-4})$, which is much smaller than ![]() $O(10^{-3})$ in the lower strip. Figure 7(c,d) plots the variations of
$O(10^{-3})$ in the lower strip. Figure 7(c,d) plots the variations of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ with
$|\tilde {b}|$ with ![]() $\omega _s$ at
$\omega _s$ at ![]() $\theta _s=52.987^{\circ }$, which is the resonant angle. Two sharp peaks at
$\theta _s=52.987^{\circ }$, which is the resonant angle. Two sharp peaks at ![]() $\omega _s=0.257$ and
$\omega _s=0.257$ and ![]() $0.702$ are observed. As
$0.702$ are observed. As ![]() $\omega _s$ approaches
$\omega _s$ approaches ![]() $0.257$ (the resonant frequency),
$0.257$ (the resonant frequency), ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ become unbounded as is shown by enlarged views near
$|\tilde {b}|$ become unbounded as is shown by enlarged views near ![]() $\omega _s=0.257$, signalling the onset of resonance, while the zoomed views near
$\omega _s=0.257$, signalling the onset of resonance, while the zoomed views near ![]() $\omega _s=0.702$ show the abrupt rise of
$\omega _s=0.702$ show the abrupt rise of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ to their peak values in the upper strip. Figure 7(e,f) shows the variations of
$|\tilde {b}|$ to their peak values in the upper strip. Figure 7(e,f) shows the variations of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ with
$|\tilde {b}|$ with ![]() $\omega _s$ at
$\omega _s$ at ![]() $\theta _s=61.4^{\circ }$. The patterns resemble those at
$\theta _s=61.4^{\circ }$. The patterns resemble those at ![]() $\theta _s=40^{\circ }$.
$\theta _s=40^{\circ }$.

Figure 7. Variations of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ with
$|\tilde {b}|$ with ![]() $\omega _{s}$ at
$\omega _{s}$ at ![]() $\theta _s=40^{\circ }$ (a,b),
$\theta _s=40^{\circ }$ (a,b), ![]() $52.987^{\circ }$ (c,d) and
$52.987^{\circ }$ (c,d) and ![]() $61.4^{\circ }$ (e,f).
$61.4^{\circ }$ (e,f).
4. Fundamental resonance
It was demonstrated in the previous section that, for the acoustic wave satisfying the resonant condition, resonant over-reflection takes place, with the reflected wave coinciding with a neutral radiating mode. We considered the response of the boundary layer at a fixed location to impinging waves of different frequencies and incident angles. In this setting, the resonance occurs for a specific pairing of ![]() $\omega _s$ and
$\omega _s$ and ![]() $\theta _s$. An alternative view is to consider the response of the boundary layer at different
$\theta _s$. An alternative view is to consider the response of the boundary layer at different ![]() $x_3$ to the same incident wave with a fixed
$x_3$ to the same incident wave with a fixed ![]() $\omega _s$ and
$\omega _s$ and ![]() $\theta _s$, and then the resonance takes place at a streamwise location
$\theta _s$, and then the resonance takes place at a streamwise location ![]() $x_{3,s}$. In the vicinity of this position, the reflected wave evolves in the streamwise direction into the radiating mode. The generation and evolution of such a mode will be explored in this section. The excitation process is similar to the receptivity of T-S waves studied in Qin & Wu (Reference Qin and Wu2016), but the difference is that the present radiating mode is of inviscid nature and on the upper (right) branch of the neutral curve, and thus has a critical layer, which is sensitive to nonlinear effects. The radiating mode locally excited is likely to develop nonlinearly on a relatively short length scale. Another fact is that a non-neutral radiating mode is likely to be present upstream of the resonance location, and when approaching the resonant (neutral) position, it is likely to have acquired, through the accumulated growth, a large enough amplitude to become nonlinear (Leib Reference Leib1991; Wu Reference Wu2019), while it is also influenced substantially by the incident sound. For locally excited and pre-existing radiating modes, the direct effect of the impinging sound can be accounted for by an appropriate amplitude equation of the mode, which is to be derived. Depending on the intensity of the acoustic wave, the critical-layer dynamics may be different. The excitation and evolution of the radiating mode in both the non-equilibrium parallel and equilibrium non-parallel regimes will be analysed in the following.
$x_{3,s}$. In the vicinity of this position, the reflected wave evolves in the streamwise direction into the radiating mode. The generation and evolution of such a mode will be explored in this section. The excitation process is similar to the receptivity of T-S waves studied in Qin & Wu (Reference Qin and Wu2016), but the difference is that the present radiating mode is of inviscid nature and on the upper (right) branch of the neutral curve, and thus has a critical layer, which is sensitive to nonlinear effects. The radiating mode locally excited is likely to develop nonlinearly on a relatively short length scale. Another fact is that a non-neutral radiating mode is likely to be present upstream of the resonance location, and when approaching the resonant (neutral) position, it is likely to have acquired, through the accumulated growth, a large enough amplitude to become nonlinear (Leib Reference Leib1991; Wu Reference Wu2019), while it is also influenced substantially by the incident sound. For locally excited and pre-existing radiating modes, the direct effect of the impinging sound can be accounted for by an appropriate amplitude equation of the mode, which is to be derived. Depending on the intensity of the acoustic wave, the critical-layer dynamics may be different. The excitation and evolution of the radiating mode in both the non-equilibrium parallel and equilibrium non-parallel regimes will be analysed in the following.
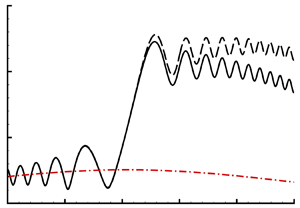
We note that nonlinear evolution and excitation were simultaneously included in the work by Hall & Smith (Reference Hall and Smith1982) on the T-S mode in an incompressible boundary layer forced by a moving wavy wall. There the focus was on the vicinity of the lower-branch neutral curve. Since the T-S wave upstream experiences considerable decay, the nonlinearity effect is associated with the locally excited mode, and is expected to be significant only if the external forcing is sufficiently strong.
4.1. Non-equilibrium parallel regime
The scaling argument in § 2.3.1 shows that the radiating mode evolves nonlinearly with the rate ![]() $\tilde \mu =\tilde {\epsilon }^{2/5}$ when its amplitude
$\tilde \mu =\tilde {\epsilon }^{2/5}$ when its amplitude ![]() $\tilde \epsilon =O(R^{-5/6})$, and such a mode may be excited and/or affected by the incident sound of a much smaller magnitude
$\tilde \epsilon =O(R^{-5/6})$, and such a mode may be excited and/or affected by the incident sound of a much smaller magnitude ![]() $\tilde {\epsilon }_s=\tilde {\epsilon }\tilde \mu =O(R^{-7/6})$ due to resonance. Detuning effects may be included by allowing the wavenumber of the sound to differ from that of the radiating mode by an
$\tilde {\epsilon }_s=\tilde {\epsilon }\tilde \mu =O(R^{-7/6})$ due to resonance. Detuning effects may be included by allowing the wavenumber of the sound to differ from that of the radiating mode by an ![]() $O(\tilde \mu )$ amount, that is,
$O(\tilde \mu )$ amount, that is,
where ![]() $\tilde \alpha _d$ is an
$\tilde \alpha _d$ is an ![]() $O(1)$ detuning parameter.
$O(1)$ detuning parameter.
4.1.1. Main layer
In the main layer, the disturbance expands as
where ![]() $E=\exp ({\mathrm {i}\alpha (x-ct)})$ is the carrier wave, and the first term represents a radiating mode, which may be locally excited and/or propagates from upstream with
$E=\exp ({\mathrm {i}\alpha (x-ct)})$ is the carrier wave, and the first term represents a radiating mode, which may be locally excited and/or propagates from upstream with ![]() $\tilde {A}(\tilde {x})$ being its amplitude function. Substitution of (4.2) into (2.2) followed by linearisation yields the leading-order equations for the disturbance
$\tilde {A}(\tilde {x})$ being its amplitude function. Substitution of (4.2) into (2.2) followed by linearisation yields the leading-order equations for the disturbance
Elimination of ![]() $\hat {\rho }_0$,
$\hat {\rho }_0$, ![]() $\hat {u}_0$,
$\hat {u}_0$, ![]() $\hat {v}_0$ and
$\hat {v}_0$ and ![]() $\hat {\theta }_0$ leads to the familiar compressible Rayleigh equation (2.29) for the leading-order pressure
$\hat {\theta }_0$ leads to the familiar compressible Rayleigh equation (2.29) for the leading-order pressure ![]() $\hat {p}_0$. As
$\hat {p}_0$. As ![]() $y\rightarrow \infty$,
$y\rightarrow \infty$,
which represents an outgoing wave that persists away from the main layer. Here, ![]() $\mathscr {C}_{\infty }$ is a constant that is determined by normalisation of the eigenfunction.
$\mathscr {C}_{\infty }$ is a constant that is determined by normalisation of the eigenfunction.
Let ![]() $\hat {\eta }\equiv y-y_c\rightarrow 0$, the solution near the critical level
$\hat {\eta }\equiv y-y_c\rightarrow 0$, the solution near the critical level ![]() $y_c$ is obtained using the Frobenius method as
$y_c$ is obtained using the Frobenius method as
where ![]() $\phi _a$ and
$\phi _a$ and ![]() $\phi _b$ have the same expressions as
$\phi _b$ have the same expressions as ![]() $\phi _{sa}$ and
$\phi _{sa}$ and ![]() $\phi _{sb}$ given by (3.6) and (3.7), respectively, with
$\phi _{sb}$ given by (3.6) and (3.7), respectively, with ![]() $\alpha$ replacing
$\alpha$ replacing ![]() $\alpha _{s}$. It follows from (4.3b)–(4.3d) that, as
$\alpha _{s}$. It follows from (4.3b)–(4.3d) that, as ![]() $\hat {\eta }\rightarrow 0$,
$\hat {\eta }\rightarrow 0$,
The temperature perturbation exhibits the same simple-pole singularity as that of an inflectional mode (Goldstein & Leib Reference Goldstein and Leib1989), while the logarithmic singularity is present only for a supersonic mode, whose critical level does not correspond to the generalised inflection point (Leib Reference Leib1991). Equation (4.6) indicates a jump of ![]() $\hat {u}_0$
$\hat {u}_0$
At the next order, the second terms in the expansion (4.2), ![]() $(\hat {\rho }_1, \hat {u}_1, \hat {v}_1, \hat {p}_1, \hat {\theta }_1)$, are found to satisfy the inhomogeneous version of (4.3a)–(4.3e) (Qin Reference Qin2024). By eliminating
$(\hat {\rho }_1, \hat {u}_1, \hat {v}_1, \hat {p}_1, \hat {\theta }_1)$, are found to satisfy the inhomogeneous version of (4.3a)–(4.3e) (Qin Reference Qin2024). By eliminating ![]() $\hat {\rho }_1$,
$\hat {\rho }_1$, ![]() $\hat {u}_1$,
$\hat {u}_1$, ![]() $\hat {v}_1$ and
$\hat {v}_1$ and ![]() $\hat {\theta }_1$ from those equations, we can show that
$\hat {\theta }_1$ from those equations, we can show that ![]() $\hat {p}_1$ satisfies an inhomogeneous Rayleigh equation (Wu Reference Wu2005; Qin Reference Qin2024)
$\hat {p}_1$ satisfies an inhomogeneous Rayleigh equation (Wu Reference Wu2005; Qin Reference Qin2024)
where we have put
 \begin{align} \varDelta_1 &=
\biggl\{\frac{2\bar{U}^\prime}{\bar{U}-c}\biggl(\frac{\bar{U}_1}{\bar{U}-c}-
\frac{\bar{U}_1^\prime}{\bar{U}^\prime}\biggr)+\frac{\bar{T}^\prime}{\bar{T}}\biggl(
\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-
\frac{\bar{T}_1}{\bar{T}} \biggr) \biggr\}\hat{p}_0^\prime
\nonumber\\ &\quad +\alpha^2
M^2\frac{(\bar{U}-c)^2}{\bar{T}}\left(
\frac{2\bar{U}_1}{\bar{U}-c}-\frac{\bar{T}_1}{\bar{T}}
\right)\hat{p}_0. \end{align}
\begin{align} \varDelta_1 &=
\biggl\{\frac{2\bar{U}^\prime}{\bar{U}-c}\biggl(\frac{\bar{U}_1}{\bar{U}-c}-
\frac{\bar{U}_1^\prime}{\bar{U}^\prime}\biggr)+\frac{\bar{T}^\prime}{\bar{T}}\biggl(
\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-
\frac{\bar{T}_1}{\bar{T}} \biggr) \biggr\}\hat{p}_0^\prime
\nonumber\\ &\quad +\alpha^2
M^2\frac{(\bar{U}-c)^2}{\bar{T}}\left(
\frac{2\bar{U}_1}{\bar{U}-c}-\frac{\bar{T}_1}{\bar{T}}
\right)\hat{p}_0. \end{align}
As ![]() $y\rightarrow \infty$, the incident acoustic wave must be included in the far-field boundary condition, which reads
$y\rightarrow \infty$, the incident acoustic wave must be included in the far-field boundary condition, which reads
 \begin{align} \hat{p}_1 &\sim p_I\exp({\mathrm{i}\tilde\alpha_d\tilde{x}})[\exp({\mathrm{i}\alpha q y}) +\hat{\mathscr{R}}(\tilde{x})\exp({-\mathrm{i}\alpha q y})] \nonumber\\ &\quad +q^{-1}[1-M^2(1-c)]\mathscr{C}_{\infty}\tilde{A}^\prime y\exp({-\mathrm{i}\alpha q y}). \end{align}
\begin{align} \hat{p}_1 &\sim p_I\exp({\mathrm{i}\tilde\alpha_d\tilde{x}})[\exp({\mathrm{i}\alpha q y}) +\hat{\mathscr{R}}(\tilde{x})\exp({-\mathrm{i}\alpha q y})] \nonumber\\ &\quad +q^{-1}[1-M^2(1-c)]\mathscr{C}_{\infty}\tilde{A}^\prime y\exp({-\mathrm{i}\alpha q y}). \end{align}
On the other hand, by the method of dominant balance we deduce that, as ![]() $y\rightarrow y_c$,
$y\rightarrow y_c$,
 \begin{align} \hat{p}_1 &\sim \frac{\alpha^2}{\bar{T}_c}\left( \frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A} \right) \left\{ \hat{\eta}-\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\hat{\eta}^2\ln|\hat{\eta}| \right.\nonumber\\ &\quad \left.-\left[ a^{{\pm}}+\frac{1}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \right]\hat{\eta}^2 +\frac{1}{3}j\hat{\eta}^3\ln|\hat{\eta}| \right\}+\frac{\bar{U}_c^\prime}{\bar{T}_c}(\mathrm{i}\alpha \tilde{A}^\prime)\hat{\eta}^2 \nonumber\\ &\quad +\left( \frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x}_1 \tilde{A} \right)j_1\hat{\eta}^3\ln|\hat{\eta}| +c^{{\pm}}\phi_a +d\left[ \phi_b+\frac{\alpha^2}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\ln|\hat{\eta}|\phi_a \right], \end{align}
\begin{align} \hat{p}_1 &\sim \frac{\alpha^2}{\bar{T}_c}\left( \frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A} \right) \left\{ \hat{\eta}-\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\hat{\eta}^2\ln|\hat{\eta}| \right.\nonumber\\ &\quad \left.-\left[ a^{{\pm}}+\frac{1}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \right]\hat{\eta}^2 +\frac{1}{3}j\hat{\eta}^3\ln|\hat{\eta}| \right\}+\frac{\bar{U}_c^\prime}{\bar{T}_c}(\mathrm{i}\alpha \tilde{A}^\prime)\hat{\eta}^2 \nonumber\\ &\quad +\left( \frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x}_1 \tilde{A} \right)j_1\hat{\eta}^3\ln|\hat{\eta}| +c^{{\pm}}\phi_a +d\left[ \phi_b+\frac{\alpha^2}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\ln|\hat{\eta}|\phi_a \right], \end{align}
where ![]() $c^{\pm }$ and
$c^{\pm }$ and ![]() $d$ are arbitrary functions of
$d$ are arbitrary functions of ![]() $\tilde {x}$, and the constants,
$\tilde {x}$, and the constants, ![]() $j$ and
$j$ and ![]() $j_1$, have the expressions
$j_1$, have the expressions
 \begin{gather} j=\frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime} -\left(\frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2 +\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 +3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -2\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\frac{\bar{U}_c^\prime}{\bar{U}_c}, \end{gather}
\begin{gather} j=\frac{\bar{T}_c^{\prime\prime}}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime\prime}}{\bar{U}_c^\prime} -\left(\frac{\bar{T}_c^\prime}{\bar{T}_c} \right)^2 +\left(\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 +3\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2 -2\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\frac{\bar{U}_c^\prime}{\bar{U}_c}, \end{gather} It follows from the ![]() $x$- and
$x$- and ![]() $y$-momentum equations that
$y$-momentum equations that
Thus, the jump of ![]() $\hat {u}_1$ is found to relate to
$\hat {u}_1$ is found to relate to ![]() $(c^+ - c^-)$ by the equation
$(c^+ - c^-)$ by the equation
In order for the inhomogeneous equation (4.10) to have an acceptable solution, it has to satisfy a solvability condition. This can be derived by multiplying both sides of (4.10) by ![]() $\hat {p}_0\bar {T}/(\bar {U}-c)^2$ and integrating from
$\hat {p}_0\bar {T}/(\bar {U}-c)^2$ and integrating from ![]() $0$ to
$0$ to ![]() $\infty$, leading to
$\infty$, leading to
where use has been made of the impermeability condition ![]() $\hat {p}_0^\prime (0)=\hat {p}_{1,y}|_{y=0}=0$, and
$\hat {p}_0^\prime (0)=\hat {p}_{1,y}|_{y=0}=0$, and
 \begin{align} I_1 &= \int_{0}^{\infty}
\biggl\{\biggl[\frac{2\bar{U}^\prime}{\bar{U}-c}
\biggl(\frac{\bar{U}_1}{\bar{U}-c}-\frac{\bar{U}_1^\prime}{\bar{U}^\prime}
\biggr) +\frac{\bar{T}^\prime}{\bar{T}}
\biggl(\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-\frac{\bar{T}_1}{\bar{T}}
\biggr)\biggr]
\frac{\bar{T}\hat{p}_0\hat{p}_0^\prime}{(\bar{U}-c)^2} \nonumber\\ &\quad
\vphantom{\left[\frac{2\bar{U}^\prime}{\bar{U}-c}
\left(\frac{\bar{U}_1}{\bar{U}-c}-\frac{\bar{U}_1^\prime}{\bar{U}^\prime}
\right) +\frac{\bar{T}^\prime}{\bar{T}}
\left(\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-\frac{\bar{T}_1}{\bar{T}}
\right)\right]}
+\alpha^2M^2\left(\frac{2\bar{U}_1}{\bar{U}-c}-\frac{\bar{T}_1}{\bar{T}}\right)
\hat{p}_0^2\biggr\}{\rm d} y,
\end{align}
\begin{align} I_1 &= \int_{0}^{\infty}
\biggl\{\biggl[\frac{2\bar{U}^\prime}{\bar{U}-c}
\biggl(\frac{\bar{U}_1}{\bar{U}-c}-\frac{\bar{U}_1^\prime}{\bar{U}^\prime}
\biggr) +\frac{\bar{T}^\prime}{\bar{T}}
\biggl(\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-\frac{\bar{T}_1}{\bar{T}}
\biggr)\biggr]
\frac{\bar{T}\hat{p}_0\hat{p}_0^\prime}{(\bar{U}-c)^2} \nonumber\\ &\quad
\vphantom{\left[\frac{2\bar{U}^\prime}{\bar{U}-c}
\left(\frac{\bar{U}_1}{\bar{U}-c}-\frac{\bar{U}_1^\prime}{\bar{U}^\prime}
\right) +\frac{\bar{T}^\prime}{\bar{T}}
\left(\frac{\bar{T}_1^\prime}{\bar{T}^\prime}-\frac{\bar{T}_1}{\bar{T}}
\right)\right]}
+\alpha^2M^2\left(\frac{2\bar{U}_1}{\bar{U}-c}-\frac{\bar{T}_1}{\bar{T}}\right)
\hat{p}_0^2\biggr\}{\rm d} y,
\end{align}
It should be noted that both sides of (4.18) contain singular terms, which turn out to be of the same form, and hence are cancelled out in such a manner that the integrals ![]() $I_1$ and
$I_1$ and ![]() $I_2$ are interpreted as Hadamard finite parts. By applying the far-field condition (4.4) and (4.12), we obtain
$I_2$ are interpreted as Hadamard finite parts. By applying the far-field condition (4.4) and (4.12), we obtain
 \begin{align} & \frac{1}{\bar{U}_c^\prime}\left\{ 3(c^+-c^-)-\frac{2\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A} \right) \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)(a^+-a^-) -\alpha^2 d(a^+-a^-) \right\} \nonumber\\ &\quad -\frac{2\mathrm{i}\alpha q\mathscr{C}_{\infty}}{(1-c)^2}p_I\exp({\mathrm{i}\tilde\alpha_d\tilde{x}}) =-\left(\frac{2\mathrm{i} c}{\alpha}I_2 \tilde{A}^\prime-I_1\bar{x}_1 \tilde{A}\right). \end{align}
\begin{align} & \frac{1}{\bar{U}_c^\prime}\left\{ 3(c^+-c^-)-\frac{2\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A} \right) \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)(a^+-a^-) -\alpha^2 d(a^+-a^-) \right\} \nonumber\\ &\quad -\frac{2\mathrm{i}\alpha q\mathscr{C}_{\infty}}{(1-c)^2}p_I\exp({\mathrm{i}\tilde\alpha_d\tilde{x}}) =-\left(\frac{2\mathrm{i} c}{\alpha}I_2 \tilde{A}^\prime-I_1\bar{x}_1 \tilde{A}\right). \end{align}
The jumps ![]() $(a^+-a^-)$ and
$(a^+-a^-)$ and ![]() $(c^+-c^-)$ will be determined by analysing the critical-layer dynamics.
$(c^+-c^-)$ will be determined by analysing the critical-layer dynamics.
4.1.2. Critical layer
The singularity of the main-layer solution is to be removed by introducing the non-equilibrium and viscous effects within the critical layer, which determine the critical-layer width to be ![]() $O(\tilde {\epsilon }^{2/5})$, and so the appropriate local transverse coordinate is
$O(\tilde {\epsilon }^{2/5})$, and so the appropriate local transverse coordinate is
The asymptote of the inviscid solution, (4.5) and (4.6)–(4.8), suggests that the perturbation in the critical layer expands as
Strictly speaking, the expansions actually contain logarithm terms, but they are not needed in the calculation of the jumps and hence are not written out for brevity. Substituting (4.23) into (2.2), we then obtain the equations governing the terms at different orders in the expansion.
At leading order, inspection of the ![]() $x$- and
$x$- and ![]() $y$-momentum equations gives
$y$-momentum equations gives
Expansion of the energy equation shows that
with the operator ![]() $\mathscr {L}_p$ being defined by
$\mathscr {L}_p$ being defined by
Equation (4.25) is solved by use of Fourier transform to give
where we have put ![]() $\bar {Y}\equiv Y+(\bar {U}_{1c}/\bar {U}_c^\prime )\bar {x}_1$ and
$\bar {Y}\equiv Y+(\bar {U}_{1c}/\bar {U}_c^\prime )\bar {x}_1$ and ![]() $s_p={\frac {1}{3}}\lambda (\alpha \bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c Pr^{-1}$.
$s_p={\frac {1}{3}}\lambda (\alpha \bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c Pr^{-1}$.
At the next order, expansion of the continuity and ![]() $x$-momentum equations yields
$x$-momentum equations yields
where ![]() $\mathscr {L}_\mu$ is the same as
$\mathscr {L}_\mu$ is the same as ![]() $\mathscr {L}_p$ provided that
$\mathscr {L}_p$ provided that ![]() $Pr$ is set to unity. The above two equations can be combined to obtain an equation for
$Pr$ is set to unity. The above two equations can be combined to obtain an equation for ![]() $U_{1,Y}$, which is solved to give
$U_{1,Y}$, which is solved to give
 \begin{align} U_{1,Y} &= \mathrm{i}\alpha\bar{U}_c^\prime\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{T}_c\bar{\mu}_c(1-Pr^{-1})} \int_{0}^{\infty} [1-\exp({-(s_p-s)\xi^3})] \nonumber\\ &\quad \times\exp(-s\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi)\tilde{A}(\tilde{x}-c\xi)\,{\rm d}\xi \nonumber\\ &\quad -\mathrm{i}\alpha\bar{U}_c^\prime\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \int_{0}^{\infty} \exp(-s\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi)\tilde{A}(\tilde{x}-c\xi)\,{\rm d}\xi, \end{align}
\begin{align} U_{1,Y} &= \mathrm{i}\alpha\bar{U}_c^\prime\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{T}_c\bar{\mu}_c(1-Pr^{-1})} \int_{0}^{\infty} [1-\exp({-(s_p-s)\xi^3})] \nonumber\\ &\quad \times\exp(-s\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi)\tilde{A}(\tilde{x}-c\xi)\,{\rm d}\xi \nonumber\\ &\quad -\mathrm{i}\alpha\bar{U}_c^\prime\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \int_{0}^{\infty} \exp(-s\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi)\tilde{A}(\tilde{x}-c\xi)\,{\rm d}\xi, \end{align}
where ![]() $s={\frac {1}{3}}\lambda (\alpha \bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c$. Matching
$s={\frac {1}{3}}\lambda (\alpha \bar {U}_c^\prime )^2\bar {T}_c\bar {\mu }_c$. Matching ![]() $U_1$ with its outer counterpart determines the jump
$U_1$ with its outer counterpart determines the jump
The self-interaction of the fundamental mode at quadratic level generates a mean-flow distortion, which interacts in turn with the fundamental at cubic level. The analysis is presented in Appendix B. The key outcome is the nonlinear jump (B8). Inserting the jumps (4.30) and (B8) into (4.21), we obtain the evolution equation for the amplitude function ![]() $\tilde {A}$ (cf. Leib Reference Leib1991)
$\tilde {A}$ (cf. Leib Reference Leib1991)
 \begin{align} \tilde{A}^\prime(\tilde{x}) &= \sigma\bar{x}_1 \tilde{A}+\varUpsilon\!\int_{0}^{\infty} \!\!\!\int_{0}^{\infty}\! K(\xi,\eta)\tilde{A}(\tilde{x}-c\xi) \tilde{A}(\tilde{x}-c\xi-c\eta)\tilde{A}^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\tilde{F}\exp({\mathrm{i}\tilde\alpha_d\tilde{x}}), \end{align}
\begin{align} \tilde{A}^\prime(\tilde{x}) &= \sigma\bar{x}_1 \tilde{A}+\varUpsilon\!\int_{0}^{\infty} \!\!\!\int_{0}^{\infty}\! K(\xi,\eta)\tilde{A}(\tilde{x}-c\xi) \tilde{A}(\tilde{x}-c\xi-c\eta)\tilde{A}^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\tilde{F}\exp({\mathrm{i}\tilde\alpha_d\tilde{x}}), \end{align}where
 \begin{gather} \sigma=(-\mathrm{i}\alpha/c)\left\{ I_1+\frac{\alpha^2}{\bar{T}_c}\left[ \frac{\bar{U}_{1c}}{\bar{U}_c^\prime} \left(j-2\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2\right)-j_1 \right]{\rm \pi}\mathrm{i}\right\}/G, \end{gather}
\begin{gather} \sigma=(-\mathrm{i}\alpha/c)\left\{ I_1+\frac{\alpha^2}{\bar{T}_c}\left[ \frac{\bar{U}_{1c}}{\bar{U}_c^\prime} \left(j-2\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)^2\right)-j_1 \right]{\rm \pi}\mathrm{i}\right\}/G, \end{gather}with
 \begin{equation} G=2I_2+\frac{\alpha^2}{\bar{T}_c\bar{U}_c^\prime} \left[j-2\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 \right]{\rm \pi}\mathrm{i}. \end{equation}
\begin{equation} G=2I_2+\frac{\alpha^2}{\bar{T}_c\bar{U}_c^\prime} \left[j-2\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right)^2 \right]{\rm \pi}\mathrm{i}. \end{equation}The amplitude equation (4.31) is inhomogeneous with the forcing representing the impact of the incident sound, and it describes both the excitation and evolution of the radiating mode.
4.1.3. Nonlinear response
Consider now the physical processes which are described by (4.31). The noise level in the conventional wind tunnel is of ![]() $O(10^{-3})$ (Masutti et al. Reference Masutti, Spinosa, Chazot and Carbonaro2012; Cerminara et al. Reference Cerminara, Durant, André, Sandham and Taylor2019), but in flight conditions it can be one to two orders of magnitude lower (Schneider Reference Schneider2008, Reference Schneider2015). It is impossible to infer from the overall noise level the amplitude of a component, but just as a rule of thumb, we take
$O(10^{-3})$ (Masutti et al. Reference Masutti, Spinosa, Chazot and Carbonaro2012; Cerminara et al. Reference Cerminara, Durant, André, Sandham and Taylor2019), but in flight conditions it can be one to two orders of magnitude lower (Schneider Reference Schneider2008, Reference Schneider2015). It is impossible to infer from the overall noise level the amplitude of a component, but just as a rule of thumb, we take ![]() $p_s=O(10^{-4})$. Recall that the pressure of the acoustic wave takes the form
$p_s=O(10^{-4})$. Recall that the pressure of the acoustic wave takes the form ![]() $p_s=\tilde \epsilon _s p_I\exp ({\mathrm {i}(\alpha _{s}{x}+\gamma _{s}{y}-\omega _{s}{t})})+\mathrm {c.c.}$, and it follows that the rescaled amplitude of the incident sound
$p_s=\tilde \epsilon _s p_I\exp ({\mathrm {i}(\alpha _{s}{x}+\gamma _{s}{y}-\omega _{s}{t})})+\mathrm {c.c.}$, and it follows that the rescaled amplitude of the incident sound
for Reynolds numbers in the range of ![]() $10^4$–
$10^4$–![]() $10^5$. Varying
$10^5$. Varying ![]() $p_I$ in the above range with a fixed
$p_I$ in the above range with a fixed ![]() $R$ alternatively corresponds to different
$R$ alternatively corresponds to different ![]() $p_s$.
$p_s$.
The inhomogeneous amplitude equation (4.31) admits an equilibrium solution of the form
where ![]() $a_e$ is a complex constant to be determined. This solution represents the nonlinear boundary-layer response to the incident sound. Substitution of (4.37) into (4.31) yields
$a_e$ is a complex constant to be determined. This solution represents the nonlinear boundary-layer response to the incident sound. Substitution of (4.37) into (4.31) yields
where we have put ![]() $\kappa _0=\sigma \bar {x}_1$, and
$\kappa _0=\sigma \bar {x}_1$, and
On writing ![]() $a_e=|a_e|\,\mathrm {e}^{\mathrm {i}\phi }$ and
$a_e=|a_e|\,\mathrm {e}^{\mathrm {i}\phi }$ and ![]() $\tilde {F}=|\tilde {F}|\,\mathrm {e}^{\mathrm {i}\theta _F}$ (
$\tilde {F}=|\tilde {F}|\,\mathrm {e}^{\mathrm {i}\theta _F}$ (![]() $-{\rm \pi} <\theta _F\leq {\rm \pi}$), (4.38) becomes
$-{\rm \pi} <\theta _F\leq {\rm \pi}$), (4.38) becomes
where ![]() $\theta =\theta _F-\phi$. Separation of the real and imaginary parts gives
$\theta =\theta _F-\phi$. Separation of the real and imaginary parts gives
Eliminating ![]() $\theta$ leads to the response equation
$\theta$ leads to the response equation
where we have put ![]() $b_e=|a_e|^2>0$. From (4.41a,b), we obtain
$b_e=|a_e|^2>0$. From (4.41a,b), we obtain ![]() $\theta =\theta _0$ or
$\theta =\theta _0$ or ![]() $\theta =\theta _0+{\rm \pi}$, where
$\theta =\theta _0+{\rm \pi}$, where
The phase of the nonlinear response can be obtained as ![]() $\phi =\theta _F-\theta$.
$\phi =\theta _F-\theta$.
The dependence of the nonlinear response on ![]() $\bar {x}_1$ for various values of
$\bar {x}_1$ for various values of ![]() $p_I$ and
$p_I$ and ![]() $\tilde \alpha _d$ is shown in figure 8. The nonlinear response attains its maximum at some point, beyond which it decreases rapidly. The maximum value of
$\tilde \alpha _d$ is shown in figure 8. The nonlinear response attains its maximum at some point, beyond which it decreases rapidly. The maximum value of ![]() $|a_e|$ increases with the sound magnitude
$|a_e|$ increases with the sound magnitude ![]() $p_I$, indicating that sound waves of higher intensity induce larger boundary-layer response. Note that the response would have been infinite at a particular value of
$p_I$, indicating that sound waves of higher intensity induce larger boundary-layer response. Note that the response would have been infinite at a particular value of ![]() $\bar {x}_1=\tilde \alpha _d/\sigma$ if nonlinearity were ignored, but remains finite in the presence of the latter, which plays a regularising role. For large
$\bar {x}_1=\tilde \alpha _d/\sigma$ if nonlinearity were ignored, but remains finite in the presence of the latter, which plays a regularising role. For large ![]() $p_I$,
$p_I$, ![]() $a_e$ scales as
$a_e$ scales as ![]() $p_I^{1/3}$. Changing the detuning parameter
$p_I^{1/3}$. Changing the detuning parameter ![]() $\tilde \alpha _d$ simply shifts the nonlinear response curve, but the overall behaviour remains almost the same. It should be noted that the equilibrium solution is only physically meaningful for
$\tilde \alpha _d$ simply shifts the nonlinear response curve, but the overall behaviour remains almost the same. It should be noted that the equilibrium solution is only physically meaningful for ![]() $\bar {x}_1<0$ because when
$\bar {x}_1<0$ because when ![]() $\bar {x}_1=O(R^{-1/3})$ and negative, the equilibrium solution evolves into the radiating mode as will be described in § 4.2.
$\bar {x}_1=O(R^{-1/3})$ and negative, the equilibrium solution evolves into the radiating mode as will be described in § 4.2.

Figure 8. Effects of the forcing and detuning on the nonlinear response with ![]() $\lambda =1$. (a) Effects of
$\lambda =1$. (a) Effects of ![]() $p_I$ on
$p_I$ on ![]() $a_e$ with
$a_e$ with ![]() $\tilde \alpha _d=0$. (b) Effects of
$\tilde \alpha _d=0$. (b) Effects of ![]() $\tilde \alpha _d$ on
$\tilde \alpha _d$ on ![]() $a_e$ with
$a_e$ with ![]() $p_I=5$.
$p_I=5$.
4.1.4. Effects on the linear growth rate
In general, the solution to (4.31) can be written as
By substituting (4.44) into (4.31), we obtain
 \begin{align} A_0^\prime(\tilde{x}) &= (\kappa_{0}-\mathrm{i}\tilde\alpha_d)A_0 +\varUpsilon|a_e|^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^*\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0(\tilde{x}-c\xi)A_0(\tilde{x}-c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0(\tilde{x}-c\xi)A_0(\tilde{x}-c\xi-c\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi. \end{align}
\begin{align} A_0^\prime(\tilde{x}) &= (\kappa_{0}-\mathrm{i}\tilde\alpha_d)A_0 +\varUpsilon|a_e|^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^*\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0(\tilde{x}-c\xi)A_0(\tilde{x}-c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0(\tilde{x}-c\xi)A_0(\tilde{x}-c\xi-c\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi. \end{align}This may be viewed as describing the stability of the nonlinear response, but more appropriately as describing the instability of the boundary layer in the presence of the impinging sound, which now appears multiplicatively despite the fact that it originally enters as an additive term in (4.31).
Linearising the above equation, we have
 \begin{align} A_0^\prime(\tilde{x}) &= (\kappa_{0}-\mathrm{i}\tilde\alpha_d)A_0 +\varUpsilon|a_e|^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi. \end{align}
\begin{align} A_0^\prime(\tilde{x}) &= (\kappa_{0}-\mathrm{i}\tilde\alpha_d)A_0 +\varUpsilon|a_e|^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)[A_0(\tilde{x}-c\xi)+A_0(\tilde{x}-c\xi-c\eta)]\,{\rm d}\eta{\rm d}\xi \nonumber\\ &\quad +\varUpsilon a_e^2\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)A_0^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi. \end{align}Let us seek a solution of the form
where ![]() $a_r$ and
$a_r$ and ![]() $a_i$ are both complex constants. Then
$a_i$ are both complex constants. Then ![]() $A_0$ can be written as
$A_0$ can be written as
Substitution of (4.48) into (4.46) and collection of terms proportional to ![]() $\mathrm {e}^{\kappa \tilde {x}}$ and
$\mathrm {e}^{\kappa \tilde {x}}$ and ![]() $\mathrm {e}^{\kappa ^*\tilde {x}}$ leads to the eigenvalue problem
$\mathrm {e}^{\kappa ^*\tilde {x}}$ leads to the eigenvalue problem
 \begin{align} & \begin{pmatrix} \kappa_{0r}+\varUpsilon_r |a_e|^2\chi_0+(\varUpsilon a_e^2)_r \bar\chi_0 & -\kappa_{0i}+\tilde\alpha_d-\varUpsilon_i |a_e|^2\chi_0+(\varUpsilon a_e^2)_i \bar\chi_0 \\ \kappa_{0i}-\tilde\alpha_d+\varUpsilon_i |a_e|^2\chi_0+(\varUpsilon a_e^2)_i \bar\chi_0 & \kappa_{0r}+\varUpsilon_r |a_e|^2\chi_0-(\varUpsilon a_e^2)_r \bar\chi_0 \end{pmatrix} \begin{pmatrix} a_r \\ a_i \end{pmatrix} \nonumber\\ &\quad =\kappa \begin{pmatrix} a_r \\ a_i \end{pmatrix}, \end{align}
\begin{align} & \begin{pmatrix} \kappa_{0r}+\varUpsilon_r |a_e|^2\chi_0+(\varUpsilon a_e^2)_r \bar\chi_0 & -\kappa_{0i}+\tilde\alpha_d-\varUpsilon_i |a_e|^2\chi_0+(\varUpsilon a_e^2)_i \bar\chi_0 \\ \kappa_{0i}-\tilde\alpha_d+\varUpsilon_i |a_e|^2\chi_0+(\varUpsilon a_e^2)_i \bar\chi_0 & \kappa_{0r}+\varUpsilon_r |a_e|^2\chi_0-(\varUpsilon a_e^2)_r \bar\chi_0 \end{pmatrix} \begin{pmatrix} a_r \\ a_i \end{pmatrix} \nonumber\\ &\quad =\kappa \begin{pmatrix} a_r \\ a_i \end{pmatrix}, \end{align}where we have put
 \begin{align} \chi_0 &= \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)(\exp({-\kappa c\xi})+\exp({-\kappa c\xi-\kappa c\eta}))\,{\rm d}\eta{\rm d}\xi \nonumber\\ &=\int_{0}^{\infty} [K_0(\xi)+K_1(\xi)]\exp({-2s\xi^3-\kappa c\xi})\,{\rm d}\xi, \end{align}
\begin{align} \chi_0 &= \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)(\exp({-\kappa c\xi})+\exp({-\kappa c\xi-\kappa c\eta}))\,{\rm d}\eta{\rm d}\xi \nonumber\\ &=\int_{0}^{\infty} [K_0(\xi)+K_1(\xi)]\exp({-2s\xi^3-\kappa c\xi})\,{\rm d}\xi, \end{align}
here, ![]() $K_0$ and
$K_0$ and ![]() $K_1$ are given by
$K_1$ are given by
 \begin{equation} \left.\begin{gathered} K_0=\left( \frac{1}{3s}+\frac{1}{3s_p} \right)\exp({-(s_p-s)\xi^3}) +\frac{\bar{T}_c}{\bar{T}_c^\prime}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\frac{1}{3s}\\ \quad -\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left[ \frac{1}{3s}-\frac{1}{3s_p}\exp({-2(s_p-s)\xi^3}) \right],\\ K_1 = \left( \frac{\xi^2}{3s\xi^2+\kappa c}+\frac{\xi^2}{3s_p\xi^2+\kappa c}\right)\exp({-(s_p-s)\xi^3}) +\frac{\bar{T}_c}{\bar{T}_c^\prime}\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right) \frac{\xi^2}{3s\xi^2+\kappa c} \\ \quad -\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left[ \frac{\xi^2}{3s\xi^2+\kappa c}-\frac{\xi^2}{3s_p\xi^2+\kappa c}\exp({-2(s_p-s)\xi^3}) \right] . \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} K_0=\left( \frac{1}{3s}+\frac{1}{3s_p} \right)\exp({-(s_p-s)\xi^3}) +\frac{\bar{T}_c}{\bar{T}_c^\prime}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\frac{1}{3s}\\ \quad -\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left[ \frac{1}{3s}-\frac{1}{3s_p}\exp({-2(s_p-s)\xi^3}) \right],\\ K_1 = \left( \frac{\xi^2}{3s\xi^2+\kappa c}+\frac{\xi^2}{3s_p\xi^2+\kappa c}\right)\exp({-(s_p-s)\xi^3}) +\frac{\bar{T}_c}{\bar{T}_c^\prime}\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right) \frac{\xi^2}{3s\xi^2+\kappa c} \\ \quad -\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left[ \frac{\xi^2}{3s\xi^2+\kappa c}-\frac{\xi^2}{3s_p\xi^2+\kappa c}\exp({-2(s_p-s)\xi^3}) \right] . \end{gathered}\right\} \end{equation}
The requirement that ![]() $a_r$ and
$a_r$ and ![]() $a_i$ are non-vanishing gives the characteristic equation for the modified growth rate
$a_i$ are non-vanishing gives the characteristic equation for the modified growth rate
The function ![]() $\mathcal {F}$ is real if
$\mathcal {F}$ is real if ![]() $\kappa$ is, and thus, if the equation
$\kappa$ is, and thus, if the equation ![]() $\mathcal {F}=0$ admits a complex root
$\mathcal {F}=0$ admits a complex root ![]() $\kappa$, so does its complex conjugate. The equation is solved numerically using Newton iteration. The corresponding eigenvector
$\kappa$, so does its complex conjugate. The equation is solved numerically using Newton iteration. The corresponding eigenvector ![]() $(a_r, a_i)$ is obtained from (4.49) and written as
$(a_r, a_i)$ is obtained from (4.49) and written as
where ![]() $(a_r, a_i)$ is normalised such that
$(a_r, a_i)$ is normalised such that ![]() $|a_{r0}|^2+|a_{i0}|^2=1$, and
$|a_{r0}|^2+|a_{i0}|^2=1$, and ![]() $a_0=|a_0|\,\mathrm {e}^{\mathrm {i}\phi _0}$ is a complex constant. Thus the perturbation
$a_0=|a_0|\,\mathrm {e}^{\mathrm {i}\phi _0}$ is a complex constant. Thus the perturbation ![]() $A_0$ can be written as
$A_0$ can be written as
Figure 9 shows the effects of ![]() $p_I$ on the modified growth rate
$p_I$ on the modified growth rate ![]() $\kappa _r$. In general,
$\kappa _r$. In general, ![]() $\kappa _r$ is enhanced by the impinging sound, especially in the region where the nonlinear response is significant (cf. figure 8). As
$\kappa _r$ is enhanced by the impinging sound, especially in the region where the nonlinear response is significant (cf. figure 8). As ![]() $\bar {x}_1\rightarrow -\infty$,
$\bar {x}_1\rightarrow -\infty$, ![]() $\kappa _r$ approaches the unperturbed growth rate
$\kappa _r$ approaches the unperturbed growth rate ![]() $\kappa _{0r}$. The modified growth rate increases with
$\kappa _{0r}$. The modified growth rate increases with ![]() $p_I$. Since the function
$p_I$. Since the function ![]() $\mathcal {F}$ is real for real values of
$\mathcal {F}$ is real for real values of ![]() $\kappa$, it may admit real roots for certain parameters. Indeed, the solution changes from a complex conjugate pair to two real roots at certain positions with one being significantly larger than the other. These real roots are associated with the ‘phase-locking’ phenomenon, that is, we can write
$\kappa$, it may admit real roots for certain parameters. Indeed, the solution changes from a complex conjugate pair to two real roots at certain positions with one being significantly larger than the other. These real roots are associated with the ‘phase-locking’ phenomenon, that is, we can write ![]() $A_0=|\check {a}_0|\exp ({\mathrm {i}\check \phi _0+\kappa \tilde {x}})$, where
$A_0=|\check {a}_0|\exp ({\mathrm {i}\check \phi _0+\kappa \tilde {x}})$, where ![]() $\check {a}_0=2|a_0|[|a_{r0}|\cos (\theta _1+\phi _0)+\mathrm {i}|a_{i0}|\cos (\theta _2+\phi _0)]\equiv |\check {a}_0| \exp ({\mathrm {i}\check \phi _0})$. Now the total amplitude
$\check {a}_0=2|a_0|[|a_{r0}|\cos (\theta _1+\phi _0)+\mathrm {i}|a_{i0}|\cos (\theta _2+\phi _0)]\equiv |\check {a}_0| \exp ({\mathrm {i}\check \phi _0})$. Now the total amplitude ![]() $\tilde {A}$ can be expressed as
$\tilde {A}$ can be expressed as ![]() $\tilde {A}=(|a_e|\,\mathrm {e}^{\mathrm {i}\phi }+|\check {a}_0|\exp ({\mathrm {i}\check \phi _0+\kappa \tilde {x}})) \exp ({\mathrm {i}\tilde \alpha _d\tilde {x}})$, indicating that the phases of the nonlinear response and the perturbation are ‘locked’ in the sense that their difference is independent of
$\tilde {A}=(|a_e|\,\mathrm {e}^{\mathrm {i}\phi }+|\check {a}_0|\exp ({\mathrm {i}\check \phi _0+\kappa \tilde {x}})) \exp ({\mathrm {i}\tilde \alpha _d\tilde {x}})$, indicating that the phases of the nonlinear response and the perturbation are ‘locked’ in the sense that their difference is independent of ![]() $\tilde {x}$.
$\tilde {x}$.

Figure 9. Effects of the forcing on the modified growth rate ![]() $\kappa$ with
$\kappa$ with ![]() $\tilde \alpha _d=-1$ and
$\tilde \alpha _d=-1$ and ![]() $\lambda =1$: (a)
$\lambda =1$: (a) ![]() $\kappa _r$ and (b)
$\kappa _r$ and (b) ![]() $\kappa _i$. The dashed line represents the linear growth rate in the absence of the incident sound.
$\kappa _i$. The dashed line represents the linear growth rate in the absence of the incident sound.
Figure 10 shows the variation of the modified growth rate with ![]() $\bar {x}_1$ for three values of
$\bar {x}_1$ for three values of ![]() $\tilde \alpha _d$. Altering
$\tilde \alpha _d$. Altering ![]() $\tilde \alpha _d$ shifts the distribution of both
$\tilde \alpha _d$ shifts the distribution of both ![]() $\kappa _r$ and
$\kappa _r$ and ![]() $\kappa _i$. Again, the complex roots
$\kappa _i$. Again, the complex roots ![]() $\kappa$ develop into two branches of real roots in the region where the nonlinear response is large. All these results indicate that, for the parameters examined, the impinging sound enhances the linear growth rate substantially.
$\kappa$ develop into two branches of real roots in the region where the nonlinear response is large. All these results indicate that, for the parameters examined, the impinging sound enhances the linear growth rate substantially.

Figure 10. Effects of detuning on the modified growth rate ![]() $\kappa$ with
$\kappa$ with ![]() $p_I=5$ and
$p_I=5$ and ![]() $\lambda =1$: (a)
$\lambda =1$: (a) ![]() $\kappa _r$ and (b)
$\kappa _r$ and (b) ![]() $\kappa _i$. The dashed line represents the linear growth rate in the absence of the incident sound.
$\kappa _i$. The dashed line represents the linear growth rate in the absence of the incident sound.
4.1.5. Nonlinear evolution
We proceed to consider the effect of the impinging sound on the nonlinear development by solving numerically the nonlinear amplitude equation (4.45), subject to the appropriate initial condition (4.55) as ![]() $\tilde {x}\rightarrow -\infty$. The sixth-order Adams–Moulton method is used, and the integral term is approximated by Simpson's rule. Results of the effects are shown in figure 11. The amplitude always develops into a singularity at some point. Increasing the intensity of the sound wave advances the blow-up behaviour (figure 11a). We also examine the effects of viscosity on the nonlinear development, which generally delays the occurrence of the finite-distance singularity (figure 11b), similar to what has been found in previous studies of free-mode evolution (Goldstein & Leib Reference Goldstein and Leib1989; Wu et al. Reference Wu, Lee and Cowley1993).
$\tilde {x}\rightarrow -\infty$. The sixth-order Adams–Moulton method is used, and the integral term is approximated by Simpson's rule. Results of the effects are shown in figure 11. The amplitude always develops into a singularity at some point. Increasing the intensity of the sound wave advances the blow-up behaviour (figure 11a). We also examine the effects of viscosity on the nonlinear development, which generally delays the occurrence of the finite-distance singularity (figure 11b), similar to what has been found in previous studies of free-mode evolution (Goldstein & Leib Reference Goldstein and Leib1989; Wu et al. Reference Wu, Lee and Cowley1993).

Figure 11. Effects of sound intensity and viscosity on the nonlinear evolution of the radiating mode. (a) Nonlinear development for different values of ![]() $p_I$ with
$p_I$ with ![]() $\lambda =1$. (b) Nonlinear development for different values of
$\lambda =1$. (b) Nonlinear development for different values of ![]() $\lambda$ with
$\lambda$ with ![]() $p_I=5$. The dashed lines represent the corresponding linear solution (4.55). Here, we have taken
$p_I=5$. The dashed lines represent the corresponding linear solution (4.55). Here, we have taken ![]() $\bar {x}_1=-7$,
$\bar {x}_1=-7$, ![]() $\tilde \alpha _d=-1$ and
$\tilde \alpha _d=-1$ and ![]() $a_0=1$.
$a_0=1$.
4.2. Equilibrium non-parallel regime
As is shown in § 2.3.2, a sound influences nonlinearly the excitation and evolution of the radiating mode in the equilibrium regime when its magnitude ![]() $\bar {\epsilon }_s=\bar {\epsilon }R^{-1/2}=O(R^{-17/12})$, and its frequency/wavenumber is the same/close to those of the radiating mode, that is,
$\bar {\epsilon }_s=\bar {\epsilon }R^{-1/2}=O(R^{-17/12})$, and its frequency/wavenumber is the same/close to those of the radiating mode, that is,
where ![]() $\bar \alpha _d$ is an
$\bar \alpha _d$ is an ![]() $O(1)$ detuning parameter. For
$O(1)$ detuning parameter. For ![]() $R=10^{4}\mbox {--}10^{5}$,
$R=10^{4}\mbox {--}10^{5}$, ![]() $\bar {p}_I=p_s/\bar {\epsilon }_s=p_s/R^{-17/12}\approx 46.4\mbox {--}1211.5$.
$\bar {p}_I=p_s/\bar {\epsilon }_s=p_s/R^{-17/12}\approx 46.4\mbox {--}1211.5$.
4.2.1. The amplitude equation
The analysis in the main layer is only slightly modified with expansion (4.2) being replaced by
The corresponding solvability condition (4.21) becomes
 \begin{align} & \frac{1}{\bar{U}_c^\prime}\left\{ 3(c^+-c^-)-\frac{2\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\bar{A}^\prime-\bar{U}_{1c}\bar{x} \bar{A} \right) \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)(a^+-a^-) -\alpha^2 d(a^+-a^-) \right\} \nonumber\\ &\quad -\frac{2\mathrm{i}\alpha q\mathscr{C}_{\infty}}{(1-c)^2}\bar{p}_I\exp({\mathrm{i}\bar\alpha_d\bar{x}}) =-\left(\frac{2\mathrm{i} c}{\alpha}I_2 \bar{A}^\prime-I_1\bar{x} \bar{A}\right), \end{align}
\begin{align} & \frac{1}{\bar{U}_c^\prime}\left\{ 3(c^+-c^-)-\frac{2\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\bar{A}^\prime-\bar{U}_{1c}\bar{x} \bar{A} \right) \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)(a^+-a^-) -\alpha^2 d(a^+-a^-) \right\} \nonumber\\ &\quad -\frac{2\mathrm{i}\alpha q\mathscr{C}_{\infty}}{(1-c)^2}\bar{p}_I\exp({\mathrm{i}\bar\alpha_d\bar{x}}) =-\left(\frac{2\mathrm{i} c}{\alpha}I_2 \bar{A}^\prime-I_1\bar{x} \bar{A}\right), \end{align}
which corresponds to (4.21) but with the parameter ![]() $\bar {x}_1$ being replaced by variable
$\bar {x}_1$ being replaced by variable ![]() $\bar {x}$. The jump
$\bar {x}$. The jump ![]() $(a^+-a^-)$ remains as (4.30), while
$(a^+-a^-)$ remains as (4.30), while ![]() $(c^+-c^-)$ was given in Wu (Reference Wu2005) (see also Qin Reference Qin2024), that is,
$(c^+-c^-)$ was given in Wu (Reference Wu2005) (see also Qin Reference Qin2024), that is,
 \begin{align} c^+-c^- &= \frac{1}{3}\frac{\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\bar{A}^\prime-\bar{U}_{1c}\bar{x} \bar{A} \right)j{\rm \pi}\mathrm{i} +\left( \frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x} \bar{A} \right)j_1{\rm \pi}\mathrm{i} \nonumber\\ &\quad +d\frac{\alpha^2}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right){\rm \pi}\mathrm{i} +\frac{\varLambda}{3}\bar{A}|\bar{A}|^2, \end{align}
\begin{align} c^+-c^- &= \frac{1}{3}\frac{\alpha^2}{\bar{T}_c} \left( \frac{\mathrm{i} c}{\alpha}\bar{A}^\prime-\bar{U}_{1c}\bar{x} \bar{A} \right)j{\rm \pi}\mathrm{i} +\left( \frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x} \bar{A} \right)j_1{\rm \pi}\mathrm{i} \nonumber\\ &\quad +d\frac{\alpha^2}{3}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right){\rm \pi}\mathrm{i} +\frac{\varLambda}{3}\bar{A}|\bar{A}|^2, \end{align}
where ![]() $\varLambda$ is given by
$\varLambda$ is given by
 \begin{align} \varLambda &=-\frac{2{\rm \pi}\mathrm{i}\alpha^4\bar{U}_c^\prime}{3\bar{T}_c^2\bar{\mu}_c} \left\{\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{T}_c\bar{\mu}_c(1-Pr^{-1})} (Pr^{4/3}-1)+\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \right.\nonumber\\ &\quad + \left.\frac{\bar{T}_c^\prime}{\bar{T}_c}(1+Pr)^{2/3}(2Pr)^{1/3} \right\}(2s)^{-1/3}\varGamma \left({\frac{1}{3}}\right), \end{align}
\begin{align} \varLambda &=-\frac{2{\rm \pi}\mathrm{i}\alpha^4\bar{U}_c^\prime}{3\bar{T}_c^2\bar{\mu}_c} \left\{\frac{\bar{T}_c^\prime(\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1})}{\bar{T}_c\bar{\mu}_c(1-Pr^{-1})} (Pr^{4/3}-1)+\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right) \right.\nonumber\\ &\quad + \left.\frac{\bar{T}_c^\prime}{\bar{T}_c}(1+Pr)^{2/3}(2Pr)^{1/3} \right\}(2s)^{-1/3}\varGamma \left({\frac{1}{3}}\right), \end{align}
with ![]() $\varGamma$ denoting the gamma function and
$\varGamma$ denoting the gamma function and ![]() $s$ being the same as that in (4.29) provided that
$s$ being the same as that in (4.29) provided that ![]() $\lambda$ is set to unity. Inserting (4.30) and (4.59) into (4.58), we obtain the amplitude equation for
$\lambda$ is set to unity. Inserting (4.30) and (4.59) into (4.58), we obtain the amplitude equation for ![]() $\bar {A}$,
$\bar {A}$,
where ![]() $\sigma$ is given in (4.32),
$\sigma$ is given in (4.32), ![]() $\bar {F}=\tilde {F}$ as given by (4.34) and
$\bar {F}=\tilde {F}$ as given by (4.34) and
4.2.2. The initial amplitude without oncoming free modes
On dropping in (4.61) the nonlinear term, which is negligible in the upstream region, and solving the linear equation, the initial condition is specified as
where ![]() $\breve {a}_0$ is an arbitrary constant. It should be noted that, although the first term is a complementary solution of the linearised version of (4.61), it does not represent a free oncoming mode. This is because the first term is exponentially small in the upstream region, whereas the second term is algebraically small, and when approximated asymptotically, the remainder contains the exponentially small term corresponding to the free mode. Therefore our immediate task is to determine the specific value of
$\breve {a}_0$ is an arbitrary constant. It should be noted that, although the first term is a complementary solution of the linearised version of (4.61), it does not represent a free oncoming mode. This is because the first term is exponentially small in the upstream region, whereas the second term is algebraically small, and when approximated asymptotically, the remainder contains the exponentially small term corresponding to the free mode. Therefore our immediate task is to determine the specific value of ![]() $\breve {a}_0$ such that the free mode is absent in the upstream region. This is achieved by using the idea of optimal truncation in asymptotic approximation.
$\breve {a}_0$ such that the free mode is absent in the upstream region. This is achieved by using the idea of optimal truncation in asymptotic approximation.
For that purpose, we split the integration interval into ![]() $(0,\tau _0)$ and
$(0,\tau _0)$ and ![]() $(\tau _0,\bar {x})$ and perform integration by parts to the integral over the latter to obtain
$(\tau _0,\bar {x})$ and perform integration by parts to the integral over the latter to obtain
 \begin{align} \bar{A}(\bar{x}) &=
\exp({\sigma\bar{x}^2/2})\left[ \breve{a}_0+ \bar{F}
\left(I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1 \cdot 3 \cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}
\right.\right.\nonumber\\ &\quad
+\exp({\mathrm{i}\bar\alpha_d\bar{x}-\sigma\bar{x}^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\bar{x})^{2n+1}}
\nonumber\\ &\quad
\vphantom{\left(I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}
\right.} + \left.\left.(-1)^N\int_{\bar{x}}^{\tau_0}
\frac{\exp({\mathrm{i}\bar\alpha_d\tau-\sigma\tau^2/2})
\sigma^{N+1}1\cdot 3\cdot 5\cdots(2N+1)}
{(\mathrm{i}\bar\alpha_d-\sigma\tau)^{2N+2}}\,{\rm d}\tau\vphantom{\sum_{n=0}^{N}}\right)\right],
\end{align}
\begin{align} \bar{A}(\bar{x}) &=
\exp({\sigma\bar{x}^2/2})\left[ \breve{a}_0+ \bar{F}
\left(I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1 \cdot 3 \cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}
\right.\right.\nonumber\\ &\quad
+\exp({\mathrm{i}\bar\alpha_d\bar{x}-\sigma\bar{x}^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\bar{x})^{2n+1}}
\nonumber\\ &\quad
\vphantom{\left(I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})\sum_{n=0}^{N}
\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}
\right.} + \left.\left.(-1)^N\int_{\bar{x}}^{\tau_0}
\frac{\exp({\mathrm{i}\bar\alpha_d\tau-\sigma\tau^2/2})
\sigma^{N+1}1\cdot 3\cdot 5\cdots(2N+1)}
{(\mathrm{i}\bar\alpha_d-\sigma\tau)^{2N+2}}\,{\rm d}\tau\vphantom{\sum_{n=0}^{N}}\right)\right],
\end{align}
where ![]() $\tau _0$ is constant and
$\tau _0$ is constant and
The optimal truncation of the asymptotic expansion is the one that makes the remainder exponentially small by retaining the right number of terms, ![]() $N=N_{op}$, where
$N=N_{op}$, where ![]() $N_{op}$ is the maximum number of terms whose size is monotonically decreasing for a fixed large negative
$N_{op}$ is the maximum number of terms whose size is monotonically decreasing for a fixed large negative ![]() $\bar {x}$, and is dependent of
$\bar {x}$, and is dependent of ![]() $\bar {x}$. The expression for
$\bar {x}$. The expression for ![]() $N_{op}$ is determined as follows. Let
$N_{op}$ is determined as follows. Let ![]() $f_n$ be the
$f_n$ be the ![]() $n$th term in (4.64). Then consider the ratio of the two consecutive terms
$n$th term in (4.64). Then consider the ratio of the two consecutive terms
for a large ![]() $\bar {x}=\bar {x}_{\infty }$. If we require
$\bar {x}=\bar {x}_{\infty }$. If we require ![]() $|\,f_{n+1}/f_n|<1$, then
$|\,f_{n+1}/f_n|<1$, then
Thus the terms in the expansion are in decreasing order for ![]() $n\leq N_{op}$, where
$n\leq N_{op}$, where
with ![]() $[I]$ representing the largest integer that is smaller than
$[I]$ representing the largest integer that is smaller than ![]() $I$; the magnitude of the terms with
$I$; the magnitude of the terms with ![]() $n>N_{op}$ increases. With the optimal truncation, the remainder is made sufficiently small. The complementary solution would be absent if we choose
$n>N_{op}$ increases. With the optimal truncation, the remainder is made sufficiently small. The complementary solution would be absent if we choose ![]() $\breve {a}_0$ to be
$\breve {a}_0$ to be
 \begin{equation}
\breve{a}_0=\bar{a}_{op}\equiv-\bar{F}\biggl[I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})
\sum_{n=0}^{N_{op}}\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}\biggr].
\end{equation}
\begin{equation}
\breve{a}_0=\bar{a}_{op}\equiv-\bar{F}\biggl[I_0-\exp({\mathrm{i}\bar\alpha_d\tau_0-\sigma\tau_0^2/2})
\sum_{n=0}^{N_{op}}\frac{\sigma^n (-1)^n 1\cdot 3\cdot 5\cdots(2n-1)}{(\mathrm{i}\bar\alpha_d-\sigma\tau_0)^{2n+1}}\biggr].
\end{equation}
The values of ![]() $\bar {a}_{op}$ calculated using (4.69) are listed in table 1 for
$\bar {a}_{op}$ calculated using (4.69) are listed in table 1 for ![]() $\bar \alpha _d=0$ and
$\bar \alpha _d=0$ and ![]() $4$. We evaluate the linear solution (4.63) and solve the nonlinear equation (4.61) with the initial condition being imposed at different upstream positions
$4$. We evaluate the linear solution (4.63) and solve the nonlinear equation (4.61) with the initial condition being imposed at different upstream positions ![]() $\bar {x}_{\infty }$ with
$\bar {x}_{\infty }$ with ![]() $\breve {a}_0=\bar {a}_{op}$. As is shown in figure 12, the solutions starting from different
$\breve {a}_0=\bar {a}_{op}$. As is shown in figure 12, the solutions starting from different ![]() $\bar {x}_{\infty }$ overlap each other, suggesting that the particular initial amplitude is independent of the upstream position; the initial condition with
$\bar {x}_{\infty }$ overlap each other, suggesting that the particular initial amplitude is independent of the upstream position; the initial condition with ![]() $\breve {a}_0=\bar {a}_{op}$ represents solely the locally forced response.
$\breve {a}_0=\bar {a}_{op}$ represents solely the locally forced response.
Table 1. The initial amplitude without oncoming free modes determined by the optimal truncation for ![]() $\bar {p}_I=115.94$.
$\bar {p}_I=115.94$.


Figure 12. Linear and nonlinear evolution for ![]() $\bar {p}_I=115.94$ starting from different upstream positions
$\bar {p}_I=115.94$ starting from different upstream positions ![]() $\bar {x}_{\infty }$; (a)
$\bar {x}_{\infty }$; (a) ![]() $\bar \alpha _d=0$ and
$\bar \alpha _d=0$ and ![]() $\breve {a}_0=-22.011-16.921\mathrm {i}$, (b)
$\breve {a}_0=-22.011-16.921\mathrm {i}$, (b) ![]() $\bar \alpha _d=4$ and
$\bar \alpha _d=4$ and ![]() $\breve {a}_0=-2.042+0.241\mathrm {i}$.
$\breve {a}_0=-2.042+0.241\mathrm {i}$.
5. Non-parallelism and the composite amplitude equation
Having obtained the amplitude equations in the non-equilibrium parallel and equilibrium non-parallel regimes, respectively, it is straightforward to construct a composite amplitude equation that accommodates both regimes. The respective validity regions and the associated length scales are shown in figure 13.

Figure 13. A sketch illustrating different evolution regimes.
5.1. Construction of the composite amplitude equation
Recall that, in the equilibrium regime, the evolution occurs in the vicinity of the neutral position (figure 13)
and the amplitude equation is (4.61) with ![]() $\bar \alpha _d$ being defined by (4.56a,b). On the other hand, in the non-equilibrium regime, where without loss of generality the Haberman parameter is taken to be
$\bar \alpha _d$ being defined by (4.56a,b). On the other hand, in the non-equilibrium regime, where without loss of generality the Haberman parameter is taken to be ![]() $\lambda =1$, the evolution occurs in the vicinity of the neutral position
$\lambda =1$, the evolution occurs in the vicinity of the neutral position
and the amplitude is governed by (4.31) with ![]() $\tilde \alpha _d$ being specified by (4.1a,b).
$\tilde \alpha _d$ being specified by (4.1a,b).
Let us first construct the composite solution starting from the non-equilibrium regime. Noting (2.18), i.e.
we can approximate the base flow by
Following Wu & Huerre (Reference Wu and Huerre2009), we construct a composite amplitude equation by retaining the ![]() $O(R^{-2/3})$ term in (5.4) so that the first term on the right-hand side of (4.31) is modified to
$O(R^{-2/3})$ term in (5.4) so that the first term on the right-hand side of (4.31) is modified to ![]() $\sigma (\bar {x}_1+R^{-1/3}\tilde {x})$, and the carrier of the forcing becomes
$\sigma (\bar {x}_1+R^{-1/3}\tilde {x})$, and the carrier of the forcing becomes ![]() $\exp ({\mathrm {i}\tilde \alpha _d(\tilde {x}+R^{1/3}\bar {x}_1+R^{2/3}x_{3,n})})$. From (5.1) and (5.3) follows
$\exp ({\mathrm {i}\tilde \alpha _d(\tilde {x}+R^{1/3}\bar {x}_1+R^{2/3}x_{3,n})})$. From (5.1) and (5.3) follows
Note that, in the equilibrium regime, we expanded the perturbation as
where
whilst, in the non-equilibrium regime, we expand the perturbation as
where
Thus we have the relations ![]() $\bar {A}(\bar {x})=R^{1/12}\tilde {A}(\tilde {x})$ and
$\bar {A}(\bar {x})=R^{1/12}\tilde {A}(\tilde {x})$ and ![]() $\bar {p}_I=R^{1/4}p_I$ (
$\bar {p}_I=R^{1/4}p_I$ (![]() $\bar {F}=R^{1/4}\tilde {F}$). On using these relations as well as (5.5), and noting
$\bar {F}=R^{1/4}\tilde {F}$). On using these relations as well as (5.5), and noting ![]() $\bar {\alpha }_d=R^{1/6}\tilde \alpha _d$, the amplitude equation (4.31) is rewritten as
$\bar {\alpha }_d=R^{1/6}\tilde \alpha _d$, the amplitude equation (4.31) is rewritten as
 \begin{align} \bar{A}^\prime(\bar{x}) &= \sigma\bar{x}\bar{A} +\varUpsilon R^{2/3}\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta;\bar{s}) \bar{A}(\bar{x}-c\xi)\bar{A}(\bar{x}-c\xi-c\eta) \nonumber\\ &\quad \times \bar{A}^*(\bar{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi +\bar{F}\exp({\mathrm{i}\bar{\alpha}_d\bar{x}}), \end{align}
\begin{align} \bar{A}^\prime(\bar{x}) &= \sigma\bar{x}\bar{A} +\varUpsilon R^{2/3}\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta;\bar{s}) \bar{A}(\bar{x}-c\xi)\bar{A}(\bar{x}-c\xi-c\eta) \nonumber\\ &\quad \times \bar{A}^*(\bar{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi +\bar{F}\exp({\mathrm{i}\bar{\alpha}_d\bar{x}}), \end{align}
where ![]() $\bar {s}=sR^{1/2}$, and we have taken
$\bar {s}=sR^{1/2}$, and we have taken ![]() $x_{3,n}=0$ without loss of generality.
$x_{3,n}=0$ without loss of generality.
The same composite amplitude equation may alternatively be constructed starting from the equilibrium regime by retaining the small non-equilibrium term in the critical-layer operator, which then becomes
In Appendix C, we show that the evolution problems in the equilibrium and non-equilibrium regimes can be properly recovered from the composite theory.
The initial condition of the composite amplitude equation (5.10) is obtained by neglecting the nonlinear term, leading to
We can write ![]() $\breve {a}_0=\bar {a}_{op}+\hat {a}_0$ so that the term
$\breve {a}_0=\bar {a}_{op}+\hat {a}_0$ so that the term ![]() $\hat {a}_0\exp ({\sigma \bar {x}^2/2})$ represents the free mode.
$\hat {a}_0\exp ({\sigma \bar {x}^2/2})$ represents the free mode.
5.2. Effects of forcing and free modes
We first solve the composite amplitude equation (5.10) without forcing (i.e. ![]() $\bar {F}=0$). The results are shown in figure 14. For all the values of
$\bar {F}=0$). The results are shown in figure 14. For all the values of ![]() $\breve {a}_0$ examined, the numerical solution and the corresponding initial condition overlap as expected in the upstream linear phase. For small values of
$\breve {a}_0$ examined, the numerical solution and the corresponding initial condition overlap as expected in the upstream linear phase. For small values of ![]() $\breve {a}_0$, the numerical solution remains linear in the entire course of the development. As the initial amplitude becomes larger,
$\breve {a}_0$, the numerical solution remains linear in the entire course of the development. As the initial amplitude becomes larger, ![]() $\bar {A}$ amplifies faster than in the linear limit, suggesting that nonlinear effects enhance the growth of the free radiating mode before it attenuates. When
$\bar {A}$ amplifies faster than in the linear limit, suggesting that nonlinear effects enhance the growth of the free radiating mode before it attenuates. When ![]() $\breve {a}_0$ exceeds a threshold value, the solution blows up at a finite distance.
$\breve {a}_0$ exceeds a threshold value, the solution blows up at a finite distance.
Next, we solve the composite amplitude equation (5.10) numerically for a range of forcing amplitude ![]() $\bar {p}_I$ with
$\bar {p}_I$ with ![]() $\breve {a}_0$ taken to be
$\breve {a}_0$ taken to be ![]() $\breve {a}_0=\bar {a}_{op}$ (
$\breve {a}_0=\bar {a}_{op}$ (![]() $\hat {a}_0=0$), so that there is no oncoming free mode. Each solution represents the locally excited disturbance through resonance and describes its subsequent development into a radiating mode. The solutions are presented in figure 15. The corresponding linear solution (5.12), the solution to (4.61) in the equilibrium regime and the nonlinear response in the non-equilibrium regime (recast in terms of the coordinate of the composite theory, (C3)) are also plotted for comparison. For small values of
$\hat {a}_0=0$), so that there is no oncoming free mode. Each solution represents the locally excited disturbance through resonance and describes its subsequent development into a radiating mode. The solutions are presented in figure 15. The corresponding linear solution (5.12), the solution to (4.61) in the equilibrium regime and the nonlinear response in the non-equilibrium regime (recast in terms of the coordinate of the composite theory, (C3)) are also plotted for comparison. For small values of ![]() $\bar {p}_I$, the perturbation remains weak that the solutions to the composite and equilibrium amplitude equations overlap with the linear solution in the whole range (figure 15a). After reaching its peak value, the amplitude decays in an oscillatory manner. For a moderate value of
$\bar {p}_I$, the perturbation remains weak that the solutions to the composite and equilibrium amplitude equations overlap with the linear solution in the whole range (figure 15a). After reaching its peak value, the amplitude decays in an oscillatory manner. For a moderate value of ![]() $\bar {p}_I$, the nonlinear effect comes into play during the attenuation phase, causing a slow decay of the disturbance in the downstream region, while the non-equilibrium effect is rather small, as indicated by the agreement between the composite and equilibrium solutions (figure 15b). However, non-equilibrium effect becomes significant with further increase of
$\bar {p}_I$, the nonlinear effect comes into play during the attenuation phase, causing a slow decay of the disturbance in the downstream region, while the non-equilibrium effect is rather small, as indicated by the agreement between the composite and equilibrium solutions (figure 15b). However, non-equilibrium effect becomes significant with further increase of ![]() $\bar {p}_I$ (figure 15c) and suppresses the disturbance. When
$\bar {p}_I$ (figure 15c) and suppresses the disturbance. When ![]() $\bar {p}_I$ is large enough, instead of attenuation, the disturbance amplifies in the downstream region, and appears to terminate at a finite-distance singularity (figure 15d). On entering the nonlinear stage, non-equilibrium becomes important, as indicated by the fact that the solution to the composite amplitude equation saturates/grows at a smaller rate than that in the equilibrium regime.
$\bar {p}_I$ is large enough, instead of attenuation, the disturbance amplifies in the downstream region, and appears to terminate at a finite-distance singularity (figure 15d). On entering the nonlinear stage, non-equilibrium becomes important, as indicated by the fact that the solution to the composite amplitude equation saturates/grows at a smaller rate than that in the equilibrium regime.

Figure 15. Effects of the forcing on the evolution predicted by the composite amplitude equation (5.10) with ![]() $\bar \alpha _d=0$ and
$\bar \alpha _d=0$ and ![]() $\breve {a}_0=\bar {a}_{op}$ (
$\breve {a}_0=\bar {a}_{op}$ (![]() $\hat {a}_0=0$) for
$\hat {a}_0=0$) for ![]() $\bar {p}_I=3$ (a),
$\bar {p}_I=3$ (a), ![]() $\bar {p}_I=6$ (b),
$\bar {p}_I=6$ (b), ![]() $\bar {p}_I=10$ (c) and
$\bar {p}_I=10$ (c) and ![]() $\bar {p}_I=15$ (d). Solid lines: solution to (5.10) with
$\bar {p}_I=15$ (d). Solid lines: solution to (5.10) with ![]() $R=10^4$; dashed lines: linear solution (5.12); dashed-dotted lines: solution to (4.61) in the equilibrium regime; (red) dashed-dotted-dotted lines: nonlinear response given by (C3) in terms of the coordinate of the composite theory.
$R=10^4$; dashed lines: linear solution (5.12); dashed-dotted lines: solution to (4.61) in the equilibrium regime; (red) dashed-dotted-dotted lines: nonlinear response given by (C3) in terms of the coordinate of the composite theory.
Figure 16 shows the effects of the forcing (i.e. ![]() $\bar {p}_I$) on the evolution in the presence of a pre-existing free mode (
$\bar {p}_I$) on the evolution in the presence of a pre-existing free mode (![]() $\hat {a}_0\neq 0$). Two cases are considered, for which the free mode remains bounded (figure 16a) and blows up (figure 16b). While the amplitude upstream increases monotonically in the case of either solely a free mode (figure 14) or just the locally forced disturbance (figure 15), when both are present their total amplitude becomes oscillatory even in the earlier linear stage. Figure 16(a) shows that moderate forcing inhibits the mode, whereas further increase of the forcing enhances the amplification of the disturbance and may lead to blow-up. Similar behaviours are observed in figure 16(b), where moderate forcing delays the development of a finite-distance singularity and sufficiently large forcing does the opposite.
$\hat {a}_0\neq 0$). Two cases are considered, for which the free mode remains bounded (figure 16a) and blows up (figure 16b). While the amplitude upstream increases monotonically in the case of either solely a free mode (figure 14) or just the locally forced disturbance (figure 15), when both are present their total amplitude becomes oscillatory even in the earlier linear stage. Figure 16(a) shows that moderate forcing inhibits the mode, whereas further increase of the forcing enhances the amplification of the disturbance and may lead to blow-up. Similar behaviours are observed in figure 16(b), where moderate forcing delays the development of a finite-distance singularity and sufficiently large forcing does the opposite.

Figure 16. Effects of the forcing on the evolution in the presence of a pre-existing free mode with an initial amplitude ![]() $\hat {a}_0$: (a)
$\hat {a}_0$: (a) ![]() $\hat {a}_0=3$ and (b)
$\hat {a}_0=3$ and (b) ![]() $\hat {a}_0=5$.
$\hat {a}_0=5$.
We consider further the evolution of the combined free and locally excited modes. The solutions to the composite amplitude equation for a fixed ![]() $\bar {p}_I=10$ but different initial amplitudes of the free mode are displayed in figure 17. A free mode with initial amplitudes
$\bar {p}_I=10$ but different initial amplitudes of the free mode are displayed in figure 17. A free mode with initial amplitudes ![]() $\hat {a}_0=1$ and
$\hat {a}_0=1$ and ![]() $3$ influences the overall behaviour of the evolution appreciably (figure 17b,c). Interestingly, the free mode suppresses the disturbance downstream (figure 17c). However, when its initial amplitude is increased to
$3$ influences the overall behaviour of the evolution appreciably (figure 17b,c). Interestingly, the free mode suppresses the disturbance downstream (figure 17c). However, when its initial amplitude is increased to ![]() $\hat {a}_0=5$, the free mode promotes the disturbance instead, causing the latter to blow up at a finite distance (figure 17d). The phase of the initial amplitude of the free mode also plays an important role in the evolution, as is displayed in figure 18. Figure 18(a) shows that changing the phase either suppresses or promotes the disturbance significantly. The free mode with particular phases can cause a finite-distance singularity even though the mode with the same initial magnitude but different phases saturates. The important role of the phase is also observed for the case where the disturbance blows up, as is shown in figure 18(b): the shift of the phase either advances or delays the formation of finite-distance singularity.
$\hat {a}_0=5$, the free mode promotes the disturbance instead, causing the latter to blow up at a finite distance (figure 17d). The phase of the initial amplitude of the free mode also plays an important role in the evolution, as is displayed in figure 18. Figure 18(a) shows that changing the phase either suppresses or promotes the disturbance significantly. The free mode with particular phases can cause a finite-distance singularity even though the mode with the same initial magnitude but different phases saturates. The important role of the phase is also observed for the case where the disturbance blows up, as is shown in figure 18(b): the shift of the phase either advances or delays the formation of finite-distance singularity.

Figure 17. Evolution of the combined free and locally excited modes. The solid lines represent the solution to the composite amplitude equation (5.10) with ![]() $R=10^4$,
$R=10^4$, ![]() $\bar {p}_I=10$,
$\bar {p}_I=10$, ![]() $\bar \alpha _d=0$ and
$\bar \alpha _d=0$ and ![]() $\breve {a}_0=\bar {a}_{op}+\hat {a}_0$ for
$\breve {a}_0=\bar {a}_{op}+\hat {a}_0$ for ![]() $\hat {a}_0=0$ (a),
$\hat {a}_0=0$ (a), ![]() $\hat {a}_0=1$ (b),
$\hat {a}_0=1$ (b), ![]() $\hat {a}_0=3$ (c) and
$\hat {a}_0=3$ (c) and ![]() $\hat {a}_0=5$ (d). The dashed lines represent the nonlinear solution to (4.61), and the dashed-dotted lines represent the nonlinear evolution of a free mode with the same
$\hat {a}_0=5$ (d). The dashed lines represent the nonlinear solution to (4.61), and the dashed-dotted lines represent the nonlinear evolution of a free mode with the same ![]() $\hat {a}_0$ but without forcing.
$\hat {a}_0$ but without forcing.

Figure 18. Effects of the phase of the free-mode initial amplitude, ![]() $\hat {a}_0\equiv |\hat {a}_0|\,\mathrm {e}^{\mathrm {i}\psi }$, on the evolution of the combined free and locally excited modes with
$\hat {a}_0\equiv |\hat {a}_0|\,\mathrm {e}^{\mathrm {i}\psi }$, on the evolution of the combined free and locally excited modes with ![]() $R=10^4$,
$R=10^4$, ![]() $\bar {p}_I=10$ and
$\bar {p}_I=10$ and ![]() $\bar \alpha _d=0$ for
$\bar \alpha _d=0$ for ![]() $|\hat {a}_0|=3$ (a) and
$|\hat {a}_0|=3$ (a) and ![]() $|\hat {a}_0|=5$ (b).
$|\hat {a}_0|=5$ (b).
6. Mach wave radiation
Similar to its counterpart on a free shear layer and a circular jet (Tam & Burton Reference Tam and Burton1984a,Reference Tam and Burtonb), a supersonic instability mode on a boundary layer undergoing amplification–attenuation can radiate a highly directional sound wave in the form of a Mach wave beam, as was described by Wu (Reference Wu2005). We shall follow his asymptotic approach to determine the complete structure of the Mach wave beam, formally in the non-parallel equilibrium regime. The disturbance outside of the boundary layer, ![]() $(\tilde \rho, \tilde {u}, \tilde {v}, \tilde {p}, \tilde \theta )$, is governed by the linearised Euler equations. Eliminating
$(\tilde \rho, \tilde {u}, \tilde {v}, \tilde {p}, \tilde \theta )$, is governed by the linearised Euler equations. Eliminating ![]() $\tilde \rho$,
$\tilde \rho$, ![]() $\tilde {u}$,
$\tilde {u}$, ![]() $\tilde {v}$ and
$\tilde {v}$ and ![]() $\tilde \theta$ from these equations leads to the wave equation for the pressure
$\tilde \theta$ from these equations leads to the wave equation for the pressure ![]() $\tilde {p}$
$\tilde {p}$
 \begin{equation} \mathscr{L}_w\tilde{p}\equiv\left\{M^2\left(\frac{\partial}{\partial{t}}+\frac{\partial}{\partial{x}} \right)^2 -\left( \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2} \right) \right\}\tilde{p}=0. \end{equation}
\begin{equation} \mathscr{L}_w\tilde{p}\equiv\left\{M^2\left(\frac{\partial}{\partial{t}}+\frac{\partial}{\partial{x}} \right)^2 -\left( \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2} \right) \right\}\tilde{p}=0. \end{equation}6.1. Near field of the Mach wave beam
As in Wu (Reference Wu2005), the main-layer expansion (4.57) becomes disordered when ![]() $y=O(R^{1/2})$ in view of the solution (4.12) for the pressure. The appropriate solution can be sought by introducing the variable
$y=O(R^{1/2})$ in view of the solution (4.12) for the pressure. The appropriate solution can be sought by introducing the variable
Accordingly, by the multiple-scale method, we have
The perturbation now expands as
 \begin{align} (\tilde\rho, \tilde{u}, \tilde{v}, \tilde{p}, \tilde\theta) &= \bar\epsilon_s R^{1/2}[(\rho_0, u_0, v_0, p_0, \theta_0)+R^{-1/2}(\rho_1, u_1, v_1, p_1, \theta_1) \nonumber\\ &\quad +R^{-1}(\rho_2, u_2, v_2, p_2, \theta_2)+\cdots]. \end{align}
\begin{align} (\tilde\rho, \tilde{u}, \tilde{v}, \tilde{p}, \tilde\theta) &= \bar\epsilon_s R^{1/2}[(\rho_0, u_0, v_0, p_0, \theta_0)+R^{-1/2}(\rho_1, u_1, v_1, p_1, \theta_1) \nonumber\\ &\quad +R^{-1}(\rho_2, u_2, v_2, p_2, \theta_2)+\cdots]. \end{align}
Substitution of the above expansion for ![]() $\tilde {p}$ into (6.1) leads to the equation for the leading-order pressure,
$\tilde {p}$ into (6.1) leads to the equation for the leading-order pressure, ![]() $\mathscr {L}_w p_0=0$. The solution may be written in the form
$\mathscr {L}_w p_0=0$. The solution may be written in the form
where ![]() $q=\sqrt {M^2(1-c)^2-1}$, and
$q=\sqrt {M^2(1-c)^2-1}$, and ![]() $\bar {p}_0$ is determined by considering the second-order term.
$\bar {p}_0$ is determined by considering the second-order term.
Proceeding to the next order, we obtain the equation for ![]() $p_1$
$p_1$
It is worth pointing out that ![]() $p_1$ contains the incident wave, which satisfies the homogeneous equation and thus does not affect the radiation directly. In order to remove the secular terms in the expansion, the term proportional to
$p_1$ contains the incident wave, which satisfies the homogeneous equation and thus does not affect the radiation directly. In order to remove the secular terms in the expansion, the term proportional to ![]() $p_0$ on the right-hand side of the above equation is required to be zero, from which and (6.5), we obtain
$p_0$ on the right-hand side of the above equation is required to be zero, from which and (6.5), we obtain
which satisfies the boundary condition through matching with the main-layer solution
The solution to (6.7)–(6.8) is found by the method of characteristic lines as
which indicates that the amplitude modulation propagates along the characteristic lines
6.2. Far field of the Mach wave beam
As was pointed out by Wu (Reference Wu2005), the expansion (6.4) and the solution (6.9) are no longer valid in the far field corresponding to the region
To construct the valid solution in this far field, we introduce the variable
and it follows that
The expansion for the pressure takes the form
 \begin{align} \tilde{p} &= \bar\epsilon_s R^{1/2}[\tilde{p}_0(\bar{\xi},\tilde{y}) +R^{-1}\tilde{p}_1(\bar{\xi},\tilde{y})+\cdots]\exp({\mathrm{i}\alpha(x-ct-qy)}) \nonumber\\ &\quad +\bar\epsilon_s\bar{p}_I\exp({\mathrm{i}\alpha(x-ct+qy)})+\mathrm{c.c.}. \end{align}
\begin{align} \tilde{p} &= \bar\epsilon_s R^{1/2}[\tilde{p}_0(\bar{\xi},\tilde{y}) +R^{-1}\tilde{p}_1(\bar{\xi},\tilde{y})+\cdots]\exp({\mathrm{i}\alpha(x-ct-qy)}) \nonumber\\ &\quad +\bar\epsilon_s\bar{p}_I\exp({\mathrm{i}\alpha(x-ct+qy)})+\mathrm{c.c.}. \end{align}
Again the leading-order term satisfies the wave equation, but the secular condition for ![]() $\tilde {p}_1$ leads to (Wu Reference Wu2005)
$\tilde {p}_1$ leads to (Wu Reference Wu2005)
which is different from (6.7). Matching with the near-field solution (6.9) gives the boundary condition
Equation (6.15) with (6.16) is solved by Fourier transform to give
For a linear free mode, ![]() $\bar {A}(\bar {x})=\bar {a}_0\exp ({\sigma \bar {x}^2/2})$, and the solution has the explicit expression
$\bar {A}(\bar {x})=\bar {a}_0\exp ({\sigma \bar {x}^2/2})$, and the solution has the explicit expression
 \begin{equation} |\tilde{p}_0(\bar{\xi},\tilde{y})|=\left\lvert 1+\frac{\mathrm{i} M^2 c^2\sigma}{\alpha q^3}\tilde{y}\right\rvert^{-1/2} \left\lvert \mathscr{C}_{\infty}\bar{a}_0\exp\left\{ \frac{1}{2}\sigma\bar{\xi}^2 /\left( 1+\frac{\mathrm{i} M^2 c^2\sigma}{\alpha q^3}\tilde{y} \right)\right\} \right\rvert. \end{equation}
\begin{equation} |\tilde{p}_0(\bar{\xi},\tilde{y})|=\left\lvert 1+\frac{\mathrm{i} M^2 c^2\sigma}{\alpha q^3}\tilde{y}\right\rvert^{-1/2} \left\lvert \mathscr{C}_{\infty}\bar{a}_0\exp\left\{ \frac{1}{2}\sigma\bar{\xi}^2 /\left( 1+\frac{\mathrm{i} M^2 c^2\sigma}{\alpha q^3}\tilde{y} \right)\right\} \right\rvert. \end{equation}6.3. Numerical evaluation
To compute the distribution of the sound field, we rewrite the far-field pressure (6.17) as
 \begin{align} \tilde{p}_0(\check{x},\check{y}) &= \frac{R^{1/4}\exp({{\rm \pi}\mathrm{i}/4})}{|\sigma_r|^{1/4}\sqrt{\check{y}}} \sqrt{\frac{\alpha q^3}{2{\rm \pi} M^2 c^2}}\mathscr{C}_{\infty} \int_{-\infty}^{\infty} \bar{A}(\zeta/\sqrt{|\sigma_r|})\exp\left\{-\frac{\mathrm{i}\alpha q^3 R^{1/2}}{2 M^2 c^2\sqrt{|\sigma_r|}\check{y}} \right.\nonumber\\ &\quad \left.\vphantom{\frac{\mathrm{i}\alpha q^3 R^{1/2}}{2 M^2 c^2\sqrt{|\sigma_r|}\check{y}}} \times[\check{x}-q^{-1}(M^2(1-c)-1)\check{y}-\zeta]^2 \right\}\,{\rm d}\zeta, \end{align}
\begin{align} \tilde{p}_0(\check{x},\check{y}) &= \frac{R^{1/4}\exp({{\rm \pi}\mathrm{i}/4})}{|\sigma_r|^{1/4}\sqrt{\check{y}}} \sqrt{\frac{\alpha q^3}{2{\rm \pi} M^2 c^2}}\mathscr{C}_{\infty} \int_{-\infty}^{\infty} \bar{A}(\zeta/\sqrt{|\sigma_r|})\exp\left\{-\frac{\mathrm{i}\alpha q^3 R^{1/2}}{2 M^2 c^2\sqrt{|\sigma_r|}\check{y}} \right.\nonumber\\ &\quad \left.\vphantom{\frac{\mathrm{i}\alpha q^3 R^{1/2}}{2 M^2 c^2\sqrt{|\sigma_r|}\check{y}}} \times[\check{x}-q^{-1}(M^2(1-c)-1)\check{y}-\zeta]^2 \right\}\,{\rm d}\zeta, \end{align}where we have introduced
As a highlight of the structure of the sound field, we first study the case of a linear free mode and consider the analytical formula (6.18) in terms of the variables ![]() $\check {x}$ and
$\check {x}$ and ![]() $\check {y}$. Let us write
$\check {y}$. Let us write ![]() $|\tilde {p}_0(\bar {\xi },\tilde {y})|$ as
$|\tilde {p}_0(\bar {\xi },\tilde {y})|$ as
where we have put
 \begin{equation} \left.\begin{gathered} H(\kern0.06em \check{y})=(1-\sigma_i\check{Q}\check{y})^2+(\sigma_r\check{Q}\check{y})^2,\quad \check{Q}=\frac{M^2c^2}{R^{1/2}\sqrt{|\sigma_r|}\alpha q^3},\\ \check{q}=\frac{M^2(1-c)-1}{q},\quad \check{\sigma}_r=\frac{\sigma_r}{|\sigma_r|}. \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} H(\kern0.06em \check{y})=(1-\sigma_i\check{Q}\check{y})^2+(\sigma_r\check{Q}\check{y})^2,\quad \check{Q}=\frac{M^2c^2}{R^{1/2}\sqrt{|\sigma_r|}\alpha q^3},\\ \check{q}=\frac{M^2(1-c)-1}{q},\quad \check{\sigma}_r=\frac{\sigma_r}{|\sigma_r|}. \end{gathered}\right\} \end{equation}
In order to locate a possible maximum/minimum (or saddle point) of ![]() $F(\check {x},\check {y})$, we seek stationary point(s) by setting
$F(\check {x},\check {y})$, we seek stationary point(s) by setting ![]() $\partial F/\partial \check {x}=0$ and
$\partial F/\partial \check {x}=0$ and ![]() $\partial F/\partial \check {y}=0$. The first of the above equations implies that
$\partial F/\partial \check {y}=0$. The first of the above equations implies that ![]() $\check {x}=\check {q}\check {y}$, use of which in the second gives
$\check {x}=\check {q}\check {y}$, use of which in the second gives ![]() $\partial H(\kern0.06em \check {y})/\partial \check {y}=0$. The above equation yields a unique stationary point
$\partial H(\kern0.06em \check {y})/\partial \check {y}=0$. The above equation yields a unique stationary point ![]() $(\check {x}_s,\check {y}_s)$,
$(\check {x}_s,\check {y}_s)$,
which indicates that a stationary point with ![]() $\check {y}_s>0$ exists only when
$\check {y}_s>0$ exists only when ![]() $\sigma _i>0$. It is noted that the characteristic line emanating from the origin passes through the stationary point.
$\sigma _i>0$. It is noted that the characteristic line emanating from the origin passes through the stationary point.
Next, we evaluate the second-order derivatives of ![]() $F(\check {x},\check {y})$ at
$F(\check {x},\check {y})$ at ![]() $(\check {x}_s,\check {y}_s)$, and find that
$(\check {x}_s,\check {y}_s)$, and find that
 \begin{equation} \check{\varDelta}(\check{x}_s,\check{y}_s)\equiv\frac{\partial^2 F}{\partial\check{x}^2} \frac{\partial^2 F}{\partial\check{y}^2} -\left( \frac{\partial^2 F}{\partial\check{x}\partial\check{y}} \right)^2 =-\frac{1}{2}F^2\check{\sigma}_r\frac{(\sigma_r^2+\sigma_i^2)\check{Q}^2}{H^2}>0. \end{equation}
\begin{equation} \check{\varDelta}(\check{x}_s,\check{y}_s)\equiv\frac{\partial^2 F}{\partial\check{x}^2} \frac{\partial^2 F}{\partial\check{y}^2} -\left( \frac{\partial^2 F}{\partial\check{x}\partial\check{y}} \right)^2 =-\frac{1}{2}F^2\check{\sigma}_r\frac{(\sigma_r^2+\sigma_i^2)\check{Q}^2}{H^2}>0. \end{equation}
Thus, we conclude that the stationary point ![]() $(\check {x}_s,\check {y}_s)$ is a local maximum.
$(\check {x}_s,\check {y}_s)$ is a local maximum.
For the present case, we have ![]() $\sigma _i>0$, so that there is a stationary point with
$\sigma _i>0$, so that there is a stationary point with ![]() $\check {y}_s>0$, which turns out to be the maximum. The fact that
$\check {y}_s>0$, which turns out to be the maximum. The fact that ![]() $\sigma _i>0$ in the present case is consistent with the result of Chuvakhov & Fedorov (Reference Chuvakhov and Fedorov2016). Figures 3 and 9 of their paper show that the phase speed decreases as the mode passes through the neutral point, indicating that the streamwise wavenumber increases and hence its derivative with respect to the streamwise coordinate at the neutral position is positive. Since in our theory
$\sigma _i>0$ in the present case is consistent with the result of Chuvakhov & Fedorov (Reference Chuvakhov and Fedorov2016). Figures 3 and 9 of their paper show that the phase speed decreases as the mode passes through the neutral point, indicating that the streamwise wavenumber increases and hence its derivative with respect to the streamwise coordinate at the neutral position is positive. Since in our theory ![]() $\sigma _i$ is proportional to that derivative, it is positive. As a validation of our numerical code evaluating (6.19), we compare the result of the analytical formula (6.18) with the numerical evaluation of (6.19) in figure 19. The two are in complete agreement. Figure 19(b), which is a locally enlarged view of the ‘focal region’, shows that the stationary point is indeed a local maximum. For the case of
$\sigma _i$ is proportional to that derivative, it is positive. As a validation of our numerical code evaluating (6.19), we compare the result of the analytical formula (6.18) with the numerical evaluation of (6.19) in figure 19. The two are in complete agreement. Figure 19(b), which is a locally enlarged view of the ‘focal region’, shows that the stationary point is indeed a local maximum. For the case of ![]() $\sigma _i\leq 0$, no physically meaningful stationary point exists; contours of the sound intensity are lobed, as is shown in Wu (Reference Wu2005).
$\sigma _i\leq 0$, no physically meaningful stationary point exists; contours of the sound intensity are lobed, as is shown in Wu (Reference Wu2005).
We now turn to the acoustic field of a nonlinearly evolving mode with and without the incident sound. The pressure contours predicted using the solutions to the composite amplitude equation (5.10) with ![]() $R=10^4$ are displayed in figure 20. The pressure contours without an impinging sound are shown in figure 20(a) with the far field in figure 20(b). The emitted sound wave focuses first towards the point where the intensity attains its maximum, beyond which the contours feature a main lobe flanked by two secondary beams. The contours are rather smooth. Figure 20(c) depicts the pressure contours of a locally excited mode by the incident sound without any oncoming free mode. The distinct feature is that the contours exhibit multiple spikes. This is due to amplitude oscillations caused by the forcing. The structure in the far field is illustrated in figure 20(d). Figure 20(e) shows the acoustic field in the case where a free radiating mode is present in addition to the locally excited mode. The far-field region in figure 20(f) shows that multiple spikes are again present as a result of the amplitude oscillations. In summary, the pattern of the Mach wave radiation is substantially changed in the presence of the impinging sound.
$R=10^4$ are displayed in figure 20. The pressure contours without an impinging sound are shown in figure 20(a) with the far field in figure 20(b). The emitted sound wave focuses first towards the point where the intensity attains its maximum, beyond which the contours feature a main lobe flanked by two secondary beams. The contours are rather smooth. Figure 20(c) depicts the pressure contours of a locally excited mode by the incident sound without any oncoming free mode. The distinct feature is that the contours exhibit multiple spikes. This is due to amplitude oscillations caused by the forcing. The structure in the far field is illustrated in figure 20(d). Figure 20(e) shows the acoustic field in the case where a free radiating mode is present in addition to the locally excited mode. The far-field region in figure 20(f) shows that multiple spikes are again present as a result of the amplitude oscillations. In summary, the pattern of the Mach wave radiation is substantially changed in the presence of the impinging sound.

Figure 20. Contours of the far-field pressure ![]() $|\tilde {p}_0|$ using the solution to the composite amplitude equation (5.10) with
$|\tilde {p}_0|$ using the solution to the composite amplitude equation (5.10) with ![]() $R=10^4$. Panels show (a)
$R=10^4$. Panels show (a) ![]() $\bar {p}_I=0$ and
$\bar {p}_I=0$ and ![]() $\breve {a}_0=3$, (c)
$\breve {a}_0=3$, (c) ![]() $\bar {p}_I=10$ and
$\bar {p}_I=10$ and ![]() $\breve {a}_0=\bar {a}_{op}$, (e)
$\breve {a}_0=\bar {a}_{op}$, (e) ![]() $\bar {p}_I=10$ and
$\bar {p}_I=10$ and ![]() $\breve {a}_0=\bar {a}_{op}+3$. (b,d,f) Show the far field of (a,c,e), respectively.
$\breve {a}_0=\bar {a}_{op}+3$. (b,d,f) Show the far field of (a,c,e), respectively.
7. Summary and conclusions
The present paper has investigated the effects of impinging sound waves on linear and nonlinear instability of supersonic boundary layers at asymptotically large Reynolds numbers. The focus is on the flow conditions (Mach number and wall temperatures) under which there exists a radiating mode, which remains finite at the outer edge of the boundary layer and emits a Mach wave. We identified and described a particularly important mechanism, referred to as fundamental resonance, through which the radiating mode and the impinging sound with the same frequency and wavenumber interact effectively. As a result, the latter can, even with a rather low amplitude, alters substantially the linear and nonlinear evolution of the radiating mode.
In order to provide the context for this mechanism, we first considered reflection of an impinging slow sound wave by the boundary layer. The boundary-layer response, consisting of the absorbed and reflected waves, is predicted by a primarily inviscid analysis supplemented by a jump condition across the critical level, which is derived by analysing the viscous critical layer. We introduced the reflection coefficient ![]() $\mathscr {R}$, defined as the ratio of the magnitude of the outgoing wave to that of the incident wave. The scaled sound pressure
$\mathscr {R}$, defined as the ratio of the magnitude of the outgoing wave to that of the incident wave. The scaled sound pressure ![]() $|\tilde {b}|$ at the critical level was used to measure the absorbed disturbance. We monitored the values of
$|\tilde {b}|$ at the critical level was used to measure the absorbed disturbance. We monitored the values of ![]() $|\mathscr {R}|$ and
$|\mathscr {R}|$ and ![]() $|\tilde {b}|$ in a broad range of the incident angle and frequency, and found that both are extraordinarily large for a small subset of the sound incident angle and frequency. Furthermore, for a specific pairing of incidence angle and frequency,
$|\tilde {b}|$ in a broad range of the incident angle and frequency, and found that both are extraordinarily large for a small subset of the sound incident angle and frequency. Furthermore, for a specific pairing of incidence angle and frequency, ![]() $\mathscr {R}$ becomes infinite, which is referred to as resonant over-reflection, and the reflected wave corresponds to the neutral radiating mode. The infinite reflection coefficient signals high sensitivity of the radiating mode to this particular incident sound wave.
$\mathscr {R}$ becomes infinite, which is referred to as resonant over-reflection, and the reflected wave corresponds to the neutral radiating mode. The infinite reflection coefficient signals high sensitivity of the radiating mode to this particular incident sound wave.
The resonant over-reflection implies that, among broadband external acoustic disturbances, there exist ones whose wavenumber and frequency would coincide with those of the neutral radiating mode at each streamwise location. As a result, fundamental resonance takes place between the sound and the instability mode. The excitation of the radiating mode as well as its evolution were described by using the nonlinear critical-layer theory. Depending on the magnitude of the sound, the amplitude equations are derived in the non-equilibrium parallel and equilibrium non-parallel regimes, respectively. In the non-equilibrium regime, which occurs when the incident sound is sufficiently strong, the amplitude equation admits an equilibrium solution representing the nonlinear response, which modifies the linear growth rate of the mode significantly. In the nonlinear evolution stage, the incident sound wave promotes nonlinear amplification and advances the eventual blow-up. In the equilibrium regime, in addition to the pre-existing free mode, the locally forced response evolves into a radiating mode. The evolution depends on both the intensity of the incident sound and the amplitude of the pre-existing free mode. With the amplitude equations derived for the two distinguished regimes, we then constructed a composite amplitude equation that takes into account non-parallel and non-equilibrium effects simultaneously. This equation was solved numerically, and solutions showed that the incident sound influences the evolution significantly: with moderate intensity it inhibits the disturbance, but enhances amplification when the intensity is sufficiently large. The most obvious effect of the impinging sound wave is that the amplitude undergoes vigorous oscillations, whether attenuating or amplifying. The amplitude evolution predicted by the composite amplitude equation was then used to study the Mach wave radiation process. The Mach wave in the far field is drastically altered by the impinging sound wave: the characteristic simple lobed beam is replaced by a highly complex directivity.
The present theoretical investigation provides physical insights into how acoustic waves originated from the environment may influence the instability and acoustic radiation of supersonic boundary layers. The rather striking phenomena revealed and described are important when incident sound waves of an appreciable level are present, but may also be relevant if the experimental data are to be extrapolated to flight conditions. The results may be of relevance for flow control using acoustic actuation.
Finally, we comment on related issues that require further investigation. Free-stream acoustic waves in reality have a broadband spectrum whereas our theory considered a single discrete component. The simplification was based on the observation that, among all possible components, only those in a narrow band centred at the particular component with the same frequency and wavenumber of the radiating mode can take part in the fundamental resonance. Only one such component was considered in this paper for simplicity, but the analysis can be generalised to include a continuum of components in the narrow band, in which case the amplitude function ![]() $A$ would be allowed to modulate simultaneously in time. Another issue concerns the fact that solutions to the amplitude equations blow up for a certain range of parameters. The present weakly nonlinear theory becomes invalid close to the blow-up location, where the disturbance would evolve on the short scale comparable to the boundary-layer thickness and be governed by the Euler equations (Leib Reference Leib1991). It is also possible that the primary disturbance becomes susceptible to secondary instability. Either of the scenarios signals a cascade into small scales, the implication of which is unclear, but it might undermine the quantitative usefulness of asymptotic solutions as was argued by Cowley (Reference Cowley2001). Predicting ensuing rapid evolution and/or onset of small-scale motions is a major challenge.
$A$ would be allowed to modulate simultaneously in time. Another issue concerns the fact that solutions to the amplitude equations blow up for a certain range of parameters. The present weakly nonlinear theory becomes invalid close to the blow-up location, where the disturbance would evolve on the short scale comparable to the boundary-layer thickness and be governed by the Euler equations (Leib Reference Leib1991). It is also possible that the primary disturbance becomes susceptible to secondary instability. Either of the scenarios signals a cascade into small scales, the implication of which is unclear, but it might undermine the quantitative usefulness of asymptotic solutions as was argued by Cowley (Reference Cowley2001). Predicting ensuing rapid evolution and/or onset of small-scale motions is a major challenge.
Acknowledgements
The referees are thanked for their comments and suggestions, which helped us improve the manuscript.
Funding
F.Q. acknowledges the support of an EPSRC-IDS scholarship from the Department of Mathematics of Imperial College London.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Computation of neutral eigenmode and reflection coefficient
A.1. Computation of the neutral eigenmode
To solve Rayleigh equation (2.30) numerically, we recast it into a system of first-order differential equations. The integration starts at a position slightly beneath the critical level, ![]() $\eta _c-\tilde {d}$, with the initial values
$\eta _c-\tilde {d}$, with the initial values ![]() $\bar \phi _a(\eta _c-\tilde {d})$,
$\bar \phi _a(\eta _c-\tilde {d})$, ![]() $\bar \phi _a^\prime (\eta _c-\tilde {d})$,
$\bar \phi _a^\prime (\eta _c-\tilde {d})$, ![]() $\bar \phi _b(\eta _c-\tilde {d})$ and
$\bar \phi _b(\eta _c-\tilde {d})$ and ![]() $\bar \phi _b^\prime (\eta _c-\tilde {d})$ calculated using (2.34) and (2.35). The governing equations are marched from
$\bar \phi _b^\prime (\eta _c-\tilde {d})$ calculated using (2.34) and (2.35). The governing equations are marched from ![]() $\eta =\eta _c-\tilde {d}$ to
$\eta =\eta _c-\tilde {d}$ to ![]() $\eta =0$ by the fourth-order Runge–Kutta method, leading to
$\eta =0$ by the fourth-order Runge–Kutta method, leading to ![]() $( \bar {p}_a(0), \bar {p}_a^\prime (0) )$ and
$( \bar {p}_a(0), \bar {p}_a^\prime (0) )$ and ![]() $( \bar {p}_b(0), \bar {p}_b^\prime (0) )$ at the wall. Imposing the first of the boundary condition (2.31), we obtain
$( \bar {p}_b(0), \bar {p}_b^\prime (0) )$ at the wall. Imposing the first of the boundary condition (2.31), we obtain
A second integration starts from the position ![]() $\eta =\eta _e=20$, which represents the far field. According to (2.32), the initial condition can be taken as
$\eta =\eta _e=20$, which represents the far field. According to (2.32), the initial condition can be taken as
The governing equations are marched from ![]() $\eta =\eta _e$ to
$\eta =\eta _e$ to ![]() $\eta =\eta _c+\tilde {d}$ again by the fourth-order Runge–Kutta method, yielding
$\eta =\eta _c+\tilde {d}$ again by the fourth-order Runge–Kutta method, yielding ![]() $( \hat {p}_0(\eta _c+\tilde {d}), \hat {p}_0^\prime (\eta _c+\tilde {d}) )$ just above the critical level. Equating
$( \hat {p}_0(\eta _c+\tilde {d}), \hat {p}_0^\prime (\eta _c+\tilde {d}) )$ just above the critical level. Equating ![]() $\mathscr {C}_{\infty }( \hat {p}_0(\eta _c+\tilde {d}), \hat {p}_0^\prime (\eta _c+\tilde {d}) )$ to the corresponding local analytical solution (2.33) at
$\mathscr {C}_{\infty }( \hat {p}_0(\eta _c+\tilde {d}), \hat {p}_0^\prime (\eta _c+\tilde {d}) )$ to the corresponding local analytical solution (2.33) at ![]() $\eta _c+\tilde {d}$, we obtain a pair of equations, eliminating from which the constant
$\eta _c+\tilde {d}$, we obtain a pair of equations, eliminating from which the constant ![]() $\mathscr {C}_{\infty }$ yields the expression for
$\mathscr {C}_{\infty }$ yields the expression for ![]() $\bar {a}^+$
$\bar {a}^+$
 \begin{equation} \bar{a}^+=\frac{\hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_b(\eta_c+\tilde{d})- \hat{p}_0(\eta_c+\tilde{d})\bar\phi_b^\prime(\eta_c+\tilde{d})} {\hat{p}_0(\eta_c+\tilde{d})\bar\phi_a^\prime(\eta_c+\tilde{d})-\hat{p}_0^\prime (\eta_c+\tilde{d})\bar\phi_a(\eta_c+\tilde{d})}. \end{equation}
\begin{equation} \bar{a}^+=\frac{\hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_b(\eta_c+\tilde{d})- \hat{p}_0(\eta_c+\tilde{d})\bar\phi_b^\prime(\eta_c+\tilde{d})} {\hat{p}_0(\eta_c+\tilde{d})\bar\phi_a^\prime(\eta_c+\tilde{d})-\hat{p}_0^\prime (\eta_c+\tilde{d})\bar\phi_a(\eta_c+\tilde{d})}. \end{equation}In addition, a linear critical-layer analysis (presented in § 4.1) determines the jump
which corresponds to, as is well known, the phase of the logarithm in the Frobenius solution changing by ![]() $-{\rm \pi}$ as
$-{\rm \pi}$ as ![]() $\eta$ goes from
$\eta$ goes from ![]() $\eta _c^+$ to
$\eta _c^+$ to ![]() $\eta _c^-$. From (A1), (A3) and (A4) follows the dispersion relation
$\eta _c^-$. From (A1), (A3) and (A4) follows the dispersion relation
 \begin{align} \varDelta(\alpha,c) &\equiv \frac{\hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_b(\eta_c+\tilde{d})- \hat{p}_0(\eta_c+\tilde{d})\bar\phi_b^\prime(\eta_c+\tilde{d})} {\hat{p}_0(\eta_c+\tilde{d})\bar\phi_a^\prime(\eta_c+\tilde{d})- \hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_a(\eta_c+\tilde{d})} \nonumber\\ &\quad +\bar{p}_b^\prime(0)/\bar{p}_a^\prime(0)-\frac{\alpha^2\bar{T}_c^2}{3} \left(\frac{2\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right){\rm \pi}\mathrm{i}=0. \end{align}
\begin{align} \varDelta(\alpha,c) &\equiv \frac{\hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_b(\eta_c+\tilde{d})- \hat{p}_0(\eta_c+\tilde{d})\bar\phi_b^\prime(\eta_c+\tilde{d})} {\hat{p}_0(\eta_c+\tilde{d})\bar\phi_a^\prime(\eta_c+\tilde{d})- \hat{p}_0^\prime(\eta_c+\tilde{d})\bar\phi_a(\eta_c+\tilde{d})} \nonumber\\ &\quad +\bar{p}_b^\prime(0)/\bar{p}_a^\prime(0)-\frac{\alpha^2\bar{T}_c^2}{3} \left(\frac{2\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right){\rm \pi}\mathrm{i}=0. \end{align}
The Newton–Raphson method is employed to solve the dispersion relation for an initial guess of ![]() $(\alpha,c)$.
$(\alpha,c)$.
A.2. Computation of the reflection coefficient and boundary-layer response
For a given pairing ![]() $(\alpha _{s}, c_s)$, the reflection coefficient
$(\alpha _{s}, c_s)$, the reflection coefficient ![]() $\mathscr {R}$ and boundary-layer response are determined by using a combination of analytical results and numerical method. Using the similarity solution for
$\mathscr {R}$ and boundary-layer response are determined by using a combination of analytical results and numerical method. Using the similarity solution for ![]() $\bar {U}$ and
$\bar {U}$ and ![]() $\bar {T}$, (3.3) for
$\bar {T}$, (3.3) for ![]() $\check {p}_s$ is recast in terms of
$\check {p}_s$ is recast in terms of ![]() $\eta$ and then written as a system of first-order ordinary differential equations.
$\eta$ and then written as a system of first-order ordinary differential equations.
Near the critical level ![]() $\eta _c$ (i.e.
$\eta _c$ (i.e. ![]() $\breve {\eta }\equiv \eta -\eta _c\rightarrow 0$), the pressure takes the form
$\breve {\eta }\equiv \eta -\eta _c\rightarrow 0$), the pressure takes the form
where ![]() $\tilde \phi _{a}$ and
$\tilde \phi _{a}$ and ![]() $\tilde \phi _{b}$ have the same expressions as (2.34) and (2.35), respectively, with
$\tilde \phi _{b}$ have the same expressions as (2.34) and (2.35), respectively, with ![]() $\alpha$ being replaced by
$\alpha$ being replaced by ![]() $\alpha _{s}$. Integrating from
$\alpha _{s}$. Integrating from ![]() $\eta =\eta _c-\tilde {d}$ to
$\eta =\eta _c-\tilde {d}$ to ![]() $\eta =0$ with the initial conditions
$\eta =0$ with the initial conditions ![]() $(\tilde \phi _a(\eta _c-\tilde {d}),\tilde \phi ^\prime _a(\eta _c-\tilde {d}))$ and
$(\tilde \phi _a(\eta _c-\tilde {d}),\tilde \phi ^\prime _a(\eta _c-\tilde {d}))$ and ![]() $(\tilde \phi _b(\eta _c-\tilde {d}),\tilde \phi ^\prime _b(\eta _c-\tilde {d}))$, we obtain
$(\tilde \phi _b(\eta _c-\tilde {d}),\tilde \phi ^\prime _b(\eta _c-\tilde {d}))$, we obtain ![]() $(p_a(0),p_a^\prime (0))$ and
$(p_a(0),p_a^\prime (0))$ and ![]() $(p_b(0),p_b^\prime (0))$, respectively. Then use of the impermeability condition gives
$(p_b(0),p_b^\prime (0))$, respectively. Then use of the impermeability condition gives
In the far field, the pressure takes the form
Given the initial values ![]() $(\exp ({\mathrm {i}\gamma _{s}\eta _e}),\mathrm {i}\gamma _{s}\exp ({\mathrm {i}\gamma _{s}\eta _e}))$ and
$(\exp ({\mathrm {i}\gamma _{s}\eta _e}),\mathrm {i}\gamma _{s}\exp ({\mathrm {i}\gamma _{s}\eta _e}))$ and ![]() $(\exp ({-\mathrm {i}\gamma _{s}\eta _e}),-\mathrm {i}\gamma _{s}\exp ({-\mathrm {i}\gamma _{s}\eta _e}))$, the governing equations are marched from
$(\exp ({-\mathrm {i}\gamma _{s}\eta _e}),-\mathrm {i}\gamma _{s}\exp ({-\mathrm {i}\gamma _{s}\eta _e}))$, the governing equations are marched from ![]() $\eta =\eta _e$ to
$\eta =\eta _e$ to ![]() $\eta =\eta _c+\tilde {d}$ by the fourth-order Runge–Kutta method, leading to
$\eta =\eta _c+\tilde {d}$ by the fourth-order Runge–Kutta method, leading to ![]() $(p_i(\eta _c+\tilde {d}),p_i^\prime (\eta _c+\tilde {d}))$ and
$(p_i(\eta _c+\tilde {d}),p_i^\prime (\eta _c+\tilde {d}))$ and ![]() $(p_r(\eta _c+\tilde {d}),p_r^\prime (\eta _c+\tilde {d}))$ above the critical level. Equating the numerical solution to the analytical formula (A6) yields
$(p_r(\eta _c+\tilde {d}),p_r^\prime (\eta _c+\tilde {d}))$ above the critical level. Equating the numerical solution to the analytical formula (A6) yields
In addition, the jump condition can be written as
where
From (A7) and (A9)–(A11), we obtain the reflection coefficient
 \begin{equation} \mathscr{R}(\alpha_{s},c_s)=\frac{\mathcal{B}p_i(\eta_c+\tilde{d})-\mathcal{A}p_i^\prime(\eta_c+\tilde{d})} {\mathcal{A}p_r^\prime(\eta_c+\tilde{d})-\mathcal{B}p_r(\eta_c+\tilde{d})}, \end{equation}
\begin{equation} \mathscr{R}(\alpha_{s},c_s)=\frac{\mathcal{B}p_i(\eta_c+\tilde{d})-\mathcal{A}p_i^\prime(\eta_c+\tilde{d})} {\mathcal{A}p_r^\prime(\eta_c+\tilde{d})-\mathcal{B}p_r(\eta_c+\tilde{d})}, \end{equation}where we have put
We introduce the scaled quantity ![]() $\tilde {b}\equiv b_s/p_I$, which measures the response in the critical layer. Substituting the expression of
$\tilde {b}\equiv b_s/p_I$, which measures the response in the critical layer. Substituting the expression of ![]() $\mathscr {R}$ into (A9), we find that
$\mathscr {R}$ into (A9), we find that
Appendix B. The mean-flow distortion and interaction at the cubic level
The mean-flow distortion driven by the nonlinear interaction of the fundamental wave is found to satisfy the equations
where the asterisk indicates the complex conjugate. Equation (B1c) is solved to give
 \begin{align} \varTheta_M &= \mathrm{i}\alpha^3\bar{T}_c^\prime\bar{U}_c^\prime\! \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} \!\xi\exp(-s_p\xi^3-3s_p\xi^2\eta \nonumber\\ &\quad +\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi) \tilde{A}(\tilde{x}-c\eta)\tilde{A}^*(\tilde{x}-c\eta-c\xi)\,{\rm d}\eta{\rm d}\xi. \end{align}
\begin{align} \varTheta_M &= \mathrm{i}\alpha^3\bar{T}_c^\prime\bar{U}_c^\prime\! \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} \!\xi\exp(-s_p\xi^3-3s_p\xi^2\eta \nonumber\\ &\quad +\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi) \tilde{A}(\tilde{x}-c\eta)\tilde{A}^*(\tilde{x}-c\eta-c\xi)\,{\rm d}\eta{\rm d}\xi. \end{align}
Equations (B1a) and (B1c) imply that ![]() $V_M=\lambda \bar {\mu }_c Pr^{-1}\varTheta _{M,Y}$, which is inserted into (B1b) to obtain
$V_M=\lambda \bar {\mu }_c Pr^{-1}\varTheta _{M,Y}$, which is inserted into (B1b) to obtain
We find the solution to be
 \begin{align} U_{M,YY} &= \alpha^4(\bar{U}_c^\prime)^3\frac{\bar{T}_c^\prime}{\bar{T}_c}\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} \xi^2\exp(-s_p\xi^3-3s\xi^2\eta+\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi) \nonumber\\ &\quad \times \left[1-\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left( \exp({(s_p-s)\xi^3})-\exp({3(s-s_p)\xi^2\eta}) \right) \right.\nonumber\\ &\quad + \left.\frac{\bar{T}_c}{\bar{T}_c^\prime}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\exp({(s_p-s)\xi^3})\right] \nonumber\\ &\quad \times \tilde{A}(\tilde{x}-c\eta)\tilde{A}^*(\tilde{x}-c\eta-c\xi)\,{\rm d}\eta{\rm d}\xi. \end{align}
\begin{align} U_{M,YY} &= \alpha^4(\bar{U}_c^\prime)^3\frac{\bar{T}_c^\prime}{\bar{T}_c}\int_{0}^{\infty}\!\!\!\int_{0}^{\infty} \xi^2\exp(-s_p\xi^3-3s\xi^2\eta+\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi) \nonumber\\ &\quad \times \left[1-\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} \left( \exp({(s_p-s)\xi^3})-\exp({3(s-s_p)\xi^2\eta}) \right) \right.\nonumber\\ &\quad + \left.\frac{\bar{T}_c}{\bar{T}_c^\prime}\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\exp({(s_p-s)\xi^3})\right] \nonumber\\ &\quad \times \tilde{A}(\tilde{x}-c\eta)\tilde{A}^*(\tilde{x}-c\eta-c\xi)\,{\rm d}\eta{\rm d}\xi. \end{align}Now we proceed to consider the fundamental regenerated by the cubic interaction, whose governing equations are found to be
In order to find ![]() $U_2$ and hence the jump, we must calculate the temperature component
$U_2$ and hence the jump, we must calculate the temperature component ![]() $\varTheta _2$. Equation (B5c) is thus solved to give
$\varTheta _2$. Equation (B5c) is thus solved to give
 \begin{align} \varTheta_2 &=-\mathrm{i}\alpha^5(\bar{U}_c^\prime)^2\bar{T}_c^\prime\int_{0}^{\infty}\!\!\!\int_{0}^{\infty}\!\!\!\int_{-\zeta}^{\infty} \zeta^2\exp[-s_p\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi-2s_p\zeta^3-3s_p\zeta^2\eta] \nonumber\\ &\quad \times \tilde{A}(\tilde{x}-c\xi-c\zeta)\tilde{A}(\tilde{x}-c\xi-c\zeta-c\eta) \tilde{A}^*(\tilde{x}-c\xi-2c\zeta-c\eta)\,{\rm d}\xi{\rm d}\eta{\rm d}\zeta. \end{align}
\begin{align} \varTheta_2 &=-\mathrm{i}\alpha^5(\bar{U}_c^\prime)^2\bar{T}_c^\prime\int_{0}^{\infty}\!\!\!\int_{0}^{\infty}\!\!\!\int_{-\zeta}^{\infty} \zeta^2\exp[-s_p\xi^3-\mathrm{i}\alpha\bar{U}_c^\prime\bar{Y}\xi-2s_p\zeta^3-3s_p\zeta^2\eta] \nonumber\\ &\quad \times \tilde{A}(\tilde{x}-c\xi-c\zeta)\tilde{A}(\tilde{x}-c\xi-c\zeta-c\eta) \tilde{A}^*(\tilde{x}-c\xi-2c\zeta-c\eta)\,{\rm d}\xi{\rm d}\eta{\rm d}\zeta. \end{align}Equations (B5a) and (B5b) can be reduced to
The jump of ![]() $U_2$ can be obtained by performing Fourier transform of the above equation and setting the transform variable to zero. Matching
$U_2$ can be obtained by performing Fourier transform of the above equation and setting the transform variable to zero. Matching ![]() $U_2$ with the outer solution (4.17) determines the jump
$U_2$ with the outer solution (4.17) determines the jump
 \begin{align} c^+-c^- &= \frac{1}{3}\frac{\alpha^2}{\bar{T}_c} \left(\frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A}\right)j{\rm \pi}\mathrm{i} + \left(\frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x}_1 \tilde{A}\right)j_1{\rm \pi}\mathrm{i} +d\frac{\alpha^2}{3}\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right){\rm \pi}\mathrm{i} \nonumber\\ &\quad -\frac{2{\rm \pi}\mathrm{i}\alpha^6(\bar{U}_c^\prime)^3\bar{T}_c^\prime}{3\bar{T}_c^2} \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)\tilde{A}(\tilde{x}-c\xi)\tilde{A}(\tilde{x}-c\xi-c\eta) \nonumber\\ &\quad \times\tilde{A}^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi, \end{align}
\begin{align} c^+-c^- &= \frac{1}{3}\frac{\alpha^2}{\bar{T}_c} \left(\frac{\mathrm{i} c}{\alpha}\tilde{A}^\prime-\bar{U}_{1c}\bar{x}_1 \tilde{A}\right)j{\rm \pi}\mathrm{i} + \left(\frac{\alpha^2\bar{U}_c^\prime}{3\bar{T}_c}\bar{x}_1 \tilde{A}\right)j_1{\rm \pi}\mathrm{i} +d\frac{\alpha^2}{3}\left(\frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime}\right){\rm \pi}\mathrm{i} \nonumber\\ &\quad -\frac{2{\rm \pi}\mathrm{i}\alpha^6(\bar{U}_c^\prime)^3\bar{T}_c^\prime}{3\bar{T}_c^2} \int_{0}^{\infty}\!\!\!\int_{0}^{\infty} K(\xi,\eta)\tilde{A}(\tilde{x}-c\xi)\tilde{A}(\tilde{x}-c\xi-c\eta) \nonumber\\ &\quad \times\tilde{A}^*(\tilde{x}-2c\xi-c\eta)\,{\rm d}\eta{\rm d}\xi, \end{align}
where the linear part of the jump corresponds to the ![]() $(-{\rm \pi} )$ phase jump of the logarithmic singularity in (4.13), and the kernel function
$(-{\rm \pi} )$ phase jump of the logarithmic singularity in (4.13), and the kernel function
 \begin{align} K(\xi,\eta) &= \xi^2\exp[-s(2\xi^3+3\xi^2\eta)]\left\{\exp[-(s_p-s)\xi^3] \vphantom{\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)}\right.\nonumber\\ &\quad +\exp[-(s_p-s)\xi^3-3(s_p-s)\xi^2\eta] \nonumber\\ &\quad - \left.\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} [1-\exp(-(s_p-s)(2\xi^3+3\xi^2\eta))]+\frac{\bar{T}_c}{\bar{T}_c^\prime} \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\right\}. \end{align}
\begin{align} K(\xi,\eta) &= \xi^2\exp[-s(2\xi^3+3\xi^2\eta)]\left\{\exp[-(s_p-s)\xi^3] \vphantom{\left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)}\right.\nonumber\\ &\quad +\exp[-(s_p-s)\xi^3-3(s_p-s)\xi^2\eta] \nonumber\\ &\quad - \left.\frac{\bar{T}_c\bar{\mu}_c^\prime-\bar{\mu}_c Pr^{-1}}{\bar{\mu}_c(1-Pr^{-1})} [1-\exp(-(s_p-s)(2\xi^3+3\xi^2\eta))]+\frac{\bar{T}_c}{\bar{T}_c^\prime} \left( \frac{\bar{T}_c^\prime}{\bar{T}_c}-\frac{\bar{U}_c^{\prime\prime}}{\bar{U}_c^\prime} \right)\right\}. \end{align}Appendix C. Recovery of the equilibrium and non-equilibrium regimes from the composite theory
In this appendix, we show that the amplitude equations in the equilibrium and non-equilibrium regimes can be recovered from the composite amplitude equation (5.10) as the appropriate limiting cases.
First, consider recovery of the equilibrium regime. Following Wu & Huerre (Reference Wu and Huerre2009), we perform the substitution ![]() $\xi \rightarrow R^{-1/6}\xi$ and
$\xi \rightarrow R^{-1/6}\xi$ and ![]() $\eta \rightarrow R^{-1/6}\eta$ and take the limit
$\eta \rightarrow R^{-1/6}\eta$ and take the limit ![]() $R\gg 1$ in (5.10). The latter then reduces to (4.61).
$R\gg 1$ in (5.10). The latter then reduces to (4.61).
Next, recall that in the non-equilibrium regime we have the nonlinear response ![]() $a_e\exp ({\mathrm {i}\tilde \alpha _d\tilde {x}})$, where
$a_e\exp ({\mathrm {i}\tilde \alpha _d\tilde {x}})$, where ![]() $a_e(\bar {x}_1)$ is governed by (4.38). Let
$a_e(\bar {x}_1)$ is governed by (4.38). Let ![]() $\bar {A}_e$ denote the corresponding nonlinear response written in terms of the scaled quantities and coordinate in the composite theory. Then we have
$\bar {A}_e$ denote the corresponding nonlinear response written in terms of the scaled quantities and coordinate in the composite theory. Then we have
where we have put ![]() $\tilde {x}=0$ in (5.5). By using (C1) and noting
$\tilde {x}=0$ in (5.5). By using (C1) and noting
the response equation (4.38) is rewritten as
Figure 21 compares the nonlinear response with the solution to the composite amplitude equation in the absence of an oncoming free mode. The two solutions overlap in the upstream region, suggesting that the former can be recovered from the latter in the upstream limit. An enlarged view, figure 21(b), shows that the solution to the composite amplitude equation evolves through a stage which is nonlinear and captured by the nonlinear response.

Figure 21. Comparison between the nonlinear response and the solution to the composite amplitude equation without an oncoming free mode for ![]() $\bar {p}_I=160$ and
$\bar {p}_I=160$ and ![]() $\bar {\alpha }_d=0$. Solid lines: solution to (5.10) with
$\bar {\alpha }_d=0$. Solid lines: solution to (5.10) with ![]() $R=10^4$; dotted lines: linear solution (5.12); dashed-dotted lines: nonlinear response governed by (C3). (b) Zooms into a range in (a).
$R=10^4$; dotted lines: linear solution (5.12); dashed-dotted lines: nonlinear response governed by (C3). (b) Zooms into a range in (a).
We consider next the evolution of the perturbation with the growth rate modified by the nonlinear response. The perturbation in the non-equilibrium regime satisfies the initial condition (4.55) with the modified growth rate ![]() $\kappa$ being given by (4.53), and the eigenvector
$\kappa$ being given by (4.53), and the eigenvector ![]() $(a_r, a_i)$ given in (4.54a,b). Let
$(a_r, a_i)$ given in (4.54a,b). Let ![]() $\bar {A}_0$ denote the corresponding perturbation under the scaling of the composite theory, that is,
$\bar {A}_0$ denote the corresponding perturbation under the scaling of the composite theory, that is, ![]() $\bar {A}_0(\bar {x})=R^{1/12}A_0(\tilde {x})$. On noting (5.5), the perturbation can be written as
$\bar {A}_0(\bar {x})=R^{1/12}A_0(\tilde {x})$. On noting (5.5), the perturbation can be written as
where the modified growth rate ![]() $\bar \kappa \equiv R^{1/6}\kappa$ and the eigenvector
$\bar \kappa \equiv R^{1/6}\kappa$ and the eigenvector ![]() $(\bar {a}_r, \bar {a}_i)$ satisfy the same equations as (4.53) and (4.54a,b) in the non-equilibrium regime, respectively, provided that the parameter
$(\bar {a}_r, \bar {a}_i)$ satisfy the same equations as (4.53) and (4.54a,b) in the non-equilibrium regime, respectively, provided that the parameter ![]() $\bar {x}_1$ is replaced by the variable
$\bar {x}_1$ is replaced by the variable ![]() $\bar {x}$ and the parameters
$\bar {x}$ and the parameters ![]() $\varUpsilon$ and
$\varUpsilon$ and ![]() $s$ are replaced by
$s$ are replaced by ![]() $\bar \varUpsilon$ and
$\bar \varUpsilon$ and ![]() $\bar {s}$ with
$\bar {s}$ with
Similarly, the rescaled nonlinear evolution equation for the perturbation in the composite theory has the same form as (4.45) in the non-equilibrium regime, provided that ![]() $\bar {x}_1$ is replaced by
$\bar {x}_1$ is replaced by ![]() $\bar {x}$ and the rescaled quantities in (C5a,b) are used.
$\bar {x}$ and the rescaled quantities in (C5a,b) are used.
In order to compare the solution to the composite amplitude equation (5.10) in the presence of an oncoming free mode with the nonlinear response plus the nonlinear perturbation, the constants ![]() $|\bar {a}_0|$ and
$|\bar {a}_0|$ and ![]() $\bar \phi _0$ are first determined by fitting
$\bar \phi _0$ are first determined by fitting ![]() $\bar {A}_e+\bar {A}_0$ with the composite solution at a particular location
$\bar {A}_e+\bar {A}_0$ with the composite solution at a particular location ![]() $\bar {x}=-10$. The resulting initial condition (C4) is used to solve the rescaled version of the nonlinear evolution equation (4.45). Figure 22 shows the comparison between the two solutions. The sum of
$\bar {x}=-10$. The resulting initial condition (C4) is used to solve the rescaled version of the nonlinear evolution equation (4.45). Figure 22 shows the comparison between the two solutions. The sum of ![]() $\bar {A}_e$ and
$\bar {A}_e$ and ![]() $\bar {A}_0$ represents the nonlinear response and the nonlinear perturbation under the scaling of the composite theory. There is good agreement between the two solutions. This indicates that the composite theory captures the characteristics of the non-equilibrium effects.
$\bar {A}_0$ represents the nonlinear response and the nonlinear perturbation under the scaling of the composite theory. There is good agreement between the two solutions. This indicates that the composite theory captures the characteristics of the non-equilibrium effects.

Figure 22. Comparison between the nonlinear response plus the nonlinear perturbation and the solution to the composite amplitude equation (5.10) in the presence of an oncoming free mode with ![]() $\hat {a}_0=3$ for
$\hat {a}_0=3$ for ![]() $\bar {p}_I=160$,
$\bar {p}_I=160$, ![]() $\bar {\alpha }_d=0$ and
$\bar {\alpha }_d=0$ and ![]() $R=10^4$.
$R=10^4$.