1. Introduction
Transport in Poiseuille flow within a channel is a classical problem that has served to advance the understanding of the fundamental features of advection–dispersion of scalars such as solutes and temperature, going back to the classical works on asymptotic dispersion of Taylor (Reference Taylor1953) and Aris (Reference Aris1956). Partially absorbing channel walls, where a transported scalar that diffuses into the walls is consumed proportionally to its local concentration, can represent a variety of physical processes, such as reactive solute consumption or sorption in porous or fractured media (Battiato et al. Reference Battiato, Tartakovsky, Tartakovsky and Scheibe2011), heat transport in pipes, rock fractures or other conduits (Lungu & Moffatt Reference Lungu and Moffatt1982), absorption in biological tissues (Davidson & Schroter Reference Davidson and Schroter1983), and chromatography (Sankarasubramanian & Gill Reference Sankarasubramanian and Gill1973; Balakotaiah, Chang & Smith Reference Balakotaiah, Chang and Smith1995). In what follows, we adopt the language of reactive solute transport for concreteness and ease of exposition.
Traditionally, the conservative problem is treated in terms of the method of moments (Aris Reference Aris1956), in which differential equations can be derived for successively higher moments along the longitudinal (mean flow) direction, averaged along the transverse direction(s). In addition to asymptotic mean velocities and dispersion coefficients, the evolution of the longitudinal plume towards normality can also be quantified using this type of approach (Chatwin Reference Chatwin1970). The question of how surface reaction affects effective advective velocities and dispersion has received much attention (Sankarasubramanian & Gill Reference Sankarasubramanian and Gill1973; De Gance & Johns Reference De Gance and Johns1978b; Lungu & Moffatt Reference Lungu and Moffatt1982; Shapiro & Brenner Reference Shapiro and Brenner1986; Balakotaiah et al. Reference Balakotaiah, Chang and Smith1995; Mikelić, Devigne & Van Duijn Reference Mikelić, Devigne and Van Duijn2006; Biswas & Sen Reference Biswas and Sen2007). Sankarasubramanian & Gill (Reference Sankarasubramanian and Gill1973), followed by De Gance & Johns (Reference De Gance and Johns1978a,Reference De Gance and Johnsb), generalized the asymptotic theory of Taylor (Reference Taylor1953) and Aris (Reference Aris1956) to the case of absorbing walls, and computed dispersive approximations to the longitudinal concentration field. A treatment in terms of series expansions of the longitudinal moments in Fourier space is given by Lungu & Moffatt (Reference Lungu and Moffatt1982). These works derive differential equations for longitudinal moments at asymptotic times, and in particular give a detailed account of effective plume velocities and dispersion coefficients. Intuitively, solute removal preferentially depletes low-velocity areas, and these works quantify the corresponding increase in average plume velocity, as well as the reduction in dispersion due to the associated decrease in the variability of sampled velocities. Later, Barton (Reference Barton1984) derived a general framework for computing the time-dependent moments and asymptotic solutions based on eigenfunction expansions, extending his previous work (Barton Reference Barton1983) and that of Chatwin (Reference Chatwin1970) for the conservative problem. More recently, a stochastic formulation was developed by Biswas & Sen (Reference Biswas and Sen2007). Although we focus here on a linear, irreversible reaction, we note that when forward reaction is accompanied by the reverse reaction, such as in chromatographic applications where sorption is accompanied by desorption, the net effect at late times is a decrease in plume velocity characterized by a retardation factor associated with the average time that the solute remains sorbed to the channel walls (Paine, Carbonell & Whitaker Reference Paine, Carbonell and Whitaker1983; Balakotaiah et al. Reference Balakotaiah, Chang and Smith1995; Jiang et al. Reference Jiang, Zeng, Fu and Wu2022). These two scenarios and the time scales governing the different regimes can be reconciled within a unified description (Zhang, Hesse & Wang Reference Zhang, Hesse and Wang2017). The linear irreversible picture applies, for example, over time scales where the reverse reaction may be neglected and local surface reactant concentrations may be approximated as constant, or when thermally conducting walls may be approximated as a thermal reservoir.
Despite these significant advances, previous work has focused mainly on the transverse-averaged moments and resulting approximations for the longitudinal concentration field. The present work offers a fresh perspective on this classical problem from the point of view of transverse mass and velocity distributions. The work of Barton (Reference Barton1984) provides a formal means to compute the dependency of longitudinal moments on transverse position and has been used to analyse the evolution of transverse averages and breakthrough curves (Yasuda Reference Yasuda1984; Guan & Chen Reference Guan and Chen2024). Here, we provide an alternative approach to analyse the asymptotic transverse variability in plume concentrations and advective velocities directly and in detail. Transverse distributions are relevant in the current context due to their fundamental role in spatial Markov models of transport in heterogeneous systems, which describe transport in terms of a stochastic evolution of velocities along solute trajectories over fixed spatial increments (Le Borgne, Dentz & Carrera Reference Le Borgne, Dentz and Carrera2008; Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016; Sherman et al. Reference Sherman, Paster, Porta and Bolster2019, Reference Sherman, Engdahl, Porta and Bolster2021; Puyguiraud, Gouze & Dentz Reference Puyguiraud, Gouze and Dentz2021; Aquino & Le Borgne Reference Aquino and Le Borgne2021b). Recent theoretical, numerical and experimental advances regarding flow and transport in biological systems such as lung tissue (Sznitman Reference Sznitman2021) and blood vessel networks in the brain (Goirand, Le Borgne & Lorthois Reference Goirand, Le Borgne and Lorthois2021) and tumours (Dewhirst & Secomb Reference Dewhirst and Secomb2017) underline the importance of transport and surface exchange for processes ranging from drug delivery to oxygen uptake and metabolic waste disposal. The question of how surface reaction modifies velocity distributions across solute plumes is thus central for the development of upscaled models of reactive transport in natural subsurface systems and other heterogeneous media.
We first address the following question: does the transverse distribution of solute concentrations, normalized by surviving mass, admit an asymptotic form for large times and travel distances from a given initial condition? We find that the answer is affirmative, and we derive explicit expressions for equilibrium mass, velocity and breakthrough distributions for arbitrary reaction rate. To characterize breakthrough distributions, it turns out to be necessary to determine the asymptotic mean plume velocity. To this end, we provide an analysis that highlights the role of subleading transverse variability in the mean plume position, while reproducing previous results based on the method of moments (Lungu & Moffatt Reference Lungu and Moffatt1982; Barton Reference Barton1984). We show in particular that the equality of flux-weighted (i.e. weighted by local velocities) and breakthrough (i.e. associated with flux over a control plane) distributions that has been established for conservative transport (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016; Puyguiraud et al. Reference Puyguiraud, Gouze and Dentz2021) breaks down in the presence of reaction, and that the mean plume velocity as a function of time is no longer fully characterized by the transverse distribution of flow velocities sampled by the plume at a given time. The extent of these effects depends on medium geometry and is more pronounced for flow in a cylindrical channel than between parallel plates.
The paper is organized as follows. In § 2, we formalize the problem and present the governing equations. In § 3, we introduce the transverse distributions and related average quantities that we then compute and compare to simulations for large times and travel distances in § 4, in both two dimensions (flow between parallel plates) and three dimensions (flow in a cylindrical channel). Section 5 presents an overall discussion and conclusions. Ancillary details and derivations can be found in the appendices.
2. Transport in a channel with reactive walls
Consider Poiseuille flow through an infinite channel of fixed cross-section, and a solute undergoing advective–diffusive transport within the channel. We begin by introducing some notation. We denote the channel by ![]() $\varOmega$ and an arbitrary cross-section by
$\varOmega$ and an arbitrary cross-section by ![]() $\varOmega _\perp$, and the channel radius by
$\varOmega _\perp$, and the channel radius by ![]() $a$ (half-width in two dimensions). We consider a Cartesian coordinate system with the origin at the channel centre and such that
$a$ (half-width in two dimensions). We consider a Cartesian coordinate system with the origin at the channel centre and such that ![]() $x$ is oriented along the channel. We denote spatial positions by
$x$ is oriented along the channel. We denote spatial positions by ![]() $\boldsymbol {x} = (x,\boldsymbol {x}_\perp ) \in \varOmega$, with
$\boldsymbol {x} = (x,\boldsymbol {x}_\perp ) \in \varOmega$, with ![]() $\boldsymbol {x}_\perp \in \varOmega _\perp$ equal to
$\boldsymbol {x}_\perp \in \varOmega _\perp$ equal to ![]() $y$ in two dimensions and to
$y$ in two dimensions and to ![]() $(y,z)$ in three dimensions. We use the notation
$(y,z)$ in three dimensions. We use the notation ![]() $|\varLambda |$ applied to a
$|\varLambda |$ applied to a ![]() $d_\varLambda$-dimensional spatial domain
$d_\varLambda$-dimensional spatial domain ![]() $\varLambda$ to denote its
$\varLambda$ to denote its ![]() $d_\varLambda$-dimensional measure (volume for
$d_\varLambda$-dimensional measure (volume for ![]() $d_\varLambda =3$, area for
$d_\varLambda =3$, area for ![]() $d_\varLambda =2$, and number of points for
$d_\varLambda =2$, and number of points for ![]() $d_\varLambda =1$). For example, the cross-sectional area is given by
$d_\varLambda =1$). For example, the cross-sectional area is given by ![]() $|\varOmega _\perp |={\rm \pi} a^2$ for a cylindrical channel in three dimensions (
$|\varOmega _\perp |={\rm \pi} a^2$ for a cylindrical channel in three dimensions (![]() $\varOmega _\perp$ has dimension two, so
$\varOmega _\perp$ has dimension two, so ![]() $|\varOmega _\perp |$ is an area) and
$|\varOmega _\perp |$ is an area) and ![]() $|\varOmega _\perp |=2a$ for two spatial dimensions (
$|\varOmega _\perp |=2a$ for two spatial dimensions (![]() $|\varOmega _\perp |$ is a length). Finally, we denote partial derivatives with respect to a variable
$|\varOmega _\perp |$ is a length). Finally, we denote partial derivatives with respect to a variable ![]() $\xi$ by
$\xi$ by ![]() $\partial _\xi$.
$\partial _\xi$.
Within the channel, ![]() $\boldsymbol {x} \in \varOmega$, solute concentrations obey the advection–dispersion equation
$\boldsymbol {x} \in \varOmega$, solute concentrations obey the advection–dispersion equation
where ![]() $t$ is time,
$t$ is time, ![]() $D$ is the diffusion coefficient, and for stratified, fully-developed channel flow, the spatial (Eulerian) velocity profile
$D$ is the diffusion coefficient, and for stratified, fully-developed channel flow, the spatial (Eulerian) velocity profile ![]() $v_E(\boldsymbol {x}_\perp )$ is a function of
$v_E(\boldsymbol {x}_\perp )$ is a function of ![]() $\boldsymbol {x}_\perp \in \varOmega _\perp$ only:
$\boldsymbol {x}_\perp \in \varOmega _\perp$ only:
where ![]() $v_M$ is the maximum velocity, attained at the centre of the channel (
$v_M$ is the maximum velocity, attained at the centre of the channel (![]() $\boldsymbol {x}_\perp = 0$). We define the Péclet number as
$\boldsymbol {x}_\perp = 0$). We define the Péclet number as
where
is the Eulerian mean velocity.
Solute diffusion coefficients in both environmental and engineering applications are commonly in the range ![]() $10^{-10}\unicode{x2013}10^{-9}\ \mathrm {m}^2\ \mathrm {s}^{-1}$, whereas common flow rates and relevant length scales (such as the pore, pipe or blood vessel diameter, or the fracture aperture) vary substantially and are often not independent. For example, subsurface flows through porous and fractured media usually range from approximately
$10^{-10}\unicode{x2013}10^{-9}\ \mathrm {m}^2\ \mathrm {s}^{-1}$, whereas common flow rates and relevant length scales (such as the pore, pipe or blood vessel diameter, or the fracture aperture) vary substantially and are often not independent. For example, subsurface flows through porous and fractured media usually range from approximately ![]() $\textit {Pe}=10^{-2}$ to
$\textit {Pe}=10^{-2}$ to ![]() $\textit {Pe}=10^4$, with advection-dominated conditions
$\textit {Pe}=10^4$, with advection-dominated conditions ![]() $(\textit {Pe}>1)$ being common, in particular in fractures (de Marsily Reference de Marsily1986). In chromatography, the Péclet number is usually between unity and a few hundred (Gritti & Guiochon Reference Gritti and Guiochon2013), although it should be noted that turbulent effects may be non-negligible in engineering applications such as chromatography and flow cell batteries. Typical flow rates in blood capillary networks (Ivanov, Kalinina & Levkovich Reference Ivanov, Kalinina and Levkovich1981) are of the order of
$(\textit {Pe}>1)$ being common, in particular in fractures (de Marsily Reference de Marsily1986). In chromatography, the Péclet number is usually between unity and a few hundred (Gritti & Guiochon Reference Gritti and Guiochon2013), although it should be noted that turbulent effects may be non-negligible in engineering applications such as chromatography and flow cell batteries. Typical flow rates in blood capillary networks (Ivanov, Kalinina & Levkovich Reference Ivanov, Kalinina and Levkovich1981) are of the order of ![]() $\mathrm {mm}\ \mathrm {s}^{-1}$, with vessel diameters of the order of
$\mathrm {mm}\ \mathrm {s}^{-1}$, with vessel diameters of the order of ![]() $\mathrm {\mu }\mathrm {m}$, corresponding to a typical
$\mathrm {\mu }\mathrm {m}$, corresponding to a typical ![]() $\textit {Pe}$ of approximately
$\textit {Pe}$ of approximately ![]() $1$–
$1$–![]() $10$. For heat transport in fractures, the thermal diffusivity is commonly approximately
$10$. For heat transport in fractures, the thermal diffusivity is commonly approximately ![]() $10^{-7}\ \mathrm {m}^2\ \mathrm {s}$, and
$10^{-7}\ \mathrm {m}^2\ \mathrm {s}$, and ![]() $\textit {Pe}\sim 10\unicode{x2013}10^2$ (de Marsily Reference de Marsily1986).
$\textit {Pe}\sim 10\unicode{x2013}10^2$ (de Marsily Reference de Marsily1986).
The cross-section concentration, obtained by integrating out the longitudinal coordinate ![]() $x$, is
$x$, is
Within ![]() $\varOmega _\perp$, the cross-section concentration obeys the diffusion equation
$\varOmega _\perp$, the cross-section concentration obeys the diffusion equation
which can be verified by integrating out ![]() $x$ in (2.1), and applying natural boundary conditions at
$x$ in (2.1), and applying natural boundary conditions at ![]() $x=\pm \infty$, i.e. setting the limit as
$x=\pm \infty$, i.e. setting the limit as ![]() $|x|\to \infty$ of
$|x|\to \infty$ of ![]() $c$ and its derivative to zero, which is needed to ensure finite mass in an infinite domain. Here and throughout,
$c$ and its derivative to zero, which is needed to ensure finite mass in an infinite domain. Here and throughout, ![]() $\boldsymbol {\nabla }_\perp$ represents the gradient with respect to the transverse coordinates. We consider this problem subject to a given initial condition
$\boldsymbol {\nabla }_\perp$ represents the gradient with respect to the transverse coordinates. We consider this problem subject to a given initial condition ![]() $c_\perp (\boldsymbol {x}_\perp ;0)$, which is determined from the initial concentration field
$c_\perp (\boldsymbol {x}_\perp ;0)$, which is determined from the initial concentration field ![]() $c(\boldsymbol {x};0)$ according to (2.5).
$c(\boldsymbol {x};0)$ according to (2.5).
Surface reaction can be represented through the boundary conditions. Linear depletion at a constant surface rate ![]() $k_A$
$k_A$ ![]() $[LT^{-1}]$ corresponds to partially absorbing boundaries, i.e. the Robin boundary conditions
$[LT^{-1}]$ corresponds to partially absorbing boundaries, i.e. the Robin boundary conditions
where ![]() $\boldsymbol {n}_\perp (\boldsymbol {x}_\perp )$ is the outward normal at the point
$\boldsymbol {n}_\perp (\boldsymbol {x}_\perp )$ is the outward normal at the point ![]() $\boldsymbol {x}_\perp$ on the boundary
$\boldsymbol {x}_\perp$ on the boundary ![]() $\partial \varOmega _\perp$. For the conservative problem,
$\partial \varOmega _\perp$. For the conservative problem, ![]() $k_A=0$, this reduces to a reflecting boundary,
$k_A=0$, this reduces to a reflecting boundary, ![]() $\boldsymbol {n}_\perp \boldsymbol {\cdot }\boldsymbol {\nabla }_\perp c_\perp |_{\partial \varOmega _\perp }=0$, while for instantaneous reaction,
$\boldsymbol {n}_\perp \boldsymbol {\cdot }\boldsymbol {\nabla }_\perp c_\perp |_{\partial \varOmega _\perp }=0$, while for instantaneous reaction, ![]() $k_A\to \infty$, we have a fully absorbing boundary,
$k_A\to \infty$, we have a fully absorbing boundary, ![]() $c_\perp |_{\partial \varOmega _\perp } = 0$. We define the Damköhler number
$c_\perp |_{\partial \varOmega _\perp } = 0$. We define the Damköhler number ![]() $\textit {Da}$ as the ratio of the characteristic diffusion and reaction times
$\textit {Da}$ as the ratio of the characteristic diffusion and reaction times ![]() $\tau _D$ and
$\tau _D$ and ![]() $\tau _R$ associated with the channel radius
$\tau _R$ associated with the channel radius ![]() $a$:
$a$:
Because the reaction rate ![]() $k_A$ depends on both the thermodynamics of the reaction and the surface concentrations of reactants at the interface, the Damköhler number for solute transport problems can vary over a very broad range of orders of magnitude. For heat transport, we have
$k_A$ depends on both the thermodynamics of the reaction and the surface concentrations of reactants at the interface, the Damköhler number for solute transport problems can vary over a very broad range of orders of magnitude. For heat transport, we have ![]() $\textit {Da}=aH/(2K)$, where
$\textit {Da}=aH/(2K)$, where ![]() $H$ is the surface conductance or heat transfer coefficient, and
$H$ is the surface conductance or heat transfer coefficient, and ![]() $K$ is the thermal conductivity of the surface (Carslaw & Jaeger Reference Carslaw and Jaeger1986). For example, for subsurface transport in fractured rock, we have
$K$ is the thermal conductivity of the surface (Carslaw & Jaeger Reference Carslaw and Jaeger1986). For example, for subsurface transport in fractured rock, we have ![]() $K\sim \mathrm {W}\ \mathrm {m}^{-1}\ \mathrm {K}^{-1}$ (Carslaw & Jaeger Reference Carslaw and Jaeger1986) and
$K\sim \mathrm {W}\ \mathrm {m}^{-1}\ \mathrm {K}^{-1}$ (Carslaw & Jaeger Reference Carslaw and Jaeger1986) and ![]() $H\sim 10\unicode{x2013}10^2\ \mathrm {W}\ \mathrm {m}^{-2}\ \mathrm {K}^{-1}$ (Heinze Reference Heinze2021), so that, using
$H\sim 10\unicode{x2013}10^2\ \mathrm {W}\ \mathrm {m}^{-2}\ \mathrm {K}^{-1}$ (Heinze Reference Heinze2021), so that, using ![]() $a\sim 10^{-6}\unicode{x2013}10^{-2}\ \mathrm {m}$, we estimate typical values of
$a\sim 10^{-6}\unicode{x2013}10^{-2}\ \mathrm {m}$, we estimate typical values of ![]() $\textit {Da}$ in the range
$\textit {Da}$ in the range ![]() $10^{-5}\unicode{x2013}1$.
$10^{-5}\unicode{x2013}1$.
It has been established that as for the traditional conservative problem (Taylor Reference Taylor1953; Aris Reference Aris1956), the concentration plume for the reactive problem approaches a Gaussian shape along the longitudinal direction at late times (Chatwin Reference Chatwin1970; Biswas & Sen Reference Biswas and Sen2007). The effective (Taylor) dispersion coefficient is then given by
where ![]() $\eta$ is a dimensionless constant that depends on the domain geometry and decreases monotonically with
$\eta$ is a dimensionless constant that depends on the domain geometry and decreases monotonically with ![]() $\textit {Da}$, quantifying the decrease in longitudinal dispersion due to the reduced variability in sampled velocities (Lungu & Moffatt Reference Lungu and Moffatt1982). For the two-dimensional (2-D) channel,
$\textit {Da}$, quantifying the decrease in longitudinal dispersion due to the reduced variability in sampled velocities (Lungu & Moffatt Reference Lungu and Moffatt1982). For the two-dimensional (2-D) channel, ![]() $\eta =2/105 \approx 1.9\times 10^{-2}$ for the conservative problem, and
$\eta =2/105 \approx 1.9\times 10^{-2}$ for the conservative problem, and ![]() $\eta =9{\rm \pi} ^{-6}(75{\rm \pi} ^2-{\rm \pi} ^4-630)/45 \approx 2.7\times 10^{-3}$ for
$\eta =9{\rm \pi} ^{-6}(75{\rm \pi} ^2-{\rm \pi} ^4-630)/45 \approx 2.7\times 10^{-3}$ for ![]() $\textit {Da}\to \infty$. The corresponding values for the three-dimensional (3-D) problem are
$\textit {Da}\to \infty$. The corresponding values for the three-dimensional (3-D) problem are ![]() $\eta =1/48 \approx 2.1\times 10^{-2}$ and
$\eta =1/48 \approx 2.1\times 10^{-2}$ and ![]() $\eta \approx 5.0\times 10^{-3}$.
$\eta \approx 5.0\times 10^{-3}$.
3. Transverse distributions
In this section, we introduce different probability density functions (p.d.f.s) of interest across the transverse direction, before proceeding to discuss the corresponding asymptotic equilibria in § 4. In Appendix A, we discuss how these quantities can be represented in terms of concentration moments in the classical Aris–Barton formulation (Barton Reference Barton1984).
3.1. Surviving mass
The total mass at time ![]() $t$ can be expressed as
$t$ can be expressed as
We use the notation ![]() $\int _\varOmega \,{\rm d}\kern0.06em \boldsymbol{x} = \int {{\rm d}\kern0.06em x} \int {{\rm d}y} \int {\rm d}z$ for multi-dimensional integrals. For
$\int _\varOmega \,{\rm d}\kern0.06em \boldsymbol{x} = \int {{\rm d}\kern0.06em x} \int {{\rm d}y} \int {\rm d}z$ for multi-dimensional integrals. For ![]() $M(t)\neq 1$,
$M(t)\neq 1$, ![]() $c_\perp (\cdot ;t)$ is a density, but not a p.d.f., because it is not normalized to unit integral. The p.d.f.
$c_\perp (\cdot ;t)$ is a density, but not a p.d.f., because it is not normalized to unit integral. The p.d.f. ![]() $p_t(\cdot ;t)$ of surviving mass, which describes the transverse mass profile along the cross-section at time
$p_t(\cdot ;t)$ of surviving mass, which describes the transverse mass profile along the cross-section at time ![]() $t$, is given by
$t$, is given by
If it exists, the corresponding equilibrium p.d.f. is
3.2. Velocity at fixed time
A velocity p.d.f. describes the probability density of encountering a certain velocity in a spatial domain, sampled according to some prescribed distribution. For the flow profile (2.2), we may disregard the longitudinal direction and consider only the cross-section. We first introduce the Eulerian velocity p.d.f. ![]() $p_E$, which is defined as the probability density associated with finding a certain velocity magnitude value at a uniformly random spatial location. We also define the flux-weighted Eulerian p.d.f.
$p_E$, which is defined as the probability density associated with finding a certain velocity magnitude value at a uniformly random spatial location. We also define the flux-weighted Eulerian p.d.f.
where the Eulerian mean velocity, defined in (2.4), obeys ![]() $\overline {v_E}=\int _0^{v_M} {\rm d}v\,v\,p_E(v)$. We denote the flux-weighted mean velocity by
$\overline {v_E}=\int _0^{v_M} {\rm d}v\,v\,p_E(v)$. We denote the flux-weighted mean velocity by
The transverse velocity p.d.f. at fixed time, ![]() $p_{v_t}(\cdot ;t)$, is obtained by sampling spatial locations according to the p.d.f.
$p_{v_t}(\cdot ;t)$, is obtained by sampling spatial locations according to the p.d.f. ![]() $p_t(\cdot ;t)$, which describes the probability density of surviving mass at a given time as a function of cross-section positions, rather than uniformly. If
$p_t(\cdot ;t)$, which describes the probability density of surviving mass at a given time as a function of cross-section positions, rather than uniformly. If ![]() $p_t^\infty$ exists, then this velocity p.d.f. also admits an equilibrium given by
$p_t^\infty$ exists, then this velocity p.d.f. also admits an equilibrium given by
where
are the radial distances from the channel centre where the velocity magnitude equals ![]() $v$ for the Poiseuille flow profile (2.2). Here and in similar contexts, we use the slight abuse of notation
$v$ for the Poiseuille flow profile (2.2). Here and in similar contexts, we use the slight abuse of notation ![]() $p_t^\infty [r_\perp (v)] = p_t^\infty (\boldsymbol {x}_\perp )|_{|\boldsymbol {x}_\perp | = r_\perp (v)}$ for convenience. Note that
$p_t^\infty [r_\perp (v)] = p_t^\infty (\boldsymbol {x}_\perp )|_{|\boldsymbol {x}_\perp | = r_\perp (v)}$ for convenience. Note that ![]() $p_{v_t}^\infty$ reduces to the Eulerian p.d.f.
$p_{v_t}^\infty$ reduces to the Eulerian p.d.f. ![]() $p_E$ if
$p_E$ if ![]() $p_t^\infty (\boldsymbol {x}_\perp ) = 1/|\varOmega _\perp |$, i.e. if mass is distributed uniformly along the cross-section. Further details on the Eulerian and flux-weighted Eulerian p.d.f.s, including table 2 summarizing useful quantities and a derivation of (3.6), are given in Appendix B.
$p_t^\infty (\boldsymbol {x}_\perp ) = 1/|\varOmega _\perp |$, i.e. if mass is distributed uniformly along the cross-section. Further details on the Eulerian and flux-weighted Eulerian p.d.f.s, including table 2 summarizing useful quantities and a derivation of (3.6), are given in Appendix B.
The mean velocity associated with ![]() $p_{v_t}^\infty$ is
$p_{v_t}^\infty$ is
Finally, we introduce the fixed-time flux-weighted velocity p.d.f., corresponding to assigning a weight proportional to the local velocity to the sampling of spatial locations:
where the spatial sampling p.d.f. is obtained by flux-weighting the surviving mass p.d.f. (3.3):
The relationship between these p.d.f.s and solute breakthrough over a control plane is discussed in § 3.3. The associated mean velocity is
One might reasonably suppose the asymptotic mean of the fixed-time velocity p.d.f., ![]() $v_t^\infty$ (3.8), to correspond to the asymptotic mean velocity of the solute plume at large fixed times. While this is true for conservative transport (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016), it is in fact not the case for the reactive problem. To see why, first recall that the mean plume velocity
$v_t^\infty$ (3.8), to correspond to the asymptotic mean velocity of the solute plume at large fixed times. While this is true for conservative transport (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016), it is in fact not the case for the reactive problem. To see why, first recall that the mean plume velocity ![]() $v_P(t)$ as a function of time is defined as the rate of change of the mean plume position
$v_P(t)$ as a function of time is defined as the rate of change of the mean plume position ![]() $m_P(t)$, which is given by
$m_P(t)$, which is given by
Taking the time derivative gives
where ![]() $\alpha = M^{-1}\,|{\rm d}M/{\rm d}t|$ is the effective reaction rate across the solute plume (units of inverse time). Integrating the advection–dispersion equation (ADE) (2.1) in
$\alpha = M^{-1}\,|{\rm d}M/{\rm d}t|$ is the effective reaction rate across the solute plume (units of inverse time). Integrating the advection–dispersion equation (ADE) (2.1) in ![]() $\varOmega$ and assuming that the equilibrium distribution
$\varOmega$ and assuming that the equilibrium distribution ![]() $p^\infty _t$ exists, we find that the late-time effective rate is constant:
$p^\infty _t$ exists, we find that the late-time effective rate is constant:
Again using the ADE (2.1) to substitute for ![]() $\partial _t c(\boldsymbol {x},t)$ in (3.13) and performing the appropriate integrations, we find for late times that
$\partial _t c(\boldsymbol {x},t)$ in (3.13) and performing the appropriate integrations, we find for late times that
where
 \begin{equation} m(\boldsymbol{x}_\perp, t) = \frac{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, x\, c(\boldsymbol{x},t)}{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, c(\boldsymbol{x},t)} = \frac{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, x\,c(\boldsymbol{x},t)}{M(t)\, p_t^\infty(\boldsymbol{x}_\perp)}, \quad m_W(t)=m(\boldsymbol{x}_\perp{\in}\partial\varOmega_\perp,t) \end{equation}
\begin{equation} m(\boldsymbol{x}_\perp, t) = \frac{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, x\, c(\boldsymbol{x},t)}{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, c(\boldsymbol{x},t)} = \frac{\displaystyle\int_{-\infty}^\infty {{\rm d}\kern0.06em x}\, x\,c(\boldsymbol{x},t)}{M(t)\, p_t^\infty(\boldsymbol{x}_\perp)}, \quad m_W(t)=m(\boldsymbol{x}_\perp{\in}\partial\varOmega_\perp,t) \end{equation}
are the mean longitudinal plume positions given an arbitrary transverse position ![]() $\boldsymbol {x}_\perp$ and a position
$\boldsymbol {x}_\perp$ and a position ![]() $\boldsymbol {x}_\perp$ at the channel walls, respectively.
$\boldsymbol {x}_\perp$ at the channel walls, respectively.
Reactive consumption cannot lead to a maximum velocity larger than ![]() $v_M$, the centre-channel velocity. However, according to (3.15), if
$v_M$, the centre-channel velocity. However, according to (3.15), if ![]() $m_P(t) - m_W(t)$ grew asymptotically as time
$m_P(t) - m_W(t)$ grew asymptotically as time ![]() $t\to \infty$, so would the mean plume velocity
$t\to \infty$, so would the mean plume velocity ![]() $v_P(t)$. Thus
$v_P(t)$. Thus ![]() $m_P(t) - m_W(t)$ must be at most constant at late times, and we find from (3.15) that
$m_P(t) - m_W(t)$ must be at most constant at late times, and we find from (3.15) that ![]() $v_P(t)$ is constant at late times. For the conservative problem, it is well known that the mean plume velocity approaches the Eulerian mean velocity
$v_P(t)$ is constant at late times. For the conservative problem, it is well known that the mean plume velocity approaches the Eulerian mean velocity ![]() $\overline {v_E}$. Since reaction depletes mass in low-velocity regions, the late-time plume velocity must not be smaller than
$\overline {v_E}$. Since reaction depletes mass in low-velocity regions, the late-time plume velocity must not be smaller than ![]() $\overline {v_E}$ and must therefore be non-zero, so that
$\overline {v_E}$ and must therefore be non-zero, so that ![]() $m_P(t)$ must grow asymptotically. Then the fact that
$m_P(t)$ must grow asymptotically. Then the fact that ![]() $m_P(t) - m_W(t)$ cannot grow at late times implies
$m_P(t) - m_W(t)$ cannot grow at late times implies ![]() $m_P(t) = m_W(t)$ to leading order. On the other hand, by definition,
$m_P(t) = m_W(t)$ to leading order. On the other hand, by definition, ![]() $v_P(t) = {\rm d}m_P(t)/{\rm d}t$, and we conclude that to leading order
$v_P(t) = {\rm d}m_P(t)/{\rm d}t$, and we conclude that to leading order ![]() $v_P(t) = {\rm d}m_W(t)/{\rm d}t$ also. Therefore,
$v_P(t) = {\rm d}m_W(t)/{\rm d}t$ also. Therefore, ![]() $m_W(t) \sim v_P^\infty t$ asymptotically, with the equilibrium mean plume velocity given by
$m_W(t) \sim v_P^\infty t$ asymptotically, with the equilibrium mean plume velocity given by
As we will show below, it turns out that ![]() $v_P^\infty \geq v _t^\infty \geq \overline {v_E}$, where the equalities hold only for the conservative problem. This may also be seen using the more traditional method of moments, which has been used to compute
$v_P^\infty \geq v _t^\infty \geq \overline {v_E}$, where the equalities hold only for the conservative problem. This may also be seen using the more traditional method of moments, which has been used to compute ![]() $v_P^\infty$ (Lungu & Moffatt Reference Lungu and Moffatt1982). The present approach clarifies the physical origin of this effect: even though the global mean plume position equals the mean plume position at the wall to leading order at late times, the subleading difference of these quantities contributes at leading order to the asymptotic mean plume velocity in (3.15).
$v_P^\infty$ (Lungu & Moffatt Reference Lungu and Moffatt1982). The present approach clarifies the physical origin of this effect: even though the global mean plume position equals the mean plume position at the wall to leading order at late times, the subleading difference of these quantities contributes at leading order to the asymptotic mean plume velocity in (3.15).
In order to compute ![]() $v_P^\infty$ below, we consider the auxiliary quantity
$v_P^\infty$ below, we consider the auxiliary quantity
From this definition, we have at late times
Multiplying the ADE (2.1) by ![]() $x/M(t)$, integrating out
$x/M(t)$, integrating out ![]() $x$, and rearranging terms, we obtain an evolution equation for
$x$, and rearranging terms, we obtain an evolution equation for ![]() $f$. At late times, it reads
$f$. At late times, it reads
with the reactive boundary condition (2.7) applied to ![]() $f$, and an initial condition
$f$, and an initial condition ![]() $f(\boldsymbol {x}_\perp, 0)$ determined by the initial concentration field according to (3.18). This equation has the form of the transverse ADE (2.6) in terms of differential operators, but with an additional linear production term at rate
$f(\boldsymbol {x}_\perp, 0)$ determined by the initial concentration field according to (3.18). This equation has the form of the transverse ADE (2.6) in terms of differential operators, but with an additional linear production term at rate ![]() $\alpha ^\infty$, and a source term given by the velocity field weighted by the surviving mass distribution. We will analyse the late-time behaviour of (3.20) in more detail separately for the 2-D and 3-D channels in what follows. In particular, we will find that
$\alpha ^\infty$, and a source term given by the velocity field weighted by the surviving mass distribution. We will analyse the late-time behaviour of (3.20) in more detail separately for the 2-D and 3-D channels in what follows. In particular, we will find that
where the constant-in-time mean-position discrepancy at late times ![]() $\Delta m(\boldsymbol {x}_\perp )$ obeys
$\Delta m(\boldsymbol {x}_\perp )$ obeys
where ![]() $\Delta m_W = \Delta m(\boldsymbol {x}_\perp \in \partial \varOmega _\perp )$, so that (3.15) for the mean plume velocity is satisfied.
$\Delta m_W = \Delta m(\boldsymbol {x}_\perp \in \partial \varOmega _\perp )$, so that (3.15) for the mean plume velocity is satisfied.
3.3. Breakthrough over a fixed control plane
The breakthrough of mass as a function of time is a standard metric that represents the total advective mass flux passing a control plane at a fixed longitudinal position. Here, we consider breakthrough profiles, by which we mean the profile of the mass flux per area as a function of transverse position over the control plane. As before, we are interested in the existence of equilibrium profiles when normalized by surviving mass. Thus we define the breakthrough p.d.f., i.e. the breakthrough profile normalized by the total mass that crosses a control plane at position ![]() $x$ over all times, and we seek its equilibrium form:
$x$ over all times, and we seek its equilibrium form:
 \begin{equation} p_s(\boldsymbol{x}_\perp; x) = \frac{\displaystyle\int_0^\infty {\rm d}t\, v_E(\boldsymbol{x}_\perp)\,c(\boldsymbol{x}, t)}{\displaystyle\int_{\varOmega_\perp} {\rm d}\kern0.06em \boldsymbol{x}_\perp\int_0^\infty {\rm d}t\,v_E(\boldsymbol{x}_\perp)\,c(\boldsymbol{x},t)}, \quad p_s^\infty(\boldsymbol{x}_\perp) = \lim_{x\to\infty} p_s(\boldsymbol{x}_\perp; x). \end{equation}
\begin{equation} p_s(\boldsymbol{x}_\perp; x) = \frac{\displaystyle\int_0^\infty {\rm d}t\, v_E(\boldsymbol{x}_\perp)\,c(\boldsymbol{x}, t)}{\displaystyle\int_{\varOmega_\perp} {\rm d}\kern0.06em \boldsymbol{x}_\perp\int_0^\infty {\rm d}t\,v_E(\boldsymbol{x}_\perp)\,c(\boldsymbol{x},t)}, \quad p_s^\infty(\boldsymbol{x}_\perp) = \lim_{x\to\infty} p_s(\boldsymbol{x}_\perp; x). \end{equation} The advective mass flux is locally proportional to the flow velocity. At large distances, the crossing times are also large, so that we may expect the equilibrium breakthrough p.d.f. to result from flux-weighting the surviving mass p.d.f., i.e. ![]() $p_s^\infty =p_{t,F}^\infty$; see (3.10). This is indeed the case for the conservative problem (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016), but, surprisingly, the equality does not hold exactly for the reactive problem due to the subleading contributions
$p_s^\infty =p_{t,F}^\infty$; see (3.10). This is indeed the case for the conservative problem (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016), but, surprisingly, the equality does not hold exactly for the reactive problem due to the subleading contributions ![]() $\Delta m(\boldsymbol {x}_\perp )$ to the mean plume position discussed in the previous subsection (see (3.21)). To see this, consider that, as already discussed, the plume is Gaussian along the longitudinal direction at late times (Chatwin Reference Chatwin1970; Biswas & Sen Reference Biswas and Sen2007). We thus write the concentration field as
$\Delta m(\boldsymbol {x}_\perp )$ to the mean plume position discussed in the previous subsection (see (3.21)). To see this, consider that, as already discussed, the plume is Gaussian along the longitudinal direction at late times (Chatwin Reference Chatwin1970; Biswas & Sen Reference Biswas and Sen2007). We thus write the concentration field as
where ![]() $G(\cdot ; \xi, \sigma ^2)$ is the Gaussian p.d.f. of mean
$G(\cdot ; \xi, \sigma ^2)$ is the Gaussian p.d.f. of mean ![]() $\xi$ and variance
$\xi$ and variance ![]() $\sigma ^2$, the mean plume position is given by (3.21), and the Taylor dispersion coefficient
$\sigma ^2$, the mean plume position is given by (3.21), and the Taylor dispersion coefficient ![]() $D_e$ is given by (2.9). We have established in (3.14) that the mass decays at a constant rate
$D_e$ is given by (2.9). We have established in (3.14) that the mass decays at a constant rate ![]() $\alpha ^\infty$ at late times, which is equivalent to saying the late-time decay of mass is exponential at rate
$\alpha ^\infty$ at late times, which is equivalent to saying the late-time decay of mass is exponential at rate ![]() $\alpha ^\infty$. Thus the time integrals in (3.23a) are proportional to the Laplace transform over time of the Gaussian p.d.f. in (3.24) evaluated at
$\alpha ^\infty$. Thus the time integrals in (3.23a) are proportional to the Laplace transform over time of the Gaussian p.d.f. in (3.24) evaluated at ![]() $\alpha ^\infty$, which, for
$\alpha ^\infty$, which, for ![]() $x\geq \Delta m(\boldsymbol {x}_\perp )$, is given by
$x\geq \Delta m(\boldsymbol {x}_\perp )$, is given by
 \begin{align} \mathcal{L}_tG[x;v_P^\infty t \!+\! \Delta m(\boldsymbol{x}_\perp), 2D_e t](\alpha^\infty) = \frac{\exp\left[-\dfrac{v_P^\infty}{2D_e}\left(\sqrt{1\!+\!\dfrac{4D_e\alpha^\infty}{(v_P^\infty)^2}}-1\right)[x-\Delta m(\boldsymbol{x}_\perp)]\right]}{v_P^\infty\sqrt{1+4D_e\alpha^\infty/(v_P^\infty)^2}}. \end{align}
\begin{align} \mathcal{L}_tG[x;v_P^\infty t \!+\! \Delta m(\boldsymbol{x}_\perp), 2D_e t](\alpha^\infty) = \frac{\exp\left[-\dfrac{v_P^\infty}{2D_e}\left(\sqrt{1\!+\!\dfrac{4D_e\alpha^\infty}{(v_P^\infty)^2}}-1\right)[x-\Delta m(\boldsymbol{x}_\perp)]\right]}{v_P^\infty\sqrt{1+4D_e\alpha^\infty/(v_P^\infty)^2}}. \end{align}
The requirement ![]() $x\geq \Delta m(\boldsymbol {x}_\perp )$ is needed because the Gaussian approximation deteriorates at smaller
$x\geq \Delta m(\boldsymbol {x}_\perp )$ is needed because the Gaussian approximation deteriorates at smaller ![]() $x$. For a given time
$x$. For a given time ![]() $t>0$, the peak of the Gaussian is located at
$t>0$, the peak of the Gaussian is located at ![]() $x=v_P^\infty t+\Delta m$, which implies
$x=v_P^\infty t+\Delta m$, which implies ![]() $x-\Delta m = v_P^\infty t$. This means that under this approximation, the peak at a position
$x-\Delta m = v_P^\infty t$. This means that under this approximation, the peak at a position ![]() $x<\Delta m$ would occur before
$x<\Delta m$ would occur before ![]() $t=0$, resulting in a change of sign of the square root term within the exponential in the Laplace transform. Using (3.25), we conclude that
$t=0$, resulting in a change of sign of the square root term within the exponential in the Laplace transform. Using (3.25), we conclude that
 \begin{equation} p_s^\infty(\boldsymbol{x}_\perp) = \frac{\beta(\boldsymbol{x}_\perp)\,v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}{ \displaystyle\int_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, \beta(\boldsymbol{x}_\perp)\,v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}, \end{equation}
\begin{equation} p_s^\infty(\boldsymbol{x}_\perp) = \frac{\beta(\boldsymbol{x}_\perp)\,v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}{ \displaystyle\int_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, \beta(\boldsymbol{x}_\perp)\,v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}, \end{equation}where
 \begin{align} \beta(\boldsymbol{x}_\perp) = \exp({\gamma \alpha^\infty\,\Delta m(\boldsymbol{x}_\perp)/\overline{v_E}}), \quad \gamma = \frac{2\overline{v_E}}{v_P^\infty}\left[1+\sqrt{1+\frac{4\mu_1^2\overline{v_E}^2}{(v_P^\infty)^2\,\textit{Pe}^2}(1+\eta\,\textit{Pe}^2)}\right]^{{-}1}. \end{align}
\begin{align} \beta(\boldsymbol{x}_\perp) = \exp({\gamma \alpha^\infty\,\Delta m(\boldsymbol{x}_\perp)/\overline{v_E}}), \quad \gamma = \frac{2\overline{v_E}}{v_P^\infty}\left[1+\sqrt{1+\frac{4\mu_1^2\overline{v_E}^2}{(v_P^\infty)^2\,\textit{Pe}^2}(1+\eta\,\textit{Pe}^2)}\right]^{{-}1}. \end{align}
Here, we have used the fact that ![]() $\mu _1^2 = 2\tau _D\alpha ^\infty$ is a constant that depends only on the geometry of the problem and on the Damköhler number, as we will see below. Note that
$\mu _1^2 = 2\tau _D\alpha ^\infty$ is a constant that depends only on the geometry of the problem and on the Damköhler number, as we will see below. Note that ![]() $\gamma \approx \textit {Pe}/\mu _1$ for
$\gamma \approx \textit {Pe}/\mu _1$ for ![]() $\textit {Pe}\ll 2\mu _1\overline {v_E}/v_P^\infty$,
$\textit {Pe}\ll 2\mu _1\overline {v_E}/v_P^\infty$, ![]() $\eta ^{-1/2}$, whereas in the opposite limit of large
$\eta ^{-1/2}$, whereas in the opposite limit of large ![]() $\textit {Pe}$,
$\textit {Pe}$, ![]() $\gamma$ approaches a constant,
$\gamma$ approaches a constant, ![]() $\gamma \approx 2\overline {v_E}/v_P^\infty [1+(1+4\mu _1^2\overline {v_E}^2\eta /(v_P^\infty )^2)^{1/2}]^{-1} \approx \overline {v_E}/v_P^\infty$. In the last approximation, we have used the fact that the term involving
$\gamma \approx 2\overline {v_E}/v_P^\infty [1+(1+4\mu _1^2\overline {v_E}^2\eta /(v_P^\infty )^2)^{1/2}]^{-1} \approx \overline {v_E}/v_P^\infty$. In the last approximation, we have used the fact that the term involving ![]() $\eta$ turns out to be small compared to
$\eta$ turns out to be small compared to ![]() $1$ for both the 2-D and 3-D problems. We note that
$1$ for both the 2-D and 3-D problems. We note that ![]() $\gamma \approx \overline {v_E}/v_P^\infty$ is recovered if the plume is approximated as a Dirac delta rather than a Gaussian along the longitudinal direction. As shown in what follows, the dimensionless quantity
$\gamma \approx \overline {v_E}/v_P^\infty$ is recovered if the plume is approximated as a Dirac delta rather than a Gaussian along the longitudinal direction. As shown in what follows, the dimensionless quantity ![]() $\alpha ^\infty \,\Delta m(\boldsymbol {x}_\perp )/\overline {v_E}$ does not depend on the Péclet number, and
$\alpha ^\infty \,\Delta m(\boldsymbol {x}_\perp )/\overline {v_E}$ does not depend on the Péclet number, and ![]() $\gamma$ increases monotonically with
$\gamma$ increases monotonically with ![]() $\textit {Pe}$. The correction factor
$\textit {Pe}$. The correction factor ![]() $\beta$ is thus largest and, more importantly, most spatially variable as
$\beta$ is thus largest and, more importantly, most spatially variable as ![]() $\textit {Pe}\to \infty$. Formally, the factor
$\textit {Pe}\to \infty$. Formally, the factor ![]() $\gamma$ is also largest as
$\gamma$ is also largest as ![]() $\eta \to 0$ for a given
$\eta \to 0$ for a given ![]() $\textit {Pe}$, with
$\textit {Pe}$, with ![]() $\eta$ depending on
$\eta$ depending on ![]() $\textit {Da}$ and geometry, although we find that the value of
$\textit {Da}$ and geometry, although we find that the value of ![]() $\eta$ has negligible impact for the problems treated here, irrespective of the value of
$\eta$ has negligible impact for the problems treated here, irrespective of the value of ![]() $\textit {Pe}$. This means that while the mean plume velocity
$\textit {Pe}$. This means that while the mean plume velocity ![]() $v_P^\infty$ is required to estimate
$v_P^\infty$ is required to estimate ![]() $\gamma$, a detailed treatment of dispersion is not. For the conservative problem,
$\gamma$, a detailed treatment of dispersion is not. For the conservative problem, ![]() $\alpha ^\infty = 0$, so
$\alpha ^\infty = 0$, so ![]() $\beta (\boldsymbol {x}_\perp ) = 1$ and
$\beta (\boldsymbol {x}_\perp ) = 1$ and ![]() $p_s^\infty = p_{t,F}^\infty$, as expected.
$p_s^\infty = p_{t,F}^\infty$, as expected.
We thus conclude that for the reactive problem, breakthrough is favoured where ![]() $\Delta m>0$, and suppressed where
$\Delta m>0$, and suppressed where ![]() $\Delta m <0$, in addition to the natural flux-weighting caused by considering advective breakthrough at fixed distance. From the preceding discussion, based on (3.24), we see that this enhancement or suppression of breakthrough is due to the fact that transverse positions where the mean plume position is locally larger are associated with a larger mass at the time of crossing, because solute arrives earlier and is therefore less subject to reaction on average. We find in what follows that the differences between
$\Delta m <0$, in addition to the natural flux-weighting caused by considering advective breakthrough at fixed distance. From the preceding discussion, based on (3.24), we see that this enhancement or suppression of breakthrough is due to the fact that transverse positions where the mean plume position is locally larger are associated with a larger mass at the time of crossing, because solute arrives earlier and is therefore less subject to reaction on average. We find in what follows that the differences between ![]() $p_s^\infty$ and
$p_s^\infty$ and ![]() $p_{t,F}^\infty$ are non-zero but small for all
$p_{t,F}^\infty$ are non-zero but small for all ![]() $\textit {Da}>0$ and
$\textit {Da}>0$ and ![]() $\textit {Pe}>0$ for the 2-D channel, and are more pronounced for the 3-D channel, even at moderate
$\textit {Pe}>0$ for the 2-D channel, and are more pronounced for the 3-D channel, even at moderate ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}$. In both the 2-D and 3-D cases, the differences between the mean
$\textit {Pe}$. In both the 2-D and 3-D cases, the differences between the mean ![]() $v_t^\infty$ of the fixed-time transverse velocity p.d.f. and the mean plume velocity
$v_t^\infty$ of the fixed-time transverse velocity p.d.f. and the mean plume velocity ![]() $v_P^\infty$, which also result from the same effect, are appreciable starting at moderate
$v_P^\infty$, which also result from the same effect, are appreciable starting at moderate ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}$. It is interesting to note that as we will see,
$\textit {Pe}$. It is interesting to note that as we will see, ![]() $\Delta m$ is non-zero even for the conservative problem, although it no longer plays a role at late times because it does not interact with reaction to create the necessary mass differences.
$\Delta m$ is non-zero even for the conservative problem, although it no longer plays a role at late times because it does not interact with reaction to create the necessary mass differences.
Finally, we consider the velocity p.d.f. associated with breakthrough over a control plane at a given distance from injection. Analogously to (3.6), we have the relationship
 \begin{equation} p_{v_s}^\infty(v) = |\varOmega_\perp|\,p_s^\infty[r_\perp(v)]\,p_E(v) = |\varOmega_\perp|\,p_t^\infty[r_\perp(v)]\,\frac{\beta[r_\perp(v)]\,\overline{v_E}\, p_F(v)}{\displaystyle\int\nolimits_0^{v_M}{\rm d}v\,\beta[r_\perp(v)]\,v\,p_{v,t}^\infty(v)}. \end{equation}
\begin{equation} p_{v_s}^\infty(v) = |\varOmega_\perp|\,p_s^\infty[r_\perp(v)]\,p_E(v) = |\varOmega_\perp|\,p_t^\infty[r_\perp(v)]\,\frac{\beta[r_\perp(v)]\,\overline{v_E}\, p_F(v)}{\displaystyle\int\nolimits_0^{v_M}{\rm d}v\,\beta[r_\perp(v)]\,v\,p_{v,t}^\infty(v)}. \end{equation}Its mean,
 \begin{align} v_s^\infty \!=\! \int_0^{v_M} {\rm d}v\, v\,p_{v_s}^\infty(v) = \frac{\displaystyle\int\nolimits_0^{v_M} {\rm d}v\,\beta[r_\perp(v)]\,v^2\,p_{v_t}^\infty(v)} {\displaystyle\int\nolimits_0^{v_M} {\rm d}v\,\beta[r_\perp(v)]\,v\,p_{v_t}^\infty(v)} = \frac{\displaystyle\int\nolimits_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, \beta(\boldsymbol{x}_\perp)\,v_E^2(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}{ \displaystyle\int\nolimits_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\,\beta(\boldsymbol{x}_\perp)\, v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}, \end{align}
\begin{align} v_s^\infty \!=\! \int_0^{v_M} {\rm d}v\, v\,p_{v_s}^\infty(v) = \frac{\displaystyle\int\nolimits_0^{v_M} {\rm d}v\,\beta[r_\perp(v)]\,v^2\,p_{v_t}^\infty(v)} {\displaystyle\int\nolimits_0^{v_M} {\rm d}v\,\beta[r_\perp(v)]\,v\,p_{v_t}^\infty(v)} = \frac{\displaystyle\int\nolimits_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, \beta(\boldsymbol{x}_\perp)\,v_E^2(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}{ \displaystyle\int\nolimits_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\,\beta(\boldsymbol{x}_\perp)\, v_E(\boldsymbol{x}_\perp)\,p_t^\infty(\boldsymbol{x}_\perp)}, \end{align}
represents the mean solute velocity upon crossing a far control plane, i.e. at a longitudinal position far from the initial condition irrespective of the crossing time. Note that for the conservative problem, this velocity p.d.f. is obtained by flux-weighting the fixed-time velocity p.d.f. That is, in that case, ![]() $p_{v_s}^\infty (v) = p_{v_t,F}^\infty (v)$ and
$p_{v_s}^\infty (v) = p_{v_t,F}^\infty (v)$ and ![]() $v_s^\infty =v_{t,F}^\infty$; see (3.9) and (3.11).
$v_s^\infty =v_{t,F}^\infty$; see (3.9) and (3.11).
4. Equilibrium distributions
In this section, we determine the transverse equilibrium distributions for surviving mass, breakthrough and velocity introduced in § 3. The main asymptotic quantities discussed in this section are summarized in table 1 for ease of reference. Consider first the conservative problem. The asymptotic concentration field for large times is constant over the cross-section, so that ![]() $p_t^\infty (\boldsymbol {x}_\perp )=1/|\varOmega _\perp |$. Thus, in this case, the asymptotic p.d.f. of velocities at fixed time coincides with the Eulerian p.d.f.,
$p_t^\infty (\boldsymbol {x}_\perp )=1/|\varOmega _\perp |$. Thus, in this case, the asymptotic p.d.f. of velocities at fixed time coincides with the Eulerian p.d.f., ![]() $p_{v_t}^\infty =p_E$. Since, as already discussed, the correction factor
$p_{v_t}^\infty =p_E$. Since, as already discussed, the correction factor ![]() $\beta (\boldsymbol {x}_\perp )$ in (3.26) is unity in this case, breakthrough p.d.f.s are obtained by flux-weighting. Thus we have
$\beta (\boldsymbol {x}_\perp )$ in (3.26) is unity in this case, breakthrough p.d.f.s are obtained by flux-weighting. Thus we have ![]() $p_s^\infty =p_{t,F}^\infty = v_E/(|\varOmega _\perp |\,\overline {v_E})$ and
$p_s^\infty =p_{t,F}^\infty = v_E/(|\varOmega _\perp |\,\overline {v_E})$ and ![]() $p_{v_s}^\infty =p_{v_t,F}^\infty =p_F$, as expected (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016).
$p_{v_s}^\infty =p_{v_t,F}^\infty =p_F$, as expected (Dentz et al. Reference Dentz, Kang, Comolli, Le Borgne and Lester2016).
Table 1. Main equilibrium quantities discussed in the text, along with important equations.

In what follows, we analyse the reactive problem separately for flow between flat plates (2-D channel) and flow in a cylindrical pipe (3-D channel). We compare our results to numerical simulations obtained using a standard finite-volume method in OpenFOAM (OpenCFD Ltd 2022). For the simulations, we fix a moderate Péclet number ![]() $\textit {Pe} = 2$, and consider three values of the Damköhler number,
$\textit {Pe} = 2$, and consider three values of the Damköhler number, ![]() $\textit {Da}=10^{-1}$,
$\textit {Da}=10^{-1}$, ![]() $1$ and
$1$ and ![]() $10$, corresponding to slow, moderate and fast reaction compared to diffusion at the scale of the channel radius (see Appendix C for further details).
$10$, corresponding to slow, moderate and fast reaction compared to diffusion at the scale of the channel radius (see Appendix C for further details).
4.1. Two-dimensional channel
In this case, the diffusion equation (2.6) with boundary conditions (2.7) and initial condition ![]() $c_\perp (y;0)$ has the solution (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
$c_\perp (y;0)$ has the solution (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
 \begin{equation} c_\perp(y;t) = \sum_{n\geq 1}\exp\left({-\frac{\mu_n^2 t}{2\tau_D}}\right) \frac{\phi_n(y)}{ab_n}\int_{{-}a}^{a} {{\rm d}y}'\,\phi_n(y')\,c_\perp(y';0), \end{equation}
\begin{equation} c_\perp(y;t) = \sum_{n\geq 1}\exp\left({-\frac{\mu_n^2 t}{2\tau_D}}\right) \frac{\phi_n(y)}{ab_n}\int_{{-}a}^{a} {{\rm d}y}'\,\phi_n(y')\,c_\perp(y';0), \end{equation}where
and ![]() $\mu _n$ are the positive solutions to
$\mu _n$ are the positive solutions to
Trigonometric manipulation yields two useful alternate forms of this relation:
The ![]() $\mu _n$ dictate the rate of decay of mode
$\mu _n$ dictate the rate of decay of mode ![]() $n$ in (4.1a) through the exponential factor. While they cannot in general be determined analytically, by ordering the solutions so that
$n$ in (4.1a) through the exponential factor. While they cannot in general be determined analytically, by ordering the solutions so that ![]() $\mu _n<\mu _{n+1}$, it holds that the
$\mu _n<\mu _{n+1}$, it holds that the ![]() $n=1$ mode is dominant for
$n=1$ mode is dominant for ![]() $t\gtrsim 2\tau _D/(\mu _2^2-\mu _1^2)$, so that for large times,
$t\gtrsim 2\tau _D/(\mu _2^2-\mu _1^2)$, so that for large times,
The dependency of ![]() $\mu _1$ on
$\mu _1$ on ![]() $\textit {Da}$ is shown in figure 1, along with the 3-D case discussed in § 4.2 for comparison. Analytical results for the low and high Damköhler limits are derived in § E.1.
$\textit {Da}$ is shown in figure 1, along with the 3-D case discussed in § 4.2 for comparison. Analytical results for the low and high Damköhler limits are derived in § E.1.

Figure 1. Slowest decay mode constant ![]() $\mu _1$ as a function of
$\mu _1$ as a function of ![]() $\textit {Da}$ for the 2-D and 3-D channels. The solid lines are obtained by finding the smallest solution to (4.1d) and (4.18b) numerically. The analytical limiting forms (E1) and (F1) for small
$\textit {Da}$ for the 2-D and 3-D channels. The solid lines are obtained by finding the smallest solution to (4.1d) and (4.18b) numerically. The analytical limiting forms (E1) and (F1) for small ![]() $\textit {Da}$, and (E2) and (F2) for large
$\textit {Da}$, and (E2) and (F2) for large ![]() $\textit {Da}$, are shown as dashed lines for
$\textit {Da}$, are shown as dashed lines for ![]() $\textit {Da}\leq 1$ and
$\textit {Da}\leq 1$ and ![]() $\textit {Da}\geq 1$, respectively.
$\textit {Da}\geq 1$, respectively.
The onset of the asymptotic regime depends only weakly on the reaction time ![]() $\tau _R$, through the dependence of the decay mode constants
$\tau _R$, through the dependence of the decay mode constants ![]() $\mu _n$ on the Damköhler number. Indeed,
$\mu _n$ on the Damköhler number. Indeed, ![]() $\mu _2^2-\mu _1^2$ grows monotonically from
$\mu _2^2-\mu _1^2$ grows monotonically from ![]() ${\approx }10$ to
${\approx }10$ to ![]() ${\approx }20$ for the 2-D case, so that the characteristic time for the onset of the asymptotic regime decreases with
${\approx }20$ for the 2-D case, so that the characteristic time for the onset of the asymptotic regime decreases with ![]() $\textit {Da}$ but is always of the order of a tenth of the diffusion time. It may seem surprising that the time
$\textit {Da}$ but is always of the order of a tenth of the diffusion time. It may seem surprising that the time ![]() $\tau _R$ does not enter more directly, but this can be understood as follows. In the high-
$\tau _R$ does not enter more directly, but this can be understood as follows. In the high-![]() $\textit {Da}$ limit, the reaction is transport-limited, so that the transition to the asymptotic regime is controlled by diffusion. On the other hand, in the low
$\textit {Da}$ limit, the reaction is transport-limited, so that the transition to the asymptotic regime is controlled by diffusion. On the other hand, in the low ![]() $\textit {Da}$ limit, the equilibrium profile is close to homogeneous, so that little reaction is necessary to achieve it, and the diffusive homogenization time remains the most important control. Similar considerations are valid for the 3-D case, for which
$\textit {Da}$ limit, the equilibrium profile is close to homogeneous, so that little reaction is necessary to achieve it, and the diffusive homogenization time remains the most important control. Similar considerations are valid for the 3-D case, for which ![]() $\mu _2^2-\mu _1^2$ grows monotonically from
$\mu _2^2-\mu _1^2$ grows monotonically from ![]() ${\approx }15$ to
${\approx }15$ to ![]() ${\approx }25$.
${\approx }25$.
4.1.1. Surviving mass and breakthrough
From (3.2) and (4.2), we obtain the equilibrium surviving mass p.d.f.
 \begin{equation} p_t^\infty(y) = \frac{\phi_1(y)}{\displaystyle\int\nolimits_{{-}a}^a {{\rm d}y}'\,\phi_1(y')} = \frac{\mu_1^2}{4a\,\textit{Da}}\left(\cos\left[\mu_1\left(1+\frac{y}{a}\right)\right]+\frac{2\,\textit{Da}}{\mu_1}\sin\left[\mu_1\left(1+\frac{y}{a}\right)\right]\right), \end{equation}
\begin{equation} p_t^\infty(y) = \frac{\phi_1(y)}{\displaystyle\int\nolimits_{{-}a}^a {{\rm d}y}'\,\phi_1(y')} = \frac{\mu_1^2}{4a\,\textit{Da}}\left(\cos\left[\mu_1\left(1+\frac{y}{a}\right)\right]+\frac{2\,\textit{Da}}{\mu_1}\sin\left[\mu_1\left(1+\frac{y}{a}\right)\right]\right), \end{equation}where we have used (4.1e) and some trigonometric manipulation.
We conclude that for arbitrary reaction rate and including ![]() $\textit {Da}\to \infty$, the transverse distribution of surviving mass admits an asymptotic form that is independent of the initial condition. From (4.1a), we also conclude immediately that the late-time reaction rate is constant and given by the slowest decay mode,
$\textit {Da}\to \infty$, the transverse distribution of surviving mass admits an asymptotic form that is independent of the initial condition. From (4.1a), we also conclude immediately that the late-time reaction rate is constant and given by the slowest decay mode,
This result can be verified to agree with (3.14) by direct calculation using (4.3) and the trigonometric relations (4.1e). The fact that the asymptotic rate is constant is consistent with the existence of a transverse equilibrium distribution. The relationship to recent descriptions in terms of first passage times (Aquino & Le Borgne Reference Aquino and Le Borgne2021a; Aquino et al. Reference Aquino, Le Borgne and Heyman2023) is discussed in Appendix D.
To obtain the flux-weighted surviving mass p.d.f. ![]() $p_{t,F}^\infty$, we flux-weight (4.3) according to (3.10):
$p_{t,F}^\infty$, we flux-weight (4.3) according to (3.10):
see also (4.13) below for the mean of the fixed-time velocity p.d.f. The limiting forms of ![]() $p_t^\infty$ and
$p_t^\infty$ and ![]() $p_{t,F}^\infty$ for small and large
$p_{t,F}^\infty$ for small and large ![]() $\textit {Da}$ are derived in § E.1.
$\textit {Da}$ are derived in § E.1.
To obtain the true breakthrough p.d.f. ![]() $p_s^\infty$ associated with flux over a fixed control plane, we must take into account the correction factor
$p_s^\infty$ associated with flux over a fixed control plane, we must take into account the correction factor ![]() $\beta (y) = \exp [\gamma \alpha ^\infty \,\Delta m(y)/\overline {v_E}]$; see (3.26). Because of the normalization, any differences between
$\beta (y) = \exp [\gamma \alpha ^\infty \,\Delta m(y)/\overline {v_E}]$; see (3.26). Because of the normalization, any differences between ![]() $p_s^\infty$ and
$p_s^\infty$ and ![]() $p_{t,F}^\infty$ result from variability in the mean-position discrepancy
$p_{t,F}^\infty$ result from variability in the mean-position discrepancy ![]() $\Delta m(y)$ with respect to the cross-section position
$\Delta m(y)$ with respect to the cross-section position ![]() $y$. To compute it, we must solve (3.20) for the auxiliary quantity
$y$. To compute it, we must solve (3.20) for the auxiliary quantity ![]() $f(y,t)$. Since the differential operators are the same as for the transverse ADE (2.6), this equation has the same propagator, except that the decay modes are modified by the production term at rate
$f(y,t)$. Since the differential operators are the same as for the transverse ADE (2.6), this equation has the same propagator, except that the decay modes are modified by the production term at rate ![]() $\alpha ^\infty$. The solution for the 2-D channel, reflecting the presence of a source term
$\alpha ^\infty$. The solution for the 2-D channel, reflecting the presence of a source term ![]() $p_t^\infty (y)v_E(y)$, is (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
$p_t^\infty (y)v_E(y)$, is (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
 \begin{align} f(y,t) &= \sum_{n\geq 1}\frac{\phi_n(y)}{ab_n}\left[\exp\left({-\left(\frac{\mu_n^2}{2\tau_D}-\alpha^\infty\right)t}\right) \int_{{-}a}^a {{\rm d}y}'\, \phi_n(y')\,f(y',0)\right. \end{align}
\begin{align} f(y,t) &= \sum_{n\geq 1}\frac{\phi_n(y)}{ab_n}\left[\exp\left({-\left(\frac{\mu_n^2}{2\tau_D}-\alpha^\infty\right)t}\right) \int_{{-}a}^a {{\rm d}y}'\, \phi_n(y')\,f(y',0)\right. \end{align}
where the ![]() $\phi _n$ and
$\phi _n$ and ![]() $\mu _n$ are the same as in (4.1a). We assume that the initial condition
$\mu _n$ are the same as in (4.1a). We assume that the initial condition ![]() $f(y,0)\propto \int {{\rm d}\kern0.06em x}\,x\,c(x,y,0)$ does not depend on
$f(y,0)\propto \int {{\rm d}\kern0.06em x}\,x\,c(x,y,0)$ does not depend on ![]() $y$, which holds for any initial condition of constant width along the longitudinal direction. We then set
$y$, which holds for any initial condition of constant width along the longitudinal direction. We then set ![]() $f(y, 0)=0$ without further loss of generality by choosing the longitudinal origin of the coordinate system to coincide with the initial mean plume position. Using (4.3) and (4.4), we obtain, for
$f(y, 0)=0$ without further loss of generality by choosing the longitudinal origin of the coordinate system to coincide with the initial mean plume position. Using (4.3) and (4.4), we obtain, for ![]() $t\gg 2\tau _D/(\mu _2^2-\mu _1^2)$,
$t\gg 2\tau _D/(\mu _2^2-\mu _1^2)$,
 \begin{align} &\quad +\sum_{n\geq 2}\frac{\phi_n(y)}{ab_n\alpha^\infty}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{{-}a}^{a} {{\rm d}y}'\,p_t^\infty(y')\,\phi_n(y')\,v_E(y'). \end{align}
\begin{align} &\quad +\sum_{n\geq 2}\frac{\phi_n(y)}{ab_n\alpha^\infty}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{{-}a}^{a} {{\rm d}y}'\,p_t^\infty(y')\,\phi_n(y')\,v_E(y'). \end{align}The first term is associated with the mean plume velocity as discussed below. From the second term and (3.19a,b) and (3.21), we conclude that the late-time mean-position discrepancy obeys
 \begin{equation} \frac{\alpha^\infty}{\overline{v_E}}\,\Delta m(y) ={-}\frac{3}{2p_t^\infty(y)}\sum_{n\geq 2}\frac{\phi_n(y)}{b_n}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{{-}1}^{1} {\rm d}u\,u^2\,p_t^\infty(au)\,\phi_n(au), \end{equation}
\begin{equation} \frac{\alpha^\infty}{\overline{v_E}}\,\Delta m(y) ={-}\frac{3}{2p_t^\infty(y)}\sum_{n\geq 2}\frac{\phi_n(y)}{b_n}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{{-}1}^{1} {\rm d}u\,u^2\,p_t^\infty(au)\,\phi_n(au), \end{equation}
where we have used the fact that ![]() $p_t^\infty (y)\propto \phi _1(y)$ and the
$p_t^\infty (y)\propto \phi _1(y)$ and the ![]() $\phi _n$ are a set of orthogonal modes (i.e. the product
$\phi _n$ are a set of orthogonal modes (i.e. the product ![]() $\phi _n \phi _m$ integrates to zero for
$\phi _n \phi _m$ integrates to zero for ![]() $n\neq m$). We note that for an initial condition where
$n\neq m$). We note that for an initial condition where ![]() $f(y,0)$ is not constant, there is an additional contribution to
$f(y,0)$ is not constant, there is an additional contribution to ![]() $\Delta m(y)$ given by
$\Delta m(y)$ given by ![]() $\phi _1(y)/(a b_1)\int {{\rm d}y}'\, \phi _1(y')\,f(y',0)$, which cannot be fully removed by a choice of coordinate origin. We are not aware of a closed-form solution of (4.10) for arbitrary
$\phi _1(y)/(a b_1)\int {{\rm d}y}'\, \phi _1(y')\,f(y',0)$, which cannot be fully removed by a choice of coordinate origin. We are not aware of a closed-form solution of (4.10) for arbitrary ![]() $\textit {Da}$. However, rather surprisingly, the remaining integration and sum can both be performed analytically in the limit of large
$\textit {Da}$. However, rather surprisingly, the remaining integration and sum can both be performed analytically in the limit of large ![]() $\textit {Da}$ to yield the simple form
$\textit {Da}$ to yield the simple form
Unfortunately, the denominator in (3.26) must still be computed numerically. As mentioned in § 3.3, ![]() $\Delta m$ is non-zero even for the reactive problem. In that case, proceeding similarly using the conservative solution (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016), we obtain
$\Delta m$ is non-zero even for the reactive problem. In that case, proceeding similarly using the conservative solution (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016), we obtain
We find by numerical computation according to (4.10), using the values of ![]() $\mu _n$ up to
$\mu _n$ up to ![]() $n=6$ reported in Carslaw & Jaeger (Reference Carslaw and Jaeger1986), that this result is approached continuously in the limit of small
$n=6$ reported in Carslaw & Jaeger (Reference Carslaw and Jaeger1986), that this result is approached continuously in the limit of small ![]() $\textit {Da}$.
$\textit {Da}$.
Figure 2(a) illustrates the dependency of the factor ![]() $\gamma$ on Péclet number (see (3.26)), and figure 2(b) shows a comparison between
$\gamma$ on Péclet number (see (3.26)), and figure 2(b) shows a comparison between ![]() $p_s^\infty$ and
$p_s^\infty$ and ![]() $p_{t,F}^\infty$ at large
$p_{t,F}^\infty$ at large ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}$, showing little difference. The value of
$\textit {Pe}$, showing little difference. The value of ![]() $\eta$ in
$\eta$ in ![]() $\gamma$ depends on the Damköhler number, as discussed in relation to (2.9) for Taylor dispersion. However, this dependency makes no appreciable difference in either two or three dimensions for the quantities reported here, and we employ
$\gamma$ depends on the Damköhler number, as discussed in relation to (2.9) for Taylor dispersion. However, this dependency makes no appreciable difference in either two or three dimensions for the quantities reported here, and we employ ![]() $\eta =0$ in (3.26b) here and in what follows. The largest error in
$\eta =0$ in (3.26b) here and in what follows. The largest error in ![]() $\gamma$ occurs for
$\gamma$ occurs for ![]() $\textit {Pe}\to \infty$ and
$\textit {Pe}\to \infty$ and ![]() $\textit {Da}\to \infty$, with a relative value of about
$\textit {Da}\to \infty$, with a relative value of about ![]() $4\times 10^{-3}$ in two dimensions, and
$4\times 10^{-3}$ in two dimensions, and ![]() $2\times 10^{-4}$ in three dimensions. The error decreases to zero as
$2\times 10^{-4}$ in three dimensions. The error decreases to zero as ![]() $\textit {Da}\to 0$. The results for the p.d.f.s under the approximation
$\textit {Da}\to 0$. The results for the p.d.f.s under the approximation ![]() $p_s^\infty \approx p_{t,F}^\infty$ are shown in figure 3 for different
$p_s^\infty \approx p_{t,F}^\infty$ are shown in figure 3 for different ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}=2$. As expected, since the effect of
$\textit {Pe}=2$. As expected, since the effect of ![]() $\beta$ is small at large
$\beta$ is small at large ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}$, the agreement is good across all values of
$\textit {Pe}$, the agreement is good across all values of ![]() $\textit {Da}$.
$\textit {Da}$.
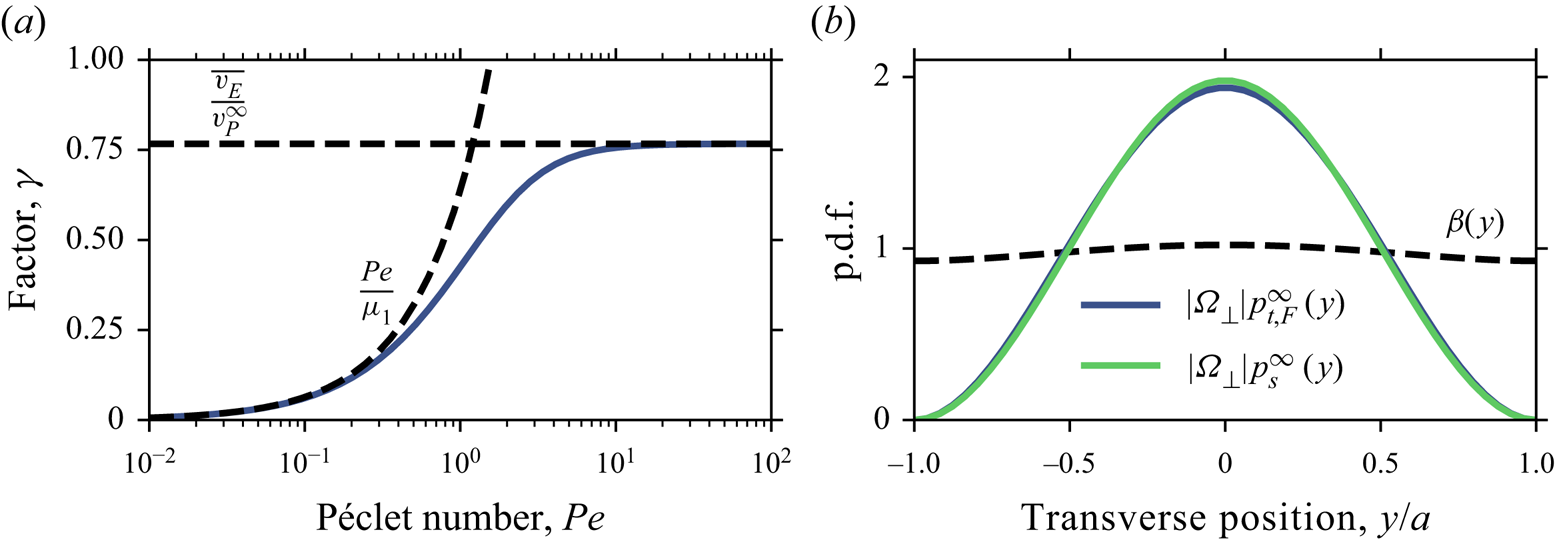
Figure 2. Effect of the mean-position discrepancy ![]() $\Delta m(y)$ on the breakthrough p.d.f.
$\Delta m(y)$ on the breakthrough p.d.f. ![]() $p_s^\infty$ for the 2-D channel. The mean-position discrepancy generates differences between the flux-weighted p.d.f.
$p_s^\infty$ for the 2-D channel. The mean-position discrepancy generates differences between the flux-weighted p.d.f. ![]() $p_{t,F}^\infty$ and the true breakthrough p.d.f.
$p_{t,F}^\infty$ and the true breakthrough p.d.f. ![]() $p_s^\infty$ through the factor
$p_s^\infty$ through the factor ![]() $\beta (y)=\exp [-\gamma \alpha ^\infty \,\Delta m(y)/\overline {v_E}]$ in (3.26). (a) Plot of
$\beta (y)=\exp [-\gamma \alpha ^\infty \,\Delta m(y)/\overline {v_E}]$ in (3.26). (a) Plot of ![]() $\gamma$ as a function of Péclet number
$\gamma$ as a function of Péclet number ![]() $\textit {Pe}$ in the limit of infinite
$\textit {Pe}$ in the limit of infinite ![]() $\textit {Da}$, with the low- and high-
$\textit {Da}$, with the low- and high-![]() $\textit {Pe}$ behaviours shown as dashed lines.(b) Comparison of
$\textit {Pe}$ behaviours shown as dashed lines.(b) Comparison of ![]() $p_s^\infty$ ((3.26) and (4.10)) and
$p_s^\infty$ ((3.26) and (4.10)) and ![]() $p_{t,F}^\infty$ (E6) in the limit of large
$p_{t,F}^\infty$ (E6) in the limit of large ![]() $\textit {Da}$ and
$\textit {Da}$ and ![]() $\textit {Pe}$, showing that differences are minor for the 2-D channel; the factor
$\textit {Pe}$, showing that differences are minor for the 2-D channel; the factor ![]() $\beta (y)$, which is below
$\beta (y)$, which is below ![]() $1$ near the channel walls and above
$1$ near the channel walls and above ![]() $1$ near the channel centre but always close to unity, is shown as a dashed line.
$1$ near the channel centre but always close to unity, is shown as a dashed line.

Figure 3. Equilibrium surviving mass and breakthrough p.d.f.s ![]() $p_t^\infty$ and
$p_t^\infty$ and ![]() $p_s^\infty$ in the 2-D channel, for (a)
$p_s^\infty$ in the 2-D channel, for (a) ![]() $\textit {Da}=10^{-1}$, (b)
$\textit {Da}=10^{-1}$, (b) ![]() $\textit {Da}=1$, and (c)
$\textit {Da}=1$, and (c) ![]() $\textit {Da}=10$. Symbols show the results of numerical simulations. The theoretical predictions approximate the breakthrough p.d.f.
$\textit {Da}=10$. Symbols show the results of numerical simulations. The theoretical predictions approximate the breakthrough p.d.f. ![]() $p_s^\infty$ as the flux-weighted p.d.f.
$p_s^\infty$ as the flux-weighted p.d.f. ![]() $p_{t,F}^\infty$ as discussed in the text. The solid lines in (a,c) show the analytical limit forms (E3) and (E5) for low
$p_{t,F}^\infty$ as discussed in the text. The solid lines in (a,c) show the analytical limit forms (E3) and (E5) for low ![]() $\textit {Da}$, and (E4) and (E6) for high
$\textit {Da}$, and (E4) and (E6) for high ![]() $\textit {Da}$, respectively. The solid lines in (b) show the analytical solutions (4.3) and (4.5) with
$\textit {Da}$, respectively. The solid lines in (b) show the analytical solutions (4.3) and (4.5) with ![]() $\mu _1$ computed numerically according to (4.1d).
$\mu _1$ computed numerically according to (4.1d).
4.1.2. Velocity
Using (2.2), (3.8) and (4.3), we determine the asymptotic mean of the fixed-time velocity p.d.f. as
As discussed in § 3.2, this is smaller than the mean plume velocity ![]() $v_P^\infty$, which describes the rate of change of the plume centre of mass at late times. We find from (3.17) and (4.8) that
$v_P^\infty$, which describes the rate of change of the plume centre of mass at late times. We find from (3.17) and (4.8) that
This result is equivalent to that reported in Lungu & Moffatt (Reference Lungu and Moffatt1982). Using (4.3) for ![]() $p_t^\infty$, (4.11) for
$p_t^\infty$, (4.11) for ![]() $\alpha _\infty \,\Delta m(y)/\overline {v_E}$, (4.13) and (4.14) for
$\alpha _\infty \,\Delta m(y)/\overline {v_E}$, (4.13) and (4.14) for ![]() $v_t^\infty /\overline {v_E}$ and
$v_t^\infty /\overline {v_E}$ and ![]() $v_P^\infty /\overline {v_E}$, and
$v_P^\infty /\overline {v_E}$, and ![]() $\Delta m_W=\Delta m(\pm a)$, we find by direct calculation that (3.22) is satisfied as expected.
$\Delta m_W=\Delta m(\pm a)$, we find by direct calculation that (3.22) is satisfied as expected.
In line with the discussion for the breakthrough p.d.f., we approximate the true average breakthrough velocity ![]() $v_s^\infty$ by the flux-weighted mean
$v_s^\infty$ by the flux-weighted mean ![]() $v_{t,F}^\infty$. Proceeding similarly to the calculation of
$v_{t,F}^\infty$. Proceeding similarly to the calculation of ![]() $v_t^\infty$, using (3.11), we obtain
$v_t^\infty$, using (3.11), we obtain
These results are shown as a function of ![]() $\textit {Da}$ in figure 4(a) (see § E.2 for the derivation of the high- and low-
$\textit {Da}$ in figure 4(a) (see § E.2 for the derivation of the high- and low-![]() $\textit {Da}$ forms). The 3-D case, discussed in detail in § 4.2, is shown in figure 4(b) for comparison.
$\textit {Da}$ forms). The 3-D case, discussed in detail in § 4.2, is shown in figure 4(b) for comparison.

Figure 4. Equilibrium mean of the transverse velocity p.d.f. in time ![]() $v_t^\infty$, its flux-weighted counterpart
$v_t^\infty$, its flux-weighted counterpart ![]() $v_{t,F}^\infty$, mean plume velocity
$v_{t,F}^\infty$, mean plume velocity ![]() $v_P^\infty$, and mean breakthrough velocity
$v_P^\infty$, and mean breakthrough velocity ![]() $v_s^\infty$, as a function of
$v_s^\infty$, as a function of ![]() $\textit {Da}$ for (a) the 2-D channel and (b) the 3-D channel. The solid lines corresponding to
$\textit {Da}$ for (a) the 2-D channel and (b) the 3-D channel. The solid lines corresponding to ![]() $v_t^\infty$,
$v_t^\infty$, ![]() $v_P^\infty$ and
$v_P^\infty$ and ![]() $v_{t,F}^\infty$ are the analytical solutions (a) (4.13), (4.14) and (4.15), and (b) (4.24), (4.25) and (4.26). The corresponding dashed lines show the analytical limit forms for low and high
$v_{t,F}^\infty$ are the analytical solutions (a) (4.13), (4.14) and (4.15), and (b) (4.24), (4.25) and (4.26). The corresponding dashed lines show the analytical limit forms for low and high ![]() $\textit {Da}$: (a) (E7), (E9) and (E11), and (E8), (E10) and (E12); (b) (F7), (F9) and (F11), and (F8), (F10) and (F12). Solid lines corresponding to
$\textit {Da}$: (a) (E7), (E9) and (E11), and (E8), (E10) and (E12); (b) (F7), (F9) and (F11), and (F8), (F10) and (F12). Solid lines corresponding to ![]() $v_s^\infty$ employ (3.28), together with (4.10) for (a) and (4.23) for (b); these lines use Péclet number
$v_s^\infty$ employ (3.28), together with (4.10) for (a) and (4.23) for (b); these lines use Péclet number ![]() $\textit {Pe}\to \infty$. Symbols show the results of numerical simulations for
$\textit {Pe}\to \infty$. Symbols show the results of numerical simulations for ![]() $\textit {Da}=10^{-1}$,
$\textit {Da}=10^{-1}$, ![]() $1$ and
$1$ and ![]() $10$.
$10$.
It is interesting to note that for both the 2-D and 3-D channels, we have ![]() $\overline {v_E}<\overline {v_F}< v_t^\infty < v_{t,F}^\infty < v_s^\infty < v_P^\infty$ as
$\overline {v_E}<\overline {v_F}< v_t^\infty < v_{t,F}^\infty < v_s^\infty < v_P^\infty$ as ![]() $\textit {Da}\to \infty$. In this high-
$\textit {Da}\to \infty$. In this high-![]() $\textit {Da}$ limit, there is a noticeable difference corresponding to an increase of approximately
$\textit {Da}$ limit, there is a noticeable difference corresponding to an increase of approximately ![]() $7\,\%$ and
$7\,\%$ and ![]() $13\,\%$ between
$13\,\%$ between ![]() $v_t^\infty$ and
$v_t^\infty$ and ![]() $v_P^\infty$ in two and three dimensions, respectively. The plume velocity
$v_P^\infty$ in two and three dimensions, respectively. The plume velocity ![]() $v_P^\infty$ differs from the fixed-time flux-weighted velocity
$v_P^\infty$ differs from the fixed-time flux-weighted velocity ![]() $v_{t,F}^\infty$ by only approximately
$v_{t,F}^\infty$ by only approximately ![]() $1\,\%$ and
$1\,\%$ and ![]() $2\,\%$, respectively, and the fixed-time average velocity
$2\,\%$, respectively, and the fixed-time average velocity ![]() $v_t^\infty$ is similar to the Eulerian flux-weighted mean velocity
$v_t^\infty$ is similar to the Eulerian flux-weighted mean velocity ![]() $\overline {v_F}$ rather than to the Eulerian mean velocity
$\overline {v_F}$ rather than to the Eulerian mean velocity ![]() $\overline {v_E}$, differing by about
$\overline {v_E}$, differing by about ![]() $1\,\%$ in the 2-D case, and
$1\,\%$ in the 2-D case, and ![]() $4\,\%$ in the 3-D case. The average breakthrough velocity
$4\,\%$ in the 3-D case. The average breakthrough velocity ![]() $v_s^\infty$ is approximately halfway between
$v_s^\infty$ is approximately halfway between ![]() $v_P^\infty$ and
$v_P^\infty$ and ![]() $v_{t,F}^\infty$ in both cases. This should be contrasted with the conservative problem, for which
$v_{t,F}^\infty$ in both cases. This should be contrasted with the conservative problem, for which ![]() $v_t^\infty =v_P^\infty =\overline {v_E}$ and
$v_t^\infty =v_P^\infty =\overline {v_E}$ and ![]() $v_s^\infty =v_{t,F}^\infty =\overline {v_F}$. As shown in table 2,
$v_s^\infty =v_{t,F}^\infty =\overline {v_F}$. As shown in table 2, ![]() $\overline {v_F}$ is larger than the mean flow velocity
$\overline {v_F}$ is larger than the mean flow velocity ![]() $\overline {v_E}$ by
$\overline {v_E}$ by ![]() $20\,\%$ and approximately
$20\,\%$ and approximately ![]() $33\,\%$ in two and three dimensions; thus the mean plume velocity increases by approximately
$33\,\%$ in two and three dimensions; thus the mean plume velocity increases by approximately ![]() $30\,\%$ and
$30\,\%$ and ![]() $56\,\%$ as
$56\,\%$ as ![]() $\textit{Da} \to \infty$.
$\textit{Da} \to \infty$.
Table 2. Eulerian and flux-weighted Eulerian flow velocity p.d.f.s and associated quantities for Poiseuille flow between two flat plates (spatial dimension ![]() $d=2$) and in a cylindrical channel (
$d=2$) and in a cylindrical channel (![]() $d=3$).
$d=3$).
It is easy to see that the relationship ![]() $\overline {v_E}\leq \overline {v_F}$ always holds, with the equality holding if and only if the flow is uniform, due to fact that
$\overline {v_E}\leq \overline {v_F}$ always holds, with the equality holding if and only if the flow is uniform, due to fact that ![]() $\overline {v_F}$ assigns more weight to higher velocities. The same argument shows that
$\overline {v_F}$ assigns more weight to higher velocities. The same argument shows that ![]() $v_t^\infty \leq v _{t,F}^\infty$, and similarly, because breakthrough at fixed distance is naturally associated with a flux-weighting according to the local velocities,
$v_t^\infty \leq v _{t,F}^\infty$, and similarly, because breakthrough at fixed distance is naturally associated with a flux-weighting according to the local velocities, ![]() $v_t^\infty \leq v _s^\infty$. Since reaction happens at the channel walls, it leads to an increase of the velocities sampled by the plume, and therefore to an increase in the different Lagrangian (i.e. associated with sampling by the solute rather than characteristic of the flow) average velocities
$v_t^\infty \leq v _s^\infty$. Since reaction happens at the channel walls, it leads to an increase of the velocities sampled by the plume, and therefore to an increase in the different Lagrangian (i.e. associated with sampling by the solute rather than characteristic of the flow) average velocities ![]() $v_t^\infty$,
$v_t^\infty$, ![]() $v_{t,F}^\infty$,
$v_{t,F}^\infty$, ![]() $v_s^\infty$ and
$v_s^\infty$ and ![]() $v_P^\infty$. Thus it is also easy to see that for the reactive problem,
$v_P^\infty$. Thus it is also easy to see that for the reactive problem, ![]() $\overline {v_E}< v_t^\infty,v_P^\infty$ and
$\overline {v_E}< v_t^\infty,v_P^\infty$ and ![]() $\overline {v_F}< v_{t,F}^\infty,v_s^\infty$. We have seen that the inequality
$\overline {v_F}< v_{t,F}^\infty,v_s^\infty$. We have seen that the inequality ![]() $v_{t,F}^\infty < v_s^\infty$ of two averages that are identical for the conservative problem arises from the interaction between the subleading moment discrepancy
$v_{t,F}^\infty < v_s^\infty$ of two averages that are identical for the conservative problem arises from the interaction between the subleading moment discrepancy ![]() $\Delta m$ and reaction. Indeed, breakthrough is favoured where
$\Delta m$ and reaction. Indeed, breakthrough is favoured where ![]() $\Delta m>0$, because the earlier arrival of Lagrangian trajectories at these positions means a shorter exposure to reaction; see (3.26). Given that
$\Delta m>0$, because the earlier arrival of Lagrangian trajectories at these positions means a shorter exposure to reaction; see (3.26). Given that ![]() $\Delta m\neq 0$, it is intuitive that the mean plume position for a given transverse position is larger where the flow velocity is larger. This mechanism acts in addition to the natural flux-weighting associated with breakthrough, and leads to
$\Delta m\neq 0$, it is intuitive that the mean plume position for a given transverse position is larger where the flow velocity is larger. This mechanism acts in addition to the natural flux-weighting associated with breakthrough, and leads to ![]() $v_{t,F}^\infty < v_s^\infty$. For a similar reason,
$v_{t,F}^\infty < v_s^\infty$. For a similar reason, ![]() $v_t^\infty < v_P^\infty$; see (3.15). It should be noted that these qualitative arguments are not sufficient to ensure that for sufficiently fast reaction, the fixed-time averages
$v_t^\infty < v_P^\infty$; see (3.15). It should be noted that these qualitative arguments are not sufficient to ensure that for sufficiently fast reaction, the fixed-time averages ![]() $v_P^\infty$ and
$v_P^\infty$ and ![]() $v_t^\infty$ become larger than the flux-weighted Eulerian average
$v_t^\infty$ become larger than the flux-weighted Eulerian average ![]() $\overline {v_F}$, and similarly that
$\overline {v_F}$, and similarly that ![]() $v_P^\infty$ becomes larger than both the Lagrangian flux-weighted average
$v_P^\infty$ becomes larger than both the Lagrangian flux-weighted average ![]() $v_{t,F}^\infty$ and the breakthrough average
$v_{t,F}^\infty$ and the breakthrough average ![]() $v_s^\infty$, as we observe in figure 4. In other words, this discussion does not guarantee that this happens at finite
$v_s^\infty$, as we observe in figure 4. In other words, this discussion does not guarantee that this happens at finite ![]() $\textit {Da}$ for an arbitrary flow configuration.
$\textit {Da}$ for an arbitrary flow configuration.
We also note in this context that the inequality of Lagrangian and Eulerian average velocities is not limited to the reactive problem when considering early times. For the conservative problem, the classical Taylor dispersion picture implies that the asymptotic fixed-time transverse average velocity and the plume velocity both equal the average flow velocity ![]() $\overline {v_E}$, and similarly the average flux-weighted and breakthrough velocities equal
$\overline {v_E}$, and similarly the average flux-weighted and breakthrough velocities equal ![]() $\overline {v_F}$. However, this is not true at pre-asymptotic times, when these quantities may differ as the initial plume deforms as it samples the flow, and complex pre-asymptotic distributions of transverse concentration and breakthrough may develop (Guan & Chen Reference Guan and Chen2024).
$\overline {v_F}$. However, this is not true at pre-asymptotic times, when these quantities may differ as the initial plume deforms as it samples the flow, and complex pre-asymptotic distributions of transverse concentration and breakthrough may develop (Guan & Chen Reference Guan and Chen2024).
Next, we turn to the asymptotic velocity p.d.f.s. For the fixed-time p.d.f., using (3.6), (3.7) and (4.3), we obtain
Recall that the maximum velocity is ![]() $v_M=3\overline {v_E}/2$ for two dimensions. For
$v_M=3\overline {v_E}/2$ for two dimensions. For ![]() $v\ll v_M$, we find by Taylor expansion that the low-velocity behaviour is flat, as for the conservative case. However, as
$v\ll v_M$, we find by Taylor expansion that the low-velocity behaviour is flat, as for the conservative case. However, as ![]() $\textit {Da}\to \infty$ and
$\textit {Da}\to \infty$ and ![]() $\mu _1\to {\rm \pi}/2$, the
$\mu _1\to {\rm \pi}/2$, the ![]() $v$-independent term vanishes. The low-velocity plateau, which accounts for contributions from the shear layer near the channel walls, is thus lower for higher
$v$-independent term vanishes. The low-velocity plateau, which accounts for contributions from the shear layer near the channel walls, is thus lower for higher ![]() $\textit {Da}$, and occurs for smaller
$\textit {Da}$, and occurs for smaller ![]() $v$. The approach to this plateau is
$v$. The approach to this plateau is ![]() $\sim v$, and the scaling of the p.d.f. thus becomes linear in
$\sim v$, and the scaling of the p.d.f. thus becomes linear in ![]() $v$ as
$v$ as ![]() $\textit {Da}\to \infty$. For
$\textit {Da}\to \infty$. For ![]() $v\approx v_M$, corresponding to positions near the centre of the channel, we have
$v\approx v_M$, corresponding to positions near the centre of the channel, we have ![]() $p_{v_t}^\infty (v)\sim 1/\sqrt {v-v_M}$ as for the conservative case, irrespective of
$p_{v_t}^\infty (v)\sim 1/\sqrt {v-v_M}$ as for the conservative case, irrespective of ![]() $\textit {Da}$ (see § E.2 for further details on the low- and high-
$\textit {Da}$ (see § E.2 for further details on the low- and high-![]() $\textit {Da}$ limits).
$\textit {Da}$ limits).
In line with the results for the breakthrough p.d.f., we approximate the true velocity p.d.f. ![]() $p_{v_s}^\infty$ associated with breakthrough at fixed distance by the flux-weighted p.d.f.
$p_{v_s}^\infty$ associated with breakthrough at fixed distance by the flux-weighted p.d.f. ![]() $p_{v_t,F}^\infty$. Flux-weighting (4.16) and using (4.13), we find
$p_{v_t,F}^\infty$. Flux-weighting (4.16) and using (4.13), we find
The low-velocity scaling is now linear for finite ![]() $\textit {Da}$, and becomes quadratic as
$\textit {Da}$, and becomes quadratic as ![]() $\textit {Da}\to \infty$. As before, for high velocities
$\textit {Da}\to \infty$. As before, for high velocities ![]() $v\approx v_M$, the scaling is
$v\approx v_M$, the scaling is ![]() $p_{v_t,F}^\infty (v)\sim 1/\sqrt {v-v_M}$, irrespective of
$p_{v_t,F}^\infty (v)\sim 1/\sqrt {v-v_M}$, irrespective of ![]() $\textit {Da}$. The flux-weighted approximation agrees well with numerical simulations, as can be seen in figure 5.
$\textit {Da}$. The flux-weighted approximation agrees well with numerical simulations, as can be seen in figure 5.

Figure 5. Equilibrium velocity p.d.f. in time ![]() $p_{v_t}^\infty$ and breakthrough velocity p.d.f.
$p_{v_t}^\infty$ and breakthrough velocity p.d.f. ![]() $p_{v_s}^\infty$ in the 2-D channel, for (a)
$p_{v_s}^\infty$ in the 2-D channel, for (a) ![]() $\textit {Da}=10^{-1}$, (b)
$\textit {Da}=10^{-1}$, (b) ![]() $\textit {Da}=1$, and (c)
$\textit {Da}=1$, and (c) ![]() $\textit {Da}=10$. Symbols show the results of numerical simulations. The theoretical predictions approximate
$\textit {Da}=10$. Symbols show the results of numerical simulations. The theoretical predictions approximate ![]() $p_{v_s}^\infty$ as the flux-weighted p.d.f.
$p_{v_s}^\infty$ as the flux-weighted p.d.f. ![]() $p_{v_t,F}^\infty$ as discussed in the text. The solid lines in (a,c) show the analytical limit forms (E13) and (E15) for low
$p_{v_t,F}^\infty$ as discussed in the text. The solid lines in (a,c) show the analytical limit forms (E13) and (E15) for low ![]() $\textit {Da}$, and (E14) and (E16) for high
$\textit {Da}$, and (E14) and (E16) for high ![]() $\textit {Da}$, respectively. The solid lines in (b) show the analytical solutions (4.16) and (4.17), with
$\textit {Da}$, respectively. The solid lines in (b) show the analytical solutions (4.16) and (4.17), with ![]() $\mu _1$ computed numerically according to (4.1d). Dotted lines show the Eulerian and flux-weighted Eulerian velocity p.d.f.s
$\mu _1$ computed numerically according to (4.1d). Dotted lines show the Eulerian and flux-weighted Eulerian velocity p.d.f.s ![]() $p_E(v)$ and
$p_E(v)$ and ![]() $p_F(v)$, which equal
$p_F(v)$, which equal ![]() $p_{v_t}^\infty$ and
$p_{v_t}^\infty$ and ![]() $p_{v_s}^\infty =p_{v_t,F}^\infty$ for the conservative problem.
$p_{v_s}^\infty =p_{v_t,F}^\infty$ for the conservative problem.
4.2. Three-dimensional channel
Similarly to the 2-D case, decay modes of order higher than the first can be neglected at late times for transport in a cylindrical channel. Furthermore, in this case, symmetry ensures that any angular variability in the initial concentration along the channel cross-section vanishes at late times. The late-time solution for transverse concentrations is thus associated with the slowest radial decay mode and is given by (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
 \begin{align}
c_\perp(\boldsymbol{x}_\perp, t) &= \frac{2}{a^2\,{\rm
J}_1^2(\mu_1)}\,\frac{(2\,\textit{Da})^2}{\mu_1^2+(2\,\textit{Da})^2}\exp\left(\frac{-\mu_1^2t}{2\tau_D}\right){\rm
J}_0\left(\mu_1\,\frac{|\boldsymbol{x}_\perp|}{a}\right)\nonumber\\ &\quad \times \int_0^a
{\rm d}r\, r\, {\rm
J}_0\left(\mu_1\,\frac{r}{a}\right)c_\perp(r, 0),
\end{align}
\begin{align}
c_\perp(\boldsymbol{x}_\perp, t) &= \frac{2}{a^2\,{\rm
J}_1^2(\mu_1)}\,\frac{(2\,\textit{Da})^2}{\mu_1^2+(2\,\textit{Da})^2}\exp\left(\frac{-\mu_1^2t}{2\tau_D}\right){\rm
J}_0\left(\mu_1\,\frac{|\boldsymbol{x}_\perp|}{a}\right)\nonumber\\ &\quad \times \int_0^a
{\rm d}r\, r\, {\rm
J}_0\left(\mu_1\,\frac{r}{a}\right)c_\perp(r, 0),
\end{align}
where ![]() ${\rm J}_\nu$ is the Bessel function of the first kind of order
${\rm J}_\nu$ is the Bessel function of the first kind of order ![]() $\nu$, and
$\nu$, and ![]() $\mu _1$ is the smallest positive root of
$\mu _1$ is the smallest positive root of
Using the well-known recurrence relation ![]() $2\alpha \,{\rm J}_\alpha (x)/x = {\rm J}_{\alpha -1}(x)+{\rm J}_{\alpha +1}(x)$ (Abramowitz & Stegun Reference Abramowitz and Stegun1964) for
$2\alpha \,{\rm J}_\alpha (x)/x = {\rm J}_{\alpha -1}(x)+{\rm J}_{\alpha +1}(x)$ (Abramowitz & Stegun Reference Abramowitz and Stegun1964) for ![]() $\alpha =1, 2$, we find that the latter is equivalent to
$\alpha =1, 2$, we find that the latter is equivalent to
The behaviour of ![]() $\mu _1$ as a function of
$\mu _1$ as a function of ![]() $\textit {Da}$ is shown in figure 1(b); see § F.1 for the derivation of the asymptotic forms. Note that the
$\textit {Da}$ is shown in figure 1(b); see § F.1 for the derivation of the asymptotic forms. Note that the ![]() $n$th radial mode decays exponentially at rate
$n$th radial mode decays exponentially at rate ![]() $\mu _n^2/(2\tau _D)$ as for the 2-D case, although the values of
$\mu _n^2/(2\tau _D)$ as for the 2-D case, although the values of ![]() $\mu _n$ are different because they now solve (4.18b).
$\mu _n$ are different because they now solve (4.18b).
4.2.1. Surviving mass and breakthrough
From (4.18a), we obtain the surviving mass p.d.f.
Again, we conclude in particular that an equilibrium form independent of the initial condition exists for all ![]() $\textit {Da}$, including
$\textit {Da}$, including ![]() $\textit {Da}\to \infty$. As before, the asymptotic reaction rate is given by
$\textit {Da}\to \infty$. As before, the asymptotic reaction rate is given by
Flux-weighting, we find
see also the result for the fixed-time average velocity in (4.24) below. The limiting forms of these two p.d.f.s for ![]() $\textit {Da}\to 0$ and
$\textit {Da}\to 0$ and ![]() $\textit {Da}\to \infty$ are discussed in § F.1.
$\textit {Da}\to \infty$ are discussed in § F.1.
To find the breakthrough p.d.f. ![]() $p_s^\infty$, we must solve (3.20). As for the 2-D case, we assume that the initial condition
$p_s^\infty$, we must solve (3.20). As for the 2-D case, we assume that the initial condition ![]() $f(\boldsymbol {x}_\perp,0)\propto \int {{\rm d}\kern0.06em x}\,x\,c(x,\boldsymbol {x}_\perp,0)$ does not depend on
$f(\boldsymbol {x}_\perp,0)\propto \int {{\rm d}\kern0.06em x}\,x\,c(x,\boldsymbol {x}_\perp,0)$ does not depend on ![]() $\boldsymbol {x}_\perp$, and we set
$\boldsymbol {x}_\perp$, and we set ![]() $f(\boldsymbol {x}_\perp, 0)=0$ without further loss of generality. Analogously to the 2-D channel, the solution for
$f(\boldsymbol {x}_\perp, 0)=0$ without further loss of generality. Analogously to the 2-D channel, the solution for ![]() $t\gg 2\tau _D/(\mu _2^2-\mu _1^2)$ is now (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
$t\gg 2\tau _D/(\mu _2^2-\mu _1^2)$ is now (Polyanin & Nazaikinskii Reference Polyanin and Nazaikinskii2016)
 \begin{align} f(\boldsymbol{x}_\perp,t) &=\frac{8{\rm \pi}^2a^2 \mu_1^{{-}2} t\, p_t^\infty(\boldsymbol{x}_\perp)}{1+(\mu_1/2\,\textit{Da})^2} \int_{0}^{a} {\rm d}r\,r(p_t^\infty)^2(r)\,v_E(r) \nonumber\\ &\quad +\frac{2}{a^2\alpha^\infty}\sum_{n\geq 2}\frac{{\rm J}_1^{{-}2}(\mu_n)\,{\rm J}_0(\mu_n\,|\boldsymbol{x}_\perp|/a)}{1+(\mu_n/2\,\textit{Da})^2}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{0}^{a} {\rm d}r\,r\,p_t^\infty(r)\,{\rm J}_0(\mu_n r/a)\,v_E(r). \end{align}
\begin{align} f(\boldsymbol{x}_\perp,t) &=\frac{8{\rm \pi}^2a^2 \mu_1^{{-}2} t\, p_t^\infty(\boldsymbol{x}_\perp)}{1+(\mu_1/2\,\textit{Da})^2} \int_{0}^{a} {\rm d}r\,r(p_t^\infty)^2(r)\,v_E(r) \nonumber\\ &\quad +\frac{2}{a^2\alpha^\infty}\sum_{n\geq 2}\frac{{\rm J}_1^{{-}2}(\mu_n)\,{\rm J}_0(\mu_n\,|\boldsymbol{x}_\perp|/a)}{1+(\mu_n/2\,\textit{Da})^2}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\int_{0}^{a} {\rm d}r\,r\,p_t^\infty(r)\,{\rm J}_0(\mu_n r/a)\,v_E(r). \end{align}As before, the first term is associated with the mean plume velocity (see below), and from (3.19a,b) and (3.21) we conclude from the second term that
 \begin{align} \frac{\alpha^\infty}{\overline{v_E}}\,\Delta m(\boldsymbol{x}_\perp) &={-}4\sum_{n\geq 2}\frac{{\rm J}_0(\mu_n\,|\boldsymbol{x}_\perp|/a)}{{\rm J}_1^2(\mu_n)\,{\rm J}_0(\mu_1\,|\boldsymbol{x}_\perp|/a)}\, \frac{(2\,\textit{Da})^2}{(2\,\textit{Da})^2+\mu_n^2}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\nonumber\\ &\quad\times\int_{0}^{1} {\rm d}u\,u^3\,{\rm J}_0(\mu_1 u)\,{\rm J}_0(\mu_n u). \end{align}
\begin{align} \frac{\alpha^\infty}{\overline{v_E}}\,\Delta m(\boldsymbol{x}_\perp) &={-}4\sum_{n\geq 2}\frac{{\rm J}_0(\mu_n\,|\boldsymbol{x}_\perp|/a)}{{\rm J}_1^2(\mu_n)\,{\rm J}_0(\mu_1\,|\boldsymbol{x}_\perp|/a)}\, \frac{(2\,\textit{Da})^2}{(2\,\textit{Da})^2+\mu_n^2}\,\frac{\mu_1^2}{\mu_n^2-\mu_1^2}\nonumber\\ &\quad\times\int_{0}^{1} {\rm d}u\,u^3\,{\rm J}_0(\mu_1 u)\,{\rm J}_0(\mu_n u). \end{align}We are not aware of a closed-form solution for either the integral or the sum in this case.
Recall that the mean-position discrepancy affects the breakthrough p.d.f. ![]() $p_s^\infty$ through the factor
$p_s^\infty$ through the factor ![]() $\beta (\boldsymbol {x}_\perp )$ in (3.26). The
$\beta (\boldsymbol {x}_\perp )$ in (3.26). The ![]() $\beta$ profiles for different values of the Péclet number at infinite
$\beta$ profiles for different values of the Péclet number at infinite ![]() $\textit {Da}$ are shown in figure 6(a), along with a comparison between the resulting
$\textit {Da}$ are shown in figure 6(a), along with a comparison between the resulting ![]() $p_s^\infty$ and the flux-weighted p.d.f.
$p_s^\infty$ and the flux-weighted p.d.f. ![]() $p_{t,F}^\infty$ in figure 6(b). Although the difference to the flux-weighted p.d.f. is not dramatic, it is substantially more pronounced than in the 2-D case, and clearly discernible at the channel centre. At
$p_{t,F}^\infty$ in figure 6(b). Although the difference to the flux-weighted p.d.f. is not dramatic, it is substantially more pronounced than in the 2-D case, and clearly discernible at the channel centre. At ![]() $\textit {Pe}=2$, the results are similar to those for
$\textit {Pe}=2$, the results are similar to those for ![]() $\textit {Pe}\to \infty$, which explains the good agreement found between simulations at
$\textit {Pe}\to \infty$, which explains the good agreement found between simulations at ![]() $\textit {Pe}=2$ and theory for
$\textit {Pe}=2$ and theory for ![]() $\textit {Pe}\to \infty$ for the mean breakthrough velocity in figure 4(b). The results for the surviving mass and breakthrough p.d.f.s are shown in figure 7 for different
$\textit {Pe}\to \infty$ for the mean breakthrough velocity in figure 4(b). The results for the surviving mass and breakthrough p.d.f.s are shown in figure 7 for different ![]() $\textit {Da}$ at
$\textit {Da}$ at ![]() $\textit {Pe}=2$. As expected, the differences between
$\textit {Pe}=2$. As expected, the differences between ![]() $p_s^\infty$ and
$p_s^\infty$ and ![]() $p_{t,F}^\infty$ become more pronounced with increasing
$p_{t,F}^\infty$ become more pronounced with increasing ![]() $\textit {Da}$, but are already visible at
$\textit {Da}$, but are already visible at ![]() $\textit {Da}=10^{-1}$.
$\textit {Da}=10^{-1}$.
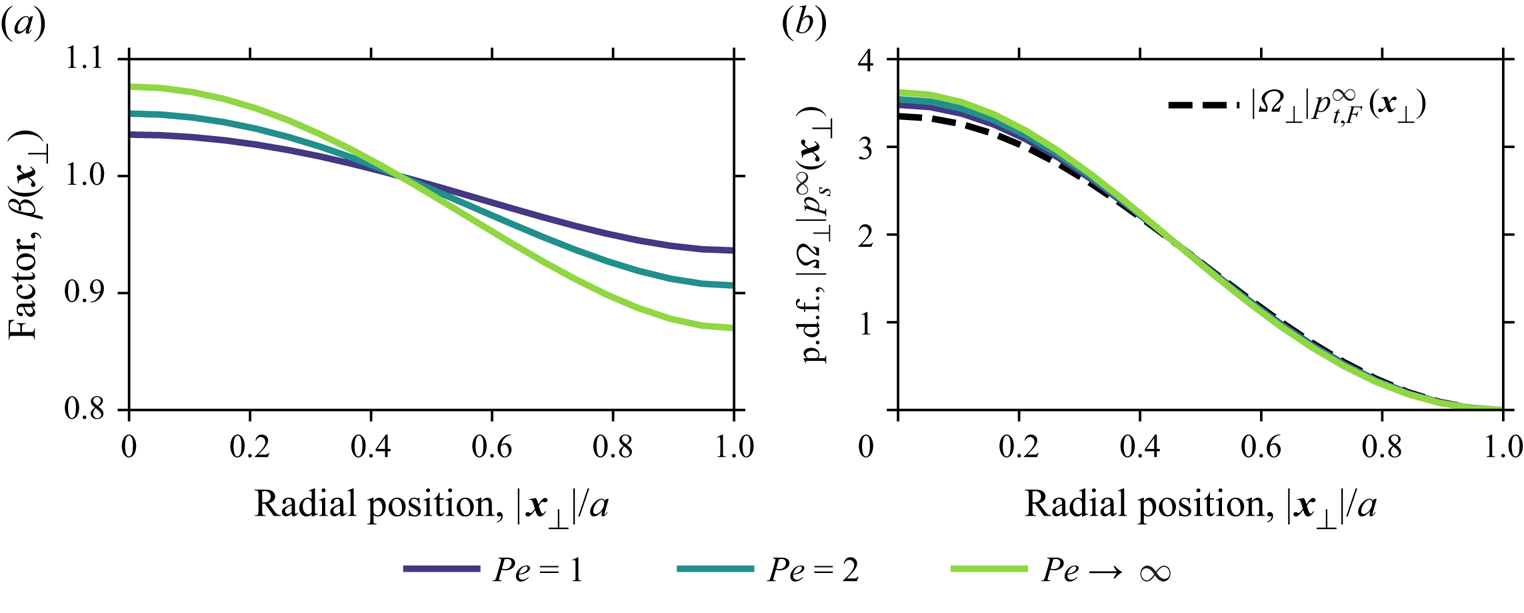
Figure 6. Effect of the mean-position discrepancy ![]() $\Delta m(\boldsymbol {x}_\perp )$ on the breakthrough p.d.f.
$\Delta m(\boldsymbol {x}_\perp )$ on the breakthrough p.d.f. ![]() $p_s^\infty$ for the 3-D channel. The mean-position discrepancy generates differences between the flux-weighted p.d.f.
$p_s^\infty$ for the 3-D channel. The mean-position discrepancy generates differences between the flux-weighted p.d.f. ![]() $p_{t,F}^\infty$ and the true breakthrough p.d.f.
$p_{t,F}^\infty$ and the true breakthrough p.d.f. ![]() $p_s^\infty$ through the factor
$p_s^\infty$ through the factor ![]() $\beta (\boldsymbol {x}_\perp )$ in (3.26). (a) Behaviour of
$\beta (\boldsymbol {x}_\perp )$ in (3.26). (a) Behaviour of ![]() $\beta$ in the limit of infinite
$\beta$ in the limit of infinite ![]() $\textit {Da}$, for different values of Péclet number
$\textit {Da}$, for different values of Péclet number ![]() $\textit {Pe}$. (b) Comparison of the resulting
$\textit {Pe}$. (b) Comparison of the resulting ![]() $p_s^\infty$ ((3.26) and (4.23), using terms up to
$p_s^\infty$ ((3.26) and (4.23), using terms up to ![]() $n=6$ in the sum according to the values of
$n=6$ in the sum according to the values of ![]() $\mu _n$ reported in Carslaw & Jaeger Reference Carslaw and Jaeger1986) to
$\mu _n$ reported in Carslaw & Jaeger Reference Carslaw and Jaeger1986) to ![]() $p_{t,F}^\infty$ (F6).
$p_{t,F}^\infty$ (F6).

Figure 7. Equilibrium surviving mass and breakthrough p.d.f.s ![]() $p_t^\infty$ and
$p_t^\infty$ and ![]() $p_s^\infty$, and flux-weighted mass p.d.f.
$p_s^\infty$, and flux-weighted mass p.d.f. ![]() $p_{t,F}^\infty$, in the 3-D channel, for (a)
$p_{t,F}^\infty$, in the 3-D channel, for (a) ![]() $\textit {Da}=10^{-1}$, (b)
$\textit {Da}=10^{-1}$, (b) ![]() $\textit {Da}=1$, and (c)
$\textit {Da}=1$, and (c) ![]() $\textit {Da}=10$. Symbols show the results of numerical simulations. The solid lines in (a,c) for
$\textit {Da}=10$. Symbols show the results of numerical simulations. The solid lines in (a,c) for ![]() $p_t^\infty$ and
$p_t^\infty$ and ![]() $p_{t,F}^\infty$ show the analytical limiting forms (F3) and (F5) for low
$p_{t,F}^\infty$ show the analytical limiting forms (F3) and (F5) for low ![]() $\textit {Da}$, and (F4) and (F6) for high
$\textit {Da}$, and (F4) and (F6) for high ![]() $\textit {Da}$. The corresponding solid lines in (b) show the analytical solutions (4.19) and (4.21), with
$\textit {Da}$. The corresponding solid lines in (b) show the analytical solutions (4.19) and (4.21), with ![]() $\mu _1$ computed numerically according to (4.18b). In all plots, the solid lines representing
$\mu _1$ computed numerically according to (4.18b). In all plots, the solid lines representing ![]() $p_s^\infty$ are computed using (3.26) and (4.23), using terms up to
$p_s^\infty$ are computed using (3.26) and (4.23), using terms up to ![]() $n=6$ in the sum according to the values of
$n=6$ in the sum according to the values of ![]() $\mu _n$ reported in Carslaw & Jaeger (Reference Carslaw and Jaeger1986).
$\mu _n$ reported in Carslaw & Jaeger (Reference Carslaw and Jaeger1986).
4.2.2. Velocity
Proceeding as for the 2-D case, but integrating (3.8) in polar coordinates and consulting table 2 for the 3-D case, we obtain for the asymptotic mean of the fixed-time velocity p.d.f.:
Using (4.22), arguments similar to those for the 2-D case lead to the asymptotic plume velocity
This result is equivalent to that reported in Lungu & Moffatt (Reference Lungu and Moffatt1982). For the flux-weighted mean velocity, we find
The different mean velocities are shown as a function of ![]() $\textit {Da}$ in figure 4(b); see also the associated discussion in §§ 4.1.2 and F.2 for the limiting forms at low and high
$\textit {Da}$ in figure 4(b); see also the associated discussion in §§ 4.1.2 and F.2 for the limiting forms at low and high ![]() $\textit {Da}$.
$\textit {Da}$.
We now turn to the asymptotic velocity p.d.f.s, again proceeding as for the one-dimensional case. First, according to (3.6), the fixed-time p.d.f. is given by
Note that in this case, the Eulerian p.d.f. ![]() $p_E(v)=1/v_M$ is independent of
$p_E(v)=1/v_M$ is independent of ![]() $v$; see table 2. Finally, for the flux-weighted p.d.f., we have
$v$; see table 2. Finally, for the flux-weighted p.d.f., we have
These velocity p.d.f.s are illustrated in figure 8 (see § F.2 for low- and high-![]() $\textit {Da}$ forms) along with the breakthrough velocity p.d.f.
$\textit {Da}$ forms) along with the breakthrough velocity p.d.f. ![]() $p_{v_s}^\infty$ from (3.27) that takes into account the mean-position discrepancy (4.23). The differences between
$p_{v_s}^\infty$ from (3.27) that takes into account the mean-position discrepancy (4.23). The differences between ![]() $p_{v_s}^\infty$ and
$p_{v_s}^\infty$ and ![]() $p_{v_t,F}^\infty$ are in line with the discussion of the breakthrough p.d.f.
$p_{v_t,F}^\infty$ are in line with the discussion of the breakthrough p.d.f. ![]() $p_s^\infty$; see figure 7.
$p_s^\infty$; see figure 7.

Figure 8. Equilibrium velocity p.d.f. at fixed time ![]() $p_{v_t}^\infty$, corresponding flux-weighted p.d.f.
$p_{v_t}^\infty$, corresponding flux-weighted p.d.f. ![]() $p_{v_t,F}^\infty$, and breakthrough velocity p.d.f.
$p_{v_t,F}^\infty$, and breakthrough velocity p.d.f. ![]() $p_{v_s}^\infty$ in the 3-D channel, for (a)
$p_{v_s}^\infty$ in the 3-D channel, for (a) ![]() $\textit {Da}=10^{-1}$, (b)
$\textit {Da}=10^{-1}$, (b) ![]() $\textit {Da}=1$, and (c)
$\textit {Da}=1$, and (c) ![]() $\textit {Da}=10$. Symbols show the results of numerical simulations. The solid lines associated with
$\textit {Da}=10$. Symbols show the results of numerical simulations. The solid lines associated with ![]() $p_{v_t}^\infty$ and
$p_{v_t}^\infty$ and ![]() $p_{v_t,F}^\infty$ in (a,c) show the analytical limit forms (F13) and (F15) for low
$p_{v_t,F}^\infty$ in (a,c) show the analytical limit forms (F13) and (F15) for low ![]() $\textit {Da}$, and (F14) and (F16) for high
$\textit {Da}$, and (F14) and (F16) for high ![]() $\textit {Da}$. The corresponding solid lines in (b) show the analytical solutions (4.27) and (4.28), with
$\textit {Da}$. The corresponding solid lines in (b) show the analytical solutions (4.27) and (4.28), with ![]() $\mu _1$ computed numerically according to (4.18b). The solid lines associated with
$\mu _1$ computed numerically according to (4.18b). The solid lines associated with ![]() $p_{v_s}^\infty$ use (3.27) in all plots, with
$p_{v_s}^\infty$ use (3.27) in all plots, with ![]() $p_s$ computed as in figure 7. Dotted lines show the Eulerian and flux-weighted Eulerian p.d.f.s, which equal
$p_s$ computed as in figure 7. Dotted lines show the Eulerian and flux-weighted Eulerian p.d.f.s, which equal ![]() $p_{v_t}^\infty$ and
$p_{v_t}^\infty$ and ![]() $p_{v_s}^\infty =p_{v_t,F}^\infty$ for the conservative problem.
$p_{v_s}^\infty =p_{v_t,F}^\infty$ for the conservative problem.
5. Discussion and conclusions
We have provided a detailed analysis of the asymptotic transverse distributions of surviving mass, velocity and breakthrough fluxes for advective–diffusive transport in Poiseuille flow between two flat plates and in a cylindrical channel. Just as for the conservative case, asymptotic forms exist, even in the limit of instantaneous reaction. In addition to qualitatively intuitive changes associated with the depletion of low-velocity regions due to reaction at the channel walls, we have also found that the equality between flux-weighted and breakthrough quantities, as well as between the mean plume velocity and the average of the transverse velocity distribution at fixed time, are modified by the presence of reaction. These effects result from variability in the mean plume position over the channel cross-section, which, despite being of subleading order in time, contributes at leading order to the mean plume velocity and results in non-vanishing asymptotic effects. As we have seen, the effect of this mechanism on breakthrough distributions is noticeable but mild, especially in the two-dimensional case. The effect on the mean plume velocity is more substantial in both cases.
The simplicity of the set-up used here in terms of the geometry, flow profile and chemical kinetics allows most of the calculations to be carried out analytically. This elucidates the underlying mechanisms and also provides analytical building blocks that can be used to develop models that are applicable to more complex scenarios. In this context, the results raise a number of questions that remain open. Does the ordering under fast reaction, ![]() $\overline {v_E}<\overline {v_F}< v_t^\infty < v_{t,F}^\infty < v_s^\infty < v_P^\infty$, of the different mean velocities discussed here hold for arbitrary geometries? What geometric features lead to larger or smaller differences between the mean plume velocity and the average of the transverse velocity distribution, and between breakthrough and flux-weighted quantities? To what extent do these results affect the formal structure and predictions of stochastic models of transport based on velocity distributions, and how can they be adapted to account for more complex geometry, flow heterogeneity and rheology, as encountered, for example, in natural porous and fractured rock formations or in biological systems? Answering these questions, in particular for the single channel and for ensembles of connected channels, will be the subject of future work.
$\overline {v_E}<\overline {v_F}< v_t^\infty < v_{t,F}^\infty < v_s^\infty < v_P^\infty$, of the different mean velocities discussed here hold for arbitrary geometries? What geometric features lead to larger or smaller differences between the mean plume velocity and the average of the transverse velocity distribution, and between breakthrough and flux-weighted quantities? To what extent do these results affect the formal structure and predictions of stochastic models of transport based on velocity distributions, and how can they be adapted to account for more complex geometry, flow heterogeneity and rheology, as encountered, for example, in natural porous and fractured rock formations or in biological systems? Answering these questions, in particular for the single channel and for ensembles of connected channels, will be the subject of future work.
Funding
T.A. acknowledges financial support through the HydroPoreII project (reference PID2022-137652NB-C42), funded by MICIU/AEI/10.13039/501100011033 and by ERDF/EU.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Transverse quantities in terms of Aris–Barton moments
Here, we relate the transverse quantities introduced in § 3 to moments in the classical Aris–Barton formulation (Barton Reference Barton1984). To this end, we define the integral operators
 \begin{equation} \left.\begin{gathered} {\rm I}_x\kern0.06em f = \int_0^\infty {{\rm d}\kern0.06em x}\,f(x) , \quad {\rm I}_\perp \kern0.06em f = \int_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, f(\boldsymbol{x}_\perp),\\ {\rm I}_t \kern0.06em f = \int_0^T{\rm d}t\,f(t), \quad {\rm I}_v f = \int_0^{v_M} f(v)\,{\rm d}v, \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} {\rm I}_x\kern0.06em f = \int_0^\infty {{\rm d}\kern0.06em x}\,f(x) , \quad {\rm I}_\perp \kern0.06em f = \int_{\varOmega_\perp}{\rm d}\kern0.06em \boldsymbol{x}_\perp\, f(\boldsymbol{x}_\perp),\\ {\rm I}_t \kern0.06em f = \int_0^T{\rm d}t\,f(t), \quad {\rm I}_v f = \int_0^{v_M} f(v)\,{\rm d}v, \end{gathered}\right\} \end{equation}
where ![]() $f$ is an arbitrary function that depends on the appropriate physical variable, and variables not affected by the operator are understood to be kept constant. We introduce the local axial moments
$f$ is an arbitrary function that depends on the appropriate physical variable, and variables not affected by the operator are understood to be kept constant. We introduce the local axial moments
where ![]() $m \in \mathbb {N}$, the hat indicates the identity function (i.e.
$m \in \mathbb {N}$, the hat indicates the identity function (i.e. ![]() $\hat x(x) = x$), and the global moments
$\hat x(x) = x$), and the global moments
Note that ![]() $M_0(t)=M(t)$, the total mass at time
$M_0(t)=M(t)$, the total mass at time ![]() $t$. An analytical treatment of these moments may be found in Barton (Reference Barton1984).
$t$. An analytical treatment of these moments may be found in Barton (Reference Barton1984).
In terms of these definitions, the transverse mass p.d.f. is given by
Its flux-weighted counterpart is
and the breakthrough p.d.f. is in turn
As discussed in the main text and in Appendix B, the velocity p.d.f.s associated with spatial sampling according to the previous p.d.f.s can be obtained through what amounts to a change of variables. That is,
where ![]() $\delta _{v_E}$ is the Dirac delta centred at
$\delta _{v_E}$ is the Dirac delta centred at ![]() $v_E$,
$v_E$, ![]() $\delta _{v_E(\boldsymbol {x}_\perp )}(v)=\delta [v_E(\boldsymbol {x}_\perp )-v]$. At equilibrium, when from symmetry considerations the transverse mass p.d.f.s must be a function of radial position only, this simplifies to
$\delta _{v_E(\boldsymbol {x}_\perp )}(v)=\delta [v_E(\boldsymbol {x}_\perp )-v]$. At equilibrium, when from symmetry considerations the transverse mass p.d.f.s must be a function of radial position only, this simplifies to
see (3.7). For the corresponding mean velocities, we have
Finally, the mean plume velocity is the rate of change of the mean plume position,
and we have for the transverse-position-dependent mean position:
so that from (3.15),
 \begin{equation} v^\infty_P = v_t^\infty + \alpha^\infty\lim_{t\to\infty}\left(\frac{M_1}{M_0} - \left.\frac{C_1}{C_0}\right|_{\boldsymbol{x}_\perp{\in}\partial\varOmega_\perp}\right). \end{equation}
\begin{equation} v^\infty_P = v_t^\infty + \alpha^\infty\lim_{t\to\infty}\left(\frac{M_1}{M_0} - \left.\frac{C_1}{C_0}\right|_{\boldsymbol{x}_\perp{\in}\partial\varOmega_\perp}\right). \end{equation}Appendix B. Flow velocity distributions
In this appendix, we provide details on the Eulerian and flux-weighted p.d.f.s associated with flow velocity at fixed times, and their relationship with the velocity p.d.f. characterizing advective velocities at fixed time. The Eulerian velocity p.d.f. is defined as the probability density associated with finding a certain velocity magnitude value at a uniformly random spatial location,
where ![]() $\delta (\cdot )$ is the Dirac delta. In order to express this p.d.f. in a more practical form, it is convenient to change variables in the integrand to explicitly use the fact that the contributions to
$\delta (\cdot )$ is the Dirac delta. In order to express this p.d.f. in a more practical form, it is convenient to change variables in the integrand to explicitly use the fact that the contributions to ![]() $p_E(v)$ arise from positions
$p_E(v)$ arise from positions ![]() $\boldsymbol {x}_\perp$ where the velocity has a specified value
$\boldsymbol {x}_\perp$ where the velocity has a specified value ![]() $v$. The Dirac delta can be expressed as a simple layer integral (Hörmander Reference Hörmander2015; Aquino & Le Borgne Reference Aquino and Le Borgne2021b)
$v$. The Dirac delta can be expressed as a simple layer integral (Hörmander Reference Hörmander2015; Aquino & Le Borgne Reference Aquino and Le Borgne2021b)
where ![]() $\varLambda (v)$ is the
$\varLambda (v)$ is the ![]() $(d-2)$-surface of points
$(d-2)$-surface of points ![]() $\boldsymbol {x}_\perp$ where
$\boldsymbol {x}_\perp$ where ![]() $v_E(\boldsymbol {x}_\perp )=v$. For channel flow, the shear rate magnitude as a function of velocity
$v_E(\boldsymbol {x}_\perp )=v$. For channel flow, the shear rate magnitude as a function of velocity ![]() $\alpha (v)=|\boldsymbol {\nabla }_\perp v_E(\boldsymbol {x}_\perp ;t)|_{\boldsymbol {x}_\perp \in \varLambda (v)}$ is well defined, as it is constant over surfaces of constant velocity. Thus, substituting in (B2), we obtain
$\alpha (v)=|\boldsymbol {\nabla }_\perp v_E(\boldsymbol {x}_\perp ;t)|_{\boldsymbol {x}_\perp \in \varLambda (v)}$ is well defined, as it is constant over surfaces of constant velocity. Thus, substituting in (B2), we obtain
Note that the surface ![]() $\varLambda (v)$ of constant velocity is composed of points of constant radial coordinate
$\varLambda (v)$ of constant velocity is composed of points of constant radial coordinate ![]() $r_\perp (v)=|\boldsymbol {x}_\perp |$ given by
$r_\perp (v)=|\boldsymbol {x}_\perp |$ given by
Recall that ![]() $a$ is the channel radius and
$a$ is the channel radius and ![]() $v_M$ is the maximum velocity, which occurs at the centre of the channel. For example, in two dimensions, this occurs at two points for
$v_M$ is the maximum velocity, which occurs at the centre of the channel. For example, in two dimensions, this occurs at two points for ![]() $v\in ]0,v_M[$, so that
$v\in ]0,v_M[$, so that ![]() $|\varLambda (v)|=2H(v_M-v)\,H(v)$, where
$|\varLambda (v)|=2H(v_M-v)\,H(v)$, where ![]() $H$ is the Heaviside step function. In what follows, we omit such Heaviside step functions for notational simplicity. Taking the derivative of the Poiseuille flow profile (2.2) with respect to
$H$ is the Heaviside step function. In what follows, we omit such Heaviside step functions for notational simplicity. Taking the derivative of the Poiseuille flow profile (2.2) with respect to ![]() $|\boldsymbol {x}_\perp |$ and substituting (B4),
$|\boldsymbol {x}_\perp |$ and substituting (B4),
We also define the flux-weighted Eulerian p.d.f. ![]() $p_F(v) = v\,p_E(v)/\overline {v_E}$. Some useful quantities relating to
$p_F(v) = v\,p_E(v)/\overline {v_E}$. Some useful quantities relating to ![]() $p_E$ and
$p_E$ and ![]() $p_F$ and their means
$p_F$ and their means ![]() $\overline {v_E}$ and
$\overline {v_E}$ and ![]() $\overline {v_F}$ for Poiseuille flow in two and three dimensions, computed according to these results, are summarized in table 2.
$\overline {v_F}$ for Poiseuille flow in two and three dimensions, computed according to these results, are summarized in table 2.
We can now generalize the discussion above leading to the Eulerian p.d.f. The transverse velocity p.d.f. at fixed time ![]() $p_{v_t}^\infty (\cdot ;t)$ is obtained by sampling spatial locations according to the p.d.f.
$p_{v_t}^\infty (\cdot ;t)$ is obtained by sampling spatial locations according to the p.d.f. ![]() $p_t(\cdot ;t)$ of cross-section positions determined by the surviving mass profile, rather than uniformly. That is,
$p_t(\cdot ;t)$ of cross-section positions determined by the surviving mass profile, rather than uniformly. That is,
Using (B2), together with the fact that the shear rate ![]() $\alpha (v)$ is constant over surfaces of constant
$\alpha (v)$ is constant over surfaces of constant ![]() $v$, we obtain
$v$, we obtain
From symmetry considerations, if the asymptotic surviving mass p.d.f. ![]() $p_t^\infty$ exists, then it must depend only on the radial coordinate, and therefore can also be expressed as a function of velocity through
$p_t^\infty$ exists, then it must depend only on the radial coordinate, and therefore can also be expressed as a function of velocity through ![]() $r_\perp (v)$; see (B4). Thus, from (B3) and (B7),
$r_\perp (v)$; see (B4). Thus, from (B3) and (B7),
Appendix C. Numerical simulations
Numerical simulations of the reactive transport problem used in the text were performed using a standard second-order finite-volume solver in OpenFOAM (OpenCFD Ltd 2022). The mean Eulerian velocity was set to ![]() $\overline {v_E}=1$, the domain radius (half-width in two dimensions) to
$\overline {v_E}=1$, the domain radius (half-width in two dimensions) to ![]() $a=1$, and the diffusion coefficient to
$a=1$, and the diffusion coefficient to ![]() $D=1/2$. A flux-weighted pulse injection one discretization cell wide near
$D=1/2$. A flux-weighted pulse injection one discretization cell wide near ![]() $x=x_0=10$ was used in all simulations. The channel inlet was placed at
$x=x_0=10$ was used in all simulations. The channel inlet was placed at ![]() $x=0$, and the outlet at
$x=0$, and the outlet at ![]() $x=100$. The normalized equilibrium results presented in the text are not affected by these parameter and initial condition choices, except for the value of Péclet number
$x=100$. The normalized equilibrium results presented in the text are not affected by these parameter and initial condition choices, except for the value of Péclet number ![]() $\textit {Pe}=2$ (defined according to (2.3)) in the case of breakthrough quantities. The boundary conditions at the inlet and outlet of the channel were absorbing, although care was taken to verify that no mass left the domain by the inlet or outlet within the times of interest. The Robin boundary condition (2.7) was imposed at the channel walls. The simulations were run up to time
$\textit {Pe}=2$ (defined according to (2.3)) in the case of breakthrough quantities. The boundary conditions at the inlet and outlet of the channel were absorbing, although care was taken to verify that no mass left the domain by the inlet or outlet within the times of interest. The Robin boundary condition (2.7) was imposed at the channel walls. The simulations were run up to time ![]() $t=100$. Damköhler numbers
$t=100$. Damköhler numbers ![]() $\textit {Da}=10^{-1}$,
$\textit {Da}=10^{-1}$, ![]() $1$ and
$1$ and ![]() $10$, defined according to (2.8a–c), were simulated.
$10$, defined according to (2.8a–c), were simulated.
For the 2-D channel, we employed a regular grid discretization with ![]() $1000$ cells in the
$1000$ cells in the ![]() $x$ direction and
$x$ direction and ![]() $20$ cells in the
$20$ cells in the ![]() $y$ direction. For the 3-D channel, we used a regular discretization in a square central region of side
$y$ direction. For the 3-D channel, we used a regular discretization in a square central region of side ![]() $1/2$ to avoid numerical issues at the centre of the channel, as shown in figure 9. The discretization along the
$1/2$ to avoid numerical issues at the centre of the channel, as shown in figure 9. The discretization along the ![]() $x$ direction was again regular using
$x$ direction was again regular using ![]() $1000$ cells. Along each of the
$1000$ cells. Along each of the ![]() $y$ and
$y$ and ![]() $z$ directions,
$z$ directions, ![]() $30$ cells were used:
$30$ cells were used: ![]() $10$ in the square central region, and
$10$ in the square central region, and ![]() $10$ on each side. The outer regions employed an expansion ratio of
$10$ on each side. The outer regions employed an expansion ratio of ![]() $25\,\%$, such that cells decreased in size towards the channel wall from the centre.
$25\,\%$, such that cells decreased in size towards the channel wall from the centre.
Figure 9. Cross-section of the 3-D-channel mesh.
The equilibrium profiles were evaluated at times ![]() $\tau$ and longitudinal positions
$\tau$ and longitudinal positions ![]() $x_0+\overline {v_E}\tau$. For the 2-D case,
$x_0+\overline {v_E}\tau$. For the 2-D case, ![]() $\tau =30$ for all values of
$\tau =30$ for all values of ![]() $\textit {Da}$. For the 3-D case,
$\textit {Da}$. For the 3-D case, ![]() $\tau =20$ for
$\tau =20$ for ![]() $\textit {Da}=10^{-1}$, and
$\textit {Da}=10^{-1}$, and ![]() $\tau =5$ for
$\tau =5$ for ![]() $\textit {Da}=1$ and
$\textit {Da}=1$ and ![]() $\textit {Da}=10$. These smaller values of
$\textit {Da}=10$. These smaller values of ![]() $\tau$ in the latter cases were used to avoid numerical issues due to very small concentration values, which affect the computation of breakthrough fluxes at large distances. In addition, in these two cases, the initial mass was multiplied by a large value to avoid errors associated with roundoff procedures employed by OpenFOAM to prevent overflow on division by small numbers. This does not affect the results after normalizing by mass because the problem is linear.
$\tau$ in the latter cases were used to avoid numerical issues due to very small concentration values, which affect the computation of breakthrough fluxes at large distances. In addition, in these two cases, the initial mass was multiplied by a large value to avoid errors associated with roundoff procedures employed by OpenFOAM to prevent overflow on division by small numbers. This does not affect the results after normalizing by mass because the problem is linear.
Surviving mass p.d.f.s ![]() $p_t$ are computed by integrating concentrations numerically over the longitudinal direction at the time of interest, using the underlying grid discretization. The breakthrough profiles
$p_t$ are computed by integrating concentrations numerically over the longitudinal direction at the time of interest, using the underlying grid discretization. The breakthrough profiles ![]() $p_s$ are computed by integrating concentrations multiplied by local velocities over time at the longitudinal position of interest, using an integration time step 0.1. Mean plume velocities
$p_s$ are computed by integrating concentrations multiplied by local velocities over time at the longitudinal position of interest, using an integration time step 0.1. Mean plume velocities ![]() $v_P^\infty$ are obtained by numerically computing the mean longitudinal position
$v_P^\infty$ are obtained by numerically computing the mean longitudinal position ![]() $m_P(t)$ at time
$m_P(t)$ at time ![]() $t=40$, and estimating
$t=40$, and estimating ![]() $v_P^\infty = [m_P(t)-x_0]/t$. The remaining mean velocities discussed in the text,
$v_P^\infty = [m_P(t)-x_0]/t$. The remaining mean velocities discussed in the text, ![]() $v_t^\infty$,
$v_t^\infty$, ![]() $v_{t,F}^\infty$ and
$v_{t,F}^\infty$ and ![]() $v_s^\infty$, are obtained by direct numerical integration according to the relevant numerically determined p.d.f.s.
$v_s^\infty$, are obtained by direct numerical integration according to the relevant numerically determined p.d.f.s.
Appendix D. Asymptotic decay rate in terms of first passage times
As shown in the present work, the asymptotic reaction rate ![]() $\alpha ^\infty$ associated with the decay of total plume mass at late times is constant and determined by the slowest decay mode of concentration,
$\alpha ^\infty$ associated with the decay of total plume mass at late times is constant and determined by the slowest decay mode of concentration,
Recently, the decay of total mass has been described in terms of first passage and return times to the reactive interface (Aquino & Le Borgne Reference Aquino and Le Borgne2021a; Aquino et al. Reference Aquino, Le Borgne and Heyman2023). In particular, for an instantaneous injection of initial mass ![]() $M_0$ in the 2-D channel, it is given in Laplace space by (Aquino & Le Borgne Reference Aquino and Le Borgne2021a)
$M_0$ in the 2-D channel, it is given in Laplace space by (Aquino & Le Borgne Reference Aquino and Le Borgne2021a)
where the tilde denotes the Laplace transform, ![]() $\lambda$ is the Laplace variable conjugate to time, and
$\lambda$ is the Laplace variable conjugate to time, and ![]() $\varPsi _0$ is the survival probability, i.e.
$\varPsi _0$ is the survival probability, i.e. ![]() $\varPsi _0(t)$ is the probability that first passage to the channel wall has not occurred by time
$\varPsi _0(t)$ is the probability that first passage to the channel wall has not occurred by time ![]() $t$ for a given initial concentration distribution in the channel. The description in terms of first passage times is particularly intuitive for
$t$ for a given initial concentration distribution in the channel. The description in terms of first passage times is particularly intuitive for ![]() $\textit {Da}\to \infty$, which corresponds to fully-absorbing walls. Then, for any geometry, the total mass is fully determined by the first passage times and is given by
$\textit {Da}\to \infty$, which corresponds to fully-absorbing walls. Then, for any geometry, the total mass is fully determined by the first passage times and is given by ![]() $M(t) = M_0\,\varPsi _0(t)$, i.e. the surviving mass is precisely the mass that has not yet reached the walls. The general result agrees with that reported in Zhang et al. (Reference Zhang, Hesse and Wang2017) for the case of a homogeneous initial distribution, for which
$M(t) = M_0\,\varPsi _0(t)$, i.e. the surviving mass is precisely the mass that has not yet reached the walls. The general result agrees with that reported in Zhang et al. (Reference Zhang, Hesse and Wang2017) for the case of a homogeneous initial distribution, for which ![]() $\tilde {\varPsi }_0(\lambda ) = [1-\tanh (\sqrt {2\tau _D\lambda })/\sqrt {2\tau _D\lambda }]/\lambda$.
$\tilde {\varPsi }_0(\lambda ) = [1-\tanh (\sqrt {2\tau _D\lambda })/\sqrt {2\tau _D\lambda }]/\lambda$.
From (D2), the late-time reaction rate can be estimated by expanding for small ![]() $\lambda$, yielding (Aquino & Le Borgne Reference Aquino and Le Borgne2021a)
$\lambda$, yielding (Aquino & Le Borgne Reference Aquino and Le Borgne2021a)
where ![]() $w_0$ is the mean first passage time, and
$w_0$ is the mean first passage time, and ![]() $s_0^2$ is the corresponding second moment. This result differs from (D1) and appears to suggest that the late-time reaction rate depends on the initial mass distribution. The reason for this discrepancy is that the small-
$s_0^2$ is the corresponding second moment. This result differs from (D1) and appears to suggest that the late-time reaction rate depends on the initial mass distribution. The reason for this discrepancy is that the small-![]() $\lambda$ expansion of the Laplace transform of a function with a finite first moment produces an approximation of the late-time behaviour that recovers the correct first moment, rather than providing the exact late-time decay. This approximation becomes exact when the original function is itself exponential. For common initial distributions, such as a uniform injection, a flux-weighted injection (
$\lambda$ expansion of the Laplace transform of a function with a finite first moment produces an approximation of the late-time behaviour that recovers the correct first moment, rather than providing the exact late-time decay. This approximation becomes exact when the original function is itself exponential. For common initial distributions, such as a uniform injection, a flux-weighted injection (![]() $\tilde {\varPsi }_0(\lambda ) = [1 - 3(1-\tanh (\sqrt {2\tau _D\lambda })/\sqrt {2\tau _D\lambda })/(2\tau _D\lambda )]/\lambda$), or a mid-channel injection (
$\tilde {\varPsi }_0(\lambda ) = [1 - 3(1-\tanh (\sqrt {2\tau _D\lambda })/\sqrt {2\tau _D\lambda })/(2\tau _D\lambda )]/\lambda$), or a mid-channel injection (![]() $\tilde {\varPsi }_0(\lambda ) = [1-\mathrm {sech}(\sqrt {2\tau _D\lambda })]/\lambda$), the exponential approximation is sound and leads to maximum relative errors of approximately
$\tilde {\varPsi }_0(\lambda ) = [1-\mathrm {sech}(\sqrt {2\tau _D\lambda })]/\lambda$), the exponential approximation is sound and leads to maximum relative errors of approximately ![]() $1\,\%$,
$1\,\%$, ![]() $0.1\,\%$ and
$0.1\,\%$ and ![]() $3\,\%$, respectively, which occur at infinite
$3\,\%$, respectively, which occur at infinite ![]() $\textit{Da}$. Thus while it may wrongly suggest that the late-time behaviour is initial-condition-dependent, the Laplace expansion approach based on the first passage time picture provides good approximations and generalizes well to more complex geometries (Aquino & Le Borgne Reference Aquino and Le Borgne2021a; Aquino et al. Reference Aquino, Le Borgne and Heyman2023). This also shows that since for
$\textit{Da}$. Thus while it may wrongly suggest that the late-time behaviour is initial-condition-dependent, the Laplace expansion approach based on the first passage time picture provides good approximations and generalizes well to more complex geometries (Aquino & Le Borgne Reference Aquino and Le Borgne2021a; Aquino et al. Reference Aquino, Le Borgne and Heyman2023). This also shows that since for ![]() $\textit {Da}\to \infty$ we have
$\textit {Da}\to \infty$ we have ![]() $\alpha ^\infty$ independent of the initial condition, the actual late-time tail of the first passage time distribution is independent of the initial mass distribution and is instead fully determined by the diffusion coefficient and the geometry of the problem.
$\alpha ^\infty$ independent of the initial condition, the actual late-time tail of the first passage time distribution is independent of the initial mass distribution and is instead fully determined by the diffusion coefficient and the geometry of the problem.
Appendix E. Damköhler expansions for the 2-D channel
In this appendix, we derive limiting forms for low and high Damöhler number ![]() $\textit {Da}$ of some of the equilibrium quantities discussed in the main text for the 2-D channel.
$\textit {Da}$ of some of the equilibrium quantities discussed in the main text for the 2-D channel.
E.1. Surviving mass
First, consider the slowest concentration decay mode ![]() $\mu _1$. For
$\mu _1$. For ![]() $\textit {Da}\ll 1$, we can Taylor expand the second form in (4.1e) around
$\textit {Da}\ll 1$, we can Taylor expand the second form in (4.1e) around ![]() $\mu =0$, to obtain
$\mu =0$, to obtain
In the opposite limit of fast reaction, ![]() $\textit {Da}\gg 1$, we expand (4.1d) around
$\textit {Da}\gg 1$, we expand (4.1d) around ![]() $\mu ={\rm \pi} /2$ and
$\mu ={\rm \pi} /2$ and ![]() $1/\textit {Da}=0$ to obtain
$1/\textit {Da}=0$ to obtain
Substituting (E1) in (4.3) and Taylor expanding for ![]() $\textit {Da}\ll 1$ yields for the surviving mass p.d.f.
$\textit {Da}\ll 1$ yields for the surviving mass p.d.f.
In particular, note that ![]() $p_t^\infty (y)=1/|\varOmega _\perp |=1/(2a)$ for
$p_t^\infty (y)=1/|\varOmega _\perp |=1/(2a)$ for ![]() $\textit {Da}=0$, as expected. Similarly, substituting (E2) and expanding for
$\textit {Da}=0$, as expected. Similarly, substituting (E2) and expanding for ![]() $\textit {Da}\gg 1$ leads to
$\textit {Da}\gg 1$ leads to
The corresponding flux-weighted p.d.f. (4.5) is, for low ![]() $\textit {Da}$,
$\textit {Da}$,
and, for high ![]() $\textit {Da}$,
$\textit {Da}$,
E.2. Velocity
For ![]() $\textit {Da}\ll 1$, we obtain the average of the fixed-time velocity p.d.f. (4.13),
$\textit {Da}\ll 1$, we obtain the average of the fixed-time velocity p.d.f. (4.13),
In particular, we recover ![]() $v_t^\infty =\overline {v_E}$ for the conservative problem, as expected. Note that in order to obtain this result to second order in
$v_t^\infty =\overline {v_E}$ for the conservative problem, as expected. Note that in order to obtain this result to second order in ![]() $\textit {Da}$ with the expansion (E1) for
$\textit {Da}$ with the expansion (E1) for ![]() $\mu _1$, it is necessary to use the first form in (4.13); for the second form, a higher-order expansion of
$\mu _1$, it is necessary to use the first form in (4.13); for the second form, a higher-order expansion of ![]() $\mu _1$ in
$\mu _1$ in ![]() $\textit {Da}$ would be necessary. The second-order accuracy is necessary to achieve first-order accuracy in
$\textit {Da}$ would be necessary. The second-order accuracy is necessary to achieve first-order accuracy in ![]() $v_{t,F}^\infty$ below. For
$v_{t,F}^\infty$ below. For ![]() $\textit {Da}\gg 1$, we have
$\textit {Da}\gg 1$, we have
For the mean plume velocity (4.14), we find, for ![]() $\textit {Da}\ll 1$,
$\textit {Da}\ll 1$,
and, for ![]() $\textit {Da}\gg 1$,
$\textit {Da}\gg 1$,
For ![]() $\textit {Da}\ll 1$, using (E1) and (E7), (4.15) for the flux-weighted average velocity reduces to
$\textit {Da}\ll 1$, using (E1) and (E7), (4.15) for the flux-weighted average velocity reduces to
Again as expected, we recover ![]() $v_{t,F}^\infty =\overline {v_F}$ in the conservative limit. For
$v_{t,F}^\infty =\overline {v_F}$ in the conservative limit. For ![]() $\textit {Da}\gg 1$,
$\textit {Da}\gg 1$,
Proceeding similarly, the ![]() $\textit {Da}\ll 1$ limit of (4.16) for the equilibrium fixed-time velocity p.d.f. is
$\textit {Da}\ll 1$ limit of (4.16) for the equilibrium fixed-time velocity p.d.f. is
and for ![]() $\textit {Da}\gg 1$ we have
$\textit {Da}\gg 1$ we have
For the equilibrium flux-weighted velocity p.d.f. (4.17), the low-![]() $\textit {Da}$ limit is
$\textit {Da}$ limit is
and for the high-![]() $\textit {Da}$ limit, we obtain
$\textit {Da}$ limit, we obtain
 \begin{align} \frac{p_{v_t,F}^\infty(v)}{p_F(v)} &\approx \frac{{\rm \pi}^3}{24}\cos\left(\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\right)\nonumber\\ &\quad \times\left(1-\left[3-\frac{{\rm \pi}^2}{4}-\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\tan\left(\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\right)\right]\frac{1}{2\,\textit{Da}}\right). \end{align}
\begin{align} \frac{p_{v_t,F}^\infty(v)}{p_F(v)} &\approx \frac{{\rm \pi}^3}{24}\cos\left(\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\right)\nonumber\\ &\quad \times\left(1-\left[3-\frac{{\rm \pi}^2}{4}-\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\tan\left(\frac{\rm \pi}{2}\sqrt{1-\frac{v}{v_M}}\right)\right]\frac{1}{2\,\textit{Da}}\right). \end{align}Appendix F. Damköhler expansions for the 3-D channel
Here, we derive limiting forms for low and high Damöhler number ![]() $\textit {Da}$ of some of the equilibrium quantities discussed in the main text for the 3-D channel.
$\textit {Da}$ of some of the equilibrium quantities discussed in the main text for the 3-D channel.
F.1. Surviving mass
Expanding (4.18b) to sixth order in ![]() $\mu$, solving for
$\mu$, solving for ![]() $\mu$, and expanding for small
$\mu$, and expanding for small ![]() $\textit {Da}$, we find for the slowest concentration decay mode:
$\textit {Da}$, we find for the slowest concentration decay mode:
For ![]() $\textit {Da}\to \infty$, we have
$\textit {Da}\to \infty$, we have ![]() $\textrm {J}_0(\mu )=0$, so that
$\textrm {J}_0(\mu )=0$, so that ![]() $\mu _1=j_{0,1}\approx 2.4048$, the smallest positive root of
$\mu _1=j_{0,1}\approx 2.4048$, the smallest positive root of ![]() $\textrm {J}_0$. Expanding
$\textrm {J}_0$. Expanding ![]() $\mu$ to first order around this value in (4.18b), we obtain the high-
$\mu$ to first order around this value in (4.18b), we obtain the high-![]() $\textit {Da}$ expansion
$\textit {Da}$ expansion
Using (4.19) and (F1), we find the low-![]() $\textit {Da}$ expansion for the surviving mass p.d.f.:
$\textit {Da}$ expansion for the surviving mass p.d.f.:
Note that, as expected, in the conservative limit we recover a uniform transverse p.d.f. ![]() $p_t^\infty (\boldsymbol {x}_\perp )=1/|\varOmega _\perp |=1/({\rm \pi} a^2)$. Based on (4.19) and (F2), we obtain the high-
$p_t^\infty (\boldsymbol {x}_\perp )=1/|\varOmega _\perp |=1/({\rm \pi} a^2)$. Based on (4.19) and (F2), we obtain the high-![]() $\textit {Da}$ expansion
$\textit {Da}$ expansion
Correspondingly, for the flux-weighted p.d.f., we find for low ![]() $\textit {Da}$
$\textit {Da}$
and for high ![]() $\textit {Da}$,
$\textit {Da}$,
 \begin{align} |\varOmega_\perp|\,p_{t,F}^\infty(\boldsymbol{x}_\perp) &\approx \frac{j_{0,1}^3\,{\rm J}_0(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}{8\,{\rm J}_1(j_{0,1})}\left(1-\frac{|\boldsymbol{x}_\perp|^2}{a^2}\right) \nonumber\\ &\quad\times\left[1-\left(8-j_{0,1}^2-\frac{2j_{0,1}\,{\rm J}_1(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}{{\rm J}_0(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}\,\frac{|\boldsymbol{x}_\perp|}{a}\right)\frac{1}{4\,\textit{Da}}\right]. \end{align}
\begin{align} |\varOmega_\perp|\,p_{t,F}^\infty(\boldsymbol{x}_\perp) &\approx \frac{j_{0,1}^3\,{\rm J}_0(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}{8\,{\rm J}_1(j_{0,1})}\left(1-\frac{|\boldsymbol{x}_\perp|^2}{a^2}\right) \nonumber\\ &\quad\times\left[1-\left(8-j_{0,1}^2-\frac{2j_{0,1}\,{\rm J}_1(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}{{\rm J}_0(j_{0,1}\,|\boldsymbol{x}_\perp|/a)}\,\frac{|\boldsymbol{x}_\perp|}{a}\right)\frac{1}{4\,\textit{Da}}\right]. \end{align}F.2. Velocity
The average of the fixed-time velocity p.d.f. (4.24), admits the low-![]() $\textit {Da}$ expansion
$\textit {Da}$ expansion
and the high-![]() $\textit {Da}$ expansion
$\textit {Da}$ expansion
 \begin{equation} \frac{v_t^\infty}{\overline{v_E}} \approx \frac{8}{j_{0,1}^2}\left(1-\frac{j_{0,1}^2-4}{4\,\textit{Da}}\right). \end{equation}
\begin{equation} \frac{v_t^\infty}{\overline{v_E}} \approx \frac{8}{j_{0,1}^2}\left(1-\frac{j_{0,1}^2-4}{4\,\textit{Da}}\right). \end{equation} For the plume velocity (4.25), we find for ![]() $\textit {Da}\ll 1$,
$\textit {Da}\ll 1$,
and for ![]() $\textit {Da}\gg 1$,
$\textit {Da}\gg 1$,
 \begin{equation} \frac{v_P^\infty}{\overline{v_E}} \approx \frac{4}{3}\left(1+\frac{1}{j_{0,1}^2}\right) - \left(1-\frac{2}{j_{0,1}^2}\right)\frac{2}{3\,\textit{Da}}. \end{equation}
\begin{equation} \frac{v_P^\infty}{\overline{v_E}} \approx \frac{4}{3}\left(1+\frac{1}{j_{0,1}^2}\right) - \left(1-\frac{2}{j_{0,1}^2}\right)\frac{2}{3\,\textit{Da}}. \end{equation}
Note that these approximations agree with those reported in Sankarasubramanian & Gill (Reference Sankarasubramanian and Gill1973) and Barton (Reference Barton1984) to the relevant order in ![]() $\textit {Da}$.
$\textit {Da}$.
For ![]() $\textit {Da}\ll 1$, we obtain the flux-weighted average velocity (4.26),
$\textit {Da}\ll 1$, we obtain the flux-weighted average velocity (4.26),
and, for ![]() $\textit {Da}\gg 1$,
$\textit {Da}\gg 1$,
 \begin{equation} \frac{v_{t,F}^\infty}{\overline{v_F}} \approx 3\,\frac{8-j_{0,1}^2}{j_{0,1}^2}\left(1-\frac{j_{0,1}^4-32}{8-j_{0,1}^2}\,\frac{1}{4\,\textit{Da}}\right). \end{equation}
\begin{equation} \frac{v_{t,F}^\infty}{\overline{v_F}} \approx 3\,\frac{8-j_{0,1}^2}{j_{0,1}^2}\left(1-\frac{j_{0,1}^4-32}{8-j_{0,1}^2}\,\frac{1}{4\,\textit{Da}}\right). \end{equation} For the equilibrium fixed-time velocity p.d.f. (4.27), we have for low ![]() $\textit {Da}$,
$\textit {Da}$,
and for high ![]() $\textit {Da}$,
$\textit {Da}$,
 \begin{equation} \frac{p_{v_t}^\infty(v)}{p_E(v)} \approx \frac{j_{0,1}\,{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}{2\,{\rm J}_1(j_{0,1})}\left[1-\left(1-\frac{j_{0,1}\,{\rm J}_1(j_{0,1}\sqrt{1-v/v_M})}{2\,{\rm J}_0(j_{0,1}\,\sqrt{1-v/v_M})}\sqrt{1-\frac{v}{v_M}}\right)\frac{1}{\textit{Da}}\right]. \end{equation}
\begin{equation} \frac{p_{v_t}^\infty(v)}{p_E(v)} \approx \frac{j_{0,1}\,{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}{2\,{\rm J}_1(j_{0,1})}\left[1-\left(1-\frac{j_{0,1}\,{\rm J}_1(j_{0,1}\sqrt{1-v/v_M})}{2\,{\rm J}_0(j_{0,1}\,\sqrt{1-v/v_M})}\sqrt{1-\frac{v}{v_M}}\right)\frac{1}{\textit{Da}}\right]. \end{equation} For the equilibrium flux-weighted velocity p.d.f. (4.28), the low-![]() $\textit {Da}$ limit is
$\textit {Da}$ limit is
and the high-![]() $\textit {Da}$ limit is
$\textit {Da}$ limit is
 \begin{align} \frac{p_{v_t,F}^\infty(v)}{p_F(v)} &\approx \frac{j_{0,1}^3\,{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}{16\,{\rm J}_1(j_{0,1})}\nonumber\\ &\quad \times\left[1-\left(8-j_{0,1}^2-\frac{2j_{0,1}\,{\rm J}_1(j_{0,1}\sqrt{1-v/v_M})}{{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}\,\sqrt{1-\frac{v}{v_M}}\right)\frac{1}{4\,\textit{Da}}\right]. \end{align}
\begin{align} \frac{p_{v_t,F}^\infty(v)}{p_F(v)} &\approx \frac{j_{0,1}^3\,{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}{16\,{\rm J}_1(j_{0,1})}\nonumber\\ &\quad \times\left[1-\left(8-j_{0,1}^2-\frac{2j_{0,1}\,{\rm J}_1(j_{0,1}\sqrt{1-v/v_M})}{{\rm J}_0(j_{0,1}\sqrt{1-v/v_M})}\,\sqrt{1-\frac{v}{v_M}}\right)\frac{1}{4\,\textit{Da}}\right]. \end{align}





















































































































