The significance of dust particles for the electron energy probability function (EEPF) and plasma oscillations is studied under varying magnetic field strength in a filamentary discharge hydrogen plasma. The experimental result shows that with an increase in dust density, the electron density decreases as a result of the charging of dust grains in the plasma background. A bi-Maxwellian EEPF is computed in both a pristine hydrogen plasma and a dust-containing plasma at different magnetic field strengths. We have observed that the increase in magnetic field decreases the lower energy electron population. The electron population of the lower energy range shows nearly identical results at magnetic field, $B\leqslant 3.7$ mT whereas the behaviour of the high-energy electron population becomes identical for a field strength $B\leqslant 5.8$ mT. From the observation, we have seen that the mid energy electron population slightly decreases and the high energy electron population slightly increases due to the presence of dust particles as compared to a pristine plasma. Further, very low energy electron population remains almost unchanged. With increase in dust density, the mid energy electron population further decreases whereas the high energy electron population slightly increases for different magnetic fields. But, no changes were observed for the very low energy electron population in the presence of dust particles. From the study of plasma oscillation, it is observed that the dominant frequency associated with the plasma oscillation is matched with the ion cyclotron frequency. The amplitude of the ion cyclotron frequency reduces with the increase of dust density which might be due to the decrease of plasma density.

Energy chirp compensation of the electron bunch (e-bunch) in a laser wakefield accelerator, which is caused by the phase space rotation in the gradient wakefield, has been applied in many schemes for low energy spread e-bunch generation. We report the experimental observation of energy chirp compensation of the e-bunch in a nonlinear laser wakefield accelerator with a negligible beam loading effect. By adjusting the acceleration length using a wedge-roof block, the chirp compensation of the accelerated e-bunch was observed via an electron spectrometer. Apart from this, some significant parameters for the compensation process, such as the longitudinal dispersion and wakefield slope at the bunch position, were also estimated. A detailed comparison between experiment and simulation shows good agreement of the wakefield and bunch parameters. These results give a clear demonstration of the longitudinal characteristics of the wakefield in a plasma and the bunch dynamics, which are important for better control of a compact laser wakefield accelerator.

Analytic treatment is presented of the electrostatic instability of an initially planar electron hole in a plasma of effectively infinite particle magnetization. It is shown that there is an unstable mode consisting of a rigid shift of the hole in the trapping direction. Its low frequency is determined by the real part of the force balance between the Maxwell stress arising from the transverse wavenumber $k$ and the kinematic jetting from the hole’s acceleration. The very low growth rate arises from a delicate balance in the imaginary part of the force between the passing-particle jetting, which is destabilizing, and the resonant response of the trapped particles, which is stabilizing. Nearly universal scalings of the complex frequency and $k$ with hole depth are derived. Particle in cell simulations show that the slow-growing instabilities previously investigated as coupled hole–wave phenomena occur at the predicted frequency, but with growth rates 2 to 4 times greater than the analytic prediction. This higher rate may be caused by a reduced resonant stabilization because of numerical phase-space diffusion in the simulations.

To properly treat the collisional transport of alpha particles due to a weakly rippled tokamak magnetic field the tangential magnetic drift due to its gradient (the $\unicode[STIX]{x1D735}B$ drift) and pitch angle scatter must be retained. Their combination gives rise to a narrow boundary layer in which collisions are able to match the finite trapped response to the ripple to the vanishing passing response of the alphas. Away from this boundary layer collisions are ineffective. There the $\unicode[STIX]{x1D735}B$ drift of the alphas balances the small radial drift of the trapped alphas caused by the ripple. A narrow collisional boundary layer is necessary since this balance does not allow the perturbed trapped alpha distribution function to vanish at the trapped–passing boundary. The solution of this boundary layer problem allows the alpha transport fluxes to be evaluated in a self-consistent manner to obtain meaningful constraints on the ripple allowable in a tokamak fusion reactor. A key result of the analysis is that collisional alpha losses are insensitive to the ripple near the equatorial plane on the outboard side where the ripple is high. As the high field side ripple is normally very small, collisional $\sqrt{\unicode[STIX]{x1D708}}$ ripple transport is unlikely to be a serious issue.

Dipole and stellarator geometries are capable of confining plasmas of arbitrary neutrality, ranging from pure electron plasmas through to quasineutral. The diocotron mode is known to be important in non-neutral plasmas and has been widely studied. However, drift mode dynamics, dominating quasineutral plasmas, has received very little by way of attention in the non-neutral context. Here, we show that non-neutral plasmas can be unstable respect to both density-gradient- and temperature-gradient-driven instabilities. A local shearless slab limit is considered for simplicity. A key feature of non-neutral plasmas is the development of strong electric fields, in this local limit of straight field line geometry, the effect of the corresponding $\boldsymbol{E}\times \boldsymbol{B}$ drift is limited to the Doppler shift of the complex frequency $\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{E}$. However, the breaking of the quasineutrality condition still leads to interesting dynamics in non-neutral plasmas. In this paper we address the behaviour of a number of gyrokinetic modes in electron–ion and electron–positron plasmas with arbitrary degree of neutrality.

It is shown that in low-beta, weakly collisional plasmas, such as the solar corona, some instances of the solar wind, the aurora, inner regions of accretion discs, their coronae and some laboratory plasmas, Alfvénic fluctuations produce no ion heating within the gyrokinetic approximation, i.e. as long as their amplitudes (at the Larmor scale) are small and their frequencies stay below the ion-Larmor frequency (even though their spatial scales can be above or below the ion Larmor scale). Thus, all low-frequency ion heating in such plasmas is due to compressive fluctuations (‘slow modes’): density perturbations and non-Maxwellian perturbations of the ion distribution function. Because these fluctuations energetically decouple from the Alfvénic ones already in the inertial range, the above conclusion means that the energy partition between ions and electrons in low-beta plasmas is decided at the outer scale, where turbulence is launched, and can be determined from magnetohydrodynamic (MHD) models of the relevant astrophysical systems. Any additional ion heating must come from non-gyrokinetic mechanisms such as cyclotron heating or the stochastic heating owing to distortions of ions’ Larmor orbits. An exception to these conclusions occurs in the Hall limit, i.e. when the ratio of the ion to electron temperatures is as low as the ion beta (equivalently, the electron beta is order unity). In this regime, slow modes couple to Alfvénic ones well above the Larmor scale (viz., at the ion inertial or ion sound scale), so the Alfvénic and compressive cascades join and then separate again into two cascades of fluctuations that linearly resemble kinetic Alfvén and ion-cyclotron waves, with the former heating electrons and the latter ions. The two cascades are shown to decouple, scalings for them are derived and it is argued physically that the two species will be heated by them at approximately equal rates.

The magnetic presheath is a boundary layer occurring when magnetized plasma is in contact with a wall and the angle $\unicode[STIX]{x1D6FC}$ between the wall and the magnetic field 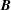$\boldsymbol{B}$ is oblique. Here, we consider the fusion-relevant case of a shallow-angle, $\unicode[STIX]{x1D6FC}\ll 1$, electron-repelling sheath, with the electron density given by a Boltzmann distribution, valid for 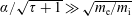$\unicode[STIX]{x1D6FC}/\sqrt{\unicode[STIX]{x1D70F}+1}\gg \sqrt{m_{\text{e}}/m_{\text{i}}}$, where 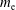$m_{\text{e}}$ is the electron mass, 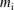$m_{\text{i}}$ is the ion mass, 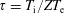$\unicode[STIX]{x1D70F}=T_{\text{i}}/ZT_{\text{e}}$, 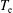$T_{\text{e}}$ is the electron temperature, 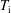$T_{\text{i}}$ is the ion temperature and $Z$ is the ionic charge state. The thickness of the magnetic presheath is of the order of a few ion sound Larmor radii 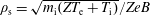$\unicode[STIX]{x1D70C}_{\text{s}}=\sqrt{m_{\text{i}}(ZT_{\text{e}}+T_{\text{i}})}/ZeB$, where e is the proton charge and 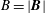$B=|\boldsymbol{B}|$ is the magnitude of the magnetic field. We study the dependence on $\unicode[STIX]{x1D70F}$ of the electrostatic potential and ion distribution function in the magnetic presheath by using a set of prescribed ion distribution functions at the magnetic presheath entrance, parameterized by $\unicode[STIX]{x1D70F}$. The kinetic model is shown to be asymptotically equivalent to Chodura’s fluid model at small ion temperature, 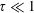$\unicode[STIX]{x1D70F}\ll 1$, for 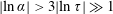$|\text{ln}\,\unicode[STIX]{x1D6FC}|>3|\text{ln}\,\unicode[STIX]{x1D70F}|\gg 1$. In this limit, despite the fact that fluid equations give a reasonable approximation to the potential, ion gyro-orbits acquire a spatial extent that occupies a large portion of the magnetic presheath. At large ion temperature, 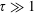$\unicode[STIX]{x1D70F}\gg 1$, relevant because 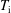$T_{\text{i}}$ is measured to be a few times larger than 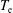$T_{\text{e}}$ near divertor targets of fusion devices, ions reach the Debye sheath entrance (and subsequently the wall) at a shallow angle whose size is given by 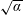$\sqrt{\unicode[STIX]{x1D6FC}}$ or 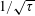$1/\sqrt{\unicode[STIX]{x1D70F}}$, depending on which is largest.

Kinetic treatments of drift tearing modes that match an inner, resonant layer solution to an external magnetohydrodynamic (MHD) solution, characterised by $\unicode[STIX]{x1D6E5}^{\prime }$, can fail to match the ideal MHD boundary condition on the parallel electric field, $E_{\Vert }=0$. In this paper we demonstrate how consideration of ion sound and ion Landau damping effects achieves this, placing the theory on a firm footing. These effects are found to modify the effective critical $\unicode[STIX]{x1D6E5}^{\prime }$ for instability of drift tearing modes, in particular for weak electron temperature gradients. The implications for a realistic hot plasma resonant layer model – involving large ion Larmor radius and semi-collisional electron physics (Connor et al., Plasma Phys. Control. Fusion, vol. 54, 2012, 035003) – are determined.

Quasisymmetric stellarators are appealing intellectually and as fusion reactor candidates since the guiding-centre particle trajectories and neoclassical transport are isomorphic to those in a tokamak, implying good confinement. Previously, quasisymmetric magnetic fields have been identified by applying black-box optimization algorithms to minimize symmetry-breaking Fourier modes of the field strength $B$. Here, instead, we directly construct magnetic fields in cylindrical coordinates that are quasisymmetric to leading order in the distance from the magnetic axis, without using optimization. The method involves solution of a one-dimensional nonlinear ordinary differential equation, originally derived by Garren & Boozer (Phys. Fluids B, vol. 3, 1991, p. 2805). We demonstrate the usefulness and accuracy of this optimization-free approach by providing the results of this construction as input to the codes VMEC and BOOZ_XFORM, confirming the purity and scaling of the magnetic spectrum. The space of magnetic fields that are quasisymmetric to this order is parameterized by the magnetic axis shape along with three other real numbers, one of which reflects the on-axis toroidal current density, and another one of which is zero for stellarator symmetry. The method here could be used to generate good initial conditions for conventional optimization, and its speed enables exhaustive searches of parameter space.

We show that when a solid plasma foil with a density gradient on the front surface is irradiated by an intense laser pulse at a grazing angle, ${\sim}80^{\circ }$, a relativistic electron vortex is excited in the near-critical-density layer after the laser pulse depletion. The vortex structure and dynamics are studied using particle-in-cell simulations. Due to the asymmetry introduced by non-uniform background density, the vortex drifts at a constant velocity, typically $0.2{-}0.3$ times the speed of light. The strong magnetic field inside the vortex leads to significant charge separation; in the corresponding electric field initially stationary protons can be captured and accelerated to twice the velocity of the vortex (100–200 MeV). A representative scenario – with laser intensity of $10^{21}~\text{W}~\text{cm}^{-2}$ – is discussed: two-dimensional simulations suggest that a quasi-monoenergetic proton beam can be obtained with a mean energy 140 MeV and an energy spread of ${\sim}10\,\%$. We derive an analytical estimate for the vortex velocity in terms of laser and plasma parameters, demonstrating that the maximum proton energy can be controlled by the incidence angle of the laser and the plasma density gradient.

Ion-temperature-gradient-driven (ITG) turbulence is compared for two quasi-symmetric (QS) stellarator configurations to determine the relationship between linear growth rates and nonlinear heat fluxes. We focus on the quasi-helically symmetric (QHS) stellarator HSX and the quasi-axisymmetric (QAS) stellarator NCSX. In normalized units, HSX exhibits higher growth rates than NCSX, while heat fluxes in gyro-Bohm units are lower in HSX. These results hold for simulations made with both adiabatic and kinetic electrons. The results show that HSX has a larger number of subdominant modes than NCSX and that eigenmodes are more spatially extended in HSX. We conclude that the consideration of nonlinear physics is necessary to accurately assess the heat flux due to ITG turbulence when comparing QS stellarator equilibria.

The concept of informativeness of nonlinear plasma physics scenarios is explained. Natural ideas of developing highly informative models of plasma kinetics are spelled out. They are applied to develop a formula that governs the drift of long Langmuir waves in spatial positions and wave vectors in a magnetized plasma due to the plasma inhomogeneity. Together with previous findings (Erofeev, Phys. Plasmas, vol. 22, 2015, 092302), the formula evidences the need for an intelligent generalization of the notion of wave energy density from usual homogeneous plasmas to inhomogeneous ones.

EDI (enhanced biDimensional pIc) is a two-dimensional (2-D) electrostatic/magnetostatic particle-in-cell (PIC) code designed to optimize plasma based systems. The code is built on an unstructured mesh of triangles, allowing for arbitrary geometries. The PIC core is comprised of a Boris leapfrog scheme that can manage multiple species. Particle tracking locates particles in the mesh, using a fast and simple priority-sorting algorithm. A magnetic field with an arbitrary topology can be imposed to study the magnetized particle dynamics. The electrostatic fields are then computed by solving Poisson’s equation with a a finite element method solver. The latter is an external solver that has been properly modified in order to be integrated into EDI. The major advantage of using an external solver directly incorporated into the EDI structure is its strong flexibility, in fact it is possible to couple together different physical problems (electrostatic, magnetostatic, etc.). EDI is written in C, which allows the rapid development of new modules. A big effort in the development of the code has been made in optimization of the linking efficiency, in order to minimize computational time. Finally, EDI is a multiplatform (Linux, Mac OS X) software.

Boundary layers in space and astrophysical plasmas are the location of complex dynamics where different mechanisms coexist and compete, eventually leading to plasma mixing. In this work, we present fully kinetic particle-in-cell simulations of different boundary layers characterized by the following main ingredients: a velocity shear, a density gradient and a magnetic gradient localized at the same position. In particular, the presence of a density gradient drives the development of the lower-hybrid drift instability (LHDI), which competes with the Kelvin–Helmholtz instability (KHI) in the development of the boundary layer. Depending on the density gradient, the LHDI can even dominate the dynamics of the layer. Because these two instabilities grow on different spatial and temporal scales, when the LHDI develops faster than the KHI an inverse cascade is generated, at least in two dimensions. This inverse cascade, starting at the LHDI kinetic scales, generates structures at scale lengths at which the KHI would typically develop. When that is the case, those structures can suppress the KHI itself because they significantly affect the underlying velocity shear gradient. We conclude that, depending on the density gradient, the velocity jump and the width of the boundary layer, the LHDI in its nonlinear phase can become the primary instability for plasma mixing. These numerical simulations show that the LHDI is likely to be a dominant process at the magnetopause of Mercury. These results are expected to be of direct impact to the interpretation of the forthcoming BepiColombo observations.

I analyse and numerically evaluate the radiation field generated by an experimentally realized embodiment of an electric polarization current whose rotating distribution pattern moves with linear speeds exceeding the speed of light in vacuum. I find that the flux density of the resulting emission (i) has a dominant value and is linearly polarized within a sharply delineated radiation beam whose orientation and polar width are determined by the range of values of the linear speeds of the rotating source distribution, and (ii) decays with the distance $d$ from the source as $d^{-\unicode[STIX]{x1D6FC}}$ in which the value of $\unicode[STIX]{x1D6FC}$ lies between $1$ and $2$ (instead of being equal to $2$ as in a conventional radiation) across the beam. In that the rate at which boundaries of the retarded distribution of such a source change with time depends on its duration monotonically, this is an intrinsically transient emission process: temporal rate of change of the energy density of the radiation generated by it has a time-averaged value that is negative (instead of being zero as in a conventional radiation) at points where the envelopes of the wave fronts emanating from the constituent volume elements of the source distribution are cusped. The difference in the fluxes of power across any two spheres centred on the source is in this case balanced by the change with time of the energy contained inside the shell bounded by those spheres. These results are relevant not only to long-range transmitters in communications technology but also to astrophysical objects containing rapidly rotating neutron stars (such as pulsars) and to the interpretation of the energetics of the multi-wavelength emissions from sources that lie at cosmological distances (such as radio and gamma-ray bursts). The analysis presented in this paper is self-contained and supersedes my earlier works on this problem.

We have numerically studied how an actual confinement magnetostatic field affects power deposition in a helicon source. We have solved the wave propagation by means of two electromagnetic solvers, namely: (i) plaSma Padova Inhomogeneous Radial Electromagnetic solver (SPIREs), a mono-dimensional finite-difference frequency-domain code, and (ii) Advanced coDe for Anisotropic Media and ANTennas (ADAMANT), a full-wave three-dimensional tool based on the method of moments. We have computed the deposited power spectrum with SPIREs, power deposition profile with ADAMANT and the antenna impedance with both codes. First we have verified the numerical accuracy of both SPIREs and ADAMNT. Then, we have analysed two configurations of magnetostatic field, namely produced by Maxwell coils, and Helmholtz coils. For each configuration we have studied three cases: (i) low density $n=10^{17}~\text{m}^{-3}$ and low magnetic field $B_{0}=250$ G; (ii) medium density $n=10^{18}~\text{m}^{-3}$ and medium magnetic field $B_{0}=500$ G; (iii) high density $n=10^{19}~\text{m}^{-3}$ and high magnetic field $B_{0}=1000$ G. We have found that the Maxwell coil configuration does not produces significant changes in the deposited power phenomenon with respect to a perfectly uniform and axial magnetostatic field. While the Helmholtz coil configuration can lead to a power spectrum peaked near the axis of the discharge.

In present and future magnetic confined fusion devices with metallic plasma-facing components (PFCs) such as JET-ILW and ITER, the calculation of the plasma composition must account for multiple impurities of a wide range of mass and charge, resolve their poloidal asymmetries and account for different central peakings for various elements. Single measurements of radiation and effective charge are not enough to characterize this complex system and a self-consistent analysis of data from multiple diagnostics is required. This contribution describes a method to calculate the plasma composition simultaneously accounting for contributions of up to two low-Z impurities, and two mid-/high-Z impurities. The analysis stems from methodologies explained in Sertoli et al. (Rev. Sci. Instrum., vol. 89 (11), 2018, 113501), expanded to include more impurities and to coherently analyse multiple diagnostics within the same framework. The example Ne-seeded JET-ILW hybrid discharge reported here shows that Be, Ne, Ni and W are necessary to simultaneously explain the observed soft X-ray emission, the W concentration measured by passive vacuum ultra-violet spectroscopy, the line-of-sight integrated measurement of the effective charge, the observed poloidal asymmetry of the soft X-ray (SXR) emission, the Ne density measured by charge-exchange-recombination spectroscopy and the line-of-sight integrals of the total radiation as measured by bolometry. This consistent picture of the elemental composition enables the calculation of the radial profiles of the effective charge, the dilution and total radiation. For the cases analysed up to now, these are often very different from the typical assumptions presently used when modelling JET-ILW discharges. This will affect, among others, the calculation of neutron rates, current density profile and heat transport. These considerations are of course valid for all present and future magnetic-controlled fusion devices which exhibit multi-material plasma-facing components, including ITER.

A method is given to rapidly compute quasisymmetric stellarator magnetic fields for plasma confinement, without the need to call a three-dimensional magnetohydrodynamic equilibrium code inside an optimization iteration. The method is based on direct solution of the equations of magnetohydrodynamic equilibrium and quasisymmetry using Garren & Boozer’s expansion about the magnetic axis (Phys Fluids B, vol. 3, 1991, p. 2805), and it is several orders of magnitude faster than the conventional optimization approach. The work here extends the method of Landreman et al. (J. Plasma Phys., vol. 85, 2019, 905850103), which was limited to flux surfaces with elliptical cross-section, to higher order in the aspect-ratio expansion. As a result, configurations can be generated with strong shaping that achieve quasisymmetry to high accuracy. Using this construction, we give the first numerical demonstrations of Garren and Boozer’s ideal scaling of quasisymmetry breaking with the cube of the inverse aspect ratio. We also demonstrate a strongly non-axisymmetric configuration (vacuum rotational transform $\unicode[STIX]{x1D704}>0.4$) in which symmetry-breaking mode amplitudes throughout a finite volume are ${<}2\times 10^{-7}$, the smallest ever reported. To generate boundary shapes of finite-minor-radius configurations, a careful analysis is given of the effect of substituting a finite minor radius into the near-axis expansion. The approach here can provide analytic insight into the space of possible quasisymmetric stellarator configurations, and it can be used to generate good initial conditions for conventional stellarator optimization.

The injection of cryogenic pellets into a magnetically confined plasma is shown to be accompanied by a considerable transfer of thermal energy from the electrons in the background plasma to the ions. The resulting ion heating can be significant, particularly in plasmas with disparate electron and ion temperatures, and can affect the energy balance of the plasma. In recent Wendelstein 7-X experiments, this mechanism can account for a substantial fraction of the ion heating power during pellet injection.

In magnetized plasma situations where magnetic fields intersect massive conducting boundaries, ‘line-tied’ boundary conditions are often used, analytically and in numerical simulations. For ideal magnetohydrodynamic (MHD) plasmas, these conditions are arrived at given the relatively long time scales for magnetic fields penetrating resistively into good conductors. Under line-tied boundary conditions, numerical simulations often exhibit what could be construed as numerical ‘noise’ emanating from the boundaries. We show here that this ‘noise’ is real. By combining numerical and analytical methods, we highlight the existence of sharp spatial structures near the conductors and confirm the appearance of short wavelength structures riding on long wavelength modes. We conclude that, for numerical fidelity, the short multiscale structures need to be resolved. Generally, the short structure widths scale as the square root of the plasma $\unicode[STIX]{x1D6FD}$.