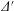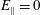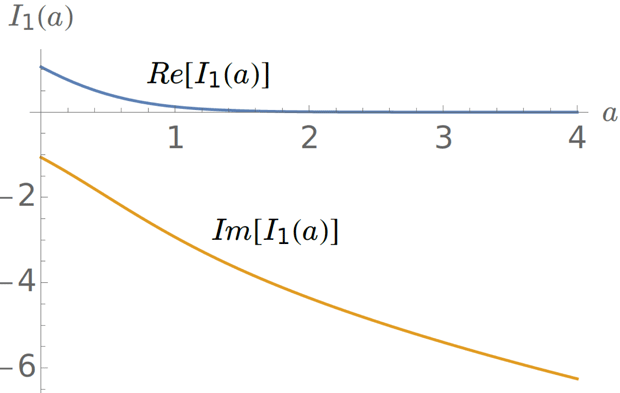1 Introduction
Tearing modes are driven by current gradients and pressure gradients in the plasma whose destabilising effects are characterised by a quantity
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
. The associated tearing of a tokamak magnetic field occurs at the resonant radius,
$\unicode[STIX]{x1D6E5}^{\prime }$
. The associated tearing of a tokamak magnetic field occurs at the resonant radius,
![]() $r=r_{0}$
, where
$r=r_{0}$
, where
![]() $m=nq(r_{0}),m$
and
$m=nq(r_{0}),m$
and
![]() $n$
are the poloidal and toroidal mode numbers of the helical instability and
$n$
are the poloidal and toroidal mode numbers of the helical instability and
![]() $q$
is the safety factor. In the vicinity of
$q$
is the safety factor. In the vicinity of
![]() $r=r_{0}$
complex kinetic effects can occur and to account for these it is convenient to treat a narrow ‘inner’ region in which these effects are included, but the equations are simplified because of the localised nature of this inner layer. Stability is then determined by matching solutions of these inner equations to outer ones, valid across the regions away from the layer (and satisfying appropriate boundary conditions at the plasma boundary and magnetic axis) where a simple ideal magnetohydrodynamic (MHD) description of the plasma suffices. The solution of the inner equations provides a quantity
$r=r_{0}$
complex kinetic effects can occur and to account for these it is convenient to treat a narrow ‘inner’ region in which these effects are included, but the equations are simplified because of the localised nature of this inner layer. Stability is then determined by matching solutions of these inner equations to outer ones, valid across the regions away from the layer (and satisfying appropriate boundary conditions at the plasma boundary and magnetic axis) where a simple ideal magnetohydrodynamic (MHD) description of the plasma suffices. The solution of the inner equations provides a quantity
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D714})$
, where
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D714})$
, where
![]() $\unicode[STIX]{x1D714}$
is the complex mode frequency, while the solution of the outer equations yields the aforementioned quantity
$\unicode[STIX]{x1D714}$
is the complex mode frequency, while the solution of the outer equations yields the aforementioned quantity
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
: the matching condition leads to a dispersion relation and a critical value of
$\unicode[STIX]{x1D6E5}^{\prime }$
: the matching condition leads to a dispersion relation and a critical value of
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
for instability.
$\unicode[STIX]{x1D6E5}^{\prime }$
for instability.
For a simple resistive MHD model (or even a cold ion model containing electron diamagnetic effects) of the inner region, the corresponding solutions match satisfactorily to the outer ones, with the perturbed parallel electric field,
![]() $E_{\Vert }$
, vanishing properly as one reaches the outer ideal MHD region. However, for a kinetic or fluid treatment of the ion physics when the ions have finite temperature, so that the effects of finite ion Larmor radius (FLR) and their parallel thermal motion or transport are included, this matching becomes more complex (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979; Cowley, Kulsrud & Hahm Reference Cowley, Kulsrud and Hahm1986; Fitzpatrick Reference Fitzpatrick1989; Connor, Hastie & Zocco Reference Connor, Hastie and Zocco2012). Even though one can match the longitudinal component of the perturbed vector potential,
$E_{\Vert }$
, vanishing properly as one reaches the outer ideal MHD region. However, for a kinetic or fluid treatment of the ion physics when the ions have finite temperature, so that the effects of finite ion Larmor radius (FLR) and their parallel thermal motion or transport are included, this matching becomes more complex (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979; Cowley, Kulsrud & Hahm Reference Cowley, Kulsrud and Hahm1986; Fitzpatrick Reference Fitzpatrick1989; Connor, Hastie & Zocco Reference Connor, Hastie and Zocco2012). Even though one can match the longitudinal component of the perturbed vector potential,
![]() $A_{\Vert }$
, from the inner region to its form in the ideal region, where
$A_{\Vert }$
, from the inner region to its form in the ideal region, where
![]() $A_{\Vert }\propto 1+(r-r_{0})\unicode[STIX]{x1D6E5}^{\prime }$
, the expression for
$A_{\Vert }\propto 1+(r-r_{0})\unicode[STIX]{x1D6E5}^{\prime }$
, the expression for
![]() $E_{\Vert }$
does not necessarily tend to zero. To accomplish this (i.e. decay of
$E_{\Vert }$
does not necessarily tend to zero. To accomplish this (i.e. decay of
![]() $E_{\Vert }$
) within the matching region, one must consider an intermediate region where ion sound and ion Landau damping become significant at the characteristic frequency of a drift tearing mode (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Consequently, the overall matching condition is modified, with an impact on the stability of the drift tearing mode. The investigation of this effect for the realistic situation in a hot plasma where the ion Larmor orbit width exceeds the reconnecting layer width associated with a semi-collisional electron model, is the subject of this paper. In this work, the intermediate region is described by a cylindrical, collisionless plasma model.
$E_{\Vert }$
) within the matching region, one must consider an intermediate region where ion sound and ion Landau damping become significant at the characteristic frequency of a drift tearing mode (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Consequently, the overall matching condition is modified, with an impact on the stability of the drift tearing mode. The investigation of this effect for the realistic situation in a hot plasma where the ion Larmor orbit width exceeds the reconnecting layer width associated with a semi-collisional electron model, is the subject of this paper. In this work, the intermediate region is described by a cylindrical, collisionless plasma model.
We note in passing that the stabilising effects of ion sound on the ‘drift collisional’ tearing mode were also presented by Bussac et al. (Reference Bussac, Edery, Pellat and Soule1978) and a simple model for the effects of ion Landau damping on the semi-collisional neoclassical drift tearing mode was given by Fitzpatrick (Reference Fitzpatrick1989), while a more fluid-like treatment of this problem was presented by Connor, Hastie & Helander (Reference Connor, Hastie and Helander2017).
In § 2 we develop the governing equations, namely the vorticity equation and Ampere’s equation, that pertain in the intermediate region. To complete these equations, we solve the collisionless kinetic equations for the perturbed parallel electron and ion currents. We obtain these solutions in § 3 by calculating in the space of the radial coordinate. However, we wish to connect this region to inner region models which feature large ion Larmor radii (as compared to the electron scales of the reconnecting layer). Since such inner region models are better dealt with in Fourier space (Pegoraro & Schep Reference Pegoraro and Schep1986), it is convenient to operate with Fourier transforms of the radially dependent perturbed fields (as in the formalism of Connor et al. (Reference Connor, Hastie and Zocco2012)), deducing the corresponding real space behaviour from their long-wavelength limit in Fourier transformed variables. The resulting intermediate region solution is then inserted into Ampere’s law in § 4 to calculate the effect of the intermediate region on
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
.
$\unicode[STIX]{x1D6E5}^{\prime }$
.
The results are characterised by a quantity
![]() $a=(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}L_{s}/2\unicode[STIX]{x1D714}_{\ast e}L_{n})((\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\ast e})/(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}+(1+\unicode[STIX]{x1D702}_{i})\unicode[STIX]{x1D714}_{\ast e}))$
. Here
$a=(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}L_{s}/2\unicode[STIX]{x1D714}_{\ast e}L_{n})((\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\ast e})/(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}+(1+\unicode[STIX]{x1D702}_{i})\unicode[STIX]{x1D714}_{\ast e}))$
. Here
![]() $\unicode[STIX]{x1D714}$
is the mode frequency,
$\unicode[STIX]{x1D714}$
is the mode frequency,
![]() $\unicode[STIX]{x1D714}_{\ast j}=mT_{j}/(e_{j}BrL_{n})$
is the diamagnetic frequency of species
$\unicode[STIX]{x1D714}_{\ast j}=mT_{j}/(e_{j}BrL_{n})$
is the diamagnetic frequency of species
![]() $j$
(
$j$
(
![]() $j=e,i$
for electrons and ions, respectively),
$j=e,i$
for electrons and ions, respectively),
![]() $1/L_{n}=\text{d}(\ln n)/\text{d}r$
with
$1/L_{n}=\text{d}(\ln n)/\text{d}r$
with
![]() $n$
the plasma density,
$n$
the plasma density,
![]() $\unicode[STIX]{x1D702}_{j}=\text{d}(\ln T_{j})/\text{d}(\ln n)$
with
$\unicode[STIX]{x1D702}_{j}=\text{d}(\ln T_{j})/\text{d}(\ln n)$
with
![]() $T_{j}$
the temperature of species
$T_{j}$
the temperature of species
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D70F}=T_{e}/T_{i}$
,
$\unicode[STIX]{x1D70F}=T_{e}/T_{i}$
,
![]() $r$
is a minor radius of the cylinder and
$r$
is a minor radius of the cylinder and
![]() $L_{s}$
is the magnetic shear length. Since drift tearing modes typically have a real frequency
$L_{s}$
is the magnetic shear length. Since drift tearing modes typically have a real frequency
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\ast e}(1+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D702}_{e})$
, where
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\ast e}(1+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D702}_{e})$
, where
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $0(1)$
(for the collisionless case,
$0(1)$
(for the collisionless case,
![]() $\unicode[STIX]{x1D6FC}=0.5$
(Drake & Lee Reference Drake and Lee1977; Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979; Cowley et al.
Reference Cowley, Kulsrud and Hahm1986), while for semi-collisional electrons,
$\unicode[STIX]{x1D6FC}=0.5$
(Drake & Lee Reference Drake and Lee1977; Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979; Cowley et al.
Reference Cowley, Kulsrud and Hahm1986), while for semi-collisional electrons,
![]() $\unicode[STIX]{x1D6FC}=0.74$
(Cowley et al.
Reference Cowley, Kulsrud and Hahm1986; Connor et al.
Reference Connor, Hastie and Zocco2012)),
$\unicode[STIX]{x1D6FC}=0.74$
(Cowley et al.
Reference Cowley, Kulsrud and Hahm1986; Connor et al.
Reference Connor, Hastie and Zocco2012)),
![]() $a$
is usually large, but for weak electron temperature gradients it too can become
$a$
is usually large, but for weak electron temperature gradients it too can become
![]() $0(1)$
. This is the situation addressed by Coppi et al. (Reference Coppi, Mark, Sugiyama and Bertin1979) and in the present work.
$0(1)$
. This is the situation addressed by Coppi et al. (Reference Coppi, Mark, Sugiyama and Bertin1979) and in the present work.
In § 5, we discuss the implications for a realistic hot plasma resonant layer model – involving large ion Larmor radius and semi-collisional electron physics (Cowley et al.
Reference Cowley, Kulsrud and Hahm1986; Connor et al.
Reference Connor, Hastie and Zocco2012). In contrast to the calculation in Coppi et al. (Reference Coppi, Mark, Sugiyama and Bertin1979), we now need both real and imaginary parts of the modified
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
. A final section discusses the results and draws conclusions.
$\unicode[STIX]{x1D6E5}^{\prime }$
. A final section discusses the results and draws conclusions.
2 Intermediate region plasma model
We consider cylindrical geometry with coordinates
![]() $r,\unicode[STIX]{x1D703},z$
and magnetic fields
$r,\unicode[STIX]{x1D703},z$
and magnetic fields
![]() $(0,B_{\unicode[STIX]{x1D703}}(r),B_{Z}(r))$
; the total field strength is
$(0,B_{\unicode[STIX]{x1D703}}(r),B_{Z}(r))$
; the total field strength is
![]() $B$
. The perturbed fields of the tearing mode involve the parallel vector potential,
$B$
. The perturbed fields of the tearing mode involve the parallel vector potential,
![]() $A_{\Vert }$
, and electrostatic potential,
$A_{\Vert }$
, and electrostatic potential,
![]() $\unicode[STIX]{x1D711}$
, with frequency
$\unicode[STIX]{x1D711}$
, with frequency
![]() $\unicode[STIX]{x1D714}$
and structure
$\unicode[STIX]{x1D714}$
and structure
![]() $A_{\Vert }\sim A(x)\text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}k_{z}z-\text{i}m\unicode[STIX]{x1D703}}$
for example. Here
$A_{\Vert }\sim A(x)\text{e}^{-\text{i}\unicode[STIX]{x1D714}t+\text{i}k_{z}z-\text{i}m\unicode[STIX]{x1D703}}$
for example. Here
![]() $x=r-r_{0}$
, where the resonant surface,
$x=r-r_{0}$
, where the resonant surface,
![]() $r_{0}$
, is given by
$r_{0}$
, is given by
![]() $k_{z}B_{Z}(r_{0})-k_{\unicode[STIX]{x1D703}}B_{\unicode[STIX]{x1D703}}(r_{0})=0$
, with
$k_{z}B_{Z}(r_{0})-k_{\unicode[STIX]{x1D703}}B_{\unicode[STIX]{x1D703}}(r_{0})=0$
, with
![]() $k_{\unicode[STIX]{x1D703}}=m/r$
, so that the wavenumber parallel to the magnetic field is
$k_{\unicode[STIX]{x1D703}}=m/r$
, so that the wavenumber parallel to the magnetic field is
![]() $k_{\Vert }=mx/rL_{s}$
, with
$k_{\Vert }=mx/rL_{s}$
, with
![]() $L_{s}$
being the magnetic shear length. In the toroidal geometry of a tokamak,
$L_{s}$
being the magnetic shear length. In the toroidal geometry of a tokamak,
![]() $k_{z}=n/R$
,
$k_{z}=n/R$
,
![]() $L_{s}=Rq/s$
, with
$L_{s}=Rq/s$
, with
![]() $R$
the major radius,
$R$
the major radius,
![]() $s=r\text{d}(\ln q)/\text{d}r$
and
$s=r\text{d}(\ln q)/\text{d}r$
and
![]() $q$
the safety factor.
$q$
the safety factor.
The electrons and ions satisfy the linearised, collisionless, kinetic equation:
Here the perturbed electron distribution,
![]() $\unicode[STIX]{x1D6FF}f_{j}$
is written
$\unicode[STIX]{x1D6FF}f_{j}$
is written
![]() $\unicode[STIX]{x1D6FF}f_{j}=-(e_{j}F_{Mj}/T_{j})\unicode[STIX]{x1D711}+g_{j}$
, where
$\unicode[STIX]{x1D6FF}f_{j}=-(e_{j}F_{Mj}/T_{j})\unicode[STIX]{x1D711}+g_{j}$
, where
![]() $F_{Mj}$
is the Maxwellian distribution for species
$F_{Mj}$
is the Maxwellian distribution for species
![]() $j$
,
$j$
,
![]() $v_{\Vert }$
is the parallel velocity and
$v_{\Vert }$
is the parallel velocity and
![]() $v_{\bot }$
the perpendicular velocity, while
$v_{\bot }$
the perpendicular velocity, while
![]() $\unicode[STIX]{x1D714}_{\ast j}^{T}=\unicode[STIX]{x1D714}_{\ast j}(1+\unicode[STIX]{x1D702}_{j}((m_{j}v^{2}/2T_{j})-3/2))$
, with
$\unicode[STIX]{x1D714}_{\ast j}^{T}=\unicode[STIX]{x1D714}_{\ast j}(1+\unicode[STIX]{x1D702}_{j}((m_{j}v^{2}/2T_{j})-3/2))$
, with
![]() $v^{2}=v_{\Vert }^{2}+v_{\bot }^{2}$
.
$v^{2}=v_{\Vert }^{2}+v_{\bot }^{2}$
.
![]() $J_{0}$
is the Bessel function of zero order with
$J_{0}$
is the Bessel function of zero order with
![]() $k_{\bot }$
, where
$k_{\bot }$
, where
![]() $k_{\bot }^{2}=k_{x}^{2}+m^{2}/r^{2}$
, being the wavenumber perpendicular to the magnetic field, and
$k_{\bot }^{2}=k_{x}^{2}+m^{2}/r^{2}$
, being the wavenumber perpendicular to the magnetic field, and
![]() $\unicode[STIX]{x1D714}_{cj}=e_{j}B/m_{j}$
, with
$\unicode[STIX]{x1D714}_{cj}=e_{j}B/m_{j}$
, with
![]() $m_{j}$
the mass of species
$m_{j}$
the mass of species
![]() $j$
, is the cyclotron frequency for species
$j$
, is the cyclotron frequency for species
![]() $j$
.
$j$
.
The stability of tearing modes can be investigated from two equations: the vorticity equation and Ampere’s law. The former is obtained by multiplying (2.1) by
![]() $e_{j}$
, integrating over velocity space, summing over the two species,
$e_{j}$
, integrating over velocity space, summing over the two species,
![]() $j$
, and applying the quasi-neutrality condition,
$j$
, and applying the quasi-neutrality condition,
![]() $\unicode[STIX]{x1D6FF}n_{e}=\unicode[STIX]{x1D6FF}n_{i}$
. The result is:
$\unicode[STIX]{x1D6FF}n_{e}=\unicode[STIX]{x1D6FF}n_{i}$
. The result is:
Here
![]() $J_{\Vert }=J_{\Vert ,i}+J_{\Vert ,e}$
is the perturbed parallel current density,
$J_{\Vert }=J_{\Vert ,i}+J_{\Vert ,e}$
is the perturbed parallel current density,
![]() $e$
the proton charge and
$e$
the proton charge and
![]() $\unicode[STIX]{x1D6E4}_{l}(b)=I_{l}(b)\text{e}^{-b}$
, where
$\unicode[STIX]{x1D6E4}_{l}(b)=I_{l}(b)\text{e}^{-b}$
, where
![]() $b=k_{\bot }^{2}T_{i}/(m_{i}\unicode[STIX]{x1D714}_{ci}^{2})$
, with
$b=k_{\bot }^{2}T_{i}/(m_{i}\unicode[STIX]{x1D714}_{ci}^{2})$
, with
![]() $I_{l}(b)$
the modified Bessel functions of order
$I_{l}(b)$
the modified Bessel functions of order
![]() $l$
. Ampere’s equation is simply:
$l$
. Ampere’s equation is simply:
where we ignore the small contribution to the left-hand side from
![]() $k_{\unicode[STIX]{x1D703}}^{2}$
as
$k_{\unicode[STIX]{x1D703}}^{2}$
as
![]() $k_{\unicode[STIX]{x1D703}}^{2}x^{2}\ll 1$
. In general, one must consider several regions in
$k_{\unicode[STIX]{x1D703}}^{2}x^{2}\ll 1$
. In general, one must consider several regions in
![]() $x$
: (i) the innermost layer,
$x$
: (i) the innermost layer,
![]() $x\sim \unicode[STIX]{x1D6FF}_{e}$
, where
$x\sim \unicode[STIX]{x1D6FF}_{e}$
, where
![]() $\unicode[STIX]{x1D6FF}_{e}$
is the width of the very narrow region where electron physics such as electron Landau damping or semi-collisional effects play a role in reconnection; (ii) at somewhat larger values of
$\unicode[STIX]{x1D6FF}_{e}$
is the width of the very narrow region where electron physics such as electron Landau damping or semi-collisional effects play a role in reconnection; (ii) at somewhat larger values of
![]() $x$
, namely
$x$
, namely
![]() $x\sim \unicode[STIX]{x1D70C}_{i}>\unicode[STIX]{x1D6FF}_{e}$
, where
$x\sim \unicode[STIX]{x1D70C}_{i}>\unicode[STIX]{x1D6FF}_{e}$
, where
![]() $\unicode[STIX]{x1D70C}_{i}=v_{Ti}/\unicode[STIX]{x1D714}_{ci}$
, with
$\unicode[STIX]{x1D70C}_{i}=v_{Ti}/\unicode[STIX]{x1D714}_{ci}$
, with
![]() $v_{Ti}$
the ion thermal velocity,
$v_{Ti}$
the ion thermal velocity,
![]() $v_{Ti}=(2T_{i}/m_{i})^{1/2}$
, is the ion Larmor radius, one must retain full finite ion Larmor radius (FLR) effects; (iii) the ‘intermediate region’,
$v_{Ti}=(2T_{i}/m_{i})^{1/2}$
, is the ion Larmor radius, one must retain full finite ion Larmor radius (FLR) effects; (iii) the ‘intermediate region’,
![]() $\unicode[STIX]{x1D714}\sim k_{\Vert }v_{Ti}$
, where full ion parallel dynamics operates (ion sound at
$\unicode[STIX]{x1D714}\sim k_{\Vert }v_{Ti}$
, where full ion parallel dynamics operates (ion sound at
![]() $x\sim (L_{s}/L_{n})^{1/2}\unicode[STIX]{x1D70C}_{i}$
and ion Landau damping at
$x\sim (L_{s}/L_{n})^{1/2}\unicode[STIX]{x1D70C}_{i}$
and ion Landau damping at
![]() $x\sim (L_{s}/L_{n})\unicode[STIX]{x1D70C}_{i}$
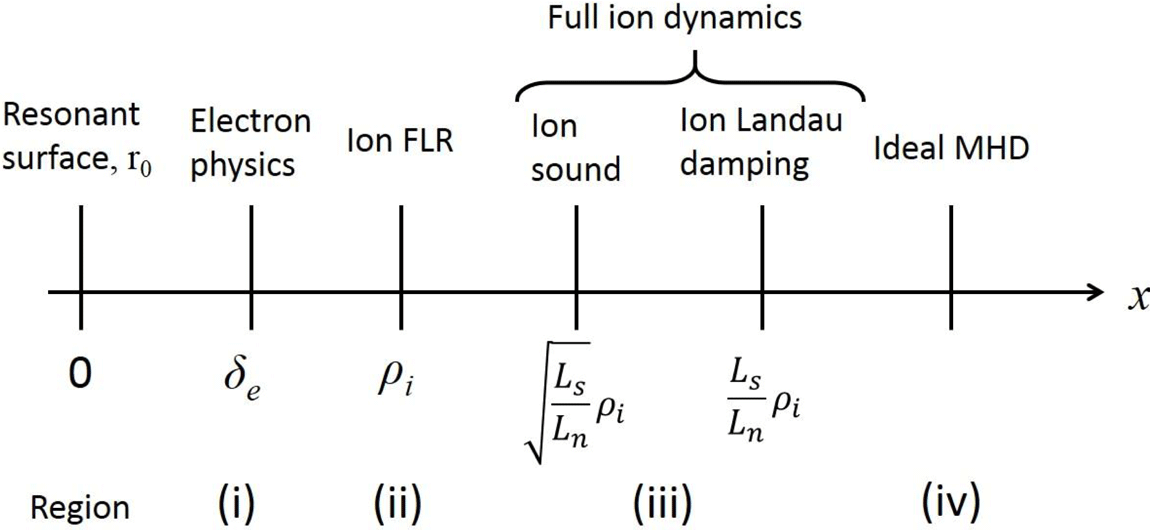
); and finally; (iv) the outer ideal MHD region. These regions are shown schematically in figure 1. Solutions of (2.2) and (2.3) must be matched through all these four regions. In earlier work Connor et al. (Reference Connor, Hastie and Zocco2012) considered this problem, but omitted the intermediate region required to ensure
$x\sim (L_{s}/L_{n})\unicode[STIX]{x1D70C}_{i}$
); and finally; (iv) the outer ideal MHD region. These regions are shown schematically in figure 1. Solutions of (2.2) and (2.3) must be matched through all these four regions. In earlier work Connor et al. (Reference Connor, Hastie and Zocco2012) considered this problem, but omitted the intermediate region required to ensure
![]() $E_{\Vert }\rightarrow 0$
as one approaches the ideal region. We now develop the equations to describe this region.
$E_{\Vert }\rightarrow 0$
as one approaches the ideal region. We now develop the equations to describe this region.

Figure 1. The regions in which different physical processes occur as the distance,
![]() $x=r-r_{0}$
, from the resonant surface,
$x=r-r_{0}$
, from the resonant surface,
![]() $r_{0}$
, increases: (i) electron reconnecting physics at a scale
$r_{0}$
, increases: (i) electron reconnecting physics at a scale
![]() $\unicode[STIX]{x1D6FF}_{e}$
; (ii) ion finite Larmor radius effects at a scale
$\unicode[STIX]{x1D6FF}_{e}$
; (ii) ion finite Larmor radius effects at a scale
![]() $\unicode[STIX]{x1D70C}_{i}$
; (iii) full ion parallel dynamics, namely ion sound at a scale
$\unicode[STIX]{x1D70C}_{i}$
; (iii) full ion parallel dynamics, namely ion sound at a scale
![]() $(L_{s}/L_{n})^{1/2}\unicode[STIX]{x1D70C}_{i}$
and ion Landau damping effects at a scale
$(L_{s}/L_{n})^{1/2}\unicode[STIX]{x1D70C}_{i}$
and ion Landau damping effects at a scale
![]() $(L_{s}/L_{n})\unicode[STIX]{x1D70C}_{i}$
; and (iv) the outer ideal MHD region.
$(L_{s}/L_{n})\unicode[STIX]{x1D70C}_{i}$
; and (iv) the outer ideal MHD region.
Expressions for the parallel current densities,
![]() $J_{\Vert ,e}$
and
$J_{\Vert ,e}$
and
![]() $J_{\Vert ,i}$
, valid in the ion sound region and when
$J_{\Vert ,i}$
, valid in the ion sound region and when
![]() $b\ll 1$
, are derived from solving the respective kinetic equations for electrons and ions, equation (2.1):
$b\ll 1$
, are derived from solving the respective kinetic equations for electrons and ions, equation (2.1):
where
![]() $E_{\Vert }=-\text{i}(k_{\Vert }\unicode[STIX]{x1D711}-\unicode[STIX]{x1D714}A_{\Vert })$
,
$E_{\Vert }=-\text{i}(k_{\Vert }\unicode[STIX]{x1D711}-\unicode[STIX]{x1D714}A_{\Vert })$
,
![]() $\unicode[STIX]{x1D701}_{i}=\unicode[STIX]{x1D714}L_{s}/k_{\unicode[STIX]{x1D703}}xv_{Ti}$
and
$\unicode[STIX]{x1D701}_{i}=\unicode[STIX]{x1D714}L_{s}/k_{\unicode[STIX]{x1D703}}xv_{Ti}$
and
![]() $Z(\unicode[STIX]{x1D701}_{i})$
is the plasma dispersion function. Making use of the long-wavelength approximation,
$Z(\unicode[STIX]{x1D701}_{i})$
is the plasma dispersion function. Making use of the long-wavelength approximation,
![]() $b\sim |\unicode[STIX]{x1D70C}_{i}^{2}\text{d}^{2}/\text{d}x^{2}|\ll 1$
, for the ions in (2.2), eliminating
$b\sim |\unicode[STIX]{x1D70C}_{i}^{2}\text{d}^{2}/\text{d}x^{2}|\ll 1$
, for the ions in (2.2), eliminating
![]() $J_{\Vert ,e,i}$
and introducing the dimensionless variable,
$J_{\Vert ,e,i}$
and introducing the dimensionless variable,
![]() $X=1/\unicode[STIX]{x1D701}_{i}$
, so that
$X=1/\unicode[STIX]{x1D701}_{i}$
, so that
![]() $X=(2L_{n}/L_{s})(\unicode[STIX]{x1D714}_{\ast i}/\unicode[STIX]{x1D714})(x/\unicode[STIX]{x1D70C}_{i})$
, we obtain the following fourth-order system describing the potentials
$X=(2L_{n}/L_{s})(\unicode[STIX]{x1D714}_{\ast i}/\unicode[STIX]{x1D714})(x/\unicode[STIX]{x1D70C}_{i})$
, we obtain the following fourth-order system describing the potentials
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $A_{\Vert }$
, replacing the former by
$A_{\Vert }$
, replacing the former by
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}/v_{Ti}$
and denoting the latter by
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D711}/v_{Ti}$
and denoting the latter by
![]() $A$
: (so that
$A$
: (so that
![]() $E_{\Vert }\propto (X\unicode[STIX]{x1D719}-A)$
):
$E_{\Vert }\propto (X\unicode[STIX]{x1D719}-A)$
):
and
 $$\begin{eqnarray}\displaystyle X\frac{\text{d}^{2}A}{\text{d}X^{2}} & = & \displaystyle \frac{\unicode[STIX]{x1D6FD}_{e}}{2}\left(\frac{L_{s}}{L_{n}}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)^{2}\left(\unicode[STIX]{x1D719}-\frac{A}{X}\right)\left[1-\frac{\unicode[STIX]{x1D714}_{\ast e}}{\unicode[STIX]{x1D714}}+\unicode[STIX]{x1D70F}\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\left(1+\frac{Z}{X}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x1D702}_{i}}{X^{2}}\left(1+\frac{Z}{X}-\frac{XZ}{2}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X\frac{\text{d}^{2}A}{\text{d}X^{2}} & = & \displaystyle \frac{\unicode[STIX]{x1D6FD}_{e}}{2}\left(\frac{L_{s}}{L_{n}}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)^{2}\left(\unicode[STIX]{x1D719}-\frac{A}{X}\right)\left[1-\frac{\unicode[STIX]{x1D714}_{\ast e}}{\unicode[STIX]{x1D714}}+\unicode[STIX]{x1D70F}\left(1-\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\right)\left(1+\frac{Z}{X}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}\frac{\unicode[STIX]{x1D702}_{i}}{X^{2}}\left(1+\frac{Z}{X}-\frac{XZ}{2}\right)\right],\end{eqnarray}$$
where
![]() $Z=Z(1/X)$
and the
$Z=Z(1/X)$
and the
![]() $\unicode[STIX]{x1D6FD}_{j}$
are the ratios of plasma to magnetic pressure for each species. These two equations can be combined to yield:
$\unicode[STIX]{x1D6FD}_{j}$
are the ratios of plasma to magnetic pressure for each species. These two equations can be combined to yield:
where
with
![]() $\hat{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\ast e}$
. The quantity
$\hat{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\ast e}$
. The quantity
![]() $Q(X)$
contains the effects of ion sound when
$Q(X)$
contains the effects of ion sound when
![]() $X\ll 1$
and ion Landau damping in the region
$X\ll 1$
and ion Landau damping in the region
![]() $X\sim 1$
. Introducing the ion sound approximation,
$X\sim 1$
. Introducing the ion sound approximation,
The validity of the ion finite Larmor radius and ion sound expansions requires these terms both to be small so that the balance of terms in (2.8), with
![]() $Q(X)$
given by (2.10), implies
$Q(X)$
given by (2.10), implies
![]() $\hat{\unicode[STIX]{x1D714}}-1\sim \unicode[STIX]{x1D702}_{e}\sim L_{n}/L_{s}<1$
.
$\hat{\unicode[STIX]{x1D714}}-1\sim \unicode[STIX]{x1D702}_{e}\sim L_{n}/L_{s}<1$
.
We shall find it to be sufficient to consider only the ion sound approximation in order to ensure
![]() $E_{\Vert }\rightarrow 0$
, the physics of ion Landau damping only playing a conceptual role that justifies the use of the ‘outward carrying energy’ wave boundary conditions, as in the theory of the electron drift wave (Pearlstein & Berk Reference Pearlstein and Berk1969).
$E_{\Vert }\rightarrow 0$
, the physics of ion Landau damping only playing a conceptual role that justifies the use of the ‘outward carrying energy’ wave boundary conditions, as in the theory of the electron drift wave (Pearlstein & Berk Reference Pearlstein and Berk1969).
Inserting the solution for
![]() $\unicode[STIX]{x1D719}$
into Ampere’s law (2.6) and integrating over
$\unicode[STIX]{x1D719}$
into Ampere’s law (2.6) and integrating over
![]() $X$
through the ion sound region yields the modification to
$X$
through the ion sound region yields the modification to
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
arising from the intermediate region (which represents ion sound and, implicitly, ion Landau damping physics and we designate it as such):
$\unicode[STIX]{x1D6E5}^{\prime }$
arising from the intermediate region (which represents ion sound and, implicitly, ion Landau damping physics and we designate it as such):
where we have used (2.8).
3 Solution in the intermediate region
At low
![]() $\unicode[STIX]{x1D6FD}_{i}$
, equation (2.6) allows us to write
$\unicode[STIX]{x1D6FD}_{i}$
, equation (2.6) allows us to write
![]() $A\equiv \text{const.}$
, since
$A\equiv \text{const.}$
, since
![]() $A_{\Vert }$
is an even function of
$A_{\Vert }$
is an even function of
![]() $x$
, which we choose to be unity:
$x$
, which we choose to be unity:
![]() $A=1$
. Introducing the following scaled variables:
$A=1$
. Introducing the following scaled variables:
equation (2.8) can then be written as
The validity of the ion FLR and ion sound expansions means that (3.2) is only valid on the domain
![]() $(L_{s}/L_{n})^{1/2}>y>(L_{n}/L_{s})^{1/2}$
, requiring
$(L_{s}/L_{n})^{1/2}>y>(L_{n}/L_{s})^{1/2}$
, requiring
![]() $(L_{n}/L_{s})\ll 1$
.
$(L_{n}/L_{s})\ll 1$
.
To solve (3.2) we adopt two different techniques, corresponding to the two components of the inhomogeneous term,
![]() $R(y)$
. For the first term,
$R(y)$
. For the first term,
![]() $R(y)\rightarrow R_{1}(y)=-a/y$
, we employ a Fourier transform for its solution,
$R(y)\rightarrow R_{1}(y)=-a/y$
, we employ a Fourier transform for its solution,
![]() $\hat{\unicode[STIX]{x1D711}}_{1}$
. For the second one,
$\hat{\unicode[STIX]{x1D711}}_{1}$
. For the second one,
![]() $R(y)\rightarrow R_{2}(y)=y/4$
, we generalise a technique due to Basu & Coppi (Reference Basu and Coppi1977), involving an integral representation of its solution,
$R(y)\rightarrow R_{2}(y)=y/4$
, we generalise a technique due to Basu & Coppi (Reference Basu and Coppi1977), involving an integral representation of its solution,
![]() $\hat{\unicode[STIX]{x1D711}}_{2}$
.
$\hat{\unicode[STIX]{x1D711}}_{2}$
.
Introducing the normalisations (3.1), the contribution to (2.11) from the ion sound term in
![]() $Q(X)$
becomes:
$Q(X)$
becomes:
(i) Solution
![]() $\hat{\unicode[STIX]{x1D711}}_{1}(y)$
$\hat{\unicode[STIX]{x1D711}}_{1}(y)$
Fourier transforming equation (3.2) with
![]() $R(y)\rightarrow R_{1}(y)=-a/y$
, we obtain an equation for
$R(y)\rightarrow R_{1}(y)=-a/y$
, we obtain an equation for
![]() $\tilde{\unicode[STIX]{x1D711}}_{1}(k)$
:
$\tilde{\unicode[STIX]{x1D711}}_{1}(k)$
:
namely
where the transform of the right-hand side is given by Pegoraro & Schep (Reference Pegoraro and Schep1986), utilising the theory for Fourier transforms of generalised functions (Gel’fand & Shilov Reference Gel’fand and Shilov1964).
This can be cast in the canonical form for parabolic cylinder functions by introducing
![]() $\unicode[STIX]{x1D705}=2k$
. The solution of (3.5) can then be written as:
$\unicode[STIX]{x1D705}=2k$
. The solution of (3.5) can then be written as:
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a) & = & \displaystyle AE(-a,\unicode[STIX]{x1D705})+BE^{\ast }(-a,\unicode[STIX]{x1D705})\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}\unicode[STIX]{x03C0}a\frac{E(-a,\unicode[STIX]{x1D705})}{W}\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E^{\ast }(-a,\unicode[STIX]{x1D705}^{\prime })\,\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}\unicode[STIX]{x03C0}a\frac{E^{\ast }(-a,\unicode[STIX]{x1D705})}{W}\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\,\text{sgn}(\unicode[STIX]{x1D705}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a) & = & \displaystyle AE(-a,\unicode[STIX]{x1D705})+BE^{\ast }(-a,\unicode[STIX]{x1D705})\nonumber\\ \displaystyle & & \displaystyle +\,\text{i}\unicode[STIX]{x03C0}a\frac{E(-a,\unicode[STIX]{x1D705})}{W}\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E^{\ast }(-a,\unicode[STIX]{x1D705}^{\prime })\,\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\nonumber\\ \displaystyle & & \displaystyle -\,\text{i}\unicode[STIX]{x03C0}a\frac{E^{\ast }(-a,\unicode[STIX]{x1D705})}{W}\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\,\text{sgn}(\unicode[STIX]{x1D705}^{\prime }),\end{eqnarray}$$
where
![]() $E(-a,\unicode[STIX]{x1D705})$
and
$E(-a,\unicode[STIX]{x1D705})$
and
![]() $E^{\ast }(-a,\unicode[STIX]{x1D705})$
are the wave-like parabolic cylinder functions (Abramowitz & Stegun Reference Abramowitz and Stegun1972), the Wronskian,
$E^{\ast }(-a,\unicode[STIX]{x1D705})$
are the wave-like parabolic cylinder functions (Abramowitz & Stegun Reference Abramowitz and Stegun1972), the Wronskian,
![]() $W=-2i$
and
$W=-2i$
and
![]() $A$
and
$A$
and
![]() $B$
are constants to be determined by applying appropriate boundary conditions.
$B$
are constants to be determined by applying appropriate boundary conditions.
The acceptable solution in configuration space (i.e.
![]() $x$
-space) is a wave carrying energy outwards from the resonant layer, eventually decaying due to ion Landau damping (Pearlstein & Berk Reference Pearlstein and Berk1969). Since the electron drift wave is a ‘backwards’ wave with group velocity opposed to its phase velocity, this translates into suppressing the wave solution with positive phase velocity in
$x$
-space) is a wave carrying energy outwards from the resonant layer, eventually decaying due to ion Landau damping (Pearlstein & Berk Reference Pearlstein and Berk1969). Since the electron drift wave is a ‘backwards’ wave with group velocity opposed to its phase velocity, this translates into suppressing the wave solution with positive phase velocity in
![]() $x$
-space. In
$x$
-space. In
![]() $k$
-space this implies supressing the one with an apparent negative phase velocity, so that
$k$
-space this implies supressing the one with an apparent negative phase velocity, so that
We also require
![]() $\hat{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},-a)$
to be odd in
$\hat{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},-a)$
to be odd in
![]() $\unicode[STIX]{x1D705}$
with
$\unicode[STIX]{x1D705}$
with
![]() $\hat{\unicode[STIX]{x1D711}}_{1}(0,a)=0$
. This requires
$\hat{\unicode[STIX]{x1D711}}_{1}(0,a)=0$
. This requires
Thus
 $$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a) & = & \displaystyle \frac{\text{i}\unicode[STIX]{x03C0}a}{W}\left[E^{\ast }(-a,\unicode[STIX]{x1D705})\int _{\unicode[STIX]{x1D705}}^{\infty }\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{E^{\ast }(-a,0)}{E(-a,0)}E(-a,\unicode[STIX]{x1D705})\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\left.E(-a,\unicode[STIX]{x1D705})\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E^{\ast }(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a) & = & \displaystyle \frac{\text{i}\unicode[STIX]{x03C0}a}{W}\left[E^{\ast }(-a,\unicode[STIX]{x1D705})\int _{\unicode[STIX]{x1D705}}^{\infty }\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{E^{\ast }(-a,0)}{E(-a,0)}E(-a,\unicode[STIX]{x1D705})\int _{0}^{\infty }\text{d}\unicode[STIX]{x1D705}^{\prime }E(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\nonumber\\ \displaystyle & & \displaystyle +\left.E(-a,\unicode[STIX]{x1D705})\int _{0}^{\unicode[STIX]{x1D705}}\text{d}\unicode[STIX]{x1D705}^{\prime }E^{\ast }(-a,\unicode[STIX]{x1D705}^{\prime })\text{sgn}(\unicode[STIX]{x1D705}^{\prime })\right].\end{eqnarray}$$
(ii) Solution
![]() $\hat{\unicode[STIX]{x1D711}}_{2}(y)$
$\hat{\unicode[STIX]{x1D711}}_{2}(y)$
Introducing
![]() $z=iy^{2}/4$
and
$z=iy^{2}/4$
and
![]() $\hat{\unicode[STIX]{x1D711}}_{2}(y)=u\exp (-z)$
into (3.2) with
$\hat{\unicode[STIX]{x1D711}}_{2}(y)=u\exp (-z)$
into (3.2) with
![]() $R(y)\rightarrow R_{2}(y)=y/4$
, we obtain the equation:
$R(y)\rightarrow R_{2}(y)=y/4$
, we obtain the equation:
for
![]() $u(z)$
. Generalising the technique of Basu & Coppi (Reference Basu and Coppi1977), we introduce the transform:
$u(z)$
. Generalising the technique of Basu & Coppi (Reference Basu and Coppi1977), we introduce the transform:
where the contour
![]() $C$
remains to be chosen for convenience. Inserting the substitution (3.11) in (3.10) leads to
$C$
remains to be chosen for convenience. Inserting the substitution (3.11) in (3.10) leads to
 $$\begin{eqnarray}\displaystyle & & \displaystyle z^{\unicode[STIX]{x1D6FD}-1}\int _{C}\text{d}tv(t)\text{e}^{zt}\left\{z^{2}(t^{2}-2t)+z\left[\left(2\unicode[STIX]{x1D6FD}+\frac{1}{2}\right)(t-1)+\text{i}a\right]+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FD}-1)+\unicode[STIX]{x1D6FD}/2\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}z^{1/2}\text{e}^{z}/2.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle z^{\unicode[STIX]{x1D6FD}-1}\int _{C}\text{d}tv(t)\text{e}^{zt}\left\{z^{2}(t^{2}-2t)+z\left[\left(2\unicode[STIX]{x1D6FD}+\frac{1}{2}\right)(t-1)+\text{i}a\right]+\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D6FD}-1)+\unicode[STIX]{x1D6FD}/2\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}z^{1/2}\text{e}^{z}/2.\end{eqnarray}$$
Choosing
![]() $\unicode[STIX]{x1D6FD}=1/2$
, which eliminates the term independent of
$\unicode[STIX]{x1D6FD}=1/2$
, which eliminates the term independent of
![]() $z$
on the right-hand side bracket, equation (3.12) simplifies to
$z$
on the right-hand side bracket, equation (3.12) simplifies to
Integrating by parts in
![]() $t$
,
$t$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle [v(t)\text{e}^{zt}(t^{2}-2t)]_{t_{1}}^{t_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{C}\text{d}t\text{e}^{zt}\left\{\frac{\text{d}}{\text{d}t}[((t^{2}-2t))v(t)]-\left[\frac{3}{2}(t-1)+\text{i}a\right]v(t)\right\}=-\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}\text{e}^{z}/2,\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle [v(t)\text{e}^{zt}(t^{2}-2t)]_{t_{1}}^{t_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\int _{C}\text{d}t\text{e}^{zt}\left\{\frac{\text{d}}{\text{d}t}[((t^{2}-2t))v(t)]-\left[\frac{3}{2}(t-1)+\text{i}a\right]v(t)\right\}=-\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}\text{e}^{z}/2,\qquad\end{eqnarray}$$
where
![]() $t_{1}$
and
$t_{1}$
and
![]() $t_{2}$
are the endpoints of contour
$t_{2}$
are the endpoints of contour
![]() $C$
and are to be chosen later for convenience.
$C$
and are to be chosen later for convenience.
Equation (3.14) is solved if
and
Equation (3.15) is satisfied by:
and (3.16) by choosing
![]() $t_{1}=0,t_{2}=1$
and the constant
$t_{1}=0,t_{2}=1$
and the constant
![]() ${\hat{c}}=\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}/2$
. Inserting solution (3.17) into (3.11) for
${\hat{c}}=\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}/2$
. Inserting solution (3.17) into (3.11) for
![]() $u(z)$
, determines
$u(z)$
, determines
![]() $\hat{\unicode[STIX]{x1D711}}_{2}(y)=u(z)\exp (-z)$
with
$\hat{\unicode[STIX]{x1D711}}_{2}(y)=u(z)\exp (-z)$
with
![]() $z=iy^{2}/4$
.
$z=iy^{2}/4$
.
4 The
 $\unicode[STIX]{x1D6E5}^{\prime }$
-integral
$\unicode[STIX]{x1D6E5}^{\prime }$
-integral
Inserting the solution
![]() $\hat{\unicode[STIX]{x1D711}}=\hat{\unicode[STIX]{x1D711}}_{1}+\hat{\unicode[STIX]{x1D711}}_{2}$
into (3.3) and integrating over
$\hat{\unicode[STIX]{x1D711}}=\hat{\unicode[STIX]{x1D711}}_{1}+\hat{\unicode[STIX]{x1D711}}_{2}$
into (3.3) and integrating over
![]() $y$
through the ion sound region yields
$y$
through the ion sound region yields
![]() $\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
, which we can express as
$\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
, which we can express as
where
and
To evaluate
![]() $\unicode[STIX]{x1D6E5}^{\prime (1)}$
we introduce the Fourier transform for
$\unicode[STIX]{x1D6E5}^{\prime (1)}$
we introduce the Fourier transform for
![]() $\hat{\unicode[STIX]{x1D711}}_{1}(y,a),\tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a)$
, perform the integration over
$\hat{\unicode[STIX]{x1D711}}_{1}(y,a),\tilde{\unicode[STIX]{x1D711}}_{1}(\unicode[STIX]{x1D705},a)$
, perform the integration over
![]() $y$
, using the resulting delta function,
$y$
, using the resulting delta function,
![]() $\unicode[STIX]{x1D6FF}(k)$
, to reduce the integral to:
$\unicode[STIX]{x1D6FF}(k)$
, to reduce the integral to:
From (3.9) we have the result:
As shown in the appendix, equation (A 10), the integral over
![]() $\unicode[STIX]{x1D705}^{\prime }$
can be performed analytically to yield:
$\unicode[STIX]{x1D705}^{\prime }$
can be performed analytically to yield:
 $$\begin{eqnarray}\text{i}\frac{\text{d}}{\text{d}k}\tilde{\unicode[STIX]{x1D711}}_{1}(k,a)_{k=0}=-\frac{\displaystyle 2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{5}{4}-\frac{\text{i}a}{2}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
$$\begin{eqnarray}\text{i}\frac{\text{d}}{\text{d}k}\tilde{\unicode[STIX]{x1D711}}_{1}(k,a)_{k=0}=-\frac{\displaystyle 2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{5}{4}-\frac{\text{i}a}{2}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
Here
![]() $F(a,b;c;z)$
is the hypergeometric function and
$F(a,b;c;z)$
is the hypergeometric function and
![]() $\unicode[STIX]{x1D6E4}(z)$
the gamma function (Abramowitz & Stegun Reference Abramowitz and Stegun1972). Thus:
$\unicode[STIX]{x1D6E4}(z)$
the gamma function (Abramowitz & Stegun Reference Abramowitz and Stegun1972). Thus:
with
 $$\begin{eqnarray}I_{0}(a)=-\frac{\displaystyle 2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{5}{4}-\frac{\text{i}a}{2}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
$$\begin{eqnarray}I_{0}(a)=-\frac{\displaystyle 2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{5}{4}-\frac{\text{i}a}{2}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
![]() $I_{0}(a)$
, not to be confused with the modified Bessel function, is displayed in figure 2.
$I_{0}(a)$
, not to be confused with the modified Bessel function, is displayed in figure 2.
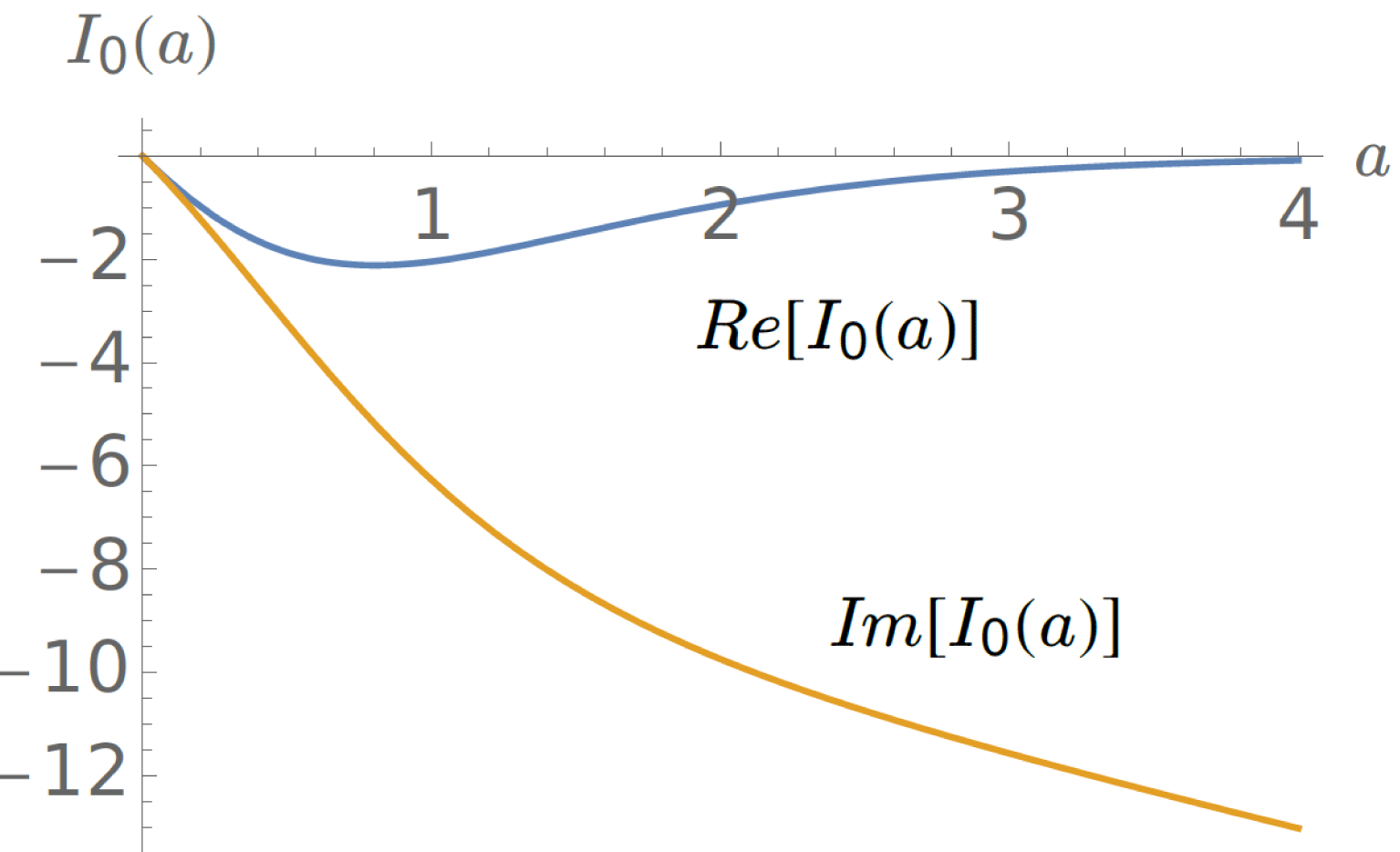
Figure 2. The real and imaginary parts of
![]() $I_{0}(a)$
as a function of the parameter
$I_{0}(a)$
as a function of the parameter
![]() $a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
$a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
Inserting
![]() $\hat{\unicode[STIX]{x1D711}}_{2}$
into integral (4.3) yields
$\hat{\unicode[STIX]{x1D711}}_{2}$
into integral (4.3) yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)}=\frac{\unicode[STIX]{x1D6FD}_{i}(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{0}^{\infty }\text{d}y\left[1-\frac{\text{i}y^{2}}{4}\int _{0}^{1}\text{d}t\exp \left(-\frac{\text{i}y^{2}t}{4}\right)(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)}=\frac{\unicode[STIX]{x1D6FD}_{i}(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\int _{0}^{\infty }\text{d}y\left[1-\frac{\text{i}y^{2}}{4}\int _{0}^{1}\text{d}t\exp \left(-\frac{\text{i}y^{2}t}{4}\right)(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}\right].\end{eqnarray}$$
Using the identity
we can rewrite (4.9) as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)} & = & \displaystyle \frac{\unicode[STIX]{x1D6FD}_{i}\left(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i}\right)}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\left\{\int _{0}^{\infty }\text{d}y\exp \left(-\frac{\text{i}y^{2}}{4}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\int _{0}^{\infty }\text{d}y\frac{\text{i}y^{2}}{4}\int _{0}^{1}\text{d}t\exp \left(-\frac{\text{i}y^{2}t}{4}\right)[1-(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}]\right\}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)} & = & \displaystyle \frac{\unicode[STIX]{x1D6FD}_{i}\left(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i}\right)}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\left\{\int _{0}^{\infty }\text{d}y\exp \left(-\frac{\text{i}y^{2}}{4}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\int _{0}^{\infty }\text{d}y\frac{\text{i}y^{2}}{4}\int _{0}^{1}\text{d}t\exp \left(-\frac{\text{i}y^{2}t}{4}\right)[1-(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}]\right\}.\qquad\end{eqnarray}$$
Now the integration over
![]() $y$
can be readily performed to yield:
$y$
can be readily performed to yield:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)} & = & \displaystyle \sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}\frac{\unicode[STIX]{x1D6FD}_{i}(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{1+\frac{1}{2}\int _{0}^{1}\text{d}t\,t^{-3/2}[1-(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}]\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}^{\prime (2)} & = & \displaystyle \sqrt{\unicode[STIX]{x03C0}}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}\frac{\unicode[STIX]{x1D6FD}_{i}(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})}{\unicode[STIX]{x1D70C}_{i}}\left(\frac{L_{s}}{L_{n}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{1+\frac{1}{2}\int _{0}^{1}\text{d}t\,t^{-3/2}[1-(1-t)^{-1/4-\text{i}a/2}(1+t)^{-1/4+\text{i}a/2}]\right\}.\end{eqnarray}$$
Thus, we require the integral
This can be evaluated analytically, as shown in (B 9) of appendix B:
 $$\begin{eqnarray}\hat{I} (a)=-1+\frac{\displaystyle \sqrt{(2\unicode[STIX]{x03C0})}\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{I} (a)=-1+\frac{\displaystyle \sqrt{(2\unicode[STIX]{x03C0})}\unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$

Figure 3. The real and imaginary parts of
![]() $I_{1}(a)$
as a function of the parameter
$I_{1}(a)$
as a function of the parameter
![]() $a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
$a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
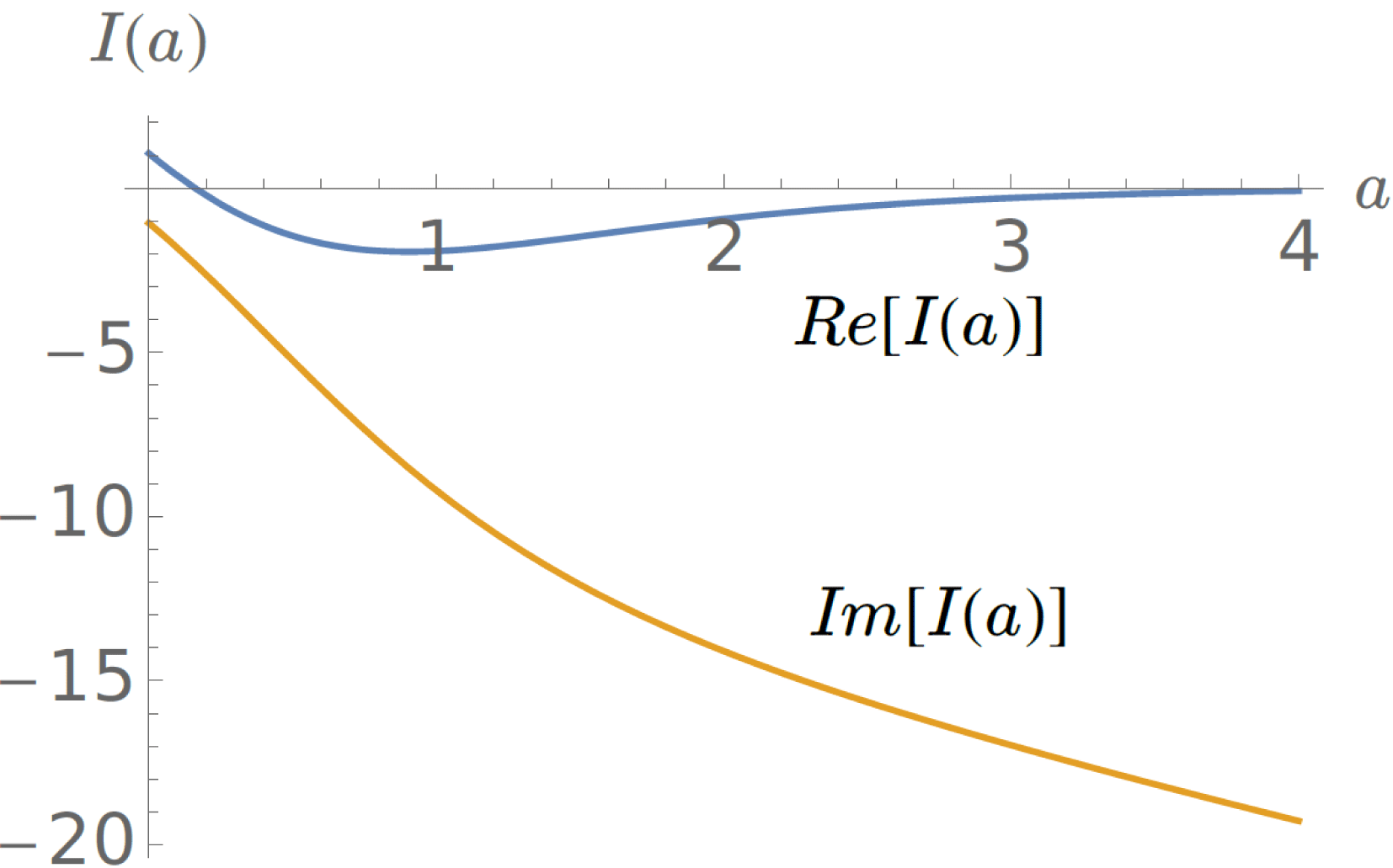
Figure 4. The real and imaginary parts of
![]() $I(a)=I_{0}(a)+I_{1}(a)$
as a function of the parameter
$I(a)=I_{0}(a)+I_{1}(a)$
as a function of the parameter
![]() $a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
$a=(L_{s}\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}/2L_{n})(\hat{\unicode[STIX]{x1D714}}-1)/(\hat{\unicode[STIX]{x1D714}}\unicode[STIX]{x1D70F}+1+\unicode[STIX]{x1D702}_{i})$
.
Thus, from (4.7) and (4.12)–(4.14) we obtain:
where
 $$\begin{eqnarray}I_{1}(a)=\sqrt{2}\unicode[STIX]{x03C0}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)},\end{eqnarray}$$
$$\begin{eqnarray}I_{1}(a)=\sqrt{2}\unicode[STIX]{x03C0}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)},\end{eqnarray}$$
which is evaluated numerically and displayed in figure 3. The combination
is plotted in figure 4. When
![]() $a=0$
, the expression (4.15) reduces to the analytic result for the real part of
$a=0$
, the expression (4.15) reduces to the analytic result for the real part of
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
quoted in Coppi et al. (Reference Coppi, Mark, Sugiyama and Bertin1979) for the case
$\unicode[STIX]{x1D6E5}^{\prime }$
quoted in Coppi et al. (Reference Coppi, Mark, Sugiyama and Bertin1979) for the case
![]() $\unicode[STIX]{x1D702}_{e}=0$
.
$\unicode[STIX]{x1D702}_{e}=0$
.
5 The effective
 $\unicode[STIX]{x1D6E5}^{\prime }$
for stability
$\unicode[STIX]{x1D6E5}^{\prime }$
for stability
The result (4.15) for
![]() $\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
, the modification to
$\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
, the modification to
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
due to the ion sound/ion Landau damping physics, can be substituted into expressions in the literature for the drift tearing mode growth rate at finite ion temperature which have ignored the presence of these effects.
$\unicode[STIX]{x1D6E5}^{\prime }$
due to the ion sound/ion Landau damping physics, can be substituted into expressions in the literature for the drift tearing mode growth rate at finite ion temperature which have ignored the presence of these effects.
For example, the semi-collisional tearing mode with large ion Larmor orbits in the absence of the ion sound intermediate layer has a growth rate
![]() $\hat{\unicode[STIX]{x1D6FE}}$
given by
$\hat{\unicode[STIX]{x1D6FE}}$
given by
![]() $\text{Im}(\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}})$
, where
$\text{Im}(\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}})$
, where
![]() $\hat{\unicode[STIX]{x1D714}}=\hat{\unicode[STIX]{x1D714}}_{0}+\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}}$
, and
$\hat{\unicode[STIX]{x1D714}}=\hat{\unicode[STIX]{x1D714}}_{0}+\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}}$
, and
![]() $\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}}$
satisfies the dispersion relation (Connor et al.
Reference Connor, Hastie and Zocco2012):
$\unicode[STIX]{x1D6FF}\hat{\unicode[STIX]{x1D714}}$
satisfies the dispersion relation (Connor et al.
Reference Connor, Hastie and Zocco2012):
Here
![]() $\hat{\unicode[STIX]{x1D714}}_{0}=(1+0.74\unicode[STIX]{x1D702}_{e})$
,
$\hat{\unicode[STIX]{x1D714}}_{0}=(1+0.74\unicode[STIX]{x1D702}_{e})$
,
![]() $\unicode[STIX]{x1D6FF}_{sc}=(\unicode[STIX]{x1D708}_{e}\unicode[STIX]{x1D70C}_{e}L_{s}^{2}/k_{\unicode[STIX]{x1D703}}v_{Te}L_{n})^{1/2}$
, with
$\unicode[STIX]{x1D6FF}_{sc}=(\unicode[STIX]{x1D708}_{e}\unicode[STIX]{x1D70C}_{e}L_{s}^{2}/k_{\unicode[STIX]{x1D703}}v_{Te}L_{n})^{1/2}$
, with
![]() $\unicode[STIX]{x1D708}_{e}$
the electron collision frequency,
$\unicode[STIX]{x1D708}_{e}$
the electron collision frequency,
![]() $\unicode[STIX]{x1D70C}_{e}$
the electron Larmor radius and
$\unicode[STIX]{x1D70C}_{e}$
the electron Larmor radius and
![]() $v_{Te}$
the electron thermal velocity, is the semi-collisional width (
$v_{Te}$
the electron thermal velocity, is the semi-collisional width (
![]() $\unicode[STIX]{x1D6FF}_{sc}\ll \unicode[STIX]{x1D70C}_{i}$
) and
$\unicode[STIX]{x1D6FF}_{sc}\ll \unicode[STIX]{x1D70C}_{i}$
) and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime } & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}\hat{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x1D70C}_{i}}\frac{(\hat{\unicode[STIX]{x1D714}}_{0}-1)^{2}}{\hat{\unicode[STIX]{x1D714}}_{0}}\left(1+\hat{\unicode[STIX]{x1D714}}_{0}\unicode[STIX]{x1D70F}-\frac{\unicode[STIX]{x1D702}_{i}}{2}\right)\ln (\unicode[STIX]{x1D70C}_{i}/(\unicode[STIX]{x1D6FF}_{sc}\hat{\unicode[STIX]{x1D714}}_{0}^{1/2}))\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x03C0}\hat{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x1D70C}_{i}}\hat{\unicode[STIX]{x1D714}}_{0}(\hat{\unicode[STIX]{x1D714}}_{0}-1)\overline{I},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime } & = & \displaystyle \frac{\sqrt{\unicode[STIX]{x03C0}}\hat{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x1D70C}_{i}}\frac{(\hat{\unicode[STIX]{x1D714}}_{0}-1)^{2}}{\hat{\unicode[STIX]{x1D714}}_{0}}\left(1+\hat{\unicode[STIX]{x1D714}}_{0}\unicode[STIX]{x1D70F}-\frac{\unicode[STIX]{x1D702}_{i}}{2}\right)\ln (\unicode[STIX]{x1D70C}_{i}/(\unicode[STIX]{x1D6FF}_{sc}\hat{\unicode[STIX]{x1D714}}_{0}^{1/2}))\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x03C0}\hat{\unicode[STIX]{x1D6FD}}}{\unicode[STIX]{x1D70C}_{i}}\hat{\unicode[STIX]{x1D714}}_{0}(\hat{\unicode[STIX]{x1D714}}_{0}-1)\overline{I},\end{eqnarray}$$
with
![]() $\hat{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{e}(L_{s}/L_{n})^{2}/2$
.
$\hat{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FD}_{e}(L_{s}/L_{n})^{2}/2$
.
![]() $\overline{I}(\hat{\unicode[STIX]{x1D714}}_{0}(\unicode[STIX]{x1D702}_{e}),\unicode[STIX]{x1D702}_{i,}\unicode[STIX]{x1D70F})$
is an integral that is negative and numerical evaluation shows that it is well represented by
$\overline{I}(\hat{\unicode[STIX]{x1D714}}_{0}(\unicode[STIX]{x1D702}_{e}),\unicode[STIX]{x1D702}_{i,}\unicode[STIX]{x1D70F})$
is an integral that is negative and numerical evaluation shows that it is well represented by
![]() $\overline{I}\cong -1.3\unicode[STIX]{x1D702}_{e}^{1/2}$
(Connor et al.
Reference Connor, Hastie and Zocco2012).Footnote
1
The first contribution to
$\overline{I}\cong -1.3\unicode[STIX]{x1D702}_{e}^{1/2}$
(Connor et al.
Reference Connor, Hastie and Zocco2012).Footnote
1
The first contribution to
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
in (5.2) is due to finite ion Larmor radius effects (FLR), while the second term represents diamagnetic effects. The most sensitive dependence of
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
in (5.2) is due to finite ion Larmor radius effects (FLR), while the second term represents diamagnetic effects. The most sensitive dependence of
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is on
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is on
![]() $\unicode[STIX]{x1D702}_{e}$
.
$\unicode[STIX]{x1D702}_{e}$
.
To introduce the effect of the intermediate ion sound layer, we replace
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
in (5.1) by
$\unicode[STIX]{x1D6E5}^{\prime }$
in (5.1) by
![]() $(\unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime })$
. Using (4.15) and (5.1), with the result for
$(\unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime })$
. Using (4.15) and (5.1), with the result for
![]() $I(a)$
displayed in figure 4, we show
$I(a)$
displayed in figure 4, we show
![]() $\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }$
, the critical value of
$\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }$
, the critical value of
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
(i.e. the value of
$\unicode[STIX]{x1D6E5}^{\prime }$
(i.e. the value of
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
for which the growth rate, as calculated from (5.1), vanishes) as a function of
$\unicode[STIX]{x1D6E5}^{\prime }$
for which the growth rate, as calculated from (5.1), vanishes) as a function of
![]() $\unicode[STIX]{x1D702}_{e}$
in figure 5, for typical values of the other parameters (
$\unicode[STIX]{x1D702}_{e}$
in figure 5, for typical values of the other parameters (
![]() $\hat{\unicode[STIX]{x1D6FD}}=0.05$
,
$\hat{\unicode[STIX]{x1D6FD}}=0.05$
,
![]() $\unicode[STIX]{x1D6FF}_{sc}/\unicode[STIX]{x1D70C}_{i}=10^{-3},\unicode[STIX]{x1D70F}=1,\unicode[STIX]{x1D702}_{i}=0,L_{n}/L_{s}=0.1$
). Because
$\unicode[STIX]{x1D6FF}_{sc}/\unicode[STIX]{x1D70C}_{i}=10^{-3},\unicode[STIX]{x1D70F}=1,\unicode[STIX]{x1D702}_{i}=0,L_{n}/L_{s}=0.1$
). Because
![]() $\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
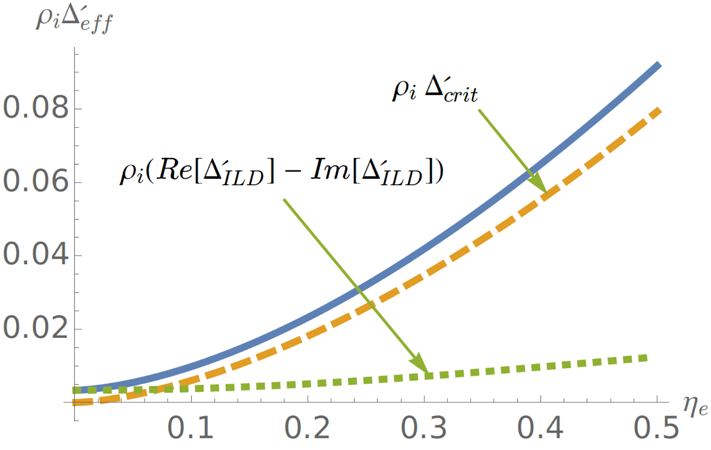
is complex, both its real and imaginary parts contribute to the growth rate in (5.1). We see that the contribution from the ion sound/ion Landau damping layer is less important than those arising from
$\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
is complex, both its real and imaginary parts contribute to the growth rate in (5.1). We see that the contribution from the ion sound/ion Landau damping layer is less important than those arising from
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, representing the FLR and diamagnetic terms, except near
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, representing the FLR and diamagnetic terms, except near
![]() $\unicode[STIX]{x1D702}_{e}=0$
where it remains finite. There it provides a persistent stabilising contribution, unlike the others, which tend to zero.
$\unicode[STIX]{x1D702}_{e}=0$
where it remains finite. There it provides a persistent stabilising contribution, unlike the others, which tend to zero.

Figure 5. The effective critical value of
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D70C}_{i}$
,
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D70C}_{i}$
,
![]() $\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }\unicode[STIX]{x1D70C}_{i}$
(full (blue) line), as a function of
$\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }\unicode[STIX]{x1D70C}_{i}$
(full (blue) line), as a function of
![]() $\unicode[STIX]{x1D702}_{e}$
for typical values of the other parameters:
$\unicode[STIX]{x1D702}_{e}$
for typical values of the other parameters:
![]() $\hat{\unicode[STIX]{x1D6FD}}=0.05$
,
$\hat{\unicode[STIX]{x1D6FD}}=0.05$
,
![]() $\unicode[STIX]{x1D6FF}_{sc}/\unicode[STIX]{x1D70C}_{i}=10^{-3}$
,
$\unicode[STIX]{x1D6FF}_{sc}/\unicode[STIX]{x1D70C}_{i}=10^{-3}$
,
![]() $\unicode[STIX]{x1D70F}=1$
,
$\unicode[STIX]{x1D70F}=1$
,
![]() $\unicode[STIX]{x1D702}_{i}=0$
,
$\unicode[STIX]{x1D702}_{i}=0$
,
![]() $L_{n}/L_{s}=0.1$
.
$L_{n}/L_{s}=0.1$
.
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is the contribution from FLR and diamagnetic effects (long dashed (brown) line), while
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
is the contribution from FLR and diamagnetic effects (long dashed (brown) line), while
![]() $(\text{Re}[\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }]-\text{Im}[\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }])$
is the contribution from the real and imaginary parts of the ion Landau damping terms (dashed (green) line).
$(\text{Re}[\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }]-\text{Im}[\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }])$
is the contribution from the real and imaginary parts of the ion Landau damping terms (dashed (green) line).
6 Discussion and conclusions
We have investigated the impact of ion sound and ion Landau damping on the effective tearing mode stability parameter,
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
, in a hot tokamak plasma. These effects are essential in ensuring the parallel electric field approaches zero as one attempts to match solutions of the inner resonant layer equations to those of the external ideal MHD model. Because the tearing mode frequency is effectively determined by the resonant layer physics and depends on
$\unicode[STIX]{x1D6E5}^{\prime }$
, in a hot tokamak plasma. These effects are essential in ensuring the parallel electric field approaches zero as one attempts to match solutions of the inner resonant layer equations to those of the external ideal MHD model. Because the tearing mode frequency is effectively determined by the resonant layer physics and depends on
![]() $\unicode[STIX]{x1D702}_{e}$
, it transpires that the effect is significant even for weak electron temperature gradients. In this situation one can introduce an intermediate region, between that where the key resonant layer physics lies and the ideal MHD region, where electron drift wave physics dominates (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Indeed, by recalling the ideas of Pearlstein & Berk (Reference Pearlstein and Berk1969) one does not need to explicitly consider the ion Landau damping region, replacing it by the boundary condition that the drift waves must only carry energy outwards. Matching solutions through this layer provides a link between the true
$\unicode[STIX]{x1D702}_{e}$
, it transpires that the effect is significant even for weak electron temperature gradients. In this situation one can introduce an intermediate region, between that where the key resonant layer physics lies and the ideal MHD region, where electron drift wave physics dominates (Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Indeed, by recalling the ideas of Pearlstein & Berk (Reference Pearlstein and Berk1969) one does not need to explicitly consider the ion Landau damping region, replacing it by the boundary condition that the drift waves must only carry energy outwards. Matching solutions through this layer provides a link between the true
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
and the effective one seen by the inner layer.
$\unicode[STIX]{x1D6E5}^{\prime }$
and the effective one seen by the inner layer.
The effect of the intermediate layer is parametrised by the quantity
![]() $a=(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}L_{s}/2\unicode[STIX]{x1D714}_{\ast e}L_{n})((\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\ast e})/(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}+(1+\unicode[STIX]{x1D702}_{i})\unicode[STIX]{x1D714}_{\ast e}))$
. Recalling that a good fit to the drift tearing mode frequency is
$a=(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}L_{s}/2\unicode[STIX]{x1D714}_{\ast e}L_{n})((\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{\ast e})/(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}+(1+\unicode[STIX]{x1D702}_{i})\unicode[STIX]{x1D714}_{\ast e}))$
. Recalling that a good fit to the drift tearing mode frequency is
![]() $\hat{\unicode[STIX]{x1D714}}_{0}=(1+0.74\unicode[STIX]{x1D702}_{e})$
(Connor et al.
Reference Connor, Hastie and Zocco2012), we see that
$\hat{\unicode[STIX]{x1D714}}_{0}=(1+0.74\unicode[STIX]{x1D702}_{e})$
(Connor et al.
Reference Connor, Hastie and Zocco2012), we see that
![]() $a$
is indeed essentially a function of
$a$
is indeed essentially a function of
![]() $\unicode[STIX]{x1D702}_{e}$
and
$\unicode[STIX]{x1D702}_{e}$
and
![]() $L_{s}/L_{n}$
. However, the validity of the theory requires the electron temperature gradient to be rather weak, with
$L_{s}/L_{n}$
. However, the validity of the theory requires the electron temperature gradient to be rather weak, with
![]() $\unicode[STIX]{x1D702}_{e}\sim L_{n}/L_{s}$
, i.e.
$\unicode[STIX]{x1D702}_{e}\sim L_{n}/L_{s}$
, i.e.
![]() $L_{T_{e}}\sim L_{s}$
, so that
$L_{T_{e}}\sim L_{s}$
, so that
![]() $a\sim 0(1)$
(Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Although the effects of the intermediate region increase as
$a\sim 0(1)$
(Coppi et al.
Reference Coppi, Mark, Sugiyama and Bertin1979). Although the effects of the intermediate region increase as
![]() $\unicode[STIX]{x1D702}_{e}$
increases, a valid treatment for
$\unicode[STIX]{x1D702}_{e}$
increases, a valid treatment for
![]() $\unicode[STIX]{x1D702}_{e}\sim 0(1)$
would require a numerical calculation involving the full effects of ion Larmor radius and ion Landau damping, as the approximations inherent in the simple electron drift wave model, namely the long-wavelength ion Larmor radius and the ion sound expansion, no longer hold.
$\unicode[STIX]{x1D702}_{e}\sim 0(1)$
would require a numerical calculation involving the full effects of ion Larmor radius and ion Landau damping, as the approximations inherent in the simple electron drift wave model, namely the long-wavelength ion Larmor radius and the ion sound expansion, no longer hold.
Given these constraints on
![]() $\unicode[STIX]{x1D702}_{e}$
, we have applied the results to a realistic hot tokamak plasma model, although in cylindrical geometry, where the ion Larmor orbit exceeds the reconnecting layer width, which itself is described by semi-collisional electron physics (Cowley et al.
Reference Cowley, Kulsrud and Hahm1986; Connor et al.
Reference Connor, Hastie and Zocco2012) and compared the stabilising effects from the ion sound/ion Landau damping physics with other stabilising effects, as a function of
$\unicode[STIX]{x1D702}_{e}$
, we have applied the results to a realistic hot tokamak plasma model, although in cylindrical geometry, where the ion Larmor orbit exceeds the reconnecting layer width, which itself is described by semi-collisional electron physics (Cowley et al.
Reference Cowley, Kulsrud and Hahm1986; Connor et al.
Reference Connor, Hastie and Zocco2012) and compared the stabilising effects from the ion sound/ion Landau damping physics with other stabilising effects, as a function of
![]() $\unicode[STIX]{x1D702}_{e}$
. The sum of these effects then leads to a critical value,
$\unicode[STIX]{x1D702}_{e}$
. The sum of these effects then leads to a critical value,
![]() $\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }$
for tearing instability. Although
$\unicode[STIX]{x1D6E5}_{\text{eff}}^{\prime }$
for tearing instability. Although
![]() $\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
is generally a less important stabilising term than the FLR and diamagnetic contributions in
$\unicode[STIX]{x1D6E5}_{\text{ILD}}^{\prime }$
is generally a less important stabilising term than the FLR and diamagnetic contributions in
![]() $\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, it persists as
$\unicode[STIX]{x1D6E5}_{\text{crit}}^{\prime }$
, it persists as
![]() $\unicode[STIX]{x1D702}_{e}\rightarrow 0$
, unlike the others.
$\unicode[STIX]{x1D702}_{e}\rightarrow 0$
, unlike the others.
The calculation in this paper is only strictly valid for a collisionless plasma slab in a sheared magnetic field geometry, as it only ignores possible curvature, collisional and trapped particle effects. However, these are weak in the range of
![]() $x\,(\unicode[STIX]{x1D70C}_{i}<x<\unicode[STIX]{x1D70C}_{i}L_{s}/L_{n})$
that is relevant for the ion dynamics involved in the calculation; it is therefore a meaningful calculation for more general geometries.
$x\,(\unicode[STIX]{x1D70C}_{i}<x<\unicode[STIX]{x1D70C}_{i}L_{s}/L_{n})$
that is relevant for the ion dynamics involved in the calculation; it is therefore a meaningful calculation for more general geometries.
Acknowledgements
This work has been part funded by the RCUK Energy Programme [grant number EP/P012450/1]. To obtain further information on the data and models underlying this paper please contact [email protected].
Appendix A. Derivation of (4.6) for
 $I_{0}(a)$
$I_{0}(a)$
This appendix leans heavily on results concerning the confluent hypergeometric functions, the hypergeometric functions and the parabolic cylinder functions, respectively from chaps 13, 15 and 19 of Abramowitz & Stegun (Reference Abramowitz and Stegun1972).
Firstly
![]() $E(-a,z)$
can be related to the usual parabolic cylinder function
$E(-a,z)$
can be related to the usual parabolic cylinder function
![]() $D_{ia-1/2}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}z)$
, so that
$D_{ia-1/2}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}z)$
, so that
Now
![]() $D_{ia-1/2}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}z)$
itself can be expressed in terms of a confluent hypergeometric function,
$D_{ia-1/2}(\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}z)$
itself can be expressed in terms of a confluent hypergeometric function,
![]() $U$
:
$U$
:
The confluent hypergeometric function,
![]() $U(a,b;x)$
, has an integral representation; using this we can write:
$U(a,b;x)$
, has an integral representation; using this we can write:
 $$\begin{eqnarray}\displaystyle & & \displaystyle U\left(\frac{1}{4}-\frac{\text{i}a}{2},\frac{1}{2};-\frac{\text{i}z^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\text{e}^{-\text{i}z^{2}/2}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\int _{1}^{\infty }\text{d}t\text{e}^{\text{i}tz^{2}/2}(t-1)^{-(\text{i}a/2+3/4)}t^{(\text{i}a/2-3/4)}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle U\left(\frac{1}{4}-\frac{\text{i}a}{2},\frac{1}{2};-\frac{\text{i}z^{2}}{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\text{e}^{-\text{i}z^{2}/2}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\int _{1}^{\infty }\text{d}t\text{e}^{\text{i}tz^{2}/2}(t-1)^{-(\text{i}a/2+3/4)}t^{(\text{i}a/2-3/4)}.\end{eqnarray}$$
This enables one to perform the integration over
![]() $z$
in the numerator of (A 1), which becomes:
$z$
in the numerator of (A 1), which becomes:
 $$\begin{eqnarray}\frac{2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\left(\frac{\unicode[STIX]{x03C0}}{2}\right)^{1/2}\int _{1}^{\infty }\text{d}t(t-1)^{-(\text{i}a/2+3/4)}t^{(\text{i}a/2-3/4)}(t-1/2)^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\left(\frac{\unicode[STIX]{x03C0}}{2}\right)^{1/2}\int _{1}^{\infty }\text{d}t(t-1)^{-(\text{i}a/2+3/4)}t^{(\text{i}a/2-3/4)}(t-1/2)^{-1/2}.\end{eqnarray}$$
Finally, introducing
![]() $u=1/t$
, result (A 4) becomes
$u=1/t$
, result (A 4) becomes
 $$\begin{eqnarray}\frac{2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\left(\frac{\unicode[STIX]{x03C0}}{2}\right)^{1/2}\int _{0}^{1}\text{d}u(1-u)^{-(\text{i}a/2+3/4)}(1-u/2)^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\left(\frac{\unicode[STIX]{x03C0}}{2}\right)^{1/2}\int _{0}^{1}\text{d}u(1-u)^{-(\text{i}a/2+3/4)}(1-u/2)^{-1/2}.\end{eqnarray}$$
Now the hypergeometric function,
![]() $F(a,b;c;x)$
also has an integral representation and one observes
$F(a,b;c;x)$
also has an integral representation and one observes
 $$\begin{eqnarray}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right)=\frac{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)\unicode[STIX]{x1D6E4}(1)}\int _{0}^{1}\text{d}tt^{-(\text{i}a/2+3/4)}(1+t)^{-1/2}\end{eqnarray}$$
$$\begin{eqnarray}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right)=\frac{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)\unicode[STIX]{x1D6E4}(1)}\int _{0}^{1}\text{d}tt^{-(\text{i}a/2+3/4)}(1+t)^{-1/2}\end{eqnarray}$$
so that, on substituting
![]() $t=1-u$
, we obtain
$t=1-u$
, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\sqrt{2}\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)\unicode[STIX]{x1D6E4}(1)}\int _{0}^{1}\text{d}u(1-u)^{-(\text{i}a/2+3/4)}(1-u/2)^{-1/2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\sqrt{2}\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{1}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)\unicode[STIX]{x1D6E4}(1)}\int _{0}^{1}\text{d}u(1-u)^{-(\text{i}a/2+3/4)}(1-u/2)^{-1/2}.\end{eqnarray}$$
Thus, result (A 5) can be rewritten as:
 $$\begin{eqnarray}\frac{\sqrt{\unicode[STIX]{x03C0}}2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\sqrt{\unicode[STIX]{x03C0}}2^{(\text{i}a/2-1/4)}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
Concerning the denominator in (A 1), we have:
 $$\begin{eqnarray}D_{ia-1/2}(0)=\frac{\displaystyle \sqrt{\unicode[STIX]{x03C0}}2^{\left(\text{i}a/2-1/4\right)}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\end{eqnarray}$$
$$\begin{eqnarray}D_{ia-1/2}(0)=\frac{\displaystyle \sqrt{\unicode[STIX]{x03C0}}2^{\left(\text{i}a/2-1/4\right)}}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}\end{eqnarray}$$
so that, finally, on using properties of the gamma function:
 $$\begin{eqnarray}I_{0}(a)=-\frac{2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
$$\begin{eqnarray}I_{0}(a)=-\frac{2\unicode[STIX]{x03C0}\text{e}^{\text{i}\unicode[STIX]{x03C0}/4}a\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}{\unicode[STIX]{x1D6E4}\left({\displaystyle \frac{5}{4}}-{\displaystyle \frac{\text{i}a}{2}}\right)}F\left(\frac{1}{2},\frac{1}{4}-\frac{\text{i}a}{2};\frac{5}{4}-\frac{\text{i}a}{2};-1\right).\end{eqnarray}$$
Appendix B. Derivation of (4.14) for
 $\hat{I} (a)$
$\hat{I} (a)$
We first need to evaluate integral
![]() $\hat{I} (a)$
in (4.13). This is integrable because the two terms in the denominator cancel as
$\hat{I} (a)$
in (4.13). This is integrable because the two terms in the denominator cancel as
![]() $t\rightarrow 0$
. It is convenient to consider it as the difference of the two diverging integrals:
$t\rightarrow 0$
. It is convenient to consider it as the difference of the two diverging integrals:
 $$\begin{eqnarray}\displaystyle \hat{I} (a) & = & \displaystyle \frac{1}{2}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\int _{\unicode[STIX]{x1D6FF}}^{1}\frac{\text{d}t}{t^{3/2}}-\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\frac{1}{2}\int _{\unicode[STIX]{x1D6FF}}^{1}\frac{\text{d}t}{t^{3/2}}(1-t)^{-\text{i}a/2-1/4}(1+t)^{\text{i}a/2-1/4}\nonumber\\ \displaystyle & \equiv & \displaystyle J_{1}(\unicode[STIX]{x1D6FF})-J_{2}(\unicode[STIX]{x1D6FF},a).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{I} (a) & = & \displaystyle \frac{1}{2}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\int _{\unicode[STIX]{x1D6FF}}^{1}\frac{\text{d}t}{t^{3/2}}-\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\frac{1}{2}\int _{\unicode[STIX]{x1D6FF}}^{1}\frac{\text{d}t}{t^{3/2}}(1-t)^{-\text{i}a/2-1/4}(1+t)^{\text{i}a/2-1/4}\nonumber\\ \displaystyle & \equiv & \displaystyle J_{1}(\unicode[STIX]{x1D6FF})-J_{2}(\unicode[STIX]{x1D6FF},a).\end{eqnarray}$$
The first is readily evaluated:
For the second we substitute,
![]() $t=1/(2v+1)$
, to obtain
$t=1/(2v+1)$
, to obtain
where
![]() $z=(1-\unicode[STIX]{x1D6FF})/2\unicode[STIX]{x1D6FF}$
. Now
$z=(1-\unicode[STIX]{x1D6FF})/2\unicode[STIX]{x1D6FF}$
. Now
![]() $J_{2}(\unicode[STIX]{x1D6FF},a)$
can be expressed in terms of the incomplete beta function,
$J_{2}(\unicode[STIX]{x1D6FF},a)$
can be expressed in terms of the incomplete beta function,
![]() $B_{1-2\unicode[STIX]{x1D6FF}}(3/4-\text{i}a/2,-1/2)$
(see §§ 1.5 and 2.53 of Erdelyi Reference Erdelyi1953):
$B_{1-2\unicode[STIX]{x1D6FF}}(3/4-\text{i}a/2,-1/2)$
(see §§ 1.5 and 2.53 of Erdelyi Reference Erdelyi1953):
The incomplete beta function can be expressed in terms of the hypergeometric function,
![]() $F(a,b;c;z)$
(Abramowitz & Stegun Reference Abramowitz and Stegun1972):
$F(a,b;c;z)$
(Abramowitz & Stegun Reference Abramowitz and Stegun1972):
 $$\begin{eqnarray}B_{1-2\unicode[STIX]{x1D6FF}}\left(\frac{3}{4}-\frac{\text{i}a}{2},-\frac{1}{2}\right)=\frac{(1-2\unicode[STIX]{x1D6FF})^{-\text{i}a/2+3/4}}{\displaystyle \left(-\frac{\text{i}a}{2}+\frac{3}{4}\right)}F\left(\frac{3}{4}-\frac{\text{i}a}{2},\frac{3}{2};\frac{7}{4}-\frac{\text{i}a}{2};1-2\unicode[STIX]{x1D6FF}\right).\end{eqnarray}$$
$$\begin{eqnarray}B_{1-2\unicode[STIX]{x1D6FF}}\left(\frac{3}{4}-\frac{\text{i}a}{2},-\frac{1}{2}\right)=\frac{(1-2\unicode[STIX]{x1D6FF})^{-\text{i}a/2+3/4}}{\displaystyle \left(-\frac{\text{i}a}{2}+\frac{3}{4}\right)}F\left(\frac{3}{4}-\frac{\text{i}a}{2},\frac{3}{2};\frac{7}{4}-\frac{\text{i}a}{2};1-2\unicode[STIX]{x1D6FF}\right).\end{eqnarray}$$
A suitable transformation for considering the limit
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
is the relation
$\unicode[STIX]{x1D6FF}\rightarrow 0$
is the relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle F(a,b;c;z)=\frac{\unicode[STIX]{x1D6E4}(c)\unicode[STIX]{x1D6E4}(c-b-a)}{\unicode[STIX]{x1D6E4}(c-a)\unicode[STIX]{x1D6E4}(c-b)}F(a,b;a+b-c+1;1-z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(1-z)^{c-a-b}\frac{\unicode[STIX]{x1D6E4}(c)\unicode[STIX]{x1D6E4}(a+b-c)}{\unicode[STIX]{x1D6E4}(a)\unicode[STIX]{x1D6E4}(b)}F(c-a,c-b;c-a-b+1;1-z),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F(a,b;c;z)=\frac{\unicode[STIX]{x1D6E4}(c)\unicode[STIX]{x1D6E4}(c-b-a)}{\unicode[STIX]{x1D6E4}(c-a)\unicode[STIX]{x1D6E4}(c-b)}F(a,b;a+b-c+1;1-z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,(1-z)^{c-a-b}\frac{\unicode[STIX]{x1D6E4}(c)\unicode[STIX]{x1D6E4}(a+b-c)}{\unicode[STIX]{x1D6E4}(a)\unicode[STIX]{x1D6E4}(b)}F(c-a,c-b;c-a-b+1;1-z),\end{eqnarray}$$
where we can then use the result
(Abramowitz & Stegun Reference Abramowitz and Stegun1972) to take the limit
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. The result is
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. The result is
 $$\begin{eqnarray}J_{2}(\unicode[STIX]{x1D6FF},a)=\frac{1}{\unicode[STIX]{x1D6FF}^{1/2}}-\sqrt{2\unicode[STIX]{x03C0}}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}J_{2}(\unicode[STIX]{x1D6FF},a)=\frac{1}{\unicode[STIX]{x1D6FF}^{1/2}}-\sqrt{2\unicode[STIX]{x03C0}}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$
Combining with the result (B 2), we obtain
 $$\begin{eqnarray}\hat{I} (a)=-1+\sqrt{2\unicode[STIX]{x03C0}}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{I} (a)=-1+\sqrt{2\unicode[STIX]{x03C0}}\frac{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{3}{4}-\frac{\text{i}a}{2}\right)}{\displaystyle \unicode[STIX]{x1D6E4}\left(\frac{1}{4}-\frac{\text{i}a}{2}\right)}.\end{eqnarray}$$
This is the result quoted in (4.14).