We show analytically that for  $\unicode[STIX]{x1D704}$-profiles similar to the one of the Wendelstein 7-X stellarator, where
$\unicode[STIX]{x1D704}$-profiles similar to the one of the Wendelstein 7-X stellarator, where  $\unicode[STIX]{x1D704}$ is the rotational transform of the equilibrium magnetic field, a highly conducting toroidal plasma is unstable to kinetically mediated pressure-driven long-wavelength reconnecting modes, of the infernal type. The modes are destabilized either by the electron temperature gradient or by a small amount of current, depending on how far from unity the average value of
$\unicode[STIX]{x1D704}$ is the rotational transform of the equilibrium magnetic field, a highly conducting toroidal plasma is unstable to kinetically mediated pressure-driven long-wavelength reconnecting modes, of the infernal type. The modes are destabilized either by the electron temperature gradient or by a small amount of current, depending on how far from unity the average value of  $\unicode[STIX]{x1D704}$ is, which is assumed to be slowly varying. We argue that, for W7-X, a broad mode with toroidal and poloidal mode numbers
$\unicode[STIX]{x1D704}$ is, which is assumed to be slowly varying. We argue that, for W7-X, a broad mode with toroidal and poloidal mode numbers 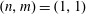 $(n,m)=(1,1)$ can be destabilized due to the strong geometric side-band coupling of the resonant kinetic electron response at locations where
$(n,m)=(1,1)$ can be destabilized due to the strong geometric side-band coupling of the resonant kinetic electron response at locations where  $\unicode[STIX]{x1D704}$ is rational for harmonics that belong to the mode family of the
$\unicode[STIX]{x1D704}$ is rational for harmonics that belong to the mode family of the 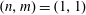 $(n,m)=(1,1)$ mode itself. In many regimes, the growth rate is insensitive to the plasma density, thus it is likely to persist in high performance W7-X discharges. For a peaked electron temperature, with a maximum of
$(n,m)=(1,1)$ mode itself. In many regimes, the growth rate is insensitive to the plasma density, thus it is likely to persist in high performance W7-X discharges. For a peaked electron temperature, with a maximum of 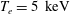 $T_{e}=5~\text{keV}$, larger than the ion temperature,
$T_{e}=5~\text{keV}$, larger than the ion temperature, 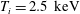 $T_{i}=2.5~\text{keV}$, and a density
$T_{i}=2.5~\text{keV}$, and a density 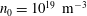 $n_{0}=10^{19}~\text{m}^{-3}$, instability is found in regimes which show plasma sawtooth activity, with growth rates of the order of tens of kiloHertz. Frequencies are either electron diamagnetic or of the ideal magnetohydrodynamic type, but sub-Alfvénic. The kinetic infernal mode is thus a good candidate for the explanation of sawtooth oscillations in present-day stellarators and poses a new challenge to the problem of stellarator reactor optimization.
$n_{0}=10^{19}~\text{m}^{-3}$, instability is found in regimes which show plasma sawtooth activity, with growth rates of the order of tens of kiloHertz. Frequencies are either electron diamagnetic or of the ideal magnetohydrodynamic type, but sub-Alfvénic. The kinetic infernal mode is thus a good candidate for the explanation of sawtooth oscillations in present-day stellarators and poses a new challenge to the problem of stellarator reactor optimization.
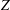 $Z$ impurities with the new impurity version of XGCa
$Z$ impurities with the new impurity version of XGCa
 $\unicode[STIX]{x1D704}$-profiles
$\unicode[STIX]{x1D704}$-profiles