The combined roughness/Reynolds number problem is explored. Existing and newly acquired data from zero pressure gradient rough-wall turbulent boundary layers are used to clarify the leading order balances of terms in the mean dynamical equation. For the variety of roughnesses examined, it is revealed that the mean viscous force retains dominant order above (and often well above) the roughness crests. Mean force balance data are shown to be usefully organized relative to the characteristic length scale, which is equal or proportional to the width of the region from the wall to where the leading order mean dynamics become described by a balance between the mean and turbulent inertia. This is equivalently the width of the region from the wall to where the mean viscous force loses leading order. For both smooth-wall and rough-wall flows, the wall-normal extent of this region consistently ends just beyond the zero-crossing of the turbulent inertia term. In smooth-wall flow this characteristic length is a known function of Reynolds number. The present analyses indicate that for rough-wall flows the wall-normal position where the mean dynamics become inertial is an irreducible function of roughness and Reynolds number, as it is an inherent function of the relative scale separations between the inner, roughness, and outer lengths. These findings indicate that, for any given roughness, new dynamical regimes will typically emerge as the Reynolds number increases. For the present range of parameters, there appear to be three identifiable regimes. These correspond to the ratio of the equivalent sand grain roughness to the characteristic length being less than, equal to, or greater than 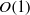 $O(1)$. The relative influences of the inner, outer, and roughness length scales on the characteristic length are explored empirically. A prediction for the decay rate of the mean vorticity is developed via extension of the smooth-wall theory. Existing data are shown to exhibit good agreement with this extension. Overall, the present results appear to expose unifying connections between the structure of smooth- and rough-wall flows. Among other findings, the present analyses show promise toward providing a self-consistent and dynamically meaningful way of identifying the domain where the wall similarity hypothesis, if operative, should hold.
$O(1)$. The relative influences of the inner, outer, and roughness length scales on the characteristic length are explored empirically. A prediction for the decay rate of the mean vorticity is developed via extension of the smooth-wall theory. Existing data are shown to exhibit good agreement with this extension. Overall, the present results appear to expose unifying connections between the structure of smooth- and rough-wall flows. Among other findings, the present analyses show promise toward providing a self-consistent and dynamically meaningful way of identifying the domain where the wall similarity hypothesis, if operative, should hold.