Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-09T05:19:31.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditional statistics of the turbulent/non-turbulent interface in a jet flow

Published online by Cambridge University Press:  29 August 2013

Markus Gampert ,
Venkat Narayanaswamy ,
Philip Schaefer  and
Norbert Peters
Markus Gampert
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
Venkat Narayanaswamy
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
Philip Schaefer
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
Norbert Peters*
Affiliation:
Institute for Combustion Technology, RWTH-Aachen University, Templergraben 64, Aachen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using two-dimensional high-speed measurements of the mixture fraction 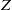$Z$ in a turbulent round jet with nozzle-based Reynolds numbers 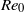$R{e}_{0} $ between 3000 and 18 440, we investigate the scalar turbulent/non-turbulent (T/NT) interface of the flow. The mixture fraction steeply changes from 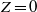$Z= 0$ to a final value which is typically larger than 0.1. Since combustion occurs in the vicinity of the stoichiometric mixture fraction, which is around 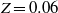$Z= 0. 06$ for typical fuel/air mixtures, it is expected to take place largely within the turbulent/non-turbulent interface. Therefore, deep understanding of this part of the flow is essential for an accurate modelling of turbulent non-premixed combustion. To this end, we use a composite model developed by Effelsberg & Peters (Combust. Flame, vol. 50, 1983, pp. 351–360) for the probability density function (p.d.f.) 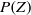$P(Z)$ which takes into account the different contributions from the fully turbulent as well as the turbulent/non-turbulent interface part of the flow. A very good agreement between the measurements and the model is observed over a wide range of axial and radial locations as well as at varying intermittency factor 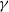$\gamma $ and shear. Furthermore, we observe a constant mean mixture fraction value in the fully turbulent region. The p.d.f. of this region is thus of non-marching character, which is attributed physically to the meandering nature of the fully turbulent core of the jet flow. Finally, the location and in particular the scaling of the thickness 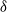$\delta $ of the scalar turbulent/non-turbulent interface are investigated. We provide the first experimental results for the thickness of the interface over the above-mentioned Reynolds number range and observe 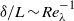$\delta / L\sim R{ e}_{\lambda }^{- 1} $, where 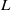$L$ is an integral length scale and 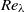$R{e}_{\lambda } $ the local Reynolds number based on the Taylor scale 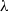$\lambda $, meaning that 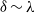$\delta \sim \lambda $. This result also supports the assumption often made in modelling of the stoichiometric scalar dissipation rate 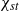${\chi }_{st} $ being a Reynolds-number-independent quantity.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 615 - 638
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexopoulos, C. C. & Keffer, J. F. 1971 Turbulent wake in a passively stratified field. Phys. Fluids 14, 216–224.CrossRefGoogle Scholar
Bilger, R. W. 1976 The structure of diffusion flames. Combust. Sci. Technol. 13, 155–170.CrossRefGoogle Scholar
Bilger, R. W. 1980 Turbulent flows with nonpremixed reactants. In Turbulent Reacting Flow (ed. Libby, P. A. & Williams, F. A.), pp. 65–111. Academic.CrossRefGoogle Scholar
Bisset, D., Hunt, J. & Rogers, M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.Google Scholar
Broadwell, J. E. & Breidenthal, R. E. 1982 A simple model for mixing and chemical reaction in a turbulent shear layer. J. Fluid Mech. 125, 397–410.Google Scholar
Brown, G. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Cannon, S., Champagne, E. & Glezer, A. 1993 Observations of large-scale structures in wakes behind axisymmetric bodies. Exp. Fluids 14, 447–450.Google Scholar
Corrsin, S. & Kistler, A. L. 1955 Free-stream boundaries of turbulent flows. NACA Rep. 1244.Google Scholar
Dimotakis, P. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Dimotakis, P., Miake-Lye, R. & Papantoniou, D. A. 1983 Structure and dynamics of round turbulent jets. Phys. Fluids 26, 3185–3192.CrossRefGoogle Scholar
Eckbreth, A. 1996 Laser Diagnostics for Combustion Temperature and Species, 2nd edn. Informa Healthcare.Google Scholar
Effelsberg, E. & Peters, N. 1983 A composite model for the conserved scalar pdf. Combust. Flame 50, 351–360.CrossRefGoogle Scholar
Fox, R. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.Google Scholar
Frank, J. & Kaiser, S. 2005 Multiscalar imaging in partially premixed jet flames with argon dilution. Combust. Flame 143, 507–523.Google Scholar
Frank, J., Kaiser, S. & Long, M. 2002 Reaction-rate, mixture-fraction, and temperature imaging in turbulent methane/air jet flames. Proc. Combust. Inst. 29, 2687–2694.CrossRefGoogle Scholar
Gampert, M., Schaefer, P., Narayanaswamy, V. & Peters, N. 2013a Gradient trajectory analysis in a jet flow for turbulent combustion modelling. J. Turbul. 14, 147–164.Google Scholar
Gampert, M., Schaefer, P. & Peters, N. 2013b Experimental investigation of dissipation element statistics in scalar fields of a jet flow. J. Fluid Mech. 724, 337–366.Google Scholar
Girimaji, S. 1991 Assumed $\beta $ -pdf model for turbulent mixing: validation and extension to multiple scalar mixing. Combust. Sci. Technol. 78, 177.Google Scholar
Goldin, G. M. & Menon, S. 1998 A comparison of scalar pdf turbulent combustion models. Combust. Flame 113 (3), 442–453.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007a Small-scale aspects of flows in proximity of the turbulent/non-turbulent interface. Phys. Fluids 19 (7), 071702.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Lüthi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small scale features of turbulent entrainment through 3D-PTV and DNS. J. Fluid Mech. 598, 465–475.Google Scholar
Holzner, M., Luethi, B., Tsinober, A. & Kinzelbach, W. 2007b Acceleration, pressure and related quantities in the proximity of the turbulent/non-turbulent interface. J. Fluid Mech. 639, 153–165.CrossRefGoogle Scholar
Hunt, J., Eames, I., da Silva, C. & Westerweel, J. 2011 Interfaces and inhomogeneous turbulence. Phil. Trans. R. Soc. Lond. A 369, 811–832.Google Scholar
Hussain, A. & Clark, A. 1981 On the coherent structure of the axisymmetric mixing layer: a flow-visualization study. J. Fluid Mech. 104, 263–294.Google Scholar
Jiang, N., Patton, R., Lempert, W. & Sutton, J. 2011 Development of high-repetition rate ch plif imaging in turbulent nonpremixed flames. Proc. Combust. 33, 767–774.CrossRefGoogle Scholar
Karasso, P. S. & Mungal, M. G. 1996 Scalar mixing and reaction in plane liquid shear layers. J. Fluid Mech. 323, 23–63.Google Scholar
Karpetis, A. & Barlow, R. 2002 Measurements of scalar dissipation in a turbulent piloted methane/air jet flame. Proc. Combust. Inst. 29, 1929–1936.Google Scholar
Kline, S., Reynolds, W., Schraub, F. & Runstadler, P. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Kollman, W. & Janicka, J. 1982 The probability density function of a passive scalar in turbulent shear flows. Phys. Fluids 25, 1755–1769.Google Scholar
Lau, J., Morris, P. & Fisher, M. 1979 Measurements in subsonic and supersonic free jets using a laser velocimeter. J. Fluid Mech. 93, 1–27.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Lin, C. & O’Brien, E. 1974 Turbulent shear flow mixing and rapid chemical reaction: an analogy. J. Fluid Mech. 64, 195–206.Google Scholar
Marusic, I. & Adrian, R. A. 2013 The eddies and scales of wall turbulence. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.). Cambridge University Press.Google Scholar
Mathew, J. & Basu, A. 2002 Some characteristics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14, 2065–2072.Google Scholar
Peters, N. 1983 On the role of quasi-one-dimensional dissipation layers in turbulent scalar mixing. Combust. Sci. Technol. 30, 1–17.CrossRefGoogle Scholar
Peters, N. 1984 Laminar diffusion flamelet models in non-premixed turbulent combustion. Prog. Energy Combust. Sci. 10, 319–339.CrossRefGoogle Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.Google Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24 (5), 055108.Google Scholar
Pitsch, H. 1996 Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 38, 453–482.CrossRefGoogle Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prasad, R. R. & Sreenivasan, K. R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7, 259–264.Google Scholar
da Silva, C. B. & Pereira, J. C. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.Google Scholar
da Silva, C. B. & Pereira, J. C. 2011 The role of coherent vortices near the turbulent/non-turbulent interface in a planar jet. Phil. Trans. R. Soc. Lond. A 369, 738–753.Google Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Talbot, B., Mazellier, N., Renou, B., Danaila, L. & Boukhalfa, M. 2009 Time-resolved velocity and concentration measurements in variable-viscosity turbulent jet flow. Exp. Fluids 47, 769–787.Google Scholar
Townsend, A. A. 1948 Local isotropy in the turbulent wake of a cylinder. Austral. J. Sci. Res. A 1, 161–174.Google Scholar
Townsend, A. A. 1949 The fully developed turbulent wake of a circular cylinder. Austral. J. Sci. Res. A 2, 451–468.Google Scholar
Wang, G., Barlow, R. & Karpetis, A. 2007 Dissipation length scales in turbulent non-premixed jet flames. Combust. Flame 148, 62–75.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. 2005 Mechanics of the turbulent nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. & Hunt, J. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33, 873–878.CrossRefGoogle Scholar
Westerweel, J., Petracci, A., Delfos, R. & Hunt, J. 2011 Characteristics of the turbulent/non-turbulent interface of a non-isothermal jet. Phil. Trans. R. Soc. Lond. A 369, 723–737.Google Scholar
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38, 577–612.CrossRefGoogle Scholar
Yoda, M., Hesselink, L. & Mungal, M. G. 1994 Instantaneous three-dimensional concentration measurements in the self-similar region of a round high-Schmidt-number jet. J. Fluid Mech. 279, 313–350.CrossRefGoogle Scholar