Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-07T09:48:28.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental verification of power-law non-Newtonian axisymmetric porous gravity currents

Published online by Cambridge University Press:  20 August 2013

Sandro Longo ,
Vittorio Di Federico ,
Luca Chiapponi  and
Renata Archetti
Sandro Longo*
Affiliation:
Dipartimento di Ingegneria Civile, Ambiente Territorio e Architettura (DICATeA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
Vittorio Di Federico
Affiliation:
Dipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Università di Bologna, Viale Risorgimento, 2, 40136 Bologna, Italy
Luca Chiapponi
Affiliation:
Dipartimento di Ingegneria Civile, Ambiente Territorio e Architettura (DICATeA), Università di Parma, Parco Area delle Scienze, 181/A, 43124 Parma, Italy
Renata Archetti
Affiliation:
Dipartimento di Ingegneria Civile, Chimica, Ambientale e dei Materiali (DICAM), Università di Bologna, Viale Risorgimento, 2, 40136 Bologna, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

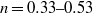We present a theoretical and experimental analysis of axisymmetric gravity currents of power-law fluids in homogeneous porous media. The non-Newtonian shear-thinning fluid is a mixture of water, glycerol and Xanthan gum ($n= 0. 33{\unicode{x2013}} 0. 53$), and it is injected into a porous layer of glass beads (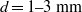$d= 1{\unicode{x2013}} 3~\mathrm{mm} $). We compare experiments conducted with constant (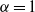$\alpha = 1$) and time-increasing (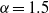$\alpha = 1. 5$ and 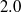$2. 0$) influxes to theoretical self-similar solutions obtained by the numerical integration of the nonlinear ordinary differential equation that describes one-dimensional transient motion. The theoretical analysis is confirmed by experimental data. In addition, the selection of the most appropriate expression for the tortuosity factor and the choice of the correct range of shear stress for the determination of the rheological parameters are shown to be crucial to obtaining a good fit between the theory and experiments.

JFM classification

Geophysical and Geological Flows: Gravity currents Non-Newtonian Flows: Non-Newtonian Flows Low-Reynolds-number flows: Porous media
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , R2
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bataller, R. C. 2008 On unsteady gravity flows of a power-law fluid through a porous medium. Appl. Maths Comput. 196, 356–362.Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2002 Transport Phenomena. John Wiley & Sons.Google Scholar
Chertock, A. 2002 On the stability of a class of self-similar solutions to the filtration-absorption equation. Eur. J. Appl. Maths 13, 179–194.Google Scholar
Dhrmadhikari, R. V. & Kale, D. D. 1985 Flow of non-Newtonian fluids through porous media. Chem. Engng Sci. 40, 527–529.Google Scholar
Di Federico, V., Archetti, R. & Longo, S. 2012 Spreading of axisymmetric non-newtonian power-law gravity currents in porous media. J. Non-Newtonian Fluid Mech. 189–190, 31–39.CrossRefGoogle Scholar
Escudier, M. P., Gouldson, I. W., Pereira, A. S., Pinho, F. T. & Poole, R. J. 2001 On the reproducibility of the rheology of shear-thinning liquids. J. Non-Newtonian Fluid Mech. 97, 99–124.Google Scholar
Helmreich, A., Vorwerk, J., Steger, R., Muller, M. & Bruun, P. O. 1995 Non-viscous effects in the flow of xanthan gum solutions through a oacked bed of spheres. Chem. Engng J. 59, 111–119.Google Scholar
Huppert, H. E. 1986 The intrusion of fluid mechanics into geology. J. Fluid Mech. 173, 557–598.Google Scholar
Kemblowski, Z. & Michniewicz, M. 1979 A new look at the laminar flow of power-law fluids through granular beds. Rheol. Acta 18, 730–739.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickle, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
Pascal, H. 1983 Nonsteady flow of non-Newtonian fluids through a porous medium. Intl J. Engng Sci. 21, 199–210.Google Scholar
Pascal, J. P. & Pascal, H. 1993 Similarity solutions to gravity flows of non-Newtonian fluids through porous media. Intl J. Non-Linear Mech. 28 (2), 157–167.Google Scholar
Savins, J. G. 1969 Non-Newtonian flow through porous media. Ind. Engng Chem. 61, 18–47.Google Scholar
Sayag, R. & Worster, M. G. 2013 Axisymmetric gravity currents of power-law fluids over a rigid horizontal surface. J. Fluid Mech. 716, R5–1–11.Google Scholar
Shenoy, A. V. 1995 Non-Newtonian fluid heat transfer in porous media. Adv. Heat Transfer 24, 102–190.Google Scholar
Simpson, J. E. 1982 Gravity currents in the laboratory, atmosphere, and ocean. Annu. Rev. Fluid Mech. 14, 213–234.Google Scholar
Smith, W. O., Foote, P. D. & Busang, P. F. 1930 Capillary retention of liquid in assemblages of homogeneous spheres. Phys. Rev. 36, 524–530.Google Scholar
Ungarish, M. 2010 An Introduction to Gravity Currents and Intrusions. CRC.Google Scholar
Whitcomb, P. J. & Macosko, C. W. 1978 Rheology of xanthan gum. J. Rheol. 22, 493–505.Google Scholar
Supplementary material: PDF

Longo et al. supplementary material

Supplementary figures

Download Longo et al. supplementary material(PDF)
PDF 4.8 MB

Longo et al. supplementary movie

Video #1: Test #8. Axisymmetric gravity current in porous medium. Intruding fluid: non-Newtonian shear-thinning fluid; ambient fluid: air; skeleton: glass beads d = 1.0 mm. Constant influx (α = 1.0) (duration 51’’).

Download Longo et al. supplementary movie(Video)
Video 7.1 MB

Longo et al. supplementary movie

Video #2: Test #12. Axisymmetric gravity current in porous medium. Intruding fluid: non-Newtonian shear-thinning fluid; ambient fluid: air; skeleton: glass beads d = 2.0 mm. Time increasing influx (α = 2) (duration 48’’).

Download Longo et al. supplementary movie(Video)
Video 7.3 MB