We prove a higher genus version of the genus 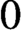 0 local-relative correspondence of van Garrel-Graber-Ruddat: for
0 local-relative correspondence of van Garrel-Graber-Ruddat: for 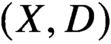 (X,D) a pair with X a smooth projective variety and D a nef smooth divisor, maximal contact Gromov-Witten theory of
(X,D) a pair with X a smooth projective variety and D a nef smooth divisor, maximal contact Gromov-Witten theory of 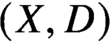 (X,D) with
(X,D) with 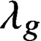 \lambda _g-insertion is related to Gromov-Witten theory of the total space of
\lambda _g-insertion is related to Gromov-Witten theory of the total space of 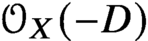 {\mathcal O}_X(-D) and local Gromov-Witten theory of D.
{\mathcal O}_X(-D) and local Gromov-Witten theory of D.
Specializing to
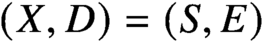 (X,D)=(S,E) for S a del Pezzo surface or a rational elliptic surface and E a smooth anticanonical divisor, we show that maximal contact Gromov-Witten theory of
(X,D)=(S,E) for S a del Pezzo surface or a rational elliptic surface and E a smooth anticanonical divisor, we show that maximal contact Gromov-Witten theory of 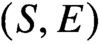 (S,E) is determined by the Gromov-Witten theory of the Calabi-Yau 3-fold
(S,E) is determined by the Gromov-Witten theory of the Calabi-Yau 3-fold 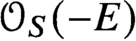 {\mathcal O}_S(-E) and the stationary Gromov-Witten theory of the elliptic curve E.
{\mathcal O}_S(-E) and the stationary Gromov-Witten theory of the elliptic curve E.
Specializing further to 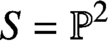 S={\mathbb P}^2, we prove that higher genus generating series of maximal contact Gromov-Witten invariants of
S={\mathbb P}^2, we prove that higher genus generating series of maximal contact Gromov-Witten invariants of 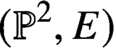 ({\mathbb P}^2,E) are quasimodular and satisfy a holomorphic anomaly equation. The proof combines the quasimodularity results and the holomorphic anomaly equations previously known for local
({\mathbb P}^2,E) are quasimodular and satisfy a holomorphic anomaly equation. The proof combines the quasimodularity results and the holomorphic anomaly equations previously known for local 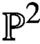 {\mathbb P}^2 and the elliptic curve.
{\mathbb P}^2 and the elliptic curve.
Furthermore, using the connection between maximal contact Gromov-Witten invariants of 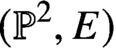 ({\mathbb P}^2,E) and Betti numbers of moduli spaces of semistable one-dimensional sheaves on
({\mathbb P}^2,E) and Betti numbers of moduli spaces of semistable one-dimensional sheaves on 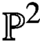 {\mathbb P}^2, we obtain a proof of the quasimodularity and holomorphic anomaly equation predicted in the physics literature for the refined topological string free energy of local
{\mathbb P}^2, we obtain a proof of the quasimodularity and holomorphic anomaly equation predicted in the physics literature for the refined topological string free energy of local 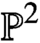 {\mathbb P}^2 in the Nekrasov-Shatashvili limit.
{\mathbb P}^2 in the Nekrasov-Shatashvili limit.