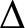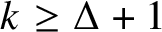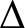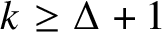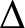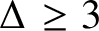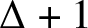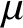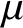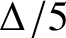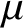1 Introduction
1.1 Hajnal–Szemerédi theorem for Borel graphs
Let G be a (simple undirected) graph with vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $E(G)$
. For a vertex
$E(G)$
. For a vertex
![]() $x \in V(G)$
, we denote the neighbourhood of x in G by
$x \in V(G)$
, we denote the neighbourhood of x in G by
![]() $N_G(x)$
and write
$N_G(x)$
and write
![]() $\deg _G(x) := \lvert N_G(x)\rvert $
for the degree of x in G. The maximum degree of G, denoted by
$\deg _G(x) := \lvert N_G(x)\rvert $
for the degree of x in G. The maximum degree of G, denoted by
![]() $\Delta (G)$
, is defined by
$\Delta (G)$
, is defined by
![]() $\Delta (G) := \mathop {\mathrm {sup}}\nolimits _{x \in V(G)} \deg _G(x)$
.
$\Delta (G) := \mathop {\mathrm {sup}}\nolimits _{x \in V(G)} \deg _G(x)$
.
Given a set
![]() $\mathcal {C}$
, a
$\mathcal {C}$
, a
![]() $\mathcal {C}$
-colouring of G is simply a mapping
$\mathcal {C}$
-colouring of G is simply a mapping
![]() $f \colon V(G) \to \mathcal {C}$
; in this context we call the elements of
$f \colon V(G) \to \mathcal {C}$
; in this context we call the elements of
![]() $\mathcal {C}$
colours. A
$\mathcal {C}$
colours. A
![]() $\mathcal {C}$
-colouring f is proper if
$\mathcal {C}$
-colouring f is proper if
![]() $f(x) \neq f(y)$
whenever x and y are adjacent in G. We will be mostly interested in the case when
$f(x) \neq f(y)$
whenever x and y are adjacent in G. We will be mostly interested in the case when
![]() $\mathcal {C}$
is finite. With a slight abuse of terminology, we refer to
$\mathcal {C}$
is finite. With a slight abuse of terminology, we refer to
![]() $\mathcal {C}$
-colourings with a fixed finite set
$\mathcal {C}$
-colourings with a fixed finite set
![]() $\mathcal {C}$
of size k, say
$\mathcal {C}$
of size k, say
![]() $\left \{1, \dotsc , k\right \}$
, as k-colourings. Here and throughout the paper, k denotes a positive integer.
$\left \{1, \dotsc , k\right \}$
, as k-colourings. Here and throughout the paper, k denotes a positive integer.
Given a
![]() $\mathcal {C}$
-colouring f, we refer to the sets
$\mathcal {C}$
-colouring f, we refer to the sets
![]() $f^{-1}(\alpha )$
for
$f^{-1}(\alpha )$
for
![]() $\alpha \in \mathcal {C}$
as the colour classes of f. A proper
$\alpha \in \mathcal {C}$
as the colour classes of f. A proper
![]() $\mathcal {C}$
-colouring of a finite graph G is equitable if every two colour classes of f differ in size by at most
$\mathcal {C}$
-colouring of a finite graph G is equitable if every two colour classes of f differ in size by at most
![]() $1$
. In particular, if
$1$
. In particular, if
![]() $\lvert V(G)\rvert $
is divisible by
$\lvert V(G)\rvert $
is divisible by
![]() $k \geq 1$
, then in an equitable k-colouring of G all colour classes must be of size precisely
$k \geq 1$
, then in an equitable k-colouring of G all colour classes must be of size precisely
![]() $\lvert V(G)\rvert /k$
. In contrast to ordinary colouring, a graph with an equitable k-colouring need not have an equitable
$\lvert V(G)\rvert /k$
. In contrast to ordinary colouring, a graph with an equitable k-colouring need not have an equitable
![]() $(k+1)$
-colouring. Nevertheless, Erdős [Reference Erdős and FiedlerErd64] conjectured that every finite graph of maximum degree
$(k+1)$
-colouring. Nevertheless, Erdős [Reference Erdős and FiedlerErd64] conjectured that every finite graph of maximum degree
![]() $\Delta $
has an equitable k-colouring for each
$\Delta $
has an equitable k-colouring for each
![]() $k \geq \Delta +1$
. Erdős’s conjecture was confirmed by Hajnal and Szemerédi:
$k \geq \Delta +1$
. Erdős’s conjecture was confirmed by Hajnal and Szemerédi:
Theorem 1.1 Hajnal–Szemerédi [Reference Hajnal, Szemerédi, Erdős, Rényi and SósHS70]
Let G be a finite graph of maximum degree
![]() $\Delta $
. If
$\Delta $
. If
![]() $k \geq \Delta +1$
, then G has an equitable k-colouring.
$k \geq \Delta +1$
, then G has an equitable k-colouring.
The original proof of Theorem 1.1 due to Hajnal and Szemerédi was surprisingly difficult, but it was significantly simplified by Mydlarz and Szemerédi (unpublished; see [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10]) and Kierstead and Kostochka [Reference Kierstead and KostochkaKK08], culminating in a two-page proof. Moreover, their argument provides an efficient algorithm that builds a desired equitable colouring [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10].
The central result of this paper is an extension of Theorem 1.1 to equitable colourings of infinite graphs. Specifically, if G is a graph whose vertex set
![]() $V(G)$
carries a probability measure, then it is natural to call a proper k-colouring f of G equitable if every colour class of f has measure
$V(G)$
carries a probability measure, then it is natural to call a proper k-colouring f of G equitable if every colour class of f has measure
![]() $1/k$
. Notice that for this definition to be sensible, we must require that every colour class of f be a measurable subset of
$1/k$
. Notice that for this definition to be sensible, we must require that every colour class of f be a measurable subset of
![]() $V(G)$
. Questions regarding the behavior of colourings, matchings and other combinatorial constructions under extra measurability constraints are studied in the area of descriptive combinatorics, which has attracted considerable attention in recent years; see [Reference Kechris and MarksKM16] for a comprehensive survey.
$V(G)$
. Questions regarding the behavior of colourings, matchings and other combinatorial constructions under extra measurability constraints are studied in the area of descriptive combinatorics, which has attracted considerable attention in recent years; see [Reference Kechris and MarksKM16] for a comprehensive survey.
Before stating our results, we need to introduce some relevant terminology. Our main references for descriptive set theory are [Reference KechrisKec95, Reference TserunyanTse16]. By a Borel graph we mean a graph G whose vertex set
![]() $V(G)$
is a standard Borel space and whose edge set
$V(G)$
is a standard Borel space and whose edge set
![]() $E(G)$
is a Borel subset of
$E(G)$
is a Borel subset of
![]() $V(G) \times V(G)$
. If G is a Borel graph and
$V(G) \times V(G)$
. If G is a Borel graph and
![]() $\mathcal {C}$
is a standard Borel space, then a
$\mathcal {C}$
is a standard Borel space, then a
![]() $\mathcal {C}$
-colouring
$\mathcal {C}$
-colouring
![]() $f \colon V(G) \to \mathcal {C}$
is Borel if it is a Borel function – that is, if preimages of Borel subsets of
$f \colon V(G) \to \mathcal {C}$
is Borel if it is a Borel function – that is, if preimages of Borel subsets of
![]() $\mathcal {C}$
under f are Borel in
$\mathcal {C}$
under f are Borel in
![]() $V(G)$
. When
$V(G)$
. When
![]() $\mathcal {C}$
is countable, this is equivalent to saying that every colour class of f is a Borel subset of
$\mathcal {C}$
is countable, this is equivalent to saying that every colour class of f is a Borel subset of
![]() $V(G)$
. The smallest cardinality of a standard Borel space
$V(G)$
. The smallest cardinality of a standard Borel space
![]() $\mathcal {C}$
such that G admits a Borel proper
$\mathcal {C}$
such that G admits a Borel proper
![]() $\mathcal {C}$
-colouring is called the Borel chromatic number of G and is denoted by
$\mathcal {C}$
-colouring is called the Borel chromatic number of G and is denoted by
![]() $\chi _{\mathrm {B}}(G)$
. Similarly, given a probability measure
$\chi _{\mathrm {B}}(G)$
. Similarly, given a probability measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
, we can talk about
$V(G)$
, we can talk about
![]() $\mu $
-measurable colourings
$\mu $
-measurable colourings
![]() $f \colon V(G) \to \mathcal {C}$
(i.e., such that f-preimages of Borel subsets of
$f \colon V(G) \to \mathcal {C}$
(i.e., such that f-preimages of Borel subsets of
![]() $\mathcal {C}$
are
$\mathcal {C}$
are
![]() $\mu $
-measurable) and define the
$\mu $
-measurable) and define the
![]() $\mu $
-measurable chromatic number
$\mu $
-measurable chromatic number
![]() $\chi _\mu (G)$
of G as the smallest cardinality of a standard Borel space
$\chi _\mu (G)$
of G as the smallest cardinality of a standard Borel space
![]() $\mathcal {C}$
such that G admits a
$\mathcal {C}$
such that G admits a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\mathcal {C}$
-colouring. Borel chromatic numbers were first introduced and systematically studied by Kechris, Solecki and Todorcevic in their seminal paper [Reference Kechris, Solecki and TodorcevicKST99]. Among several other results, they established the following fact:
$\mathcal {C}$
-colouring. Borel chromatic numbers were first introduced and systematically studied by Kechris, Solecki and Todorcevic in their seminal paper [Reference Kechris, Solecki and TodorcevicKST99]. Among several other results, they established the following fact:
Theorem 1.2 Kechris–Solecki–Todorcevic [Reference Kechris, Solecki and TodorcevicKST99, Proposition 4.6]
Let G be a Borel graph of finite maximum degree
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $\chi _{\mathrm {B}}(G) \leq \Delta +1$
.
$\chi _{\mathrm {B}}(G) \leq \Delta +1$
.
In view of Theorem 1.2, it is meaningful to ask for Borel
![]() $(\Delta +1)$
-colourings with extra properties (such as being equitable). We remark that according to a startling result of Marks [Reference MarksMar16], the upper bound
$(\Delta +1)$
-colourings with extra properties (such as being equitable). We remark that according to a startling result of Marks [Reference MarksMar16], the upper bound
![]() $\chi _{\mathrm {B}}(G) \leq \Delta + 1$
is sharp, even for acyclic graphs G.
$\chi _{\mathrm {B}}(G) \leq \Delta + 1$
is sharp, even for acyclic graphs G.
Definition 1.1. Let G be a Borel graph and let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $V(G)$
. A
$V(G)$
. A
![]() $\mu $
-equitable k-colouring of G is a
$\mu $
-equitable k-colouring of G is a
![]() $\mu $
-measurable proper k-colouring f of G such that
$\mu $
-measurable proper k-colouring f of G such that
![]() $\mu \left (f^{-1}(\alpha )\right ) = 1/k$
for every colour
$\mu \left (f^{-1}(\alpha )\right ) = 1/k$
for every colour
![]() $\alpha $
.
$\alpha $
.
Just as the definition of equitable colouring for finite graphs uses the (normalised) counting measure on
![]() $V(G)$
, Definition 1.1 is most natural for measures
$V(G)$
, Definition 1.1 is most natural for measures
![]() $\mu $
that ‘assign the same weight’ to every vertex of G. Formally, let
$\mu $
that ‘assign the same weight’ to every vertex of G. Formally, let
![]() $[\![ G ]\!]$
denote the Borel full semigroup of G – that is, the set of all Borel bijections
$[\![ G ]\!]$
denote the Borel full semigroup of G – that is, the set of all Borel bijections
![]() $\varphi \colon A \to B$
, where A and B are Borel subsets of
$\varphi \colon A \to B$
, where A and B are Borel subsets of
![]() $V(G)$
, such that for all
$V(G)$
, such that for all
![]() $x \in A$
,
$x \in A$
,
![]() $\varphi (x)$
and x are joined by a path in G. We say that Borel subsets A,
$\varphi (x)$
and x are joined by a path in G. We say that Borel subsets A,
![]() $B \subseteq V(G)$
are G-equidecomposable – in symbols,
$B \subseteq V(G)$
are G-equidecomposable – in symbols,
![]() $A \approx _G B$
– if there is
$A \approx _G B$
– if there is
![]() $\varphi \in [\![ G ]\!]$
with
$\varphi \in [\![ G ]\!]$
with
![]() $\mathrm {dom}(\varphi ) = A$
and
$\mathrm {dom}(\varphi ) = A$
and
![]() $\mathrm {im}(\varphi ) = B$
. A probability measure
$\mathrm {im}(\varphi ) = B$
. A probability measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
is said to be G-invariant if
$V(G)$
is said to be G-invariant if
![]() $\mu (A) = \mu (B)$
whenever
$\mu (A) = \mu (B)$
whenever
![]() $A \approx _G B$
. When the maximum degree of G is finite, this is equivalent to the following ‘double-counting’ identity:
$A \approx _G B$
. When the maximum degree of G is finite, this is equivalent to the following ‘double-counting’ identity:
 $$ \begin{align*} \int_A \lvert N_G(x) \cap B\rvert \mathrm{d}\mu(x) = \int_B \lvert N_G(y) \cap A\rvert \mathrm{d} \mu(y), \qquad \text{for all Borel } A, B \subseteq V(G). \end{align*} $$
$$ \begin{align*} \int_A \lvert N_G(x) \cap B\rvert \mathrm{d}\mu(x) = \int_B \lvert N_G(y) \cap A\rvert \mathrm{d} \mu(y), \qquad \text{for all Borel } A, B \subseteq V(G). \end{align*} $$
Definition 1.2. Let G be a Borel graph. A Borel-equitable k-colouring of G is a Borel proper k-colouring f of G such that
![]() $f^{-1}(\alpha ) \approx _G f^{-1}(\beta )$
for every pair of colours
$f^{-1}(\alpha ) \approx _G f^{-1}(\beta )$
for every pair of colours
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
.
$\beta $
.
It follows immediately that a Borel-equitable k-colouring of G is
![]() $\mu $
-equitable with respect to every G-invariant probability measure
$\mu $
-equitable with respect to every G-invariant probability measure
![]() $\mu $
.
$\mu $
.
We prove a version of Theorem 1.1 for Borel-equitable colourings. In order to avoid divisibility issues and thus make the statement simpler, we shall focus on aperiodic graphs – that is, those in which every connected component is infinite. However, the extension to graphs with finite components is straightforward; see, e.g., Lemma 5.1.
Theorem 1.3 Borel Hajnal–Szemerédi
Let G be an aperiodic Borel graph of finite maximum degree
![]() $\Delta $
. If
$\Delta $
. If
![]() $k \geq \Delta + 1$
, then G has a Borel-equitable k-colouring.
$k \geq \Delta + 1$
, then G has a Borel-equitable k-colouring.
Additionally, we show that if a given colouring f is ‘approximately equitable’, then f is actually ‘close’ to an equitable colouring. To make this precise, we need a couple more definitions. A subset
![]() $A \subseteq V(G)$
is G-invariant if it is a union of connected components of G – that is, if no edge of G joins a vertex in A to a vertex in
$A \subseteq V(G)$
is G-invariant if it is a union of connected components of G – that is, if no edge of G joins a vertex in A to a vertex in
![]() $V(G) \setminus A$
. A G-invariant measure
$V(G) \setminus A$
. A G-invariant measure
![]() $\mu $
is G-ergodic (or simply ergodic, if G is clear from the context) if every G-invariant Borel subset of
$\mu $
is G-ergodic (or simply ergodic, if G is clear from the context) if every G-invariant Borel subset of
![]() $V(G)$
is either
$V(G)$
is either
![]() $\mu $
-null or
$\mu $
-null or
![]() $\mu $
-conull. Every G-invariant probability measure can be decomposed as a convex combination of ergodic measures; see Theorem 2.4 for a precise statement of this fact. Now, fix a nonempty finite colour set
$\mu $
-conull. Every G-invariant probability measure can be decomposed as a convex combination of ergodic measures; see Theorem 2.4 for a precise statement of this fact. Now, fix a nonempty finite colour set
![]() $\mathcal {C}$
and let
$\mathcal {C}$
and let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $V(G)$
. The
$V(G)$
. The
![]() $\mu $
-discrepancy of a
$\mu $
-discrepancy of a
![]() $\mu $
-measurable
$\mu $
-measurable
![]() $\mathcal {C}$
-colouring f is defined by the formula
$\mathcal {C}$
-colouring f is defined by the formula
 $$ \begin{align*} {\mathrm{disc}}_\mu(f) := \max_{\alpha \in \mathcal{C}} \left\lvert\mu\left(f^{-1}(\alpha)\right) - \lvert\mathcal{C}\rvert^{-1}\right\rvert. \end{align*} $$
$$ \begin{align*} {\mathrm{disc}}_\mu(f) := \max_{\alpha \in \mathcal{C}} \left\lvert\mu\left(f^{-1}(\alpha)\right) - \lvert\mathcal{C}\rvert^{-1}\right\rvert. \end{align*} $$
The
![]() $\mu $
-distance between two
$\mu $
-distance between two
![]() $\mathcal {C}$
-colourings
$\mathcal {C}$
-colourings
![]() $f, g$
is defined as
$f, g$
is defined as
We establish the following strengthening of Theorem 1.3:
Theorem 1.4 Stable Borel Hajnal–Szemerédi
Let G be an aperiodic Borel graph of finite maximum degree
![]() $\Delta $
and let f be a Borel proper k-colouring of G, where
$\Delta $
and let f be a Borel proper k-colouring of G, where
![]() $k \geq \Delta + 1$
.
$k \geq \Delta + 1$
.
-
(a) For every G-invariant probability measure
 $\mu $
, there is a
$\mu $
, there is a
 $\mu $
-equitable k-colouring g such that (1.3)
$\mu $
-equitable k-colouring g such that (1.3) $$ \begin{align} {\mathrm{dist}}_\mu(f, g) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align} $$
$$ \begin{align} {\mathrm{dist}}_\mu(f, g) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align} $$
-
(b) Furthermore, G has a Borel-equitable k-colouring g such that formula (1.3) holds for every ergodic G-invariant probability measure
 $\mu $
simultaneously.
$\mu $
simultaneously.
We did not make an effort to optimise the coefficient
![]() $7^{k+1}$
in front of
$7^{k+1}$
in front of
![]() ${\mathrm {disc}}_\mu (f)$
in formula (1.3); however, even with more care, our proof techniques seem to lead to exponential dependence on k. It would be interesting to know whether exponential dependence is necessary; in principle, it might even be possible to replace
${\mathrm {disc}}_\mu (f)$
in formula (1.3); however, even with more care, our proof techniques seem to lead to exponential dependence on k. It would be interesting to know whether exponential dependence is necessary; in principle, it might even be possible to replace
![]() $7^{k+1}$
by a linear function of k.
$7^{k+1}$
by a linear function of k.
1.2 Equitable
 $\Delta $
-colourings
$\Delta $
-colourings
By Brooks’ theorem [Reference DiestelDie00, Theorem 5.2.4], ‘most’ connected finite graphs of maximum degree
![]() $\Delta $
can be properly coloured using only
$\Delta $
can be properly coloured using only
![]() $\Delta $
colours; the only exceptions are odd cycles and complete graphs. For equitable
$\Delta $
colours; the only exceptions are odd cycles and complete graphs. For equitable
![]() $\Delta $
-colourings, at least one new class of pathological examples is known: the complete bipartite graphs
$\Delta $
-colourings, at least one new class of pathological examples is known: the complete bipartite graphs
![]() $K_{\Delta ,\Delta }$
for odd
$K_{\Delta ,\Delta }$
for odd
![]() $\Delta $
. The following analogue of Brooks’ theorem was conjectured by Chen, Lih and Wu:
$\Delta $
. The following analogue of Brooks’ theorem was conjectured by Chen, Lih and Wu:
Conjecture 1.5 Chen–Lih–Wu [Reference Chen, Lih and WuCLW94]
Let G be a connected finite graph of maximum degree
![]() $\Delta \geq 1$
. Then G has an equitable
$\Delta \geq 1$
. Then G has an equitable
![]() $\Delta $
-colouring, unless
$\Delta $
-colouring, unless
-
(a)
 $\Delta =2$
and G is an odd cycle,
$\Delta =2$
and G is an odd cycle, -
(b)
 $G \cong K_{\Delta +1}$
or
$G \cong K_{\Delta +1}$
or -
(c)
 $\Delta $
is odd and
$\Delta $
is odd and
 $G \cong K_{\Delta ,\Delta }$
.
$G \cong K_{\Delta ,\Delta }$
.
To date, Conjecture 1.5 remains open. However, some partial results are known; see [Reference Lih, Pardalos, Du and GrahamLih13] for a survey. In particular, Kostochka and Nakprasit proved that G has an equitable
![]() $\Delta $
-colouring provided that
$\Delta $
-colouring provided that
 $$ \begin{align*} d(G) := \frac{\sum_{x \in V(G)} \deg_G(x)}{\lvert V(G\rvert|} = \frac{2\lvert E(G)\rvert}{\lvert V(G)\rvert} \end{align*} $$
$$ \begin{align*} d(G) := \frac{\sum_{x \in V(G)} \deg_G(x)}{\lvert V(G\rvert|} = \frac{2\lvert E(G)\rvert}{\lvert V(G)\rvert} \end{align*} $$
(the average degree of G) is considerably smaller than
![]() $\Delta $
:
$\Delta $
:
Theorem 1.6 Kostochka–Nakprasit [Reference Kostochka and NakprasitKN05, Theorem 1]
Let G be a finite graph of maximum degree
![]() $\Delta \geq 46$
and without a clique on
$\Delta \geq 46$
and without a clique on
![]() $\Delta +1$
vertices. If the average degree of G is at most
$\Delta +1$
vertices. If the average degree of G is at most
![]() $\Delta /5$
, then G admits an equitable
$\Delta /5$
, then G admits an equitable
![]() $\Delta $
-colouring.
$\Delta $
-colouring.
Our second main result is a measurable version of Theorem 1.6. Unfortunately, Brooks’ theorem fails in the setting of Borel colourings (as mentioned earlier, Marks [Reference MarksMar16] showed that the bound
![]() $\chi _{\mathrm {B}}(G) \leq \Delta + 1$
is sharp even for acyclic graphs G). However, Conley, Marks and Tucker-Drob established a version of Brooks’ theorem for measurable colourings:
$\chi _{\mathrm {B}}(G) \leq \Delta + 1$
is sharp even for acyclic graphs G). However, Conley, Marks and Tucker-Drob established a version of Brooks’ theorem for measurable colourings:
Theorem 1.7 Measurable Brooks; Conley–Marks–Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMT16, Theorem 1.2(1)]
Let G be a Borel graph of finite maximum degree
![]() $\Delta \geq 3$
and without a clique on
$\Delta \geq 3$
and without a clique on
![]() $\Delta + 1$
vertices. Then
$\Delta + 1$
vertices. Then
![]() $\chi _\mu (G) \leq \Delta $
for every probability measure
$\chi _\mu (G) \leq \Delta $
for every probability measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
.
$V(G)$
.
Thus, there is still hope of constructing
![]() $\mu $
-equitable
$\mu $
-equitable
![]() $\Delta $
-colourings. For a Borel graph G of finite maximum degree and a probability measure
$\Delta $
-colourings. For a Borel graph G of finite maximum degree and a probability measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
, let the
$V(G)$
, let the
![]() $\mu $
-average degree of G be
$\mu $
-average degree of G be
 $$ \begin{align*} d_\mu(G) := \int_{V(G)} \deg_G(x) \mathrm{d} \mu(x). \end{align*} $$
$$ \begin{align*} d_\mu(G) := \int_{V(G)} \deg_G(x) \mathrm{d} \mu(x). \end{align*} $$
Readers who are familiar with measurable graph theory will notice that
![]() $d_\mu (G) = 2\mathsf {C}_\mu (G)$
, where
$d_\mu (G) = 2\mathsf {C}_\mu (G)$
, where
![]() $\mathsf {C}_\mu (G)$
is the cost of G (see [Reference Kechris and MillerKM04, Chapter III]). Recall that a measure
$\mathsf {C}_\mu (G)$
is the cost of G (see [Reference Kechris and MillerKM04, Chapter III]). Recall that a measure
![]() $\mu $
is called atomless if
$\mu $
is called atomless if
![]() $\mu (\left \{x\right \}) = 0$
for every point x. (In particular, if G is an aperiodic Borel graph, then every G-invariant probability measure on
$\mu (\left \{x\right \}) = 0$
for every point x. (In particular, if G is an aperiodic Borel graph, then every G-invariant probability measure on
![]() $V(G)$
is atomless.) We prove the following measurable analogue of Theorem 1.6:
$V(G)$
is atomless.) We prove the following measurable analogue of Theorem 1.6:
Theorem 1.8. Let G be a Borel graph of finite maximum degree
![]() $\Delta \geq 3$
and without a clique on
$\Delta \geq 3$
and without a clique on
![]() $\Delta + 1$
vertices. If
$\Delta + 1$
vertices. If
![]() $\mu $
is an atomless G-invariant probability measure on
$\mu $
is an atomless G-invariant probability measure on
![]() $V(G)$
such that
$V(G)$
such that
![]() $d_\mu (G) \leq \Delta /5$
, then G has a
$d_\mu (G) \leq \Delta /5$
, then G has a
![]() $\mu $
-equitable
$\mu $
-equitable
![]() $\Delta $
-colouring.
$\Delta $
-colouring.
It is possible that the upper bound on
![]() $d_\mu (G)$
in Theorem 1.8 is not actually necessary. Indeed, we suspect that the following version of Conjecture 1.5 should hold in full generality:
$d_\mu (G)$
in Theorem 1.8 is not actually necessary. Indeed, we suspect that the following version of Conjecture 1.5 should hold in full generality:
Conjecture 1.9. Let G be an aperiodic Borel graph of finite maximum degree
![]() $\Delta \geq 3$
and let
$\Delta \geq 3$
and let
![]() $\mu $
be a G-invariant probability measure on
$\mu $
be a G-invariant probability measure on
![]() $V(G)$
. Then G has a
$V(G)$
. Then G has a
![]() $\mu $
-equitable
$\mu $
-equitable
![]() $\Delta $
-colouring.
$\Delta $
-colouring.
1.3 Domination for partial
 $\Delta $
-colourings
$\Delta $
-colourings
In order to prove Theorem 1.6, Kostochka and Nakprasit established a useful auxiliary result concerning the relationship between
![]() $\Delta $
-colourings of a finite graph G and those of its subgraphs. Let G be a graph and let
$\Delta $
-colourings of a finite graph G and those of its subgraphs. Let G be a graph and let
![]() $\mathcal {C}$
be a set. A partial
$\mathcal {C}$
be a set. A partial
![]() $\mathcal {C}$
-colouring of G is a function
$\mathcal {C}$
-colouring of G is a function
![]() $f \colon U \to \mathcal {C}$
with
$f \colon U \to \mathcal {C}$
with
![]() $U \subseteq V(G)$
; to indicate that f is a partial
$U \subseteq V(G)$
; to indicate that f is a partial
![]() $\mathcal {C}$
-colouring, we write
$\mathcal {C}$
-colouring, we write
![]() $f \colon V(G) \rightharpoonup \mathcal {C}$
. A partial
$f \colon V(G) \rightharpoonup \mathcal {C}$
. A partial
![]() $\mathcal {C}$
-colouring f is proper if
$\mathcal {C}$
-colouring f is proper if
![]() $f(x) \neq f(y)$
whenever
$f(x) \neq f(y)$
whenever
![]() $x, y \in \mathrm {dom}(f)$
are adjacent. Given partial
$x, y \in \mathrm {dom}(f)$
are adjacent. Given partial
![]() $\mathcal {C}$
-colourings
$\mathcal {C}$
-colourings
![]() $f, g$
of a finite graph G, we say that f dominates g – in symbols,
$f, g$
of a finite graph G, we say that f dominates g – in symbols,
![]() $f \succcurlyeq g$
– if
$f \succcurlyeq g$
– if
 $\left \lvert f^{-1}(\alpha )\right \rvert \geq \left \lvert g^{-1}(\alpha )\right \rvert $
for all
$\left \lvert f^{-1}(\alpha )\right \rvert \geq \left \lvert g^{-1}(\alpha )\right \rvert $
for all
![]() $\alpha \in \mathcal {C}$
. In particular, if f is an extension of g (i.e., if
$\alpha \in \mathcal {C}$
. In particular, if f is an extension of g (i.e., if
![]() $f \supseteq g$
), then f dominates g; but in general the relation
$f \supseteq g$
), then f dominates g; but in general the relation
![]() $f \succcurlyeq g$
says nothing about the values that f and g take at individual vertices.
$f \succcurlyeq g$
says nothing about the values that f and g take at individual vertices.
Theorem 1.10 Kostochka–Nakprasit [Reference Kostochka and NakprasitKN05, Theorem 2]
Let G be a finite graph of maximum degree
![]() $\Delta \geq 3$
and without a clique on
$\Delta \geq 3$
and without a clique on
![]() $\Delta + 1$
vertices. If g is a proper partial
$\Delta + 1$
vertices. If g is a proper partial
![]() $\Delta $
-colouring of G, then G has a proper
$\Delta $
-colouring of G, then G has a proper
![]() $\Delta $
-colouring f such that
$\Delta $
-colouring f such that
![]() $f \succcurlyeq g$
.
$f \succcurlyeq g$
.
Unsurprisingly, our proof of Theorem 1.8 similarly relies on a measurable version of Theorem 1.10. To state it, we extend the notion of domination for partial colourings to the measurable context in the obvious way. Namely, if G is a Borel graph and
![]() $\mu $
is a probability measure on
$\mu $
is a probability measure on
![]() $V(G)$
, then given a pair of
$V(G)$
, then given a pair of
![]() $\mu $
-measurable partial colourings
$\mu $
-measurable partial colourings
![]() $f, g$
, we say that f dominates g with respect to
$f, g$
, we say that f dominates g with respect to
![]() $\mu $
– in symbols,
$\mu $
– in symbols,
![]() $f \succcurlyeq _\mu g$
– if
$f \succcurlyeq _\mu g$
– if
![]() $\mu \left (f^{-1}(\alpha )\right ) \geq \mu \left (g^{-1}(\alpha )\right )$
for every colour
$\mu \left (f^{-1}(\alpha )\right ) \geq \mu \left (g^{-1}(\alpha )\right )$
for every colour
![]() $\alpha $
.
$\alpha $
.
Theorem 1.11 Measurable domination
Let G be a Borel graph of finite maximum degree
![]() $\Delta \geq 3$
and without a clique on
$\Delta \geq 3$
and without a clique on
![]() $\Delta + 1$
vertices, and let
$\Delta + 1$
vertices, and let
![]() $\mu $
be a G-invariant probability measure on
$\mu $
be a G-invariant probability measure on
![]() $V(G)$
. If g is a
$V(G)$
. If g is a
![]() $\mu $
-measurable proper partial
$\mu $
-measurable proper partial
![]() $\Delta $
-colouring of G, then G has a
$\Delta $
-colouring of G, then G has a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\Delta $
-colouring f such that
$\Delta $
-colouring f such that
![]() $f \succcurlyeq _\mu g$
.
$f \succcurlyeq _\mu g$
.
In combination with Theorem 1.3, Theorem 1.11 yields the following corollary:
Corollary 1.12 Almost equitable
 $\Delta $
-colourings
$\Delta $
-colourings
Let G be an aperiodic Borel graph of finite maximum degree
![]() $\Delta \geq 3$
and let
$\Delta \geq 3$
and let
![]() $\mu $
be a G-invariant probability measure on
$\mu $
be a G-invariant probability measure on
![]() $V(G)$
. Then G has a
$V(G)$
. Then G has a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\Delta $
-colouring f such that
$\Delta $
-colouring f such that
![]() $\mu \left (f^{-1}(\alpha )\right ) \geq 1/(\Delta + 1)$
for every colour
$\mu \left (f^{-1}(\alpha )\right ) \geq 1/(\Delta + 1)$
for every colour
![]() $\alpha $
.
$\alpha $
.
Proof. By Theorem 1.3, G has a
![]() $\mu $
-equitable
$\mu $
-equitable
![]() $(\Delta + 1)$
-colouring h. Fix an arbitrary colour
$(\Delta + 1)$
-colouring h. Fix an arbitrary colour
![]() $\beta $
and let g be the partial
$\beta $
and let g be the partial
![]() $\Delta $
-colouring of G obtained from h by uncolouring all the vertices in
$\Delta $
-colouring of G obtained from h by uncolouring all the vertices in
![]() $h^{-1}(\beta )$
. Then every colour class of g has measure precisely
$h^{-1}(\beta )$
. Then every colour class of g has measure precisely
![]() $1/(\Delta + 1)$
, and thus applying Theorem 1.11 to this g yields the desired
$1/(\Delta + 1)$
, and thus applying Theorem 1.11 to this g yields the desired
![]() $\Delta $
-colouring f.
$\Delta $
-colouring f.
It turns out that to prove Theorem 1.11, we must first strengthen Theorem 1.10 by extending it to the list-colouring context. This phenomenon is not uncommon in graph-colouring theory; for example, the proof of Theorem 1.7 due to Conley, Marks and Tucker-Drob relies in a similar fashion on the list-colouring version of Brooks’ theorem (see Theorem 1.13). As we believe our list-colouring analogue of Theorem 1.10 to be of independent interest, we describe it here.
List colouring is a generalisation of graph colouring that was introduced independently by Vizing [Reference VizingViz] and Erdős, Rubin and Taylor [Reference Erdős, Rubin and TaylorERT79]. A list assignment for a graph G is a mapping
![]() $\mathcal {L}$
that assigns to each vertex
$\mathcal {L}$
that assigns to each vertex
![]() $x \in V(G)$
a set
$x \in V(G)$
a set
![]() $\mathcal {L}(x)$
, called the list of x. An
$\mathcal {L}(x)$
, called the list of x. An
![]() $\mathcal {L}$
-colouring of G is a function f with domain
$\mathcal {L}$
-colouring of G is a function f with domain
![]() $V(G)$
such that
$V(G)$
such that
![]() $f(x) \in \mathcal {L}(x)$
for all
$f(x) \in \mathcal {L}(x)$
for all
![]() $x \in V(G)$
; similarly, a partial
$x \in V(G)$
; similarly, a partial
![]() $\mathcal {L}$
-colouring is a function f with
$\mathcal {L}$
-colouring is a function f with
![]() $\mathrm {dom}(f) \subseteq V(G)$
such that
$\mathrm {dom}(f) \subseteq V(G)$
such that
![]() $f(x) \in \mathcal {L}(x)$
for all
$f(x) \in \mathcal {L}(x)$
for all
![]() $x \in \mathrm {dom}(f)$
. A (partial)
$x \in \mathrm {dom}(f)$
. A (partial)
![]() $\mathcal {L}$
-colouring f is proper if
$\mathcal {L}$
-colouring f is proper if
![]() $f(x) \neq f(y)$
whenever x and y are adjacent. Note that ordinary graph colouring is a special case of list colouring, with all lists being the same.
$f(x) \neq f(y)$
whenever x and y are adjacent. Note that ordinary graph colouring is a special case of list colouring, with all lists being the same.
A list assignment
![]() $\mathcal {L}$
for a graph G is called a degree-list assignment if
$\mathcal {L}$
for a graph G is called a degree-list assignment if
![]() $\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
for all
$\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
for all
![]() $x \in V(G)$
. A fundamental result of Borodin [Reference BorodinBor79] and Erdős, Rubin and Taylor [Reference Erdős, Rubin and TaylorERT79], which can be seen as an extension of Brooks’ theorem to list colouring, provides a complete characterisation of graphs G that are not
$x \in V(G)$
. A fundamental result of Borodin [Reference BorodinBor79] and Erdős, Rubin and Taylor [Reference Erdős, Rubin and TaylorERT79], which can be seen as an extension of Brooks’ theorem to list colouring, provides a complete characterisation of graphs G that are not
![]() $\mathcal {L}$
-colourable with respect to some degree-list assignment
$\mathcal {L}$
-colourable with respect to some degree-list assignment
![]() $\mathcal {L}$
. To state it, we need to recall a few definitions. Given a vertex
$\mathcal {L}$
. To state it, we need to recall a few definitions. Given a vertex
![]() $x \in V(G)$
, we write
$x \in V(G)$
, we write
![]() $G-x$
for the subgraph of G obtained by deleting x and all the edges incident to x. A cut-vertex in a connected graph G is a vertex
$G-x$
for the subgraph of G obtained by deleting x and all the edges incident to x. A cut-vertex in a connected graph G is a vertex
![]() $x \in V(G)$
such that
$x \in V(G)$
such that
![]() $G - x$
has at least two connected components. A block in a graph G is a maximal subgraph of G without a cut-vertex. A connected graph G is called a Gallai tree if every block in G is a clique or an odd cycle (see Figure 1).
$G - x$
has at least two connected components. A block in a graph G is a maximal subgraph of G without a cut-vertex. A connected graph G is called a Gallai tree if every block in G is a clique or an odd cycle (see Figure 1).

Figure 1 A fragment of an infinite Gallai tree.
Theorem 1.13 Brooks for list colouring; Borodin [Reference BorodinBor79]; Erdős–Rubin–Taylor [Reference Erdős, Rubin and TaylorERT79]
Let G be a connected finite graph that is not a Gallai tree and let
![]() $\mathcal {L}$
be a degree/list assignment for G. Then G has a proper
$\mathcal {L}$
be a degree/list assignment for G. Then G has a proper
![]() $\mathcal {L}$
-colouring.
$\mathcal {L}$
-colouring.
If f and g are partial
![]() $\mathcal {L}$
-colourings of a finite graph G, we say that f dominates g – in symbols,
$\mathcal {L}$
-colourings of a finite graph G, we say that f dominates g – in symbols,
![]() $f \succcurlyeq g$
– if
$f \succcurlyeq g$
– if
 $\left \lvert f^{-1}(\alpha )\right \rvert \geq \left \lvert g^{-1}(\alpha )\right \rvert $
for all
$\left \lvert f^{-1}(\alpha )\right \rvert \geq \left \lvert g^{-1}(\alpha )\right \rvert $
for all
![]() $\alpha \in \bigcup \left \{\mathcal {L}(x) : x \in V(G)\right \}$
. At first glance, this notion of domination may seem too strong, since each colour
$\alpha \in \bigcup \left \{\mathcal {L}(x) : x \in V(G)\right \}$
. At first glance, this notion of domination may seem too strong, since each colour
![]() $\alpha $
is available to only a subset of the vertices. Nevertheless, it turns out that this is the right notion for strengthening Theorem 1.13 and extending Theorem 1.10 to the list-colouring framework:
$\alpha $
is available to only a subset of the vertices. Nevertheless, it turns out that this is the right notion for strengthening Theorem 1.13 and extending Theorem 1.10 to the list-colouring framework:
Theorem 1.14 Domination for list colouring
Let G be a connected finite graph that is not a Gallai tree and let
![]() $\mathcal {L}$
be a degree/list assignment for G. Suppose that g is a partial proper
$\mathcal {L}$
be a degree/list assignment for G. Suppose that g is a partial proper
![]() $\mathcal {L}$
-colouring of G. Then G has a proper
$\mathcal {L}$
-colouring of G. Then G has a proper
![]() $\mathcal {L}$
-colouring f with
$\mathcal {L}$
-colouring f with
![]() $f \succcurlyeq g$
.
$f \succcurlyeq g$
.
1.4 Outline of the remainder of the paper
After the preliminary Section 2, we proceed to prove Theorem 1.4 (and thus also Theorem 1.3) in Section 3. The bulk of Section 3 is concerned with building
![]() $\mu $
-equitable colourings for a fixed probability measure
$\mu $
-equitable colourings for a fixed probability measure
![]() $\mu $
; the tools that are then used to obtain a complete proof of Theorem 1.4 in the purely Borel setting are the uniform ergodic decomposition theorem of Farrell and Varadarajan (see Theorem 2.4), which helps us treat all G-invariant probability measures simultaneously, and the properties of compressible graphs (see Section 3.5), which allow us to handle the case when there are no G-invariant probability measures to begin with. In Section 4 we prove Theorem 1.14 and then use it to deduce Theorem 1.11. A key role in the derivation of Theorem 1.11 is played by the method of one-ended subforests developed by Conley, Marks and Tucker-Drob in [Reference Conley, Marks and Tucker-DrobCMT16]. Finally, in Section 5 we prove Theorem 1.8.
$\mu $
; the tools that are then used to obtain a complete proof of Theorem 1.4 in the purely Borel setting are the uniform ergodic decomposition theorem of Farrell and Varadarajan (see Theorem 2.4), which helps us treat all G-invariant probability measures simultaneously, and the properties of compressible graphs (see Section 3.5), which allow us to handle the case when there are no G-invariant probability measures to begin with. In Section 4 we prove Theorem 1.14 and then use it to deduce Theorem 1.11. A key role in the derivation of Theorem 1.11 is played by the method of one-ended subforests developed by Conley, Marks and Tucker-Drob in [Reference Conley, Marks and Tucker-DrobCMT16]. Finally, in Section 5 we prove Theorem 1.8.
2 Preliminaries
2.0.1 Finite sets
For a set A, let
![]() $\left [A\right ]^{<\infty }$
denote the set of all finite subsets of A. If X is a standard Borel space, then
$\left [A\right ]^{<\infty }$
denote the set of all finite subsets of A. If X is a standard Borel space, then
![]() $\left [X\right ]^{<\infty }$
also carries a natural standard Borel structure. One way to see this is to fix a Borel linear ordering on X (such an ordering exists, since by [Reference KechrisKec95, Theorem 15.6], X is isomorphic to a Borel subset of
$\left [X\right ]^{<\infty }$
also carries a natural standard Borel structure. One way to see this is to fix a Borel linear ordering on X (such an ordering exists, since by [Reference KechrisKec95, Theorem 15.6], X is isomorphic to a Borel subset of
![]() $\mathbb {R}$
) and identify
$\mathbb {R}$
) and identify
![]() $\left [X\right ]^{<\infty }$
with the set of all strictly increasing finite sequences of elements of X. It is a useful observation that there exists a Borel map
$\left [X\right ]^{<\infty }$
with the set of all strictly increasing finite sequences of elements of X. It is a useful observation that there exists a Borel map
![]() $p \colon \left [X\right ]^{<\infty }\setminus \left \{\varnothing \right \} \to X$
such that
$p \colon \left [X\right ]^{<\infty }\setminus \left \{\varnothing \right \} \to X$
such that
![]() $p(S) \in S$
for all
$p(S) \in S$
for all
![]() $S \in \left [X\right ]^{<\infty } \setminus \left \{\varnothing \right \}$
; for example, for a fixed Borel linear ordering on X, the function
$S \in \left [X\right ]^{<\infty } \setminus \left \{\varnothing \right \}$
; for example, for a fixed Borel linear ordering on X, the function
![]() $S \mapsto \min S$
works.
$S \mapsto \min S$
works.
2.0.2 Graphs
We say that a graph G is locally countable (resp., locally finite) if every vertex of G has countably (resp., finitely) many neighbours. For
![]() $U \subseteq V(G)$
,
$U \subseteq V(G)$
,
![]() $N_G(U)$
denotes the neighbourhood of U in G – that is, the set of all vertices of G that have a neighbour in U – and
$N_G(U)$
denotes the neighbourhood of U in G – that is, the set of all vertices of G that have a neighbour in U – and
![]() $G[U]$
denotes the subgraph of G induced by U – that is, the graph with vertex set U and edge set
$G[U]$
denotes the subgraph of G induced by U – that is, the graph with vertex set U and edge set
![]() $\left \{(x,y) \in E(G) : x, y \in U\right \}$
. A connected component of G is a maximal subset
$\left \{(x,y) \in E(G) : x, y \in U\right \}$
. A connected component of G is a maximal subset
![]() $C \subseteq V(G)$
such that
$C \subseteq V(G)$
such that
![]() $G[C]$
is a connected graph.
$G[C]$
is a connected graph.
We shall use the following standard extension of Theorem 1.2:
Proposition 2.1 ess. Kechris–Solecki–Todorcevic [Reference Kechris, Solecki and TodorcevicKST99, Proposition 4.6]
Let G be a locally countable Borel graph such that
![]() $\chi _{\mathrm {B}}(G) \leq \aleph _0$
, and let
$\chi _{\mathrm {B}}(G) \leq \aleph _0$
, and let
![]() $\mathcal {C}$
be a standard Borel space of colours. Let
$\mathcal {C}$
be a standard Borel space of colours. Let
![]() $\mathcal {L} \colon V(G) \to \left [\mathcal {C}\right ]^{<\infty }$
be a Borel list assignment. If g is a Borel proper partial
$\mathcal {L} \colon V(G) \to \left [\mathcal {C}\right ]^{<\infty }$
be a Borel list assignment. If g is a Borel proper partial
![]() $\mathcal {L}$
-colouring of G, then G has a Borel inclusion-maximal proper partial
$\mathcal {L}$
-colouring of G, then G has a Borel inclusion-maximal proper partial
![]() $\mathcal {L}$
-colouring f such that
$\mathcal {L}$
-colouring f such that
![]() $f \supseteq g$
.
$f \supseteq g$
.
Proof. We may assume that
![]() $g = \varnothing $
; otherwise, pass to the subgraph
$g = \varnothing $
; otherwise, pass to the subgraph
![]() $G\left [V(G) \setminus \mathrm {dom}(g)\right ]$
and replace
$G\left [V(G) \setminus \mathrm {dom}(g)\right ]$
and replace
![]() $\mathcal {L}$
by the list assignment
$\mathcal {L}$
by the list assignment
![]() $x \mapsto \mathcal {L}(x) \setminus \left \{g(y) : y \in N_G(x) \cap \mathrm {dom}(g)\right \}$
. Let
$x \mapsto \mathcal {L}(x) \setminus \left \{g(y) : y \in N_G(x) \cap \mathrm {dom}(g)\right \}$
. Let
![]() $\vartheta \colon V(G) \to {\mathbb {N}}$
be a Borel proper colouring. Fix a Borel linear ordering on
$\vartheta \colon V(G) \to {\mathbb {N}}$
be a Borel proper colouring. Fix a Borel linear ordering on
![]() $\mathcal {C}$
and recursively define partial
$\mathcal {C}$
and recursively define partial
![]() $\mathcal {L}$
-colourings
$\mathcal {L}$
-colourings
![]() $f_n \colon \vartheta ^{-1}(n) \rightharpoonup \mathcal {C}$
as follows: set
$f_n \colon \vartheta ^{-1}(n) \rightharpoonup \mathcal {C}$
as follows: set
 $$ \begin{align*} \mathcal{L}_n(x) := \mathcal{L}(x) \setminus \left\{\alpha : \text{there is } y \in N_G(x) \text{ with } \vartheta(y) < n \text{ and } f_{\vartheta(y)}(y) = \alpha\right\}, \end{align*} $$
$$ \begin{align*} \mathcal{L}_n(x) := \mathcal{L}(x) \setminus \left\{\alpha : \text{there is } y \in N_G(x) \text{ with } \vartheta(y) < n \text{ and } f_{\vartheta(y)}(y) = \alpha\right\}, \end{align*} $$
and let
![]() $f_n(x)$
be the smallest colour in
$f_n(x)$
be the smallest colour in
![]() $\mathcal {L}_n(x)$
if
$\mathcal {L}_n(x)$
if
![]() $\mathcal {L}_n(x) \neq \varnothing $
, leaving
$\mathcal {L}_n(x) \neq \varnothing $
, leaving
![]() $f_n(x)$
undefined otherwise. Then the union
$f_n(x)$
undefined otherwise. Then the union
![]() $f := \bigcup _{n=0}^\infty f_n$
is a Borel inclusion-maximal proper partial
$f := \bigcup _{n=0}^\infty f_n$
is a Borel inclusion-maximal proper partial
![]() $\mathcal {L}$
-colouring of G, as desired.
$\mathcal {L}$
-colouring of G, as desired.
It is a useful observation that if f is an inclusion-maximal proper partial
![]() $\mathcal {C}$
-colouring of a graph G, then each vertex
$\mathcal {C}$
-colouring of a graph G, then each vertex
![]() $x \in V(G) \setminus \mathrm {dom}(f)$
has at least one neighbour of every colour
$x \in V(G) \setminus \mathrm {dom}(f)$
has at least one neighbour of every colour
![]() $\alpha \in \mathcal {C}$
, and in particular,
$\alpha \in \mathcal {C}$
, and in particular,
![]() $\deg _G(x) \geq \lvert \mathcal {C}\rvert $
. Combining this observation with Proposition 2.1, we obtain the following:
$\deg _G(x) \geq \lvert \mathcal {C}\rvert $
. Combining this observation with Proposition 2.1, we obtain the following:
Corollary 2.2. Let G be a Borel graph of finite maximum degree
![]() $\Delta $
and let
$\Delta $
and let
![]() $k \geq \Delta + 1$
. If g is a Borel proper partial k-colouring of G, then G has a Borel proper k-colouring f such that
$k \geq \Delta + 1$
. If g is a Borel proper partial k-colouring of G, then G has a Borel proper k-colouring f such that
![]() $f \supseteq g$
.
$f \supseteq g$
.
Proof. This is immediate from Proposition 2.1 (note that
![]() $\chi _{\mathrm {B}}(G) \leq \Delta + 1 < \aleph _0$
, by Theorem 1.2).
$\chi _{\mathrm {B}}(G) \leq \Delta + 1 < \aleph _0$
, by Theorem 1.2).
A subset
![]() $I \subseteq V(G)$
is G-independent if
$I \subseteq V(G)$
is G-independent if
![]() $I \cap N_G(I) = \varnothing $
(thus, every colour class in a proper colouring of G is G-independent). The following is a variation of [Reference Kechris, Solecki and TodorcevicKST99, Proposition 4.2]:
$I \cap N_G(I) = \varnothing $
(thus, every colour class in a proper colouring of G is G-independent). The following is a variation of [Reference Kechris, Solecki and TodorcevicKST99, Proposition 4.2]:
Corollary 2.3 ess. Kechris–Solecki–Todorcevic [Reference Kechris, Solecki and TodorcevicKST99, Proposition 4.2]
Let G be a locally countable Borel graph such that
![]() $\chi _{\mathrm {B}}(G) \leq \aleph _0$
and let
$\chi _{\mathrm {B}}(G) \leq \aleph _0$
and let
![]() $J \subseteq V(G)$
be a Borel G-independent set. Then there is a Borel maximal G-independent set
$J \subseteq V(G)$
be a Borel G-independent set. Then there is a Borel maximal G-independent set
![]() $I \subseteq V(G)$
with
$I \subseteq V(G)$
with
![]() $I \supseteq J$
.
$I \supseteq J$
.
Proof. Apply Proposition 2.1 with
![]() $\mathcal {L} \colon x \mapsto \left \{0\right \}$
and
$\mathcal {L} \colon x \mapsto \left \{0\right \}$
and
![]() $g \colon J \to \left \{0\right \} \colon x \mapsto 0$
.
$g \colon J \to \left \{0\right \} \colon x \mapsto 0$
.
2.0.3 Measures
Let X be a standard Borel space. We use
![]() $\mathsf {Prob}(X)$
to denote the set of all probability measures on X. We equip
$\mathsf {Prob}(X)$
to denote the set of all probability measures on X. We equip
![]() $\mathsf {Prob}(X)$
with the
$\mathsf {Prob}(X)$
with the
![]() $\sigma $
-algebra generated by the maps
$\sigma $
-algebra generated by the maps
![]() $\mu \mapsto \mu (A)$
, where A is a Borel subset of X; this makes
$\mu \mapsto \mu (A)$
, where A is a Borel subset of X; this makes
![]() $\mathsf {Prob}(X)$
into a standard Borel space [Reference KechrisKec95, Section 17.E].
$\mathsf {Prob}(X)$
into a standard Borel space [Reference KechrisKec95, Section 17.E].
Let G be a locally countable Borel graph. We write
![]() $\mathsf {Inv}(G)$
(resp.,
$\mathsf {Inv}(G)$
(resp.,
![]() $\mathsf {Erg}(G)$
) to denote the set of all G-invariant (resp., G-invariant and ergodic) probability measures on
$\mathsf {Erg}(G)$
) to denote the set of all G-invariant (resp., G-invariant and ergodic) probability measures on
![]() $V(G)$
. Note that
$V(G)$
. Note that
![]() $\mathsf {Inv}(G)$
is a Borel subset of
$\mathsf {Inv}(G)$
is a Borel subset of
![]() $\mathsf {Prob}(V(G))$
, and
$\mathsf {Prob}(V(G))$
, and
![]() $\mathsf {Erg}(G)$
is a Borel subset of
$\mathsf {Erg}(G)$
is a Borel subset of
![]() $\mathsf {Inv}(G)$
[Reference KechrisKec19, Theorem 4.10]. A function on
$\mathsf {Inv}(G)$
[Reference KechrisKec19, Theorem 4.10]. A function on
![]() $V(G)$
is G-invariant if it is constant on each connected component of G. Hence, a subset
$V(G)$
is G-invariant if it is constant on each connected component of G. Hence, a subset
![]() $A \subseteq V(G)$
is G-invariant if and only if its characteristic function is G-invariant. Observe that if
$A \subseteq V(G)$
is G-invariant if and only if its characteristic function is G-invariant. Observe that if
![]() $\mu \in \mathsf {Inv}(G)$
and
$\mu \in \mathsf {Inv}(G)$
and
![]() $A \subseteq V(G)$
is
$A \subseteq V(G)$
is
![]() $\mu $
-null, then
$\mu $
-null, then
![]() $A \subseteq B$
for some G-invariant
$A \subseteq B$
for some G-invariant
![]() $\mu $
-null Borel set B. The following result plays a crucial role in our proof of Theorem 1.3:
$\mu $
-null Borel set B. The following result plays a crucial role in our proof of Theorem 1.3:
Theorem 2.4 Uniform ergodic decomposition; Farrell [Reference FarrellFar62], Varadarajan [Reference VaradarajanVar63]; see [Reference KechrisKec19, Theorem 4.11]
Let G be a locally countable Borel graph. If
![]() $\mathsf {Inv}(G) \neq \varnothing $
, then
$\mathsf {Inv}(G) \neq \varnothing $
, then
![]() $\mathsf {Erg}(G) \neq \varnothing $
and there is a surjective G-invariant Borel mapping
$\mathsf {Erg}(G) \neq \varnothing $
and there is a surjective G-invariant Borel mapping
![]() $V(G) \to \mathsf {Erg}(G) \colon x \mapsto \mu _x$
such that
$V(G) \to \mathsf {Erg}(G) \colon x \mapsto \mu _x$
such that
-
(E1) for each
 $\mu \in \mathsf {Erg}(G)$
, the set
$\mu \in \mathsf {Erg}(G)$
, the set
 $\left \{x \in V(G) : \mu _x = \mu \right \}$
is
$\left \{x \in V(G) : \mu _x = \mu \right \}$
is
 $\mu $
-conull, and
$\mu $
-conull, and -
(E2) if
 $\mu \in \mathsf {Inv}(G)$
, then
$\mu \in \mathsf {Inv}(G)$
, then
 $\mu = \int _X \mu _x \mathrm {d} \mu (x)$
.
$\mu = \int _X \mu _x \mathrm {d} \mu (x)$
.
For more information about this result, and about invariant measures in general, see [Reference KechrisKec19, Section 4].
3 Proof of the Hajnal–Szemerédi theorem for Borel graphs
3.1 Recolouring moves and perfect colourings
Assumptions for Section 3.1
Fix a Borel graph G of finite maximum degree
![]() $\Delta $
with vertex set V and edge set E; a finite set of colours
$\Delta $
with vertex set V and edge set E; a finite set of colours
![]() $\mathcal {C}$
of size
$\mathcal {C}$
of size
![]() $k \geq \Delta + 1$
; and
$k \geq \Delta + 1$
; and
![]() $\mu \in \mathsf {Inv}(G)$
.
$\mu \in \mathsf {Inv}(G)$
.
A recolouring move is a partial map
![]() $\varphi \colon V \rightharpoonup \mathcal {C}$
such that
$\varphi \colon V \rightharpoonup \mathcal {C}$
such that
![]() $\mathrm {dom}(\varphi )$
is a nonempty finite set contained in a single connected component of G. The set of all recolouring moves is denoted by
$\mathrm {dom}(\varphi )$
is a nonempty finite set contained in a single connected component of G. The set of all recolouring moves is denoted by
![]() $\mathsf {RM}$
. If we view each recolouring move as a finite subset of
$\mathsf {RM}$
. If we view each recolouring move as a finite subset of
![]() $V \times \mathcal {C}$
, then
$V \times \mathcal {C}$
, then
![]() $\mathsf {RM}$
becomes a Borel subset of
$\mathsf {RM}$
becomes a Borel subset of
![]() $\left [V \times \mathcal {C}\right ]^{<\infty }$
. Given
$\left [V \times \mathcal {C}\right ]^{<\infty }$
. Given
![]() $m \in {\mathbb {N}}^+$
, let
$m \in {\mathbb {N}}^+$
, let
![]() $\mathsf {RM}_m$
denote the (Borel) set of all recolouring moves
$\mathsf {RM}_m$
denote the (Borel) set of all recolouring moves
![]() $\varphi $
with
$\varphi $
with
![]() $\lvert \mathrm {dom}(\varphi )\rvert \leq m$
. For
$\lvert \mathrm {dom}(\varphi )\rvert \leq m$
. For
![]() $M \subseteq \mathsf {RM}$
, define
$M \subseteq \mathsf {RM}$
, define
![]() $\mathrm {dom}(M) := \bigcup \left \{\mathrm {dom}(\varphi ) : \varphi \in M\right \}$
and
$\mathrm {dom}(M) := \bigcup \left \{\mathrm {dom}(\varphi ) : \varphi \in M\right \}$
and
![]() $\mu (M) := \mu (\mathrm {dom}(M))$
. For each
$\mu (M) := \mu (\mathrm {dom}(M))$
. For each
![]() $x \in V$
, there are countably many recolouring moves
$x \in V$
, there are countably many recolouring moves
![]() $\varphi $
with
$\varphi $
with
![]() $\mathrm {dom}(\varphi ) \ni x$
; it follows from the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10] that
$\mathrm {dom}(\varphi ) \ni x$
; it follows from the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10] that
![]() $\mathrm {dom}(M)$
is Borel for every Borel set
$\mathrm {dom}(M)$
is Borel for every Borel set
![]() $M \subseteq \mathsf {RM}$
.
$M \subseteq \mathsf {RM}$
.
For a proper
![]() $\mathcal {C}$
-colouring f of G and
$\mathcal {C}$
-colouring f of G and
![]() $\varphi \in \mathsf {RM}$
, we define a colouring
$\varphi \in \mathsf {RM}$
, we define a colouring
![]() $f \oplus \varphi \colon V \to \mathcal {C}$
by the formula
$f \oplus \varphi \colon V \to \mathcal {C}$
by the formula
 $$ \begin{align*} (f \oplus \varphi)(x) := \begin{cases} \varphi(x) &\text{if } x \in \mathrm{dom}(\varphi),\\ f(x) &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} (f \oplus \varphi)(x) := \begin{cases} \varphi(x) &\text{if } x \in \mathrm{dom}(\varphi),\\ f(x) &\text{otherwise}. \end{cases} \end{align*} $$
The colouring
![]() $f \oplus \varphi $
is the result of applying the recolouring move
$f \oplus \varphi $
is the result of applying the recolouring move
![]() $\varphi $
to f, and we say that a recolouring move
$\varphi $
to f, and we say that a recolouring move
![]() $\varphi $
is acceptable for f if
$\varphi $
is acceptable for f if
![]() $f \oplus \varphi $
is again a proper colouring of G. For each colour
$f \oplus \varphi $
is again a proper colouring of G. For each colour
![]() $\alpha \in \mathcal {C}$
, let
$\alpha \in \mathcal {C}$
, let

In other words,
![]() is the change, between f and
is the change, between f and
![]() $f \oplus \varphi $
, in the number of vertices of colour
$f \oplus \varphi $
, in the number of vertices of colour
![]() $\alpha $
among the elements of
$\alpha $
among the elements of
![]() $\mathrm {dom}(\varphi )$
. Define the following two (disjoint) sets of colours:
$\mathrm {dom}(\varphi )$
. Define the following two (disjoint) sets of colours:
Assuming that f is
![]() $\mu $
-measurable, we say that
$\mu $
-measurable, we say that
![]() $\varphi $
improves f with respect to
$\varphi $
improves f with respect to
![]() $\mu $
if
$\mu $
if
-
(I1)
 $\varphi $
is acceptable for f and
$\varphi $
is acceptable for f and -
(I2) there is and
 $\alpha \in \mathcal {D}^+(f, \varphi )$
such that for all
$\alpha \in \mathcal {D}^+(f, \varphi )$
such that for all
 $\beta \in \mathcal {D}^-(f, \varphi )$
, we have
$\beta \in \mathcal {D}^-(f, \varphi )$
, we have
 $\mu \left (f^{-1}(\alpha )\right ) < \mu \left (f^{-1}(\beta )\right )$
.
$\mu \left (f^{-1}(\alpha )\right ) < \mu \left (f^{-1}(\beta )\right )$
.
Informally, (I2) states that some ‘small’ colour class has a net gain of vertices upon the recolouring move
![]() $\varphi $
. Given a set
$\varphi $
. Given a set
![]() $M \subseteq \mathsf {RM}$
, we say that a proper
$M \subseteq \mathsf {RM}$
, we say that a proper
![]() $\mathcal {C}$
-colouring f of G is
$\mathcal {C}$
-colouring f of G is
![]() $(\mu , M)$
-perfect if
$(\mu , M)$
-perfect if
The main result of this subsection is that
![]() $(\mu , \mathsf {RM}_3)$
-perfect colourings must be
$(\mu , \mathsf {RM}_3)$
-perfect colourings must be
![]() $\mu $
-equitable. In other words, if a colouring is not
$\mu $
-equitable. In other words, if a colouring is not
![]() $\mu $
-equitable, it can be improved by a recolouring move
$\mu $
-equitable, it can be improved by a recolouring move
![]() $\varphi $
with
$\varphi $
with
![]() $\lvert \mathrm {dom}(\varphi )\rvert \leq 3$
, and furthermore, such recolouring moves cover a subset of V of positive measure. Our proof of this fact is an adaptation of the proof of the Hajnal–Szemerédi theorem from [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10].
$\lvert \mathrm {dom}(\varphi )\rvert \leq 3$
, and furthermore, such recolouring moves cover a subset of V of positive measure. Our proof of this fact is an adaptation of the proof of the Hajnal–Szemerédi theorem from [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10].
Lemma 3.1. If a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\mathcal {C}$
-colouring f of G is
$\mathcal {C}$
-colouring f of G is
![]() $(\mu , \mathsf {RM}_3)$
-perfect, then it is
$(\mu , \mathsf {RM}_3)$
-perfect, then it is
![]() $\mu $
-equitable.
$\mu $
-equitable.
Proof. Suppose, toward a contradiction, that f is a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\mathcal {C}$
-colouring of G that is
$\mathcal {C}$
-colouring of G that is
![]() $(\mu , \mathsf {RM}_3)$
-perfect but not
$(\mu , \mathsf {RM}_3)$
-perfect but not
![]() $\mu $
-equitable. After passing to a
$\mu $
-equitable. After passing to a
![]() $\mu $
-conull G-invariant Borel subset of V, we may assume that in fact no recolouring move
$\mu $
-conull G-invariant Borel subset of V, we may assume that in fact no recolouring move
![]() $\varphi \in \mathsf {RM}_3$
improves f with respect to
$\varphi \in \mathsf {RM}_3$
improves f with respect to
![]() $\mu $
.
$\mu $
.
For
![]() $\gamma \in \mathcal {C}$
, let
$\gamma \in \mathcal {C}$
, let
![]() $V_\gamma := f^{-1}(\gamma )$
be the corresponding colour class. Define
$V_\gamma := f^{-1}(\gamma )$
be the corresponding colour class. Define
![]() $a := \min _{\gamma \in \mathcal {C}} \mu \left (V_\gamma \right )$
and
$a := \min _{\gamma \in \mathcal {C}} \mu \left (V_\gamma \right )$
and
Since f is not
![]() $\mu $
-equitable,
$\mu $
-equitable,
![]() $\mathcal {B} \neq \varnothing $
. Define
$\mathcal {B} \neq \varnothing $
. Define
 $b := \lvert \mathcal {B}\rvert ^{-1} \sum _{\beta \in \mathcal {B}} \mu \left (V_\beta \right )$
and notice that
$b := \lvert \mathcal {B}\rvert ^{-1} \sum _{\beta \in \mathcal {B}} \mu \left (V_\beta \right )$
and notice that
![]() $a < 1/k < b$
. Set
$a < 1/k < b$
. Set
Claim 3.1.1. If
![]() $\alpha \in \mathcal {A}$
, then every vertex
$\alpha \in \mathcal {A}$
, then every vertex
![]() $x \in B$
has a neighbour in
$x \in B$
has a neighbour in
![]() $V_\alpha $
.
$V_\alpha $
.
Proof. Suppose
![]() $\beta \in \mathcal {B}$
and
$\beta \in \mathcal {B}$
and
![]() $x \in V_\beta $
has no neighbour in
$x \in V_\beta $
has no neighbour in
![]() $V_\alpha $
. Consider the recolouring move
$V_\alpha $
. Consider the recolouring move
![]() $\varphi := \left \{(x, \alpha )\right \}$
(see Figure 2). The assumption on x ensures that
$\varphi := \left \{(x, \alpha )\right \}$
(see Figure 2). The assumption on x ensures that
![]() $\varphi $
is acceptable for f. Since
$\varphi $
is acceptable for f. Since
![]() $\mathcal {D}^+(f, \varphi ) = \left \{\alpha \right \}$
,
$\mathcal {D}^+(f, \varphi ) = \left \{\alpha \right \}$
,
![]() $\mathcal {D}^-(f, \varphi ) = \left \{\beta \right \}$
and
$\mathcal {D}^-(f, \varphi ) = \left \{\beta \right \}$
and
![]() $\mu (V_\alpha ) < \mu \left (V_\beta \right )$
, we conclude that
$\mu (V_\alpha ) < \mu \left (V_\beta \right )$
, we conclude that
![]() $\varphi $
improves f with respect to
$\varphi $
improves f with respect to
![]() $\mu $
.
$\mu $
.

Figure 2 The recolouring move from Claim 3.1.1.
Given
![]() $x \in B$
and
$x \in B$
and
![]() $y \in A$
, we say that y is a solo neighbour of x if y is the unique neighbour of x with the colour
$y \in A$
, we say that y is a solo neighbour of x if y is the unique neighbour of x with the colour
![]() $f(y)$
. (This notion plays a similarly central role in [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10].) For
$f(y)$
. (This notion plays a similarly central role in [Reference Kierstead, Kostochka, Mydlarz and SzemerédiKie+10].) For
![]() $y \in A$
, define
$y \in A$
, define
Claim 3.1.2. Let
![]() $\alpha , \alpha ' \in \mathcal {A}$
be distinct and set
$\alpha , \alpha ' \in \mathcal {A}$
be distinct and set
![]() $y \in V_\alpha $
. If
$y \in V_\alpha $
. If
![]() $S(y) \neq \varnothing $
, then y has a neighbour in
$S(y) \neq \varnothing $
, then y has a neighbour in
![]() $V_{\alpha '}$
.
$V_{\alpha '}$
.
Proof. Take any
![]() $x \in S(y)$
and define
$x \in S(y)$
and define
![]() $\beta := f(x)$
. Suppose that y has no neighbour in
$\beta := f(x)$
. Suppose that y has no neighbour in
![]() $V_{\alpha '}$
and consider the recolouring move
$V_{\alpha '}$
and consider the recolouring move
![]() $\varphi := \left \{(x, \alpha ), (y, \alpha ')\right \}$
(see Figure 3). Since y is not adjacent to any vertex in
$\varphi := \left \{(x, \alpha ), (y, \alpha ')\right \}$
(see Figure 3). Since y is not adjacent to any vertex in
![]() $V_{\alpha '}$
, and the only neighbour of x that is coloured
$V_{\alpha '}$
, and the only neighbour of x that is coloured
![]() $\alpha $
is y,
$\alpha $
is y,
![]() $\varphi $
is acceptable for f. But
$\varphi $
is acceptable for f. But
![]() $\mathcal {D}^+(f, \varphi ) = \left \{\alpha '\right \}, \varphi ) = \left \{\beta \right \}$
and
$\mathcal {D}^+(f, \varphi ) = \left \{\alpha '\right \}, \varphi ) = \left \{\beta \right \}$
and
![]() $\mu \left (V_{\alpha '}\right ) < \mu \left (V_\beta \right )$
, so
$\mu \left (V_{\alpha '}\right ) < \mu \left (V_\beta \right )$
, so
![]() $\varphi $
improves f with respect to
$\varphi $
improves f with respect to
![]() $\mu $
.
$\mu $
.

Figure 3 The recolouring move from Claim 3.1.2.
Claim 3.1.3. If
![]() $y \in A$
, then the induced subgraph
$y \in A$
, then the induced subgraph
![]() $G[S(y)]$
is a clique.
$G[S(y)]$
is a clique.
Proof. Suppose, toward a contradiction, that
![]() $G[S(y)]$
is not a clique. This means that there are two distinct nonadjacent vertices
$G[S(y)]$
is not a clique. This means that there are two distinct nonadjacent vertices
![]() $x, x' \in S(y)$
. Define
$x, x' \in S(y)$
. Define
![]() $\alpha := f(y)$
,
$\alpha := f(y)$
,
![]() $\beta := f(x)$
and
$\beta := f(x)$
and
![]() $\beta ' := f(x')$
. Observe that there is a colour
$\beta ' := f(x')$
. Observe that there is a colour
![]() $\gamma \neq \alpha $
such that
$\gamma \neq \alpha $
such that
Otherwise y would have, in addition to x and
![]() $x'$
, at least one neighbour in every colour class
$x'$
, at least one neighbour in every colour class
![]() $V_\gamma $
except for
$V_\gamma $
except for
![]() $V_\alpha $
, which would yield
$V_\alpha $
, which would yield
![]() $\deg _G(y) \geq 2 + (k-1) = k+1> \Delta $
. Now fix any
$\deg _G(y) \geq 2 + (k-1) = k+1> \Delta $
. Now fix any
![]() $\gamma \neq \alpha $
satisfying equation (3.3) and consider the recolouring move
$\gamma \neq \alpha $
satisfying equation (3.3) and consider the recolouring move
![]() $\varphi := \left \{(x, \alpha ),(x', \alpha ),(y, \gamma )\right \}$
(see Figure 4). The choice of x,
$\varphi := \left \{(x, \alpha ),(x', \alpha ),(y, \gamma )\right \}$
(see Figure 4). The choice of x,
![]() $x'$
and
$x'$
and
![]() $\gamma $
implies that
$\gamma $
implies that
![]() $\varphi $
is acceptable for f. Since
$\varphi $
is acceptable for f. Since
![]() $\alpha \in \mathcal {D}^+(f, \varphi )$
,
$\alpha \in \mathcal {D}^+(f, \varphi )$
,
![]() $\mathcal {D}^-(f, \varphi ) \subseteq \left \{\beta , \beta '\right \}$
and
$\mathcal {D}^-(f, \varphi ) \subseteq \left \{\beta , \beta '\right \}$
and
![]() $\mu (V_\alpha ) < \mu \left (V_\beta \right )$
,
$\mu (V_\alpha ) < \mu \left (V_\beta \right )$
,
![]() $\mu \left (V_{\beta '}\right )$
, we conclude that
$\mu \left (V_{\beta '}\right )$
, we conclude that
![]() $\varphi $
improves f with respect to
$\varphi $
improves f with respect to
![]() $\mu $
.
$\mu $
.

Figure 4 The recolouring move from Claim 3.1.3.
Claim 3.1.4. We have
![]() $\Delta \geq 2\lvert \mathcal {B}\rvert +1$
.
$\Delta \geq 2\lvert \mathcal {B}\rvert +1$
.
Proof. Fix an arbitrary colour
![]() $\alpha \in \mathcal {A}$
. Let X be the set of all vertices
$\alpha \in \mathcal {A}$
. Let X be the set of all vertices
![]() $x \in B$
that have a solo neighbour in
$x \in B$
that have a solo neighbour in
![]() $V_\alpha $
, and let Y be the set of all vertices
$V_\alpha $
, and let Y be the set of all vertices
![]() $y \in V_\alpha $
that have a neighbour in X. By Claim 3.1.2, every vertex
$y \in V_\alpha $
that have a neighbour in X. By Claim 3.1.2, every vertex
![]() $y \in Y$
has at least
$y \in Y$
has at least
![]() $\lvert \mathcal {A}\rvert - 1 = k - \lvert \mathcal {B}\rvert - 1$
neighbours in A, and thus
$\lvert \mathcal {A}\rvert - 1 = k - \lvert \mathcal {B}\rvert - 1$
neighbours in A, and thus
This immediately yields
 $$ \begin{align} \int_{V_{\alpha}} \lvert N_G(y) \cap B\rvert \mathrm{d} \mu(y) \leq \Delta \mu(V_\alpha) - (k - \lvert\mathcal{B}\rvert - 1) \mu(Y). \end{align} $$
$$ \begin{align} \int_{V_{\alpha}} \lvert N_G(y) \cap B\rvert \mathrm{d} \mu(y) \leq \Delta \mu(V_\alpha) - (k - \lvert\mathcal{B}\rvert - 1) \mu(Y). \end{align} $$
On the other hand, we have
 $$ \begin{align*}\hspace{7.8pc} \mu(X) &= \int_{X} 1 \mathrm{d} \mu(x) \\ &= \int_{X} \lvert N_G(x) \cap Y\rvert \mathrm{d}\mu(x) &\qquad\qquad\qquad {(\text{by the definition of}\ X\ \text{and}\ Y)}\\ &= \int_{Y} \lvert N_G(y) \cap X\rvert \mathrm{d}\mu(y) &\qquad\qquad\qquad {(\mu\ \text{is}\ G\text{-invariant})} \\ &\leq (\Delta - k + \lvert\mathcal{B}\rvert + 1) \mu(Y). &\qquad\qquad\qquad {(\text{by formula (3.4)})} \end{align*} $$
$$ \begin{align*}\hspace{7.8pc} \mu(X) &= \int_{X} 1 \mathrm{d} \mu(x) \\ &= \int_{X} \lvert N_G(x) \cap Y\rvert \mathrm{d}\mu(x) &\qquad\qquad\qquad {(\text{by the definition of}\ X\ \text{and}\ Y)}\\ &= \int_{Y} \lvert N_G(y) \cap X\rvert \mathrm{d}\mu(y) &\qquad\qquad\qquad {(\mu\ \text{is}\ G\text{-invariant})} \\ &\leq (\Delta - k + \lvert\mathcal{B}\rvert + 1) \mu(Y). &\qquad\qquad\qquad {(\text{by formula (3.4)})} \end{align*} $$
This together with Claim 3.1.1 gives
 $$ \begin{align} \int_{B} \lvert N_G(x) \cap V_\alpha\rvert \mathrm{d} \mu(x) \geq 2\mu(B) - \mu(X) \geq 2\mu(B) - (\Delta - k + \lvert\mathcal{B}\rvert + 1) \mu(Y). \end{align} $$
$$ \begin{align} \int_{B} \lvert N_G(x) \cap V_\alpha\rvert \mathrm{d} \mu(x) \geq 2\mu(B) - \mu(X) \geq 2\mu(B) - (\Delta - k + \lvert\mathcal{B}\rvert + 1) \mu(Y). \end{align} $$
Since
![]() $\mu $
is G-invariant, we can combine formulas (3.6) and (3.5) to get
$\mu $
is G-invariant, we can combine formulas (3.6) and (3.5) to get
Recalling that
![]() $\mu (V_\alpha ) = a$
and
$\mu (V_\alpha ) = a$
and
![]() $\mu (B) = \lvert \mathcal {B}\rvert b$
, we can rewrite the last inequality as
$\mu (B) = \lvert \mathcal {B}\rvert b$
, we can rewrite the last inequality as
After moving all the terms to one side and using the fact that
![]() $b> a$
, we obtain
$b> a$
, we obtain
 $$ \begin{align*} \Delta - 2\lvert\mathcal{B}\rvert + (\Delta -2k + 2 \lvert\mathcal{B}\rvert +2)\frac{\mu(Y)}{b}> 0. \end{align*} $$
$$ \begin{align*} \Delta - 2\lvert\mathcal{B}\rvert + (\Delta -2k + 2 \lvert\mathcal{B}\rvert +2)\frac{\mu(Y)}{b}> 0. \end{align*} $$
Since
![]() $0 \leq \mu (Y)/b < \mu (Y)/a \leq 1$
, at least one of the following two inequalities holds:
$0 \leq \mu (Y)/b < \mu (Y)/a \leq 1$
, at least one of the following two inequalities holds:
The second of these inequalities necessarily fails, since
![]() $2\Delta - 2k + 2 \leq 2\Delta - 2(\Delta + 1) + 2 = 0$
. Hence, we must have
$2\Delta - 2k + 2 \leq 2\Delta - 2(\Delta + 1) + 2 = 0$
. Hence, we must have
![]() $\Delta - 2\lvert \mathcal {B}\rvert> 0$
, and thus
$\Delta - 2\lvert \mathcal {B}\rvert> 0$
, and thus
![]() $\Delta \geq 2\lvert \mathcal {B}\rvert +1$
, as desired.
$\Delta \geq 2\lvert \mathcal {B}\rvert +1$
, as desired.
We are now ready for the final stage of the argument. At least one of the colour classes
![]() $V_\beta $
,
$V_\beta $
,
![]() $\beta \in \mathcal {B}$
, has measure at least b, so by taking J to be any such colour class and applying Corollary 2.3 to the induced subgraph
$\beta \in \mathcal {B}$
, has measure at least b, so by taking J to be any such colour class and applying Corollary 2.3 to the induced subgraph
![]() $G[B]$
, we obtain a Borel maximal G-independent subset
$G[B]$
, we obtain a Borel maximal G-independent subset
![]() $I \subseteq B$
such that
$I \subseteq B$
such that
![]() $\mu (I) \geq b$
. For each
$\mu (I) \geq b$
. For each
![]() $x \in I$
, let
$x \in I$
, let
![]() $\Sigma (x)$
be the set of all solo neighbours of x. Then, on the one hand,
$\Sigma (x)$
be the set of all solo neighbours of x. Then, on the one hand,
while on the other hand,
![]() $\lvert N_G(x) \cap A\rvert \leq \Delta - \lvert N_G(x) \cap B\rvert $
, which yields
$\lvert N_G(x) \cap A\rvert \leq \Delta - \lvert N_G(x) \cap B\rvert $
, which yields
Since I is G-independent, Claim 3.1.3 implies that the sets
![]() $\Sigma (x)$
,
$\Sigma (x)$
,
![]() $x \in I$
, are pairwise disjoint. Using the fact that
$x \in I$
, are pairwise disjoint. Using the fact that
![]() $\bigcup _{x \in I} \Sigma (x) \subseteq A$
and the G-invariance of
$\bigcup _{x \in I} \Sigma (x) \subseteq A$
and the G-invariance of
![]() $\mu $
, we conclude that
$\mu $
, we conclude that
 $$ \begin{align*} \mu(A) \geq \int_{I} \lvert\Sigma(x)\rvert \mathrm{d}\mu(x). \end{align*} $$
$$ \begin{align*} \mu(A) \geq \int_{I} \lvert\Sigma(x)\rvert \mathrm{d}\mu(x). \end{align*} $$
From formula (3.7), it follows that
 $$ \begin{align*} \int_I \lvert\Sigma(x)\rvert \mathrm{d}\mu(x) \geq (2k - 2\lvert\mathcal{B}\rvert - \Delta) \mu(I) + \int_I \lvert N_G(x) \cap B\rvert \mathrm{d} \mu(x). \end{align*} $$
$$ \begin{align*} \int_I \lvert\Sigma(x)\rvert \mathrm{d}\mu(x) \geq (2k - 2\lvert\mathcal{B}\rvert - \Delta) \mu(I) + \int_I \lvert N_G(x) \cap B\rvert \mathrm{d} \mu(x). \end{align*} $$
Since I is a maximal G-independent subset of B, every vertex
![]() $z \in B \setminus I$
has a neighbour in I, and thus
$z \in B \setminus I$
has a neighbour in I, and thus
 $$ \begin{align*} \int_I \lvert N_G(x) \cap B\rvert \mathrm{d} \mu(x) = \int_{B \setminus I} \lvert N_G(z) \cap I\rvert \mathrm{d} \mu(z) \geq \mu(B \setminus I) = \mu(B) - \mu(I). \end{align*} $$
$$ \begin{align*} \int_I \lvert N_G(x) \cap B\rvert \mathrm{d} \mu(x) = \int_{B \setminus I} \lvert N_G(z) \cap I\rvert \mathrm{d} \mu(z) \geq \mu(B \setminus I) = \mu(B) - \mu(I). \end{align*} $$
To summarise, we have
Claim 3.1.4 and the inequality
![]() $k \geq \Delta +1$
yield
$k \geq \Delta +1$
yield
![]() $2k-2\lvert \mathcal {B}\rvert -\Delta - 1> 0$
. Hence, since
$2k-2\lvert \mathcal {B}\rvert -\Delta - 1> 0$
. Hence, since
![]() $\mu (I) \geq b$
, the right-hand side of formula (3.8) could only decrease if we replace
$\mu (I) \geq b$
, the right-hand side of formula (3.8) could only decrease if we replace
![]() $\mu (I)$
by b, so
$\mu (I)$
by b, so
Using
![]() $\mu (B) = \lvert \mathcal {B}\rvert b$
,
$\mu (B) = \lvert \mathcal {B}\rvert b$
,
![]() $\mu (A) = \lvert \mathcal {A}\rvert a = (k - \lvert \mathcal {B}\rvert )a$
and
$\mu (A) = \lvert \mathcal {A}\rvert a = (k - \lvert \mathcal {B}\rvert )a$
and
![]() $b> a$
, we obtain
$b> a$
, we obtain
which after simplifying becomes
![]() $k < \Delta + 1$
. This is a contradiction, and Lemma 3.1 is proved.
$k < \Delta + 1$
. This is a contradiction, and Lemma 3.1 is proved.
Roughly speaking, our strategy now is to start with an arbitrary proper colouring
![]() $f_0$
and repeatedly apply recolouring moves that improve it, producing an infinite sequence of colourings
$f_0$
and repeatedly apply recolouring moves that improve it, producing an infinite sequence of colourings
![]() $(f_n)_{n=0}^\infty $
. We then intend to show that this sequence converges to some ‘limit’ colouring
$(f_n)_{n=0}^\infty $
. We then intend to show that this sequence converges to some ‘limit’ colouring
![]() $f_\infty $
that cannot be improved by a recolouring move anymore (at least on a
$f_\infty $
that cannot be improved by a recolouring move anymore (at least on a
![]() $\mu $
-conull set), and hence by Lemma 3.1,
$\mu $
-conull set), and hence by Lemma 3.1,
![]() $f_\infty $
must be
$f_\infty $
must be
![]() $\mu $
-equitable. For this approach to work, we must argue that the ‘limit’ colouring
$\mu $
-equitable. For this approach to work, we must argue that the ‘limit’ colouring
![]() $f_\infty $
actually exists. This will be done using the Borel–Cantelli lemma: we will prove that
$f_\infty $
actually exists. This will be done using the Borel–Cantelli lemma: we will prove that
![]() $\sum _{n = 0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1}) < \infty $
, which implies that the pointwise limit
$\sum _{n = 0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1}) < \infty $
, which implies that the pointwise limit
![]() $\lim _{n \to \infty } f_n(x)$
exists for
$\lim _{n \to \infty } f_n(x)$
exists for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in V$
. To obtain an upper bound on
$x \in V$
. To obtain an upper bound on
![]() $\sum _{n = 0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1})$
, we will require a certain technical result (namely Lemma 3.2) that is proven in the next subsection. At this point we should note that our argument would be quite a bit simpler (and we would have no need of Lemma 3.2) if it were possible to control the recolouring process by some numerical parameter – for instance, if we could ensure that
$\sum _{n = 0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1})$
, we will require a certain technical result (namely Lemma 3.2) that is proven in the next subsection. At this point we should note that our argument would be quite a bit simpler (and we would have no need of Lemma 3.2) if it were possible to control the recolouring process by some numerical parameter – for instance, if we could ensure that
![]() ${\mathrm {disc}}_\mu (f_{n+1}) < {\mathrm {disc}}_\mu (f_n)$
. Unfortunately, this is not the case; the culprit is the recolouring move from Claim 3.1.3 (see Figure 4), during which a vertex may be added to a colour class
${\mathrm {disc}}_\mu (f_{n+1}) < {\mathrm {disc}}_\mu (f_n)$
. Unfortunately, this is not the case; the culprit is the recolouring move from Claim 3.1.3 (see Figure 4), during which a vertex may be added to a colour class
![]() $\left (\text {namely }V_\gamma \right )$
that is already ‘too large’.
$\left (\text {namely }V_\gamma \right )$
that is already ‘too large’.
3.2 Comparing distributions
Assumptions for Section 3.2
Fix a finite set of colours
![]() $\mathcal {C}$
of size
$\mathcal {C}$
of size
![]() $k \geq 1$
.
$k \geq 1$
.
As usual, for a function
![]() $\omega \colon \mathcal {C} \to \mathbb {R}$
, we write
$\omega \colon \mathcal {C} \to \mathbb {R}$
, we write
![]() $\lVert \omega \rVert _1 := \sum _{\alpha \in \mathcal {C}} \lvert \omega (\alpha )\rvert $
. A distribution (on
$\lVert \omega \rVert _1 := \sum _{\alpha \in \mathcal {C}} \lvert \omega (\alpha )\rvert $
. A distribution (on
![]() $\mathcal {C}$
) is a function
$\mathcal {C}$
) is a function
![]() $\omega \colon \mathcal {C} \to [0,1]$
such that
$\omega \colon \mathcal {C} \to [0,1]$
such that
![]() $\lVert \omega \rVert _1 = 1$
. The discrepancy of a distribution
$\lVert \omega \rVert _1 = 1$
. The discrepancy of a distribution
![]() $\omega $
is
$\omega $
is
 $$ \begin{align*} {\mathrm{disc}}(\omega) := \max_{\alpha \in \mathcal{C}} \left\lvert\omega(\alpha) - 1/k\right\rvert. \end{align*} $$
$$ \begin{align*} {\mathrm{disc}}(\omega) := \max_{\alpha \in \mathcal{C}} \left\lvert\omega(\alpha) - 1/k\right\rvert. \end{align*} $$
Given a pair of distributions
![]() $\omega $
and
$\omega $
and
![]() $\eta $
, we define the following two (disjoint) sets of colours:
$\eta $
, we define the following two (disjoint) sets of colours:
Observe the similarity between this definition and expression (3.2). We say that
![]() $\eta $
is more equitable than
$\eta $
is more equitable than
![]() $\omega $
– in symbols,
$\omega $
– in symbols,
![]() $\omega \vartriangleleft \eta $
– if there is a colour
$\omega \vartriangleleft \eta $
– if there is a colour
![]() $\alpha \in \mathcal {D}^+(\omega , \eta )$
such that for all
$\alpha \in \mathcal {D}^+(\omega , \eta )$
such that for all
![]() $\beta \in \mathcal {D}^-(\omega , \eta )$
, we have
$\beta \in \mathcal {D}^-(\omega , \eta )$
, we have
![]() $\eta (\alpha ) \leq \eta (\beta )$
, and we write
$\eta (\alpha ) \leq \eta (\beta )$
, and we write
![]() $\omega \trianglelefteq \eta $
to mean that
$\omega \trianglelefteq \eta $
to mean that
![]() $\omega \vartriangleleft \eta $
or
$\omega \vartriangleleft \eta $
or
![]() $\omega = \eta $
. Notice that the relation
$\omega = \eta $
. Notice that the relation
![]() $\vartriangleleft $
is antisymmetric and irreflexive; however, it is not transitive when
$\vartriangleleft $
is antisymmetric and irreflexive; however, it is not transitive when
![]() $k \geq 3$
. Nevertheless, the transitive closure of
$k \geq 3$
. Nevertheless, the transitive closure of
![]() $\vartriangleleft $
is a strict partial order on distributions, which justifies our use of the order-like symbol ‘
$\vartriangleleft $
is a strict partial order on distributions, which justifies our use of the order-like symbol ‘
![]() $\vartriangleleft $
’.Footnote
1
We also point out that if
$\vartriangleleft $
’.Footnote
1
We also point out that if
![]() $\eta (\alpha ) = 1/k$
for all
$\eta (\alpha ) = 1/k$
for all
![]() $\alpha \in \mathcal {C}$
(i.e., if
$\alpha \in \mathcal {C}$
(i.e., if
![]() $\eta $
is the uniform distribution), then
$\eta $
is the uniform distribution), then
![]() $\eta $
is more equitable than all other distributions
$\eta $
is more equitable than all other distributions
![]() $\omega $
.
$\omega $
.
Lemma 3.2. Let
![]() $(\omega _n)_{n=0}^\infty $
be a sequence of distributions on
$(\omega _n)_{n=0}^\infty $
be a sequence of distributions on
![]() $\mathcal {C}$
such that for all
$\mathcal {C}$
such that for all
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
![]() $\omega _n \trianglelefteq \omega _{n+1}$
. Suppose that there is a real number
$\omega _n \trianglelefteq \omega _{n+1}$
. Suppose that there is a real number
![]() $A \geq 1$
such that for all
$A \geq 1$
such that for all
![]() $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
![]() $\alpha \in \mathcal {D}^+(\omega _n, \omega _{n+1})$
,
$\alpha \in \mathcal {D}^+(\omega _n, \omega _{n+1})$
,
Then
 $$ \begin{align*} \sum_{n=0}^\infty \lVert\omega_{n+1} - \omega_{n}\rVert_1 \leq \frac{(1+A)^{k+1}}{A} \cdot {\mathrm{disc}}(\omega_0) < \infty. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty \lVert\omega_{n+1} - \omega_{n}\rVert_1 \leq \frac{(1+A)^{k+1}}{A} \cdot {\mathrm{disc}}(\omega_0) < \infty. \end{align*} $$
Proof. For each distribution
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
![]() $\omega ^\ast \colon \left \{1, \dotsc , k\right \} \to [0,1]$
denote the mapping obtained by putting the values of
$\omega ^\ast \colon \left \{1, \dotsc , k\right \} \to [0,1]$
denote the mapping obtained by putting the values of
![]() $\omega $
in nondecreasing order; that is, the lists
$\omega $
in nondecreasing order; that is, the lists
contain the same elements, and also
![]() $\omega ^\ast (1) \leq \omega ^\ast (2) \leq \dotsb \leq \omega ^\ast (k)$
.
$\omega ^\ast (1) \leq \omega ^\ast (2) \leq \dotsb \leq \omega ^\ast (k)$
.
Claim 3.2.1. For all distributions
![]() $\omega $
and
$\omega $
and
![]() $\eta $
, we have
$\eta $
, we have
![]() $\lVert \omega ^\ast - \eta ^\ast \rVert _1 \leq \lVert \omega - \eta \rVert _1$
.
$\lVert \omega ^\ast - \eta ^\ast \rVert _1 \leq \lVert \omega - \eta \rVert _1$
.
Proof. For each
![]() $\alpha \in \mathcal {C}$
, let
$\alpha \in \mathcal {C}$
, let
![]() $I_\alpha $
be the open interval with endpoints
$I_\alpha $
be the open interval with endpoints
![]() $\omega (\alpha )$
and
$\omega (\alpha )$
and
![]() $\eta (\alpha )$
. Similarly, for each
$\eta (\alpha )$
. Similarly, for each
![]() $1 \leq i \leq k$
, let
$1 \leq i \leq k$
, let
![]() $J_i$
be the open interval with endpoints
$J_i$
be the open interval with endpoints
![]() $\omega ^\ast (i)$
and
$\omega ^\ast (i)$
and
![]() $\eta ^\ast (i)$
. Then
$\eta ^\ast (i)$
. Then
 $$ \begin{align} \lVert\omega - \eta\rVert_1 = \sum_{\alpha \in \mathcal{C}} \text{length}(I_\alpha) \qquad \text{and} \qquad \lVert\omega^\ast - \eta^\ast\rVert_1 = \sum_{i=1}^k \text{length}(J_i). \end{align} $$
$$ \begin{align} \lVert\omega - \eta\rVert_1 = \sum_{\alpha \in \mathcal{C}} \text{length}(I_\alpha) \qquad \text{and} \qquad \lVert\omega^\ast - \eta^\ast\rVert_1 = \sum_{i=1}^k \text{length}(J_i). \end{align} $$
Define
![]() $S := \left \{\omega (\alpha ), \ \eta (\alpha ) : \alpha \in \mathcal {C}\right \}$
. Note that the set S is finite. We shall argue that for each
$S := \left \{\omega (\alpha ), \ \eta (\alpha ) : \alpha \in \mathcal {C}\right \}$
. Note that the set S is finite. We shall argue that for each
![]() $x \in \mathbb {R}\setminus S$
, the number of colours
$x \in \mathbb {R}\setminus S$
, the number of colours
![]() $\alpha $
with
$\alpha $
with
![]() $x \in I_\alpha $
is not less than the number of indices i with
$x \in I_\alpha $
is not less than the number of indices i with
![]() $x \in J_i$
; in view of equation (3.9), this immediately yields the claim. Take any
$x \in J_i$
; in view of equation (3.9), this immediately yields the claim. Take any
![]() $x \in \mathbb {R}\setminus S$
and define
$x \in \mathbb {R}\setminus S$
and define
Then x is in precisely
![]() $\lvert \tau (x) - \sigma (x)\rvert $
of the intervals
$\lvert \tau (x) - \sigma (x)\rvert $
of the intervals
![]() $J_i$
,
$J_i$
,
![]() $1 \leq i \leq k$
. On the other hand, if
$1 \leq i \leq k$
. On the other hand, if
![]() $\tau (x) \geq \sigma (x)$
, then there are at least
$\tau (x) \geq \sigma (x)$
, then there are at least
![]() $\tau (x) - \sigma (x)$
colours
$\tau (x) - \sigma (x)$
colours
![]() $\alpha $
with
$\alpha $
with
![]() $\omega (\alpha ) < x < \eta (\alpha )$
, whereas if
$\omega (\alpha ) < x < \eta (\alpha )$
, whereas if
![]() $\sigma (x) \geq \tau (x)$
, then there are at least
$\sigma (x) \geq \tau (x)$
, then there are at least
![]() $\sigma (x) - \tau (x)$
colours
$\sigma (x) - \tau (x)$
colours
![]() $\alpha $
with
$\alpha $
with
![]() $\eta (\alpha ) < x < \omega (\alpha )$
. In either case, x belongs to at least
$\eta (\alpha ) < x < \omega (\alpha )$
. In either case, x belongs to at least
![]() $\lvert \tau (x) - \sigma (x)\rvert $
of the intervals
$\lvert \tau (x) - \sigma (x)\rvert $
of the intervals
![]() $I_\alpha $
,
$I_\alpha $
,
![]() $\alpha \in \mathcal {C}$
, and hence we are done.
$\alpha \in \mathcal {C}$
, and hence we are done.
The proof of Lemma 3.2 rests on the following key observation:
Claim 3.2.2. Suppose that
![]() $\omega $
and
$\omega $
and
![]() $\eta $
are distributions on
$\eta $
are distributions on
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\omega \vartriangleleft \eta $
. Then there is an index
$\omega \vartriangleleft \eta $
. Then there is an index
![]() $\ell $
such that
$\ell $
such that
![]() $\omega ^\ast (i) \leq \eta ^\ast (i)$
for all
$\omega ^\ast (i) \leq \eta ^\ast (i)$
for all
![]() $1 \leq i \leq \ell $
, and there is a colour
$1 \leq i \leq \ell $
, and there is a colour
![]() $\alpha \in \mathcal {D}^+(\omega , \eta )$
with
$\alpha \in \mathcal {D}^+(\omega , \eta )$
with
 $$ \begin{align} \sum_{i=1}^\ell \eta^\ast(i) - \sum_{i=1}^\ell \omega^\ast(i) \geq \eta(\alpha) - \omega(\alpha). \end{align} $$
$$ \begin{align} \sum_{i=1}^\ell \eta^\ast(i) - \sum_{i=1}^\ell \omega^\ast(i) \geq \eta(\alpha) - \omega(\alpha). \end{align} $$
Proof. Let
![]() $\alpha \in \mathcal {D}^+(\omega , \eta )$
be such that for all
$\alpha \in \mathcal {D}^+(\omega , \eta )$
be such that for all
![]() $\beta \in \mathcal {D}^-(\omega , \eta )$
, we have
$\beta \in \mathcal {D}^-(\omega , \eta )$
, we have
![]() $\eta (\alpha ) \leq \eta (\beta )$
; and let
$\eta (\alpha ) \leq \eta (\beta )$
; and let
![]() $\ell $
be the least index such that
$\ell $
be the least index such that
![]() $\eta ^\ast (\ell ) = \eta (\alpha )$
. We claim that this choice of
$\eta ^\ast (\ell ) = \eta (\alpha )$
. We claim that this choice of
![]() $\ell $
and
$\ell $
and
![]() $\alpha $
works.
$\alpha $
works.
To begin with, fix a bijection
![]() $\left \{1, \dotsc , k\right \} \to \mathcal {C} \colon i \mapsto \alpha _i$
such that
$\left \{1, \dotsc , k\right \} \to \mathcal {C} \colon i \mapsto \alpha _i$
such that
![]() $\eta ^\ast (i) = \eta (\alpha _i)$
for all
$\eta ^\ast (i) = \eta (\alpha _i)$
for all
![]() $1 \leq i \leq k$
, and
$1 \leq i \leq k$
, and
![]() $\alpha _\ell = \alpha $
. Consider any
$\alpha _\ell = \alpha $
. Consider any
![]() $1 \leq i \leq \ell $
. We have
$1 \leq i \leq \ell $
. We have
![]() $\eta (\alpha _i) = \eta ^\ast (i) \leq \eta ^\ast (\ell )$
, where equality holds if and only if
$\eta (\alpha _i) = \eta ^\ast (i) \leq \eta ^\ast (\ell )$
, where equality holds if and only if
![]() $i = \ell $
. By the choice of
$i = \ell $
. By the choice of
![]() $\alpha $
, this yields
$\alpha $
, this yields
![]() $\alpha _i \not \in \mathcal {D}^-(\omega , \eta )$
, and therefore
$\alpha _i \not \in \mathcal {D}^-(\omega , \eta )$
, and therefore
![]() $\omega (\alpha _i) \leq \eta (\alpha _i) = \eta ^\ast (i)$
. Thus, there are at least i colours – namely
$\omega (\alpha _i) \leq \eta (\alpha _i) = \eta ^\ast (i)$
. Thus, there are at least i colours – namely
![]() $\alpha _1, \dotsc , \alpha _i$
– for which the value of
$\alpha _1, \dotsc , \alpha _i$
– for which the value of
![]() $\omega $
does not exceed
$\omega $
does not exceed
![]() $\eta ^\ast (i)$
. But this precisely means that
$\eta ^\ast (i)$
. But this precisely means that
![]() $\eta ^\ast (i) \geq \omega ^\ast (i)$
, as desired.
$\eta ^\ast (i) \geq \omega ^\ast (i)$
, as desired.
Next we prove formula (3.10). Let
![]() $1 \leq t \leq \ell $
be the largest index such that
$1 \leq t \leq \ell $
be the largest index such that
![]() $\omega ^\ast (t) \leq \omega (\alpha )$
(such a t exists, as
$\omega ^\ast (t) \leq \omega (\alpha )$
(such a t exists, as
![]() $\omega ^\ast (1) \leq \omega (\alpha )$
). We claim that if
$\omega ^\ast (1) \leq \omega (\alpha )$
). We claim that if
![]() $t < s \leq \ell $
, then
$t < s \leq \ell $
, then
![]() $\omega ^\ast (s) \leq \eta ^\ast (s-1)$
. Indeed, suppose, toward a contradiction, that
$\omega ^\ast (s) \leq \eta ^\ast (s-1)$
. Indeed, suppose, toward a contradiction, that
![]() $\omega ^\ast (s)> \eta ^\ast (s-1)$
. Then
$\omega ^\ast (s)> \eta ^\ast (s-1)$
. Then
![]() $\omega ^\ast (s-1) \leq \eta ^\ast (s-1) < \omega ^\ast (s)$
, meaning that the only colours for which the value of
$\omega ^\ast (s-1) \leq \eta ^\ast (s-1) < \omega ^\ast (s)$
, meaning that the only colours for which the value of
![]() $\omega $
is at most
$\omega $
is at most
![]() $\eta ^\ast (s-1)$
are
$\eta ^\ast (s-1)$
are
![]() $\alpha _1, \dotsc , \alpha _{s-1}$
. Since
$\alpha _1, \dotsc , \alpha _{s-1}$
. Since
![]() $\alpha = \alpha _\ell $
is not among them,
$\alpha = \alpha _\ell $
is not among them,
![]() $\omega (\alpha ) \geq \omega ^\ast (s)$
, contradicting the choice of t and the fact that
$\omega (\alpha ) \geq \omega ^\ast (s)$
, contradicting the choice of t and the fact that
![]() $s> t$
. Now we can write
$s> t$
. Now we can write
 $$ \begin{align*}\hspace{1.5pc} \sum_{i=1}^\ell \eta^\ast(i) - \sum_{i=1}^\ell \omega^\ast(i) &= \eta^\ast(\ell) + \sum_{s=t+1}^\ell \left(\eta^\ast(s-1) - \omega^\ast(s)\right) - \omega^\ast(t) \,+\, \sum_{i = 1}^{t-1} \left(\eta^\ast(i) - \omega^\ast(i)\right) \\ &\geq \eta^\ast(\ell) - \omega^\ast(t) \qquad\qquad\qquad\qquad \ \ \, ({\text{the other summands are nonnegative}}) \\[4pt] &\geq \eta(\alpha) - \omega(\alpha), \qquad\qquad\qquad\qquad({\text{since}\ \eta^\ast(\ell) = \eta(\alpha)\ \text{and}\ \omega^\ast(t) \leq \omega(\alpha)}) \end{align*} $$
$$ \begin{align*}\hspace{1.5pc} \sum_{i=1}^\ell \eta^\ast(i) - \sum_{i=1}^\ell \omega^\ast(i) &= \eta^\ast(\ell) + \sum_{s=t+1}^\ell \left(\eta^\ast(s-1) - \omega^\ast(s)\right) - \omega^\ast(t) \,+\, \sum_{i = 1}^{t-1} \left(\eta^\ast(i) - \omega^\ast(i)\right) \\ &\geq \eta^\ast(\ell) - \omega^\ast(t) \qquad\qquad\qquad\qquad \ \ \, ({\text{the other summands are nonnegative}}) \\[4pt] &\geq \eta(\alpha) - \omega(\alpha), \qquad\qquad\qquad\qquad({\text{since}\ \eta^\ast(\ell) = \eta(\alpha)\ \text{and}\ \omega^\ast(t) \leq \omega(\alpha)}) \end{align*} $$
as desired.
Now let
![]() $(\omega _n)_{n=0}^\infty $
be as in the statement of Lemma 3.2. Define
$(\omega _n)_{n=0}^\infty $
be as in the statement of Lemma 3.2. Define
 $S_n(\ell ) := \sum _{i=1}^\ell \omega ^\ast _n(i)$
for each
$S_n(\ell ) := \sum _{i=1}^\ell \omega ^\ast _n(i)$
for each
![]() $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
![]() $1 \leq \ell \leq k$
. Define
$1 \leq \ell \leq k$
. Define
![]() $R := \left \{n \in {\mathbb {N}} : \omega _n \neq \omega _{n+1}\right \}$
. Claim 3.2.2 shows that for every
$R := \left \{n \in {\mathbb {N}} : \omega _n \neq \omega _{n+1}\right \}$
. Claim 3.2.2 shows that for every
![]() $n \in R$
, there exist an index
$n \in R$
, there exist an index
![]() $\ell _n$
and a colour
$\ell _n$
and a colour
![]() $\alpha _n \in \mathcal {D}^+(\omega , \eta )$
such that
$\alpha _n \in \mathcal {D}^+(\omega , \eta )$
such that
![]() $\omega ^\ast _n(i) \leq \omega ^\ast _{n+1}(i)$
for all
$\omega ^\ast _n(i) \leq \omega ^\ast _{n+1}(i)$
for all
![]() $1 \leq i \leq \ell _n$
, and also
$1 \leq i \leq \ell _n$
, and also
For each
![]() $\ell $
, define
$\ell $
, define
![]() $R_\ell := \left \{n \in R : \ell _n = \ell \right \}$
and
$R_\ell := \left \{n \in R : \ell _n = \ell \right \}$
and
 $R_{<\ell } := \left \{n \in R : \ell _n < \ell \right \} = \bigcup _{i=1}^{\ell -1} R_i$
. We will show that
$R_{<\ell } := \left \{n \in R : \ell _n < \ell \right \} = \bigcup _{i=1}^{\ell -1} R_i$
. We will show that
 $$ \begin{align} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \frac{(1+A)^\ell - 1}{A} \cdot {\mathrm{disc}}(\omega_0). \end{align} $$
$$ \begin{align} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \frac{(1+A)^\ell - 1}{A} \cdot {\mathrm{disc}}(\omega_0). \end{align} $$
Once inequality (3.12) is proved, we obtain, using formula (3.11), that
 $$ \begin{align*} \sum_{n=0}^\infty \lVert\omega_{n+1} - \omega_n\rVert_1 &\leq A \cdot \sum_{n\in R} \left(S_{n+1}(\ell_n) - S_n(\ell_n)\right) \\ &= A \cdot \sum_{\ell=1}^k \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \\ &\leq \sum_{\ell=1}^k \left((1+A)^\ell - 1\right) \cdot {\mathrm{disc}}(\omega_0) = \frac{(1+A)^{k+1} - (k+1)A - 1}{A}\cdot {\mathrm{disc}}(\omega_0)\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \, ({\text{by formula (3.12)}}) \\ &\leq \frac{(1+A)^{k+1}}{A} \cdot {\mathrm{disc}}(\omega_0), \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty \lVert\omega_{n+1} - \omega_n\rVert_1 &\leq A \cdot \sum_{n\in R} \left(S_{n+1}(\ell_n) - S_n(\ell_n)\right) \\ &= A \cdot \sum_{\ell=1}^k \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \\ &\leq \sum_{\ell=1}^k \left((1+A)^\ell - 1\right) \cdot {\mathrm{disc}}(\omega_0) = \frac{(1+A)^{k+1} - (k+1)A - 1}{A}\cdot {\mathrm{disc}}(\omega_0)\\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \, ({\text{by formula (3.12)}}) \\ &\leq \frac{(1+A)^{k+1}}{A} \cdot {\mathrm{disc}}(\omega_0), \end{align*} $$
as desired. To prove formula (3.12), we use induction on
![]() $\ell $
, so suppose that the inequality holds with
$\ell $
, so suppose that the inequality holds with
![]() $\ell $
replaced by any
$\ell $
replaced by any
![]() $1 \leq i < \ell $
. Notice that if
$1 \leq i < \ell $
. Notice that if
![]() $\ell _n \geq \ell $
, then
$\ell _n \geq \ell $
, then
![]() $S_{n+1}(\ell ) - S_n(\ell ) \geq 0$
. Hence, for each
$S_{n+1}(\ell ) - S_n(\ell ) \geq 0$
. Hence, for each
![]() $m \in {\mathbb {N}}$
,
$m \in {\mathbb {N}}$
,
 $$ \begin{align*} \ell \cdot {\mathrm{disc}}(\omega_0) \geq \frac{\ell}{k} - S_0(\ell) &\geq S_{m+1}(\ell) - S_0(\ell) = \sum_{n = 0}^{m} \left(S_{n+1}(\ell) - S_n(\ell)\right) \\ &\geq \sum_{\substack{n \in R_\ell \\ n \leq m}} \left(S_{n+1}(\ell) - S_n(\ell)\right) - \sum_{\substack{n \in R_{< \ell} \\ n \leq m}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert. \end{align*} $$
$$ \begin{align*} \ell \cdot {\mathrm{disc}}(\omega_0) \geq \frac{\ell}{k} - S_0(\ell) &\geq S_{m+1}(\ell) - S_0(\ell) = \sum_{n = 0}^{m} \left(S_{n+1}(\ell) - S_n(\ell)\right) \\ &\geq \sum_{\substack{n \in R_\ell \\ n \leq m}} \left(S_{n+1}(\ell) - S_n(\ell)\right) - \sum_{\substack{n \in R_{< \ell} \\ n \leq m}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert. \end{align*} $$
As m here is arbitrary, we conclude that
 $$ \begin{align*} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \ell \cdot {\mathrm{disc}}(\omega_0) + \sum_{n \in R_{< \ell}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert. \end{align*} $$
$$ \begin{align*} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \ell \cdot {\mathrm{disc}}(\omega_0) + \sum_{n \in R_{< \ell}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert. \end{align*} $$
We can now write the following chain of inequalities:
 $$ \begin{align*} \hspace{3.2pc} \sum_{n \in R_{< \ell}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert &\leq \sum_{n \in R_{< \ell}} \left\lVert\omega^\ast_{n+1} - \omega^\ast_n \right\rVert_1 \\ &\leq \sum_{n \in R_{< \ell}} \left\lVert\omega_{n+1} - \omega_n \right\rVert_1 & \qquad ({\text{by Claim 3.2.1}}) \\ &\leq A \cdot \sum_{i=1}^{\ell-1} \sum_{n \in R_i} \left(S_{n+1}(i) - S_n(i)\right) & \qquad ({\text{by formula (3.11)}} )\\ &\leq \sum_{i = 1}^{\ell-1} \left((1+A)^i - 1\right) \cdot {\mathrm{disc}}(\omega_0). & \qquad ({\text{by the inductive hypothesis}}) \end{align*} $$
$$ \begin{align*} \hspace{3.2pc} \sum_{n \in R_{< \ell}} \left\lvert S_{n+1}(\ell) - S_n(\ell)\right\rvert &\leq \sum_{n \in R_{< \ell}} \left\lVert\omega^\ast_{n+1} - \omega^\ast_n \right\rVert_1 \\ &\leq \sum_{n \in R_{< \ell}} \left\lVert\omega_{n+1} - \omega_n \right\rVert_1 & \qquad ({\text{by Claim 3.2.1}}) \\ &\leq A \cdot \sum_{i=1}^{\ell-1} \sum_{n \in R_i} \left(S_{n+1}(i) - S_n(i)\right) & \qquad ({\text{by formula (3.11)}} )\\ &\leq \sum_{i = 1}^{\ell-1} \left((1+A)^i - 1\right) \cdot {\mathrm{disc}}(\omega_0). & \qquad ({\text{by the inductive hypothesis}}) \end{align*} $$
Therefore,
 $$ \begin{align*} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \ell \cdot {\mathrm{disc}}(\omega_0)+ \sum_{i = 1}^{\ell-1} \left((1+A)^i - 1\right) \cdot {\mathrm{disc}}(\omega_0) = \frac{(1+A)^{\ell}-1}{A} \cdot {\mathrm{disc}}(\omega_0), \end{align*} $$
$$ \begin{align*} \sum_{n \in R_\ell} \left(S_{n+1}(\ell) - S_n(\ell)\right) \leq \ell \cdot {\mathrm{disc}}(\omega_0)+ \sum_{i = 1}^{\ell-1} \left((1+A)^i - 1\right) \cdot {\mathrm{disc}}(\omega_0) = \frac{(1+A)^{\ell}-1}{A} \cdot {\mathrm{disc}}(\omega_0), \end{align*} $$
and the proof is complete.
3.3 Perfecting a colouring
Assumptions for Section 3.3
Fix an aperiodic Borel graph G of finite maximum degree
![]() $\Delta $
with vertex set V and edge set E and a finite set of colours
$\Delta $
with vertex set V and edge set E and a finite set of colours
![]() $\mathcal {C}$
of size
$\mathcal {C}$
of size
![]() $k \geq \Delta + 1$
.
$k \geq \Delta + 1$
.
Let
![]() $f \colon V \to \mathcal {C}$
be a Borel colouring. Given a probability measure
$f \colon V \to \mathcal {C}$
be a Borel colouring. Given a probability measure
![]() $\mu $
on V, f gives rise to the push-forward distribution
$\mu $
on V, f gives rise to the push-forward distribution
![]() $f_\ast (\mu )$
on
$f_\ast (\mu )$
on
![]() $\mathcal {C}$
defined by
$\mathcal {C}$
defined by
![]() $f_\ast (\mu )(\alpha ) := \mu \left (f^{-1}(\alpha )\right )$
. Note that
$f_\ast (\mu )(\alpha ) := \mu \left (f^{-1}(\alpha )\right )$
. Note that
![]() ${\mathrm {disc}}(f_\ast (\mu )) = {\mathrm {disc}}_\mu (f)$
.
${\mathrm {disc}}(f_\ast (\mu )) = {\mathrm {disc}}_\mu (f)$
.
Lemma 3.3. If
![]() $\mu $
is a probability measure on V and
$\mu $
is a probability measure on V and
![]() $f, g \colon V \to \mathcal {C}$
are
$f, g \colon V \to \mathcal {C}$
are
![]() $\mu $
-measurable, then
$\mu $
-measurable, then
Proof. For
![]() $\alpha , \beta \in \mathcal {C}$
, define
$\alpha , \beta \in \mathcal {C}$
, define
![]() $V_{\alpha \beta } := f^{-1}(\alpha ) \cap g^{-1}(\beta )$
. Then, for each fixed
$V_{\alpha \beta } := f^{-1}(\alpha ) \cap g^{-1}(\beta )$
. Then, for each fixed
![]() $\alpha \in \mathcal {C}$
,
$\alpha \in \mathcal {C}$
,
 $$ \begin{align*} \left\lvert\mu\left(f^{-1}(\alpha)\right) - \mu\left(g^{-1}(\alpha)\right)\right\rvert = \left\lvert\sum_{\beta \in \mathcal{C}} \mu\left(V_{\alpha \beta}\right) - \sum_{\beta \in \mathcal{C}} \mu\left(V_{\beta \alpha}\right) \right\rvert \leq \sum_{\substack{\beta \in \mathcal{C}\\\beta \neq \alpha}} \left(\mu\left(V_{\alpha \beta}\right) + \mu\left(V_{\beta \alpha}\right)\right) \end{align*} $$
$$ \begin{align*} \left\lvert\mu\left(f^{-1}(\alpha)\right) - \mu\left(g^{-1}(\alpha)\right)\right\rvert = \left\lvert\sum_{\beta \in \mathcal{C}} \mu\left(V_{\alpha \beta}\right) - \sum_{\beta \in \mathcal{C}} \mu\left(V_{\beta \alpha}\right) \right\rvert \leq \sum_{\substack{\beta \in \mathcal{C}\\\beta \neq \alpha}} \left(\mu\left(V_{\alpha \beta}\right) + \mu\left(V_{\beta \alpha}\right)\right) \end{align*} $$
and therefore,
 $$ \begin{align*} \hspace{-16pt}\lVert f_\ast(\mu)-g_\ast(\mu)\rVert_1 \leq \sum_{\alpha \in \mathcal{C}} \sum_{\substack{\beta \in \mathcal{C}\\\beta \neq \alpha}} \left(\mu\left(V_{\alpha \beta}\right) + \mu\left(V_{\beta \alpha}\right)\right) = 2 \cdot \sum_{\substack{\alpha, \beta \in \mathcal{C}\\\alpha \neq \beta}} \mu\left(V_{\alpha \beta}\right) = 2 \cdot {\mathrm{dist}}_\mu(f,g).\\[-55pt] \end{align*} $$
$$ \begin{align*} \hspace{-16pt}\lVert f_\ast(\mu)-g_\ast(\mu)\rVert_1 \leq \sum_{\alpha \in \mathcal{C}} \sum_{\substack{\beta \in \mathcal{C}\\\beta \neq \alpha}} \left(\mu\left(V_{\alpha \beta}\right) + \mu\left(V_{\beta \alpha}\right)\right) = 2 \cdot \sum_{\substack{\alpha, \beta \in \mathcal{C}\\\alpha \neq \beta}} \mu\left(V_{\alpha \beta}\right) = 2 \cdot {\mathrm{dist}}_\mu(f,g).\\[-55pt] \end{align*} $$
Starting with a Borel proper
![]() $\mathcal {C}$
-colouring f, we wish to apply recolouring moves in order to make the distribution
$\mathcal {C}$
-colouring f, we wish to apply recolouring moves in order to make the distribution
![]() $f_\ast (\mu )$
more equitable. Since applying a single recolouring move changes f on only a finite set of vertices, we have to be able to apply infinitely many recolouring moves simultaneously, but we must take care that the moves do not interfere with each other. Say that a set
$f_\ast (\mu )$
more equitable. Since applying a single recolouring move changes f on only a finite set of vertices, we have to be able to apply infinitely many recolouring moves simultaneously, but we must take care that the moves do not interfere with each other. Say that a set
![]() $M \subseteq \mathsf {RM}$
is G-separated if for every two distinct recolouring moves
$M \subseteq \mathsf {RM}$
is G-separated if for every two distinct recolouring moves
![]() $\varphi , \varphi ' \in M$
,
$\varphi , \varphi ' \in M$
,
-
(S1)
 $\mathrm {dom}(\varphi ) \cap \mathrm {dom}(\varphi ') = \varnothing $
and
$\mathrm {dom}(\varphi ) \cap \mathrm {dom}(\varphi ') = \varnothing $
and -
(S2) there are no edges in G between
 $\mathrm {dom}(\varphi )$
and
$\mathrm {dom}(\varphi )$
and
 $\mathrm {dom}(\varphi ')$
.
$\mathrm {dom}(\varphi ')$
.
For a Borel G-separated set
![]() $M \subseteq \mathsf {RM}$
, define a (Borel) colouring
$M \subseteq \mathsf {RM}$
, define a (Borel) colouring
![]() $f \oplus M \colon V \to \mathcal {C}$
via
$f \oplus M \colon V \to \mathcal {C}$
via
 $$ \begin{align*} (f \oplus M)(x) := \begin{cases} \varphi(x) &\text{if } \varphi \in M \text{ and } x \in \mathrm{dom}(\varphi),\\ f(x) &\text{if } x \not \in \mathrm{dom}(M). \end{cases} \end{align*} $$
$$ \begin{align*} (f \oplus M)(x) := \begin{cases} \varphi(x) &\text{if } \varphi \in M \text{ and } x \in \mathrm{dom}(\varphi),\\ f(x) &\text{if } x \not \in \mathrm{dom}(M). \end{cases} \end{align*} $$
In other words,
![]() $f \oplus M$
is the result of simultaneously applying every recolouring move
$f \oplus M$
is the result of simultaneously applying every recolouring move
![]() $\varphi \in M$
. This is well defined by (S1). Notice that if every recolouring move
$\varphi \in M$
. This is well defined by (S1). Notice that if every recolouring move
![]() $\varphi \in M$
is acceptable for f, then
$\varphi \in M$
is acceptable for f, then
![]() $f \oplus M$
is a proper colouring of G by (S2).
$f \oplus M$
is a proper colouring of G by (S2).
To better control the properties of
![]() $f \oplus M$
, it is convenient to assume that the recolouring moves in M are somewhat similar to each other. Specifically, given a Borel proper
$f \oplus M$
, it is convenient to assume that the recolouring moves in M are somewhat similar to each other. Specifically, given a Borel proper
![]() $\mathcal {C}$
-colouring f of G, an integer
$\mathcal {C}$
-colouring f of G, an integer
![]() $m \in {\mathbb {N}}^+$
and disjoint nonempty sets
$m \in {\mathbb {N}}^+$
and disjoint nonempty sets
![]() $\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
, let
$\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
, let
![]() $\mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
denote the set of all recolouring moves
$\mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
denote the set of all recolouring moves
![]() $\varphi \in \mathsf {RM}_m$
such that
$\varphi \in \mathsf {RM}_m$
such that
![]() $\varphi $
is acceptable for f and
$\varphi $
is acceptable for f and
Note that the set
![]() $\mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
is Borel. If
$\mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
is Borel. If
![]() $M \subseteq \mathsf {RM}_m\left (f;\mathcal {D}^+, \mathcal {D}^-\right )$
is a Borel G-separated subset and
$M \subseteq \mathsf {RM}_m\left (f;\mathcal {D}^+, \mathcal {D}^-\right )$
is a Borel G-separated subset and
![]() $\mu $
is a G-invariant probability measure on V, then either
$\mu $
is a G-invariant probability measure on V, then either
![]() $\mu (M) = 0$
or
$\mu (M) = 0$
or
Lemma 3.4. Let f be a Borel proper
![]() $\mathcal {C}$
-colouring of G. Fix
$\mathcal {C}$
-colouring of G. Fix
![]() $m \in {\mathbb {N}}^+$
and disjoint nonempty sets
$m \in {\mathbb {N}}^+$
and disjoint nonempty sets
![]() $\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
. If
$\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
. If
![]() $M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
is a Borel G-separated set, then for every G-invariant probability measure
$M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
is a Borel G-separated set, then for every G-invariant probability measure
![]() $\mu $
the following are true:
$\mu $
the following are true:
-
(1)
 ${\mathrm {dist}}_\mu (f,f \oplus M) \leq m \cdot \lVert f_\ast (\mu )-(f \oplus M)_\ast (\mu )\rVert _1$
and
${\mathrm {dist}}_\mu (f,f \oplus M) \leq m \cdot \lVert f_\ast (\mu )-(f \oplus M)_\ast (\mu )\rVert _1$
and -
(2) for all
 $\alpha \in \mathcal {D}^+$
, we have
$\alpha \in \mathcal {D}^+$
, we have
 $\lVert f_\ast (\mu )-(f \oplus M)_\ast (\mu )\rVert _1 \leq 2m \cdot \left (\mu \left ((f \oplus M)^{-1}(\alpha )\right ) - \mu \left (f^{-1}(\alpha )\right )\right )$
.
$\lVert f_\ast (\mu )-(f \oplus M)_\ast (\mu )\rVert _1 \leq 2m \cdot \left (\mu \left ((f \oplus M)^{-1}(\alpha )\right ) - \mu \left (f^{-1}(\alpha )\right )\right )$
.
Proof. Since each
![]() $\varphi \in M$
has finite domain, there is a Borel function
$\varphi \in M$
has finite domain, there is a Borel function
![]() $p \colon M \to V$
such that
$p \colon M \to V$
such that
![]() $p(\varphi ) \in \mathrm {dom}(\varphi )$
for every
$p(\varphi ) \in \mathrm {dom}(\varphi )$
for every
![]() $\varphi \in M$
(see Section 2.0.1). Set
$\varphi \in M$
(see Section 2.0.1). Set
![]() $P := \mathrm {im}(p)$
. Note that P is Borel, as it is the image of a Borel set under an injective Borel function [Reference KechrisKec95, Corollary 15.2]. Since for each
$P := \mathrm {im}(p)$
. Note that P is Borel, as it is the image of a Borel set under an injective Borel function [Reference KechrisKec95, Corollary 15.2]. Since for each
![]() $\varphi \in M$
we have
$\varphi \in M$
we have
![]() $\lvert \mathrm {dom}(\varphi ) \cap P\rvert = 1$
and
$\lvert \mathrm {dom}(\varphi ) \cap P\rvert = 1$
and
![]() $\lvert \mathrm {dom}(\varphi )\rvert \leq m$
, and since
$\lvert \mathrm {dom}(\varphi )\rvert \leq m$
, and since
![]() $\mu $
is G-invariant, we conclude that
$\mu $
is G-invariant, we conclude that
![]() $\mu (P) \geq \mu (M)/m$
. For each
$\mu (P) \geq \mu (M)/m$
. For each
![]() $x \in P$
, let
$x \in P$
, let
![]() $\varphi _x \in M$
be the unique recolouring move such that
$\varphi _x \in M$
be the unique recolouring move such that
![]() $p(\varphi _x) = x$
. The G-invariance of
$p(\varphi _x) = x$
. The G-invariance of
![]() $\mu $
yields that for each
$\mu $
yields that for each
![]() $\alpha \in \mathcal {C}$
,
$\alpha \in \mathcal {C}$
,

where
is defined in expression (3.1). Crucially,
![]() $M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
, which means that
$M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
, which means that
for all
![]() $\alpha \in \mathcal {D}^+$
and
$\alpha \in \mathcal {D}^+$
and
![]() $\varphi \in M$
. Hence, for any
$\varphi \in M$
. Hence, for any
![]() $\alpha \in \mathcal {D}^+$
, we can write
$\alpha \in \mathcal {D}^+$
, we can write
 $$ \begin{align*} \lVert f_\ast(\mu)-(f \oplus M)_\ast(\mu)\rVert_1 &\geq \mu\left((f \oplus M)^{-1}(\alpha)\right) - \mu\left(f^{-1}(\alpha)\right) \\ &\geq \int_P 1 \mathrm{d}\mu(x) = \mu(P) \geq \frac{\mu(M)}{m} \\ &\geq \frac{{\mathrm{dist}}_\mu(f, f \oplus M)}{m}\\ &\geq \frac{1}{2m}\cdot \lVert f_\ast(\mu)-(f \oplus M)_\ast(\mu)\rVert_1.\qquad\qquad\qquad ({\text{by Lemma 3.3}}) &\\[-42pt]\end{align*} $$
$$ \begin{align*} \lVert f_\ast(\mu)-(f \oplus M)_\ast(\mu)\rVert_1 &\geq \mu\left((f \oplus M)^{-1}(\alpha)\right) - \mu\left(f^{-1}(\alpha)\right) \\ &\geq \int_P 1 \mathrm{d}\mu(x) = \mu(P) \geq \frac{\mu(M)}{m} \\ &\geq \frac{{\mathrm{dist}}_\mu(f, f \oplus M)}{m}\\ &\geq \frac{1}{2m}\cdot \lVert f_\ast(\mu)-(f \oplus M)_\ast(\mu)\rVert_1.\qquad\qquad\qquad ({\text{by Lemma 3.3}}) &\\[-42pt]\end{align*} $$
The following lemma is the main result of this subsection:
Lemma 3.5. Let f be a Borel proper
![]() $\mathcal {C}$
-colouring of G. Fix an integer
$\mathcal {C}$
-colouring of G. Fix an integer
![]() $m \in {\mathbb {N}}^+$
and disjoint nonempty sets
$m \in {\mathbb {N}}^+$
and disjoint nonempty sets
![]() $\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
. Let
$\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
. Let
![]() $M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
be a Borel G-separated set.
$M \subseteq \mathsf {RM}_m\left (f; \mathcal {D}^+, \mathcal {D}^-\right )$
be a Borel G-separated set.
-
(a) For every G-invariant probability measure
 $\mu $
, there is a Borel proper
$\mu $
, there is a Borel proper
 $\mathcal {C}$
-colouring g such that
$\mathcal {C}$
-colouring g such that-
(P1)
 ${\mathrm {dist}}_\mu (f,g) \leq m \cdot \lVert f_\ast (\mu )-g_\ast (\mu )\rVert _1$
;
${\mathrm {dist}}_\mu (f,g) \leq m \cdot \lVert f_\ast (\mu )-g_\ast (\mu )\rVert _1$
; -
(P2) for all
 $\alpha \in \mathcal {D}^+(f_\ast (\mu ), g_\ast (\mu ))$
, we have
$\alpha \in \mathcal {D}^+(f_\ast (\mu ), g_\ast (\mu ))$
, we have
 $\lVert f_\ast (\mu )-g_\ast (\mu )\rVert _1 \leq 2m \cdot \left (\mu \left (g^{-1}(\alpha )\right ) - \mu \left (f^{-1}(\alpha )\right )\right )$
;
$\lVert f_\ast (\mu )-g_\ast (\mu )\rVert _1 \leq 2m \cdot \left (\mu \left (g^{-1}(\alpha )\right ) - \mu \left (f^{-1}(\alpha )\right )\right )$
; -
(P3)
 $f_\ast (\mu ) \trianglelefteq g_\ast (\mu )$
; and
$f_\ast (\mu ) \trianglelefteq g_\ast (\mu )$
; and -
(P4) g is
 $(\mu , M)$
-perfect.
$(\mu , M)$
-perfect.
-
-
(b) Furthermore, G admits a Borel proper
 $\mathcal {C}$
-colouring g such that statements (P1)–(P1) hold for every ergodic G-invariant probability measure
$\mathcal {C}$
-colouring g such that statements (P1)–(P1) hold for every ergodic G-invariant probability measure
 $\mu $
simultaneously.
$\mu $
simultaneously.
Proof. Since G is aperiodic, every G-invariant probability measure is atomless, so if M is countable, then we can simply take
![]() $g = f$
. Hence, we may assume that M is uncountable. Due to the Borel isomorphism theorem [Reference KechrisKec95, Theorem 15.6], we can fix a Borel bijection
$g = f$
. Hence, we may assume that M is uncountable. Due to the Borel isomorphism theorem [Reference KechrisKec95, Theorem 15.6], we can fix a Borel bijection
![]() $\mathbb {R}_{\geq 0} \to M \colon t \mapsto \varphi _t$
. For
$\mathbb {R}_{\geq 0} \to M \colon t \mapsto \varphi _t$
. For
![]() $t \in \mathbb {R}_{\geq 0} \cup \left \{\infty \right \}$
, define
$t \in \mathbb {R}_{\geq 0} \cup \left \{\infty \right \}$
, define
![]() $M_t := \left \{\varphi _s : 0 \leq s < t\right \}$
. In particular,
$M_t := \left \{\varphi _s : 0 \leq s < t\right \}$
. In particular,
![]() $M_0 = \varnothing $
and
$M_0 = \varnothing $
and
![]() $M_\infty = M$
. Define
$M_\infty = M$
. Define
![]() $f_t := f \oplus M_t$
.
$f_t := f \oplus M_t$
.
Now let
![]() $\mu $
be a G-invariant probability measure. Observe the following facts:
$\mu $
be a G-invariant probability measure. Observe the following facts:
-
• For each
 $\alpha \in \mathcal {D}^+$
, the function
$\alpha \in \mathcal {D}^+$
, the function
 $t \mapsto \mu \left (f_t^{-1}(\alpha )\right )$
is nondecreasing.
$t \mapsto \mu \left (f_t^{-1}(\alpha )\right )$
is nondecreasing. -
• For each
 $\beta \in \mathcal {D}^-$
, the function
$\beta \in \mathcal {D}^-$
, the function
 $t \mapsto \mu \left (f_t^{-1}(\beta )\right )$
is nonincreasing.
$t \mapsto \mu \left (f_t^{-1}(\beta )\right )$
is nonincreasing. -
• For each
 $\gamma \in \mathcal {C} \setminus \left (\mathcal {D}^+ \cup \mathcal {D}^-\right )$
, the function
$\gamma \in \mathcal {C} \setminus \left (\mathcal {D}^+ \cup \mathcal {D}^-\right )$
, the function
 $t \mapsto \mu \left (f_t^{-1}(\gamma )\right )$
is constant.
$t \mapsto \mu \left (f_t^{-1}(\gamma )\right )$
is constant.
Furthermore, since
![]() $\mu $
is atomless, we have the following additional fact:
$\mu $
is atomless, we have the following additional fact:
-
• For each
 $\gamma \in \mathcal {C}$
, the function
$\gamma \in \mathcal {C}$
, the function
 $t \mapsto \mu \left (f^{-1}_t(\gamma )\right )$
is continuous.
$t \mapsto \mu \left (f^{-1}_t(\gamma )\right )$
is continuous.
By definition,
![]() $f_\ast (\mu ) \trianglelefteq (f_t)_\ast (\mu )$
if and only if either
$f_\ast (\mu ) \trianglelefteq (f_t)_\ast (\mu )$
if and only if either
![]() $f_\ast (\mu ) = (f_t)_\ast (\mu )$
or there is an
$f_\ast (\mu ) = (f_t)_\ast (\mu )$
or there is an
![]() $\alpha \in \mathcal {D}^+$
such that
$\alpha \in \mathcal {D}^+$
such that
 $$ \begin{align*} \mu\left(f_t^{-1}(\alpha)\right) \leq \mu\left(f_t^{-1}(\beta)\right) \qquad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
$$ \begin{align*} \mu\left(f_t^{-1}(\alpha)\right) \leq \mu\left(f_t^{-1}(\beta)\right) \qquad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
This shows that the set of all
![]() $t \in \mathbb {R}_{\geq 0} \cup \left \{\infty \right \}$
such that
$t \in \mathbb {R}_{\geq 0} \cup \left \{\infty \right \}$
such that
![]() $f_\ast (\mu ) \trianglelefteq (f_t)_\ast (\mu )$
is closed. Hence, if we define
$f_\ast (\mu ) \trianglelefteq (f_t)_\ast (\mu )$
is closed. Hence, if we define
then
![]() $f_\ast (\mu ) \trianglelefteq (g_\mu )_\ast (\mu )$
. Also, by Lemma 3.4, statements (P1) and (P1) hold with
$f_\ast (\mu ) \trianglelefteq (g_\mu )_\ast (\mu )$
. Also, by Lemma 3.4, statements (P1) and (P1) hold with
![]() $g_\mu $
in place of g.
$g_\mu $
in place of g.
Claim 3.5.1. The colouring
![]() $g_\mu $
is
$g_\mu $
is
![]() $(\mu , M)$
-perfect.
$(\mu , M)$
-perfect.
Proof. We will show that in fact there is no recolouring move
![]() $\varphi \in M$
that improves
$\varphi \in M$
that improves
![]() $g_\mu $
. Indeed, suppose that
$g_\mu $
. Indeed, suppose that
![]() $\varphi \in M$
improves
$\varphi \in M$
improves
![]() $g_\mu $
. Then
$g_\mu $
. Then
![]() $\varphi \not \in M_{T\left (\mu \right )}$
, as otherwise we would have
$\varphi \not \in M_{T\left (\mu \right )}$
, as otherwise we would have
![]() $\varphi \subseteq g_\mu $
. In particular, this means that
$\varphi \subseteq g_\mu $
. In particular, this means that
![]() $T(\mu ) < \infty $
. Since
$T(\mu ) < \infty $
. Since
![]() $\varphi $
improves
$\varphi $
improves
![]() $g_\mu $
, we can fix
$g_\mu $
, we can fix
![]() $\alpha \in \mathcal {D}^+$
such that
$\alpha \in \mathcal {D}^+$
such that
 $$ \begin{align*} s\mu\left(g_\mu^{-1}(\alpha)\right) < \mu\left(g_\mu^{-1}(\beta)\right) \quad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
$$ \begin{align*} s\mu\left(g_\mu^{-1}(\alpha)\right) < \mu\left(g_\mu^{-1}(\beta)\right) \quad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
The functions
![]() $t \mapsto \mu \left (f_t^{-1}(\gamma )\right )$
,
$t \mapsto \mu \left (f_t^{-1}(\gamma )\right )$
,
![]() $\gamma \in \mathcal {C}$
, are continuous, so there is some
$\gamma \in \mathcal {C}$
, are continuous, so there is some
![]() $\varepsilon> 0$
satisfying
$\varepsilon> 0$
satisfying
 $$ \begin{align*} \mu\left(f_{T\left(\mu\right) + \varepsilon}^{-1}(\alpha)\right) < \mu\left(f_{T\left(\mu\right) + \varepsilon}^{-1}(\beta)\right) \quad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
$$ \begin{align*} \mu\left(f_{T\left(\mu\right) + \varepsilon}^{-1}(\alpha)\right) < \mu\left(f_{T\left(\mu\right) + \varepsilon}^{-1}(\beta)\right) \quad \text{for all } \beta \in \mathcal{D}^-. \end{align*} $$
This is a contradiction of the choice of
![]() $T(\mu )$
.
$T(\mu )$
.
The foregoing observations show that with respect to the measure
![]() $\mu $
, statements (P1)–(P1) hold with
$\mu $
, statements (P1)–(P1) hold with
![]() $g_\mu $
in place of g, which yields part (a) of the lemma. To prove part (b), we use the uniform ergodic decomposition theorem. The statement is vacuous if
$g_\mu $
in place of g, which yields part (a) of the lemma. To prove part (b), we use the uniform ergodic decomposition theorem. The statement is vacuous if
![]() $\mathsf {Erg}(G) = \varnothing $
, so assume that
$\mathsf {Erg}(G) = \varnothing $
, so assume that
![]() $\mathsf {Erg}(G) \neq \varnothing $
and let
$\mathsf {Erg}(G) \neq \varnothing $
and let
![]() $V \to \mathsf {Erg}(G) \colon x \mapsto \mu _x$
be a G-invariant Borel surjection given by Theorem 2.4. Notice that due to [Reference KechrisKec95, Theorem 17.25], the function
$V \to \mathsf {Erg}(G) \colon x \mapsto \mu _x$
be a G-invariant Borel surjection given by Theorem 2.4. Notice that due to [Reference KechrisKec95, Theorem 17.25], the function
is Borel. Hence, if we set
![]() $T(x) := T(\mu _x)$
for each
$T(x) := T(\mu _x)$
for each
![]() $x \in V$
and define
$x \in V$
and define
then g is a Borel
![]() $\mathcal {C}$
-colouring of G, and this colouring g has all the desired properties. Indeed, for each
$\mathcal {C}$
-colouring of G, and this colouring g has all the desired properties. Indeed, for each
![]() $\mu \in \mathsf {Erg}(G)$
, g agrees with
$\mu \in \mathsf {Erg}(G)$
, g agrees with
![]() $g_\mu $
on the
$g_\mu $
on the
![]() $\mu $
-conull G-invariant set
$\mu $
-conull G-invariant set
![]() $\left \{x \in V : \mu _x = \mu \right \}$
, and thus inherits the properties pertaining to
$\left \{x \in V : \mu _x = \mu \right \}$
, and thus inherits the properties pertaining to
![]() $\mu $
from
$\mu $
from
![]() $g_\mu $
.
$g_\mu $
.
3.4
 $\mu $
-Equitability
$\mu $
-Equitability
Assumptions for Section 3.4
Fix an aperiodic Borel graph G of finite maximum degree
![]() $\Delta $
with vertex set V and edge set E and a finite set of colours
$\Delta $
with vertex set V and edge set E and a finite set of colours
![]() $\mathcal {C}$
of size
$\mathcal {C}$
of size
![]() $k \geq \Delta + 1$
.
$k \geq \Delta + 1$
.
Lemma 3.6. Let f be a Borel proper
![]() $\mathcal {C}$
-colouring of G.
$\mathcal {C}$
-colouring of G.
-
(a) For every G-invariant probability measure
 $\mu $
, there is a
$\mu $
, there is a
 $\mu $
/equitable
$\mu $
/equitable
 $\mathcal {C}$
-colouring g such that (3.13)
$\mathcal {C}$
-colouring g such that (3.13) $$ \begin{align} {\mathrm{dist}}_\mu(f,g) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align} $$
$$ \begin{align} {\mathrm{dist}}_\mu(f,g) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align} $$
-
(b) Furthermore, G has a Borel proper
 $\mathcal {C}$
-colouring g such that for every ergodic G-invariant probability measure
$\mathcal {C}$
-colouring g such that for every ergodic G-invariant probability measure
 $\mu $
, g is
$\mu $
, g is
 $\mu $
-equitable and satisfies formula (3.13).
$\mu $
-equitable and satisfies formula (3.13).
Note that in view of the uniform ergodic decomposition theorem (specifically, Theorem 2.4(E2)), the colouring g given by Lemma 3.6(b) is in fact
![]() $\mu $
-equitable for all
$\mu $
-equitable for all
![]() $\mu \in \mathsf {Inv}(G)$
.
$\mu \in \mathsf {Inv}(G)$
.
Proof. The proofs of parts (a) and (b) of the lemma are virtually the same, except that the former relies on Lemma 3.5(a) and the latter on Lemma 3.5(b). We give the proof of part (a) and highlight the only place where it needs to be modified to prove part (b).
We start by partitioning
![]() $\mathsf {RM}$
into countably many Borel G-separated sets.
$\mathsf {RM}$
into countably many Borel G-separated sets.
Claim 3.6.1. There is a Borel function
![]() $c \colon \mathsf {RM} \to {\mathbb {N}}$
such that for each
$c \colon \mathsf {RM} \to {\mathbb {N}}$
such that for each
![]() $r \in {\mathbb {N}}$
,
$r \in {\mathbb {N}}$
,
![]() $c^{-1}(r)$
is G-separated.
$c^{-1}(r)$
is G-separated.
Proof. It will be more convenient to construct a Borel function
![]() $c \colon \mathsf {RM} \to {\mathbb {N}}^2$
such that for each pair
$c \colon \mathsf {RM} \to {\mathbb {N}}^2$
such that for each pair
![]() $(r_0,r_1) \in {\mathbb {N}}^2$
,
$(r_0,r_1) \in {\mathbb {N}}^2$
,
![]() $c^{-1}(r_0,r_1)$
is G-separated; this is sufficient, as the set
$c^{-1}(r_0,r_1)$
is G-separated; this is sufficient, as the set
![]() ${\mathbb {N}}^2$
is countable. With a slight (but standard) abuse of notation, let
${\mathbb {N}}^2$
is countable. With a slight (but standard) abuse of notation, let
![]() $\left [G\right ]^{<\infty }$
denote the set of all
$\left [G\right ]^{<\infty }$
denote the set of all
![]() $S \in \left [V\right ]^{<\infty }\setminus \left \{\varnothing \right \}$
such that every two elements of S are joined by a path in G. The proof of [Reference Kechris and MillerKM04, Lemma 7.3] shows that there exists a Borel function
$S \in \left [V\right ]^{<\infty }\setminus \left \{\varnothing \right \}$
such that every two elements of S are joined by a path in G. The proof of [Reference Kechris and MillerKM04, Lemma 7.3] shows that there exists a Borel function
![]() $\vartheta \colon \left [G\right ]^{<\infty } \to {\mathbb {N}}$
such that for each
$\vartheta \colon \left [G\right ]^{<\infty } \to {\mathbb {N}}$
such that for each
![]() $r \in {\mathbb {N}}$
, the sets in
$r \in {\mathbb {N}}$
, the sets in
![]() $\vartheta ^{-1}(r)$
are pairwise disjoint. The mapping
$\vartheta ^{-1}(r)$
are pairwise disjoint. The mapping
![]() $c_0 \colon \mathsf {RM} \to {\mathbb {N}} \colon \varphi \mapsto \vartheta (\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )))$
almost does the trick; the only problem is that two distinct recolouring moves
$c_0 \colon \mathsf {RM} \to {\mathbb {N}} \colon \varphi \mapsto \vartheta (\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )))$
almost does the trick; the only problem is that two distinct recolouring moves
![]() $\varphi , \psi $
may satisfy
$\varphi , \psi $
may satisfy
![]() $\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )) = \mathrm {dom}(\psi ) \cup N_G(\mathrm {dom}(\psi ))$
, in which case
$\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )) = \mathrm {dom}(\psi ) \cup N_G(\mathrm {dom}(\psi ))$
, in which case
![]() $c_0(\varphi ) = c_0(\psi )$
. However, for each
$c_0(\varphi ) = c_0(\psi )$
. However, for each
![]() $S \in \left [G\right ]^{<\infty }$
, there are only finitely many
$S \in \left [G\right ]^{<\infty }$
, there are only finitely many
![]() $\varphi \in \mathsf {RM}$
with
$\varphi \in \mathsf {RM}$
with
![]() $\mathrm {dom}(\varphi ) \cup N_G(\varphi ) = S$
. Hence, by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10], there is a Borel function
$\mathrm {dom}(\varphi ) \cup N_G(\varphi ) = S$
. Hence, by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10], there is a Borel function
![]() $c_1 \colon \mathsf {RM} \to {\mathbb {N}}$
such that if
$c_1 \colon \mathsf {RM} \to {\mathbb {N}}$
such that if
![]() $\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )) = \mathrm {dom}(\psi ) \cup N_G(\mathrm {dom}(\psi ))$
for distinct
$\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi )) = \mathrm {dom}(\psi ) \cup N_G(\mathrm {dom}(\psi ))$
for distinct
![]() $\varphi , \psi \in \mathsf {RM}$
, then
$\varphi , \psi \in \mathsf {RM}$
, then
![]() $c_1(\varphi ) \neq c_1(\psi )$
. Then we can set
$c_1(\varphi ) \neq c_1(\psi )$
. Then we can set
![]() $c(\varphi ) := (c_0(\varphi ), c_1(\varphi ))$
.
$c(\varphi ) := (c_0(\varphi ), c_1(\varphi ))$
.
Now let
![]() $\mu $
be a G-invariant probability measure. We recursively construct a sequence of Borel proper
$\mu $
be a G-invariant probability measure. We recursively construct a sequence of Borel proper
![]() $\mathcal {C}$
-colourings
$\mathcal {C}$
-colourings
![]() $f_n$
,
$f_n$
,
![]() $n \in {\mathbb {N}}$
, as follows. Fix a Borel function
$n \in {\mathbb {N}}$
, as follows. Fix a Borel function
![]() $c \colon \mathsf {RM} \to {\mathbb {N}}$
as in Claim 3.6.1. Let
$c \colon \mathsf {RM} \to {\mathbb {N}}$
as in Claim 3.6.1. Let
 $\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right )_{n \in {\mathbb {N}}}$
be a sequence of triples such that
$\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right )_{n \in {\mathbb {N}}}$
be a sequence of triples such that
-
(R1) for all
 $n\in {\mathbb {N}}$
,
$n\in {\mathbb {N}}$
,
 $r_n \in {\mathbb {N}}$
and
$r_n \in {\mathbb {N}}$
and
 $\mathcal {D}^+_n, \mathcal {D}^-_n$
are disjoint nonempty subsets of
$\mathcal {D}^+_n, \mathcal {D}^-_n$
are disjoint nonempty subsets of
 $\mathcal {C}$
; and
$\mathcal {C}$
; and -
(R2) every triple
 $\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
as in (R1) appears in the sequence
$\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
as in (R1) appears in the sequence
 $\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right )_{n \in {\mathbb {N}}}$
infinitely often.
$\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right )_{n \in {\mathbb {N}}}$
infinitely often.
Set
![]() $f_0 := f$
. Once
$f_0 := f$
. Once
![]() $f_n$
is defined, set
$f_n$
is defined, set
 $$ \begin{align*} M_n := \mathsf{RM}_3\left(f_n; \mathcal{D}^+_n, \mathcal{D}^-_n\right) \cap c^{-1}(r_n). \end{align*} $$
$$ \begin{align*} M_n := \mathsf{RM}_3\left(f_n; \mathcal{D}^+_n, \mathcal{D}^-_n\right) \cap c^{-1}(r_n). \end{align*} $$
Intersecting with
![]() $c^{-1}(r_n)$
ensures that
$c^{-1}(r_n)$
ensures that
![]() $M_n$
is G-separated, so we can apply Lemma 3.5(a) with
$M_n$
is G-separated, so we can apply Lemma 3.5(a) with
in order to obtain a Borel proper
![]() $\mathcal {C}$
-colouring
$\mathcal {C}$
-colouring
![]() $f_{n+1}$
such that:
$f_{n+1}$
such that:
-
(P1)
 ${\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq 3 \cdot \lVert (f_n)_\ast (\mu )-(f_{n+1})_\ast (\mu )\rVert _1$
;
${\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq 3 \cdot \lVert (f_n)_\ast (\mu )-(f_{n+1})_\ast (\mu )\rVert _1$
; -
(P2) for all
 $\alpha \in \mathcal {D}^+((f_n)_\ast (\mu ), (f_{n+1})_\ast (\mu ))$
, we have
$\alpha \in \mathcal {D}^+((f_n)_\ast (\mu ), (f_{n+1})_\ast (\mu ))$
, we have  $$ \begin{align*} \lVert(f_n)_\ast(\mu) - (f_{n+1})_\ast(\mu)\rVert_1 \leq 6 \cdot \left(\mu\left(f_{n+1}^{-1}(\alpha)\right) - \mu\left(f_n^{-1}(\alpha)\right)\right); \end{align*} $$
$$ \begin{align*} \lVert(f_n)_\ast(\mu) - (f_{n+1})_\ast(\mu)\rVert_1 \leq 6 \cdot \left(\mu\left(f_{n+1}^{-1}(\alpha)\right) - \mu\left(f_n^{-1}(\alpha)\right)\right); \end{align*} $$
-
(P3)
 $(f_n)_\ast (\mu ) \trianglelefteq (f_{n+1})_\ast (\mu )$
; and
$(f_n)_\ast (\mu ) \trianglelefteq (f_{n+1})_\ast (\mu )$
; and -
(P4)
 $f_{n+1}$
is
$f_{n+1}$
is
 $(\mu , M_n)$
-perfect.
$(\mu , M_n)$
-perfect.
To establish part (b) of the lemma, we instead apply Lemma 3.5(b) to obtain a Borel proper
![]() $\mathcal {C}$
-colouring
$\mathcal {C}$
-colouring
![]() $f_{n+1}$
that satisfies (P1)–(P4) for every
$f_{n+1}$
that satisfies (P1)–(P4) for every
![]() $\mu \in \mathsf {Erg}(G)$
. When the sequence
$\mu \in \mathsf {Erg}(G)$
. When the sequence
![]() $f_n$
,
$f_n$
,
![]() $n \in {\mathbb {N}}$
, is constructed, we define a Borel partial
$n \in {\mathbb {N}}$
, is constructed, we define a Borel partial
![]() $\mathcal {C}$
-colouring
$\mathcal {C}$
-colouring
![]() $f_\infty \colon V \rightharpoonup \mathcal {C}$
via the pointwise limit
$f_\infty \colon V \rightharpoonup \mathcal {C}$
via the pointwise limit
 $$ \begin{align*} f_\infty(x) := \lim_{n \to \infty} f_n(x). \end{align*} $$
$$ \begin{align*} f_\infty(x) := \lim_{n \to \infty} f_n(x). \end{align*} $$
Since each
![]() $f_n$
is a proper colouring,
$f_n$
is a proper colouring,
![]() $f_\infty $
is also proper, and since
$f_\infty $
is also proper, and since
![]() $k \geq \Delta + 1$
, we can extend
$k \geq \Delta + 1$
, we can extend
![]() $f_\infty $
to a Borel proper
$f_\infty $
to a Borel proper
![]() $\mathcal {C}$
-colouring g using Corollary 2.2. We claim that this g is as desired.
$\mathcal {C}$
-colouring g using Corollary 2.2. We claim that this g is as desired.
To begin with, notice that conditions (P2) and (P3) enable us to apply Lemma 3.2 to the sequence
![]() $((f_n)_\ast (\mu ))_{n \in {\mathbb {N}}}$
with
$((f_n)_\ast (\mu ))_{n \in {\mathbb {N}}}$
with
![]() $A = 6$
and conclude, using (P1), that
$A = 6$
and conclude, using (P1), that
 $$ \begin{align*} \sum_{n=0}^\infty {\mathrm{dist}}_\mu(f_n, f_{n+1}) \leq 3 \cdot \sum_{n=0}^\infty \lVert(f_n)_\ast(\mu) - (f_{n+1})_\ast(\mu)\rVert_1 \leq \frac{7^{k+1}}{2} \cdot {\mathrm{disc}}_\mu(f) < \infty. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty {\mathrm{dist}}_\mu(f_n, f_{n+1}) \leq 3 \cdot \sum_{n=0}^\infty \lVert(f_n)_\ast(\mu) - (f_{n+1})_\ast(\mu)\rVert_1 \leq \frac{7^{k+1}}{2} \cdot {\mathrm{disc}}_\mu(f) < \infty. \end{align*} $$
By the Borel–Cantelli lemma, this implies that
![]() $f_\infty $
is defined for
$f_\infty $
is defined for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in V$
; furthermore,
$x \in V$
; furthermore,
 $$ \begin{align*} {\mathrm{dist}}_\mu(f, g) = {\mathrm{dist}}_\mu(f, f_\infty) \leq \frac{7^{k+1}}{2} \cdot {\mathrm{disc}}_\mu(f). \end{align*} $$
$$ \begin{align*} {\mathrm{dist}}_\mu(f, g) = {\mathrm{dist}}_\mu(f, f_\infty) \leq \frac{7^{k+1}}{2} \cdot {\mathrm{disc}}_\mu(f). \end{align*} $$
(For simplicity, we bound the latter expression by
![]() $7^{k+1} \cdot {\mathrm {disc}}_\mu (f)$
in formula (3.13).) It remains to show that g is
$7^{k+1} \cdot {\mathrm {disc}}_\mu (f)$
in formula (3.13).) It remains to show that g is
![]() $\mu $
-equitable. To this end, we pass to a
$\mu $
-equitable. To this end, we pass to a
![]() $\mu $
-conull G-invariant Borel subset of V and assume that
$\mu $
-conull G-invariant Borel subset of V and assume that
![]() $g = f_\infty $
. Suppose, toward a contradiction, that g is not
$g = f_\infty $
. Suppose, toward a contradiction, that g is not
![]() $\mu $
-equitable. Then, by Lemma 3.1, g is not
$\mu $
-equitable. Then, by Lemma 3.1, g is not
![]() $(\mu , \mathsf {RM}_3)$
-perfect – that is,
$(\mu , \mathsf {RM}_3)$
-perfect – that is,
As there are only countably many triples
![]() $\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
with
$\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
with
![]() $r \in {\mathbb {N}}$
and
$r \in {\mathbb {N}}$
and
![]() $\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
disjoint and nonempty, we can choose
$\mathcal {D}^+, \mathcal {D}^- \subseteq \mathcal {C}$
disjoint and nonempty, we can choose
![]() $\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
such that
$\left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
such that
 $$ \begin{align} \mu\left(\left\{\varphi \in \mathsf{RM}_3\left(g; \mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) : \varphi\ \text{improves}\ g\ \text{with respect to}\ \mu\right\}\right)> 0. \end{align} $$
$$ \begin{align} \mu\left(\left\{\varphi \in \mathsf{RM}_3\left(g; \mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) : \varphi\ \text{improves}\ g\ \text{with respect to}\ \mu\right\}\right)> 0. \end{align} $$
Claim 3.6.2. If
![]() $\varphi \in \mathsf {RM}_3\left (g; \mathcal {D}^+, \mathcal {D}^-\right )$
, then for all sufficiently large
$\varphi \in \mathsf {RM}_3\left (g; \mathcal {D}^+, \mathcal {D}^-\right )$
, then for all sufficiently large
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
-
(a)
 $\varphi \in \mathsf {RM}_3\left (f_n; \mathcal {D}^+, \mathcal {D}^-\right )$
and
$\varphi \in \mathsf {RM}_3\left (f_n; \mathcal {D}^+, \mathcal {D}^-\right )$
and -
(b) if
 $\varphi $
improves g with respect to
$\varphi $
improves g with respect to
 $\mu $
, then
$\mu $
, then
 $\varphi $
also improves
$\varphi $
also improves
 $f_n$
with respect to
$f_n$
with respect to
 $\mu $
.
$\mu $
.
Proof. (a) This statement is implied by the fact that for all sufficiently large
![]() $n \in {\mathbb {N}}$
,
$n \in {\mathbb {N}}$
,
![]() $f_n$
and g agree on
$f_n$
and g agree on
![]() $\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi ))$
(since, by our assumption,
$\mathrm {dom}(\varphi ) \cup N_G(\mathrm {dom}(\varphi ))$
(since, by our assumption,
![]() $g = f_\infty $
).
$g = f_\infty $
).
(b) This follows from (a) and the observation that if
![]() $\alpha , \beta \in \mathcal {C}$
are such that
$\alpha , \beta \in \mathcal {C}$
are such that
![]() $\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
, then
$\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
, then
![]() $\mu \left (f_n^{-1}(\alpha )\right ) < \mu \left (f_n^{-1}(\beta )\right )$
for all large enough
$\mu \left (f_n^{-1}(\alpha )\right ) < \mu \left (f_n^{-1}(\beta )\right )$
for all large enough
![]() $n \in {\mathbb {N}}$
.
$n \in {\mathbb {N}}$
.
Claim 3.6.2 and formula (3.14) together show that there is
![]() $n_0 \in {\mathbb {N}}$
such that for all
$n_0 \in {\mathbb {N}}$
such that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
 $$ \begin{align*} \mu\left(\left\{\varphi \in \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) : \varphi\ \text{improves}\ f_n\ \text{with respect to} \mu\right\}\right)> 0. \end{align*} $$
$$ \begin{align*} \mu\left(\left\{\varphi \in \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) : \varphi\ \text{improves}\ f_n\ \text{with respect to} \mu\right\}\right)> 0. \end{align*} $$
This precisely means that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
 $$ \begin{align*} f_n\ \text{is not}\ \left(\mu, \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r)\right)\text{-perfect}. \end{align*} $$
$$ \begin{align*} f_n\ \text{is not}\ \left(\mu, \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r)\right)\text{-perfect}. \end{align*} $$
But this is a contradiction, as there is
![]() $n \geq n_0$
with
$n \geq n_0$
with
![]() $\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right ) = \left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
, so
$\left (r_n, \mathcal {D}^+_n, \mathcal {D}^-_n\right ) = \left (r, \mathcal {D}^+, \mathcal {D}^-\right )$
, so
 $$ \begin{align*} \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) = M_n, \end{align*} $$
$$ \begin{align*} \mathsf{RM}_3\left(f_n;\mathcal{D}^+, \mathcal{D}^-\right) \cap c^{-1}(r) = M_n, \end{align*} $$
and
![]() $f_{n+1}$
is
$f_{n+1}$
is
![]() $(\mu , M_n)$
-perfect by (P4).
$(\mu , M_n)$
-perfect by (P4).
3.5 Compressible graphs
In this subsection we consider the case when G is a Borel graph without any G-invariant probability measures; this situation is complementary to the one in Lemma 3.6. We begin by assembling some basic facts about such graphs. Throughout this subsection, G denotes a locally countable Borel graph.
A (not necessarily finite) measure
![]() $\nu $
on a subset
$\nu $
on a subset
![]() $U \subseteq V(G)$
is G-invariant if
$U \subseteq V(G)$
is G-invariant if
![]() $\nu (A) = \nu (B)$
whenever
$\nu (A) = \nu (B)$
whenever
![]() $A, B \subseteq U$
and
$A, B \subseteq U$
and
![]() $A \approx _G B$
. Note that G-invariance for a measure
$A \approx _G B$
. Note that G-invariance for a measure
![]() $\nu $
on
$\nu $
on
![]() $U \subseteq V(G)$
is in general stronger than
$U \subseteq V(G)$
is in general stronger than
![]() $G[U]$
-invariance. There is a useful combinatorial characterisation, due to Nadkarni [Reference NadkarniNad90] and subsequently generalised by Becker and Kechris [Reference Becker and KechrisBK96, Chapter 4], of Borel sets
$G[U]$
-invariance. There is a useful combinatorial characterisation, due to Nadkarni [Reference NadkarniNad90] and subsequently generalised by Becker and Kechris [Reference Becker and KechrisBK96, Chapter 4], of Borel sets
![]() $U \subseteq V(G)$
that do not support G-invariant probability measures, which we shall state after a few definitions. The G-saturation of a subset
$U \subseteq V(G)$
that do not support G-invariant probability measures, which we shall state after a few definitions. The G-saturation of a subset
![]() $U \subseteq V(G)$
, denoted by
$U \subseteq V(G)$
, denoted by
![]() $[U]_G$
, is the union of all connected components of G that intersect U. Observe that if
$[U]_G$
, is the union of all connected components of G that intersect U. Observe that if
![]() $A, B \subseteq V(G)$
are Borel subsets such that
$A, B \subseteq V(G)$
are Borel subsets such that
![]() $A \approx _G B$
, then
$A \approx _G B$
, then
![]() $[A]_G = [B]_G$
. Since G is locally countable, the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10] implies that G-saturations of Borel sets are Borel. A Borel set
$[A]_G = [B]_G$
. Since G is locally countable, the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10] implies that G-saturations of Borel sets are Borel. A Borel set
![]() $U \subseteq V(G)$
is
$U \subseteq V(G)$
is
-
• G-compressible if there is a Borel subset
 $A \subseteq U$
with
$A \subseteq U$
with
 $[A]_G = [U]_G$
and
$[A]_G = [U]_G$
and
 $U \approx _G U \setminus A$
, and
$U \approx _G U \setminus A$
, and -
• G-paradoxical if there is a Borel partition
 $U = U_0 \sqcup U_1$
with
$U = U_0 \sqcup U_1$
with
 $U_0 \approx _G U_1 \approx _G U$
.
$U_0 \approx _G U_1 \approx _G U$
.
The graph G itself is called compressible if
![]() $V(G)$
is a G-compressible set. Note that if G is compressible, then every G-invariant Borel subset
$V(G)$
is a G-compressible set. Note that if G is compressible, then every G-invariant Borel subset
![]() $U \subseteq V(G)$
is G-compressible.
$U \subseteq V(G)$
is G-compressible.
Theorem 3.7 ess. Nadkarni [Reference NadkarniNad90]
Let G be a locally countable Borel graph and let
![]() $U \subseteq V(G)$
be a Borel subset. The following statements are equivalent:
$U \subseteq V(G)$
be a Borel subset. The following statements are equivalent:
-
(i) U is not G-compressible.
-
(ii) U is not G-paradoxical.
-
(iii) There is a G-invariant probability measure
 $\nu $
on U.
$\nu $
on U. -
(iv) There is a G-invariant measure
 $\mu $
on
$\mu $
on
 $V(G)$
with
$V(G)$
with
 $0 < \mu (U) < \infty $
.
$0 < \mu (U) < \infty $
.
Proof. The equivalence (i)
![]() $\Longleftrightarrow $
(ii) is proven in [Reference Dougherty, Jackson and KechrisDJK94, Proposition 2.1]; Nadkarni’s theorem [Reference Becker and KechrisBK96, Theorem 4.3.1] gives (i)
$\Longleftrightarrow $
(ii) is proven in [Reference Dougherty, Jackson and KechrisDJK94, Proposition 2.1]; Nadkarni’s theorem [Reference Becker and KechrisBK96, Theorem 4.3.1] gives (i)
![]() $\Longleftrightarrow $
(iii); and (iii)
$\Longleftrightarrow $
(iii); and (iii)
![]() $\Longleftrightarrow $
(iv) follows by [Reference Dougherty, Jackson and KechrisDJK94, Proposition 3.2].
$\Longleftrightarrow $
(iv) follows by [Reference Dougherty, Jackson and KechrisDJK94, Proposition 3.2].
For compressible graphs G, the relation
![]() $\approx _G$
can be understood quite well; for instance, Chen [Reference ChenChe18] showed that if G is compressible, the set of all
$\approx _G$
can be understood quite well; for instance, Chen [Reference ChenChe18] showed that if G is compressible, the set of all
![]() $\approx _G$
-equivalence classes of Borel subsets of
$\approx _G$
-equivalence classes of Borel subsets of
![]() $V(G)$
forms a cardinal algebra in the sense of Tarski [Reference TarskiTar49]. We will make use of the following:
$V(G)$
forms a cardinal algebra in the sense of Tarski [Reference TarskiTar49]. We will make use of the following:
Proposition 3.8 [Reference Dougherty, Jackson and KechrisDJK94, Proposition 2.2]
Let G be a locally countable Borel graph and let
![]() $U \subseteq V(G)$
be a Borel subset. If U is G-compressible, then
$U \subseteq V(G)$
be a Borel subset. If U is G-compressible, then
![]() $U \approx _G [U]_G$
.
$U \approx _G [U]_G$
.
Corollary 3.9. Let G be a compressible Borel graph of finite maximum degree
![]() $\Delta $
. If
$\Delta $
. If
![]() $U \subseteq V(G)$
is a Borel subset such that
$U \subseteq V(G)$
is a Borel subset such that
![]() $N_G(U) \approx _G V(G)$
, then
$N_G(U) \approx _G V(G)$
, then
![]() $U \approx _G V(G)$
as well.
$U \approx _G V(G)$
as well.
Proof. Suppose, toward a contradiction, that
![]() $U \not \approx _G V(G)$
. Proposition 3.8 then shows that, since
$U \not \approx _G V(G)$
. Proposition 3.8 then shows that, since
![]() $V(G) = [N_G(U)]_G \subseteq [U]_G$
, the set U is not G-compressible. By Theorem 3.7, there is a G-invariant measure
$V(G) = [N_G(U)]_G \subseteq [U]_G$
, the set U is not G-compressible. By Theorem 3.7, there is a G-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
with
$V(G)$
with
![]() $0 < \mu (U) < \infty $
. But then
$0 < \mu (U) < \infty $
. But then
contradicting the compressibility of G.
Corollary 3.10. Let G be a compressible locally countable Borel graph and let f be a Borel proper k-colouring of G. The following statements are equivalent:
-
(i) f is Borel-equitable.
-
(ii) For every colour
 $\alpha $
,
$\alpha $
,
 $f^{-1}(\alpha ) \approx _G V(G)$
.
$f^{-1}(\alpha ) \approx _G V(G)$
. -
(iii) For every colour
 $\alpha $
,
$\alpha $
,
 $\left [f^{-1}(\alpha )\right ]_G = V(G)$
and
$\left [f^{-1}(\alpha )\right ]_G = V(G)$
and
 $f^{-1}(\alpha )$
is G-compressible.
$f^{-1}(\alpha )$
is G-compressible.
Proof. The implication (ii)
![]() $\Longrightarrow $
(i) is clear, and (iii)
$\Longrightarrow $
(i) is clear, and (iii)
![]() $\Longrightarrow $
(ii) follows by Proposition 3.8. To prove (i)
$\Longrightarrow $
(ii) follows by Proposition 3.8. To prove (i)
![]() $\Longrightarrow $
(iii), let f be Borel-equitable. This clearly implies that
$\Longrightarrow $
(iii), let f be Borel-equitable. This clearly implies that
 $\left [f^{-1}(\alpha )\right ]_G = V(G)$
for every colour
$\left [f^{-1}(\alpha )\right ]_G = V(G)$
for every colour
![]() $\alpha $
, so it remains to show that
$\alpha $
, so it remains to show that
![]() $f^{-1}(\alpha )$
is G-compressible. Take any nonzero G-invariant measure
$f^{-1}(\alpha )$
is G-compressible. Take any nonzero G-invariant measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
. Since f is Borel-equitable, all the colour classes of f have the same
$V(G)$
. Since f is Borel-equitable, all the colour classes of f have the same
![]() $\mu $
-measure, and hence
$\mu $
-measure, and hence
 $$ \begin{align*} \infty = \mu(V(G)) = k \cdot \mu\left(f^{-1}(\alpha)\right). \end{align*} $$
$$ \begin{align*} \infty = \mu(V(G)) = k \cdot \mu\left(f^{-1}(\alpha)\right). \end{align*} $$
This shows that
![]() $f^{-1}(\alpha )$
is G-compressible, by Theorem 3.7.
$f^{-1}(\alpha )$
is G-compressible, by Theorem 3.7.
In addition to the equivalence relation
![]() $\approx _G$
, it is useful to consider the preorder
$\approx _G$
, it is useful to consider the preorder
![]() $\preccurlyeq _G$
, defined as follows: given Borel sets
$\preccurlyeq _G$
, defined as follows: given Borel sets
![]() $A, B \subseteq V(G)$
, we write
$A, B \subseteq V(G)$
, we write
![]() $A \preccurlyeq _G B$
(or, equivalently,
$A \preccurlyeq _G B$
(or, equivalently,
![]() $B \succcurlyeq _G A$
) if
$B \succcurlyeq _G A$
) if
![]() $A \approx _G B'$
for some Borel
$A \approx _G B'$
for some Borel
![]() $B' \subseteq B$
. Additionally, if
$B' \subseteq B$
. Additionally, if
![]() $A \approx _G B'$
and for some Borel
$A \approx _G B'$
and for some Borel
![]() $B' \subseteq B$
such that
$B' \subseteq B$
such that
![]() $[B]_G = [B \setminus B']_G$
, then we write
$[B]_G = [B \setminus B']_G$
, then we write
![]() $A \prec _G B$
(or, equivalently,
$A \prec _G B$
(or, equivalently,
![]() $B \succ _G A$
). Thus, in particular, a Borel set
$B \succ _G A$
). Thus, in particular, a Borel set
![]() $U \subseteq V(G)$
is G-compressible if and only if
$U \subseteq V(G)$
is G-compressible if and only if
![]() $U \prec _G U$
. Note that if
$U \prec _G U$
. Note that if
![]() $A \preccurlyeq _G B$
, then
$A \preccurlyeq _G B$
, then
![]() $[A]_G \subseteq [B]_G$
and
$[A]_G \subseteq [B]_G$
and
![]() $\mu (A) \leq \mu (B)$
for every G-invariant measure
$\mu (A) \leq \mu (B)$
for every G-invariant measure
![]() $\mu $
. Furthermore, if
$\mu $
. Furthermore, if
![]() $A \prec _G B$
, then
$A \prec _G B$
, then
![]() $\mu (A) < \mu (B)$
for every G-invariant measure
$\mu (A) < \mu (B)$
for every G-invariant measure
![]() $\mu $
such that
$\mu $
such that
![]() $\mu ([B]_G)> 0$
. Indeed, if
$\mu ([B]_G)> 0$
. Indeed, if
![]() $A \approx _G B'$
, where
$A \approx _G B'$
, where
![]() $B' \subseteq B$
satisfies
$B' \subseteq B$
satisfies
![]() $[B]_G = [B \setminus B']_G$
, then
$[B]_G = [B \setminus B']_G$
, then
![]() $\mu (A) = \mu (B') = \mu (B) - \mu (B\setminus B')$
; and if
$\mu (A) = \mu (B') = \mu (B) - \mu (B\setminus B')$
; and if
![]() $\mu ([B]_G)> 0$
, then
$\mu ([B]_G)> 0$
, then
![]() $\mu (B \setminus B')> 0$
as well.
$\mu (B \setminus B')> 0$
as well.
It is clear that the relation
![]() $\preccurlyeq _G$
on Borel subsets of
$\preccurlyeq _G$
on Borel subsets of
![]() $V(G)$
is reflexive and transitive, and a standard Cantor–Schröder–Bernstein-type argument shows that
$V(G)$
is reflexive and transitive, and a standard Cantor–Schröder–Bernstein-type argument shows that
![]() $A \approx _G B$
if and only if
$A \approx _G B$
if and only if
![]() $A \preccurlyeq _G B$
and
$A \preccurlyeq _G B$
and
![]() $B \preccurlyeq _G A$
. While the relation
$B \preccurlyeq _G A$
. While the relation
![]() $\preccurlyeq _G$
generally fails to be a total preorder, any two Borel subsets of
$\preccurlyeq _G$
generally fails to be a total preorder, any two Borel subsets of
![]() $V(G)$
can be made
$V(G)$
can be made
![]() $\preccurlyeq _G$
-comparable by passing to suitable G-invariant subsets:
$\preccurlyeq _G$
-comparable by passing to suitable G-invariant subsets:
Proposition 3.11 [Reference Becker and KechrisBK96, Lemma 4.5.1]
Let G be a locally countable Borel graph and let
![]() $A, B \subseteq V(G)$
be Borel sets. Then there is a partition
$A, B \subseteq V(G)$
be Borel sets. Then there is a partition
![]() $V(G) = V_\prec \sqcup V_\approx \sqcup V_\succ $
of
$V(G) = V_\prec \sqcup V_\approx \sqcup V_\succ $
of
![]() $V(G)$
into three G-invariant Borel subsets such that
$V(G)$
into three G-invariant Borel subsets such that
Corollary 3.12. Let G be a locally countable Borel graph and let
![]() $A, B \subseteq V(G)$
be Borel sets. If
$A, B \subseteq V(G)$
be Borel sets. If
![]() $\mu (A) = \mu (B)$
for all
$\mu (A) = \mu (B)$
for all
![]() $\mu \in \mathsf {Erg}(G)$
, then there is a partition
$\mu \in \mathsf {Erg}(G)$
, then there is a partition
![]() $V(G) = V_0 \sqcup V_1$
of
$V(G) = V_0 \sqcup V_1$
of
![]() $V(G)$
into two G-invariant Borel sets such that
$V(G)$
into two G-invariant Borel sets such that
![]() $A \cap V_0 \approx _G B \cap V_0$
and
$A \cap V_0 \approx _G B \cap V_0$
and
![]() $V_1$
is G-compressible.
$V_1$
is G-compressible.
Proof. Let
![]() $V(G) = V_\prec \sqcup V_\approx \sqcup V_\succ $
be a partition given by Proposition 3.11 applied to A and B. Consider any
$V(G) = V_\prec \sqcup V_\approx \sqcup V_\succ $
be a partition given by Proposition 3.11 applied to A and B. Consider any
![]() $\mu \in \mathsf {Erg}(G)$
. Since
$\mu \in \mathsf {Erg}(G)$
. Since
![]() $\mu $
is ergodic, precisely one of
$\mu $
is ergodic, precisely one of
![]() $V_\prec $
,
$V_\prec $
,
![]() $V_\approx $
or
$V_\approx $
or
![]() $V_\succ $
must be
$V_\succ $
must be
![]() $\mu $
-conull. Since
$\mu $
-conull. Since
![]() $\mu (A) = \mu (B)$
by assumption, this implies that
$\mu (A) = \mu (B)$
by assumption, this implies that
![]() $\mu (V_\approx ) = 1$
and
$\mu (V_\approx ) = 1$
and
![]() $\mu (V_\prec \sqcup V_\succ ) = 0$
. As this holds for all
$\mu (V_\prec \sqcup V_\succ ) = 0$
. As this holds for all
![]() $\mu \in \mathsf {Erg}(G)$
, we conclude using Theorems 2.4 and 3.7 that the set
$\mu \in \mathsf {Erg}(G)$
, we conclude using Theorems 2.4 and 3.7 that the set
![]() $V_\prec \sqcup V_\succ $
is G-compressible. Hence, we can set
$V_\prec \sqcup V_\succ $
is G-compressible. Hence, we can set
![]() $V_0 := V_\approx $
and
$V_0 := V_\approx $
and
![]() $V_1 := V_\prec \sqcup V_\succ $
.
$V_1 := V_\prec \sqcup V_\succ $
.
Corollary 3.13. Let G be a compressible locally countable Borel graph. Suppose that
![]() $U_0, U_1 \subseteq V(G)$
are Borel subsets with
$U_0, U_1 \subseteq V(G)$
are Borel subsets with
![]() $U_0 \cup U_1 \approx _G V(G)$
. Then there is a partition
$U_0 \cup U_1 \approx _G V(G)$
. Then there is a partition
![]() $V(G) = V_0 \sqcup V_1$
of
$V(G) = V_0 \sqcup V_1$
of
![]() $V(G)$
into two G-invariant Borel sets satisfying
$V(G)$
into two G-invariant Borel sets satisfying
![]() $U_0 \cap V_0 \approx _G V_0$
and
$U_0 \cap V_0 \approx _G V_0$
and
![]() $U_1 \cap V_1 \approx _G V_1$
.
$U_1 \cap V_1 \approx _G V_1$
.
Proof. Without loss of generality, we may assume that
![]() $U_0 \cup U_1 = V(G)$
. From Proposition 3.11 we obtain a partition
$U_0 \cup U_1 = V(G)$
. From Proposition 3.11 we obtain a partition
![]() $V(G) = V_0 \sqcup V_1$
of
$V(G) = V_0 \sqcup V_1$
of
![]() $V(G)$
into two G-invariant Borel sets such that
$V(G)$
into two G-invariant Borel sets such that
We claim that these
![]() $V_0, V_1$
are as desired. Suppose that, say,
$V_0, V_1$
are as desired. Suppose that, say,
![]() $U_0 \cap V_0 \not \approx _G V_0$
. Since
$U_0 \cap V_0 \not \approx _G V_0$
. Since
![]() $V(G) = U_0 \cup U_1$
, the relation
$V(G) = U_0 \cup U_1$
, the relation
![]() $U_1 \cap V_0 \preccurlyeq _G U_0 \cap V_0$
implies
$U_1 \cap V_0 \preccurlyeq _G U_0 \cap V_0$
implies
![]() $[U_0 \cap V_0]_G = V_0$
. By Proposition 3.8, the set
$[U_0 \cap V_0]_G = V_0$
. By Proposition 3.8, the set
![]() $U_0 \cap V_0$
must be not G-compressible, so let
$U_0 \cap V_0$
must be not G-compressible, so let
![]() $\mu $
be a G-invariant measure on
$\mu $
be a G-invariant measure on
![]() $V(G)$
such that
$V(G)$
such that
![]() $0 < \mu (U_0 \cap V_0) < \infty $
. Since
$0 < \mu (U_0 \cap V_0) < \infty $
. Since
![]() $U_1 \cap V_0 \preccurlyeq _G U_0 \cap V_0$
, we conclude that
$U_1 \cap V_0 \preccurlyeq _G U_0 \cap V_0$
, we conclude that
contradicting the G-compressibility of
![]() $V_0$
.
$V_0$
.
Lemma 3.14. Let G be a compressible Borel graph of finite maximum degree. Let
![]() $I, J \subseteq V(G)$
be disjoint Borel G-independent sets and suppose that
$I, J \subseteq V(G)$
be disjoint Borel G-independent sets and suppose that
![]() $I \approx _G V(G)$
. Then there exist disjoint Borel G-independent sets
$I \approx _G V(G)$
. Then there exist disjoint Borel G-independent sets
![]() $I'$
and
$I'$
and
![]() $J'$
such that
$J'$
such that
![]() $I' \cup J' = I \cup J$
and
$I' \cup J' = I \cup J$
and
![]() $I' \approx _G J' \approx _G V(G)$
.
$I' \approx _G J' \approx _G V(G)$
.
Proof. Applying Corollary 3.13 with
![]() $I \setminus N_G(J)$
and
$I \setminus N_G(J)$
and
![]() $I \cap N_G(J)$
in place of
$I \cap N_G(J)$
in place of
![]() $U_0$
and
$U_0$
and
![]() $U_1$
, we obtain a partition
$U_1$
, we obtain a partition
![]() $V(G) = V_0 \sqcup V_1$
of
$V(G) = V_0 \sqcup V_1$
of
![]() $V(G)$
into two G-invariant Borel sets such that
$V(G)$
into two G-invariant Borel sets such that
Since we can treat the induced subgraphs
![]() $G[V_0]$
and
$G[V_0]$
and
![]() $G[V_1]$
separately, we may assume that either
$G[V_1]$
separately, we may assume that either
![]() $V_0 = V(G)$
or
$V_0 = V(G)$
or
![]() $V_1 = V(G)$
. Now we consider the two cases.
$V_1 = V(G)$
. Now we consider the two cases.
If
![]() $V_0 = V(G)$
and
$V_0 = V(G)$
and
![]() $I \setminus N_G(J) \approx _G V(G)$
, then by Theorem 3.7, the set
$I \setminus N_G(J) \approx _G V(G)$
, then by Theorem 3.7, the set
![]() $I \setminus N_G(J)$
is G-paradoxical, so there is a partition
$I \setminus N_G(J)$
is G-paradoxical, so there is a partition
![]() $I \setminus N_G(J) = I_0 \sqcup I_1$
of I into two Borel sets satisfying
$I \setminus N_G(J) = I_0 \sqcup I_1$
of I into two Borel sets satisfying
![]() $I_0 \approx _G I_1 \approx _G V(G)$
. This allows us to set
$I_0 \approx _G I_1 \approx _G V(G)$
. This allows us to set
![]() $I' := I \setminus I_1 = (I \cap N_G(J)) \cup I_0$
and
$I' := I \setminus I_1 = (I \cap N_G(J)) \cup I_0$
and
![]() $J' := J \cup I_1$
.
$J' := J \cup I_1$
.
On the other hand, if
![]() $V_1 = V(G)$
and
$V_1 = V(G)$
and
![]() $I \cap N_G(J) \approx _G V(G)$
, then
$I \cap N_G(J) \approx _G V(G)$
, then
![]() $J \approx _G V(G)$
by Corollary 3.9, and hence we can simply take
$J \approx _G V(G)$
by Corollary 3.9, and hence we can simply take
![]() $I' := I$
and
$I' := I$
and
![]() $J' := J$
.
$J' := J$
.
We are now ready to state and prove the main result of this subsection:
Theorem 3.15. Let G be a compressible Borel graph of finite maximum degree. If
![]() $\chi _{\mathrm {B}}(G) \leq k$
, then G has a Borel-equitable k-colouring.
$\chi _{\mathrm {B}}(G) \leq k$
, then G has a Borel-equitable k-colouring.
Proof. Let
![]() $\mathcal {C}$
be a k-element set of colours and let
$\mathcal {C}$
be a k-element set of colours and let
![]() $f \colon V(G) \to \mathcal {C}$
be a Borel proper colouring of G. It follows from Corollary 3.13 that there is a partition
$f \colon V(G) \to \mathcal {C}$
be a Borel proper colouring of G. It follows from Corollary 3.13 that there is a partition
![]() $V(G) = \bigsqcup _{\alpha \in \mathcal {C}} V_\alpha $
of
$V(G) = \bigsqcup _{\alpha \in \mathcal {C}} V_\alpha $
of
![]() $V(G)$
into G-invariant Borel sets satisfying
$V(G)$
into G-invariant Borel sets satisfying
![]() $f^{-1}(\alpha ) \cap V_\alpha \approx _G V_\alpha $
for each
$f^{-1}(\alpha ) \cap V_\alpha \approx _G V_\alpha $
for each
![]() $\alpha \in \mathcal {C}$
. As we can deal with the induced subgraphs
$\alpha \in \mathcal {C}$
. As we can deal with the induced subgraphs
![]() $G[V_\alpha ]$
individually, we may assume that
$G[V_\alpha ]$
individually, we may assume that
![]() $V(G) = V_\alpha $
for some
$V(G) = V_\alpha $
for some
![]() $\alpha \in \mathcal {C}$
and thus
$\alpha \in \mathcal {C}$
and thus
![]() $f^{-1}(\alpha ) \approx _G V(G)$
. Theorem 3.15 then follows through a sequence of
$f^{-1}(\alpha ) \approx _G V(G)$
. Theorem 3.15 then follows through a sequence of
![]() $k-1$
applications of Lemma 3.14.
$k-1$
applications of Lemma 3.14.
We remark, incidentally, that the conclusion of Theorem 3.15 may fail if the assumption of finite maximum degree is replaced by local finiteness; the reason is that in a locally finite graph G, a set that is not G-compressible can still have a G-compressible neighbourhood (in contrast to Corollary 3.9). We sketch a counterexample. Take any aperiodic locally finite Borel graph G such that
![]() $\lvert \mathsf {Erg}(G)\rvert = 1$
(such graphs are called uniquely ergodic) and let
$\lvert \mathsf {Erg}(G)\rvert = 1$
(such graphs are called uniquely ergodic) and let
![]() $\mu $
be the unique ergodic G-invariant probability measure on
$\mu $
be the unique ergodic G-invariant probability measure on
![]() $V(G)$
. Then
$V(G)$
. Then
![]() $\mu $
is atomless, so we can partition
$\mu $
is atomless, so we can partition
![]() $V(G)$
as
$V(G)$
as
![]() $V(G) = \bigsqcup _{n=1}^\infty V_n$
, where each
$V(G) = \bigsqcup _{n=1}^\infty V_n$
, where each
![]() $V_n$
is a Borel set with
$V_n$
is a Borel set with
![]() $\mu (V_n) = 2^{-n}$
. For each
$\mu (V_n) = 2^{-n}$
. For each
![]() $x \in V(G)$
, let
$x \in V(G)$
, let
![]() $n(x) \in {\mathbb {N}}^+$
denote the index such that
$n(x) \in {\mathbb {N}}^+$
denote the index such that
![]() $x \in V_{n(x)}$
, and let H be the graph with vertex set
$x \in V_{n(x)}$
, and let H be the graph with vertex set
 $$ \begin{align*} V(H) := \left\{(x, i) : x \in V(G) \text{ and } 1 \leq i \leq 2^{n(x)}\right\}, \end{align*} $$
$$ \begin{align*} V(H) := \left\{(x, i) : x \in V(G) \text{ and } 1 \leq i \leq 2^{n(x)}\right\}, \end{align*} $$
in which two vertices
![]() $(x, i)$
and
$(x, i)$
and
![]() $(y,j)$
are adjacent if and only if
$(y,j)$
are adjacent if and only if
![]() $y \in \left \{x\right \} \cup N_G(x)$
and exactly one of i or j is equal to
$y \in \left \{x\right \} \cup N_G(x)$
and exactly one of i or j is equal to
![]() $1$
. It is clear that H is locally finite, and since
$1$
. It is clear that H is locally finite, and since
 $$ \begin{align*} \int_{V(G)} 2^{n(x)} \mathrm{d}\mu(x) = \sum_{n=1}^\infty 2^n \cdot \mu(V_n) = \infty, \end{align*} $$
$$ \begin{align*} \int_{V(G)} 2^{n(x)} \mathrm{d}\mu(x) = \sum_{n=1}^\infty 2^n \cdot \mu(V_n) = \infty, \end{align*} $$
it is not hard to see that H is compressible. Furthermore, H has a Borel proper
![]() $2$
-colouring, namely the function
$2$
-colouring, namely the function
![]() $V(H) \to \left \{1,2\right \} \colon (x,i) \mapsto \min \left \{i, 2\right \}$
. Nevertheless, we claim that in every Borel proper
$V(H) \to \left \{1,2\right \} \colon (x,i) \mapsto \min \left \{i, 2\right \}$
. Nevertheless, we claim that in every Borel proper
![]() $2$
-colouring of H, one of the colour classes must be not H-compressible (and hence, by Corollary 3.10, such a colouring cannot be Borel-equitable). Indeed, let
$2$
-colouring of H, one of the colour classes must be not H-compressible (and hence, by Corollary 3.10, such a colouring cannot be Borel-equitable). Indeed, let
![]() $f \colon V(H) \to \left \{1,2\right \}$
be a Borel proper
$f \colon V(H) \to \left \{1,2\right \}$
be a Borel proper
![]() $2$
-colouring of H. If
$2$
-colouring of H. If
![]() $U \subseteq V(H)$
is a connected component of H, then f must assign the same colour to every vertex in
$U \subseteq V(H)$
is a connected component of H, then f must assign the same colour to every vertex in
![]() $U \cap (V(G) \times \left \{1\right \})$
(since any two such vertices are joined by a path of even length in H). In other words, the function
$U \cap (V(G) \times \left \{1\right \})$
(since any two such vertices are joined by a path of even length in H). In other words, the function
![]() $V(G) \to \left \{1,2\right \} \colon x \mapsto f(x,1)$
is G-invariant. Since the measure
$V(G) \to \left \{1,2\right \} \colon x \mapsto f(x,1)$
is G-invariant. Since the measure
![]() $\mu $
is ergodic, there is a colour
$\mu $
is ergodic, there is a colour
![]() $\alpha $
such that
$\alpha $
such that
![]() $f(x,1) = \alpha $
for a
$f(x,1) = \alpha $
for a
![]() $\mu $
-conull set of
$\mu $
-conull set of
![]() $x \in V(G)$
. But this means that the push-forward of
$x \in V(G)$
. But this means that the push-forward of
![]() $\mu $
under the map
$\mu $
under the map
![]() $V(G) \to V(H) \colon x \mapsto (x,1)$
is an H-invariant probability measure on
$V(G) \to V(H) \colon x \mapsto (x,1)$
is an H-invariant probability measure on
![]() $f^{-1}(\alpha )$
, showing that the colour class
$f^{-1}(\alpha )$
, showing that the colour class
![]() $f^{-1}(\alpha )$
is not H-compressible.
$f^{-1}(\alpha )$
is not H-compressible.
3.6 Finishing the proof of Theorem 1.4
We are now in a position to complete the proof of Theorem 1.4. Part (a) is given by Lemma 3.6(a), so it remains to verify part (b). To this end, we fix an aperiodic Borel graph G of finite maximum degree
![]() $\Delta $
with vertex set V and edge set E and a finite set of colours
$\Delta $
with vertex set V and edge set E and a finite set of colours
![]() $\mathcal {C}$
of size
$\mathcal {C}$
of size
![]() $k \geq \Delta + 1$
. Let
$k \geq \Delta + 1$
. Let
![]() $f \colon V \to \mathcal {C}$
be a Borel proper colouring of G. By Lemma 3.6(b), there exists a Borel proper colouring
$f \colon V \to \mathcal {C}$
be a Borel proper colouring of G. By Lemma 3.6(b), there exists a Borel proper colouring
![]() $h \colon V \to \mathcal {C}$
such that for all
$h \colon V \to \mathcal {C}$
such that for all
![]() $\mu \in \mathsf {Erg}(G)$
, h is
$\mu \in \mathsf {Erg}(G)$
, h is
![]() $\mu $
-equitable and
$\mu $
-equitable and
 $$ \begin{align*} {\mathrm{dist}}_\mu(f,h) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align*} $$
$$ \begin{align*} {\mathrm{dist}}_\mu(f,h) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f). \end{align*} $$
By applying Corollary 3.12 to each pair of colour classes of h and using the fact that finite (and even countable) unions of G-compressible sets are G-compressible, we obtain a partition
![]() $V = V_0 \sqcup V_1$
of V into two G-invariant Borel subsets such that
$V = V_0 \sqcup V_1$
of V into two G-invariant Borel subsets such that
-
• the sets
 $h^{-1}(\alpha ) \cap V_0$
,
$h^{-1}(\alpha ) \cap V_0$
,
 $\alpha \in \mathcal {C}$
, are pairwise G-equidecomposable and
$\alpha \in \mathcal {C}$
, are pairwise G-equidecomposable and -
• the set
 $V_1$
is G-compressible.
$V_1$
is G-compressible.
By Theorem 3.15, the graph
![]() $G[V_1]$
has a Borel-equitable colouring
$G[V_1]$
has a Borel-equitable colouring
![]() $h' \colon V_1 \to \mathcal {C}$
. Define
$h' \colon V_1 \to \mathcal {C}$
. Define
![]() $g \colon V \to \mathcal {C}$
by
$g \colon V \to \mathcal {C}$
by
 $$ \begin{align*} g(x) := \begin{cases} h(x) &\text{if } x \in V_0,\\ h'(x) &\text{if } x \in V_1. \end{cases} \end{align*} $$
$$ \begin{align*} g(x) := \begin{cases} h(x) &\text{if } x \in V_0,\\ h'(x) &\text{if } x \in V_1. \end{cases} \end{align*} $$
Then g is a Borel-equitable k-colouring of G such that for each
![]() $\mu \in \mathsf {Erg}(G)$
,
$\mu \in \mathsf {Erg}(G)$
,
 $$ \begin{align*} {\mathrm{dist}}_\mu(f,g) = {\mathrm{dist}}_\mu(f,h) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f), \end{align*} $$
$$ \begin{align*} {\mathrm{dist}}_\mu(f,g) = {\mathrm{dist}}_\mu(f,h) \leq 7^{k+1} \cdot {\mathrm{disc}}_\mu(f), \end{align*} $$
4 Domination for partial colourings
4.1 Domination for list colouring
In this subsection, we prove Theorem 1.14. Our strategy is to reduce the theorem, through a series of auxiliary lemmas, to Theorem 1.10.
Lemma 4.1. Let G be a connected finite graph and let
![]() $\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
$\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
![]() $\mathcal {L}$
-colouring of G. Then for each vertex
$\mathcal {L}$
-colouring of G. Then for each vertex
![]() $u \in V(G)$
, G has a partial proper
$u \in V(G)$
, G has a partial proper
![]() $\mathcal {L}$
-colouring f with
$\mathcal {L}$
-colouring f with
![]() $\mathrm {dom}(f) \supseteq V(G) \setminus \left \{u\right \}$
and
$\mathrm {dom}(f) \supseteq V(G) \setminus \left \{u\right \}$
and
![]() $f \succcurlyeq g$
.
$f \succcurlyeq g$
.
Proof. Suppose, toward a contradiction, that the tuple
![]() $(G, \mathcal {L}, g, u)$
forms a counterexample that minimises
$(G, \mathcal {L}, g, u)$
forms a counterexample that minimises
![]() $\lvert V(G)\rvert $
. Then, clearly,
$\lvert V(G)\rvert $
. Then, clearly,
![]() $\lvert V(G)\rvert \geq 2$
. Without loss of generality, we may assume that the partial proper
$\lvert V(G)\rvert \geq 2$
. Without loss of generality, we may assume that the partial proper
![]() $\mathcal {L}$
-colouring g is inclusion-maximal. This means that for each
$\mathcal {L}$
-colouring g is inclusion-maximal. This means that for each
![]() $x \in V(G) \setminus \mathrm {dom}(g)$
, every colour in
$x \in V(G) \setminus \mathrm {dom}(g)$
, every colour in
![]() $\mathcal {L}(x)$
is assigned by g to some neighbour of x. Since
$\mathcal {L}(x)$
is assigned by g to some neighbour of x. Since
![]() $\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
, we conclude that
$\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
, we conclude that
![]() $N_G(x) \subseteq \mathrm {dom}(g)$
, and for each
$N_G(x) \subseteq \mathrm {dom}(g)$
, and for each
![]() $\alpha \in \mathcal {L}(x)$
, there is exactly one
$\alpha \in \mathcal {L}(x)$
, there is exactly one
![]() $y \in N_G(x)$
, with
$y \in N_G(x)$
, with
![]() $g(y) = \alpha $
.
$g(y) = \alpha $
.
Consider now an arbitrary vertex
![]() $z \in V(G) \setminus \left \{u\right \}$
such that the subgraph
$z \in V(G) \setminus \left \{u\right \}$
such that the subgraph
![]() $G - z$
is connected (for example, if T is a spanning subtree of G, then any leaf of T distinct from u is such). If
$G - z$
is connected (for example, if T is a spanning subtree of G, then any leaf of T distinct from u is such). If
![]() $z \not \in \mathrm {dom}(g)$
, then pick any vertex
$z \not \in \mathrm {dom}(g)$
, then pick any vertex
![]() $y \in N_G(z)$
. Since y is the unique neighbour of z with the colour
$y \in N_G(z)$
. Since y is the unique neighbour of z with the colour
![]() $g(y)$
, we may replace g by the partial colouring
$g(y)$
, we may replace g by the partial colouring
![]() $g^\ast $
with domain
$g^\ast $
with domain
![]() $\left (\mathrm {dom}(g) \setminus \left \{y\right \}\right ) \cup \left \{z\right \}$
defined by
$\left (\mathrm {dom}(g) \setminus \left \{y\right \}\right ) \cup \left \{z\right \}$
defined by
 $$ \begin{align*} g^\ast(x) := \begin{cases} g(x) &\text{if } x \in \mathrm{dom}(g) \setminus \left\{y\right\},\\ g(y) &\text{if } x = z. \end{cases} \end{align*} $$
$$ \begin{align*} g^\ast(x) := \begin{cases} g(x) &\text{if } x \in \mathrm{dom}(g) \setminus \left\{y\right\},\\ g(y) &\text{if } x = z. \end{cases} \end{align*} $$
Therefore, we may assume that
![]() $z \in \mathrm {dom}(g)$
. Let
$z \in \mathrm {dom}(g)$
. Let
![]() $g'$
be the restriction of g onto
$g'$
be the restriction of g onto
![]() $\mathrm {dom}(g) \cap \left (V(G) \setminus \left \{z\right \}\right )$
. For each
$\mathrm {dom}(g) \cap \left (V(G) \setminus \left \{z\right \}\right )$
. For each
![]() $x \in V(G) \setminus \left \{z\right \}$
, define
$x \in V(G) \setminus \left \{z\right \}$
, define
 $$ \begin{align*} \mathcal{L}'(x) := \begin{cases} \mathcal{L}(x) \setminus \left\{g(z)\right\} &\text{if } x \in N_G(z),\\ \mathcal{L}(x) &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{L}'(x) := \begin{cases} \mathcal{L}(x) \setminus \left\{g(z)\right\} &\text{if } x \in N_G(z),\\ \mathcal{L}(x) &\text{otherwise}. \end{cases} \end{align*} $$
Then
![]() $\mathcal {L}'$
is a degree-list assignment for
$\mathcal {L}'$
is a degree-list assignment for
![]() $G-z$
and
$G-z$
and
![]() $g'$
is a partial proper
$g'$
is a partial proper
![]() $\mathcal {L}'$
-colouring. By the minimality of
$\mathcal {L}'$
-colouring. By the minimality of
![]() $\lvert V(G)\rvert $
,
$\lvert V(G)\rvert $
,
![]() $G - z$
has a partial proper
$G - z$
has a partial proper
![]() $\mathcal {L}'$
-colouring
$\mathcal {L}'$
-colouring
![]() $f'$
such that
$f'$
such that
![]() $\mathrm {dom}(f) \supseteq V(G) \setminus \left \{z,u\right \}$
and
$\mathrm {dom}(f) \supseteq V(G) \setminus \left \{z,u\right \}$
and
![]() $f' \succcurlyeq g'$
. But then the partial colouring
$f' \succcurlyeq g'$
. But then the partial colouring
![]() $f := f' \cup \left \{(z, g(z))\right \}$
satisfies the conclusion of the lemma.
$f := f' \cup \left \{(z, g(z))\right \}$
satisfies the conclusion of the lemma.
Lemma 4.2. Let G be a connected finite graph and let
![]() $\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
$\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
![]() $\mathcal {L}$
-colouring of G. If G has no proper
$\mathcal {L}$
-colouring of G. If G has no proper
![]() $\mathcal {L}$
-colouring f with
$\mathcal {L}$
-colouring f with
![]() $f \succcurlyeq g$
, then
$f \succcurlyeq g$
, then
![]() $\lvert \mathcal {L}(x)\rvert = \deg _G(x)$
for all
$\lvert \mathcal {L}(x)\rvert = \deg _G(x)$
for all
![]() $x \in V(G)$
.
$x \in V(G)$
.
Proof. Suppose that
![]() $x \in V(G)$
satisfies
$x \in V(G)$
satisfies
![]() $\lvert \mathcal {L}(x)\rvert \geq \deg _G(x) + 1$
. Due to Lemma 4.1, we may assume that
$\lvert \mathcal {L}(x)\rvert \geq \deg _G(x) + 1$
. Due to Lemma 4.1, we may assume that
![]() $\mathrm {dom}(g) = V(G) \setminus \left \{x\right \}$
. Then there is a colour in
$\mathrm {dom}(g) = V(G) \setminus \left \{x\right \}$
. Then there is a colour in
![]() $\mathcal {L}(x)$
that is not assigned by g to any of the neighbours of x, and hence g can be extended to a proper
$\mathcal {L}(x)$
that is not assigned by g to any of the neighbours of x, and hence g can be extended to a proper
![]() $\mathcal {L}$
-colouring of G – a contradiction.
$\mathcal {L}$
-colouring of G – a contradiction.
Lemma 4.3. Let G be a connected finite graph without a cut-vertex and let
![]() $\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
$\mathcal {L}$
be a degree-list assignment for G. Suppose that g is a partial proper
![]() $\mathcal {L}$
-colouring of G. If G has no proper
$\mathcal {L}$
-colouring of G. If G has no proper
![]() $\mathcal {L}$
-colouring f with
$\mathcal {L}$
-colouring f with
![]() $f \succcurlyeq g$
, then all the lists
$f \succcurlyeq g$
, then all the lists
![]() $\mathcal {L}(x)$
,
$\mathcal {L}(x)$
,
![]() $x \in V(G)$
, are equal to each other.
$x \in V(G)$
, are equal to each other.
Proof. The statement is vacuous if
![]() $\lvert V(G)\rvert \leq 1$
, so assume that
$\lvert V(G)\rvert \leq 1$
, so assume that
![]() $\lvert V(G)\rvert \geq 2$
. Since G is connected, it suffices to show that
$\lvert V(G)\rvert \geq 2$
. Since G is connected, it suffices to show that
![]() $\mathcal {L}(x) = \mathcal {L}(y)$
whenever x and y are adjacent. Suppose, toward a contradiction, that x and y are adjacent vertices and
$\mathcal {L}(x) = \mathcal {L}(y)$
whenever x and y are adjacent. Suppose, toward a contradiction, that x and y are adjacent vertices and
![]() $\beta \in \mathcal {L}(x) \setminus \mathcal {L}(y)$
. Due to Lemma 4.1, we may assume that
$\beta \in \mathcal {L}(x) \setminus \mathcal {L}(y)$
. Due to Lemma 4.1, we may assume that
![]() $\mathrm {dom}(g) = V(G) \setminus \left \{x\right \}$
. Since
$\mathrm {dom}(g) = V(G) \setminus \left \{x\right \}$
. Since
![]() $\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
and g cannot be extended to a proper
$\lvert \mathcal {L}(x)\rvert \geq \deg _G(x)$
and g cannot be extended to a proper
![]() $\mathcal {L}$
-colouring of G, every colour in
$\mathcal {L}$
-colouring of G, every colour in
![]() $\mathcal {L}(x)$
is assigned by g to a single neighbour of x. In particular, there is a unique vertex
$\mathcal {L}(x)$
is assigned by g to a single neighbour of x. In particular, there is a unique vertex
![]() $z \in N_G(x)$
with
$z \in N_G(x)$
with
![]() $g(z) = \beta $
. Note that
$g(z) = \beta $
. Note that
![]() $z \neq y$
, since
$z \neq y$
, since
![]() $\beta \not \in \mathcal {L}(y)$
.
$\beta \not \in \mathcal {L}(y)$
.
Let
![]() $g'$
be the restriction of g onto
$g'$
be the restriction of g onto
![]() $\mathrm {dom}(g) \cap \left (V(G) \setminus \left \{x, z\right \}\right )$
. For each
$\mathrm {dom}(g) \cap \left (V(G) \setminus \left \{x, z\right \}\right )$
. For each
![]() $u \in V(G) \setminus \left \{x\right \}$
, define
$u \in V(G) \setminus \left \{x\right \}$
, define
 $$ \begin{align*} \mathcal{L}'(u) := \begin{cases} \mathcal{L}(u) \setminus \left\{\beta\right\} &\text{if } u \in N_G(x),\\ \mathcal{L}(u) &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{L}'(u) := \begin{cases} \mathcal{L}(u) \setminus \left\{\beta\right\} &\text{if } u \in N_G(x),\\ \mathcal{L}(u) &\text{otherwise}. \end{cases} \end{align*} $$
Then
![]() $\mathcal {L}'$
is a degree-list assignment for
$\mathcal {L}'$
is a degree-list assignment for
![]() $G-x$
and
$G-x$
and
![]() $g'$
is a partial proper
$g'$
is a partial proper
![]() $\mathcal {L}'$
-colouring. Furthermore, since
$\mathcal {L}'$
-colouring. Furthermore, since
![]() $\beta \not \in \mathcal {L}(y)$
, we have
$\beta \not \in \mathcal {L}(y)$
, we have
![]() $\lvert \mathcal {L}'(y)\rvert \geq \deg _{G - x}(y) + 1$
. Since G has no cut-vertices, the graph
$\lvert \mathcal {L}'(y)\rvert \geq \deg _{G - x}(y) + 1$
. Since G has no cut-vertices, the graph
![]() $G - x$
is connected, so we may apply Lemma 4.2 to conclude that
$G - x$
is connected, so we may apply Lemma 4.2 to conclude that
![]() $G-x$
has a proper
$G-x$
has a proper
![]() $\mathcal {L}'$
-colouring
$\mathcal {L}'$
-colouring
![]() $f'$
such that
$f'$
such that
![]() $f' \succcurlyeq g'$
. But then
$f' \succcurlyeq g'$
. But then
![]() $f := f' \cup \left \{(x, \beta )\right \}$
is a proper
$f := f' \cup \left \{(x, \beta )\right \}$
is a proper
![]() $\mathcal {L}$
-colouring of G with
$\mathcal {L}$
-colouring of G with
![]() $f \succcurlyeq g$
– a contradiction.
$f \succcurlyeq g$
– a contradiction.
We are ready to finish the proof of Theorem 1.14. Let G be a connected finite graph that is not a Gallai tree and let
![]() $\mathcal {L}$
be a degree-list assignment for G. Let g be a partial proper
$\mathcal {L}$
be a degree-list assignment for G. Let g be a partial proper
![]() $\mathcal {L}$
-colouring of G and suppose, toward a contradiction, that G has no proper
$\mathcal {L}$
-colouring of G and suppose, toward a contradiction, that G has no proper
![]() $\mathcal {L}$
-colouring f with
$\mathcal {L}$
-colouring f with
![]() $f \succcurlyeq g$
. Since G is not a Gallai tree, it has a block that is neither a clique nor an odd cycle. Let
$f \succcurlyeq g$
. Since G is not a Gallai tree, it has a block that is neither a clique nor an odd cycle. Let
![]() $U \subseteq V(G)$
be the vertex set of such a block and fix any
$U \subseteq V(G)$
be the vertex set of such a block and fix any
![]() $u \in U$
. Due to Lemma 4.1, we may assume that
$u \in U$
. Due to Lemma 4.1, we may assume that
![]() $\mathrm {dom}(g) = V(G) \setminus \left \{u\right \}$
and then replace G by
$\mathrm {dom}(g) = V(G) \setminus \left \{u\right \}$
and then replace G by
![]() $G[U]$
, g by its restriction to U and
$G[U]$
, g by its restriction to U and
![]() $\mathcal {L}$
by the list assignment
$\mathcal {L}$
by the list assignment
![]() $\mathcal {L}'(x) := \mathcal {L}(x) \setminus \left \{g(y) : y \in N_G(x) \setminus U\right \}$
. In this way we arrange that G is a graph without cut-vertices that is clique nor an odd cycle. Let
$\mathcal {L}'(x) := \mathcal {L}(x) \setminus \left \{g(y) : y \in N_G(x) \setminus U\right \}$
. In this way we arrange that G is a graph without cut-vertices that is clique nor an odd cycle. Let
![]() $\Delta $
be the maximum degree of G. By Lemma 4.3, all the lists
$\Delta $
be the maximum degree of G. By Lemma 4.3, all the lists
![]() $\mathcal {L}(x)$
,
$\mathcal {L}(x)$
,
![]() $x \in V(G)$
, are the same, and by Lemma 4.2 they all have size
$x \in V(G)$
, are the same, and by Lemma 4.2 they all have size
![]() $\Delta $
. Hence, if
$\Delta $
. Hence, if
![]() $\Delta \geq 3$
, then we are done, by Theorem 1.10. On the other hand, if
$\Delta \geq 3$
, then we are done, by Theorem 1.10. On the other hand, if
![]() $\Delta \leq 2$
, then G must be an even cycle. In that case, since g is a proper
$\Delta \leq 2$
, then G must be an even cycle. In that case, since g is a proper
![]() $2$
-colouring of the even path
$2$
-colouring of the even path
![]() $G-u$
, the neighbours of u are coloured the same by g, so g can be extended to a proper
$G-u$
, the neighbours of u are coloured the same by g, so g can be extended to a proper
![]() $2$
-colouring of G.
$2$
-colouring of G.
4.2 One-ended subforests and measurable domination
Given a function
![]() $\varphi $
, we say that a sequence
$\varphi $
, we say that a sequence
![]() $x_0, x_1, \dotsc $
is
$x_0, x_1, \dotsc $
is
![]() $\varphi $
-descending if
$\varphi $
-descending if
![]() $\varphi (x_{n+1}) = x_n$
for all
$\varphi (x_{n+1}) = x_n$
for all
![]() $n \in {\mathbb {N}}$
. A function
$n \in {\mathbb {N}}$
. A function
![]() $\varphi $
is one-ended if there is no infinite
$\varphi $
is one-ended if there is no infinite
![]() $\varphi $
-descending sequence. Let G be a locally finite graph. Given a set
$\varphi $
-descending sequence. Let G be a locally finite graph. Given a set
![]() $A \subseteq V(G)$
, an A-one-ended subforest of G is a one-ended function
$A \subseteq V(G)$
, an A-one-ended subforest of G is a one-ended function
![]() $\varphi \colon V(G) \setminus A \to V(G)$
such that each
$\varphi \colon V(G) \setminus A \to V(G)$
such that each
![]() $x \in V(G)\setminus A$
is adjacent to
$x \in V(G)\setminus A$
is adjacent to
![]() $\varphi (x)$
in G. The word ‘subforest’ is used here because if
$\varphi (x)$
in G. The word ‘subforest’ is used here because if
![]() $\varphi $
is an A-one-ended subforest of G, then the graph with vertex set
$\varphi $
is an A-one-ended subforest of G, then the graph with vertex set
![]() $V(G)$
and edges joining each
$V(G)$
and edges joining each
![]() $x \in V(G) \setminus A$
to
$x \in V(G) \setminus A$
to
![]() $\varphi (x)$
is an acyclic subgraph of G. Given an A-one-ended subforest
$\varphi (x)$
is an acyclic subgraph of G. Given an A-one-ended subforest
![]() $\varphi $
of G, we define the
$\varphi $
of G, we define the
![]() $\varphi $
-height of a vertex
$\varphi $
-height of a vertex
![]() $x \in V(G)$
– in symbols,
$x \in V(G)$
– in symbols,
![]() $h_\varphi (x)$
– to be the greatest
$h_\varphi (x)$
– to be the greatest
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
![]() $x \in \mathrm {im}(\varphi ^n)$
(such an n exists, since
$x \in \mathrm {im}(\varphi ^n)$
(such an n exists, since
![]() $\varphi $
is one-ended and G is locally finite). By definition,
$\varphi $
is one-ended and G is locally finite). By definition,
![]() $h_\varphi (x) = 0$
if and only if
$h_\varphi (x) = 0$
if and only if
![]() $x \not \in \mathrm {im}(\varphi )$
. Note that
$x \not \in \mathrm {im}(\varphi )$
. Note that
![]() $h_\varphi (\varphi (x))> h_\varphi (x)$
for all
$h_\varphi (\varphi (x))> h_\varphi (x)$
for all
![]() $x \in V(G) \setminus A$
.
$x \in V(G) \setminus A$
.
Conley, Marks and Tucker-Drob developed the technique of one-ended subforests in order to prove a measurable version of Brooks’ theorem [Reference Conley, Marks and Tucker-DrobCMT16] (see Theorem 1.7). In particular, they showed that if G is a Borel graph of finite maximum degree
![]() $\Delta $
and
$\Delta $
and
![]() $A \subseteq V(G)$
is a Borel set such that G has a Borel A-one-ended subforest, then G has a Borel proper partial
$A \subseteq V(G)$
is a Borel set such that G has a Borel A-one-ended subforest, then G has a Borel proper partial
![]() $\Delta $
-colouring f with
$\Delta $
-colouring f with
![]() $\mathrm {dom}(f) \supseteq V(G) \setminus A$
[Reference Conley, Marks and Tucker-DrobCMT16, Lemma 3.9]. We strengthen this result by adding a domination requirement on f. Recall from Section 3.5 that, given Borel sets
$\mathrm {dom}(f) \supseteq V(G) \setminus A$
[Reference Conley, Marks and Tucker-DrobCMT16, Lemma 3.9]. We strengthen this result by adding a domination requirement on f. Recall from Section 3.5 that, given Borel sets
![]() $A, B \subseteq V(G)$
, we write
$A, B \subseteq V(G)$
, we write
![]() $A \preccurlyeq _G B$
(or, equivalently,
$A \preccurlyeq _G B$
(or, equivalently,
![]() $B \succcurlyeq _G A$
) if
$B \succcurlyeq _G A$
) if
![]() $A \approx _G B'$
for some Borel subset
$A \approx _G B'$
for some Borel subset
![]() $B' \subseteq B$
. For a pair of Borel partial colourings
$B' \subseteq B$
. For a pair of Borel partial colourings
![]() $f, g$
of G, we say that f Borel-dominates g – in symbols,
$f, g$
of G, we say that f Borel-dominates g – in symbols,
![]() $f \succcurlyeq _G g$
– if
$f \succcurlyeq _G g$
– if
![]() $f^{-1}(\alpha ) \succcurlyeq _G g^{-1}(\alpha )$
for every colour
$f^{-1}(\alpha ) \succcurlyeq _G g^{-1}(\alpha )$
for every colour
![]() $\alpha $
. Note that if
$\alpha $
. Note that if
![]() $f \succcurlyeq _G g$
, then
$f \succcurlyeq _G g$
, then
![]() $f \succcurlyeq _\mu g$
for every G-invariant probability measure
$f \succcurlyeq _\mu g$
for every G-invariant probability measure
![]() $\mu $
on
$\mu $
on
![]() $V(G)$
.
$V(G)$
.
Lemma 4.4. Let G be a Borel graph of finite maximum degree
![]() $\Delta $
and let
$\Delta $
and let
![]() $A \subseteq V(G)$
be a Borel set such that G has a Borel A-one-ended subforest. If g is a Borel proper partial
$A \subseteq V(G)$
be a Borel set such that G has a Borel A-one-ended subforest. If g is a Borel proper partial
![]() $\Delta $
-colouring of G, then G has a Borel proper partial
$\Delta $
-colouring of G, then G has a Borel proper partial
![]() $\Delta $
-colouring f with
$\Delta $
-colouring f with
![]() $\mathrm {dom}(f) \supseteq V(G) \setminus A$
and
$\mathrm {dom}(f) \supseteq V(G) \setminus A$
and
![]() $f \succcurlyeq _G g$
.
$f \succcurlyeq _G g$
.
Proof. Fix a Borel A-one-ended subforest
![]() $\varphi $
of G. For each
$\varphi $
of G. For each
![]() $n \in {\mathbb {N}}$
, set
$n \in {\mathbb {N}}$
, set
 $$ \begin{align*} V_n := \left\{x \in V(G) : h_\varphi(x) = n\right\} \qquad \text{and} \qquad V_{< n} := \left\{x \in V(G) : h_\varphi(x) < n\right\}. \end{align*} $$
$$ \begin{align*} V_n := \left\{x \in V(G) : h_\varphi(x) = n\right\} \qquad \text{and} \qquad V_{< n} := \left\{x \in V(G) : h_\varphi(x) < n\right\}. \end{align*} $$
Let
![]() $\mathcal {C}$
be a set of colours of size
$\mathcal {C}$
be a set of colours of size
![]() $\Delta $
and let g be a Borel proper partial
$\Delta $
and let g be a Borel proper partial
![]() $\mathcal {C}$
-colouring of G. We recursively construct a sequence of Borel proper partial
$\mathcal {C}$
-colouring of G. We recursively construct a sequence of Borel proper partial
![]() $\mathcal {C}$
-colourings
$\mathcal {C}$
-colourings
![]() $(f_n)_{n=0}^\infty $
, starting with
$(f_n)_{n=0}^\infty $
, starting with
![]() $f_0 := g$
. We will ensure that each
$f_0 := g$
. We will ensure that each
![]() $f_n$
has the following properties:
$f_n$
has the following properties:
-
(D1)
 $\mathrm {dom}(f_n) \supseteq V_{< n} \setminus A$
.
$\mathrm {dom}(f_n) \supseteq V_{< n} \setminus A$
. -
(D2) If
 $x \in V_{< n} \cap \mathrm {dom}(f_n)$
, then
$x \in V_{< n} \cap \mathrm {dom}(f_n)$
, then
 $f_{n+1}(x) = f_{n}(x)$
.
$f_{n+1}(x) = f_{n}(x)$
. -
(D3) For each colour
 $\alpha \in \mathcal {C}$
and every vertex
$\alpha \in \mathcal {C}$
and every vertex
 $y \in f_n^{-1}(\alpha ) \setminus f_{n+1}^{-1}(\alpha )$
, there is
$y \in f_n^{-1}(\alpha ) \setminus f_{n+1}^{-1}(\alpha )$
, there is
 $x \in f_{n+1}^{-1}(\alpha ) \setminus \left (A \cup f_n^{-1}(\alpha )\right )$
such that
$x \in f_{n+1}^{-1}(\alpha ) \setminus \left (A \cup f_n^{-1}(\alpha )\right )$
such that
 $h_\varphi (x) = n$
and
$h_\varphi (x) = n$
and
 $\varphi (x) = y$
.
$\varphi (x) = y$
.
Once
![]() $f_n$
is defined, we construct
$f_n$
is defined, we construct
![]() $f_{n+1}$
as follows. Let
$f_{n+1}$
as follows. Let
![]() $f_n' \supseteq f_n$
be an arbitrary Borel inclusion-maximal proper partial
$f_n' \supseteq f_n$
be an arbitrary Borel inclusion-maximal proper partial
![]() $\mathcal {C}$
-colouring (such an
$\mathcal {C}$
-colouring (such an
![]() $f_n'$
exists by Proposition 2.1). By the maximality of
$f_n'$
exists by Proposition 2.1). By the maximality of
![]() $f_n'$
, if
$f_n'$
, if
![]() $x \in V(G) \setminus \mathrm {dom}\left (f_n'\right )$
, then every neighbour of x is coloured by
$x \in V(G) \setminus \mathrm {dom}\left (f_n'\right )$
, then every neighbour of x is coloured by
![]() $f_n'$
and each colour
$f_n'$
and each colour
![]() $\alpha \in \mathcal {C}$
is used on precisely one neighbour of x. Hence, we may define
$\alpha \in \mathcal {C}$
is used on precisely one neighbour of x. Hence, we may define
![]() $f_{n+1} \colon V(G) \rightharpoonup \mathcal {C}$
by
$f_{n+1} \colon V(G) \rightharpoonup \mathcal {C}$
by
 $$ \begin{align*} f_{n+1}(x) := \begin{cases} f_n'(\varphi(x)) &\text{if } x \in V_n \setminus \left(A \cup \mathrm{dom}\left(f_n'\right)\right),\\ \text{undefined} &\text{if } x \in \varphi\left(V_n \setminus \left(A \cup \mathrm{dom}\left(f_n'\right)\right)\right),\\ f_n'(x) &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} f_{n+1}(x) := \begin{cases} f_n'(\varphi(x)) &\text{if } x \in V_n \setminus \left(A \cup \mathrm{dom}\left(f_n'\right)\right),\\ \text{undefined} &\text{if } x \in \varphi\left(V_n \setminus \left(A \cup \mathrm{dom}\left(f_n'\right)\right)\right),\\ f_n'(x) &\text{otherwise}. \end{cases} \end{align*} $$
Informally, we ‘move’ the colour from
![]() $\varphi (x)$
to x whenever
$\varphi (x)$
to x whenever
![]() $x \in V_n \setminus \left (A \cup \mathrm {dom}\left (f_n'\right )\right )$
. Conditions (D1) and (D2) are clearly satisfied. Notice also that the only vertices that are coloured in
$x \in V_n \setminus \left (A \cup \mathrm {dom}\left (f_n'\right )\right )$
. Conditions (D1) and (D2) are clearly satisfied. Notice also that the only vertices that are coloured in
![]() $f_n$
but lose their colour in
$f_n$
but lose their colour in
![]() $f_{n+1}$
are those of the form
$f_{n+1}$
are those of the form
![]() $\varphi (x)$
for some
$\varphi (x)$
for some
![]() $x \in V_n \setminus \left (A \cup \mathrm {dom}\left (f_n'\right )\right )$
, which implies (D3).
$x \in V_n \setminus \left (A \cup \mathrm {dom}\left (f_n'\right )\right )$
, which implies (D3).
The pointwise limit
![]() $f(x) := \lim _{n \to \infty } f_n(x)$
is a proper partial
$f(x) := \lim _{n \to \infty } f_n(x)$
is a proper partial
![]() $\mathcal {C}$
-colouring of G, and it follows from (D1) and (D2) that
$\mathcal {C}$
-colouring of G, and it follows from (D1) and (D2) that
![]() $\mathrm {dom}(f) \supseteq V(G) \setminus A$
. It remains to show that
$\mathrm {dom}(f) \supseteq V(G) \setminus A$
. It remains to show that
![]() $f \succcurlyeq _G g$
. To this end, set
$f \succcurlyeq _G g$
. To this end, set
and define a function
![]() $\psi \colon V(G) \to V(G)$
by setting
$\psi \colon V(G) \to V(G)$
by setting
 $$ \begin{align*} \psi(x) := \begin{cases} x &\text{if } x \in X \cup A,\\ \varphi(x) &\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \psi(x) := \begin{cases} x &\text{if } x \in X \cup A,\\ \varphi(x) &\text{otherwise}. \end{cases} \end{align*} $$
We claim that
![]() $\psi \left (f^{-1}(\alpha )\right ) \supseteq g^{-1}(\alpha )$
for every
$\psi \left (f^{-1}(\alpha )\right ) \supseteq g^{-1}(\alpha )$
for every
![]() $\alpha \in \mathcal {C}$
, which implies that
$\alpha \in \mathcal {C}$
, which implies that
![]() $f \succcurlyeq _G g$
, since the function
$f \succcurlyeq _G g$
, since the function
![]() $\psi $
has a Borel right inverse by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10]. Set
$\psi $
has a Borel right inverse by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10]. Set
![]() $\alpha \in \mathcal {C}$
and consider any
$\alpha \in \mathcal {C}$
and consider any
![]() $y \in g^{-1}(\alpha )$
. If
$y \in g^{-1}(\alpha )$
. If
![]() $y \in X$
, then
$y \in X$
, then
![]() $y \in f^{-1}(\alpha )$
and
$y \in f^{-1}(\alpha )$
and
![]() $y = \psi (y)$
. Otherwise, there is some
$y = \psi (y)$
. Otherwise, there is some
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
 $y \in f_n^{-1}(\alpha ) \setminus f_{n+1}^{-1}(\alpha )$
. Then by (D3), there is some
$y \in f_n^{-1}(\alpha ) \setminus f_{n+1}^{-1}(\alpha )$
. Then by (D3), there is some
 $x \in f_{n+1}^{-1}(\alpha ) \setminus \left (A \cup f_n^{-1}(\alpha )\right )$
with
$x \in f_{n+1}^{-1}(\alpha ) \setminus \left (A \cup f_n^{-1}(\alpha )\right )$
with
![]() $h_\varphi (x) = n$
and
$h_\varphi (x) = n$
and
![]() $\varphi (x) = y$
. Since
$\varphi (x) = y$
. Since
![]() $f_{n+1}(x) = \alpha $
but
$f_{n+1}(x) = \alpha $
but
![]() $x \not \in f_n^{-1}(\alpha )$
, we conclude that
$x \not \in f_n^{-1}(\alpha )$
, we conclude that
![]() $x \not \in X$
, so
$x \not \in X$
, so
![]() $y = \varphi (x) = \psi (x)$
. Since
$y = \varphi (x) = \psi (x)$
. Since
![]() $h_\varphi (x) = n$
, (D2) yields
$h_\varphi (x) = n$
, (D2) yields
![]() $x \in f^{-1}(\alpha )$
, and we are done.
$x \in f^{-1}(\alpha )$
, and we are done.
Given a Borel graph G and a Borel subset
![]() $A \subseteq V(G)$
, does G have a Borel A-one-ended subforest? One case in which the answer is positive is when A intersects every connected component of G:
$A \subseteq V(G)$
, does G have a Borel A-one-ended subforest? One case in which the answer is positive is when A intersects every connected component of G:
Theorem 4.5 Conley–Marks–Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMT16, Proposition 3.1]
Let G be a locally finite Borel graph and suppose that
![]() $A \subseteq V(G)$
is a Borel subset that intersects every connected component of G. Then G has a Borel A-one-ended subforest.
$A \subseteq V(G)$
is a Borel subset that intersects every connected component of G. Then G has a Borel A-one-ended subforest.
Combining this with Lemma 4.4 and Theorem 1.14, we obtain the following:
Corollary 4.6. Let G be a Borel graph of finite maximum degree
![]() $\Delta $
. Suppose that least one of the following statements holds:
$\Delta $
. Suppose that least one of the following statements holds:
-
(a) every connected component of G contains a vertex of degree less than
 $\Delta $
or
$\Delta $
or -
(b) no connected component of G is a Gallai tree.
If g is a Borel proper partial
![]() $\Delta $
-colouring of G, then G has a Borel proper
$\Delta $
-colouring of G, then G has a Borel proper
![]() $\Delta $
-colouring f with
$\Delta $
-colouring f with
![]() $f \succcurlyeq _G g$
.
$f \succcurlyeq _G g$
.
Proof. (a) Let A be the set of all
![]() $x\in V(G)$
with
$x\in V(G)$
with
![]() $\deg _G(x) < \Delta $
. By assumption, A intersects every connected component of G, so by Theorem 4.5, G has a Borel A-one-ended subforest. Thus, due to Lemma 4.4, we may assume that
$\deg _G(x) < \Delta $
. By assumption, A intersects every connected component of G, so by Theorem 4.5, G has a Borel A-one-ended subforest. Thus, due to Lemma 4.4, we may assume that
![]() $\mathrm {dom}(g) \supseteq V(G) \setminus A$
. Let
$\mathrm {dom}(g) \supseteq V(G) \setminus A$
. Let
![]() $f \supseteq g$
be a Borel inclusion-maximal proper partial
$f \supseteq g$
be a Borel inclusion-maximal proper partial
![]() $\Delta $
-colouring (such an f exists by Proposition 2.1). The maximality of f and the definition of A imply that
$\Delta $
-colouring (such an f exists by Proposition 2.1). The maximality of f and the definition of A imply that
![]() $A \subseteq \mathrm {dom}(f)$
. Therefore,
$A \subseteq \mathrm {dom}(f)$
. Therefore,
![]() $\mathrm {dom}(f) = V(G)$
, as desired.
$\mathrm {dom}(f) = V(G)$
, as desired.
(b) This argument is essentially the same as the proof of [Reference Conley, Marks and Tucker-DrobCMT16, Theorem 4.1], with Lemma 4.4 and Theorem 1.14 replacing [Reference Conley, Marks and Tucker-DrobCMT16, Lemma 3.9] and Theorem 1.13, respectively. With a slight (but standard) abuse of notation, let
![]() $\left [G\right ]^{<\infty }$
denote the set of all
$\left [G\right ]^{<\infty }$
denote the set of all
![]() $S \in \left [V\right ]^{<\infty } \setminus \left \{\varnothing \right \}$
such that every two elements of S are joined by a path in G. Let
$S \in \left [V\right ]^{<\infty } \setminus \left \{\varnothing \right \}$
such that every two elements of S are joined by a path in G. Let
![]() $W \subseteq \left [G\right ]^{<\infty }$
be the set of all
$W \subseteq \left [G\right ]^{<\infty }$
be the set of all
![]() $S \in \left [G\right ]^{<\infty }$
such that
$S \in \left [G\right ]^{<\infty }$
such that
![]() $G[S]$
is connected and not a Gallai tree. Let H be the graph with vertex set W in which two distinct vertices
$G[S]$
is connected and not a Gallai tree. Let H be the graph with vertex set W in which two distinct vertices
![]() $S, T$
are adjacent if and only if
$S, T$
are adjacent if and only if
![]() $(S \cup N_G(S)) \cap (T \cup N_G(T)) \neq \varnothing $
.
$(S \cup N_G(S)) \cap (T \cup N_G(T)) \neq \varnothing $
.
Claim 4.6.1.
![]() $\chi _{\mathrm {B}}(H) \leq \aleph _0$
.
$\chi _{\mathrm {B}}(H) \leq \aleph _0$
.
Proof. The proof of [Reference Kechris and MillerKM04, Lemma 7.3] shows that there exists a Borel function
![]() $\vartheta \colon \left [G\right ]^{<\infty } \to {\mathbb {N}}$
such that for each
$\vartheta \colon \left [G\right ]^{<\infty } \to {\mathbb {N}}$
such that for each
![]() $r \in {\mathbb {N}}$
, the sets in
$r \in {\mathbb {N}}$
, the sets in
![]() $\vartheta ^{-1}(r)$
are pairwise disjoint. The map
$\vartheta ^{-1}(r)$
are pairwise disjoint. The map
![]() $c_0 \colon W \to {\mathbb {N}} \colon S \mapsto \vartheta (S \cup N_G(S))$
is almost a proper
$c_0 \colon W \to {\mathbb {N}} \colon S \mapsto \vartheta (S \cup N_G(S))$
is almost a proper
![]() ${\mathbb {N}}$
-colouring of H; the only problem is that two distinct sets
${\mathbb {N}}$
-colouring of H; the only problem is that two distinct sets
![]() $S, T \in W$
may satisfy
$S, T \in W$
may satisfy
![]() $S \cup N_G(S) = T \cup N_G(T)$
, in which case
$S \cup N_G(S) = T \cup N_G(T)$
, in which case
![]() $c_0(S) = c_0(T)$
. However, for each
$c_0(S) = c_0(T)$
. However, for each
![]() $F \in \left [G\right ]^{<\infty }$
, there are only finitely many
$F \in \left [G\right ]^{<\infty }$
, there are only finitely many
![]() $S \in W$
with
$S \in W$
with
![]() $S \cup N_G(S) = F$
. Hence, by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10], there is a Borel map
$S \cup N_G(S) = F$
. Hence, by the Luzin–Novikov theorem [Reference KechrisKec95, Theorem 18.10], there is a Borel map
![]() $c_1 \colon W \to {\mathbb {N}}$
such that if
$c_1 \colon W \to {\mathbb {N}}$
such that if
![]() $S \cup N_G(S) = T \cup N_G(T)$
for distinct
$S \cup N_G(S) = T \cup N_G(T)$
for distinct
![]() $S, T \in W$
, then
$S, T \in W$
, then
![]() $c_1(S) \neq c_1(T)$
. Then
$c_1(S) \neq c_1(T)$
. Then
![]() $S \mapsto (c_0(S), c_1(S))$
is a Borel proper
$S \mapsto (c_0(S), c_1(S))$
is a Borel proper
![]() ${\mathbb {N}}^2$
-colouring of H.
${\mathbb {N}}^2$
-colouring of H.
From Claim 4.6.1 and Corollary 2.3 we conclude that there is a Borel maximal H-independent set
![]() $I \subseteq W$
. Set
$I \subseteq W$
. Set
![]() $A := \bigcup I$
. A connected graph is a Gallai tree if and only if all its finite connected subgraphs are Gallai trees; therefore, for every connected component C of G, there is some
$A := \bigcup I$
. A connected graph is a Gallai tree if and only if all its finite connected subgraphs are Gallai trees; therefore, for every connected component C of G, there is some
![]() $S \in W$
such that
$S \in W$
such that
![]() $S \subseteq C$
. Hence the maximality of I implies that A intersects every connected component of G. By Theorem 4.5, G has a Borel A-one-ended subforest, and thus, due to Lemma 4.4, we may assume that
$S \subseteq C$
. Hence the maximality of I implies that A intersects every connected component of G. By Theorem 4.5, G has a Borel A-one-ended subforest, and thus, due to Lemma 4.4, we may assume that
![]() $\mathrm {dom}(g) \supseteq V(G) \setminus A$
. For each vertex
$\mathrm {dom}(g) \supseteq V(G) \setminus A$
. For each vertex
![]() $x \in A$
, define
$x \in A$
, define
Then
![]() $\mathcal {L}$
is a degree-list assignment for the induced subgraph
$\mathcal {L}$
is a degree-list assignment for the induced subgraph
![]() $G[A]$
. For
$G[A]$
. For
![]() $S \in I$
, let
$S \in I$
, let
![]() $g_S \colon S \rightharpoonup \mathcal {C}$
denote the restriction of g to S, so
$g_S \colon S \rightharpoonup \mathcal {C}$
denote the restriction of g to S, so
![]() $g_S$
is a proper partial
$g_S$
is a proper partial
![]() $\mathcal {L}$
-colouring of
$\mathcal {L}$
-colouring of
![]() $G[S]$
. Since
$G[S]$
. Since
![]() $G[S]$
is a connected finite graph that is not a Gallai tree, by Theorem 1.14
$G[S]$
is a connected finite graph that is not a Gallai tree, by Theorem 1.14
![]() $G[S]$
admits a proper
$G[S]$
admits a proper
![]() $\mathcal {L}$
-colouring
$\mathcal {L}$
-colouring
![]() $f_S \colon S \to \mathcal {C}$
with
$f_S \colon S \to \mathcal {C}$
with
![]() $f_S \succcurlyeq g_S$
. Furthermore, since there are only finitely many candidates for such
$f_S \succcurlyeq g_S$
. Furthermore, since there are only finitely many candidates for such
![]() $f_S$
, the mapping
$f_S$
, the mapping
![]() $S \mapsto f_S$
can be arranged to be Borel. Now we can define a Borel proper colouring f with
$S \mapsto f_S$
can be arranged to be Borel. Now we can define a Borel proper colouring f with
![]() $f \succcurlyeq _G g$
by
$f \succcurlyeq _G g$
by
 $$ \begin{align*} f(x) := \begin{cases} g(x) &\text{if } x \in V(G) \setminus A,\\ f_S(x) &\text{if } x \in S \in I. \end{cases} \end{align*} $$
$$ \begin{align*} f(x) := \begin{cases} g(x) &\text{if } x \in V(G) \setminus A,\\ f_S(x) &\text{if } x \in S \in I. \end{cases} \end{align*} $$
(Since I is H-independent, the colouring f is indeed well defined and proper.)
To deal with graphs whose components are Gallai trees, we need another result of Conley, Marks and Tucker-Drob. For a graph G, let
![]() $\mathsf {ic}(G)$
denote the number of infinite connected components of G if it is finite, and
$\mathsf {ic}(G)$
denote the number of infinite connected components of G if it is finite, and
![]() $\infty $
otherwise. The number of ends of a connected locally finite graph G is
$\infty $
otherwise. The number of ends of a connected locally finite graph G is
 $$ \begin{align*} \mathsf{ends}(G) := \mathop{\mathrm{sup}}\limits \left\{\mathsf{ic}\left(G\left[V(G)\setminus S\right]\right) : S \in \left[V(G)\right]^{<\infty}\right\}. \end{align*} $$
$$ \begin{align*} \mathsf{ends}(G) := \mathop{\mathrm{sup}}\limits \left\{\mathsf{ic}\left(G\left[V(G)\setminus S\right]\right) : S \in \left[V(G)\right]^{<\infty}\right\}. \end{align*} $$
If
![]() $\mathsf {ends}(G) = k$
, then we say that G is k-ended. Note that
$\mathsf {ends}(G) = k$
, then we say that G is k-ended. Note that
![]() $\mathsf {ends}(G) = 0$
if and only if G is finite.
$\mathsf {ends}(G) = 0$
if and only if G is finite.
Theorem 4.7 Conley–Marks–Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMT16, proof of Theorem 4.2]
Let G be a locally finite Borel graph and let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $V(G)$
. Suppose that every connected component
$V(G)$
. Suppose that every connected component
![]() $C \subseteq V(G)$
of G has the following properties:
$C \subseteq V(G)$
of G has the following properties:
-
•
 $G[C]$
is a Gallai tree and
$G[C]$
is a Gallai tree and -
•
 $\mathsf {ends}(G[C]) \not \in \left \{0,2\right \}$
.
$\mathsf {ends}(G[C]) \not \in \left \{0,2\right \}$
.
Then there is a
![]() $\mu $
-conull G-invariant Borel subset
$\mu $
-conull G-invariant Borel subset
![]() $U \subseteq V(G)$
such that the induced subgraph
$U \subseteq V(G)$
such that the induced subgraph
![]() $G[U]$
has a Borel
$G[U]$
has a Borel
![]() $\varnothing $
-one-ended subforest.
$\varnothing $
-one-ended subforest.
We are now ready to prove Theorem 1.11.
Proof of Theorem 1.11
After passing to a
![]() $\mu $
-conull G-invariant Borel subset of
$\mu $
-conull G-invariant Borel subset of
![]() $V(G)$
, we may assume that the partial colouring g is in fact Borel. (Since the leftover
$V(G)$
, we may assume that the partial colouring g is in fact Borel. (Since the leftover
![]() $\mu $
-null set does not affect measurable domination, we may colour it simply using the usual Brooks’ theorem [Reference DiestelDie00, Theorem 5.2.4].) Partition
$\mu $
-null set does not affect measurable domination, we may colour it simply using the usual Brooks’ theorem [Reference DiestelDie00, Theorem 5.2.4].) Partition
![]() $V(G)$
into three G-invariant Borel subsets as
$V(G)$
into three G-invariant Borel subsets as
![]() $V(G) = V_0 \sqcup V_1 \sqcup V_2$
, where
$V(G) = V_0 \sqcup V_1 \sqcup V_2$
, where
-
• every connected component of
 $G[V_0]$
has a vertex of degree less than
$G[V_0]$
has a vertex of degree less than
 $\Delta $
,
$\Delta $
, -
• every vertex of
 $G[V_1]$
has degree
$G[V_1]$
has degree
 $\Delta $
and no component of
$\Delta $
and no component of
 $G[V_1]$
is a Gallai tree and
$G[V_1]$
is a Gallai tree and -
• every vertex of
 $G[V_2]$
has degree
$G[V_2]$
has degree
 $\Delta $
and every component of
$\Delta $
and every component of
 $G[V_2]$
is a Gallai tree.
$G[V_2]$
is a Gallai tree.
For each
![]() $i \in \left \{0,1,2\right \}$
, let
$i \in \left \{0,1,2\right \}$
, let
![]() $g_i$
denote the restriction of
$g_i$
denote the restriction of
![]() $g_i$
to
$g_i$
to
![]() $V_i$
. By Corollary 4.6, there exist Borel proper
$V_i$
. By Corollary 4.6, there exist Borel proper
![]() $\Delta $
-colourings
$\Delta $
-colourings
![]() $f_0$
and
$f_0$
and
![]() $f_1$
of
$f_1$
of
![]() $G[V_0]$
and
$G[V_0]$
and
![]() $G[V_1]$
, respectively, such that
$G[V_1]$
, respectively, such that
![]() $f_0 \succcurlyeq _G g_0$
and
$f_0 \succcurlyeq _G g_0$
and
![]() $f_1 \succcurlyeq _G g_1$
.
$f_1 \succcurlyeq _G g_1$
.
Now consider the graph
![]() $G[V_2]$
. Recall that a locally finite graph is regular if all its vertices have the same degree (so the graph
$G[V_2]$
. Recall that a locally finite graph is regular if all its vertices have the same degree (so the graph
![]() $G[V_2]$
is regular). Observe that the only regular
$G[V_2]$
is regular). Observe that the only regular
![]() $0$
-ended Gallai trees are cliques and odd cycles, whereas the only regular
$0$
-ended Gallai trees are cliques and odd cycles, whereas the only regular
![]() $2$
-ended Gallai trees are two-way infinite paths. This implies that since
$2$
-ended Gallai trees are two-way infinite paths. This implies that since
![]() $\Delta \geq 3$
and G does not contain a clique on
$\Delta \geq 3$
and G does not contain a clique on
![]() $\Delta + 1$
vertices,
$\Delta + 1$
vertices,
![]() $\mathsf {ends}(G[C]) \not \in \left \{0,2\right \}$
for every connected component C of
$\mathsf {ends}(G[C]) \not \in \left \{0,2\right \}$
for every connected component C of
![]() $G[V_2]$
. By Theorem 4.7, after discarding a
$G[V_2]$
. By Theorem 4.7, after discarding a
![]() $\mu $
-null G-invariant Borel set, we may assume that
$\mu $
-null G-invariant Borel set, we may assume that
![]() $G[V_2]$
admits a Borel
$G[V_2]$
admits a Borel
![]() $\varnothing $
-one-ended subforest. Hence, by Lemma 4.4, there is a Borel proper
$\varnothing $
-one-ended subforest. Hence, by Lemma 4.4, there is a Borel proper
![]() $\Delta $
-colouring
$\Delta $
-colouring
![]() $f_2$
of
$f_2$
of
![]() $G[V_2]$
with
$G[V_2]$
with
![]() $f_2 \succcurlyeq _G g_2$
. Then
$f_2 \succcurlyeq _G g_2$
. Then
![]() $f := f_0 \cup f_1 \cup f_2$
is a Borel proper
$f := f_0 \cup f_1 \cup f_2$
is a Borel proper
![]() $\Delta $
-colouring of G with
$\Delta $
-colouring of G with
![]() $f \succcurlyeq _G g$
(and hence also
$f \succcurlyeq _G g$
(and hence also
![]() $f \succcurlyeq _\mu g$
), and we are done.
$f \succcurlyeq _\mu g$
), and we are done.
5 Equitable
 $\Delta $
-colourings
$\Delta $
-colourings
5.1 Preliminary lemmas
In this section we prove Theorem 1.8. Our argument is analogous to the proof of Theorem 1.6 given in [Reference Kostochka and NakprasitKN05], modulo the changes necessary to adapt it to the measurable setting. In particular, the Hajnal–Szemerédi theorem and Theorem 1.10 are replaced by Theorems 1.3 and 1.11, respectively. (In fact, some of the final calculations presented in Section 5.2 end up being somewhat simpler than the corresponding calculations in [Reference Kostochka and NakprasitKN05].)
We start by collecting a few preliminary results. First, we need a version of Theorem 1.3 for graphs that may have finite components:
Lemma 5.1. Let G be a Borel graph of finite maximum degree
![]() $\Delta $
and let
$\Delta $
and let
![]() $\mu $
be an atomless G-invariant probability measure on
$\mu $
be an atomless G-invariant probability measure on
![]() $V(G)$
. If
$V(G)$
. If
![]() $k \geq \Delta + 1$
, then G has a
$k \geq \Delta + 1$
, then G has a
![]() $\mu $
-equitable k-colouring.
$\mu $
-equitable k-colouring.
Proof. Let
![]() $U \subseteq V(G)$
be the union of all the infinite components of G. Then U is a G-invariant Borel set, and by Theorem 1.3,
$U \subseteq V(G)$
be the union of all the infinite components of G. Then U is a G-invariant Borel set, and by Theorem 1.3,
![]() $G[U]$
has a Borel-equitable k-colouring. If
$G[U]$
has a Borel-equitable k-colouring. If
![]() $\mu (U) = 1$
, then we are done, so assume that
$\mu (U) = 1$
, then we are done, so assume that
![]() $\mu (U) < 1$
. Then, upon passing to the subgraph
$\mu (U) < 1$
. Then, upon passing to the subgraph
![]() $G\left [V(G) \setminus U\right ]$
and scaling
$G\left [V(G) \setminus U\right ]$
and scaling
![]() $\mu $
appropriately, we may assume that every component of G is finite.
$\mu $
appropriately, we may assume that every component of G is finite.
Let
![]() $\mathcal {C}$
be a set of colours of size k. By Theorem 1.2, G has a Borel proper
$\mathcal {C}$
be a set of colours of size k. By Theorem 1.2, G has a Borel proper
![]() $\mathcal {C}$
-colouring g. For each function
$\mathcal {C}$
-colouring g. For each function
![]() $\vartheta \colon \mathcal {C} \to {\mathbb {N}}$
, let
$\vartheta \colon \mathcal {C} \to {\mathbb {N}}$
, let
![]() $V_\vartheta \subseteq V(G)$
be the union of all the components C of G satisfying
$V_\vartheta \subseteq V(G)$
be the union of all the components C of G satisfying
Then
![]() $V(G) = \bigsqcup \left \{V_\vartheta : \vartheta \colon \mathcal {C} \to {\mathbb {N}}\right \}$
is a partition of G into countably many G-invariant Borel sets. Again, whenever
$V(G) = \bigsqcup \left \{V_\vartheta : \vartheta \colon \mathcal {C} \to {\mathbb {N}}\right \}$
is a partition of G into countably many G-invariant Borel sets. Again, whenever
![]() $\mu (V_\vartheta ) \neq 0$
, we may pass to the subgraph
$\mu (V_\vartheta ) \neq 0$
, we may pass to the subgraph
![]() $G[V_\vartheta ]$
and scale
$G[V_\vartheta ]$
and scale
![]() $\mu $
appropriately, thus reducing the situation to the case when
$\mu $
appropriately, thus reducing the situation to the case when
![]() $V(G) = V_\vartheta $
for some fixed
$V(G) = V_\vartheta $
for some fixed
![]() $\vartheta \colon \mathcal {C} \to {\mathbb {N}}$
. Let
$\vartheta \colon \mathcal {C} \to {\mathbb {N}}$
. Let
![]() $\mathsf {Sym}(\mathcal {C})$
denote the set of all bijections
$\mathsf {Sym}(\mathcal {C})$
denote the set of all bijections
![]() $\mathcal {C} \to \mathcal {C}$
. Since
$\mathcal {C} \to \mathcal {C}$
. Since
![]() $\mu $
is atomless and every component of G is finite, we can partition
$\mu $
is atomless and every component of G is finite, we can partition
![]() $V(G)$
into Borel G-invariant sets as
$V(G)$
into Borel G-invariant sets as
![]() $V(G) = \bigsqcup \left \{V_\pi : \pi \in \mathsf {Sym}(\mathcal {C})\right \}$
so that
$V(G) = \bigsqcup \left \{V_\pi : \pi \in \mathsf {Sym}(\mathcal {C})\right \}$
so that
![]() $\mu (V_\pi ) = 1/k!$
for all
$\mu (V_\pi ) = 1/k!$
for all
![]() $\pi \in \mathsf {Sym}(\mathcal {C})$
. Then the colouring f that sends each
$\pi \in \mathsf {Sym}(\mathcal {C})$
. Then the colouring f that sends each
![]() $x \in V_\pi $
to
$x \in V_\pi $
to
![]() $(\pi \circ g)(x)$
is
$(\pi \circ g)(x)$
is
![]() $\mu $
-equitable.
$\mu $
-equitable.
To state our next lemma we need to introduce some terminology. Let G be a Borel graph of finite maximum degree and let
![]() $\mu $
be a G-invariant probability measure on
$\mu $
be a G-invariant probability measure on
![]() $V(G)$
. Given a Borel subset
$V(G)$
. Given a Borel subset
![]() $X \subseteq V(G)$
, we define the cost of X relative to G and
$X \subseteq V(G)$
, we define the cost of X relative to G and
![]() $\mu $
by the formula
$\mu $
by the formula
 $$ \begin{align} \mathsf{C}_\mu(G; X) := \int_X \left\lvert N_G(x) \setminus X\right\rvert \mathrm{d} \mu(x) + \frac{1}{2}\int_X \lvert N_G(x) \cap X\rvert \mathrm{d} \mu(x). \end{align} $$
$$ \begin{align} \mathsf{C}_\mu(G; X) := \int_X \left\lvert N_G(x) \setminus X\right\rvert \mathrm{d} \mu(x) + \frac{1}{2}\int_X \lvert N_G(x) \cap X\rvert \mathrm{d} \mu(x). \end{align} $$
Intuitively,
![]() $\mathsf {C}_\mu (G;X)$
represents the ‘normalised’ number of edges of G incident to a vertex in X; the second summand in expression (5.1) is halved because the edges joining two vertices of X are counted twice. In particular, we have
$\mathsf {C}_\mu (G;X)$
represents the ‘normalised’ number of edges of G incident to a vertex in X; the second summand in expression (5.1) is halved because the edges joining two vertices of X are counted twice. In particular, we have
![]() $d_\mu (G) = 2\mathsf {C}_\mu (G; V(G))$
– recall that
$d_\mu (G) = 2\mathsf {C}_\mu (G; V(G))$
– recall that
![]() $d_\mu (G)$
is the
$d_\mu (G)$
is the
![]() $\mu $
-average degree of G. The G-invariance of
$\mu $
-average degree of G. The G-invariance of
![]() $\mu $
implies that if
$\mu $
implies that if
![]() $X, Y \subseteq V(G)$
are disjoint Borel sets, then
$X, Y \subseteq V(G)$
are disjoint Borel sets, then
 $$ \begin{align} \mathsf{C}_\mu(G;X \sqcup Y) = \mathsf{C}_\mu(G;X) + \mathsf{C}_\mu(G; Y) - \int_Y \lvert N_G(y) \cap X\rvert \mathrm{d} \mu(y). \end{align} $$
$$ \begin{align} \mathsf{C}_\mu(G;X \sqcup Y) = \mathsf{C}_\mu(G;X) + \mathsf{C}_\mu(G; Y) - \int_Y \lvert N_G(y) \cap X\rvert \mathrm{d} \mu(y). \end{align} $$
Note also that if
![]() $X \subseteq Y$
, then
$X \subseteq Y$
, then
![]() $\mathsf {C}_\mu (G;X) \leq \mathsf {C}_\mu (G;Y)$
.
$\mathsf {C}_\mu (G;X) \leq \mathsf {C}_\mu (G;Y)$
.
Lemma 5.2. Let G be a Borel graph of finite maximum degree and let
![]() $\mu $
be a G/invariant probability measure on
$\mu $
be a G/invariant probability measure on
![]() $V(G)$
. Then for each real number
$V(G)$
. Then for each real number
![]() $t \geq 0$
, there exists a Borel subset
$t \geq 0$
, there exists a Borel subset
![]() $X \subseteq V(G)$
with the following properties:
$X \subseteq V(G)$
with the following properties:
-
(X1)
 $\deg _G(y) < 2t$
for all
$\deg _G(y) < 2t$
for all
 $y \in V(G) \setminus X$
.
$y \in V(G) \setminus X$
. -
(X2)
 $\left \lvert N_G(y) \setminus X\right \rvert < t$
for all
$\left \lvert N_G(y) \setminus X\right \rvert < t$
for all
 $y \in V(G) \setminus X$
.
$y \in V(G) \setminus X$
. -
(X3)
 $\mathsf {C}_\mu (G; X') \geq t \mu (X')$
for every Borel set
$\mathsf {C}_\mu (G; X') \geq t \mu (X')$
for every Borel set
 $X' \subseteq X$
.
$X' \subseteq X$
.
Proof. By Theorem 1.2,
![]() $\chi _{\mathrm {B}}(G)$
is finite, so fix a Borel proper colouring
$\chi _{\mathrm {B}}(G)$
is finite, so fix a Borel proper colouring
![]() $c \colon V(G) \to \left \{0, \dotsc , k-1\right \}$
for some
$c \colon V(G) \to \left \{0, \dotsc , k-1\right \}$
for some
![]() $k \in {\mathbb {N}}^+$
. Recursively construct Borel sets
$k \in {\mathbb {N}}^+$
. Recursively construct Borel sets
![]() $X_r$
,
$X_r$
,
![]() $0 \leq r \leq k$
, as follows: Set
$0 \leq r \leq k$
, as follows: Set
 $$ \begin{align*} X_0 := \left\{x \in V(G) : \deg_G(x) \geq 2t\right\}, \end{align*} $$
$$ \begin{align*} X_0 := \left\{x \in V(G) : \deg_G(x) \geq 2t\right\}, \end{align*} $$
and once
![]() $X_r$
is defined for some
$X_r$
is defined for some
![]() $0 \leq r < k$
, define
$0 \leq r < k$
, define
We claim that the set
![]() $X := X_k$
is as desired. Condition (X1) is a consequence of the definition of
$X := X_k$
is as desired. Condition (X1) is a consequence of the definition of
![]() $X_0$
. To show (X2), suppose that
$X_0$
. To show (X2), suppose that
![]() $y \in V(G) \setminus X$
satisfies
$y \in V(G) \setminus X$
satisfies
![]() $\left \lvert N_G(y) \setminus X\right \rvert \geq t$
and define
$\left \lvert N_G(y) \setminus X\right \rvert \geq t$
and define
![]() $r := c(y)$
. Then
$r := c(y)$
. Then
![]() $\left \lvert N_G(y) \setminus X_r\right \rvert \geq \left \lvert N_G(y) \setminus X\right \rvert \geq t$
and hence
$\left \lvert N_G(y) \setminus X_r\right \rvert \geq \left \lvert N_G(y) \setminus X\right \rvert \geq t$
and hence
![]() $y \in Y_r$
. But then
$y \in Y_r$
. But then
![]() $y \in Y_r \cap c^{-1}(r) = I_r \subseteq X$
– a contradiction. It remains to verify (X3). Let
$y \in Y_r \cap c^{-1}(r) = I_r \subseteq X$
– a contradiction. It remains to verify (X3). Let
![]() $X' \subseteq X$
be a Borel subset. For each
$X' \subseteq X$
be a Borel subset. For each
![]() $0 \leq r < k$
, define
$0 \leq r < k$
, define
![]() $X_r' := X' \cap X_r$
and
$X_r' := X' \cap X_r$
and
![]() $I^{\prime }_r := X' \cap I_r$
. By repeatedly applying equation (5.2), we obtain
$I^{\prime }_r := X' \cap I_r$
. By repeatedly applying equation (5.2), we obtain
 $$ \begin{align*} \mathsf{C}_\mu(G; X') = \mathsf{C}_\mu\left(G; X_0'\right) + \sum_{r=0}^{k-1} \left(\mathsf{C}_\mu\left(G; I_r'\right) - \int_{I_r'} \left\lvert N_G(y) \cap X_r'\right\rvert \mathrm{d}\mu(y) \right). \end{align*} $$
$$ \begin{align*} \mathsf{C}_\mu(G; X') = \mathsf{C}_\mu\left(G; X_0'\right) + \sum_{r=0}^{k-1} \left(\mathsf{C}_\mu\left(G; I_r'\right) - \int_{I_r'} \left\lvert N_G(y) \cap X_r'\right\rvert \mathrm{d}\mu(y) \right). \end{align*} $$
From expression (5.1) and the definition of
![]() $X_0$
, it follows that
$X_0$
, it follows that
 $$ \begin{align*} \mathsf{C}_\mu\left(G;X_0'\right) \geq \frac{1}{2} \int_{X_0'} \deg_G(x) \mathrm{d}\mu(x) \geq t\mu\left(X_0'\right). \end{align*} $$
$$ \begin{align*} \mathsf{C}_\mu\left(G;X_0'\right) \geq \frac{1}{2} \int_{X_0'} \deg_G(x) \mathrm{d}\mu(x) \geq t\mu\left(X_0'\right). \end{align*} $$
Let
![]() $0 \leq r < k$
. The set
$0 \leq r < k$
. The set
![]() $I_r'$
is G-independent, so
$I_r'$
is G-independent, so
 $$ \begin{align*} \mathsf{C}_\mu\left(G; I_r'\right) = \int_{I_r'} \deg_G(y) \mathrm{d}\mu(y). \end{align*} $$
$$ \begin{align*} \mathsf{C}_\mu\left(G; I_r'\right) = \int_{I_r'} \deg_G(y) \mathrm{d}\mu(y). \end{align*} $$
Therefore, we have
 $$ \begin{align*} \mathsf{C}_\mu\left(G; I_r'\right) - \int_{I_r'} \left\lvert N_G(y) \cap X_r'\right\rvert \mathrm{d}\mu(y) = \int_{I_r'} \left\lvert N_G(y) \setminus X_r'\right\rvert \mathrm{d}\mu(y) \geq \int_{I_r'} \left\lvert N_G(y) \setminus X_r\right\rvert \mathrm{d}\mu(y) \geq t\mu\left(I_r'\right). \end{align*} $$
$$ \begin{align*} \mathsf{C}_\mu\left(G; I_r'\right) - \int_{I_r'} \left\lvert N_G(y) \cap X_r'\right\rvert \mathrm{d}\mu(y) = \int_{I_r'} \left\lvert N_G(y) \setminus X_r'\right\rvert \mathrm{d}\mu(y) \geq \int_{I_r'} \left\lvert N_G(y) \setminus X_r\right\rvert \mathrm{d}\mu(y) \geq t\mu\left(I_r'\right). \end{align*} $$
Putting everything together, we obtain the desired inequality
 $$ \begin{align*} \mathsf{C}_\mu(G; X') \geq t\mu\left(X_0'\right) + \sum_{r=0}^{k-1} t \mu\left(I_r'\right) = t\mu(X'). \\[-48pt] \end{align*} $$
$$ \begin{align*} \mathsf{C}_\mu(G; X') \geq t\mu\left(X_0'\right) + \sum_{r=0}^{k-1} t \mu\left(I_r'\right) = t\mu(X'). \\[-48pt] \end{align*} $$
We need one more technical lemma:
Lemma 5.3. Let G be a locally finite Borel graph and let
![]() $\mu $
be an atomless G-invariant probability measure on
$\mu $
be an atomless G-invariant probability measure on
![]() $V(G)$
. Let
$V(G)$
. Let
![]() $\mathcal {C}$
be a finite set of colours and let f be a Borel proper
$\mathcal {C}$
be a finite set of colours and let f be a Borel proper
![]() $\mathcal {C}$
-colouring of G. Then for every Borel set
$\mathcal {C}$
-colouring of G. Then for every Borel set
![]() $X \subseteq V(G)$
, there is a Borel proper
$X \subseteq V(G)$
, there is a Borel proper
![]() $\mathcal {C}$
-colouring g of G such that:
$\mathcal {C}$
-colouring g of G such that:
-
(P1)
 $g(x) = f(x)$
for all
$g(x) = f(x)$
for all
 $x \in X$
and
$x \in X$
and -
(P2) for all
 $\alpha , \beta \in \mathcal {C}$
, if
$\alpha , \beta \in \mathcal {C}$
, if
 $\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
, then
$\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
, then  $$ \begin{align*} \mu\left(\left\{y \in g^{-1}(\beta) \setminus X : N_G(y) \cap g^{-1}(\alpha) = \varnothing\right\}\right) = 0. \end{align*} $$
$$ \begin{align*} \mu\left(\left\{y \in g^{-1}(\beta) \setminus X : N_G(y) \cap g^{-1}(\alpha) = \varnothing\right\}\right) = 0. \end{align*} $$
Proof. This is a (significantly simpler) variant of the proof of Lemma 3.6. Let
![]() $(r_n, \alpha _n, \beta _n)_{n \in {\mathbb {N}}}$
be a sequence of triples such that
$(r_n, \alpha _n, \beta _n)_{n \in {\mathbb {N}}}$
be a sequence of triples such that
-
(R1) for all
 $n\in {\mathbb {N}}$
,
$n\in {\mathbb {N}}$
,
 $r_n \in {\mathbb {N}}$
and
$r_n \in {\mathbb {N}}$
and
 $\alpha _n, \beta _n \in \mathcal {C}$
are distinct colours; and
$\alpha _n, \beta _n \in \mathcal {C}$
are distinct colours; and -
(R2) every triple
 $(r, \alpha , \beta )$
as in (R1) appears in the sequence
$(r, \alpha , \beta )$
as in (R1) appears in the sequence
 $(r_n, \alpha _n, \beta _n)_{n \in {\mathbb {N}}}$
infinitely often.
$(r_n, \alpha _n, \beta _n)_{n \in {\mathbb {N}}}$
infinitely often.
Fix a Borel proper colouring
![]() $c \colon V(G) \to {\mathbb {N}}$
of G (for instance, we could take
$c \colon V(G) \to {\mathbb {N}}$
of G (for instance, we could take
![]() $c = f$
). Recursively construct Borel proper
$c = f$
). Recursively construct Borel proper
![]() $\mathcal {C}$
-colourings
$\mathcal {C}$
-colourings
![]() $f_n$
,
$f_n$
,
![]() $n \in {\mathbb {N}}$
, as follows. Set
$n \in {\mathbb {N}}$
, as follows. Set
![]() $f_0 := f$
. Once
$f_0 := f$
. Once
![]() $f_n$
is defined, we split the definition of
$f_n$
is defined, we split the definition of
![]() $f_{n+1}$
into two cases.
$f_{n+1}$
into two cases.
Case 1:
![]() $\mu \left (f_n^{-1}(\alpha _n)\right ) \geq \mu \left (f_n^{-1}(\beta _n)\right )$
. Then set
$\mu \left (f_n^{-1}(\alpha _n)\right ) \geq \mu \left (f_n^{-1}(\beta _n)\right )$
. Then set
![]() $f_{n+1} := f_n$
.
$f_{n+1} := f_n$
.
Case 2:
![]() $\mu \left (f_n^{-1}(\alpha _n)\right ) < \mu \left (f_n^{-1}(\beta _n)\right )$
. Set
$\mu \left (f_n^{-1}(\alpha _n)\right ) < \mu \left (f_n^{-1}(\beta _n)\right )$
. Set
 $$ \begin{align*} A_n := \left\{y \in f_n^{-1}(\beta_n) \setminus X : N_G(y) \cap f_n^{-1}(\alpha_n) = \varnothing\right\} \cap c^{-1}(r_n). \end{align*} $$
$$ \begin{align*} A_n := \left\{y \in f_n^{-1}(\beta_n) \setminus X : N_G(y) \cap f_n^{-1}(\alpha_n) = \varnothing\right\} \cap c^{-1}(r_n). \end{align*} $$
Subcase 2.1:
![]() $\mu \left (f_n^{-1}(\alpha _n)\right ) + \mu (A_n) \leq \mu \left (f_n^{-1}(\beta _n)\right ) - \mu (A_n)$
. Then define
$\mu \left (f_n^{-1}(\alpha _n)\right ) + \mu (A_n) \leq \mu \left (f_n^{-1}(\beta _n)\right ) - \mu (A_n)$
. Then define
![]() $B_n := A_n$
.
$B_n := A_n$
.
Subcase 2.2:
![]() $\mu \left (f_n^{-1}(\alpha _n)\right ) + \mu (A_n)> \mu \left (f_n^{-1}(\beta _n)\right ) - \mu (A_n)$
. Since
$\mu \left (f_n^{-1}(\alpha _n)\right ) + \mu (A_n)> \mu \left (f_n^{-1}(\beta _n)\right ) - \mu (A_n)$
. Since
![]() $\mu $
is atomless, we can then let
$\mu $
is atomless, we can then let
![]() $B_n \subseteq A_n$
be an arbitrary Borel subset of
$B_n \subseteq A_n$
be an arbitrary Borel subset of
![]() $A_n$
with
$A_n$
with
![]() $\mu (B_n) = \left (\mu \left (f_n^{-1}(\beta _n)\right ) - \mu \left (f_n^{-1}(\alpha _n)\right )\right )/2$
.
$\mu (B_n) = \left (\mu \left (f_n^{-1}(\beta _n)\right ) - \mu \left (f_n^{-1}(\alpha _n)\right )\right )/2$
.
Note that in both subcases we have
 $$ \begin{align} \mu(B_n) = \min \left\{A_n, \frac{\mu\left(f_n^{-1}(\beta_n)\right) - \mu\left(f_n^{-1}(\alpha_n)\right)}{2}\right\}. \end{align} $$
$$ \begin{align} \mu(B_n) = \min \left\{A_n, \frac{\mu\left(f_n^{-1}(\beta_n)\right) - \mu\left(f_n^{-1}(\alpha_n)\right)}{2}\right\}. \end{align} $$
To finish Case 2, define
 $$ \begin{align*} f_{n+1}(x) := \begin{cases} f_n(x) &\text{if } x \in V(G) \setminus B_n,\\ \alpha_n &\text{if } x \in B_n. \end{cases} \end{align*} $$
$$ \begin{align*} f_{n+1}(x) := \begin{cases} f_n(x) &\text{if } x \in V(G) \setminus B_n,\\ \alpha_n &\text{if } x \in B_n. \end{cases} \end{align*} $$
By construction,
![]() $f_{n+1}$
is proper and
$f_{n+1}$
is proper and
![]() $f_{n+1}(x) = f_n(x) = f(x)$
for all
$f_{n+1}(x) = f_n(x) = f(x)$
for all
![]() $x \in X$
.
$x \in X$
.
Now we define a Borel partial
![]() $\mathcal {C}$
-colouring
$\mathcal {C}$
-colouring
![]() $f_\infty \colon V \rightharpoonup \mathcal {C}$
via the pointwise limit
$f_\infty \colon V \rightharpoonup \mathcal {C}$
via the pointwise limit
 $$ \begin{align*} f_\infty(x) := \lim_{n \to \infty} f_n(x). \end{align*} $$
$$ \begin{align*} f_\infty(x) := \lim_{n \to \infty} f_n(x). \end{align*} $$
Since each
![]() $f_n$
is a proper colouring,
$f_n$
is a proper colouring,
![]() $f_\infty $
is also proper. We wish to show that
$f_\infty $
is also proper. We wish to show that
![]() $f_\infty $
is defined
$f_\infty $
is defined
![]() $\mu $
-almost everywhere. While this fact can be derived using Lemma 3.2, in this case we can give a simpler and more straightforward convergence argument. Let us introduce the following notation:
$\mu $
-almost everywhere. While this fact can be derived using Lemma 3.2, in this case we can give a simpler and more straightforward convergence argument. Let us introduce the following notation:
 $$ \begin{align*} \omega_n \colon \mathcal{C} \to [0,1] \colon \gamma \mapsto \mu\left(f^{-1}_n(\gamma)\right) \qquad \text{and} \qquad S_n := \frac{1}{2}\sum_{\gamma \in \mathcal{C}} \sum_{\delta \in \mathcal{C}} \left\lvert\omega_n(\gamma) - \omega_n(\delta)\right\rvert. \end{align*} $$
$$ \begin{align*} \omega_n \colon \mathcal{C} \to [0,1] \colon \gamma \mapsto \mu\left(f^{-1}_n(\gamma)\right) \qquad \text{and} \qquad S_n := \frac{1}{2}\sum_{\gamma \in \mathcal{C}} \sum_{\delta \in \mathcal{C}} \left\lvert\omega_n(\gamma) - \omega_n(\delta)\right\rvert. \end{align*} $$
Claim 5.3.1. For all
![]() $n \in {\mathbb {N}}$
, we have
$n \in {\mathbb {N}}$
, we have
![]() ${\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq (S_n - S_{n+1})/2$
.
${\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq (S_n - S_{n+1})/2$
.
Proof. If in the construction of
![]() $f_{n+1}$
Case 1 occurred, then
$f_{n+1}$
Case 1 occurred, then
![]() $f_{n+1} = f_n$
, and hence both sides of the desired inequality are
$f_{n+1} = f_n$
, and hence both sides of the desired inequality are
![]() $0$
. Now assume that Case 2 occurred. Observe that if
$0$
. Now assume that Case 2 occurred. Observe that if
![]() $a, b, c, d$
are real numbers with
$a, b, c, d$
are real numbers with
![]() $0 \leq d \leq (b-a)/2$
, then
$0 \leq d \leq (b-a)/2$
, then
By construction,
![]() ${\mathrm {dist}}_\mu (f_n, f_{n+1}) = \mu (B_n)$
. For each
${\mathrm {dist}}_\mu (f_n, f_{n+1}) = \mu (B_n)$
. For each
![]() $\gamma \in \mathcal {C}$
, we have
$\gamma \in \mathcal {C}$
, we have
 $$ \begin{align*} \omega_{n+1}(\gamma) = \begin{cases} \omega_n(\alpha_n) + \mu(B_n) &\quad \text{if } \gamma = \alpha_n,\\ \omega_n(\beta_n) - \mu(B_n) &\quad \text{if } \gamma = \beta_n,\\ \omega_n(\gamma) &\quad \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \omega_{n+1}(\gamma) = \begin{cases} \omega_n(\alpha_n) + \mu(B_n) &\quad \text{if } \gamma = \alpha_n,\\ \omega_n(\beta_n) - \mu(B_n) &\quad \text{if } \gamma = \beta_n,\\ \omega_n(\gamma) &\quad \text{otherwise}. \end{cases} \end{align*} $$
It follows from formulas (5.3) and (5.4) that for each
![]() $\gamma \in \mathcal {C}\setminus \left \{\alpha _n, \beta _n\right \}$
,
$\gamma \in \mathcal {C}\setminus \left \{\alpha _n, \beta _n\right \}$
,
Therefore,
as desired.
Claim 5.3.1 yields
![]() $\sum _{n=0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq S_0/2 < \infty $
, and hence, by the Borel–Cantelli lemma, the domain of
$\sum _{n=0}^\infty {\mathrm {dist}}_\mu (f_n, f_{n+1}) \leq S_0/2 < \infty $
, and hence, by the Borel–Cantelli lemma, the domain of
![]() $f_\infty $
is
$f_\infty $
is
![]() $\mu $
-conull. Thus, there is a
$\mu $
-conull. Thus, there is a
![]() $\mu $
-conull G-invariant Borel subset
$\mu $
-conull G-invariant Borel subset
![]() $U \subseteq \mathrm {dom}(f_\infty )$
. Define
$U \subseteq \mathrm {dom}(f_\infty )$
. Define
![]() $g \colon V(G) \to \mathcal {C}$
by sending each
$g \colon V(G) \to \mathcal {C}$
by sending each
![]() $x \in U$
to
$x \in U$
to
![]() $f_\infty (x)$
and each
$f_\infty (x)$
and each
![]() $x \in V(G)\setminus U$
to
$x \in V(G)\setminus U$
to
![]() $f(x)$
. We claim that this g is as desired. It is clear that g is proper and that
$f(x)$
. We claim that this g is as desired. It is clear that g is proper and that
![]() $g(x) = f(x)$
for all
$g(x) = f(x)$
for all
![]() $x \in X$
.
$x \in X$
.
It remains to verify (P2). To this end, let
![]() $\alpha , \beta \in \mathcal {C}$
be colours such that
$\alpha , \beta \in \mathcal {C}$
be colours such that
![]() $\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
. We shall argue that every vertex
$\mu \left (g^{-1}(\alpha )\right ) < \mu \left (g^{-1}(\beta )\right )$
. We shall argue that every vertex
![]() $y \in U \cap \left (g^{-1}(\beta ) \setminus X\right )$
has a neighbour in
$y \in U \cap \left (g^{-1}(\beta ) \setminus X\right )$
has a neighbour in
![]() $g^{-1}(\alpha )$
, which implies (P2), since
$g^{-1}(\alpha )$
, which implies (P2), since
![]() $\mu (U)=1$
. Suppose, toward a contradiction, that
$\mu (U)=1$
. Suppose, toward a contradiction, that
![]() $y \in U \cap \left (g^{-1}(\beta ) \setminus X\right )$
satisfies
$y \in U \cap \left (g^{-1}(\beta ) \setminus X\right )$
satisfies
![]() $N_G(y) \cap g^{-1}(\alpha ) = \varnothing $
. Set
$N_G(y) \cap g^{-1}(\alpha ) = \varnothing $
. Set
![]() $r := c(y)$
. Since
$r := c(y)$
. Since
![]() $\left \{y\right \} \cup N_G(y) \subseteq U$
, there is
$\left \{y\right \} \cup N_G(y) \subseteq U$
, there is
![]() $n_0 \in {\mathbb {N}}$
such that for all
$n_0 \in {\mathbb {N}}$
such that for all
![]() $n \geq n_0$
, we have
$n \geq n_0$
, we have
-
(L1)
 $f_n(y) = \beta $
and
$f_n(y) = \beta $
and
 $N_G(y) \cap f_n^{-1}(\alpha ) = \varnothing $
and
$N_G(y) \cap f_n^{-1}(\alpha ) = \varnothing $
and -
(L2)
 $\mu \left (f_n^{-1}(\alpha )\right ) < \mu \left (f_n^{-1}(\beta )\right )$
.
$\mu \left (f_n^{-1}(\alpha )\right ) < \mu \left (f_n^{-1}(\beta )\right )$
.
Take any
![]() $n \geq n_0$
with
$n \geq n_0$
with
![]() $(r_n, \alpha _n, \beta _n) = (r, \alpha , \beta )$
. It follows from (L2) that in the construction of
$(r_n, \alpha _n, \beta _n) = (r, \alpha , \beta )$
. It follows from (L2) that in the construction of
![]() $f_{n+1}$
, Case 2 occurred. Also, by (L1), we have
$f_{n+1}$
, Case 2 occurred. Also, by (L1), we have
![]() $y \in A_n$
. On the other hand,
$y \in A_n$
. On the other hand,
![]() $y \not \in B_n$
, since
$y \not \in B_n$
, since
![]() $f_{n+1}(y) = \beta \neq \alpha $
. Therefore,
$f_{n+1}(y) = \beta \neq \alpha $
. Therefore,
![]() $B_n \neq A_n$
, which implies that Subcase 2.2 occurred in the construction of
$B_n \neq A_n$
, which implies that Subcase 2.2 occurred in the construction of
![]() $f_{n+1}$
. Hence
$f_{n+1}$
. Hence
 $$ \begin{align*} \mu\left(f_n^{-1}(\alpha)\right) + \mu(B_n) = \mu\left(f_n^{-1}(\beta)\right) - \mu(B_n); \end{align*} $$
$$ \begin{align*} \mu\left(f_n^{-1}(\alpha)\right) + \mu(B_n) = \mu\left(f_n^{-1}(\beta)\right) - \mu(B_n); \end{align*} $$
that is,
 $\mu \left (f_{n+1}^{-1}(\alpha )\right ) = \mu \left (f_{n+1}^{-1}(\beta )\right )$
. But this contradicts (L2) with
$\mu \left (f_{n+1}^{-1}(\alpha )\right ) = \mu \left (f_{n+1}^{-1}(\beta )\right )$
. But this contradicts (L2) with
![]() $n+1$
in place of n.
$n+1$
in place of n.
5.2 Proof of Theorem 1.8
We are now fully equipped to prove Theorem 1.8, so let G be a Borel graph of finite maximum degree
![]() $\Delta \geq 3$
without a clique on
$\Delta \geq 3$
without a clique on
![]() $\Delta +1$
vertices, and let
$\Delta +1$
vertices, and let
![]() $\mu $
be an atomless G-invariant probability measure on
$\mu $
be an atomless G-invariant probability measure on
![]() $V(G)$
such that
$V(G)$
such that
![]() $d_\mu (G) \leq \Delta /5$
. First we use Lemma 5.2 with
$d_\mu (G) \leq \Delta /5$
. First we use Lemma 5.2 with
![]() $t = 2\Delta /5$
to find a Borel subset
$t = 2\Delta /5$
to find a Borel subset
![]() $X \subseteq V(G)$
such that
$X \subseteq V(G)$
such that
-
(X1)
 $\deg _G(y) < 4\Delta /5$
for all
$\deg _G(y) < 4\Delta /5$
for all
 $y \in V(G) \setminus X$
,
$y \in V(G) \setminus X$
, -
(X2)
 $\left \lvert N_G(y) \setminus X\right \rvert < 2\Delta /5$
for all
$\left \lvert N_G(y) \setminus X\right \rvert < 2\Delta /5$
for all
 $y \in V(G) \setminus X$
and
$y \in V(G) \setminus X$
and -
(X3)
 $\mathsf {C}_\mu (G; X') \geq (2\Delta /5) \mu (X')$
for every Borel set
$\mathsf {C}_\mu (G; X') \geq (2\Delta /5) \mu (X')$
for every Borel set
 $X' \subseteq X$
.
$X' \subseteq X$
.
Claim 5.4.
![]() $\mu (X) \leq 1/4$
.
$\mu (X) \leq 1/4$
.
Proof. This is a consequence of the following chain of inequalities:
 $$ \begin{align*} \frac{2\Delta \mu(X)}{5} \leq \mathsf{C}_\mu(G;X) \leq \mathsf{C}_\mu(G; V(G)) = \frac{d_\mu(G)}{2} \leq \frac{\Delta}{10}.\\[-42pt] \end{align*} $$
$$ \begin{align*} \frac{2\Delta \mu(X)}{5} \leq \mathsf{C}_\mu(G;X) \leq \mathsf{C}_\mu(G; V(G)) = \frac{d_\mu(G)}{2} \leq \frac{\Delta}{10}.\\[-42pt] \end{align*} $$
Next we apply Lemma 5.1 to obtain a
![]() $\mu $
-equitable
$\mu $
-equitable
![]() $(\Delta +1)$
-colouring h of the subgraph
$(\Delta +1)$
-colouring h of the subgraph
![]() $G[X]$
; here ‘
$G[X]$
; here ‘
![]() $\mu $
-equitable’ means that each colour class of h has measure
$\mu $
-equitable’ means that each colour class of h has measure
![]() $\mu (X)/(\Delta +1)$
. As in the proof of Corollary 1.12, we then uncolour one of the colour classes of h and apply Theorem 1.11 to the resulting partial colouring. This produces a
$\mu (X)/(\Delta +1)$
. As in the proof of Corollary 1.12, we then uncolour one of the colour classes of h and apply Theorem 1.11 to the resulting partial colouring. This produces a
![]() $\mu $
-measurable proper
$\mu $
-measurable proper
![]() $\Delta $
-colouring
$\Delta $
-colouring
![]() $h^\ast $
of
$h^\ast $
of
![]() $G[X]$
in which every colour class has measure at least
$G[X]$
in which every colour class has measure at least
![]() $\mu (X)/(\Delta +1)$
. After passing to a
$\mu (X)/(\Delta +1)$
. After passing to a
![]() $\mu $
-conull G-invariant Borel subset of
$\mu $
-conull G-invariant Borel subset of
![]() $V(G)$
, we may assume that
$V(G)$
, we may assume that
![]() $h^\ast $
is Borel.
$h^\ast $
is Borel.
Claim 5.5. If
![]() $S \subseteq X$
is the union of some s colour classes of
$S \subseteq X$
is the union of some s colour classes of
![]() $h^\ast $
, then
$h^\ast $
, then
 $$ \begin{align*} \frac{s\mu(X)}{\Delta + 1} \leq \mu(S) \leq \frac{(s+1) \mu(X)}{\Delta + 1}. \end{align*} $$
$$ \begin{align*} \frac{s\mu(X)}{\Delta + 1} \leq \mu(S) \leq \frac{(s+1) \mu(X)}{\Delta + 1}. \end{align*} $$
Proof. This is immediate from the fact that each colour class of
![]() $h^\ast $
has measure at least
$h^\ast $
has measure at least
![]() $\mu (X)/(\Delta + 1)$
.
$\mu (X)/(\Delta + 1)$
.
Now we use Proposition 2.1 to obtain a Borel inclusion-maximal proper partial
![]() $\Delta $
-colouring
$\Delta $
-colouring
![]() $g \supseteq h^\ast $
of G. Then
$g \supseteq h^\ast $
of G. Then
![]() $X \subseteq \mathrm {dom}(g)$
by definition; on the other hand, every vertex in
$X \subseteq \mathrm {dom}(g)$
by definition; on the other hand, every vertex in
![]() $V(G) \setminus X$
has degree less than
$V(G) \setminus X$
has degree less than
![]() $4\Delta /5 < \Delta $
, so
$4\Delta /5 < \Delta $
, so
![]() $V(G) \setminus X \subseteq \mathrm {dom}(g)$
as well. In other words,
$V(G) \setminus X \subseteq \mathrm {dom}(g)$
as well. In other words,
![]() $\mathrm {dom}(g) = V(G)$
– that is, g is a total colouring. Finally, we invoke Lemma 5.3 to produce a Borel proper
$\mathrm {dom}(g) = V(G)$
– that is, g is a total colouring. Finally, we invoke Lemma 5.3 to produce a Borel proper
![]() $\Delta $
-colouring f of G such that
$\Delta $
-colouring f of G such that
-
(P1)
 $f(x) = g(x)$
for all
$f(x) = g(x)$
for all
 $x \in X$
and
$x \in X$
and -
(P2) for any two colours
 $\alpha $
and
$\alpha $
and
 $\beta $
, if
$\beta $
, if
 $\mu \left (f^{-1}(\alpha )\right ) < \mu \left (f^{-1}(\beta )\right )$
, then
$\mu \left (f^{-1}(\alpha )\right ) < \mu \left (f^{-1}(\beta )\right )$
, then  $$ \begin{align*} \mu\left(\left\{y \in f^{-1}(\beta) \setminus X : N_G(y) \cap f^{-1}(\alpha) = \varnothing\right\}\right) = 0. \end{align*} $$
$$ \begin{align*} \mu\left(\left\{y \in f^{-1}(\beta) \setminus X : N_G(y) \cap f^{-1}(\alpha) = \varnothing\right\}\right) = 0. \end{align*} $$
We claim that this
![]() $\Delta $
-colouring f is
$\Delta $
-colouring f is
![]() $\mu $
-equitable.
$\mu $
-equitable.
Suppose, toward a contradiction, that f is not
![]() $\mu $
-equitable. Let the set of colours be
$\mu $
-equitable. Let the set of colours be
![]() $\mathcal {C}$
. For
$\mathcal {C}$
. For
![]() $\gamma \in \mathcal {C}$
, let
$\gamma \in \mathcal {C}$
, let
![]() $V_\gamma := f^{-1}(\gamma )$
be the corresponding colour class. Define
$V_\gamma := f^{-1}(\gamma )$
be the corresponding colour class. Define
 $$ \begin{align*} \mathcal{A} := \left\{\alpha \in \mathcal{C} : \mu(V_\alpha) < 1/\Delta\right\} \qquad \text{and} \qquad \mathcal{B} := \left\{\beta \in \mathcal{C} : \mu\left(V_\beta\right) \geq 1/\Delta\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{A} := \left\{\alpha \in \mathcal{C} : \mu(V_\alpha) < 1/\Delta\right\} \qquad \text{and} \qquad \mathcal{B} := \left\{\beta \in \mathcal{C} : \mu\left(V_\beta\right) \geq 1/\Delta\right\}. \end{align*} $$
Set
![]() $A := f^{-1}(\mathcal {A})$
and
$A := f^{-1}(\mathcal {A})$
and
![]() $B := f^{-1}(\mathcal {B})$
. Since f is not
$B := f^{-1}(\mathcal {B})$
. Since f is not
![]() $\mu $
-equitable,
$\mu $
-equitable,
![]() $\mathcal {A}, \mathcal {B} \neq \varnothing $
. Set
$\mathcal {A}, \mathcal {B} \neq \varnothing $
. Set
![]() $\xi := \lvert \mathcal {A}\rvert /\Delta $
.
$\xi := \lvert \mathcal {A}\rvert /\Delta $
.
Claim 5.6.
![]() $\xi < 4/5$
.
$\xi < 4/5$
.
Proof. Take any colour
![]() $\beta \in \mathcal {B}$
. Using Claims 5.4 and 5.5, we see that
$\beta \in \mathcal {B}$
. Using Claims 5.4 and 5.5, we see that
 $$ \begin{align*} \mu\left(V_\beta \cap X\right) = \mu\left((h^\ast)^{-1}(\beta)\right) \leq \frac{2\mu(X)}{\Delta+1} \leq \frac{1}{2(\Delta + 1)} < \frac{1}{\Delta} \leq \mu\left(V_\beta\right). \end{align*} $$
$$ \begin{align*} \mu\left(V_\beta \cap X\right) = \mu\left((h^\ast)^{-1}(\beta)\right) \leq \frac{2\mu(X)}{\Delta+1} \leq \frac{1}{2(\Delta + 1)} < \frac{1}{\Delta} \leq \mu\left(V_\beta\right). \end{align*} $$
Therefore,
![]() $\mu \left (V_\beta \setminus X\right )> 0$
. By (X1), each vertex in
$\mu \left (V_\beta \setminus X\right )> 0$
. By (X1), each vertex in
![]() $V_\beta \setminus X$
has degree less than
$V_\beta \setminus X$
has degree less than
![]() $4\Delta /5$
. On the other hand, by (P2),
$4\Delta /5$
. On the other hand, by (P2),
![]() $\mu $
-almost every vertex in
$\mu $
-almost every vertex in
![]() $V_\beta \setminus X$
has a neighbour in every colour class
$V_\beta \setminus X$
has a neighbour in every colour class
![]() $V_\alpha $
with
$V_\alpha $
with
![]() $\alpha \in \mathcal {A}$
. Thus, we have
$\alpha \in \mathcal {A}$
. Thus, we have
![]() $\lvert \mathcal {A}\rvert < 4\Delta /5$
, or, equivalently,
$\lvert \mathcal {A}\rvert < 4\Delta /5$
, or, equivalently,
![]() $\xi < 4/5$
, as desired.
$\xi < 4/5$
, as desired.
Following [Reference Kostochka and NakprasitKN05], define
![]() $V^+ := B \setminus X$
and
$V^+ := B \setminus X$
and
![]() $V^- := B \cap X$
.
$V^- := B \cap X$
.
Claim 5.7.
![]() $\mu (B) = \mu \left (V^+\right ) + \mu (V^-) \geq 1-\xi $
.
$\mu (B) = \mu \left (V^+\right ) + \mu (V^-) \geq 1-\xi $
.
Proof. By definition,
![]() $\mu (B) \geq \lvert \mathcal {B}\rvert /\Delta = 1- \xi $
.
$\mu (B) \geq \lvert \mathcal {B}\rvert /\Delta = 1- \xi $
.
Claim 5.8.
![]() $\mu \left (V^+\right ) < 7/10$
.
$\mu \left (V^+\right ) < 7/10$
.
Proof. Take any
![]() $\alpha \in \mathcal {A}$
. By (P2),
$\alpha \in \mathcal {A}$
. By (P2),
![]() $\mu $
-almost every vertex in
$\mu $
-almost every vertex in
![]() $V^+$
has a neighbour in
$V^+$
has a neighbour in
![]() $V_\alpha $
. Since
$V_\alpha $
. Since
![]() $\mu $
is G-invariant, this implies that
$\mu $
is G-invariant, this implies that
 $$ \begin{align*} \int_{V_\alpha} \left\lvert N_G(x) \cap V^+\right\rvert \mathrm{d}\mu(x) \geq \mu\left(V^+\right). \end{align*} $$
$$ \begin{align*} \int_{V_\alpha} \left\lvert N_G(x) \cap V^+\right\rvert \mathrm{d}\mu(x) \geq \mu\left(V^+\right). \end{align*} $$
On the other hand, we can write
 $$ \begin{align*} \hspace{3.7pc} \int_{V_\alpha} \left\lvert N_G(x) \cap V^+\right\rvert \mathrm{d}\mu(x) &\leq \int_{V_\alpha \cap X} \deg_G(x) \mathrm{d}\mu(x) + \int_{V_\alpha \setminus X} \left\lvert N_G(y) \setminus X\right\rvert \mathrm{d}\mu(y) \\ &\leq \Delta \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot\mu\left(V_\alpha \setminus X\right) \qquad\qquad\qquad\qquad({\text{by (X2)}}) \\ &= \frac{3\Delta}{5} \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot \mu(V_\alpha). \end{align*} $$
$$ \begin{align*} \hspace{3.7pc} \int_{V_\alpha} \left\lvert N_G(x) \cap V^+\right\rvert \mathrm{d}\mu(x) &\leq \int_{V_\alpha \cap X} \deg_G(x) \mathrm{d}\mu(x) + \int_{V_\alpha \setminus X} \left\lvert N_G(y) \setminus X\right\rvert \mathrm{d}\mu(y) \\ &\leq \Delta \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot\mu\left(V_\alpha \setminus X\right) \qquad\qquad\qquad\qquad({\text{by (X2)}}) \\ &= \frac{3\Delta}{5} \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot \mu(V_\alpha). \end{align*} $$
Claims 5.4 and 5.5 yield
![]() $\mu (V_\alpha \cap X) \leq 1/2(\Delta + 1) < 1/2\Delta $
. Also,
$\mu (V_\alpha \cap X) \leq 1/2(\Delta + 1) < 1/2\Delta $
. Also,
![]() $\mu (V_\alpha ) < 1/\Delta $
, since
$\mu (V_\alpha ) < 1/\Delta $
, since
![]() $\alpha \in \mathcal {A}$
. Thus
$\alpha \in \mathcal {A}$
. Thus
 $$ \begin{align*} \frac{3\Delta}{5} \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot \mu(V_\alpha) < \frac{3\Delta}{5} \cdot \frac{1}{2\Delta} + \frac{2\Delta}{5} \cdot \frac{1}{\Delta} = \frac{3}{10} + \frac{2}{5} = \frac{7}{10}, \end{align*} $$
$$ \begin{align*} \frac{3\Delta}{5} \cdot \mu(V_\alpha \cap X) + \frac{2\Delta}{5} \cdot \mu(V_\alpha) < \frac{3\Delta}{5} \cdot \frac{1}{2\Delta} + \frac{2\Delta}{5} \cdot \frac{1}{\Delta} = \frac{3}{10} + \frac{2}{5} = \frac{7}{10}, \end{align*} $$
as desired.
Claim 5.9.
![]() $\mu (V^-) < (1 - \xi )/2$
.
$\mu (V^-) < (1 - \xi )/2$
.
Proof. By Claims 5.4 and 5.5, we have
 $$ \begin{align*} \mu(V^-) \leq \frac{(\lvert\mathcal{B}\rvert + 1) \mu(X)}{\Delta+1} < \frac{\lvert\mathcal{B}\rvert + 1}{4\Delta} \leq \frac{\lvert\mathcal{B}\rvert}{2\Delta} = \frac{1-\xi}{2}.\\[-40pt] \end{align*} $$
$$ \begin{align*} \mu(V^-) \leq \frac{(\lvert\mathcal{B}\rvert + 1) \mu(X)}{\Delta+1} < \frac{\lvert\mathcal{B}\rvert + 1}{4\Delta} \leq \frac{\lvert\mathcal{B}\rvert}{2\Delta} = \frac{1-\xi}{2}.\\[-40pt] \end{align*} $$
Claim 5.10.
![]() $(4 - 10\xi ) \mu (V^-) + 10\xi (1-\xi )\leq 1$
.
$(4 - 10\xi ) \mu (V^-) + 10\xi (1-\xi )\leq 1$
.
Proof. Observe that
 $$ \begin{align*} \frac{\Delta}{10} \geq \frac{d_\mu(G)}{2} = \mathsf{C}_\mu(G; V(G)) \geq \mathsf{C}_\mu(G; V^-) + \int_{V^+} \lvert N_G(y) \cap A\rvert \mathrm{d}\mu(y). \end{align*} $$
$$ \begin{align*} \frac{\Delta}{10} \geq \frac{d_\mu(G)}{2} = \mathsf{C}_\mu(G; V(G)) \geq \mathsf{C}_\mu(G; V^-) + \int_{V^+} \lvert N_G(y) \cap A\rvert \mathrm{d}\mu(y). \end{align*} $$
Applying (X3) with
![]() $X' = V^-$
, we get
$X' = V^-$
, we get
![]() $\mathsf {C}_\mu (G;V^-) \geq (2\Delta /5)\mu (V^-)$
. Also, by (P2),
$\mathsf {C}_\mu (G;V^-) \geq (2\Delta /5)\mu (V^-)$
. Also, by (P2),
![]() $\mu $
-almost every vertex
$\mu $
-almost every vertex
![]() $y \in V^+$
has at least
$y \in V^+$
has at least
![]() $\lvert \mathcal {A}\rvert $
neighbours in A. Therefore,
$\lvert \mathcal {A}\rvert $
neighbours in A. Therefore,
 $$ \begin{align} \frac{\Delta}{10} \geq \frac{2\Delta}{5} \cdot \mu(V^-) + \lvert \mathcal{A}\rvert \cdot \mu\left(V^+\right). \end{align} $$
$$ \begin{align} \frac{\Delta}{10} \geq \frac{2\Delta}{5} \cdot \mu(V^-) + \lvert \mathcal{A}\rvert \cdot \mu\left(V^+\right). \end{align} $$
By Claim 5.7,
 $$ \begin{align*} \frac{2\Delta}{5} \cdot \mu(V^-) + \lvert\mathcal{A}\rvert \cdot \mu\left(V^+\right) \geq \left(\frac{2\Delta}{5} - \lvert\mathcal{A}\rvert\right) \cdot \mu(V^-) + \lvert\mathcal{A}\rvert \cdot (1-\xi). \end{align*} $$
$$ \begin{align*} \frac{2\Delta}{5} \cdot \mu(V^-) + \lvert\mathcal{A}\rvert \cdot \mu\left(V^+\right) \geq \left(\frac{2\Delta}{5} - \lvert\mathcal{A}\rvert\right) \cdot \mu(V^-) + \lvert\mathcal{A}\rvert \cdot (1-\xi). \end{align*} $$
Plugging this into formula (5.5) and multiplying both sides by
![]() $10/\Delta $
gives the desired result.
$10/\Delta $
gives the desired result.
Claim 5.11.
![]() $\xi < 2/5$
.
$\xi < 2/5$
.
Proof. Suppose that
![]() $\xi \geq 2/5$
. Then
$\xi \geq 2/5$
. Then
![]() $4-10\xi \leq 0$
, so it follows from Claim 5.10 that
$4-10\xi \leq 0$
, so it follows from Claim 5.10 that
 $$ \begin{align*} 1 &\geq (4 - 10\xi) \mu(V^-) + 10\xi(1-\xi) \\ &\geq (2-5\xi)(1-\xi) + 10\xi(1-\xi). \qquad\qquad({\text{by Claim 5.9}}) \end{align*} $$
$$ \begin{align*} 1 &\geq (4 - 10\xi) \mu(V^-) + 10\xi(1-\xi) \\ &\geq (2-5\xi)(1-\xi) + 10\xi(1-\xi). \qquad\qquad({\text{by Claim 5.9}}) \end{align*} $$
In other words, we have
![]() $5\xi ^2 - 3\xi - 1 \geq 0$
. This inequality implies that either
$5\xi ^2 - 3\xi - 1 \geq 0$
. This inequality implies that either
 $\xi \leq \left (3-\sqrt {29}\right )/10 < 0$
, which is impossible, or
$\xi \leq \left (3-\sqrt {29}\right )/10 < 0$
, which is impossible, or
 $\xi \geq \left (3+\sqrt {29}\right )/10 = 0.83\dotsc> 4/5$
, contradicting Claim 5.6.
$\xi \geq \left (3+\sqrt {29}\right )/10 = 0.83\dotsc> 4/5$
, contradicting Claim 5.6.
We are ready for the coup de grâce. Since
![]() $\xi < 2/5$
, we have
$\xi < 2/5$
, we have
![]() $4-10\xi> 0$
, so Claim 5.10 yields
$4-10\xi> 0$
, so Claim 5.10 yields
 $$ \begin{align*} \mu(V^-) \leq \frac{1 - 10\xi(1-\xi)}{4-10\xi} = \frac{10\xi^2 - 10\xi + 1}{4-10\xi}. \end{align*} $$
$$ \begin{align*} \mu(V^-) \leq \frac{1 - 10\xi(1-\xi)}{4-10\xi} = \frac{10\xi^2 - 10\xi + 1}{4-10\xi}. \end{align*} $$
From this and Claim 5.7 we obtain
 $$ \begin{align*} \mu\left(V^+\right) \geq 1 - \xi - \frac{10\xi^2 - 10\xi + 1}{4-10\xi} = \frac{3-4\xi}{4-10\xi}. \end{align*} $$
$$ \begin{align*} \mu\left(V^+\right) \geq 1 - \xi - \frac{10\xi^2 - 10\xi + 1}{4-10\xi} = \frac{3-4\xi}{4-10\xi}. \end{align*} $$
The function
![]() $t \mapsto (3-4t)/(4 - 10t)$
is increasing for
$t \mapsto (3-4t)/(4 - 10t)$
is increasing for
![]() $0 \leq t < 2/5$
, so
$0 \leq t < 2/5$
, so
![]() $\mu \left (V^+\right )$
is at least the value of this function at
$\mu \left (V^+\right )$
is at least the value of this function at
![]() $t = 0$
– that is,
$t = 0$
– that is,
![]() $\mu \left (V^+\right ) \geq 3/4$
. Since
$\mu \left (V^+\right ) \geq 3/4$
. Since
![]() $3/4> 7/10$
, this contradicts Claim 5.8 and completes the proof of Theorem 1.8.
$3/4> 7/10$
, this contradicts Claim 5.8 and completes the proof of Theorem 1.8.
Acknowledgements
We are very grateful to Ruiyuan (Ronnie) Chen for insightful discussions and, in particular, for drawing our attention to some of the facts concerning compressible graphs that are mentioned in Section 3.5. We are also grateful to the anonymous referees for their helpful suggestions.
Conflict of Interest
None.
Financial support
The first author is partially supported by NSF grant DMS-2045412. The second author is partially supported by NSF grant DMS-1855579.