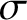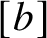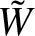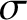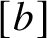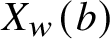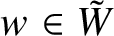1. Introduction
1.1. Motivation
The notion of the affine Deligne–Lusztig variety was introduced by Rapoport in [Reference RapoportRa05]. It plays an important role in arithmetic geometry and the Langlands programme. One of the main motivations comes from the reduction of Shimura varieties. In this paper we focus on the affine Deligne–Lusztig varieties in the affine flag variety. In this case, the affine Deligne–Lusztig varieties are closely related to the Shimura varieties with Iwahori level structure. On the special fibres, there are two important stratifications:
-
• Newton stratification, indexed by specific
 $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
 $[b]$
in the associated p-adic group
$[b]$
in the associated p-adic group -
• Kottwitz–Rapoport stratification, indexed by specific elements w in the associated Iwahori–Weyl group
A fundamental question is to determine when the intersection of a Newton stratum indexed by
![]() $[b]$
and a Kottwitz–Rapoport stratum indexed by w is nonempty and to determine its dimension. Such an intersection is closely related to the affine Deligne–Lusztig variety
$[b]$
and a Kottwitz–Rapoport stratum indexed by w is nonempty and to determine its dimension. Such an intersection is closely related to the affine Deligne–Lusztig variety
![]() $X_w(b)$
(see, e.g., [Reference He and RapoportHR17]). In a parallel story over function fields, affine Deligne–Lusztig varieties also arise naturally in the study of local shtukas (see, e.g., [Reference Hartl and ViehmannHV11]).
$X_w(b)$
(see, e.g., [Reference He and RapoportHR17]). In a parallel story over function fields, affine Deligne–Lusztig varieties also arise naturally in the study of local shtukas (see, e.g., [Reference Hartl and ViehmannHV11]).
Motivated by the study of Shimura varieties and local shtukas, we would like to understand the following fundamental questions on affine Deligne–Lusztig varieties:
-
• When is the affine Deligne–Lusztig variety nonempty?
-
• If nonempty, what is its dimension?
It is also worth pointing out that much information on affine Deligne–Lusztig varieties in partial affine flag varieties (which are closely related to Shimura varieties with other parahoric level structures) can be deduced from the information on affine Deligne-Lusztig varieties in the affine flag variety.
1.2. The main result
In this paper we determine, for any given
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
, the nonemptiness pattern and dimension formula of
$[b]$
, the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
for most w in the Iwahori–Weyl group
$X_w(b)$
for most w in the Iwahori–Weyl group
![]() $\tilde {W}$
. To state the result, we introduce some notation first. For simplicity, we will consider here only the split groups
$\tilde {W}$
. To state the result, we introduce some notation first. For simplicity, we will consider here only the split groups
![]() ${\mathbf G}$
. The general case will be studied in the body of the paper.
${\mathbf G}$
. The general case will be studied in the body of the paper.
The Iwahori–Weyl group
![]() $\tilde {W}$
is the semidirect product of the coweight lattice with the relative Weyl group
$\tilde {W}$
is the semidirect product of the coweight lattice with the relative Weyl group
![]() $W_0$
. We may write
$W_0$
. We may write
![]() $\tilde {W}$
as
$\tilde {W}$
as
![]() $\tilde {W}=\sqcup _{\lambda \text { is dominant}} W_0 t^{\lambda } W_0$
. For any
$\tilde {W}=\sqcup _{\lambda \text { is dominant}} W_0 t^{\lambda } W_0$
. For any
![]() $w \in W_0 t^{\lambda } W_0$
, we set
$w \in W_0 t^{\lambda } W_0$
, we set
![]() $\lambda _w=\lambda $
. The
$\lambda _w=\lambda $
. The
![]() $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
![]() $[b]$
are classified by Kottwitz [Reference KottwitzKo85] via two invariants: the image under the Kottwitz map
$[b]$
are classified by Kottwitz [Reference KottwitzKo85] via two invariants: the image under the Kottwitz map
![]() $\kappa $
and the Newton point
$\kappa $
and the Newton point
![]() $\nu _b$
(which is a dominant rational coweight). By Mazur’s inequality for affine Deligne–Lusztig varieties in the affine Grassmannian [Reference GashiGa10], we deduce that if
$\nu _b$
(which is a dominant rational coweight). By Mazur’s inequality for affine Deligne–Lusztig varieties in the affine Grassmannian [Reference GashiGa10], we deduce that if
![]() $X_w(b) \neq \emptyset $
, then
$X_w(b) \neq \emptyset $
, then
![]() $\kappa (w)=\kappa (b)$
and
$\kappa (w)=\kappa (b)$
and
![]() $\lambda _w \ge \nu _b$
with respect to the dominance order of the rational coweights.
$\lambda _w \ge \nu _b$
with respect to the dominance order of the rational coweights.
The converse, however, is far from being true. The main result of this paper is the following:
Theorem 1.1. Let
![]() $w \in \tilde {W}$
. Suppose that w is in a shrunken Weyl chamber. If
$w \in \tilde {W}$
. Suppose that w is in a shrunken Weyl chamber. If
![]() $\kappa (w)=\kappa (b)$
,
$\kappa (w)=\kappa (b)$
,
![]() $\lambda _w-\nu _b$
is a linear combination of the simple coroots with all the coefficients positive and
$\lambda _w-\nu _b$
is a linear combination of the simple coroots with all the coefficients positive and
![]() $\lambda _w^{\flat \mkern -2.4mu\flat } \ge \nu _b$
, then we have a complete description of the nonemptiness pattern and dimension formula for
$\lambda _w^{\flat \mkern -2.4mu\flat } \ge \nu _b$
, then we have a complete description of the nonemptiness pattern and dimension formula for
![]() $X_w(b)$
.
$X_w(b)$
.
We refer to Section 2.2 for the definition of shrunken Weyl chambers, Section 5.2 for the definition of
![]() $-^{\flat \mkern -2.4mu\flat }$
and Theorem 6.1 for the precise description of the nonemptiness pattern and dimension formula. These assumptions are satisfied for example when
$-^{\flat \mkern -2.4mu\flat }$
and Theorem 6.1 for the precise description of the nonemptiness pattern and dimension formula. These assumptions are satisfied for example when
![]() $\lambda _w \ge \nu _b+2 \rho ^\vee $
, where
$\lambda _w \ge \nu _b+2 \rho ^\vee $
, where
![]() $\rho ^\vee $
is the half sum of positive coroots (see Corollary 6.4).
$\rho ^\vee $
is the half sum of positive coroots (see Corollary 6.4).
As an application of Theorem 1.1, in joint work with Q. Yu [Reference Yu and HeHY21] we establish a dimension formula for the group-theoretic analogue of Newton strata for sufficiently large dominant coweights.
1.3. Some previous results
In [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.5.1], Görtz, Haines, Kottwitz and Reuman made several influential conjectures on the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
.
$X_w(b)$
.
First, for the basic
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
, they gave a conjecture in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.5.1 (a)] on the nonemptiness pattern and dimension formula of
$[b]$
, they gave a conjecture in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.5.1 (a)] on the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
for w in the shrunken Weyl chamber. This conjecture was established in [Reference HeHe14]. For
$X_w(b)$
for w in the shrunken Weyl chamber. This conjecture was established in [Reference HeHe14]. For
![]() $X_w(b)$
with
$X_w(b)$
with
![]() $[b]$
basic and w outside the shrunken Weyl chamber, in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.4.2] they gave a conjecture on the nonemptiness pattern. This conjecture is established in [Reference Görtz, He and NieGHN15]. But for
$[b]$
basic and w outside the shrunken Weyl chamber, in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.4.2] they gave a conjecture on the nonemptiness pattern. This conjecture is established in [Reference Görtz, He and NieGHN15]. But for
![]() $[b]$
basic and w outside the shrunken Weyl chamber, no conjectural dimension formula of
$[b]$
basic and w outside the shrunken Weyl chamber, no conjectural dimension formula of
![]() $X_w(b)$
has even been formulated so far.
$X_w(b)$
has even been formulated so far.
For arbitrary
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
, they made an interesting conjecture in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.5.1 (b)] which predicts the difference of the dimensions of
$[b]$
, they made an interesting conjecture in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Conjecture 9.5.1 (b)] which predicts the difference of the dimensions of
![]() $X_w(b)$
and
$X_w(b)$
and
![]() $X_w(b_{basic})$
, where
$X_w(b_{basic})$
, where
![]() $[b_{basic}]$
is the unique basic
$[b_{basic}]$
is the unique basic
![]() $\sigma $
-conjugacy class such that
$\sigma $
-conjugacy class such that
![]() $\kappa (b)=\kappa (b_{basic})$
. In this conjecture, w is not required to be shrunken, but the length of w is required to be big enough with some (unspecified) lower bound. In later works, we studied
$\kappa (b)=\kappa (b_{basic})$
. In this conjecture, w is not required to be shrunken, but the length of w is required to be big enough with some (unspecified) lower bound. In later works, we studied
![]() $X_w(b)$
via a somewhat different direction. First, the assumption that w is in the shrunken Weyl chamber is added, as even for the basic b, the dimension formula of
$X_w(b)$
via a somewhat different direction. First, the assumption that w is in the shrunken Weyl chamber is added, as even for the basic b, the dimension formula of
![]() $X_w(b)$
with w outside the shrunken Weyl chamber is still very mysterious. Second, we would like to have a specific lower bound on w.
$X_w(b)$
with w outside the shrunken Weyl chamber is still very mysterious. Second, we would like to have a specific lower bound on w.
For split groups and the case where
![]() $[b]$
is represented by translation elements, under the ‘very shrunken’ assumption the nonemptiness pattern and the dimension formula of
$[b]$
is represented by translation elements, under the ‘very shrunken’ assumption the nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
were given in [Reference HeHe15, Theorem 2.28 & Theorem 2.34]. A similar result was obtained in [Reference Milićević, Schwer and ThomasMST19] under a different condition on w.
$X_w(b)$
were given in [Reference HeHe15, Theorem 2.28 & Theorem 2.34]. A similar result was obtained in [Reference Milićević, Schwer and ThomasMST19] under a different condition on w.
For other nonbasic
![]() $\sigma $
-conjugacy classes, little is known so far on the nonemptiness pattern and dimension formula of
$\sigma $
-conjugacy classes, little is known so far on the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
.
$X_w(b)$
.
1.4. Old strategies
We discuss several strategies used in previous work to study the nonemptiness pattern and dimension formula for
![]() $X_w(b)$
.
$X_w(b)$
.
The emptiness pattern is established via the method of P-alcove elements introduced in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Definition 2.1.1]. The upper bound of
![]() $\dim X_w(b)$
is given by the virtual dimension
$\dim X_w(b)$
is given by the virtual dimension
![]() $d_w(b)$
introduced in [Reference HeHe14, §10.1].
$d_w(b)$
introduced in [Reference HeHe14, §10.1].
In [Reference HeHe14], we combined the Deligne–Lusztig reduction with some remarkable properties of minimal length elements in their conjugacy classes in
![]() $\tilde {W}$
to establish a method to compute
$\tilde {W}$
to establish a method to compute
![]() $\dim X_w(b)$
for arbitrary w and arbitrary
$\dim X_w(b)$
for arbitrary w and arbitrary
![]() $[b]$
. As a consequence, in [Reference HeHe14, Theorem 6.1] we established the ‘dimension=degree’ theorem, which relates the dimension of affine Deligne–Lusztig varieties with the degree of the class polynomials of the affine Hecke algebras. However, the computation of the class polynomials, in general, is extremely difficult. The dimension=degree theorem does not lead to explicit descriptions of the nonemptiness pattern and the dimension formula of
$[b]$
. As a consequence, in [Reference HeHe14, Theorem 6.1] we established the ‘dimension=degree’ theorem, which relates the dimension of affine Deligne–Lusztig varieties with the degree of the class polynomials of the affine Hecke algebras. However, the computation of the class polynomials, in general, is extremely difficult. The dimension=degree theorem does not lead to explicit descriptions of the nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
.
$X_w(b)$
.
For basic
![]() $[b]$
, assume that
$[b]$
, assume that
![]() $X_w(b) \neq \emptyset $
. It remains to show that
$X_w(b) \neq \emptyset $
. It remains to show that
![]() $\dim X_w(b)$
reaches the upper bound
$\dim X_w(b)$
reaches the upper bound
![]() $d_w(b)$
. Note that for any Coxeter element c,
$d_w(b)$
. Note that for any Coxeter element c,
![]() $\dim X_c(b)$
is easy to compute. This will be used as the starting point. In [Reference HeHe14, §11], we constructed an explicit ‘reduction path’ from an element w in the shrunken Weyl chamber to an element
$\dim X_c(b)$
is easy to compute. This will be used as the starting point. In [Reference HeHe14, §11], we constructed an explicit ‘reduction path’ from an element w in the shrunken Weyl chamber to an element
![]() $w'$
with finite part a Coxeter element. By [Reference He and YangHY12, Theorem 1.1], the minimal length elements in the conjugacy class of
$w'$
with finite part a Coxeter element. By [Reference He and YangHY12, Theorem 1.1], the minimal length elements in the conjugacy class of
![]() $w'$
in
$w'$
in
![]() $\tilde {W}$
are the Coxeter elements c. This gives a reduction path from w to c and thus leads to a lower bound of
$\tilde {W}$
are the Coxeter elements c. This gives a reduction path from w to c and thus leads to a lower bound of
![]() $\dim X_w(b)$
. Fortunately, the lower bound also equals the virtual dimension
$\dim X_w(b)$
. Fortunately, the lower bound also equals the virtual dimension
![]() $d_w(b)$
. Thus we proved the nonemptiness pattern and the dimension formula of
$d_w(b)$
. Thus we proved the nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
with basic
$X_w(b)$
with basic
![]() $[b]$
.
$[b]$
.
For split groups and the case where
![]() $[b]$
is represented by translation elements, in [Reference HeHe15] we used the superset method of [Reference Görtz, Haines, Kottwitz and ReumanGHKR10] to relate the nonemptiness pattern and dimension formula of
$[b]$
is represented by translation elements, in [Reference HeHe15] we used the superset method of [Reference Görtz, Haines, Kottwitz and ReumanGHKR10] to relate the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
with
$X_w(b)$
with
![]() $X_{w'}(1)$
for a given
$X_{w'}(1)$
for a given
![]() $w'$
. Note that
$w'$
. Note that
![]() $[1]$
is a basic
$[1]$
is a basic
![]() $\sigma $
-conjugacy class. We then used the result on
$\sigma $
-conjugacy class. We then used the result on
![]() $X_{w'}(1)$
established in [Reference HeHe14] to obtain the desired result on
$X_{w'}(1)$
established in [Reference HeHe14] to obtain the desired result on
![]() $X_w(b)$
. A very different approach was introduced in [Reference Milićević, Schwer and ThomasMST19], where the authors used alcove walks and Littelmann paths to study the nonemptiness pattern and dimension formula of
$X_w(b)$
. A very different approach was introduced in [Reference Milićević, Schwer and ThomasMST19], where the authors used alcove walks and Littelmann paths to study the nonemptiness pattern and dimension formula of
![]() $X_w(b)$
.
$X_w(b)$
.
It is unclear how or whether the methods in [Reference HeHe15] or in [Reference Milićević, Schwer and ThomasMST19] for the translation elements may be generalised to arbitrary
![]() $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
![]() $[b]$
. The reduction method introduced in [Reference HeHe14] works, in theory, for an arbitrary
$[b]$
. The reduction method introduced in [Reference HeHe14] works, in theory, for an arbitrary
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
. However, constructing an explicit reduction path from a given w to a minimal length element associated to a nonbasic
$[b]$
. However, constructing an explicit reduction path from a given w to a minimal length element associated to a nonbasic
![]() $[b]$
is very challenging. Q. Yu has written a computer program to construct the reduction path for groups with small ranks. But so far it is not clear how such a reduction path may be constructed in general.
$[b]$
is very challenging. Q. Yu has written a computer program to construct the reduction path for groups with small ranks. But so far it is not clear how such a reduction path may be constructed in general.
1.5. New strategy
The new strategy in this paper is as follows. Instead of using minimal length elements as the starting point, we use the cordial elements introduced by Milićević and Viehmann in [Reference Milićević and ViehmannMV20] as the starting point. In Section 4, we construct a new family of cordial elements. For any element
![]() $w'$
in this family,
$w'$
in this family,
![]() $\dim X_{w'}(b)$
equals the virtual dimension. We then construct in Section 5 an explicit reduction path from an element w in the shrunken Weyl chamber to an element in this family. This is where the assumption
$\dim X_{w'}(b)$
equals the virtual dimension. We then construct in Section 5 an explicit reduction path from an element w in the shrunken Weyl chamber to an element in this family. This is where the assumption
![]() $\lambda _w^{\flat \mkern -2.4mu\flat } \ge \nu _b$
is used. This shows that
$\lambda _w^{\flat \mkern -2.4mu\flat } \ge \nu _b$
is used. This shows that
![]() $\dim X_w(b) \ge d_w(b)$
. Finally we use the result that
$\dim X_w(b) \ge d_w(b)$
. Finally we use the result that
![]() $\dim X_w(b) \le d_w(b)$
established in [Reference HeHe14] to prove the desired nonemptiness pattern and the dimension formula of
$\dim X_w(b) \le d_w(b)$
established in [Reference HeHe14] to prove the desired nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
.
$X_w(b)$
.
Another issue we would like to point out here is that previous works (e.g., [Reference Görtz and HeGH10]) are in less general situations (e.g., with the assumption that G is split or tamely ramified) than the one we consider here. However, in this paper we use the geometric results Theorem 3.2 and Proposition 3.3, which hold for any reductive group G, and then use combinatorics of the Iwahori–Weyl groups
![]() $\tilde {W}$
. The results from previous works that we use here are to deduce certain nice combinatorial properties of
$\tilde {W}$
. The results from previous works that we use here are to deduce certain nice combinatorial properties of
![]() $\tilde {W}$
. Thus we may apply the previous works in the more general setup here.
$\tilde {W}$
. Thus we may apply the previous works in the more general setup here.
2. Preliminaries
2.1. The reductive group
 ${\mathbf G}$
and its Iwahori–Weyl group
${\mathbf G}$
and its Iwahori–Weyl group
Let F be a nonarchimedean local field and
![]() $\breve F$
be the completion of the maximal unramified extension of F. We write
$\breve F$
be the completion of the maximal unramified extension of F. We write
![]() $\Gamma $
for
$\Gamma $
for
 $\operatorname {\mathrm {Gal}}\left (\overline F/F\right )$
, where
$\operatorname {\mathrm {Gal}}\left (\overline F/F\right )$
, where
![]() $\overline F$
is an algebraic closure of F. We write
$\overline F$
is an algebraic closure of F. We write
![]() $\Gamma _0$
for the inertia subgroup of
$\Gamma _0$
for the inertia subgroup of
![]() $\Gamma $
. Let t be a uniformiser in F.
$\Gamma $
. Let t be a uniformiser in F.
Let
![]() ${\mathbf G}$
be a connected reductive group over F. Let
${\mathbf G}$
be a connected reductive group over F. Let
![]() $\sigma $
be the Frobenius morphism of
$\sigma $
be the Frobenius morphism of
![]() $\breve F/F$
. We write
$\breve F/F$
. We write
![]() $\breve G$
for
$\breve G$
for
![]() $\mathbf G\left (\breve F\right )$
. We use the same symbol
$\mathbf G\left (\breve F\right )$
. We use the same symbol
![]() $\sigma $
for the induced Frobenius morphism on
$\sigma $
for the induced Frobenius morphism on
![]() $\breve G$
.
$\breve G$
.
We fix a maximal
![]() $\breve F$
-split torus S in
$\breve F$
-split torus S in
![]() ${\mathbf G}$
defined over F which contains a maximal F-split torus. Let T be the centraliser of S in
${\mathbf G}$
defined over F which contains a maximal F-split torus. Let T be the centraliser of S in
![]() ${\mathbf G}$
. Then T is a maximal torus. Let
${\mathbf G}$
. Then T is a maximal torus. Let
![]() $\mathcal A$
be the apartment of
$\mathcal A$
be the apartment of
![]() $\mathbf G_{\breve F}$
corresponding to
$\mathbf G_{\breve F}$
corresponding to
![]() $S_{\breve F}$
. Thus
$S_{\breve F}$
. Thus
![]() $\mathcal A$
is (noncanonically) isomorphic to
$\mathcal A$
is (noncanonically) isomorphic to
![]() $V=X_*(T)_{\Gamma _0} \otimes _{\mathbb Z} \mathbb R$
. The Frobenius
$V=X_*(T)_{\Gamma _0} \otimes _{\mathbb Z} \mathbb R$
. The Frobenius
![]() $\sigma $
naturally acts on
$\sigma $
naturally acts on
![]() $\mathcal A$
. We fix a
$\mathcal A$
. We fix a
![]() $\sigma $
-stable alcove
$\sigma $
-stable alcove
![]() $\mathfrak a$
in
$\mathfrak a$
in
![]() $\mathcal A$
, and let
$\mathcal A$
, and let
![]() $\breve I \subset \breve G$
be the Iwahori subgroup corresponding to
$\breve I \subset \breve G$
be the Iwahori subgroup corresponding to
![]() $\mathfrak a$
. Thus
$\mathfrak a$
. Thus
![]() $\breve I$
is
$\breve I$
is
![]() $\sigma $
-stable.
$\sigma $
-stable.
We denote by N the normaliser of T in
![]() ${\mathbf G}$
. The relative Weyl group
${\mathbf G}$
. The relative Weyl group
![]() $W_0$
is defined to be
$W_0$
is defined to be
![]() $N\left (\breve F\right )/T\left (\breve F\right )$
. The Iwahori–Weyl group (associated to S) is defined as
$N\left (\breve F\right )/T\left (\breve F\right )$
. The Iwahori–Weyl group (associated to S) is defined as
 $$ \begin{align*}\tilde{W}= N\left(\breve F\right)/T\left(\breve F\right) \cap \breve I.\end{align*} $$
$$ \begin{align*}\tilde{W}= N\left(\breve F\right)/T\left(\breve F\right) \cap \breve I.\end{align*} $$
For any
![]() $w \in \tilde {W}$
, we choose a representative
$w \in \tilde {W}$
, we choose a representative
![]() $\dot w$
in
$\dot w$
in
![]() $N(L)$
.
$N(L)$
.
We have a natural short exact sequence
![]() $0 \rightarrow X_*(T)_{\Gamma _0} \rightarrow \tilde {W} \rightarrow W_0 \rightarrow 0$
. We choose a special vertex of
$0 \rightarrow X_*(T)_{\Gamma _0} \rightarrow \tilde {W} \rightarrow W_0 \rightarrow 0$
. We choose a special vertex of
![]() $\mathfrak a$
and represent
$\mathfrak a$
and represent
![]() $\tilde {W}$
as a semidirect product,
$\tilde {W}$
as a semidirect product,
 $$ \begin{align*}\tilde{W}=X_*(T)_{\Gamma_0} \rtimes W_0=\left\{t^{\lambda} w; \lambda \in X_*(T)_{\Gamma_0}, w \in W_0\right\}.\end{align*} $$
$$ \begin{align*}\tilde{W}=X_*(T)_{\Gamma_0} \rtimes W_0=\left\{t^{\lambda} w; \lambda \in X_*(T)_{\Gamma_0}, w \in W_0\right\}.\end{align*} $$
The Iwahori–Weyl group
![]() $\tilde {W}$
contains the affine Weyl group
$\tilde {W}$
contains the affine Weyl group
![]() $W_a$
as a normal subgroup and we have
$W_a$
as a normal subgroup and we have
where
![]() $\Omega $
is the stabiliser of
$\Omega $
is the stabiliser of
![]() $\mathfrak a$
. The length function
$\mathfrak a$
. The length function
![]() $\ell $
and Bruhat order
$\ell $
and Bruhat order
![]() $\le $
on
$\le $
on
![]() $W_a$
extend in a natural way to
$W_a$
extend in a natural way to
![]() $\tilde {W}$
. The Frobenius
$\tilde {W}$
. The Frobenius
![]() $\sigma $
naturally acts on
$\sigma $
naturally acts on
![]() $\tilde {W}$
, in such a way that the subset
$\tilde {W}$
, in such a way that the subset
![]() $\tilde {\mathbb {S}} \subset \tilde {W}$
is stable.
$\tilde {\mathbb {S}} \subset \tilde {W}$
is stable.
For any
![]() $K \subset \tilde {\mathbb {S}}$
, we denote by
$K \subset \tilde {\mathbb {S}}$
, we denote by
![]() $W_K$
the subgroup of
$W_K$
the subgroup of
![]() $\tilde {W}$
generated by
$\tilde {W}$
generated by
![]() $s \in K$
. Let
$s \in K$
. Let
![]() ${}^K \tilde {W}$
(resp.,
${}^K \tilde {W}$
(resp.,
![]() $\tilde {W}^K$
) be the set of minimal length elements in their cosets in
$\tilde {W}^K$
) be the set of minimal length elements in their cosets in
![]() $W_K \backslash \tilde {W}$
(resp.,
$W_K \backslash \tilde {W}$
(resp.,
![]() $\tilde {W}/W_K$
).
$\tilde {W}/W_K$
).
Let
![]() $\mathbb {S} \subset \tilde {\mathbb {S}}$
be the set of simple reflections of
$\mathbb {S} \subset \tilde {\mathbb {S}}$
be the set of simple reflections of
![]() $W_0$
. By convention, the dominant Weyl chamber of V is opposite to the unique Weyl chamber containing
$W_0$
. By convention, the dominant Weyl chamber of V is opposite to the unique Weyl chamber containing
![]() $\mathfrak a$
. Let
$\mathfrak a$
. Let
![]() $\Delta $
be the set of relative simple roots determined by the dominant Weyl chamber. For any
$\Delta $
be the set of relative simple roots determined by the dominant Weyl chamber. For any
![]() $s \in \mathbb {S}$
, we denote by
$s \in \mathbb {S}$
, we denote by
![]() $\alpha _s \in \Delta $
the corresponding simple root and
$\alpha _s \in \Delta $
the corresponding simple root and
![]() $\alpha _s^\vee $
the corresponding simple coroot. We denote by
$\alpha _s^\vee $
the corresponding simple coroot. We denote by
![]() $w_{\mathbb {S}}$
the longest element of
$w_{\mathbb {S}}$
the longest element of
![]() $W_0$
.
$W_0$
.
We define the
![]() $\sigma $
-conjugation action on
$\sigma $
-conjugation action on
![]() $\breve G$
by
$\breve G$
by
![]() $g \cdot _{\sigma } g'=g g' \sigma (g) ^{-1}$
. Let
$g \cdot _{\sigma } g'=g g' \sigma (g) ^{-1}$
. Let
![]() $B(\mathbf G)$
be the set of
$B(\mathbf G)$
be the set of
![]() $\sigma $
-conjugacy classes on
$\sigma $
-conjugacy classes on
![]() $\breve G$
. The classification of the
$\breve G$
. The classification of the
![]() $\sigma $
-conjugacy classes was obtained by Kottwitz in [Reference KottwitzKo85]. Any
$\sigma $
-conjugacy classes was obtained by Kottwitz in [Reference KottwitzKo85]. Any
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
is determined by two invariants:
$[b]$
is determined by two invariants:
-
• the element
 $\kappa ([b]) \in \Omega _{\sigma }$
and
$\kappa ([b]) \in \Omega _{\sigma }$
and -
• the Newton point
 $\nu _b \in \left (\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )^+\right )^{\langle \sigma \rangle }$
.
$\nu _b \in \left (\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )^+\right )^{\langle \sigma \rangle }$
.
Here
![]() $-_{\sigma }$
denotes the
$-_{\sigma }$
denotes the
![]() $\sigma $
-coinvariants and
$\sigma $
-coinvariants and
 $\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )^+$
denotes the set of dominant elements in
$\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )^+$
denotes the set of dominant elements in
![]() $X_*(T)_{\Gamma _0}\otimes \mathbb {Q}=X_*(T)^{\Gamma _0}\otimes \mathbb {Q}$
; the action of
$X_*(T)_{\Gamma _0}\otimes \mathbb {Q}=X_*(T)^{\Gamma _0}\otimes \mathbb {Q}$
; the action of
![]() $\sigma $
on
$\sigma $
on
![]() $\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )/W_0$
is transferred to an action on
$\left (X_*(T)_{\Gamma _0, \mathbb {Q}}\right )/W_0$
is transferred to an action on
 $\left (X_*(T)_{\mathbb {Q}}\right )^+$
(L-action).
$\left (X_*(T)_{\mathbb {Q}}\right )^+$
(L-action).
For any
![]() $w \in \tilde {W}$
, we write
$w \in \tilde {W}$
, we write
![]() $\kappa (w)$
for
$\kappa (w)$
for
![]() $\kappa (\dot w)$
. It is easy to see that
$\kappa (\dot w)$
. It is easy to see that
![]() $\kappa (w)$
is independent of the choice of the representative w.
$\kappa (w)$
is independent of the choice of the representative w.
We use the convention of Bruhat and Tits that the translation element
![]() $t^{\lambda }$
acts by
$t^{\lambda }$
acts by
![]() $-\lambda $
on the apartment. In this way, we have
$-\lambda $
on the apartment. In this way, we have
![]() $\ell \left (x t^{\lambda }\right )=\ell (x)+\ell \left (t^{\lambda }\right )$
for any
$\ell \left (x t^{\lambda }\right )=\ell (x)+\ell \left (t^{\lambda }\right )$
for any
![]() $x \in W_0$
and
$x \in W_0$
and
![]() $\lambda $
dominant.
$\lambda $
dominant.
2.2. Affine Deligne–Lusztig varieties
We have the following generalisation of the Bruhat decomposition:
due to Iwahori and Matsumoto [Reference Iwahori and MatsumotoIM65] in the split case and to Bruhat and Tits [Reference Bruhat and TitsBT72] in the general case. Let
![]() $Fl=\breve G/\breve I$
be the affine flag variety. For any
$Fl=\breve G/\breve I$
be the affine flag variety. For any
![]() $b \in \breve G$
and
$b \in \breve G$
and
![]() $w \in \tilde {W}$
, we define the corresponding affine Deligne–Lusztig variety in the affine flag variety:
$w \in \tilde {W}$
, we define the corresponding affine Deligne–Lusztig variety in the affine flag variety:
 $$ \begin{align*}X_w(b)=\left\{g \breve I \in \breve G/\breve I; g ^{-1} b \sigma(g) \in \breve I \dot w \breve I\right\} \subset Fl.\end{align*} $$
$$ \begin{align*}X_w(b)=\left\{g \breve I \in \breve G/\breve I; g ^{-1} b \sigma(g) \in \breve I \dot w \breve I\right\} \subset Fl.\end{align*} $$
In the equal characteristic,
![]() $X_w(b)$
is the set of
$X_w(b)$
is the set of
![]() $\bar {\mathbb F}_q$
-points of a scheme [Reference Bhatt and ScholzeBS17].
$\bar {\mathbb F}_q$
-points of a scheme [Reference Bhatt and ScholzeBS17].
As discussed in [Reference Görtz, He and NieGHN15, §2], the study of the nonemptiness pattern and dimension formula of affine Deligne–Lusztig varieties for an arbitrary reductive group may be reduced to simple and quasi-split groups over F. From now on, we assume that
![]() ${\mathbf G}$
is simple and quasi-split over F. In this case, the
${\mathbf G}$
is simple and quasi-split over F. In this case, the
![]() $\sigma $
-action on
$\sigma $
-action on
![]() $\tilde {W}$
preserves
$\tilde {W}$
preserves
![]() $W_0$
and
$W_0$
and
![]() $X_*(T)_{\Gamma _0}$
. Moreover, we have
$X_*(T)_{\Gamma _0}$
. Moreover, we have
![]() $\sigma (\mathbb {S})=\mathbb {S}$
and
$\sigma (\mathbb {S})=\mathbb {S}$
and
![]() $\sigma (\Delta )=\Delta $
.
$\sigma (\Delta )=\Delta $
.
Now we recall the definition of the virtual dimension in [Reference HeHe14, §10.1].
Note that any element
![]() $w \in \tilde {W}$
may be written in a unique way as
$w \in \tilde {W}$
may be written in a unique way as
![]() $w=x t^\mu y$
with
$w=x t^\mu y$
with
![]() $\mu $
dominant,
$\mu $
dominant,
![]() $x, y \in W_0$
, such that
$x, y \in W_0$
, such that
![]() $t^\mu y \in {}^{\mathbb {S}} \tilde {W}$
. In this case,
$t^\mu y \in {}^{\mathbb {S}} \tilde {W}$
. In this case,
We set
Let
![]() $\mathbf J_b$
be the reductive group over F with
$\mathbf J_b$
be the reductive group over F with
 $\mathbf J_b(F)=\left \{g \in \breve G; g b \sigma (g) ^{-1}=b\right \}.$
The defect of b is defined by
$\mathbf J_b(F)=\left \{g \in \breve G; g b \sigma (g) ^{-1}=b\right \}.$
The defect of b is defined by
![]() $\text {def}(b)=\operatorname {\mathrm {rank}}_F \mathbf G-\operatorname {\mathrm {rank}}_F \mathbf J_b.$
Here for a reductive group
$\text {def}(b)=\operatorname {\mathrm {rank}}_F \mathbf G-\operatorname {\mathrm {rank}}_F \mathbf J_b.$
Here for a reductive group
![]() $\mathbb H$
defined over F,
$\mathbb H$
defined over F,
![]() $\operatorname {\mathrm {rank}}_F$
is the F-rank of the group
$\operatorname {\mathrm {rank}}_F$
is the F-rank of the group
![]() $\mathbb H$
. Let
$\mathbb H$
. Let
![]() $\rho $
be the dominant weight with
$\rho $
be the dominant weight with
![]() $\left \langle \alpha ^\vee , \rho \right \rangle =1$
for any
$\left \langle \alpha ^\vee , \rho \right \rangle =1$
for any
![]() $\alpha \in \Delta $
. The virtual dimension is defined to be
$\alpha \in \Delta $
. The virtual dimension is defined to be
 $$ \begin{align*}d_w(b)=\frac 12 \big( \ell(w) + \ell(\eta_{\sigma}(w)) -\text{def}(b) \big)-\langle\nu_b, \rho\rangle.\end{align*} $$
$$ \begin{align*}d_w(b)=\frac 12 \big( \ell(w) + \ell(\eta_{\sigma}(w)) -\text{def}(b) \big)-\langle\nu_b, \rho\rangle.\end{align*} $$
The following result is proved in [Reference HeHe14, Corollary 10.4] for residually split groups and in [Reference HeHe15, Theorem 2.30] for the general case:
Theorem 2.1. Let
![]() $b \in \breve G$
and
$b \in \breve G$
and
![]() $w \in \tilde {W}$
. Then
$w \in \tilde {W}$
. Then
![]() $\dim X_w(b) \le d_w(b)$
.
$\dim X_w(b) \le d_w(b)$
.
For any
![]() $w \in W_0$
, we denote by
$w \in W_0$
, we denote by
![]() $\operatorname {\mathrm {supp}}(w) \subset \mathbb {S}$
the set of simple reflections appearing in some (or equivalently, any) reduced expression of w. We set
$\operatorname {\mathrm {supp}}(w) \subset \mathbb {S}$
the set of simple reflections appearing in some (or equivalently, any) reduced expression of w. We set
![]() $\operatorname {\mathrm {supp}}_{\sigma }(w)=\cup _{i \in \mathbb {Z}} \sigma ^i(\operatorname {\mathrm {supp}}(w))$
.
$\operatorname {\mathrm {supp}}_{\sigma }(w)=\cup _{i \in \mathbb {Z}} \sigma ^i(\operatorname {\mathrm {supp}}(w))$
.
For any
![]() $w \in \tilde {W}$
, let
$w \in \tilde {W}$
, let
![]() $\lambda _w$
be the unique dominant coweight such that
$\lambda _w$
be the unique dominant coweight such that
![]() $w \in W_0 t^{\lambda _w} W_0$
. For any
$w \in W_0 t^{\lambda _w} W_0$
. For any
![]() $\lambda \in X_*(T)_{\Gamma _0}$
, we denote by
$\lambda \in X_*(T)_{\Gamma _0}$
, we denote by
![]() $\lambda ^{\diamondsuit }$
the average of the
$\lambda ^{\diamondsuit }$
the average of the
![]() $\sigma $
-orbit of
$\sigma $
-orbit of
![]() $\lambda $
. For any
$\lambda $
. For any
 $\lambda , \lambda ' \in X_*(T)^+_{\mathbb {Q}}$
, we write
$\lambda , \lambda ' \in X_*(T)^+_{\mathbb {Q}}$
, we write
![]() $\lambda \ge \lambda '$
if
$\lambda \ge \lambda '$
if
![]() $\lambda -\lambda ' \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
and write
$\lambda -\lambda ' \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
and write
![]() $\lambda \ge _{\mathbb {Z}} \lambda '$
if
$\lambda \ge _{\mathbb {Z}} \lambda '$
if
![]() $\lambda -\lambda ' \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha ^\vee $
. Here
$\lambda -\lambda ' \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha ^\vee $
. Here
![]() $\mathbb {N}$
is the set of natural numbers, that is, the set of nonnegative integers.
$\mathbb {N}$
is the set of natural numbers, that is, the set of nonnegative integers.
A critical strip of the apartment V is the subset
![]() $\left \{v; -1<\langle v, \alpha \rangle <0\right \}$
for a given positive root
$\left \{v; -1<\langle v, \alpha \rangle <0\right \}$
for a given positive root
![]() $\alpha $
in the reduced root system associated to the affine Weyl group
$\alpha $
in the reduced root system associated to the affine Weyl group
![]() $W_a$
. We remove all the critical strips from V and call each connected component of the remaining subset of V a shrunken Weyl chamber.
$W_a$
. We remove all the critical strips from V and call each connected component of the remaining subset of V a shrunken Weyl chamber.
3. Some combinatorial properties
3.1. Minimal length elements
For any
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $\mathcal O$
in
$\mathcal O$
in
![]() $\tilde {W}$
, we denote by
$\tilde {W}$
, we denote by
![]() $\mathcal O_{\min }$
the set of minimal length elements in
$\mathcal O_{\min }$
the set of minimal length elements in
![]() $\mathcal O$
. For
$\mathcal O$
. For
![]() $w, w' \in \tilde {W}$
and
$w, w' \in \tilde {W}$
and
![]() $s \in \tilde {\mathbb {S}}$
, we write
$s \in \tilde {\mathbb {S}}$
, we write
![]() $w {\xrightarrow {s}}_{\sigma } w'$
if
$w {\xrightarrow {s}}_{\sigma } w'$
if
![]() $w'=s w \sigma (s)$
and
$w'=s w \sigma (s)$
and
![]() $\ell (w') \le \ell (w)$
. We write
$\ell (w') \le \ell (w)$
. We write
![]() $w {\rightarrow }_{\sigma } w'$
if there is a sequence
$w {\rightarrow }_{\sigma } w'$
if there is a sequence
![]() $w=w_0, w_1, \dotsc , w_n=w'$
of elements in
$w=w_0, w_1, \dotsc , w_n=w'$
of elements in
![]() $\tilde {W}$
such that for any k,
$\tilde {W}$
such that for any k,
![]() $w_{k-1} {\xrightarrow {s}}_{\sigma } w_k$
for some
$w_{k-1} {\xrightarrow {s}}_{\sigma } w_k$
for some
![]() $s \in \tilde {\mathbb {S}}$
. We write
$s \in \tilde {\mathbb {S}}$
. We write
![]() $w \approx _{\sigma } w'$
if
$w \approx _{\sigma } w'$
if
![]() $w \rightarrow _{\sigma } w'$
and
$w \rightarrow _{\sigma } w'$
and
![]() $w' \rightarrow _{\sigma } w$
. It is easy to see that
$w' \rightarrow _{\sigma } w$
. It is easy to see that
![]() $w \approx _{\sigma } w'$
if
$w \approx _{\sigma } w'$
if
![]() $w \rightarrow _{\sigma } w'$
and
$w \rightarrow _{\sigma } w'$
and
![]() $\ell (w)=\ell (w')$
.
$\ell (w)=\ell (w')$
.
The following result is proved in [Reference He and NieHN14, §2]:
Theorem 3.1. Let
![]() $\mathcal O$
be a
$\mathcal O$
be a
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
![]() $\tilde {W}$
and
$\tilde {W}$
and
![]() $w \in {\mathcal O}$
. Then there exists
$w \in {\mathcal O}$
. Then there exists
![]() $w' \in {\mathcal O}_{\min }$
such that
$w' \in {\mathcal O}_{\min }$
such that
![]() $w \rightarrow _{\sigma } w'$
.
$w \rightarrow _{\sigma } w'$
.
Theorem 3.2. Let
![]() $b \in \breve G$
and
$b \in \breve G$
and
![]() $w \in {\mathcal O}_{\min }$
for some
$w \in {\mathcal O}_{\min }$
for some
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() ${\mathcal O}$
of
${\mathcal O}$
of
![]() $\tilde {W}$
. Then
$\tilde {W}$
. Then
![]() $X_w(b) \neq \emptyset $
if and only if
$X_w(b) \neq \emptyset $
if and only if
![]() $\dot w \in [b]$
. In this case,
$\dot w \in [b]$
. In this case,
![]() $\dim X_w(b)=\ell (w)-\langle \nu _b, 2 \rho \rangle $
.
$\dim X_w(b)=\ell (w)-\langle \nu _b, 2 \rho \rangle $
.
3.2. Deligne–Lusztig reduction
Now we recall the ‘reduction’ à la Deligne and Lusztig for affine Deligne–Lusztig varieties (see [Reference Deligne and LusztigDL76, Proof of Theorem 1.6] and [Reference Görtz and HeGH10, Corollary 2.5.3]).
Proposition 3.3. Let
![]() $b \in \breve G$
. Then
$b \in \breve G$
. Then
-
(1) if
 $w, w' \in \tilde {W}$
with
$w, w' \in \tilde {W}$
with
 $w \approx _{\sigma } w'$
, we have
$w \approx _{\sigma } w'$
, we have  $$ \begin{align*} \dim X_w(b)=\dim X_{w'}(b); \end{align*} $$
$$ \begin{align*} \dim X_w(b)=\dim X_{w'}(b); \end{align*} $$
-
(2) if
 $w \in \tilde {W}$
and
$w \in \tilde {W}$
and
 $s \in \tilde {\mathbb {S}}$
with
$s \in \tilde {\mathbb {S}}$
with
 $\ell (s w \sigma (s))=\ell (w)-2$
, we have
$\ell (s w \sigma (s))=\ell (w)-2$
, we have  $$ \begin{align*} \dim X_w(b)=\max\left\{\dim X_{s w}(b), \dim X_{s w \sigma(s)}(b)\right\}+1. \end{align*} $$
$$ \begin{align*} \dim X_w(b)=\max\left\{\dim X_{s w}(b), \dim X_{s w \sigma(s)}(b)\right\}+1. \end{align*} $$
Here, by convention, we set
![]() $\dim \emptyset =-\infty $
and
$\dim \emptyset =-\infty $
and
![]() $-\infty +n=-\infty $
for any
$-\infty +n=-\infty $
for any
![]() $n \in \mathbb {R}$
.
$n \in \mathbb {R}$
.
3.3. The relation
 $\Rightarrow $
$\Rightarrow $
Following [Reference Görtz and HeGH10, Definition 3.1.4], for
![]() $w, w' \in \tilde {W}$
we write
$w, w' \in \tilde {W}$
we write
![]() $w \Rightarrow _{\sigma } w'$
if for any
$w \Rightarrow _{\sigma } w'$
if for any
![]() $b \in \breve G$
,
$b \in \breve G$
,
Again by convention, we set
![]() $\dim \emptyset =-\infty $
. If the right-hand side is
$\dim \emptyset =-\infty $
. If the right-hand side is
![]() $-\infty $
, then the inequality holds regardless of the left-hand side. It is also easy to see that the relation is transitive.
$-\infty $
, then the inequality holds regardless of the left-hand side. It is also easy to see that the relation is transitive.
Note that by the definition of virtual dimension,
![]() $w \Rightarrow _{\sigma } w'$
if and only if for any
$w \Rightarrow _{\sigma } w'$
if and only if for any
![]() $b \in \breve G$
with
$b \in \breve G$
with
![]() $X_{w'}(b) \neq \emptyset $
,
$X_{w'}(b) \neq \emptyset $
,
![]() $X_w(b) \neq \emptyset $
, and in this case,
$X_w(b) \neq \emptyset $
, and in this case,
 $$ \begin{align*} \dim X_w(b)-\dim X_{w'}(b) \ge \frac{1}{2}\bigl( \ell(w) + \ell(\eta_{\sigma}(w)) -\ell(w')-\ell(\eta_{\sigma}(w'))\bigr). \end{align*} $$
$$ \begin{align*} \dim X_w(b)-\dim X_{w'}(b) \ge \frac{1}{2}\bigl( \ell(w) + \ell(\eta_{\sigma}(w)) -\ell(w')-\ell(\eta_{\sigma}(w'))\bigr). \end{align*} $$
We write
![]() $w \Leftrightarrow _{\sigma } w'$
if
$w \Leftrightarrow _{\sigma } w'$
if
![]() $w \Rightarrow _{\sigma } w'$
and
$w \Rightarrow _{\sigma } w'$
and
![]() $w' \Rightarrow _{\sigma } w$
.
$w' \Rightarrow _{\sigma } w$
.
3.4. The monoid structure on
 $\tilde {W}$
$\tilde {W}$
By [Reference HeHe09, Lemma 1], for any
![]() $w, w' \in \tilde {W}$
the subset
$w, w' \in \tilde {W}$
the subset
![]() $\{u w'; u \le w\}$
of
$\{u w'; u \le w\}$
of
![]() $\tilde {W}$
contains a unique maximal element which we denote by
$\tilde {W}$
contains a unique maximal element which we denote by
![]() $w \ast w'$
. Moreover,
$w \ast w'$
. Moreover,
![]() $w \ast w'=\max \{u v; u \le w, v \le w'\}$
. Hence
$w \ast w'=\max \{u v; u \le w, v \le w'\}$
. Hence
![]() $\ast $
is associative. This gives a monoid structure on
$\ast $
is associative. This gives a monoid structure on
![]() $\tilde {W}$
. If
$\tilde {W}$
. If
![]() $w_1 \le w$
and
$w_1 \le w$
and
![]() $w^{\prime }_1 \le w'$
, then
$w^{\prime }_1 \le w'$
, then
![]() $w_1 \ast w^{\prime }_1 \le w \ast w'$
.
$w_1 \ast w^{\prime }_1 \le w \ast w'$
.
4. The cordial elements
4.1. Definition
There is a natural partial ordering
![]() $\le $
on
$\le $
on
![]() $B(\mathbf G)$
defined as follows: Set
$B(\mathbf G)$
defined as follows: Set
![]() $[b], [b'] \in B(\mathbf G)$
. Then
$[b], [b'] \in B(\mathbf G)$
. Then
![]() $[b] \le [b']$
if
$[b] \le [b']$
if
![]() $\kappa (b)=\kappa (b')$
and
$\kappa (b)=\kappa (b')$
and
![]() $\nu _b \le \nu _{b'}$
.
$\nu _b \le \nu _{b'}$
.
Now we recall the cordial elements introduced by Milićević and Viehmann in [Reference Milićević and ViehmannMV20].
For any
![]() $w \in \tilde {W}$
, there is a unique maximal
$w \in \tilde {W}$
, there is a unique maximal
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]$
such that
$[b]$
such that
![]() $X_w(b) \neq \emptyset $
. We denote this
$X_w(b) \neq \emptyset $
. We denote this
![]() $\sigma $
-conjugacy class by
$\sigma $
-conjugacy class by
![]() $[b_w]$
. The element w is called cordial if
$[b_w]$
. The element w is called cordial if
![]() $\dim X_w(b_w)=d_w(b_w)$
. Equivalently, w is cordial if and only if
$\dim X_w(b_w)=d_w(b_w)$
. Equivalently, w is cordial if and only if
 $\ell (w)-\ell (\eta _{\sigma }(w))=\left \langle \nu _{b_w}, 2 \rho \right \rangle -\text {def}(b_w)$
[Reference Milićević and ViehmannMV20, Definition 3.14].
$\ell (w)-\ell (\eta _{\sigma }(w))=\left \langle \nu _{b_w}, 2 \rho \right \rangle -\text {def}(b_w)$
[Reference Milićević and ViehmannMV20, Definition 3.14].
By definition, if
![]() $w \Leftrightarrow _{\sigma } w'$
, then w is a cordial element if and only if
$w \Leftrightarrow _{\sigma } w'$
, then w is a cordial element if and only if
![]() $w'$
is a cordial element. The following result is proved in [Reference Milićević and ViehmannMV20, Theorem 1.1 & Corollary 3.17]:
$w'$
is a cordial element. The following result is proved in [Reference Milićević and ViehmannMV20, Theorem 1.1 & Corollary 3.17]:
Theorem 4.1. Let
![]() $w \in \tilde {W}$
be a cordial element. Then the following hold:
$w \in \tilde {W}$
be a cordial element. Then the following hold:
-
(1) Set
 $[b], [b'] \in B(\mathbf G)$
. If
$[b], [b'] \in B(\mathbf G)$
. If
 $[b] \le [b'] \le [b_w]$
and
$[b] \le [b'] \le [b_w]$
and
 $X_w(b) \neq \emptyset $
, then
$X_w(b) \neq \emptyset $
, then
 $X_w(b') \neq \emptyset $
.
$X_w(b') \neq \emptyset $
. -
(2) If
 $X_w(b) \neq \emptyset $
, then
$X_w(b) \neq \emptyset $
, then
 $\dim X_w(b)=d_w(b)$
.
$\dim X_w(b)=d_w(b)$
.
It is mentioned in [Reference Milićević and ViehmannMV20] that fully characterising the cordial elements is fairly difficult. In [Reference Milićević and ViehmannMV20, Theorem 1.2], some interesting families of cordial elements are provided. The main result of this section is to provide another family of cordial elements.
Theorem 4.2. Let
![]() $\lambda $
be a dominant coweight and set
$\lambda $
be a dominant coweight and set
![]() $x \in W_0$
. Then
$x \in W_0$
. Then
![]() $x t^{\lambda }$
is a cordial element and
$x t^{\lambda }$
is a cordial element and
 $\left [b_{x t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
.
$\left [b_{x t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
.
Remark 4.3. The original proof we had was a bit technical. The proof to come was suggested by E. Viehmann.
4.2. Mazur’s inequality
Recall that
![]() ${\mathbf G}$
is quasi-split over F. Let
${\mathbf G}$
is quasi-split over F. Let
![]() $\breve K \supset \breve I$
be a
$\breve K \supset \breve I$
be a
![]() $\sigma $
-stable special maximal parahoric subgroup of
$\sigma $
-stable special maximal parahoric subgroup of
![]() $\breve G$
. The nonemptiness pattern of the affine Deligne–Lusztig varieties in the affine Grassmannian
$\breve G$
. The nonemptiness pattern of the affine Deligne–Lusztig varieties in the affine Grassmannian
![]() $\breve G/\breve K$
is determined in terms of Mazur’s inequality. This was established by Gashi [Reference GashiGa10, Theorem 1.1] for unramified groups and proved in the general case in [Reference HeHe14, Theorem 7.1]. We may reformulate the result as follows:
$\breve G/\breve K$
is determined in terms of Mazur’s inequality. This was established by Gashi [Reference GashiGa10, Theorem 1.1] for unramified groups and proved in the general case in [Reference HeHe14, Theorem 7.1]. We may reformulate the result as follows:
Theorem 4.4. Let
![]() $\lambda $
be a dominant coweight and set
$\lambda $
be a dominant coweight and set
![]() $b \in \breve G$
. Then
$b \in \breve G$
. Then
![]() $[b] \cap \breve K \dot t^{\lambda } \breve K \neq \emptyset $
if and only if
$[b] \cap \breve K \dot t^{\lambda } \breve K \neq \emptyset $
if and only if
![]() $\kappa (b)=\kappa \left (t^{\lambda }\right )$
and
$\kappa (b)=\kappa \left (t^{\lambda }\right )$
and
![]() $\nu _b \le \lambda ^{\diamondsuit }$
.
$\nu _b \le \lambda ^{\diamondsuit }$
.
4.3. Proof of Theorem 4.2
Set
![]() $w \in \tilde {W}$
. By definition,
$w \in \tilde {W}$
. By definition,
![]() $[b_w]$
is the unique maximal
$[b_w]$
is the unique maximal
![]() $\sigma $
-conjugacy class that intersects
$\sigma $
-conjugacy class that intersects
![]() $\breve I \dot w \breve I$
. By [Reference ViehmannVi14, Corollary 5.6],
$\breve I \dot w \breve I$
. By [Reference ViehmannVi14, Corollary 5.6],
![]() $[b_w]$
is also the unique maximal
$[b_w]$
is also the unique maximal
![]() $\sigma $
-conjugacy class that intersects
$\sigma $
-conjugacy class that intersects
![]() $\overline {\breve I \dot w \breve I}$
. Since
$\overline {\breve I \dot w \breve I}$
. Since
![]() $t^{\lambda } \le x t^{\lambda } \le w_{\mathbb {S}} t^{\lambda }$
, we have
$t^{\lambda } \le x t^{\lambda } \le w_{\mathbb {S}} t^{\lambda }$
, we have
 $$ \begin{align*}\breve I \dot t^{\lambda} \breve I \subset \overline{\breve I \dot x \dot t^{\lambda} \breve I} \subset \overline{\breve I \dot w_{\mathbb {S}} \dot t^{\lambda} \breve I}=\overline{\breve K \dot t^{\lambda} \breve K}.\end{align*} $$
$$ \begin{align*}\breve I \dot t^{\lambda} \breve I \subset \overline{\breve I \dot x \dot t^{\lambda} \breve I} \subset \overline{\breve I \dot w_{\mathbb {S}} \dot t^{\lambda} \breve I}=\overline{\breve K \dot t^{\lambda} \breve K}.\end{align*} $$
By Theorem 4.4,
 $\left [b_{w_{\mathbb {S}} t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
. Thus
$\left [b_{w_{\mathbb {S}} t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
. Thus
 $\left [b_{x t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
.
$\left [b_{x t^{\lambda }}\right ]=\left [\dot t^{\lambda }\right ]$
.
Now
 $\nu _{b_{x t^{\lambda }}}=\lambda ^{\diamondsuit }$
and
$\nu _{b_{x t^{\lambda }}}=\lambda ^{\diamondsuit }$
and
![]() $\text {def}\left (b_{x t^{\lambda }}\right )=0$
. Hence
$\text {def}\left (b_{x t^{\lambda }}\right )=0$
. Hence
 $$ \begin{align*}\ell\left(x t^{\lambda}\right)-\ell\left(\eta_{\sigma}\left(x t^{\lambda}\right)\right)=\ell(x)+\ell\left(t^{\lambda}\right)-\ell(x)=\ell\left(t^{\lambda}\right)=\langle \lambda, 2\rho\rangle=\left\langle \lambda^{\diamondsuit}, 2 \rho\right\rangle.\end{align*} $$
$$ \begin{align*}\ell\left(x t^{\lambda}\right)-\ell\left(\eta_{\sigma}\left(x t^{\lambda}\right)\right)=\ell(x)+\ell\left(t^{\lambda}\right)-\ell(x)=\ell\left(t^{\lambda}\right)=\langle \lambda, 2\rho\rangle=\left\langle \lambda^{\diamondsuit}, 2 \rho\right\rangle.\end{align*} $$
Thus
![]() $x t^{\lambda }$
is a cordial element.
$x t^{\lambda }$
is a cordial element.
4.4. Another family of cordial elements
Set
![]() $w \in \tilde {W}$
such that
$w \in \tilde {W}$
such that
![]() $w \mathfrak a$
is in the dominant Weyl chamber–that is,
$w \mathfrak a$
is in the dominant Weyl chamber–that is,
![]() $w=w_{\mathbb {S}} t^{\lambda } y$
, where
$w=w_{\mathbb {S}} t^{\lambda } y$
, where
![]() $\lambda $
is a dominant coweight and
$\lambda $
is a dominant coweight and
![]() $y \in W_0$
with
$y \in W_0$
with
![]() $t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. It was proved by Milićević and Viehmann in [Reference Milićević and ViehmannMV20, Theorem 1.2 (a)] that w is also a cordial element.
$t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. It was proved by Milićević and Viehmann in [Reference Milićević and ViehmannMV20, Theorem 1.2 (a)] that w is also a cordial element.
Now we show that it can also be deduced from Theorem 4.2.
Set
![]() $w'=\sigma ^{-1}(y) w_{\mathbb {S}} t^{\lambda }$
. By Theorem 4.2,
$w'=\sigma ^{-1}(y) w_{\mathbb {S}} t^{\lambda }$
. By Theorem 4.2,
![]() $w'$
is a cordial element. Note that
$w'$
is a cordial element. Note that
![]() $\eta _{\sigma }(w')=\eta _{\sigma }(w)=\sigma ^{-1}(y) w_{\mathbb {S}}$
. Moreover, it is easy to see that
$\eta _{\sigma }(w')=\eta _{\sigma }(w)=\sigma ^{-1}(y) w_{\mathbb {S}}$
. Moreover, it is easy to see that
![]() $w \approx _{\sigma } w'$
. Hence
$w \approx _{\sigma } w'$
. Hence
![]() $w \Leftrightarrow _{\sigma } w'$
, and w is also a cordial element.
$w \Leftrightarrow _{\sigma } w'$
, and w is also a cordial element.
It is also worth mentioning that not every element of the form
![]() $x t^{\lambda }$
is
$x t^{\lambda }$
is
![]() $\approx _{\sigma }$
-equivalent to an element in the dominant Weyl chamber.
$\approx _{\sigma }$
-equivalent to an element in the dominant Weyl chamber.
5. From w to a cordial element
We first show the following:
Proposition 5.1. Let
![]() $\lambda , \lambda '$
be dominant coweights. Then the set
$\lambda , \lambda '$
be dominant coweights. Then the set
contains a unique minimal element with respect the dominance order
![]() $\ge _{\mathbb {Z}}$
.
$\ge _{\mathbb {Z}}$
.
Remark 5.2. The proof is due to S. Nie.
Proof. Let
![]() $\mu ^{\prime }_1, \mu ^{\prime }_2$
be dominant coweights with
$\mu ^{\prime }_1, \mu ^{\prime }_2$
be dominant coweights with
![]() $\mu ^{\prime }_1+\lambda ' \ge _{\mathbb {Z}} \lambda $
and
$\mu ^{\prime }_1+\lambda ' \ge _{\mathbb {Z}} \lambda $
and
![]() $\mu ^{\prime }_2+\lambda ' \ge _{\mathbb {Z}} \lambda $
. We may write
$\mu ^{\prime }_2+\lambda ' \ge _{\mathbb {Z}} \lambda $
. We may write
![]() $\mu ^{\prime }_1-\mu ^{\prime }_2$
as
$\mu ^{\prime }_1-\mu ^{\prime }_2$
as
![]() $\mu ^{\prime }_1-\mu ^{\prime }_2=\gamma _1-\gamma _2$
, where
$\mu ^{\prime }_1-\mu ^{\prime }_2=\gamma _1-\gamma _2$
, where
![]() $\gamma _1 \in \sum _{\alpha \in J_1} \mathbb {Z}_{>0} \alpha $
,
$\gamma _1 \in \sum _{\alpha \in J_1} \mathbb {Z}_{>0} \alpha $
,
![]() $\gamma _2 \in \sum _{\alpha \in J_2} \mathbb {Z}_{>0} \alpha $
for some
$\gamma _2 \in \sum _{\alpha \in J_2} \mathbb {Z}_{>0} \alpha $
for some
![]() $J_1, J_2 \subset \Delta $
with
$J_1, J_2 \subset \Delta $
with
![]() $J_1 \cap J_2=\emptyset $
.
$J_1 \cap J_2=\emptyset $
.
Set
![]() $\mu =\mu ^{\prime }_1-\gamma _1=\mu ^{\prime }_2-\gamma _2$
. Set
$\mu =\mu ^{\prime }_1-\gamma _1=\mu ^{\prime }_2-\gamma _2$
. Set
![]() $\alpha \in \Delta $
. Since
$\alpha \in \Delta $
. Since
![]() $J_1 \cap J_2=\emptyset $
, we have
$J_1 \cap J_2=\emptyset $
, we have
![]() $\alpha \notin J_1$
or
$\alpha \notin J_1$
or
![]() $\alpha \notin J_2$
. If
$\alpha \notin J_2$
. If
![]() $\alpha \notin J_1$
, then
$\alpha \notin J_1$
, then
 $\langle \mu , \alpha \rangle \ge \left \langle \mu ^{\prime }_1, \alpha \right \rangle \ge 0$
. If
$\langle \mu , \alpha \rangle \ge \left \langle \mu ^{\prime }_1, \alpha \right \rangle \ge 0$
. If
![]() $\alpha \notin J_2$
, then
$\alpha \notin J_2$
, then
 $\langle \mu , \alpha \rangle \ge \left \langle \mu ^{\prime }_2, \alpha \right \rangle \ge 0$
. Thus
$\langle \mu , \alpha \rangle \ge \left \langle \mu ^{\prime }_2, \alpha \right \rangle \ge 0$
. Thus
![]() $\mu $
is dominant. By definition,
$\mu $
is dominant. By definition,
![]() $\mu ^{\prime }_1 \ge _{\mathbb {Z}} \mu $
and
$\mu ^{\prime }_1 \ge _{\mathbb {Z}} \mu $
and
![]() $\mu ^{\prime }_2 \ge _{\mathbb {Z}} \mu $
. Moreover,
$\mu ^{\prime }_2 \ge _{\mathbb {Z}} \mu $
. Moreover,
 $$ \begin{align*}\lambda'-\lambda+\mu^{\prime}_1=\lambda'-\lambda+\mu^{\prime}_2+\gamma_1-\gamma_2 \in \left(\sum_{\alpha \in \Delta} \mathbb {Z}_{>0} \alpha+\gamma_1-\gamma_2\right) \cap \sum_{\alpha \in \Delta} \mathbb {Z}_{>0} \alpha.\end{align*} $$
$$ \begin{align*}\lambda'-\lambda+\mu^{\prime}_1=\lambda'-\lambda+\mu^{\prime}_2+\gamma_1-\gamma_2 \in \left(\sum_{\alpha \in \Delta} \mathbb {Z}_{>0} \alpha+\gamma_1-\gamma_2\right) \cap \sum_{\alpha \in \Delta} \mathbb {Z}_{>0} \alpha.\end{align*} $$
Since
![]() $J_1 \cap J_2=\emptyset $
, we have
$J_1 \cap J_2=\emptyset $
, we have
![]() $\lambda '-\lambda +\mu ^{\prime }_1-\gamma _1 \in \sum _{\alpha \in \Delta } \mathbb {Z}_{>0} \alpha $
. In other words,
$\lambda '-\lambda +\mu ^{\prime }_1-\gamma _1 \in \sum _{\alpha \in \Delta } \mathbb {Z}_{>0} \alpha $
. In other words,
![]() $\lambda '+\mu \ge _{\mathbb {Z}} \lambda $
.
$\lambda '+\mu \ge _{\mathbb {Z}} \lambda $
.
The statement is proved.
5.1. The normalised subtraction
For any dominant coweights
![]() $\lambda , \lambda '$
, we denote by
$\lambda , \lambda '$
, we denote by
![]() $\lambda -_{\text {dom}} \lambda '$
the unique minimal element in the set
$\lambda -_{\text {dom}} \lambda '$
the unique minimal element in the set
It is easy to see that if
![]() $\lambda -\lambda '$
is dominant, then
$\lambda -\lambda '$
is dominant, then
![]() $\lambda -_{\text {dom}} \lambda '=\lambda -\lambda '$
. We call
$\lambda -_{\text {dom}} \lambda '=\lambda -\lambda '$
. We call
![]() $-_{\text {dom}}$
the normalised subtraction. Now we prove some of its properties.
$-_{\text {dom}}$
the normalised subtraction. Now we prove some of its properties.
Corollary 5.3. Let
![]() $\lambda , \lambda '$
be dominant coweights. Let
$\lambda , \lambda '$
be dominant coweights. Let
![]() $\lambda ''$
be a dominant coweight with
$\lambda ''$
be a dominant coweight with
![]() $\lambda ' \ge _{\mathbb {Z}} \lambda ''$
. Set
$\lambda ' \ge _{\mathbb {Z}} \lambda ''$
. Set
![]() $x \in W_0$
and let
$x \in W_0$
and let
![]() $\mu $
be the unique dominant coweight in the
$\mu $
be the unique dominant coweight in the
![]() $W_0$
-orbit of
$W_0$
-orbit of
![]() $\lambda -x(\lambda '')$
. Then
$\lambda -x(\lambda '')$
. Then
![]() $\mu \ge _{\mathbb {Z}} \lambda -_{\text {dom}} \lambda '$
.
$\mu \ge _{\mathbb {Z}} \lambda -_{\text {dom}} \lambda '$
.
Proof. Note that
![]() $\mu -(\lambda -x(\lambda '')) \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
,
$\mu -(\lambda -x(\lambda '')) \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
,
![]() $\lambda ''-x(\lambda '') \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
and
$\lambda ''-x(\lambda '') \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
and
![]() $\lambda '-\lambda '' \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
. Thus
$\lambda '-\lambda '' \in \sum _{\alpha \in \Delta } \mathbb {N} \alpha $
. Thus
 $$ \begin{align*} \mu+\lambda' &=(\mu-\lambda+x(\lambda''))+\lambda-x(\lambda'')+\lambda' \\ &=(\mu-\lambda+x(\lambda''))+(\lambda''-x(\lambda''))+(\lambda'-\lambda'')+\lambda \\ & \ge_{\mathbb {Z}} \lambda.\end{align*} $$
$$ \begin{align*} \mu+\lambda' &=(\mu-\lambda+x(\lambda''))+\lambda-x(\lambda'')+\lambda' \\ &=(\mu-\lambda+x(\lambda''))+(\lambda''-x(\lambda''))+(\lambda'-\lambda'')+\lambda \\ & \ge_{\mathbb {Z}} \lambda.\end{align*} $$
Corollary 5.4. Let
![]() $\lambda , \lambda _1, \lambda _2$
be dominant coweights. Then
$\lambda , \lambda _1, \lambda _2$
be dominant coweights. Then
Proof. Set
![]() $\mu _1=(\lambda -_{\text {dom}} \lambda _1)-_{\text {dom}} \lambda _2$
and
$\mu _1=(\lambda -_{\text {dom}} \lambda _1)-_{\text {dom}} \lambda _2$
and
![]() $\mu _2=\lambda -_{\text {dom}} (\lambda _1+\lambda _2)$
. By definition,
$\mu _2=\lambda -_{\text {dom}} (\lambda _1+\lambda _2)$
. By definition,
So
![]() $\mu _1 \ge _{\mathbb {Z}} \mu _2.$
$\mu _1 \ge _{\mathbb {Z}} \mu _2.$
On the other hand,
So by definition,
![]() $\lambda _2+\mu _2 \ge _{\mathbb {Z}} \lambda -_{\text {dom}} \lambda _1$
and
$\lambda _2+\mu _2 \ge _{\mathbb {Z}} \lambda -_{\text {dom}} \lambda _1$
and
![]() $\mu _2 \ge _{\mathbb {Z}} \mu _1$
.
$\mu _2 \ge _{\mathbb {Z}} \mu _1$
.
5.2. The double flat operator
For any subset J of
![]() $\mathbb {S}$
, we denote by
$\mathbb {S}$
, we denote by
![]() $\rho ^\vee _J$
the dominant coweight with
$\rho ^\vee _J$
the dominant coweight with
 $$ \begin{align*}\left\langle\rho^\vee_J, \alpha_s\right\rangle=\begin{cases} 1 & \text{if } s \in J, \\ 0 & \text{if } s \notin J.\end{cases}\end{align*} $$
$$ \begin{align*}\left\langle\rho^\vee_J, \alpha_s\right\rangle=\begin{cases} 1 & \text{if } s \in J, \\ 0 & \text{if } s \notin J.\end{cases}\end{align*} $$
Let
![]() $\eta ^\vee _J$
be the unique dominant coweight in the
$\eta ^\vee _J$
be the unique dominant coweight in the
![]() $W_0$
-orbit of
$W_0$
-orbit of
 $-\sigma ^{-1}\left (\rho ^\vee _J\right )$
.
$-\sigma ^{-1}\left (\rho ^\vee _J\right )$
.
Set
![]() $w \in \tilde {W}$
. We write w as
$w \in \tilde {W}$
. We write w as
![]() $w=x t^{\lambda } y$
with
$w=x t^{\lambda } y$
with
![]() $\lambda $
dominant,
$\lambda $
dominant,
![]() $x, y \in W_0$
and
$x, y \in W_0$
and
![]() $t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. Let
$t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. Let
![]() $J=\{s \in \mathbb {S}; {s y<y}\}$
. Since
$J=\{s \in \mathbb {S}; {s y<y}\}$
. Since
![]() $t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
, we have
$t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
, we have
![]() $\langle \lambda , \alpha _s\rangle>0$
for any
$\langle \lambda , \alpha _s\rangle>0$
for any
![]() $s \in J$
. In particular,
$s \in J$
. In particular,
![]() $\lambda -\rho ^\vee _J$
is dominant. We set
$\lambda -\rho ^\vee _J$
is dominant. We set
 $$ \begin{align*}\lambda_w^{\flat\mkern-2.4mu\flat}=\left(\lambda-\rho^\vee_J\right)-_{\text{dom}} \eta^\vee_J=\lambda-_{\text{dom}} \left(\rho^\vee_J+\eta^\vee_J\right).\end{align*} $$
$$ \begin{align*}\lambda_w^{\flat\mkern-2.4mu\flat}=\left(\lambda-\rho^\vee_J\right)-_{\text{dom}} \eta^\vee_J=\lambda-_{\text{dom}} \left(\rho^\vee_J+\eta^\vee_J\right).\end{align*} $$
The main result of this section is as follows:
Theorem 5.5. Assume that
![]() ${\mathbf G}$
is quasi-split over F. Set
${\mathbf G}$
is quasi-split over F. Set
![]() $w \in \tilde {W}$
such that
$w \in \tilde {W}$
such that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber. Then there exist a dominant coweight
$w \mathfrak a$
is in a shrunken Weyl chamber. Then there exist a dominant coweight
![]() $\gamma $
with
$\gamma $
with
![]() $\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
and
$\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
and
![]() $a \in W_0$
with
$a \in W_0$
with
![]() $\operatorname {\mathrm {supp}}_{\sigma }(a) \supset \operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))$
such that
$\operatorname {\mathrm {supp}}_{\sigma }(a) \supset \operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))$
such that
5.3. A convenient notation
Following [Reference Görtz and HeGH10, §2.4], we give a convenient notation for varieties of tuples of elements in
![]() $Fl$
. We explain the notation by examples. Let
$Fl$
. We explain the notation by examples. Let
 $\mathcal O_w=\left \{\left (g \breve I, g \dot w \breve I\right ); g \in \breve G\right \} \subset Fl\times Fl$
. Then we set
$\mathcal O_w=\left \{\left (g \breve I, g \dot w \breve I\right ); g \in \breve G\right \} \subset Fl\times Fl$
. Then we set

Similarly,

The affine Deligne–Lusztig varieties can be written as
In all these cases, we do not distinguish between the sets given by the conditions on the relative position and the corresponding locally closed sub-ind-schemes of the product of affine flag varieties. The following result is proved in [Reference Görtz and HeGH10, Proposition 2.5.2]:
Proposition 5.6. Set
![]() $w, w'\in \tilde {W}$
, and set
$w, w'\in \tilde {W}$
, and set
![]() $w'' \in \{ ww', w \ast w' \}$
. Then the map
$w'' \in \{ ww', w \ast w' \}$
. Then the map

is surjective. Moreover, all the fibres have dimension
 $$ \begin{align*} \dim\pi^{-1}( ( g, g') ) \ge \begin{cases} \ell(w) + \ell(w') - \ell(w*w') & \text{if } w'' = w \ast w',\\ \frac 12 \bigl( \ell(w) + \ell(w') - \ell(ww') \bigr) & \text{if } w'' = ww'. \end{cases} \end{align*} $$
$$ \begin{align*} \dim\pi^{-1}( ( g, g') ) \ge \begin{cases} \ell(w) + \ell(w') - \ell(w*w') & \text{if } w'' = w \ast w',\\ \frac 12 \bigl( \ell(w) + \ell(w') - \ell(ww') \bigr) & \text{if } w'' = ww'. \end{cases} \end{align*} $$
5.4. Proof of Theorem 5.5
We write w as
![]() $w=x t^{\lambda _w} y$
with
$w=x t^{\lambda _w} y$
with
![]() $x, y \in W_0$
and
$x, y \in W_0$
and
![]() $t^{\lambda _w} y \in {}^{\mathbb {S}} \tilde {W}$
. Let
$t^{\lambda _w} y \in {}^{\mathbb {S}} \tilde {W}$
. Let
![]() $J=\{s \in \mathbb {S}; s y<y\}$
and
$J=\{s \in \mathbb {S}; s y<y\}$
and
 $J'=\left \{s \in \mathbb {S}; s\left (\lambda _w-\rho ^\vee _J\right )=\lambda _w-\rho ^\vee _J\right \}$
. We write
$J'=\left \{s \in \mathbb {S}; s\left (\lambda _w-\rho ^\vee _J\right )=\lambda _w-\rho ^\vee _J\right \}$
. We write
![]() $\sigma ^{-1}(y) x$
as
$\sigma ^{-1}(y) x$
as
![]() $\sigma ^{-1}(y)x=x' z$
for some
$\sigma ^{-1}(y)x=x' z$
for some
 $x' \in W_0^{J'}$
and
$x' \in W_0^{J'}$
and
![]() $z \in W_{J'}$
. By [Reference Görtz and HeGH10, §2.3], the assumption that
$z \in W_{J'}$
. By [Reference Görtz and HeGH10, §2.3], the assumption that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber implies that
$w \mathfrak a$
is in a shrunken Weyl chamber implies that
![]() $x \alpha _j<0$
for any
$x \alpha _j<0$
for any
![]() $j \in J'$
. In particular,
$j \in J'$
. In particular,
 $$ \begin{align} \ell\left(x z ^{-1}\right)=\ell(x)-\ell(z). \end{align} $$
$$ \begin{align} \ell\left(x z ^{-1}\right)=\ell(x)-\ell(z). \end{align} $$
Let
![]() $\gamma $
be the unique dominant coweight in the
$\gamma $
be the unique dominant coweight in the
![]() $W_0$
-orbit of
$W_0$
-orbit of
 $\lambda _w-\rho ^\vee _J+(x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right )$
. By Corollary 5.3,
$\lambda _w-\rho ^\vee _J+(x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right )$
. By Corollary 5.3,
![]() $\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
. Let
$\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
. Let
![]() $K=\{s \in \mathbb {S}; s(\gamma )=\gamma \}$
and set
$K=\{s \in \mathbb {S}; s(\gamma )=\gamma \}$
and set
 $y' \in W_0^K$
with
$y' \in W_0^K$
with
 $\lambda _w-\rho ^\vee _J+(x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right ) =y'(\gamma )$
.
$\lambda _w-\rho ^\vee _J+(x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right ) =y'(\gamma )$
.
Set
![]() $\alpha>0$
with
$\alpha>0$
with
![]() $(y') ^{-1} \alpha <0$
. Then
$(y') ^{-1} \alpha <0$
. Then
 $\left \langle \gamma , (y') ^{-1} \alpha \right \rangle \le 0$
. On the other hand, if
$\left \langle \gamma , (y') ^{-1} \alpha \right \rangle \le 0$
. On the other hand, if
 $\left \langle \gamma , (y') ^{-1} \alpha \right \rangle =0$
, then since
$\left \langle \gamma , (y') ^{-1} \alpha \right \rangle =0$
, then since
 $y' \in W_0^K$
, we have
$y' \in W_0^K$
, we have
![]() $\alpha =y' \bigl ((y') ^{-1} \alpha \bigr )<0$
. That is a contradiction. Hence
$\alpha =y' \bigl ((y') ^{-1} \alpha \bigr )<0$
. That is a contradiction. Hence
 $\langle y'(\gamma ), \alpha \rangle =\left \langle \gamma , (y') ^{-1} \alpha \right \rangle <0$
. Since
$\langle y'(\gamma ), \alpha \rangle =\left \langle \gamma , (y') ^{-1} \alpha \right \rangle <0$
. Since
![]() $\lambda _w-\rho ^\vee _J$
is dominant,
$\lambda _w-\rho ^\vee _J$
is dominant,
 $\left \langle \lambda _w-\rho ^\vee _J, \alpha \right \rangle \ge 0$
. Thus
$\left \langle \lambda _w-\rho ^\vee _J, \alpha \right \rangle \ge 0$
. Thus
 $\left \langle (x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right ), \alpha \right \rangle =\left \langle \sigma ^{-1}\left (\rho ^\vee _J\right ), x'(\alpha )\right \rangle <0$
. Since
$\left \langle (x') ^{-1} \sigma ^{-1}\left (\rho ^\vee _J\right ), \alpha \right \rangle =\left \langle \sigma ^{-1}\left (\rho ^\vee _J\right ), x'(\alpha )\right \rangle <0$
. Since
 $\sigma ^{-1}\left (\rho ^\vee _J\right )$
is dominant,
$\sigma ^{-1}\left (\rho ^\vee _J\right )$
is dominant,
![]() $x'(\alpha )<0$
. By [Reference Görtz and HeGH10, Lemma 2.6.1], we have
$x'(\alpha )<0$
. By [Reference Görtz and HeGH10, Lemma 2.6.1], we have
Set
![]() $s \in J'$
. Since
$s \in J'$
. Since
 $x' \in W_0^{J'}$
, we have
$x' \in W_0^{J'}$
, we have
![]() $\ell (x' s)=\ell (x')+1$
. Thus
$\ell (x' s)=\ell (x')+1$
. Thus
![]() $\ell (x')-\ell (y')=\ell (x' y')=\ell \bigl ((x' s) (s y') \bigr ) \ge \ell (x' s)-\ell (s y')=\ell (x')+1-\ell (s y')$
. So
$\ell (x')-\ell (y')=\ell (x' y')=\ell \bigl ((x' s) (s y') \bigr ) \ge \ell (x' s)-\ell (s y')=\ell (x')+1-\ell (s y')$
. So
![]() $\ell (s y') \ge \ell (y')+1$
. Therefore
$\ell (s y') \ge \ell (y')+1$
. Therefore
In particular, we have
 $$ \begin{align} \ell\left((y') ^{-1} z\right)=\ell(y')+\ell(z). \end{align} $$
$$ \begin{align} \ell\left((y') ^{-1} z\right)=\ell(y')+\ell(z). \end{align} $$
Set
![]() $w_1=x z ^{-1} t^{\lambda _w-\rho ^\vee _J} y'$
and
$w_1=x z ^{-1} t^{\lambda _w-\rho ^\vee _J} y'$
and
![]() $w_2=(y') ^{-1} z t^{\rho ^\vee _J} y$
. Then
$w_2=(y') ^{-1} z t^{\rho ^\vee _J} y$
. Then
![]() $w=w_1 w_2$
. By formula (5.3),
$w=w_1 w_2$
. By formula (5.3),
![]() $t^{\lambda _w-\rho ^\vee _J} y' \in {}^{\mathbb {S}} \tilde {W}$
. By the definition of J, we have
$t^{\lambda _w-\rho ^\vee _J} y' \in {}^{\mathbb {S}} \tilde {W}$
. By the definition of J, we have
![]() $t^{\rho ^\vee _J} y \in {}^{\mathbb {S}} \tilde {W}$
. Hence by equation (2.1), we have
$t^{\rho ^\vee _J} y \in {}^{\mathbb {S}} \tilde {W}$
. Hence by equation (2.1), we have
 $$ \begin{align} \ell(w)=\ell(x)+\ell\left(t^{\lambda_w}\right)-\ell(y) \end{align} $$
$$ \begin{align} \ell(w)=\ell(x)+\ell\left(t^{\lambda_w}\right)-\ell(y) \end{align} $$
 $$ \begin{align} \ell(w_1)=\ell\left(x z ^{-1}\right)+\ell\left(t^{\lambda_w-\rho^\vee_J}\right)-\ell(y') \end{align} $$
$$ \begin{align} \ell(w_1)=\ell\left(x z ^{-1}\right)+\ell\left(t^{\lambda_w-\rho^\vee_J}\right)-\ell(y') \end{align} $$
 $$ \begin{align} \ell(w_2)=\ell\left((y') ^{-1} z\right)+\ell\left(t^{\rho^\vee_J}\right)-\ell(y). \end{align} $$
$$ \begin{align} \ell(w_2)=\ell\left((y') ^{-1} z\right)+\ell\left(t^{\rho^\vee_J}\right)-\ell(y). \end{align} $$
By equations (5.1) and (5.4), we have
 $$ \begin{align} \ell(w_1)+\ell(w_2) &=\ell(x)-\ell(z)+\ell\left(t^{\lambda_w-\rho^\vee_J}\right)-\ell(y')+\ell(y')+\ell(z)+\ell\left(t^{\rho^\vee_J}\right)-\ell(y) \nonumber \\ &=\ell(x)+\ell\left(t^{\lambda_w}\right)-\ell(y)=\ell(w). \end{align} $$
$$ \begin{align} \ell(w_1)+\ell(w_2) &=\ell(x)-\ell(z)+\ell\left(t^{\lambda_w-\rho^\vee_J}\right)-\ell(y')+\ell(y')+\ell(z)+\ell\left(t^{\rho^\vee_J}\right)-\ell(y) \nonumber \\ &=\ell(x)+\ell\left(t^{\lambda_w}\right)-\ell(y)=\ell(w). \end{align} $$
By equations (5.2) and (5.4), we have
 $$ \begin{align} \ell\left((y') ^{-1} z\right)+\ell(x' y') &=\ell(y')+\ell(z)+\ell(x')-\ell(y')=\ell(x')+\ell(z) \nonumber \\ &=\ell(x'z)=\ell\left(\sigma ^{-1}(y) x\right). \end{align} $$
$$ \begin{align} \ell\left((y') ^{-1} z\right)+\ell(x' y') &=\ell(y')+\ell(z)+\ell(x')-\ell(y')=\ell(x')+\ell(z) \nonumber \\ &=\ell(x'z)=\ell\left(\sigma ^{-1}(y) x\right). \end{align} $$
By equation (5.8) we have

Set

Here the isomorphism follows from equation (5.7).
The map
![]() $(g, g_1) \mapsto (g_1, b \sigma (g))$
is a universal homeomorphism from
$(g, g_1) \mapsto (g_1, b \sigma (g))$
is a universal homeomorphism from
![]() $X_{w}(b)$
to
$X_{w}(b)$
to
![]() $X_1$
. We have
$X_1$
. We have
![]() $y \sigma \left (x z ^{-1}\right )=\sigma \left (\sigma ^{-1}(y) x z ^{-1}\right )=\sigma (x')$
and
$y \sigma \left (x z ^{-1}\right )=\sigma \left (\sigma ^{-1}(y) x z ^{-1}\right )=\sigma (x')$
and
 $$ \begin{align*}t^{\rho^\vee_J} y \sigma(w_1)=t^{\rho^\vee_J} \sigma\left(x' t^{\lambda_w-\rho^\vee_J} y'\right)=\sigma(x') \sigma\left(t^{y'(\gamma)}\right) \sigma(y')=\sigma(x' y' t^\gamma).\end{align*} $$
$$ \begin{align*}t^{\rho^\vee_J} y \sigma(w_1)=t^{\rho^\vee_J} \sigma\left(x' t^{\lambda_w-\rho^\vee_J} y'\right)=\sigma(x') \sigma\left(t^{y'(\gamma)}\right) \sigma(y')=\sigma(x' y' t^\gamma).\end{align*} $$
Let

We have
Since
![]() $\gamma $
is dominant, we have
$\gamma $
is dominant, we have
![]() $\ell (\sigma (x' y' t^\gamma ))=\ell (\sigma (x' y'))+\ell (\sigma (t^\gamma ))$
. Set
$\ell (\sigma (x' y' t^\gamma ))=\ell (\sigma (x' y'))+\ell (\sigma (t^\gamma ))$
. Set

Let
![]() $\pi : X_2 \rightarrow X_3$
be the projection map. Set
$\pi : X_2 \rightarrow X_3$
be the projection map. Set
 $N_1=\frac {\ell \left (t^{\rho ^\vee _J} y\right )+\ell \left (w_1\right )-\ell \left (x' y' t^\gamma \right )}{2}$
. By Proposition 5.6, the map
$N_1=\frac {\ell \left (t^{\rho ^\vee _J} y\right )+\ell \left (w_1\right )-\ell \left (x' y' t^\gamma \right )}{2}$
. By Proposition 5.6, the map
![]() $\pi $
is surjective and the dimension of each fibre is larger than or equal to
$\pi $
is surjective and the dimension of each fibre is larger than or equal to
![]() $N_1$
.
$N_1$
.
We show that
(a)
![]() $\dim (X_2) \ge \dim (X_3)+N_1$
.
$\dim (X_2) \ge \dim (X_3)+N_1$
.
Now suppose that
![]() $\dim (X_2)<\dim (X_3)+N_1$
. Let Z be an irreducible component of
$\dim (X_2)<\dim (X_3)+N_1$
. Let Z be an irreducible component of
![]() $X_3$
with
$X_3$
with
![]() $\dim Z=\dim X_3$
. For each irreducible component Y of
$\dim Z=\dim X_3$
. For each irreducible component Y of
![]() $\pi ^{-1} (Z)$
, we construct a closed subscheme
$\pi ^{-1} (Z)$
, we construct a closed subscheme
![]() $Z_Y$
of Z such that
$Z_Y$
of Z such that
![]() $\dim \left (\pi ^{-1}(z) \cap Y\right )<N_1$
if
$\dim \left (\pi ^{-1}(z) \cap Y\right )<N_1$
if
![]() $z \in Z-Z_Y$
. The construction is as follows.
$z \in Z-Z_Y$
. The construction is as follows.
If
![]() $\pi (Y)$
is not dense in Z, then let
$\pi (Y)$
is not dense in Z, then let
![]() $Z_Y$
be the closure of
$Z_Y$
be the closure of
![]() $\pi (Y)$
. If
$\pi (Y)$
. If
![]() $\pi (Y)$
is dense in Z, then the morphism
$\pi (Y)$
is dense in Z, then the morphism
![]() $\pi : Y \rightarrow Z$
is dominant. By [Reference Görtz and WedhornGW10, Corollary 14.116], there exists an open dense subscheme V of Z contained in
$\pi : Y \rightarrow Z$
is dominant. By [Reference Görtz and WedhornGW10, Corollary 14.116], there exists an open dense subscheme V of Z contained in
![]() $\pi (Y)$
such that for any
$\pi (Y)$
such that for any
![]() $z \in V$
, we have
$z \in V$
, we have
![]() $\dim \left (\pi ^{-1}(z) \cap Y\right )=\dim (Y)-\dim (Z) \le \dim (X_2)-\dim (X_3)<N_1$
. We set
$\dim \left (\pi ^{-1}(z) \cap Y\right )=\dim (Y)-\dim (Z) \le \dim (X_2)-\dim (X_3)<N_1$
. We set
![]() $Z_Y=Z-V$
. This finishes our construction.
$Z_Y=Z-V$
. This finishes our construction.
Note that in either case,
![]() $Z_Y$
is a proper subscheme of Z. Hence
$Z_Y$
is a proper subscheme of Z. Hence
![]() $\cup _Y Z_Y \subsetneqq Z$
. Set
$\cup _Y Z_Y \subsetneqq Z$
. Set
![]() $z \in Z-\cup _Y Z_Y$
. Then
$z \in Z-\cup _Y Z_Y$
. Then
![]() $\dim \left (\pi ^{-1}(z) \cap Y\right )<N_1$
for any irreducible component Y of
$\dim \left (\pi ^{-1}(z) \cap Y\right )<N_1$
for any irreducible component Y of
![]() $\pi ^{-1}(Z)$
. Thus
$\pi ^{-1}(Z)$
. Thus
![]() $\dim \left (\pi ^{-1}(z)\right )<N_1$
. That gives a contradiction.
$\dim \left (\pi ^{-1}(z)\right )<N_1$
. That gives a contradiction.
So (a) is proved.
Set
![]() $a =\sigma ^{-1}\left ((y')^{-1} z\right ) * (x' y')$
. Then
$a =\sigma ^{-1}\left ((y')^{-1} z\right ) * (x' y')$
. Then
 $$ \begin{align*} \operatorname{\mathrm{supp}}_{\sigma}(a) &=\operatorname{\mathrm{supp}}_{\sigma}(\sigma(a))=\operatorname{\mathrm{supp}}_{\sigma}\left((y') ^{-1} z\right) \cup \operatorname{\mathrm{supp}}_{\sigma}(\sigma(x'y')) \\[4pt] &=\operatorname{\mathrm{supp}}_{\sigma}\left((y') ^{-1} z\right) \cup \operatorname{\mathrm{supp}}_{\sigma}(x'y') \\[4pt] & \supset \operatorname{\mathrm{supp}}_{\sigma}\left(x' y' (y') ^{-1} z\right)=\operatorname{\mathrm{supp}}_{\sigma}(x' z) \\[4pt] &=\operatorname{\mathrm{supp}}_{\sigma}(\eta_{\sigma}(w)).\end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{supp}}_{\sigma}(a) &=\operatorname{\mathrm{supp}}_{\sigma}(\sigma(a))=\operatorname{\mathrm{supp}}_{\sigma}\left((y') ^{-1} z\right) \cup \operatorname{\mathrm{supp}}_{\sigma}(\sigma(x'y')) \\[4pt] &=\operatorname{\mathrm{supp}}_{\sigma}\left((y') ^{-1} z\right) \cup \operatorname{\mathrm{supp}}_{\sigma}(x'y') \\[4pt] & \supset \operatorname{\mathrm{supp}}_{\sigma}\left(x' y' (y') ^{-1} z\right)=\operatorname{\mathrm{supp}}_{\sigma}(x' z) \\[4pt] &=\operatorname{\mathrm{supp}}_{\sigma}(\eta_{\sigma}(w)).\end{align*} $$
We set

By Proposition 5.6 and the same argument as in (a),
 $$ \begin{align*}\dim(X_3) \ge \dim(X_5)+\ell\left((y') ^{-1} z\right)+\ell(x' y')-\ell(a)=\dim(X_5)+\ell(\eta_{\sigma}(w))-\ell(a).\end{align*} $$
$$ \begin{align*}\dim(X_3) \ge \dim(X_5)+\ell\left((y') ^{-1} z\right)+\ell(x' y')-\ell(a)=\dim(X_5)+\ell(\eta_{\sigma}(w))-\ell(a).\end{align*} $$
Notice that
![]() $\ell (\sigma (a t^\gamma ))=\ell (\sigma (a))+\ell (\sigma (t^\gamma ))$
. Thus the map
$\ell (\sigma (a t^\gamma ))=\ell (\sigma (a))+\ell (\sigma (t^\gamma ))$
. Thus the map
![]() $(g_1, g_4) \mapsto g_1$
gives an isomorphism
$(g_1, g_4) \mapsto g_1$
gives an isomorphism
![]() $X_5 \cong X_{\sigma \left (a t^\gamma \right )}(b)$
, which is universally homeomorphic to
$X_5 \cong X_{\sigma \left (a t^\gamma \right )}(b)$
, which is universally homeomorphic to
![]() $X_{a t^\gamma }(b)$
. If
$X_{a t^\gamma }(b)$
. If
![]() $X_{a t^\gamma }(b)\ne \emptyset $
, then
$X_{a t^\gamma }(b)\ne \emptyset $
, then
![]() $X_{\sigma \left (a t^\gamma \right )}(b) \neq \emptyset $
and
$X_{\sigma \left (a t^\gamma \right )}(b) \neq \emptyset $
and
![]() $X_{w}(b)\ne \emptyset $
. Note that
$X_{w}(b)\ne \emptyset $
. Note that
![]() $\ell \left ((y') ^{-1} z\right )+\ell (x' y')=\ell \left (\sigma ^{-1}(y) x\right )=\ell (\eta _{\sigma }(w))$
. Therefore,
$\ell \left ((y') ^{-1} z\right )+\ell (x' y')=\ell \left (\sigma ^{-1}(y) x\right )=\ell (\eta _{\sigma }(w))$
. Therefore,
 $$ \begin{align*} \dim & X_w(b)-\dim X_{a t^\gamma}(b) \\[4pt] & \ge \frac{\ell\left(t^{\rho^\vee_J} y\right)+\ell(w_1)-\ell\left(x' y' t^\gamma\right)}{2}+\ell(\eta_{\sigma}(w))-\ell(a)\\[4pt] &=\frac{\ell\left(t^{\rho^\vee_J} y\right)+\ell\left((y') ^{-1} z\right)+\ell(w_1)-\ell(x' y' t^\gamma)+\ell(x' y')-\ell(a)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2} \\[4pt] & =\frac{\ell(w_2)+\ell(w_1)-\ell(a t^\gamma)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2} \\[4pt] &=\frac{\ell(w)-\ell(a t^\gamma)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2}=d_{w}(b)-d_{a t^\gamma}(b).\end{align*} $$
$$ \begin{align*} \dim & X_w(b)-\dim X_{a t^\gamma}(b) \\[4pt] & \ge \frac{\ell\left(t^{\rho^\vee_J} y\right)+\ell(w_1)-\ell\left(x' y' t^\gamma\right)}{2}+\ell(\eta_{\sigma}(w))-\ell(a)\\[4pt] &=\frac{\ell\left(t^{\rho^\vee_J} y\right)+\ell\left((y') ^{-1} z\right)+\ell(w_1)-\ell(x' y' t^\gamma)+\ell(x' y')-\ell(a)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2} \\[4pt] & =\frac{\ell(w_2)+\ell(w_1)-\ell(a t^\gamma)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2} \\[4pt] &=\frac{\ell(w)-\ell(a t^\gamma)}{2}+\frac{\ell(\eta_{\sigma}(w))}{2}-\frac{\ell(a)}{2}=d_{w}(b)-d_{a t^\gamma}(b).\end{align*} $$
So
![]() $w \Rightarrow _{\sigma } a t^\gamma $
. The theorem is proved.
$w \Rightarrow _{\sigma } a t^\gamma $
. The theorem is proved.
6. Proof of main theorem
Now we state our main result.
Theorem 6.1. Suppose that
![]() ${\mathbf G}$
is quasi-split over F. Set
${\mathbf G}$
is quasi-split over F. Set
![]() $b \in \breve G$
and
$b \in \breve G$
and
![]() $w \in \tilde {W}$
such that
$w \in \tilde {W}$
such that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber,
$w \mathfrak a$
is in a shrunken Weyl chamber,
![]() $\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
and
$\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
and
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. Then
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. Then
![]() $X_w(b) \neq \emptyset $
if and only if
$X_w(b) \neq \emptyset $
if and only if
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. In this case,
$\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. In this case,
![]() $\dim X_w(b)=d_w(b)$
.
$\dim X_w(b)=d_w(b)$
.
Remark 6.2. It is worth mentioning that in most cases,
![]() $\lambda _w-\lambda _w^{\flat \mkern -2.4mu\flat }$
is dominant and nonzero. In this case,
$\lambda _w-\lambda _w^{\flat \mkern -2.4mu\flat }$
is dominant and nonzero. In this case,
 $\lambda _w^{\diamondsuit }-\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
. However, if
$\lambda _w^{\diamondsuit }-\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
. However, if
![]() ${\mathbf G}$
is split over F and
${\mathbf G}$
is split over F and
![]() $\lambda _w$
is a minuscule coweight, then
$\lambda _w$
is a minuscule coweight, then
![]() $\lambda _w^{\flat \mkern -2.4mu\flat }=\lambda _w$
. Thus the assumption
$\lambda _w^{\flat \mkern -2.4mu\flat }=\lambda _w$
. Thus the assumption
![]() $\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
is needed in our statement.
$\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
is needed in our statement.
We first prove the theorem and then discuss the assumptions in the statement. In particular, we will give a simple condition where the assumptions are satisfied in Corollary 6.4.
6.1. The
 $(J, w, \delta )$
-alcove elements
$(J, w, \delta )$
-alcove elements
We recall the alcove elements introduced in [Reference Görtz, Haines, Kottwitz and ReumanGHKR10] for split groups and then generalised to quasi-split groups in [Reference Görtz, He and NieGHN15].
For any
![]() $J \subset \mathbb {S}$
with
$J \subset \mathbb {S}$
with
![]() $\sigma (J)=J$
, we denote by
$\sigma (J)=J$
, we denote by
![]() $\mathbb M_J \subset \mathbf G$
the standard Levi subgroup corresponding to J and let
$\mathbb M_J \subset \mathbf G$
the standard Levi subgroup corresponding to J and let
![]() $\mathbb P_J \supset \mathbb M_J$
be the standard parabolic subgroup. Let
$\mathbb P_J \supset \mathbb M_J$
be the standard parabolic subgroup. Let
![]() $\mathbb U_{\mathbb P_J}$
be the unipotent radical of
$\mathbb U_{\mathbb P_J}$
be the unipotent radical of
![]() $\mathbb P_J$
.
$\mathbb P_J$
.
Set
![]() $J \subset \mathbb {S}$
with
$J \subset \mathbb {S}$
with
![]() $\sigma (J)=J$
and
$\sigma (J)=J$
and
![]() $x \in W_0$
. Set
$x \in W_0$
. Set
![]() $w\in \tilde {W}$
. We say that w is a
$w\in \tilde {W}$
. We say that w is a
![]() $(J, x, \sigma )$
-alcove element if
$(J, x, \sigma )$
-alcove element if
![]() $x ^{-1} w \sigma (x) \in \tilde {W}_J$
and
$x ^{-1} w \sigma (x) \in \tilde {W}_J$
and
![]() $\mathbb {}^{\dot x} \mathbb U_{\mathbb P_J}\left (\breve F\right ) \cap {}^{\dot w} \breve I \subseteq \mathbb {}^{\dot x} \mathbb U_{\mathbb P_J}\left (\breve F\right ) \cap \breve I$
. The following result is proved in [Reference Görtz, He and NieGHN15, Corollary 3.6.1].Footnote
1
$\mathbb {}^{\dot x} \mathbb U_{\mathbb P_J}\left (\breve F\right ) \cap {}^{\dot w} \breve I \subseteq \mathbb {}^{\dot x} \mathbb U_{\mathbb P_J}\left (\breve F\right ) \cap \breve I$
. The following result is proved in [Reference Görtz, He and NieGHN15, Corollary 3.6.1].Footnote
1
Theorem 6.3. Set
![]() $[b] \in B(\mathbf G)$
and
$[b] \in B(\mathbf G)$
and
![]() $w \in \tilde {W}$
. Suppose that w is a
$w \in \tilde {W}$
. Suppose that w is a
![]() $(J, x, \sigma )$
-alcove element. Let
$(J, x, \sigma )$
-alcove element. Let
![]() $\kappa _{\mathbb M_J}$
be the Kottwitz map for the group
$\kappa _{\mathbb M_J}$
be the Kottwitz map for the group
![]() $\mathbb M_J$
. If
$\mathbb M_J$
. If
![]() $\kappa _{\mathbb M_J}\left (x ^{-1} w \sigma (x)\right ) \neq \kappa _{\mathbb M_J}(b')$
for any
$\kappa _{\mathbb M_J}\left (x ^{-1} w \sigma (x)\right ) \neq \kappa _{\mathbb M_J}(b')$
for any
![]() $b' \in [b] \cap \mathbb M_J\left (\breve F\right )$
, then
$b' \in [b] \cap \mathbb M_J\left (\breve F\right )$
, then
![]() $X_w(b)=\emptyset $
.
$X_w(b)=\emptyset $
.
6.2. The emptiness pattern
Suppose that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber and
$w \mathfrak a$
is in a shrunken Weyl chamber and
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. We write w as
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. We write w as
![]() $w=x t^{\lambda } y$
with
$w=x t^{\lambda } y$
with
![]() $x, y \in W_0$
and
$x, y \in W_0$
and
![]() $t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. If
$t^{\lambda } y \in {}^{\mathbb {S}} \tilde {W}$
. If
![]() $\kappa (b) \neq \kappa (w)$
, then
$\kappa (b) \neq \kappa (w)$
, then
![]() $X_w(b)=\emptyset $
.
$X_w(b)=\emptyset $
.
Now suppose that
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\operatorname {\mathrm {supp}}_{\sigma }\left (\sigma ^{-1}(y) x\right )\neq \mathbb {S}$
. Set
$\operatorname {\mathrm {supp}}_{\sigma }\left (\sigma ^{-1}(y) x\right )\neq \mathbb {S}$
. Set
![]() $J=\operatorname {\mathrm {supp}}_{\sigma }\left (\sigma ^{-1}(y) x\right )$
. By [Reference Görtz, He and NieGHN15, Lemma 3.6.3], w is a
$J=\operatorname {\mathrm {supp}}_{\sigma }\left (\sigma ^{-1}(y) x\right )$
. By [Reference Görtz, He and NieGHN15, Lemma 3.6.3], w is a
![]() $\left (J, \sigma ^{-1}(y), \sigma \right )$
-alcove element. Set
$\left (J, \sigma ^{-1}(y), \sigma \right )$
-alcove element. Set
![]() $b' \in [b] \cap \mathbb M_J\left (\breve F\right )$
. We denote by
$b' \in [b] \cap \mathbb M_J\left (\breve F\right )$
. We denote by
 $\nu ^{\mathbb M_J}_{b'}$
the image of
$\nu ^{\mathbb M_J}_{b'}$
the image of
![]() $b'$
under the Newton map for
$b'$
under the Newton map for
![]() $\mathbb M_J$
. Then
$\mathbb M_J$
. Then
 $\nu ^{\mathbb M_J}_{b'} \in W_0 (\nu _b)$
. Hence
$\nu ^{\mathbb M_J}_{b'} \in W_0 (\nu _b)$
. Hence
 $\nu _b-\nu ^{\mathbb M_J}_{b'} \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
.
$\nu _b-\nu ^{\mathbb M_J}_{b'} \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
.
By assumption,
![]() $\lambda ^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
. Thus
$\lambda ^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
. Thus
 $\lambda ^{\diamondsuit }-\nu ^{\mathbb M_J}_{b'} \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
and cannot be written as a linear combination of the coroots in
$\lambda ^{\diamondsuit }-\nu ^{\mathbb M_J}_{b'} \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
and cannot be written as a linear combination of the coroots in
![]() $\mathbb M_J$
. Therefore
$\mathbb M_J$
. Therefore
![]() $\kappa _{\mathbb M_J}\left (\sigma ^{-1} (y) w y ^{-1}\right ) \neq \kappa _{\mathbb M_J}(b')$
. By Theorem 6.3,
$\kappa _{\mathbb M_J}\left (\sigma ^{-1} (y) w y ^{-1}\right ) \neq \kappa _{\mathbb M_J}(b')$
. By Theorem 6.3,
![]() $X_w(b)=\emptyset $
.
$X_w(b)=\emptyset $
.
6.3. Dimension formula
Suppose that
![]() $\kappa (w)=\kappa (b)$
and
$\kappa (w)=\kappa (b)$
and
![]() $\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. By Theorem 5.5, there exist a dominant coweight
$\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. By Theorem 5.5, there exist a dominant coweight
![]() $\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
and
$\gamma \ge _{\mathbb {Z}} \lambda _w^{\flat \mkern -2.4mu\flat }$
and
![]() $a \in W_0$
with
$a \in W_0$
with
![]() $\operatorname {\mathrm {supp}}_{\sigma }(a)=\mathbb {S}$
such that
$\operatorname {\mathrm {supp}}_{\sigma }(a)=\mathbb {S}$
such that
By our assumption,
 $\gamma ^{\diamondsuit } \ge \left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. By Theorem 4.2,
$\gamma ^{\diamondsuit } \ge \left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
. By Theorem 4.2,
![]() $\left [\dot t^\gamma \right ]=\left [b_{a t^\gamma }\right ]$
. Since
$\left [\dot t^\gamma \right ]=\left [b_{a t^\gamma }\right ]$
. Since
![]() $\kappa (w)=\kappa (t^\gamma )=\kappa (b)$
, we have
$\kappa (w)=\kappa (t^\gamma )=\kappa (b)$
, we have
![]() $[b] \le \left [\dot t^\gamma \right ]$
.
$[b] \le \left [\dot t^\gamma \right ]$
.
By [Reference HeHe15, Theorem 2.27],
![]() $X_{a t^\gamma }(\dot {\tau } ) \neq \emptyset $
, where
$X_{a t^\gamma }(\dot {\tau } ) \neq \emptyset $
, where
![]() $\tau \in \Omega $
with
$\tau \in \Omega $
with
![]() $\kappa (w)=\kappa (t^\gamma )=\kappa (\tau )$
. Since
$\kappa (w)=\kappa (t^\gamma )=\kappa (\tau )$
. Since
![]() $\kappa (w)=\kappa (b)$
, we have
$\kappa (w)=\kappa (b)$
, we have
![]() $[\dot \tau ] \le [b]$
.
$[\dot \tau ] \le [b]$
.
By Theorem 4.2,
![]() $a t^\gamma $
is a cordial element. Hence by Theorem 4.1(1),
$a t^\gamma $
is a cordial element. Hence by Theorem 4.1(1),
![]() $X_{a t^\gamma }(b) \neq \emptyset $
, and by Theorem 4.1(2),
$X_{a t^\gamma }(b) \neq \emptyset $
, and by Theorem 4.1(2),
![]() $\dim X_{a t^\gamma }(b)=d_{a t^\gamma }(b)$
.
$\dim X_{a t^\gamma }(b)=d_{a t^\gamma }(b)$
.
So by the definition of
![]() $\Rightarrow _{\sigma }$
, we have
$\Rightarrow _{\sigma }$
, we have
![]() $X_w(b) \neq \emptyset $
and
$X_w(b) \neq \emptyset $
and
Hence
![]() $\dim X_w(b) \ge d_w(b)$
. On the other hand, by Theorem 2.1,
$\dim X_w(b) \ge d_w(b)$
. On the other hand, by Theorem 2.1,
![]() $\dim X_w(b) \le d_w(b)$
. So
$\dim X_w(b) \le d_w(b)$
. So
![]() $\dim X_w(b)=d_w(b)$
.
$\dim X_w(b)=d_w(b)$
.
6.4. Some remarks on the condition
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
We first consider the case where
![]() $[b]$
is basic. In this case, the condition
$[b]$
is basic. In this case, the condition
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
follows directly from the condition
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
follows directly from the condition
![]() $\kappa (b)=\kappa (w)$
.
$\kappa (b)=\kappa (w)$
.
Now we consider nonbasic
![]() $[b]$
. Suppose that
$[b]$
. Suppose that
![]() $\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
. In this case, although
$\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
. In this case, although
![]() $\lambda _w-2 \rho ^\vee $
may not be dominant, its
$\lambda _w-2 \rho ^\vee $
may not be dominant, its
![]() $\sigma $
-average is dominant and is larger than or equal to
$\sigma $
-average is dominant and is larger than or equal to
![]() $\nu _b$
. By definition,
$\nu _b$
. By definition,
 $\lambda _w^{\flat \mkern -2.4mu\flat }-\left (\lambda _w-\rho ^\vee _J-\eta ^\vee _J\right ) \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
for some J. Note that
$\lambda _w^{\flat \mkern -2.4mu\flat }-\left (\lambda _w-\rho ^\vee _J-\eta ^\vee _J\right ) \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
for some J. Note that
![]() $2 \rho ^\vee -\rho ^\vee _J-\eta ^\vee _J \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
. We have
$2 \rho ^\vee -\rho ^\vee _J-\eta ^\vee _J \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
. We have
![]() $\lambda _w^{\flat \mkern -2.4mu\flat }-\left (\lambda _w-2 \rho ^\vee \right ) \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
. Hence
$\lambda _w^{\flat \mkern -2.4mu\flat }-\left (\lambda _w-2 \rho ^\vee \right ) \in \sum _{\alpha \in \Delta } \mathbb {Q}_{\ge 0} \alpha ^\vee $
. Hence
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \lambda _w^{\diamondsuit }-2 \rho ^\vee \ge \nu _b$
. It is also easy to see that
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \lambda _w^{\diamondsuit }-2 \rho ^\vee \ge \nu _b$
. It is also easy to see that
![]() $\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
.
$\lambda _w^{\diamondsuit }-\nu _b \in \sum _{\alpha \in \Delta } \mathbb {Q}_{>0} \alpha ^\vee $
.
In particular, if
![]() $\lambda _w=n \omega ^\vee $
, where
$\lambda _w=n \omega ^\vee $
, where
![]() $\omega ^\vee $
is a fundamental coweight and
$\omega ^\vee $
is a fundamental coweight and
![]() $n \gg 0$
with respect to
$n \gg 0$
with respect to
![]() $[b]$
, then
$[b]$
, then
![]() $\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
, and hence the condition
$\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
, and hence the condition
 $\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
is satisfied in this case.
$\left (\lambda _w^{\flat \mkern -2.4mu\flat }\right )^{\diamondsuit } \ge \nu _b$
is satisfied in this case.
Corollary 6.4. Suppose that
![]() ${\mathbf G}$
is simple and quasi-split over F. Set
${\mathbf G}$
is simple and quasi-split over F. Set
![]() $b \in \breve G$
and
$b \in \breve G$
and
![]() $w \in \tilde {W}$
such that
$w \in \tilde {W}$
such that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber. Suppose that
$w \mathfrak a$
is in a shrunken Weyl chamber. Suppose that
![]() $\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
. Then
$\lambda _w^{\diamondsuit } \ge \nu _b+2 \rho ^\vee $
. Then
![]() $X_w(b) \neq \emptyset $
if and only if
$X_w(b) \neq \emptyset $
if and only if
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. In this case,
$\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
. In this case,
![]() $\dim X_w(b)=d_w(b)$
.
$\dim X_w(b)=d_w(b)$
.
6.5. A side remark
By Theorem 4.4, if
![]() $X_w(b) \neq \emptyset $
, then
$X_w(b) \neq \emptyset $
, then
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\nu _b \le \lambda _w^{\diamondsuit }$
.
$\nu _b \le \lambda _w^{\diamondsuit }$
.
Set
![]() $w \in \tilde {W}$
such that
$w \in \tilde {W}$
such that
![]() $w \mathfrak a$
is in a shrunken Weyl chamber. If
$w \mathfrak a$
is in a shrunken Weyl chamber. If
![]() $\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
, then Theorem 6.1 describes the nonemptiness pattern and the dimension formula of
$\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=\mathbb {S}$
, then Theorem 6.1 describes the nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
for most of the
$X_w(b)$
for most of the
![]() $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
![]() $[b]$
with
$[b]$
with
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\nu _b \le \lambda _w^{\diamondsuit }$
.
$\nu _b \le \lambda _w^{\diamondsuit }$
.
If
![]() $\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=J \subsetneqq \mathbb {S}$
, then by [Reference Görtz, He and NieGHN15, Lemma 3.6.3] w is a
$\operatorname {\mathrm {supp}}_{\sigma }(\eta _{\sigma }(w))=J \subsetneqq \mathbb {S}$
, then by [Reference Görtz, He and NieGHN15, Lemma 3.6.3] w is a
![]() $\left (J, \sigma ^{-1}(y), \sigma \right )$
-alcove element for some
$\left (J, \sigma ^{-1}(y), \sigma \right )$
-alcove element for some
![]() $y \in W_0$
. Then the Hodge–Newton decomposition (see [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Theorem 2.1.4] for the split group and [Reference Görtz, He and NieGHN15, Propositon 2.5.1 & Theorem 3.3.1] in general) reduces the study of
$y \in W_0$
. Then the Hodge–Newton decomposition (see [Reference Görtz, Haines, Kottwitz and ReumanGHKR10, Theorem 2.1.4] for the split group and [Reference Görtz, He and NieGHN15, Propositon 2.5.1 & Theorem 3.3.1] in general) reduces the study of
![]() $X_w(b)$
to the study of a suitable affine Deligne–Lusztig variety associated to the Levi subgroup
$X_w(b)$
to the study of a suitable affine Deligne–Lusztig variety associated to the Levi subgroup
![]() $\mathbb M_J$
. One may apply Theorem 6.1 to the latter. In this way, one also obtains an explicit description of the nonemptiness pattern and the dimension formula of
$\mathbb M_J$
. One may apply Theorem 6.1 to the latter. In this way, one also obtains an explicit description of the nonemptiness pattern and the dimension formula of
![]() $X_w(b)$
for most of the
$X_w(b)$
for most of the
![]() $\sigma $
-conjugacy classes
$\sigma $
-conjugacy classes
![]() $[b]$
with
$[b]$
with
![]() $\kappa (b)=\kappa (w)$
and
$\kappa (b)=\kappa (w)$
and
![]() $\nu _b \le \lambda _w^{\diamondsuit }$
.
$\nu _b \le \lambda _w^{\diamondsuit }$
.
Acknowledgments
We thank S. Nie, E. Viehmann and Q. Yu for helpful discussions. This paper was written during a visit to H. Bao at NUS. We thank the excellent working environment there. We also thank U. Görtz, S. Nie and E. Viehmann for useful comments on a previous version of the paper. Finally, we thank the referees for their helpful suggestions.
The research was partially supported by Hong Kong RGC grant 14300220, by funds connected with the Choh-Ming Chair at CUHK, and by the Xplorer prize.
Conflict of Interest
None.