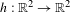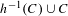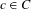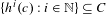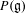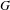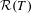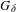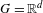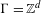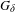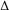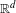Survey Article
Schrödinger operators with dynamically defined potentials
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1681-1764
-
- Article
-
- You have access
- Export citation
Research Article
Conjugacy invariants for Brouwer mapping classes
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1765-1814
-
- Article
-
- You have access
- Export citation
On a generalization of the Cartwright–Littlewood fixed point theorem for planar homeomorphisms
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1815-1824
-
- Article
-
- You have access
- Export citation
The local Hölder exponent for the dimension of invariant subsets of the circle
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1825-1840
-
- Article
-
- You have access
- Export citation
Directional recurrence and directional rigidity for infinite measure preserving actions of nilpotent lattices
-
- Published online by Cambridge University Press:
- 11 February 2016, pp. 1841-1861
-
- Article
-
- You have access
- Export citation
Embedding subshifts of finite type into the Fibonacci–Dyck shift
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 1862-1886
-
- Article
-
- You have access
- Export citation
Analytic continuation of holonomy germs of Riccati foliations along Brownian paths
-
- Published online by Cambridge University Press:
- 11 April 2016, pp. 1887-1914
-
- Article
-
- You have access
- Export citation
Self-affine sets with fibred tangents
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 1915-1934
-
- Article
-
- You have access
- Export citation
Infinite interval exchange transformations from shifts
-
- Published online by Cambridge University Press:
- 12 May 2016, pp. 1935-1965
-
- Article
-
- You have access
- Export citation
Lebesgue orbit equivalence of multidimensional Borel flows: A picturebook of tilings
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 1966-1996
-
- Article
-
- You have access
- Export citation
Singular perturbations of the unicritical polynomials with two parameters
-
- Published online by Cambridge University Press:
- 12 January 2016, pp. 1997-2016
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 37 Issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 37 Issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 August 2017, pp. b1-b2
-
- Article
-
- You have access
- Export citation