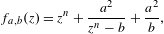Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yang, Fei
2016.
Rational maps without Herman rings.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 4,
p.
1649.
Xiao, Yingqing
and
Yang, Fei
2017.
Singular Perturbations with Multiple Poles of the Simple Polynomials.
Qualitative Theory of Dynamical Systems,
Vol. 16,
Issue. 3,
p.
731.